排序java
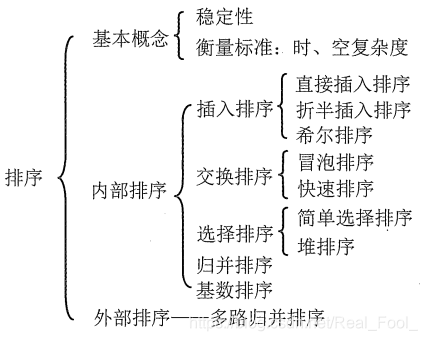
排序算法:
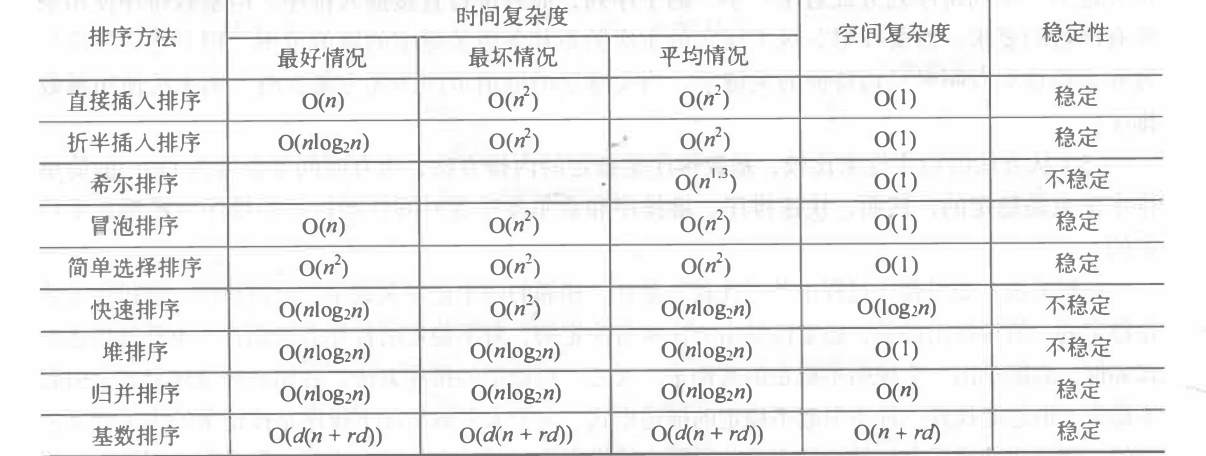
各种内郎排序方法的比较
1、插入排序
直接插人排序
直接插入排序的核心思想:
把数组分为“已排序区间”和“未排序区间”。
每次从未排序区间取一个元素,插入到已排序区间的正确位置。
| 特性 | 说明 |
|---|---|
| 时间复杂度 | 平均 O(n²),最好 O(n)(已排序) |
| 空间复杂度 | O(1) |
| 稳定性 | ✔ 稳定(不改变相等元素相对顺序) |
| 使用场景 | 数据量小或基本有序时非常快 |
java代码实现
public static void insertionSort(int[] arr) {for (int i = 1; i < arr.length; i++) {int temp = arr[i]; // 待插入的元素int j = i - 1;// 在已排序区间中寻找插入位置while (j >= 0 && arr[j] > temp) {arr[j + 1] = arr[j]; // 元素后移j--;}// 插入元素arr[j + 1] = temp;}}链表
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
public ListNode insertionSortList(ListNode head) {// 创建一个dummy节点作为新的有序链表的头ListNode dummy = new ListNode(0);ListNode curr = head;while (curr != null) {// 每次要插入的节点ListNode next = curr.next;// 找到插入位置:从dummy开始寻找第一个比 curr 大的节点ListNode temp = dummy;while (temp.next != null && temp.next.val < curr.val) {temp = temp.next;}// 将 curr 插入 temp 后面curr.next = temp.next;temp.next = curr;// 移动到下一个待处理节点curr = next;}return dummy.next;}折半插人排序
与直接插入排序相比:
直接插入排序:在已排序区间线性查找插入位置
折半插入排序:在已排序区间使用 二分查找 找位置
→ 查找插入点更快:O(log n)
→ 但整体复杂度仍然 O(n²),因为移动数组元素仍要 O(n)
public static void binaryInsertSort(int[] arr) {for (int i = 1; i < arr.length; i++) {int temp = arr[i];int left = 0;int right = i - 1;// 1️⃣ 二分查找插入位置while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] > temp) {right = mid - 1; // 插入点在左半部分} else {left = mid + 1; // 插入点在右半部分}}// 2️⃣ left 就是插入位置int insertPos = left;// 3️⃣ 将 [insertPos..i-1] 的元素往后移动for (int j = i - 1; j >= insertPos; j--) {arr[j + 1] = arr[j];}// 4️⃣ 插入元素arr[insertPos] = temp;}}希尔排序
核心思想:先让元素之间 跨较大间隔进行比较与交换(分组),逐步缩小间隔,最终进行一次普通插入排序。
这样可以提前把“小的往前放,大的往后放”,减少插入排序中大量的移动操作。
public static void shellSort(int[] arr) {int n = arr.length;// gap 序列:从 n/2 开始,每次减半for (int gap = n / 2; gap > 0; gap /= 2) {// 对每一组进行插入排序for (int i = gap; i < n; i++) {int temp = arr[i];int j = i;// 插入排序:和 gap 距离的前一个元素比较while (j - gap >= 0 && arr[j - gap] > temp) {arr[j] = arr[j - gap];j -= gap;}// 插入位置arr[j] = temp;}}}平均复杂度:取决于 gap 序列,一般 O(n^1.3 ~ n^1.5)
空间O(1)
❌ 不稳定
2、交换排序
冒泡排序
冒泡排序的核心思想:反复比较相邻元素,如果顺序错误就交换,让大的元素不断向后“冒泡”。
① 如果某一轮没有发生交换 → 数组已经有序 → 可以提前结束
② 每轮比较次数减少
| 情况 | 时间复杂度 |
|---|---|
| 最好:数组已排好序 | O(n)(因为有 swapped 优化) |
| 平均 | O(n²) |
| 最坏 | O(n²) |
| 空间复杂度 | O(1) |
| 稳定性 | ✔ 稳定 |
代码实现
public static void bubbleSort(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {boolean swapped = false; // 本轮是否有交换for (int j = 0; j < n - 1 - i; j++) {// 如果相邻元素顺序错误,交换if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;swapped = true;}}// 若本轮没有交换,提前结束if (!swapped) {break;}}}链表实现:一般为交换值
public ListNode bubbleSortList(ListNode head) {if (head == null || head.next == null) return head;boolean swapped;ListNode end = null; // 每轮冒泡后,最后的节点是有序的,不再参与比较do {swapped = false;ListNode curr = head;while (curr.next != end) {if (curr.val > curr.next.val) {// 交换节点中的数据int temp = curr.val;curr.val = curr.next.val;curr.next.val = temp;swapped = true;}curr = curr.next;}// 最后一位已排好序,下轮不再比较end = curr;} while (swapped);return head;}快速排序
快速排序核心思想
快速排序使用 分治法:
选一个基准值(pivot)
通过一趟 partition,将数组分成两部分:
左边都比 pivot 小
右边都比 pivot 大
对左右两部分递归排序
常用 Partition 方法(左右指针法)
左右指针分别从两侧向中间推进:
左指针找 大于 pivot 的元素
右指针找 小于 pivot 的元素
然后交换它们
最终右指针位置是 pivot 应在的最终位置。
代码实现:
public static void quickSort(int[] arr, int left, int right) {if (left < right) {// 获取基准值位置int pivotIndex = partition(arr, left, right);// 递归处理 pivot 左侧和右侧quickSort(arr, left, pivotIndex - 1);quickSort(arr, pivotIndex + 1, right);}}// 分区函数:返回 pivot 最终所在位置private static int partition(int[] arr, int left, int right) {int pivot = arr[left]; // 选最左元素为 pivotint l = left;int r = right;while (l < r) {// 从右侧找第一个 < pivot 的while (l < r && arr[r] >= pivot) {r--;}// 从左侧找第一个 > pivot 的while (l < r && arr[l] <= pivot) {l++;}// 交换左右指针找到的值if (l < r) {swap(arr, l, r);}}// 将 pivot 放到正确的位置(l == r)swap(arr, left, l);return l;}private static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}复杂度分析
情况 时间复杂度 最好 O(n log n)(完美二分) 平均 O(n log n) 最坏 O(n²)(原数组已近似有序,pivot 选得差) 空间复杂度:O(log n)(递归栈)
排序稳定性:不稳定
3、选择排序
简单选择
核心思想:
每一轮从 未排序区间 选择最小(或最大)元素,放到 已排序区间末尾。
特点:
不稳定(可能交换导致相同元素相对顺序改变)
空间复杂度 O(1)
时间复杂度固定 O(n²),与初始是否有序无关
public static void selectionSort(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {// 假设最小元素在 iint minIndex = i;// 在未排序区间寻找最小值for (int j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}// 交换当前元素和最小值if (minIndex != i) {int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}}}复杂度分析
情况 时间复杂度 最好 O(n²) 平均 O(n²) 最坏 O(n²) 空间 O(1) 稳定性 ❌ 不稳定
堆排序
堆排序原理
堆排序是一种 选择排序的改进版,利用 完全二叉树 的性质:
将数组构建成 大顶堆(最大值在堆顶)
将堆顶元素与数组末尾交换 → 最大元素放到最终位置
对剩余元素重新调整为大顶堆
重复以上操作,直到整个数组排序完成
特点:
时间复杂度:O(n log n)
空间复杂度:O(1)
不稳定排序
代码实现
堆的构建与调整(关键函数)
调整堆(heapify):维护子树为大顶堆
从最后一个非叶子节点开始,自底向上建堆
公式(完全二叉树数组表示):
对于以索引 0 开始的数组:
左孩子索引:
2*i + 1右孩子索引:
2*i + 2
// 堆调整函数(大根堆)
//假设r[s+l. .m]已经是堆, 将r[s.. m]调整为以r[s]为根的大根堆public static void heapAdjust(int[] arr, int s, int m) {int rc = arr[s]; // 保存当前根节点int j = 2 * s + 1; // 左孩子索引(0索引数组)while (j <= m) {// 找到左右孩子中较大的if (j < m && arr[j] < arr[j + 1]) {j++;}// 根节点比子节点大,则结束if (rc >= arr[j]) {break;}// 子节点上移arr[s] = arr[j];s = j;j = 2 * s + 1;}arr[s] = rc; // 根节点插入到正确位置}
// 建堆public static void createHeap(int[] arr) {int n = arr.length;// 从最后一个非叶子节点开始,自底向上调整for (int i = n / 2 - 1; i >= 0; i--) {heapAdjust(arr, i, n - 1);}}
// 堆排序public static void heapSort(int[] arr) {createHeap(arr); // 建大根堆// 依次将堆顶元素放到末尾,调整剩余堆for (int i = arr.length - 1; i > 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;heapAdjust(arr, 0, i - 1);}}复杂度分析
时间复杂度:O(n log n)(建堆 O(n) + 排序 O(n log n))
空间复杂度:O(1)(原地排序)
稳定性:不稳定(交换可能改变相同元素顺序)
适用场景:大量数据、要求 O(n log n) 最坏时间,且对空间敏感
4、归并排序
归并排序原理
归并排序是 典型的分治法:
分:把数组分成左右两部分
治:递归地对左右两部分排序
合:将两个有序子数组合并成一个有序数组
特点:
时间复杂度:O(n log n)
空间复杂度:O(n)(辅助数组)
稳定排序(相等元素顺序不变)
// 归并排序主函数public static void mergeSort(int[] arr) {if (arr == null || arr.length < 2) return;mergeSort(arr, 0, arr.length - 1);}private static void mergeSort(int[] arr, int left, int right) {if (left >= right) return; // 递归终止条件int mid = left + (right - left) / 2;// 递归排序左右两部分mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);// 合并两部分merge(arr, left, mid, right);}// 合并两个有序数组 arr[left..mid] 和 arr[mid+1..right]private static void merge(int[] arr, int left, int mid, int right) {int[] temp = new int[right - left + 1]; // 辅助数组int i = left; // 左子数组指针int j = mid + 1; // 右子数组指针int k = 0; // 临时数组指针while (i <= mid && j <= right) {if (arr[i] <= arr[j]) {temp[k++] = arr[i++];} else {temp[k++] = arr[j++];}}// 左子数组剩余元素while (i <= mid) {temp[k++] = arr[i++];}// 右子数组剩余元素while (j <= right) {temp[k++] = arr[j++];}// 将合并后的数组拷贝回原数组System.arraycopy(temp, 0, arr, left, temp.length);}复杂度分析
稳定性:稳定
时间复杂度:O(n log n)
空间复杂度:O(n)
适用场景:大规模数组排序、要求稳定排序
5、基数排序
基数排序是一种 非比较型排序,通常用于 整数或固定长度字符串:
按位分组:从最低位(LSD,Least Significant Digit)到最高位(MSD,Most Significant Digit)依次排序
每一位使用 稳定排序(通常用计数排序/桶排序)
最终得到有序序列
特点:
时间复杂度:O(d*(n+k))
n = 元素数量
k = 每位可能的取值范围
d = 最大数字的位数
空间复杂度:O(n+k)
稳定排序
复杂度分析
稳定性:稳定
时间复杂度:O(d*(n+k)),适合大规模整数排序
空间复杂度:O(n+k)
适用场景:整数排序、固定长度字符串排序
(1)是稳定排序。
(2)可用千链式结构, 也可用于顺序结构。
(3) 时间复杂度可以突破基千关键字比较一类方法的下界O(nlog2n), 达到O(n)。
(4)基数排序使用条件有严格的要求:需要知道各级关键字的主次关系和各级关键字的取值 范围
