C++ 哈希表 常用接口总结 力扣 1. 两数之和 每日一题 题解

零 、哈希表简介

1. 是什么？
我们可以把哈希表想象成一本“带目录的字典”：字典里的“词语”是键（key） ，“释义”是值（value） ，而“目录”就是哈希表的核心——通过特殊规则（哈希映射），把每个“词语”直接对应到某一页，这样每当我们需要找“释义”值（value） 的时候就可以直接通过“词语” **键（key）**快速定位查找。
本质上，它是一种专门存储“键-值”配对数据的容器，核心能力是“按键找值”时跳过无效遍历，直接定位。

2. 有啥用？
普通数组或链表中，要找一个数据可能得从头查到尾（比如在[2,7,11,15]里找7，得扫前两个元素），时间会随数据量增加而变长。

但哈希表通过“键→存储位置”的直接映射，平均情况下无论数据有多少，找值、存值、删值都只要1步操作，也就是我们常说的O(1)时间复杂度——这是它最核心的价值。

3. 什么时候用？
当我们写代码出现需要“频繁根据一个标识找对应数据”，且不要求数据按顺序排列时的场景时，哈希表就是最优解。对比常见的二分查找（必须先排序，只能查不能存），它的适用场景更灵活（当然付出的代价就是空间开销大相较于二分）：

• 日常开发：统计用户ID对应的订单信息（ID→订单列表）、记录网页缓存（URL→页面内容）；
• 算法题：两数之和（数值→下标）、统计单词出现次数（单词→次数）、判断重复元素（元素→是否存在）。

4. 怎么用？
不用纠结底层实现，我们直接记住两种实用方法就行：
直接用现成容器
像搭积木一样用编程语言自带的工具，比如C++里的unordered_map、Java的HashMap、Python的dict。这些容器已经帮你封装好了哈希逻辑，直接调用“存值、取值”接口就行，比如C++里hash[key] = value存值，hash[key]直接取值。

数组模拟哈希表（特定场景更高效）
当“键”的范围很小、且能转成数组下标时用这种方式，比现成容器更快。比如：
- 统计26个小写字母的出现次数：用一个大小为26的数组，字母’a’对应下标0，'b’对应1……直接用数组下标当“键”，数组值存“出现次数”；
- 注意：字符串不能直接当数组下标，需要先通过简单规则转成数字（比如把每个字符的ASCII码相加，再取数组长度的余数），但这种方式只适合简单场景。

C++哈希容器常用接口

在C++中，常用的哈希容器主要是 unordered_map（键值对存储）和 unordered_set（单值存储），它们基于哈希表实现，支持平均O(1)的插入、查找、删除操作。以下是这两个容器的核心常用接口总结：

---

unordered_map（键值对容器，key→value映射）

1.定义与初始化

#include <unordered_map>
using namespace std;// 定义：key类型为int，value类型为int（可替换为任意类型，如string、自定义结构体等）
unordered_map<int, int> hash_map;// 初始化时赋值（C++11及以上）
unordered_map<int, string> map2 = {{1, "a"}, {2, "b"}, {3, "c"}};

2. 插入键值对（insert / 直接赋值）

// 方法1 （常用）：直接赋值（更简洁，若key已存在则覆盖value）
hash_map[3] = 300;  // 插入key=3，value=300
hash_map[1] = 101;  // key=1已存在，更新value为101
// 常见用法：将数组值与数组下标绑定  目的：可以通过数组值直接找到下标
int arr[5] = {1,2,3,4,5};
for(int i = 0; i < arr.size(); i++)
{hash_map[arr[i]] = i;// 键：数组中的元素值，值：对应元素值的下标
}// 方法2：用insert插入（返回pair，first是插入的迭代器，second是是否插入成功）
hash_map.insert({1, 100});  // 插入key=1，value=100
hash_map.insert(make_pair(2, 200));  // 等价于上面

3. 查找键（find / count）

// 方法1（常用）：count(key) → 返回key出现的次数（哈希表中key唯一，故返回0或1）
if (hash_map.count(2)) {cout << "key=2存在" << endl;
} else {cout << "key=2不存在" << endl;
}// 方法2：find(key) → 返回指向该键值对的迭代器，若不存在则返回end()
// 注意find()返回的是迭代器要配合end使用，所以不常用没有count直接
// 但是从效率上考虑虽然大差不差，但是find比cound少一层要稍稍快一点
// ⭐实际刷题中差异可忽略，但面试时能说出效率的差异这点更显细节把控⭐
auto it = hash_map.find(1);
if (it != hash_map.end()) {// 找到：通过it->first获取key，it->second获取valuecout << "key=1的value是：" << it->second << endl;  // 输出101
} else {cout << "key=1不存在" << endl;
}

4. 删除键（erase）

// 方法1：通过key删除
hash_map.erase(3);  // 删除key=3的键值对// 方法2：通过迭代器删除（需先find找到）
auto it = hash_map.find(2);
if (it != hash_map.end()) {hash_map.erase(it);  // 删除迭代器指向的键值对
}

5. 其他常用接口

hash_map.size();       // 返回容器中键值对的数量
hash_map.empty();      // 判断容器是否为空（空则返回true）
hash_map.clear();      // 清空容器中所有键值对
hash_map[key];         // 获取key对应的value（若key不存在，会自动插入并默认初始化value）

---

unordered_set（单值容器，仅存储key，且key唯一）
核心价值是 “自动去重” 和 “快速查找”，适合需要 “存储一组唯一元素并频繁检查元素是否存在” 的场景
1. 定义与初始化

#include <unordered_set>
using namespace std;// 定义：存储int类型的key（可替换为其他类型）
unordered_set<int> hash_set;// 初始化时赋值
unordered_set<string> set2 = {"a", "b", "c"};

2. 插入元素（insert）

// 插入元素，若元素已存在则插入失败（返回pair，second为是否插入成功）
hash_set.insert(10);
hash_set.insert(20);
hash_set.insert(10);  // 10已存在，插入失败

3. 查找元素（find / count）

// 方法1：find(key) → 返回指向元素的迭代器，不存在则返回end()
auto it = hash_set.find(10);
if (it != hash_set.end()) {cout << "元素10存在" << endl;
}// 方法2：count(key) → 返回元素出现的次数（0或1）
if (hash_set.count(20)) {cout << "元素20存在" << endl;
}

4. 删除元素（erase）

// 方法1：通过key删除
hash_set.erase(10);// 方法2：通过迭代器删除
auto it = hash_set.find(20);
if (it != hash_set.end()) {hash_set.erase(it);
}

5. 其他常用接口

hash_set.size();    // 返回元素个数
hash_set.empty();   // 判断是否为空
hash_set.clear();   // 清空所有元素

---

注意

1. 无序性：unordered_map 和 unordered_set 中的元素是无序存储的（与插入顺序无关），若需要有序，可使用 map 和 set（基于红黑树，有序但操作复杂度为O(log n)）。
2. 键的唯一性：两者的key都不能重复，unordered_map 会覆盖重复key的value，unordered_set 会忽略重复插入的元素。
3. 自定义类型：若要存储自定义结构体，需手动实现哈希函数（重载std::hash）和相等判断（重载==），否则编译器会报错。

---

一、题目描述

题目链接：力扣 1. 两数之和

题目描述：

示例 1：
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：
输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：
输入：nums = [3,3], target = 6
输出：[0,1]

提示：
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案

二、为什么这道题值得你花几分钟的时间弄懂？

“两数之和”是哈希表的入门核心题，也是面试中“考察基础数据结构应用”的高频送分题，看似简单却暗藏玄机，价值极高。

题目核心价值
这道题之所以成为哈希表入门的“敲门砖”，本质是它能帮你彻底理解“用空间换时间”的核心思想，覆盖企业看重的基础能力：

• 数据结构选型能力：需在“暴力枚举”和“哈希表查找”中做权衡，理解不同结构对时间/空间复杂度的影响；
• 问题转化思维：将“找两个数和为target”转化为“找target - 当前数是否存在”，是解题的关键转化；
• 边界细节把控：处理重复元素（如示例3的[3,3]）、确保不重复使用同一元素，这些细节是避免出错的关键；
• 工程实践思维：哈希表的插入与查询时机、键值对设计（存数值-下标映射），直接影响代码效率和正确性。

面试考察的核心方向

1. 能否快速想到哈希表优化方案，而非局限于暴力枚举；
2. 哈希表的键值对该如何设计（为何用数值当键、下标当值）；
3. 如何避免重复使用同一元素（插入时机的选择）；
4. 面对大数据量（如nums.length=104）时，能否解释两种算法的复杂度差异；
5. 哈希表的底层实现（如unordered_map与map的区别），是否理解O(1)查找的原理。

掌握这道题，了解哈希表应用的巧妙之处，后续遇到“三数之和”“四数之和”“两数之差”等问题，都能复用“哈希表优化查找”的核心思路，面试中再遇哈希表基础题也能游刃有余。

三、算法分析

暴力算法

暴力算法的逻辑很直接：遍历数组中每一个元素，再遍历该元素之后的所有元素，判断两者之和是否等于target。

• 第一层循环固定第一个数，第二层循环寻找与第一个数相加等于target的第二个数；
• 找到后直接返回两个数的下标。

vector<int> twoSum(vector<int>& nums, int target) {for (int i = 0; i < nums.size(); i++) {for (int j = i + 1; j < nums.size(); j++) {if (nums[i] + nums[j] == target) {return {i, j};}}}return {};
}

暴力算法的另一种思路

我们上面的暴力算法是用两个循环遍历数组的时候，第一层循环固定一个数字，里面一层的循环固定的数后面去找，那么我们也可以固定一个数字项前找满足条件的数字。

vector<int> twoSum(vector<int>& nums, int target) {for (int i = 0; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] + nums[j] == target) {return {i, j};}}}return {};
}

结合哈希优化

暴力算法的核心痛点是查询效率低，而哈希表的O(1)平均查询复杂度恰好能解决这个问题。但直接存储所有元素会导致"重复使用同一元素"的问题（例如 nums = [3,3] 时，可能误将同一个3的下标返回两次）。

暴力算法的核心痛点是查询效率低，而哈希表的O(1)平均查询复杂度能解决这个问题，那么我们优化也是从这个角度下手，那么我们就可以将整个已知数组的 值-下标 的映射进行存储，我们之后对数组进行遍历，遍历到每一个元素的时候都有一个值 cat = target - nums[i] 而 cat 我们就可以通过哈希表查找是否存在，如果存在我们就可以直接获取这个值的下标，进而直接返回，用O（1）的时间查询，O（n）的时间遍历简直完美?

class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {unordered_map<int,int> hash;for(int i = 0; i < nums.size(); i++)hash[nums[i]] = i;for(int i = 0; i < nums.size(); i++){int cat = target-nums[i];if(hash[cat])return {i,hash[cat]};}return {};}
};

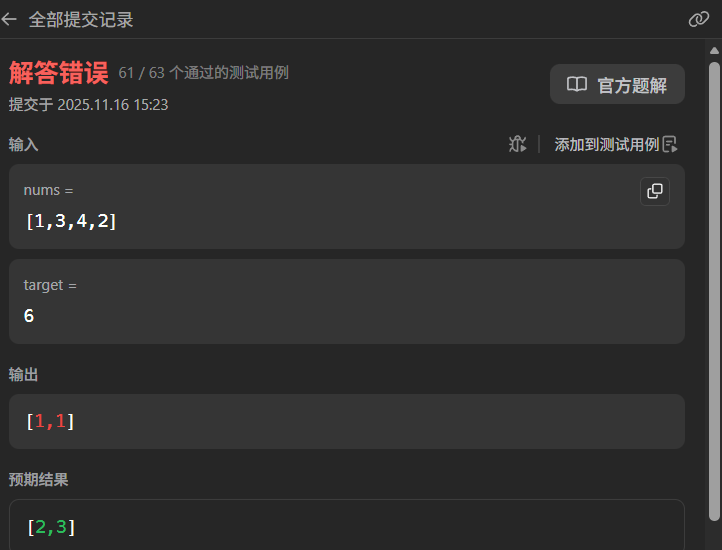
没存不出意外出意外了，那么问题在哪里呢？
我们先将所有键值对存入哈希表中，会出现重复查找同一个下标"重复使用同一元素"的问题（例如 nums = [3,3] 时，可能误将同一个3的下标返回两次），这就很不妙，如果我们进行条件判断会非常麻烦，我们有没有什么方法能够直接避免呢？

没错我们暴力的另一种思路（也就是逆向思路）这个时候就体现作用了，当我们再找前面的数字的时候一定不会并现在的数字影响到，直接避免了重发查找的问题。

也就是遍历元素时，只查询当前元素之前已存入哈希表的元素，确保不会重复使用同一个下标。具体逻辑：

• 键值对设计：key = 元素值（用于快速查询目标），value = 元素下标（用于返回结果）
• 操作顺序：先检查当前元素的互补值（target - nums[i]）是否已在哈希表中，再将当前元素存入哈希表。

开始 → 初始化空哈希表↓遍历数组中每个元素（索引i从0到n-1）→ 计算互补值 cat = target - nums[i]→ 检查哈希表中是否存在cat？├─ 是 → 返回{哈希表中cat的下标, 当前i}└─ 否 → 将{nums[i]: i}存入哈希表↓
遍历结束（实际题目保证有解，不会执行到这一步）

四、代码实现

#include <vector>
#include <unordered_map>
using namespace std;class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {unordered_map<int, int> hash;  // 存储键：数值，值：对应的下标for (int i = 0; i < nums.size(); i++) {int cat = target - nums[i];  // 计算当前元素对应的目标数if (hash.count(cat)) {       // 检查目标数是否在哈希表中return {i, hash[cat]};   // 存在则返回两个下标}hash[nums[i]] = i;           // 不存在则存入当前元素和下标}return {};  // 题目保证有答案，此句仅为兼容语法}
};

代码解析

1. 哈希表初始化：使用unordered_map（无序哈希表），查询和插入的平均时间复杂度均为O(1)；
2. 遍历数组：逐个处理每个元素，计算目标数cat；
3. 查找判断：用hash.count(cat)判断目标数是否存在（count返回0或1，因题目无重复答案）；
4. 结果返回：找到目标数则直接返回当前下标和哈希表中存储的目标数下标；
5. 元素存入：未找到则将当前元素及其下标存入哈希表，供后续元素查询。

复杂度分析

复杂度类型	分析说明	结果
时间复杂度	仅需遍历数组一次（O(n)），哈希表的查询和插入操作均为O(1)，整体由遍历主导	O(n)
空间复杂度	哈希表最坏情况下需存储所有n个元素（键值对）	O(n)

五、总结

两种算法对比

算法方式	时间复杂度	空间复杂度	核心优势	适用场景
暴力枚举	O(n²)	O(1)	逻辑简单，无需额外空间	小规模数据、快速上手编写
哈希表优化	O(n)	O(n)	效率极高，线性时间复杂度	大规模数据、面试最优解、工程实践

关键考点与避坑点

1.容器使用上的误区：用 if(hash[cat]) 判断 cat 是否存在是典型误区，在刚开始用unordered_map的使用查找键值知否存在这个哈希表中经常喜欢下意识地用 if(hash[cat]) 但是仔细思考下就会发现这个用法是错误的，unordered_map 的特性是：当访问一个不存在的键时，会自动插入该键并赋予默认值（对于 int 类型默认值为 0）。这会导致两种错误：

• 若 cat 实际不存在，hash[cat] 会返回 0，此时 if(hash[cat]) 会判定为“不存在”（逻辑正确），但会在哈希表中新增一个无效键值对（cat:0）。
• 若 cat 存在且其对应的下标恰好为 0（如示例1中 cat=2 对应下标0），if(hash[cat]) 会因 hash[cat] = 0 判定为“不存在”，直接漏掉正确答案！

2.问题转化：能否将“两数之和”转化为“单目标数查找”，是解题的核心思维。
3.数据结构选型：理解unordered_map为何优于map，以及哈希表O(1)查找的原理。
4.插入时机：必须“先查询后插入”，避免重复使用同一元素。
5.键值设计：明确“数值为键、下标为值”的设计逻辑，而非颠倒。

六、下题预告

哈希表的“查找与匹配”核心思路我们已经掌握啦！

如果面试官让我们总结下这道题目我们可以自信的对他说：“两数之和的核心是把‘找两个数’转化为‘找一个数’，用哈希表存储已经遍历过的数值和下标，实现一次遍历、O(1) 查询，将总体复杂度从 O(n²) 降到 O(n)，是典型的空间换时间思维。”

下一次我们将继续深化哈希表的应用，用 面试题 01.02. 判定是否互为字符重排 这道题，我们一起学习“哈希表统计字符频率”的经典用法，进一步巩固“用空间换时间”的思维，搞定字符串类哈希表问题！

恭喜你轻松拿下哈希表入门核心题！“两数之和”的哈希表解法虽然简单，但背后的“问题转化”和“空间换时间”思维是面试的高频考点。把这篇内容收藏起来，后续遇到哈希表相关问题，随时翻查就能快速唤醒记忆。

如果你在学习中有任何疑问——比如不同场景下的哈希表选择，或者有更优的解题思路等等，都可以发到评论区，博主看到会第一时间回复！

最后别忘了点个赞呀，你的支持就是博主持续更新优质算法内容的最大动力，我们下道题不见不散！