数据结构之二叉树-链式结构(下)
目录
前言
一、二叉树的销毁
二、层序遍历
三、判断是否为完全二叉树
四、二叉树相关算法题
1、单值二叉树
2、相同的树
3、对称二叉树(第二题拓展)
4、另一棵树的子树(第二题拓展)
5、二叉树的前序遍历
6、二叉树的构建及遍历
结束语
前言
在上一篇文章数据结构之二叉树-链式结构(上)我们对以链式结构实现二叉树进行了介绍,主要包括介绍链式二叉树的结构以及相关方法的实现,在这篇文章中我们会继续讲解剩下几个方法的实现以及层序遍历,最后为大家讲解一些非常经典的二叉树OJ题作为二叉树学习的首尾。
一、二叉树的销毁
//BinaryTree.h
//二叉树销毁
void BinaryTreeDestory(BTNode* root);//BinaryTree.c
//二叉树销毁
void BinaryTreeDestory(BTNode* root)
{if (root == NULL){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);//由于对root销毁,在形参中进行修改root不会影响实参,所以对形参置空也没用
}//Test.c
void Test1()
{BTNode* root = CreateBinaryTree();//二叉树销毁BinaryTreeDestory(root);root = NULL; //由于对root销毁,在形参中进行修改root不会影响实参,所以需要手动置空
}int main()
{Test1();return 0;
}学习了前面相关方法的实现,二叉树的销毁就没什么难度了,唯一需要注意的点就是需要后序销毁结点,原因就是先销毁根节点则左子树与右子树就找不到了。
二、层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。
层序遍历顾名思义就是一层一层的遍历:设二叉树的根结点所在层数为1,层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
实现层序遍历需要额外借助数据结构:队列
在前面学习中我们知道队列这个数据结构的特点就是先入先出,我们就是利用这个特点来实现二叉树的层序遍历。
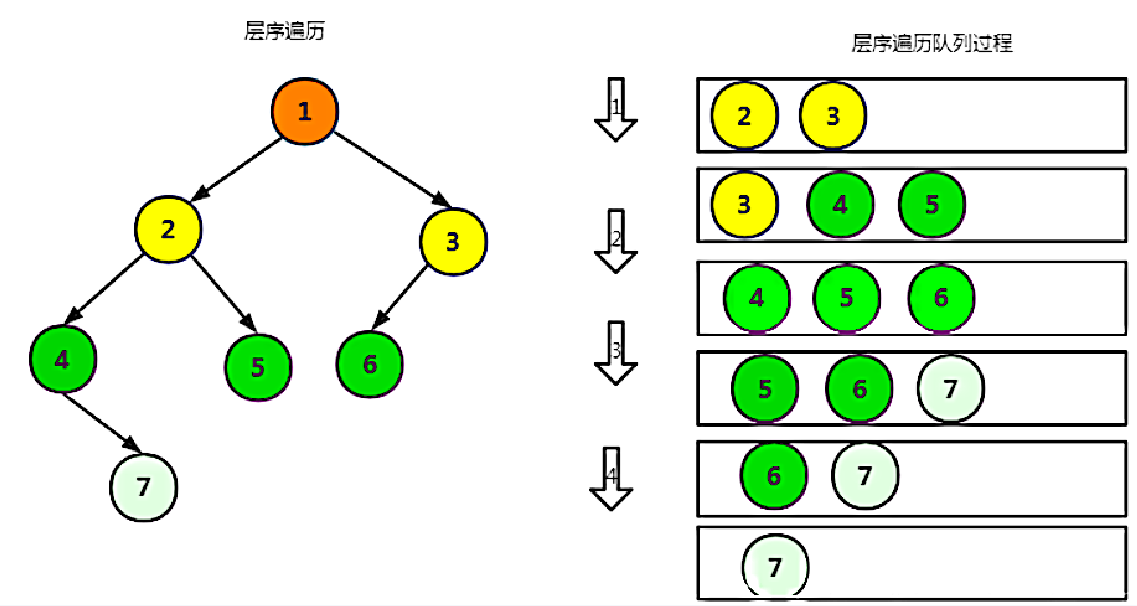
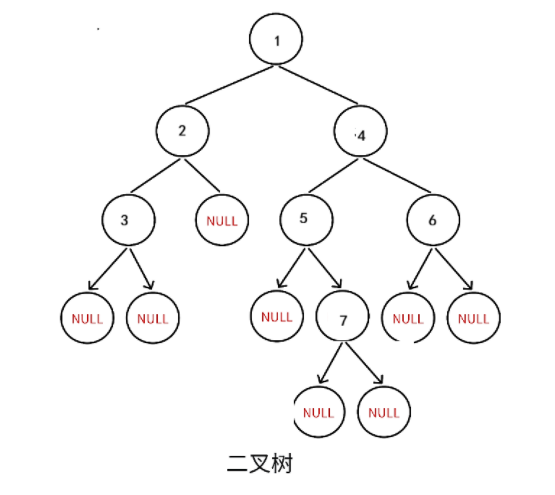
有些人可能不一定理解上面图右边是什么意思,用队列实现层序遍历的逻辑就是:首先我们将二叉树根结点放入队列中,然后将根结点取出的同时将其左子树右子树放入队列中,再删除队列结点(也就是删除头结点);然后取出左子树根结点的同时将其左子树右子树放入队列中,再删除队列结点。将上述过程进行循环直到将队列中所有数据全部取出就实现了层序遍历。由于需要利用队列,所以我们要将之前学习的数据结构之栈和队列-队列中队列相关方法实现的代码拷贝过来,唯一需要注意的是之前学习队列存放的数据都是 int 类型,但是现在我们的二叉树的结构体,所以需要将 typedef int QDataType; 的 int 改为二叉树结点地址struct BinaryTreeNode*,这里就不展示了。我们以下面的图为例,具体代码如下:
//BinatyTree.h
//层序遍历
void TreeLevelOrder(BTNode* root);//BinatyTree.c
#include "Queue.h"
//层序遍历
void TreeLevelOrder(BTNode* root)
{Queue q; //创建一个队列QueueInit(&q); //队列初始化if (root){QueuePush(&q, root);}while (QueueSize(&q)) //当队列数据删完则层序遍历结束{BTNode* rootnode = QueueFront(&q); //取出队列数据QueuePop(&q);printf("%d ", rootnode->data);if (rootnode->left)//左子树为空则不需要放入队列{QueuePush(&q, rootnode->left);}if (rootnode->right)//右子树为空则不需要放入队列{QueuePush(&q, rootnode->right);}}QueueDestroy(&q);
}//Test.c
BTNode* CreateBinaryTree()
{//创建结点BTNode* node1 = CreateNode(1);BTNode* node2 = CreateNode(2);BTNode* node3 = CreateNode(3);BTNode* node4 = CreateNode(4);BTNode* node5 = CreateNode(5);BTNode* node6 = CreateNode(6);BTNode* node7 = CreateNode(7);//连接结点构成二叉树node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;node5->right = node7;return node1;
}void Test1()
{BTNode* root = CreateBinaryTree();//层序遍历TreeLevelOrder(root);
}int main()
{Test1();return 0;
}
之所以队列能实现层序遍历的原因就是在于后加入队列的数据不会影响取出的数据顺序,也就是说比如我把结点1取出后将结点2和结点4放入队列中,当我取出结点2再将结点3放入队列时,下一次取到的还是结点4,就能保证一层的数据取完才会取到下一层的数据,也就满足层序递归的要求。
三、判断是否为完全二叉树
在数据结构之二叉树-初见介绍中我们介绍了完全二叉树的概念,这里就不过多赘述了,我们思考一下怎么去判断一个二叉树是否是完全二叉树?有些人可能就会想用递归去求出二叉树的结点个数然后去比较是否满足完全二叉树的条件。虽然这个想法如果针对于满二叉树而言的确是可行的,因为一个满二叉树如果求出了高度则结点数是固定的,但对于完全二叉树而言不可行,因为完全二叉树有个要求就是:虽然最后一层不需要满节点,但是一定要保证是连续的。而只求出结点数无法判断最后一层是否连续。
我们想一下判断是否完全二叉树是不是要一层一层去判断,如果某一层的结点不连续是不是就能说明不是完全二叉树了,这不就用到了刚刚我们学到的层序遍历了吗?没错这个问题就是利用层序遍历解决的,但也不完全是一样的。
在层序遍历中当我们遇到空结点时是选择直接跳过的,只有非空结点我们才会放入队列中;但是这个问题由于我们需要从第一个空结点开始后面是否有非空判断完全二叉树,所以一个根结点如果孩子为空结点也需要放入队列中。我们以两个二叉树为例:
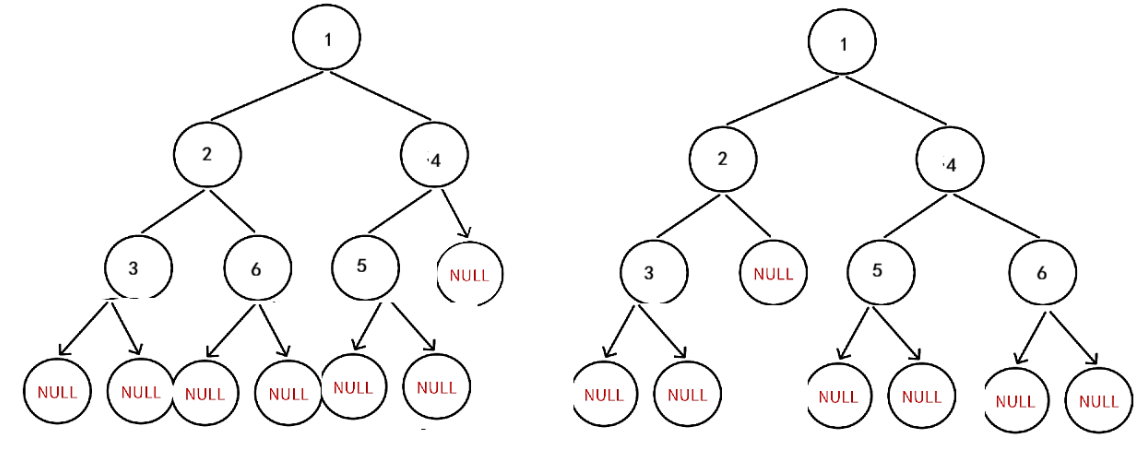
具体代码如下:
//BinaryTree.h
#include <stdbool.h>
//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);//BinaryTree.c
//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q; //创建一个队列QueueInit(&q); //队列初始化if (root){QueuePush(&q, root);}while (QueueSize(&q)) //利用层序遍历的逻辑{BTNode* rootnode = QueueFront(&q);QueuePop(&q);if (rootnode == NULL) //遇到第一个空结点则直接退出循环{break;}QueuePush(&q, rootnode->left); //孩子为空结点也需要放入队列QueuePush(&q, rootnode->right);}while (QueueSize(&q)) //此时的队列若仍有非空结点则说明不是完全二叉树,如果遍历到最后都是空结点则说明是完全二叉树{BTNode* rootnode = QueueFront(&q);QueuePop(&q);if (rootnode){return false;}}return true;
}左边的图:
//Test.c
BTNode* CreateBinaryTree()
{//创建结点BTNode* node1 = CreateNode(1);BTNode* node2 = CreateNode(2);BTNode* node3 = CreateNode(3);BTNode* node4 = CreateNode(4);BTNode* node5 = CreateNode(5);BTNode* node6 = CreateNode(6);//连接结点构成二叉树node1->left = node2;node1->right = node4;node2->left = node3;node2->right = node6;node4->left = node5;return node1;
}void Test1()
{BTNode* root = CreateBinaryTree();//判断二叉树是否是完全二叉树if (BinaryTreeComplete(root)){printf("是完全二叉树\n");}else{printf("不是完全二叉树\n");}
}int main()
{Test1();return 0;
}
右边的图:
//Test.c
BTNode* CreateBinaryTree()
{//创建结点BTNode* node1 = CreateNode(1);BTNode* node2 = CreateNode(2);BTNode* node3 = CreateNode(3);BTNode* node4 = CreateNode(4);BTNode* node5 = CreateNode(5);BTNode* node6 = CreateNode(6);//连接结点构成二叉树node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}void Test1()
{BTNode* root = CreateBinaryTree();//判断二叉树是否是完全二叉树if (BinaryTreeComplete(root)){printf("是完全二叉树\n");}else{printf("不是完全二叉树\n");}
}int main()
{Test1();return 0;
}
四、二叉树相关算法题
1、单值二叉树
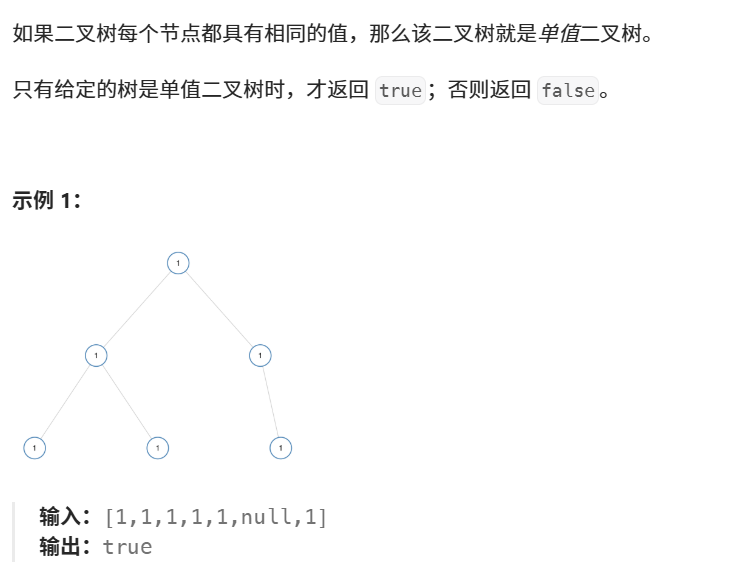
这道题的思路就是:首先判断根节点是否为空,为空则返回true,如果不为空则需要与两个孩子的值进行比较,但是如果没有孩子则无需比较,如果判断有不相同的情况则直接返回false;当根结点与孩子相同时则进行递归往下判断,具体代码如下:
bool isUnivalTree(struct TreeNode* root)
{if(root == NULL){return true;}if(root->left && root->val != root->left->val){return false;}if(root->right && root->val != root->right->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}2、相同的树
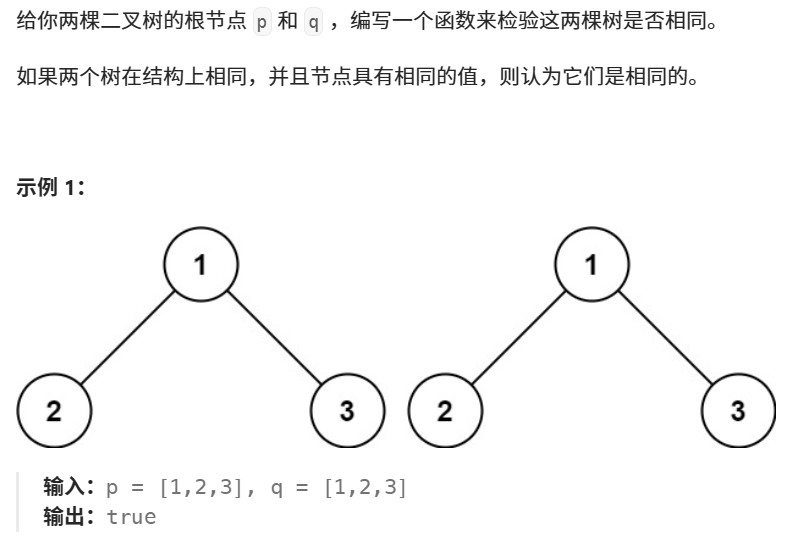
首先我们想一下怎么去证明两个树完全一样,如果是递归的思路的话是不是先判断两个树根结点是否相同,如果不相同就直接返回false了,不需要往下递归;但根结点相同的话我们就需要开始递归判断其左子树是否相同,再判断右子树是否相同;对于根的左子树而言又可以分为根和左子树右子树,这样我们的递归逻辑就出来了。
当递归到底也就是两个树同时到空结点时则返回true,但如果某次递归一个树有值但另一个树对应位置是空则说明两个树不同,直接返回false。具体代码如下;
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{if(p == NULL && q == NULL){return true;}if(p == NULL || q == NULL) //到这说明第一个if为假,也就说明p,q不同时为空//但如果两者有空的话说明树不同,返回false{return false;}if(p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}3、对称二叉树(第二题拓展)
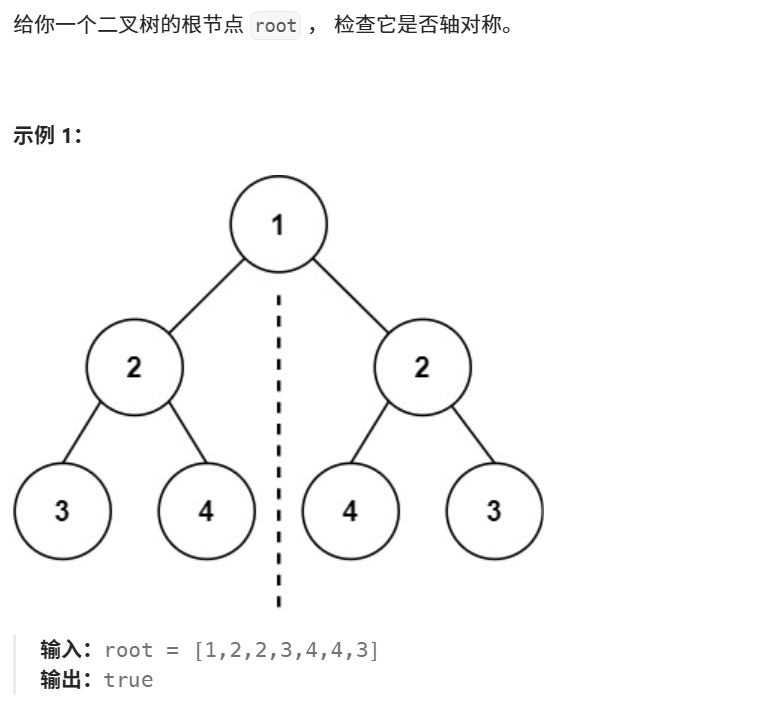
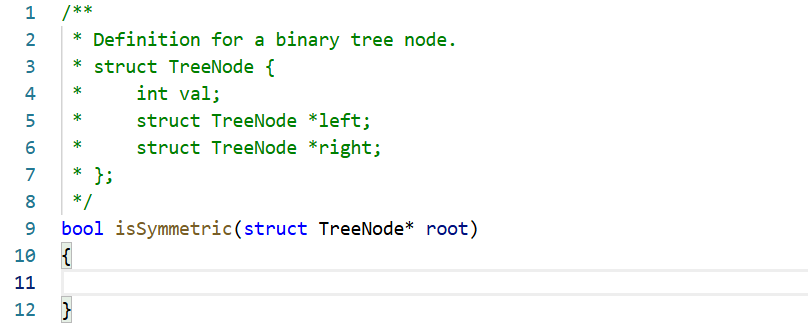
这题我们想一下怎么证明一个树是对称的,首先我们是不是要先证明根结点1的左右孩子相同,如果不相同则直接返回false;相同则开始递归,然后是不是要同时证明第二层第一个结点的左孩子和第二个结点的右孩子是否相同以及第一个结点的右孩子和第二个结点的左孩子是否相同,如果有一种情况不同就直接返回false,这样的话我们的递归就需要两个变量同时进行,所以我们还需要再自己创建一个函数;当某次递归如果其中一边不为空而另一边为空则说明树不对称也返回false,这样的话我们就会发现大致逻辑和上面一题就很类似了。
创建的函数将根结点的左子树和右子树代入,也就相当于变成两个数的判断了,与上一题不同的是本题证明的是对称而不是相同,所以需要注意的是两个树是左子树与右子树比较以及右子树与左子树比较。具体代码如下:
bool _isSymmetric(struct TreeNode* p, struct TreeNode* q)
{if(p == NULL && q == NULL){return true;}if(p == NULL || q == NULL){return false;}if(p->val != q->val){return false;}return _isSymmetric(p->left, q->right) && _isSymmetric(p->right, q->left);//证明对称是左子树与右子树比较和右子树与左子树比较,不是相同不要搞反
}bool isSymmetric(struct TreeNode* root)
{return _isSymmetric(root->left, root->right);
}4、另一棵树的子树(第二题拓展)
其实看到这个图大家就应该能先到会和第二题相关,当我们进行递归时如果某次root的值与subRoot相同时则需要开始进行比较两者是否相同。
但非常重要的点在于如果判断两者不同时不能直接返回false,原因是可能后面的递归会出现相同的情况,只是一次判断不能说明没有相同的子树,只有当递归到空结点也就是到底时,如果root的值与subRoot的值还是不同则说明没有找到返回false。具体代码如下:
bool _isSubtree(struct TreeNode* p, struct TreeNode* q)
{if(p == NULL && q == NULL){return true;}if(p == NULL || q == NULL){return false;}if(p->val != q->val){return false;}return _isSubtree(p->left, q->left) && _isSubtree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{if(root == NULL){return false;}if(root->val == subRoot->val){if(_isSubtree(root, subRoot)) //只有完全相同才能返回true,//不相同不能返回false,可能在后面的递归出现相同的情况{return true;}}return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}5、二叉树的前序遍历
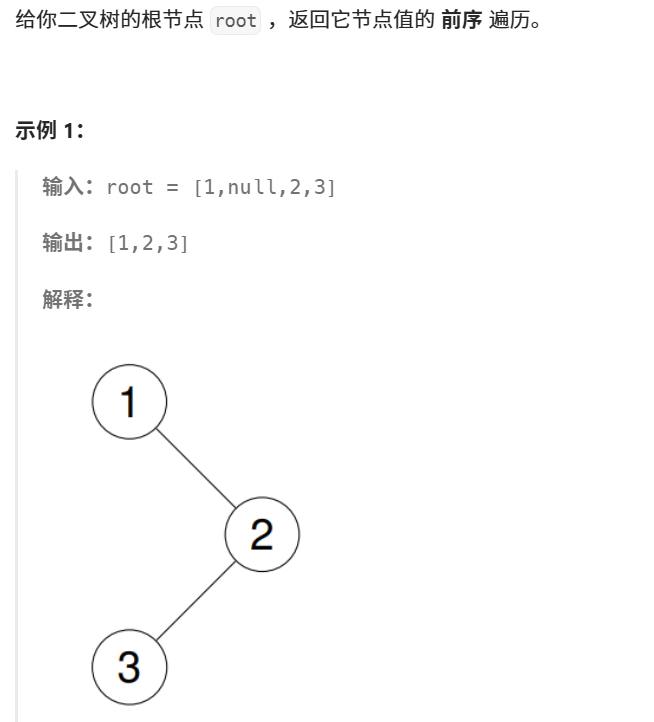
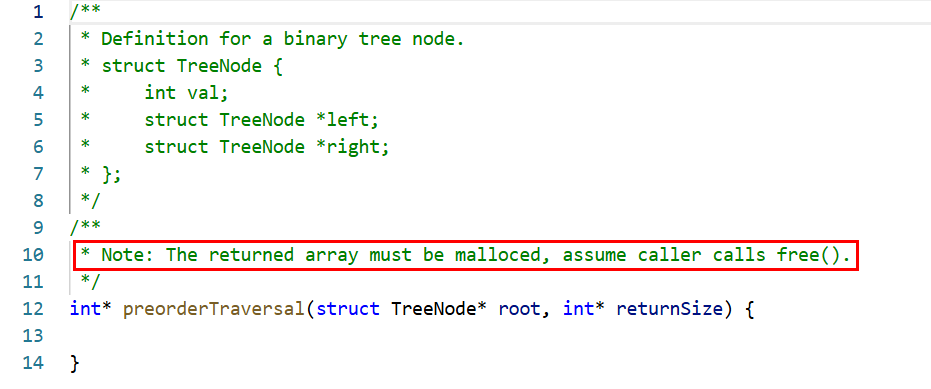
首先看到第二张图我标的红色方框意思是这道题的返回值是一个我们自己手动开辟空间的数组,也就是说我们需要将root的值传到我们自己开辟好的数组内部的。这也就是为什么函数有第二个形参returnSize,这个形参的目的就是方便我们确定开辟空间的大小。
那这道题第一步我们就需要先求出二叉树的结点个数,这个很简单,在上一篇文章数据结构之二叉树-链式结构(上)中二叉树相关方法实现已经详细讲解了。当我们得到了二叉树结点个数后就可以开辟一个符合空间大小的数组了。
那得到数组后接下来怎么做呢?我们看到题目说是返回它节点值的前序遍历,此时我们数组为空,如果要解决问题是不是就要进行一次前序遍历,通过前序遍历将二叉树的值全部传到数组中。
到这里就有一个非常需要注意的点:由于我们知道数组是有下标的,也就是我们需要创建一个变量 i ,通过 i++ 来给数组每个位置进行传值。
而如果我们函数的实参传的是 i 就会导致一个严重的问题:
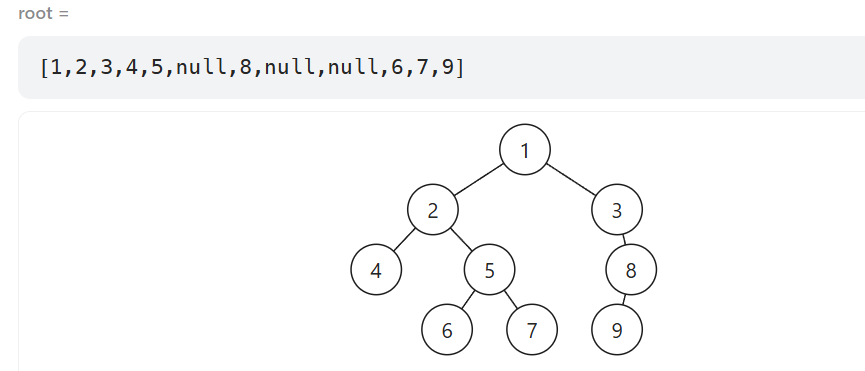

我们会发现以这个二叉树为例最后输出的只有1,3,8,9也就是二叉树的右边,原因就在于第一层我们将结点1传给数组后 i++ 让 i 变成1,此时递归到左子树进行传值。但是不管左子树怎么去传值,由于出了函数 i++ 就失效了,所以当递归返回到结点1时,此时 i 的值仍然是1,所以当递归右子树时就会把左子树递归的值全部覆盖掉。
所以为了当函数返回时 形参 i++ 也能影响实参的 i,就需要利用地址传参了。
具体代码如下:
int TreeNodeSize(struct TreeNode* root)
{if(root == NULL){return 0;}return TreeNodeSize(root->left) + TreeNodeSize(root->right) + 1;
}void PreOrder(struct TreeNode* root, int* arr, int* pi)
{if(root == NULL){return;}//前序遍历传值arr[(*pi)++] = root->val;PreOrder(root->left, arr, pi);PreOrder(root->right, arr, pi);
}int* preorderTraversal(struct TreeNode* root, int* returnSize)
{*returnSize = TreeNodeSize(root);//求出二叉树结点个数int* arr = (int*)malloc(sizeof(int) * (*returnSize)); //开辟数组int i = 0;PreOrder(root, arr, &i); //传i的地址return arr;
}这道题也有二叉树的中序遍历以及二叉树的后序遍历,但本质逻辑是一样的,只是传值的先后顺序不同,这里就不过多赘述了,大家可以自行尝试完成。
6、二叉树的构建及遍历
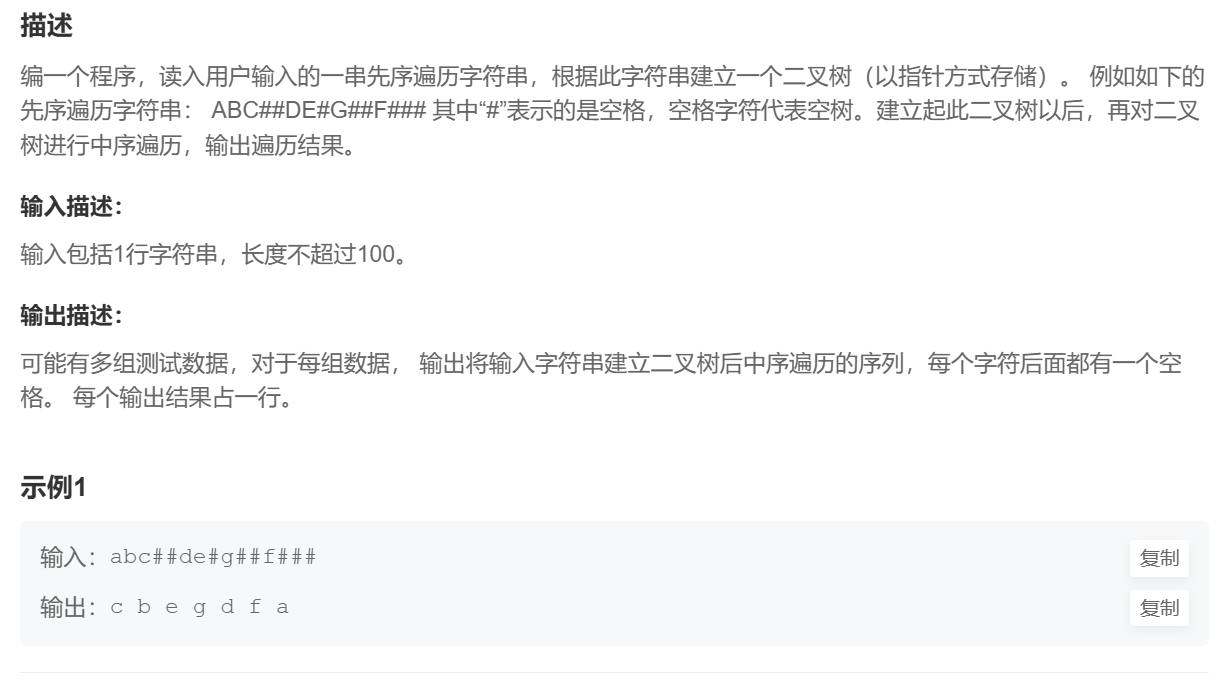
这道题虽然代码量比较多,但逻辑和前面的题都差不多,上面一题我们是通过创建一个数组将题目提供的二叉树通过前序遍历传给数组。而这道题与其相反,是题目提供一个数组,我们需要创建一个二叉树将数组的值通过前序遍历传过来,再通过中序遍历将二叉树进行打印。
具体代码如下其中有批注供大家理解:
#include <stdio.h>
#include <stdlib.h>
typedef struct BinaryTreeNode //自定义二叉树结点结构
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;int val;
}BTNode;//建立二叉树(以指针方式存储)
BTNode* CreateTree(char* arr, int* pi)
{if(arr[*pi] == '#'){(*pi)++;return NULL;} //先判断是否为#(也就是空结点),如果为空则不需要创建结点,返回NULL即可BTNode* root = (BTNode*)malloc(sizeof(BTNode));//如果不为'#'再创建根结点传值//前序遍历root->val = arr[(*pi)++]; //将数组的值传给二叉树结点root->left = CreateTree(arr, pi);root->right = CreateTree(arr, pi);return root;
}void InOrder(BTNode* root) //中序遍历打印二叉树
{if(root == NULL){return;}InOrder(root->left);printf("%c ", root->val);InOrder(root->right);
}int main()
{char arr[100];scanf("%s", arr);//建立二叉树(以指针方式存储)int i = 0;BTNode* root = CreateTree(arr, &i);//地址传参就是防止递归到空结点('#')返回时形参发生改变但实参没有影响//会导致值被覆盖的情况//中序打印InOrder(root);return 0;
}结束语
到此数据结构中以链式结构实现二叉树我们就讲解完了,相较于以顺序结构实现的二叉树-堆,链式结构的二叉树非常考验大家递归的思想,所以想要学好二叉树必须要理解清楚递归到底是在干什么,整个的递和归的逻辑是什么样子的,这些都需要非常熟悉。接下来我就会为大家讲解数据结构中的排序,希望这篇文章为大家学习二叉树能有所帮助!