考研408--数据结构--day2--顺序表及其增删改查

(以下内容全部来自上述课程)
目录
- 顺序表
- 1. 定义
- 2. 静态分配
- 3. 动态分配
- 4. 顺序表的实现
- 5. 小结
- 顺序表的插入和删除
- 1. 插入
- 2. 插入的时间复杂度
- 3. 删除
- 4. 删除的时间复杂度
- 5. 小结
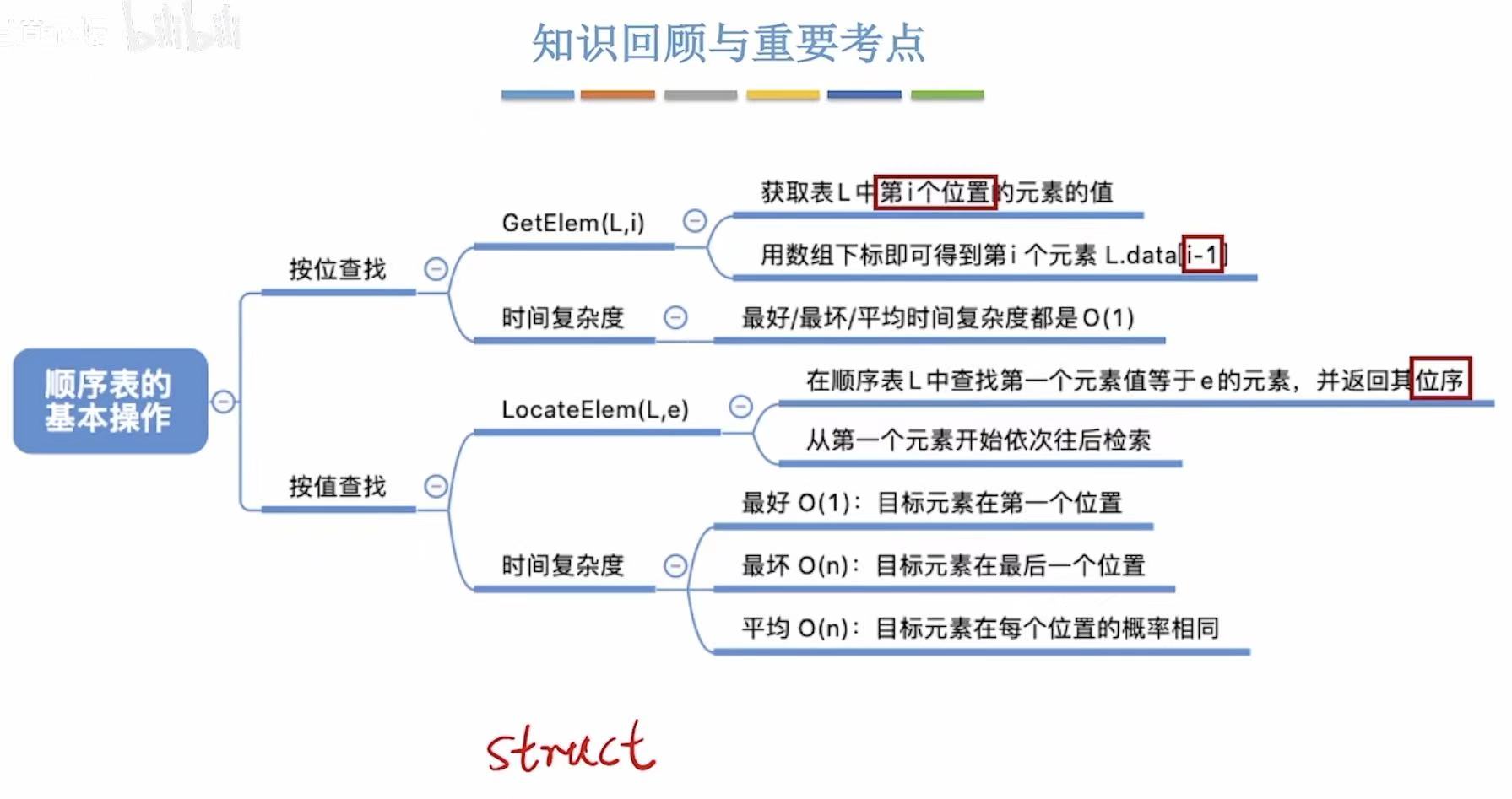
- 顺序表的基本操作
- 1. 按位查找
- 2. 按位查找的时间复杂度
- 3. 按值查找
- 4. 按值查找的时间复杂度
- 5. 小结
顺序表
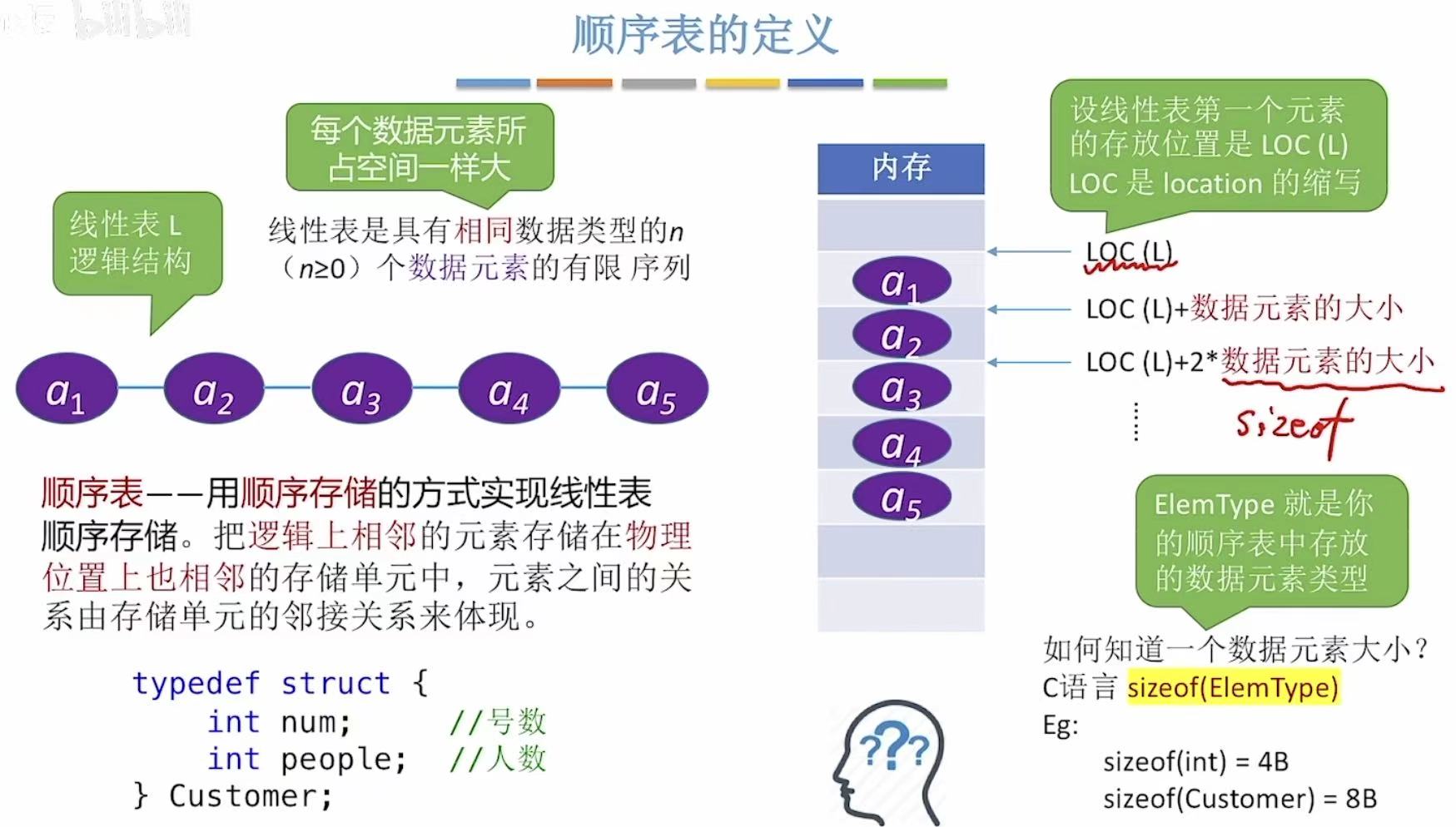
1. 定义
typedef struct:定义结构体。
顺序表:就相当于学号,每个人的学号都是有顺序的,2号之前是1号,2号之后是3号。
sizeof:获取数据元素大小。
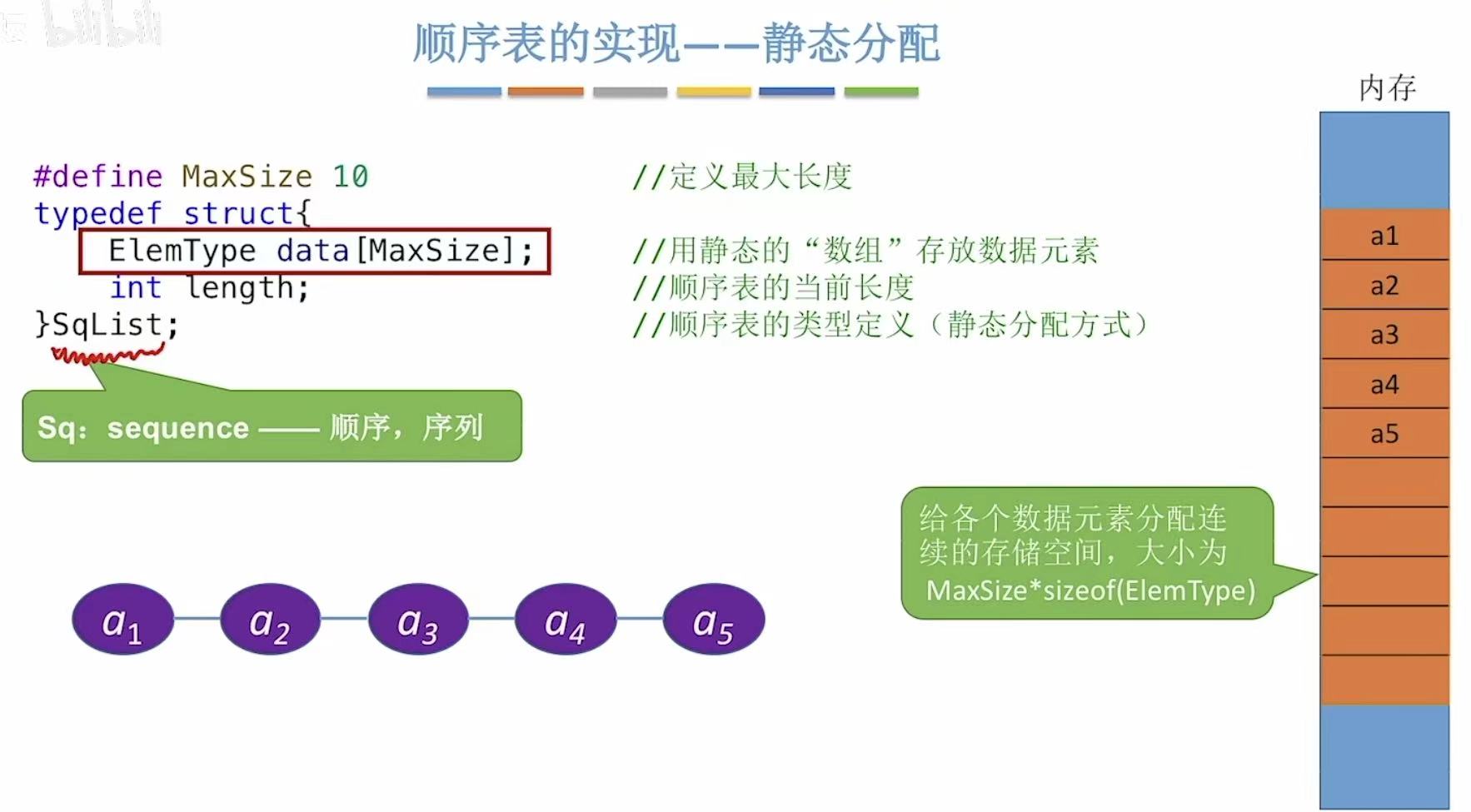
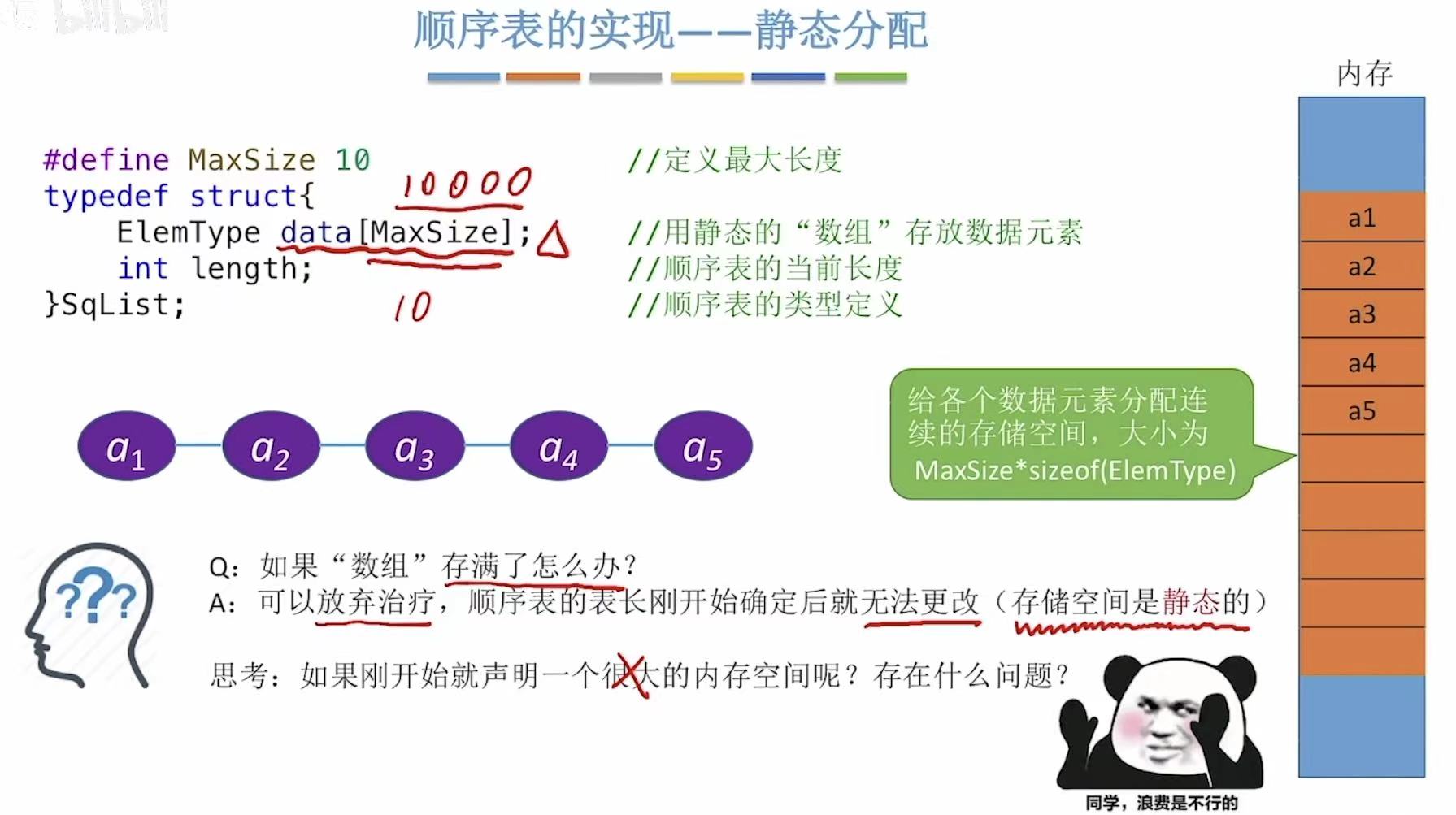
2. 静态分配
就是把顺序表的长度固定,是多大就多大,不可以调整。
标志:
#define MaxSize 10–>定义最大长度ElemType data[MaxSize];–>静态
代码:定义最大长度–>定义顺序表–>初始化顺序表–>main(使用顺序表)
内存:分配空间–>设置默认值–>将顺序表初始长度设置为0
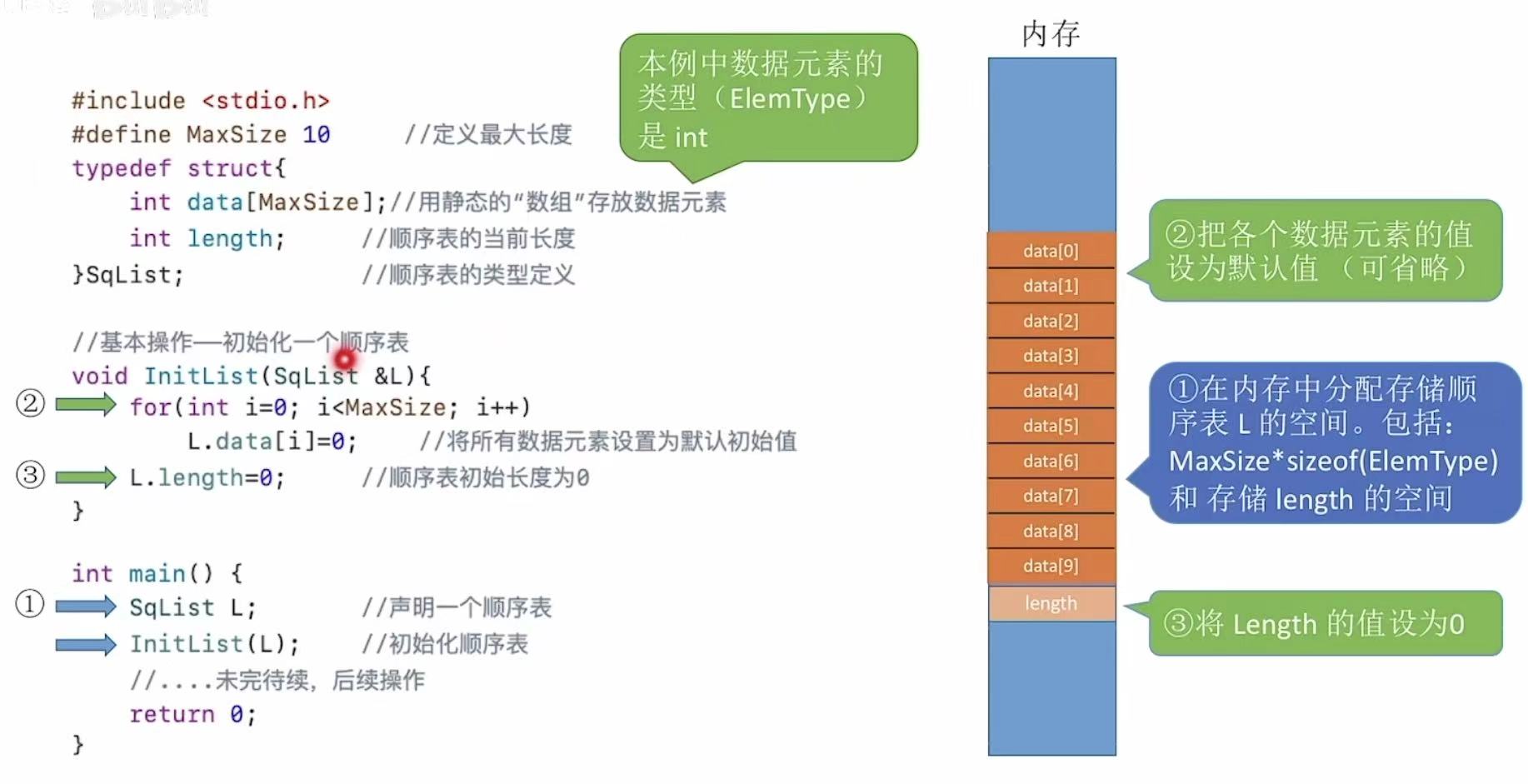
如果初始化顺序表的时候没有设置数据元素的默认值,内存中遗留的脏数据可能会影响后续存入的数据。
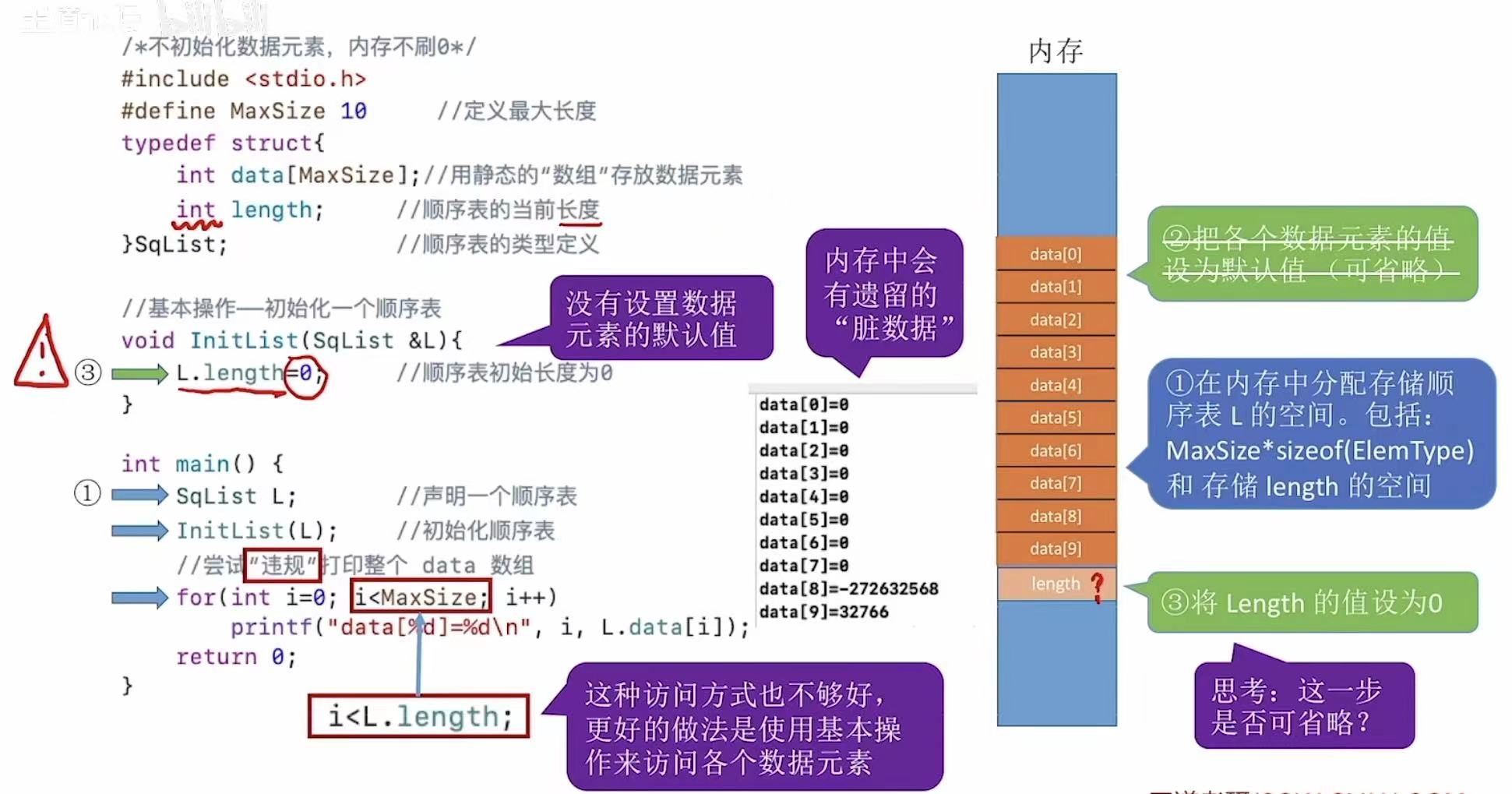
如果最开始定义了一个空间很大的顺序表,不一定都会用到,会导致空间浪费。
3. 动态分配
标志:
#define InitSize 10–>定义初始长度为10ElemType *data–>指针–>动态
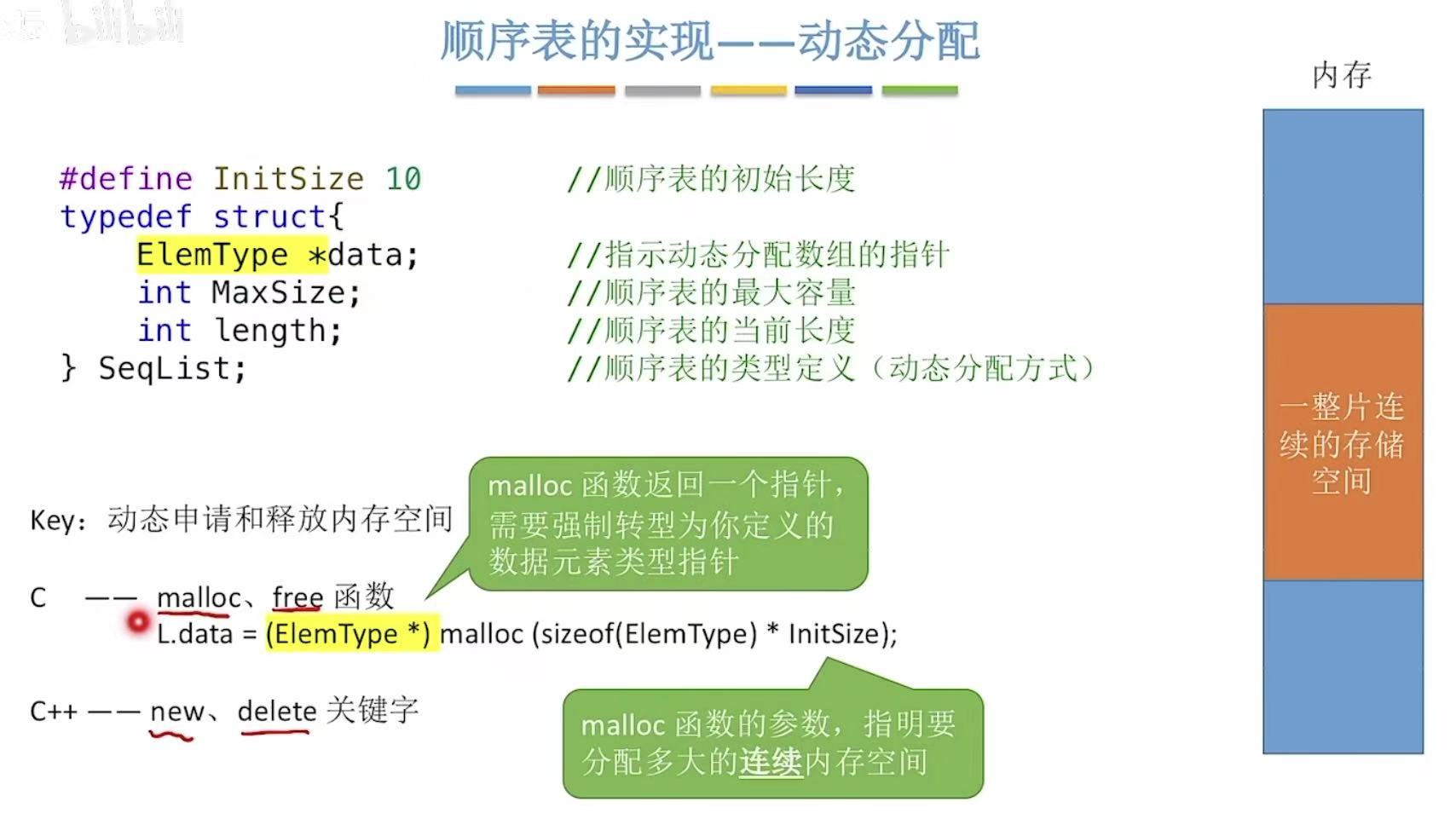
定义初始长度–>定义顺序表–>初始化顺序表–>main(使用顺序表)–>空间不够了可以增加长度
注意:说是增加长度,但其实是又重新开了(malloc)一块儿更大的地,把之前的搬到新的地方,时间开销就大了,然后把之前的地卖掉(free)。
ps:新的最大容量 = 原来的最大容量(L.MaxSize) + 传入的参数len(即L.MaxSize + len)

4. 顺序表的实现
随机访问:就像学号,你找几号,大概看在名单的哪个位置直接就能找到,所以时间复杂度为O(1)
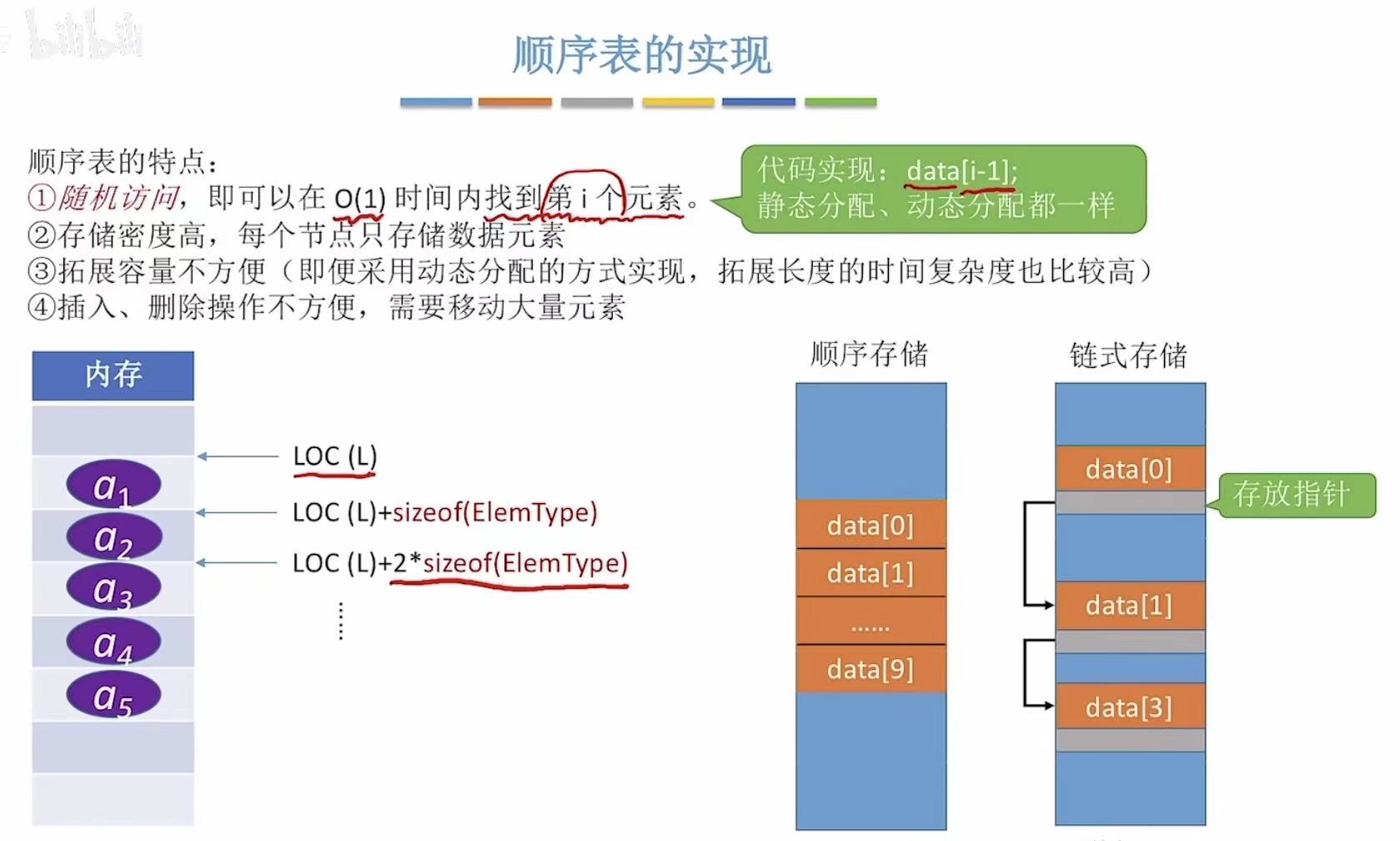
5. 小结
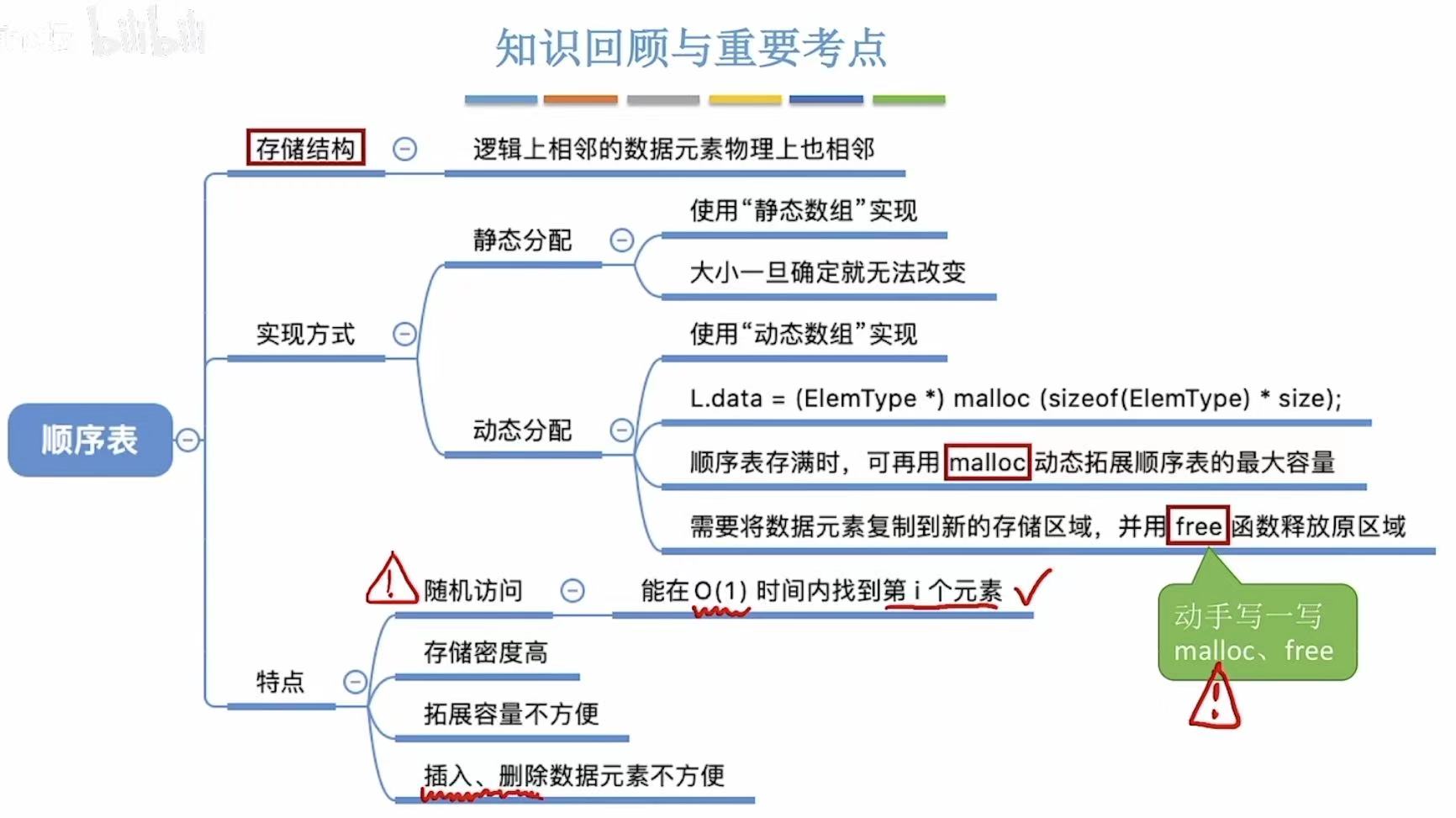
顺序表的插入和删除
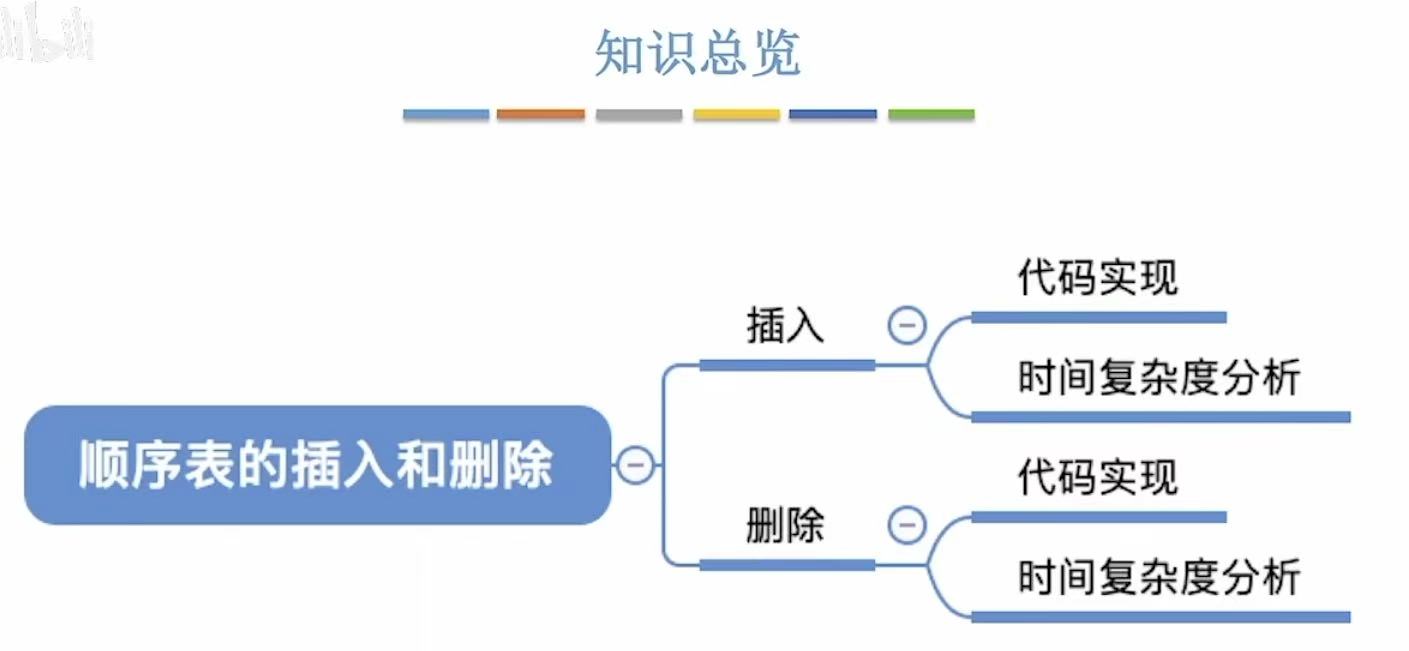
1. 插入
这样想,如果你的班级是用名字首字母的顺序排学号的,你是10号,有个插班生来到你的班级正好名字首字母在你之前,更好取代了你的位置,也就是,他变成了10号,你变成了11号,甚至连带着你之后所有的人的学号都必须+1。
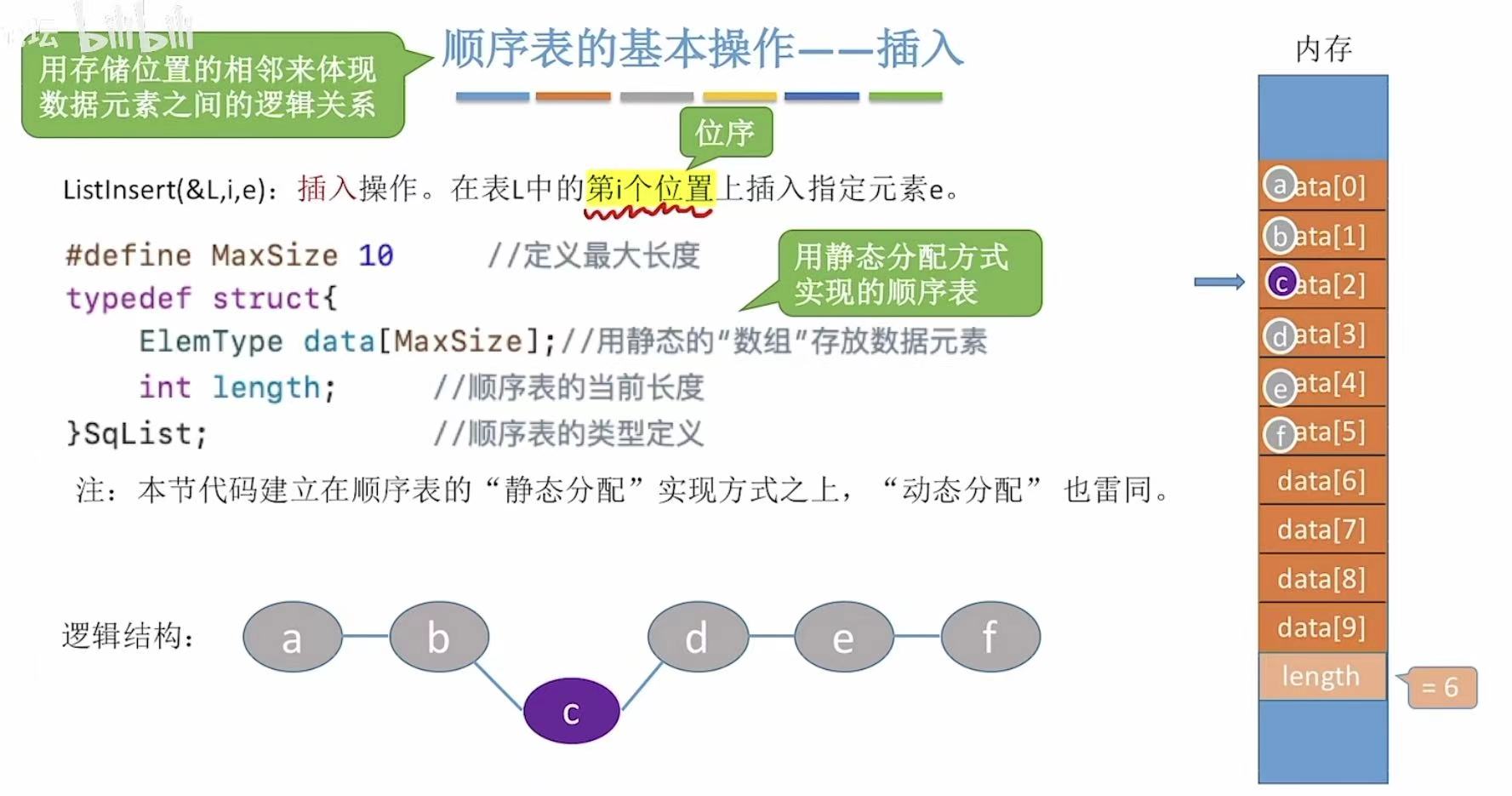
插入方法的参数:在哪里插入?–>顺序表,插入的位置?–>位序,插入谁?–>插入元素
注意:位序和数组下标的区别,数组下标从0开始,所以会比位序少1。
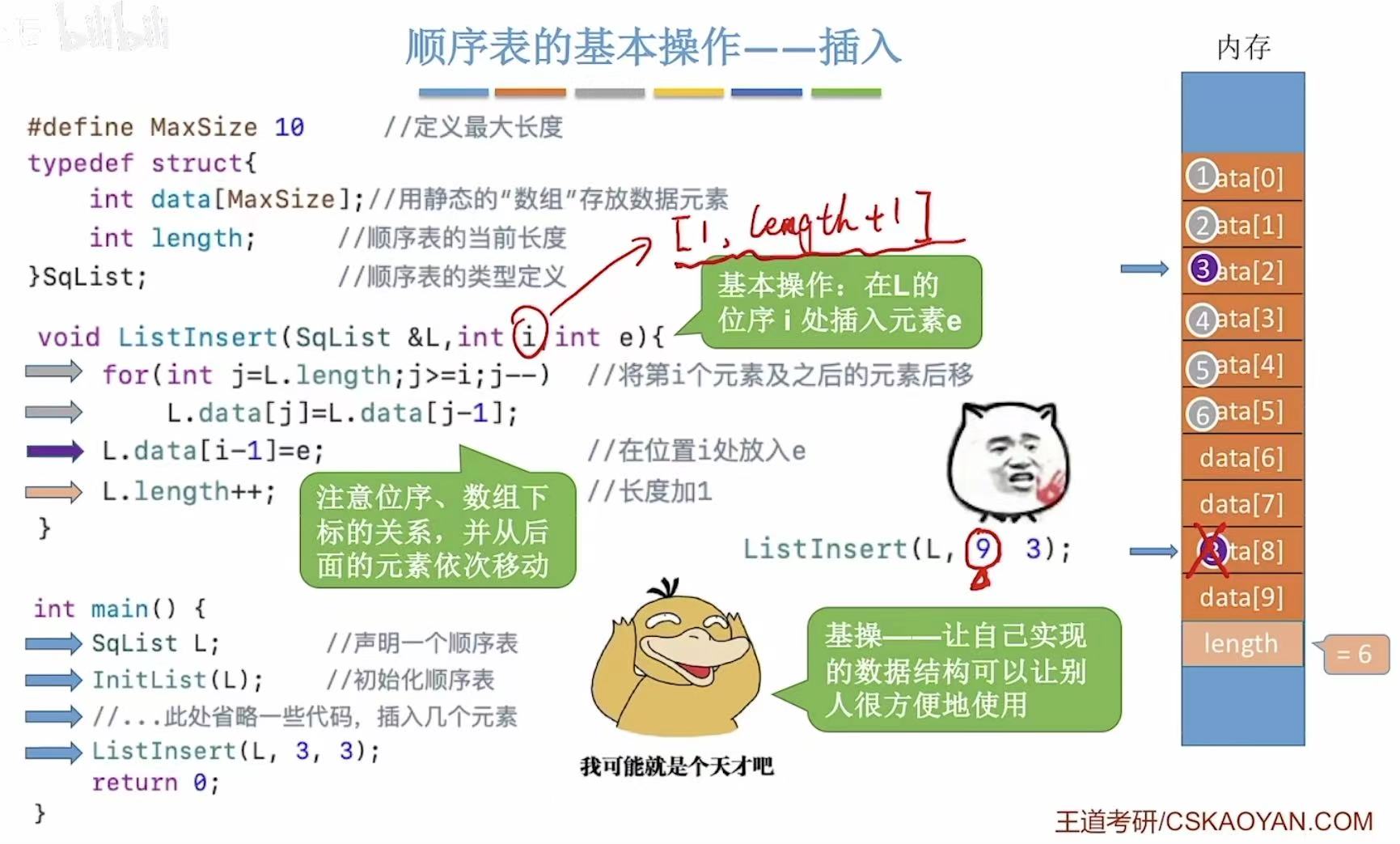

2. 插入的时间复杂度

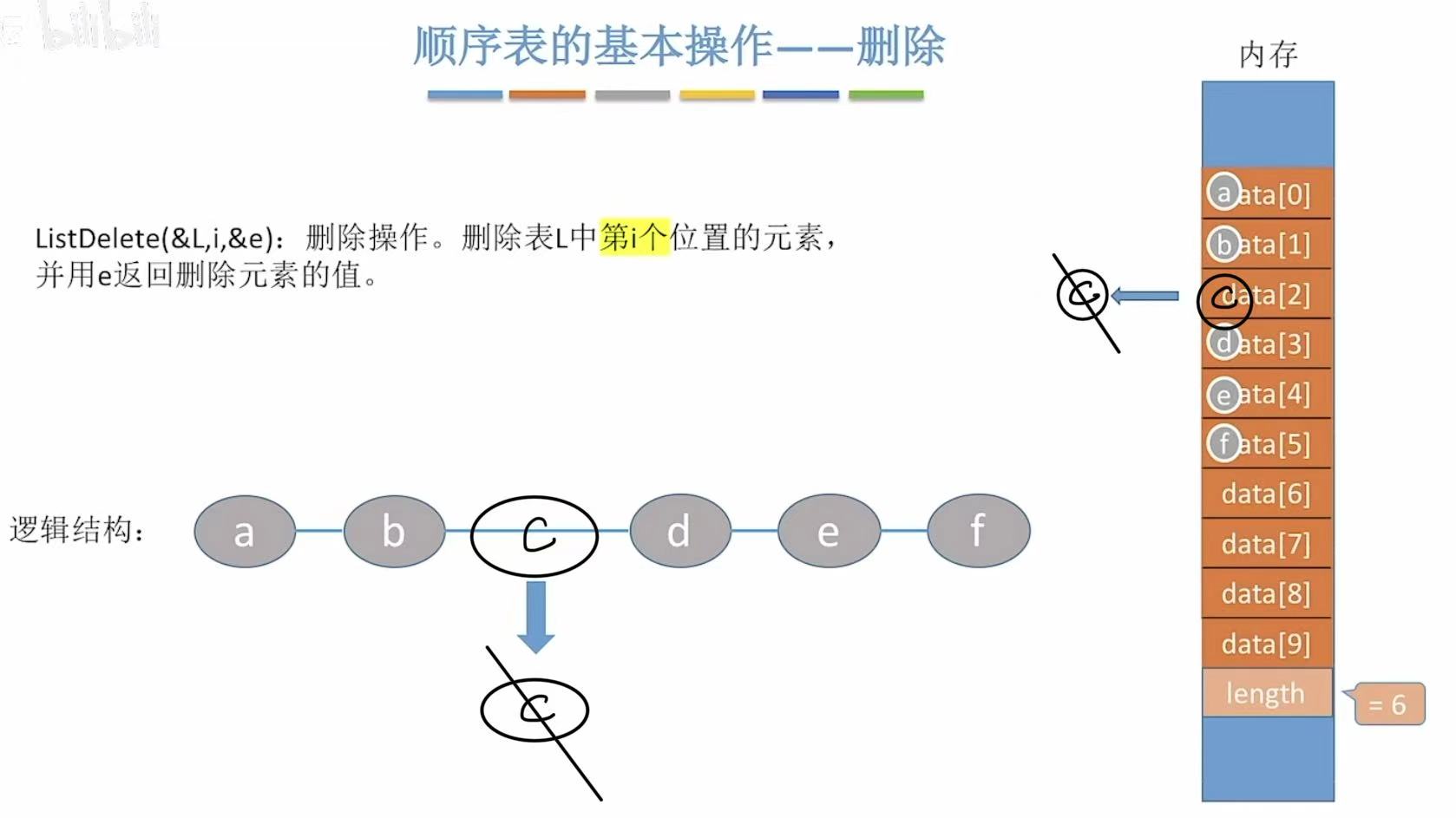
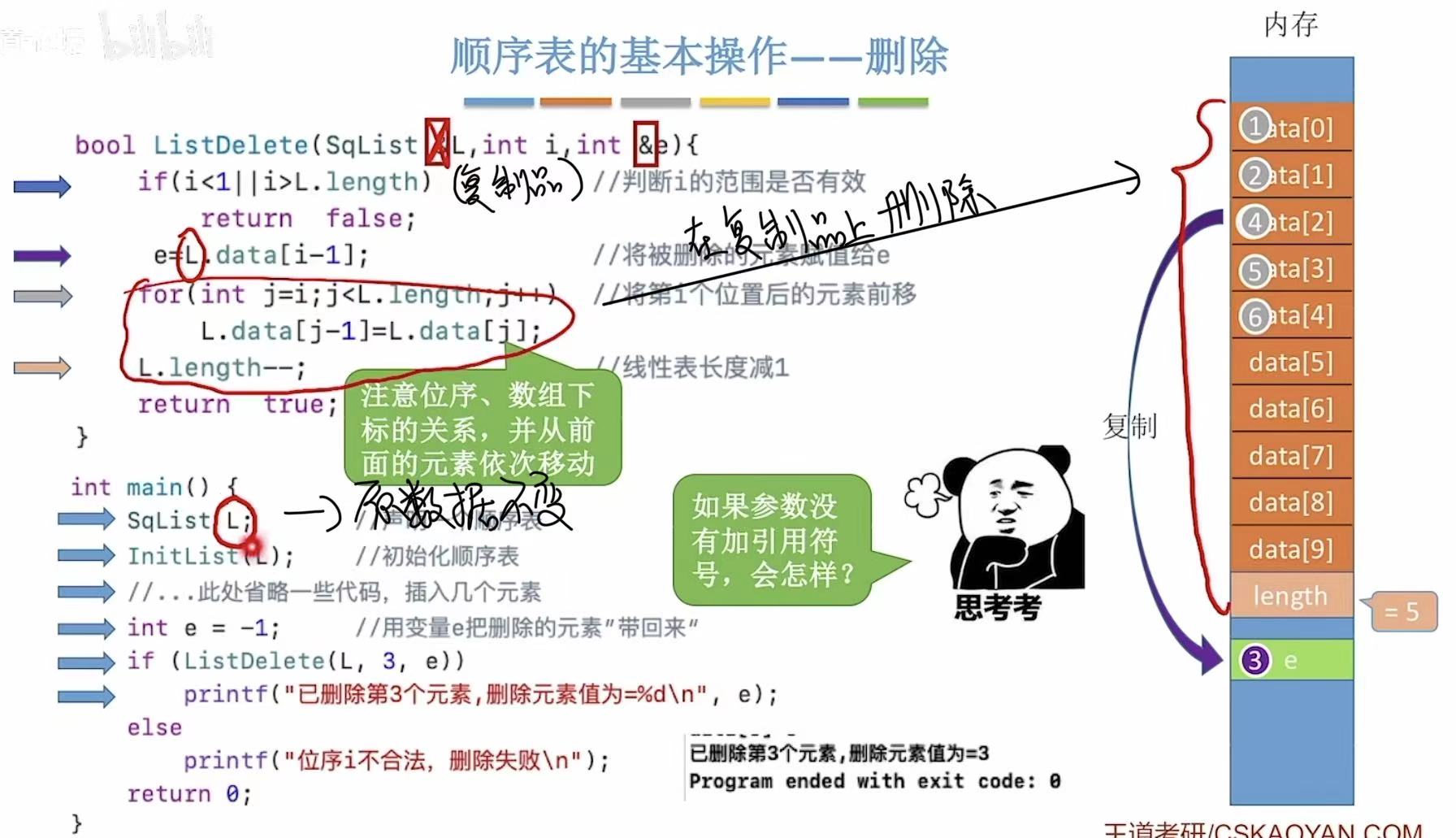
3. 删除
书接上文,插班生在你的班级呆了两天就走了,所以你又变回10号了,连带着你后面的所有人的学号也要-1,变回自己之前的学号。
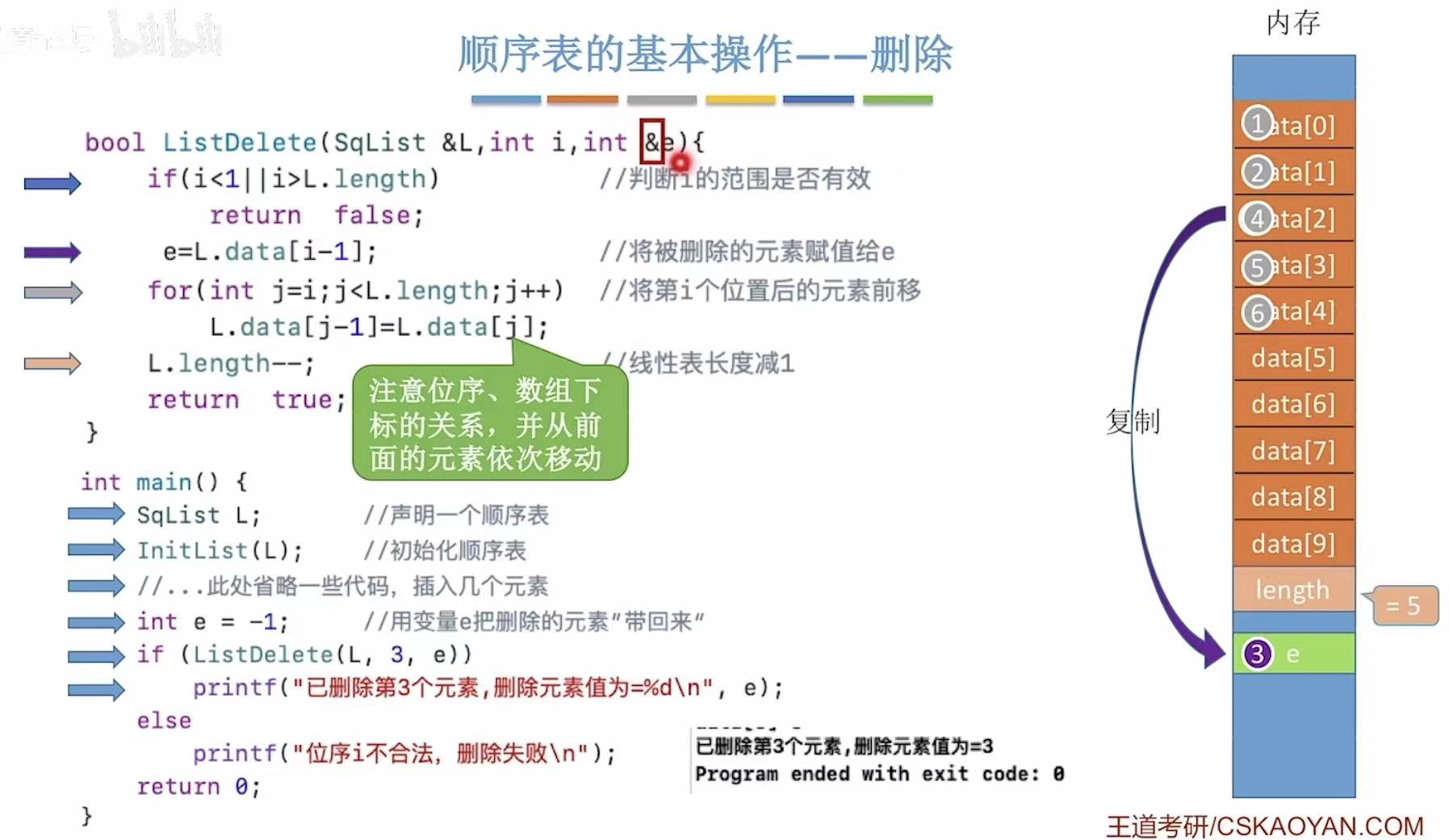
&:引用符号,代表返回数值,因为后续需要输出e的值,所以就算把e删掉了,也要复制一份留在输出的时候用。
如果e的前面没有&的话,删掉了就真的删掉了,就无法覆盖main中e的初始值-1,所以输出时就出现了错误。
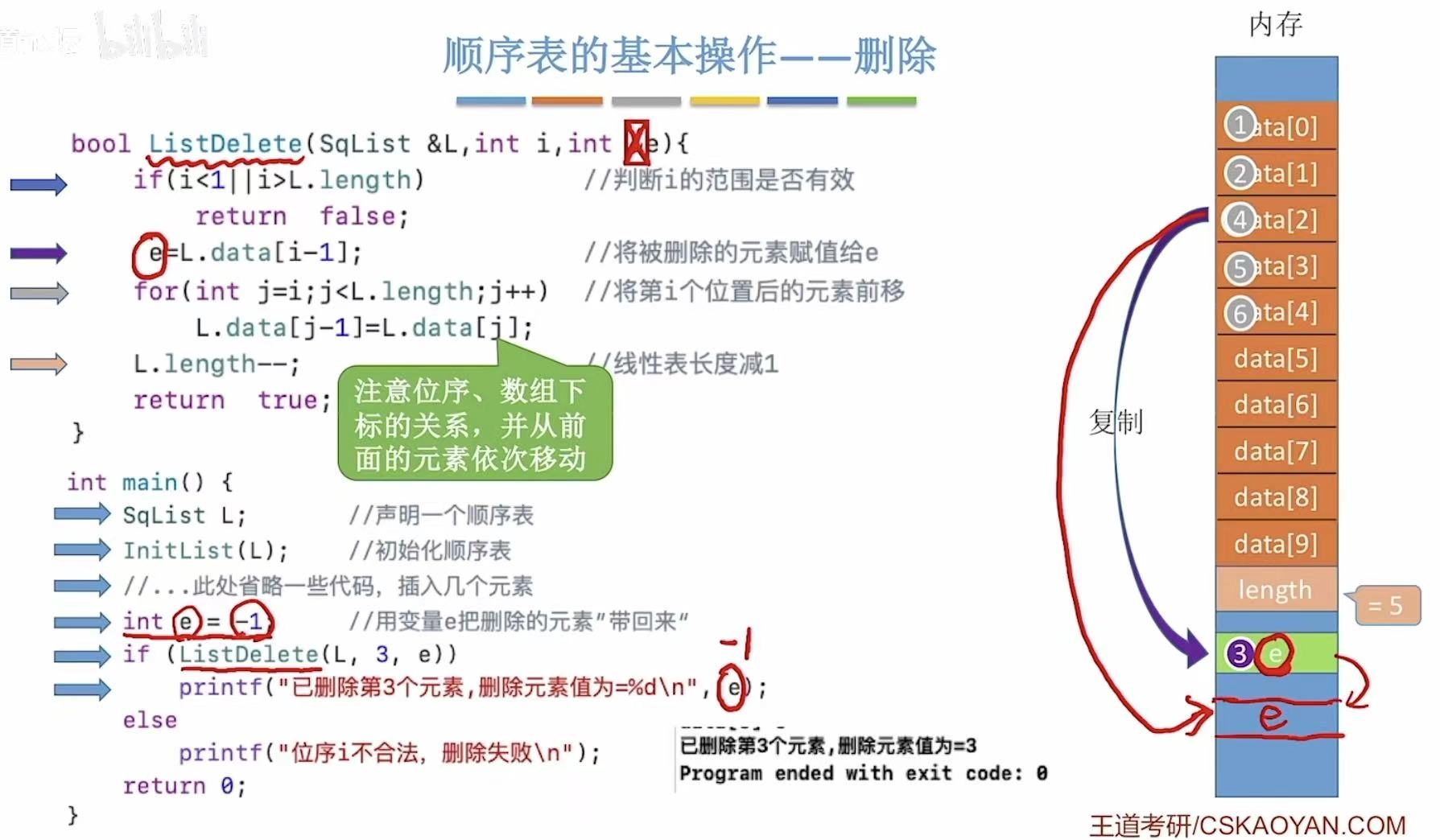
L也是同样,可以理解为有&就可以覆盖main中的初始L,所以在&L中的操作就可以同步到main的初始L上。
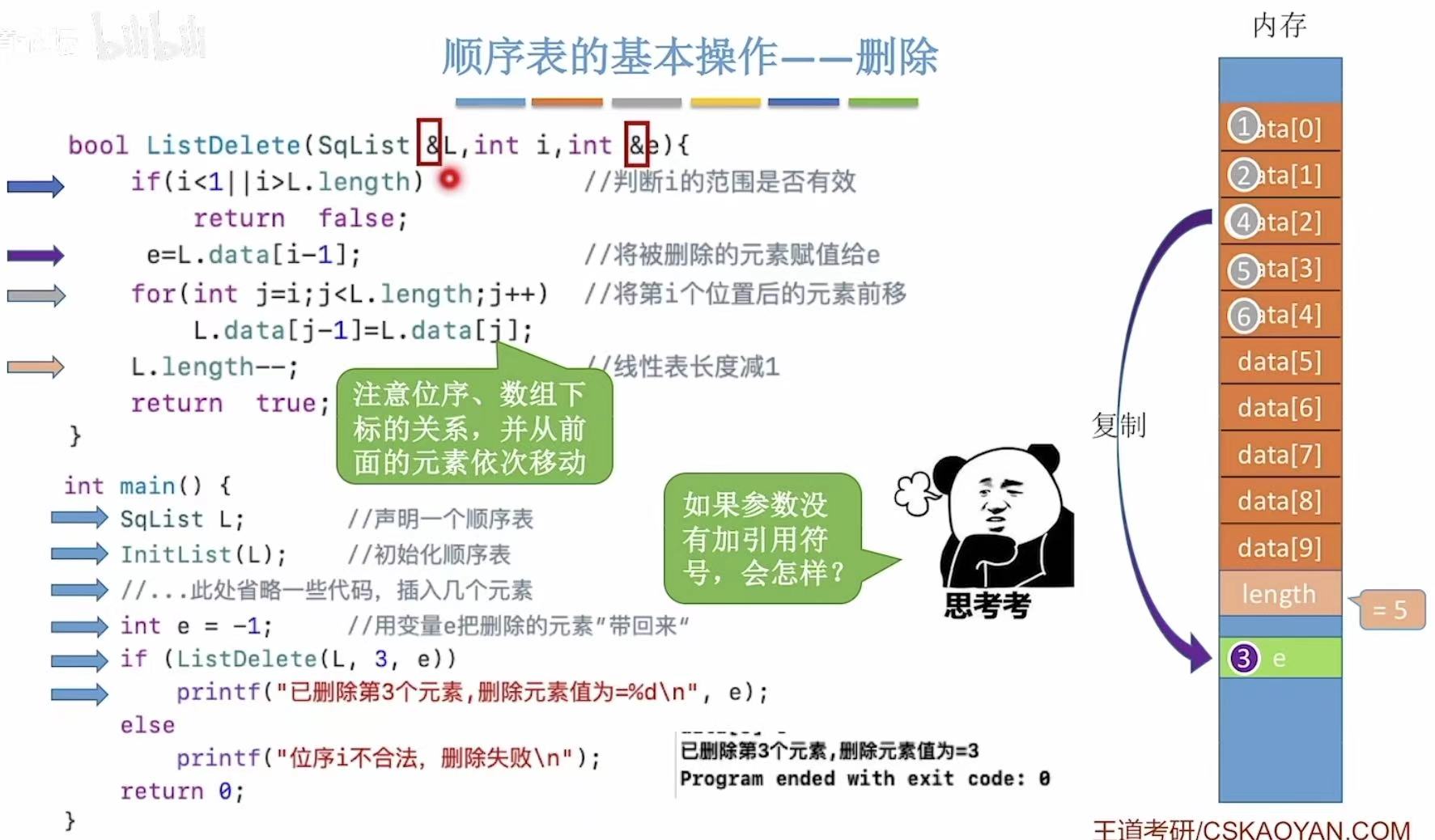
方法中的L:mian中的L的复制品
main中的L:初始L
&:同步操作
4. 删除的时间复杂度
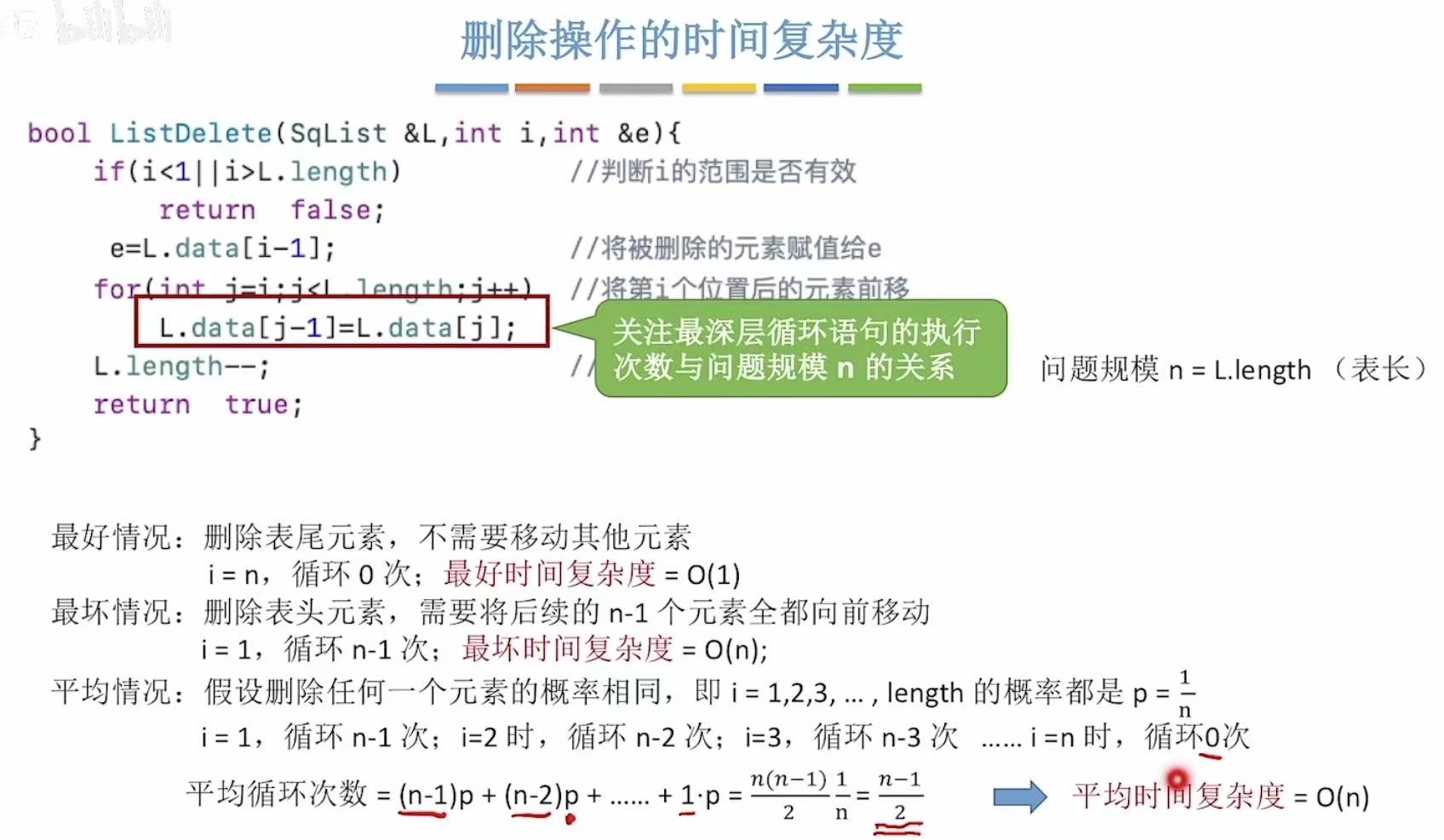
5. 小结
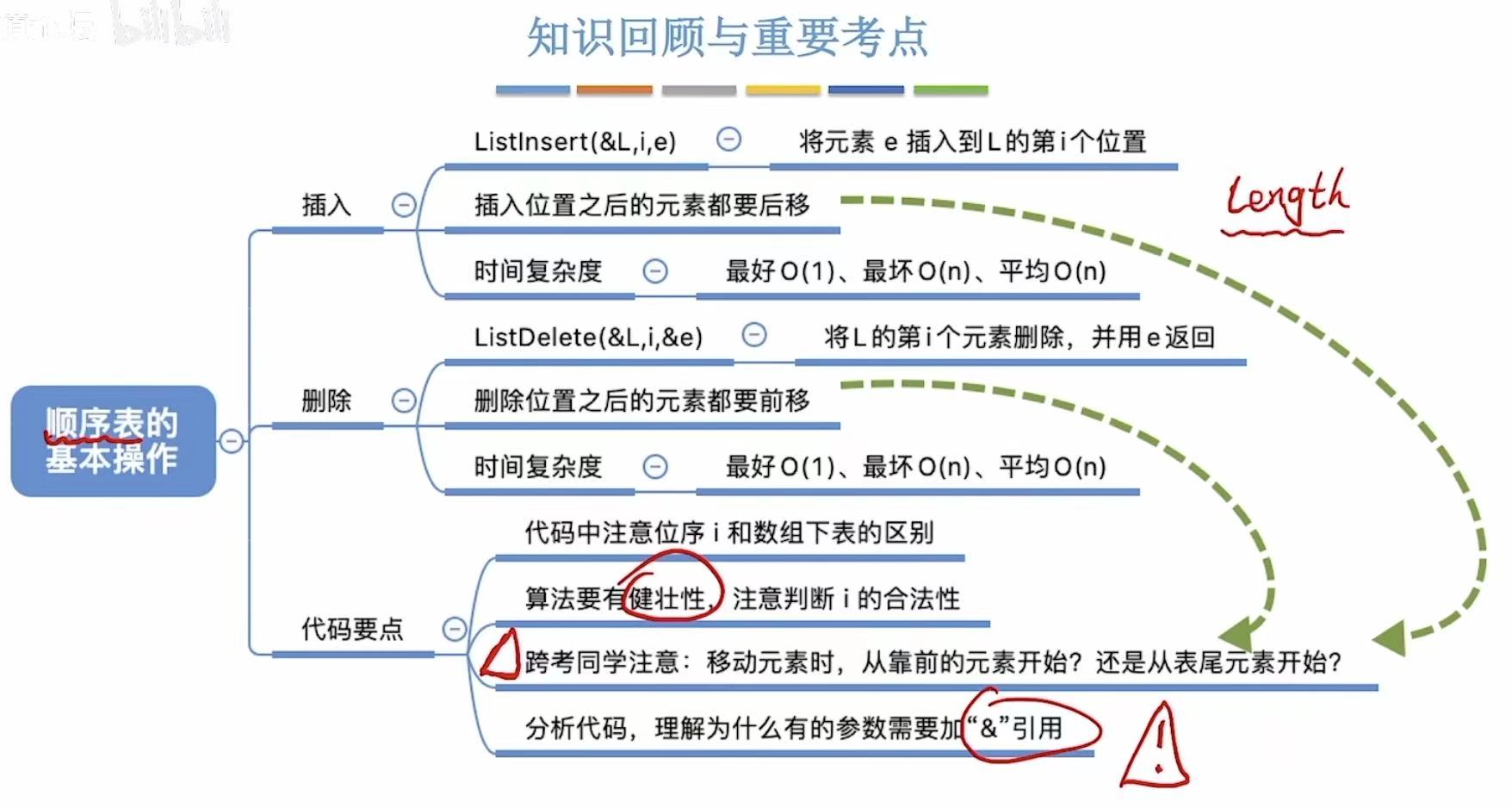
顺序表的基本操作
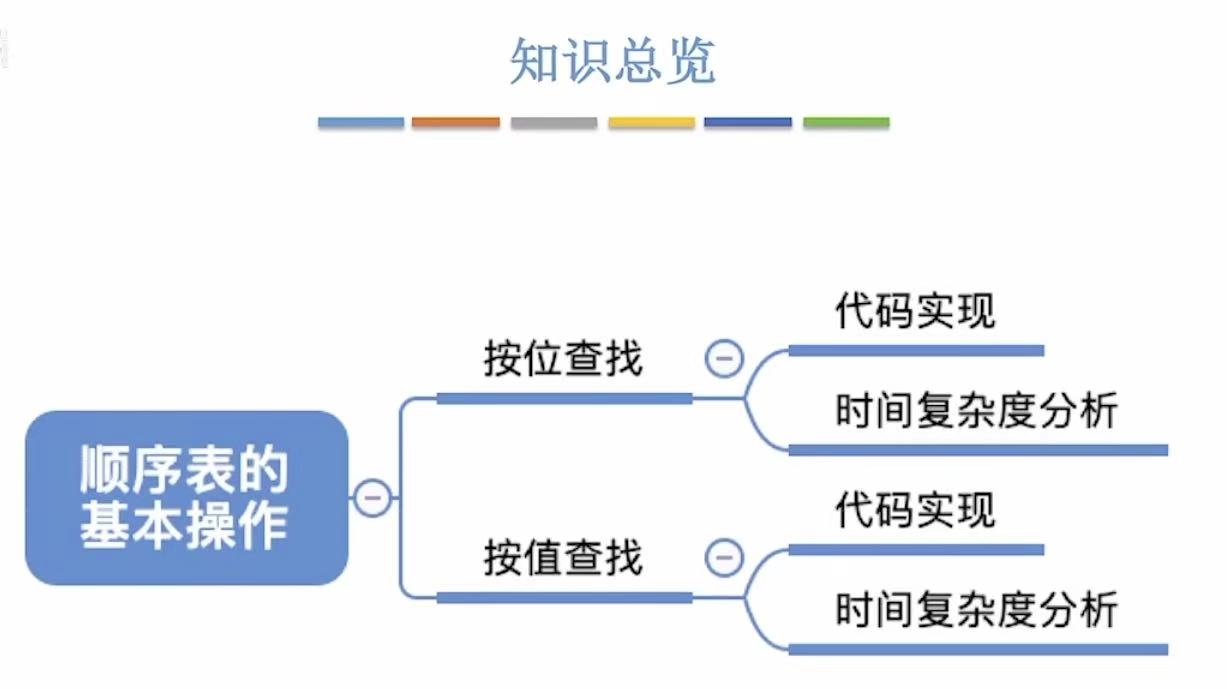
1. 按位查找
学号直查。
查找参数:在哪里找?–>顺序表,找哪位?–>位序

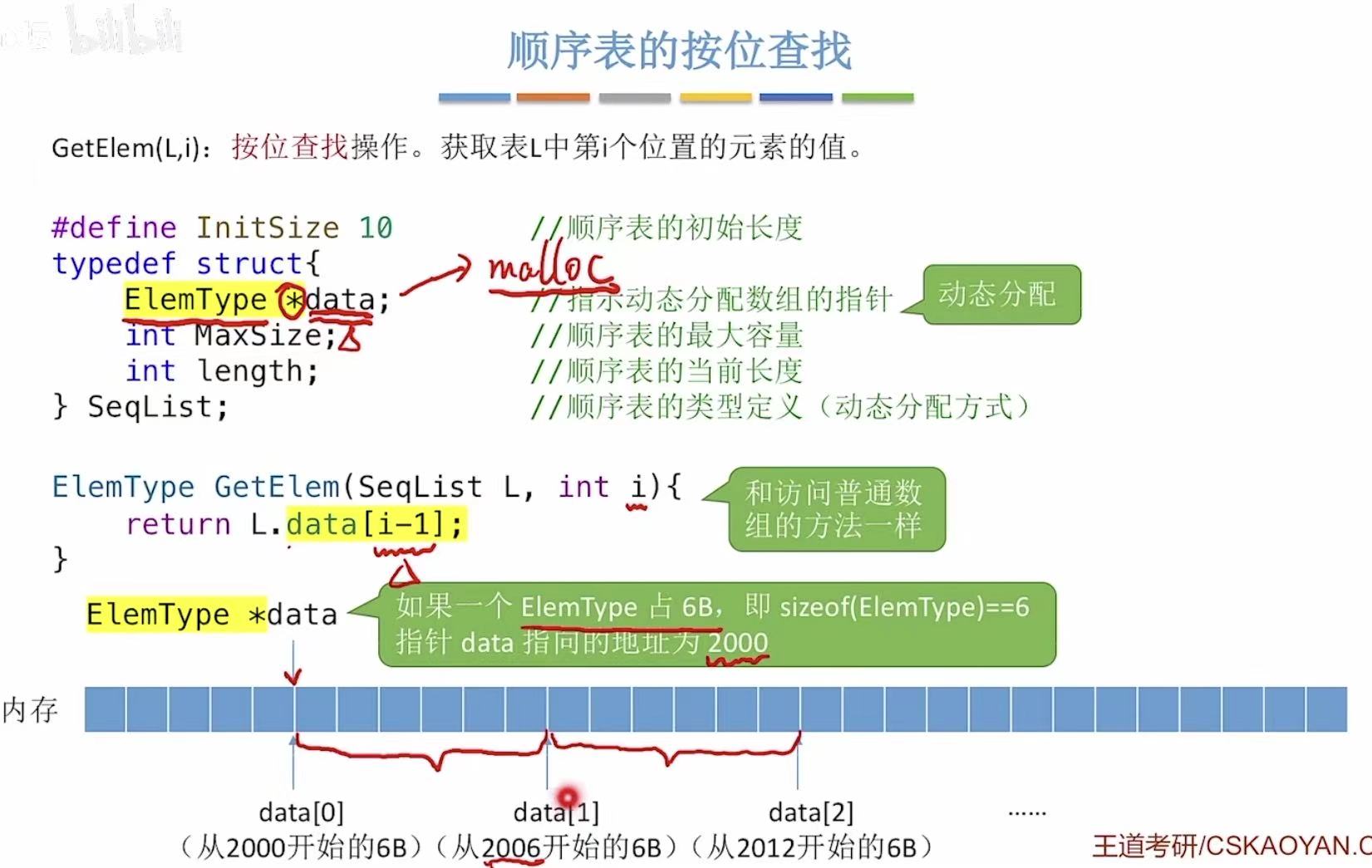
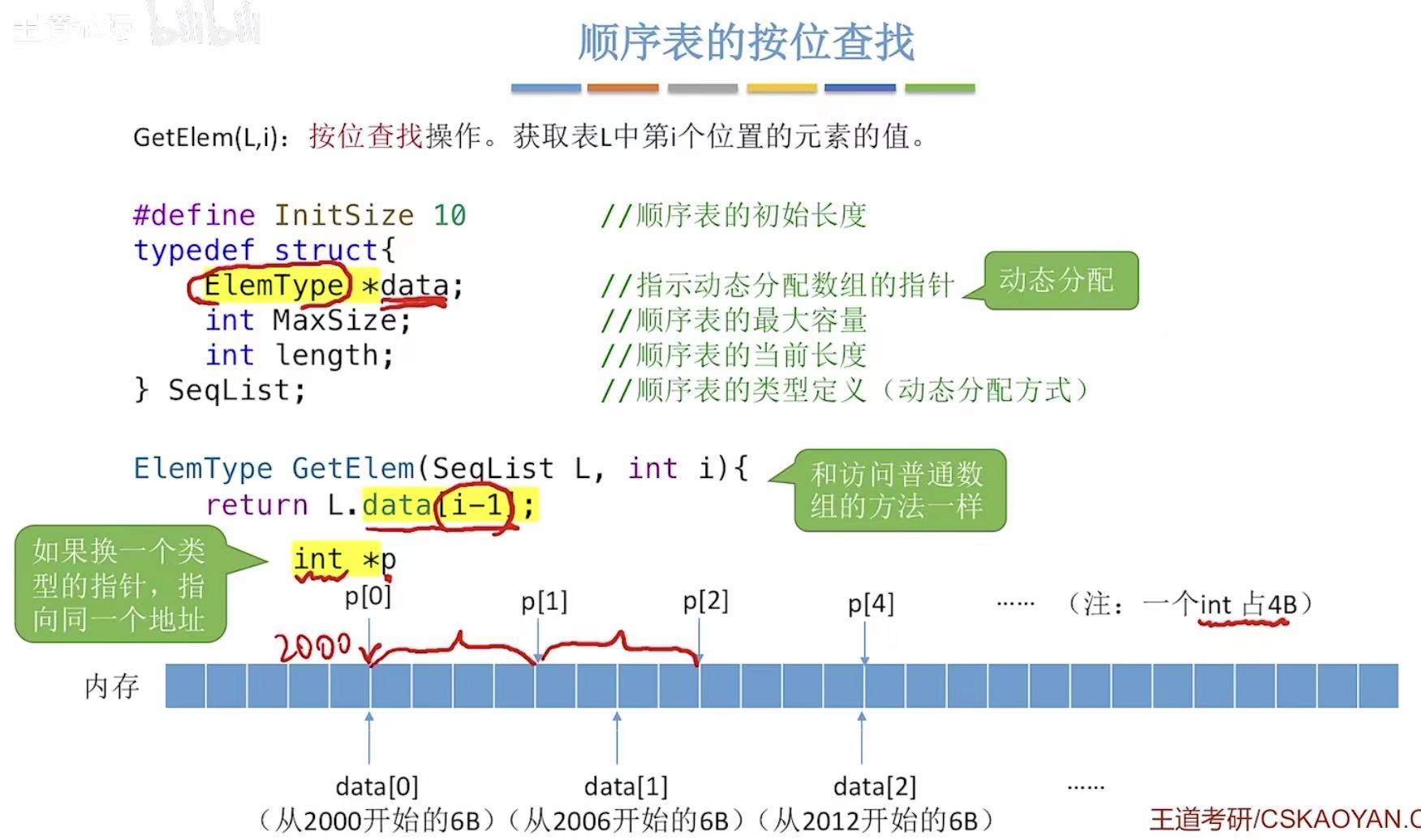
ElemType的类型不同,占的字节也不同,就会导致指针指向的位置也不同。
如果占6B,指针指向的位置是每隔6B;如果占4B,指针指向的位置是每隔4B。
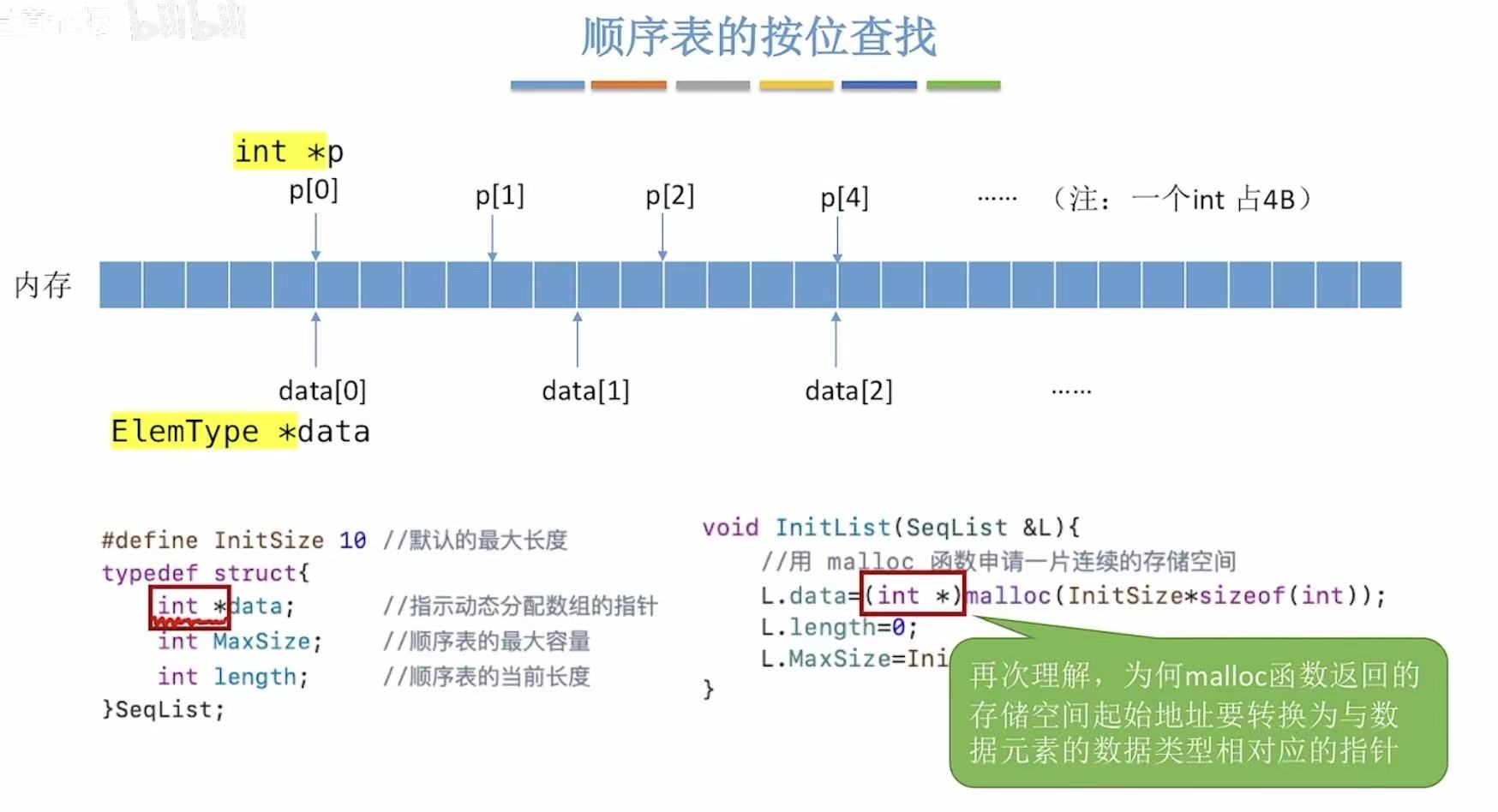
2. 按位查找的时间复杂度
类似于直接找学号,嗯,一秒钟就知道这个学号是谁了。

3. 按值查找
嗯,这次不找学号了,直接找人。


结构类型的比较
4. 按值查找的时间复杂度

5. 小结