JAVA之二叉树
1.什么是树
树指的是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做 树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的,大概的样子如下:
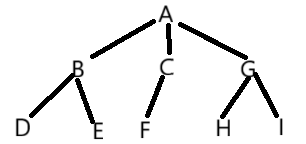
1.1树的概念
(一)结点的度
这个指的是一个结点含有子树的个数称为该结点的度,像上图A的度就是3
(二)叶子结点
当一个结点的度为零时,这个结点就称之为叶子结点,像上图的叶子结点是D,E,F,H,I
(三)树的度
这个指一棵树中所有结点的度的最大值,像上图就是树的度是3
(四)父结点
这个指的是一个结点含有子结点的话,那么这个节点就叫父结点,像上图的A是B,C,G的父结点
(五)结点的层次
从根开始算起,根为第一层,根的子结点为第二层,以此类推,像上图的层次是3
(六)树的深度
指树中结点最大的层次,如上图的深度是3
(七)非终端结点
这个指的是度不为零的结点,如上图的B,C,G,A
(八)兄弟结点
这个是指在同一根下,相邻的结点,如上图的B,C,G
(九)堂兄弟结点
这个指的是双亲在同一层的结点互为堂兄弟,如上图的E和F
(十)节点的祖先
这个指的是从根到该结点所经分支上的所有结点,如上图A是所有节点的祖先
2.二叉树
2.1二叉树的概念
二叉树指的是一颗结点的度最大不能超过二的树,它有左右之分,因此是颗有序树,如下图w所示:
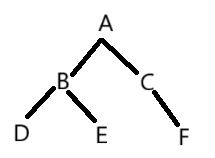
2.2特殊二叉树
(1)完全二叉函数
这个指一颗二叉树从上到下,从左到右,一次不断的进行排序,如下图所示:
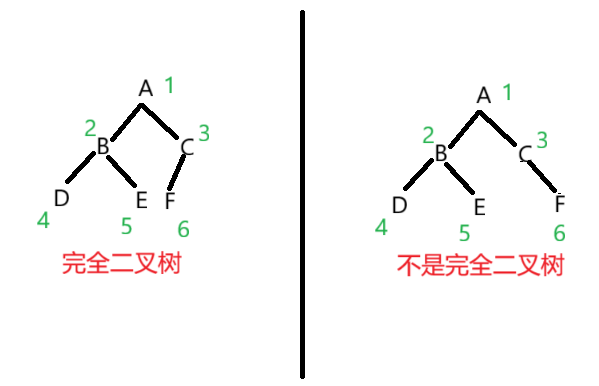
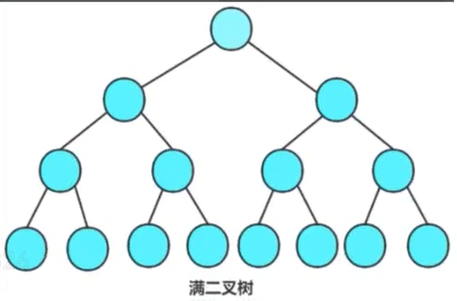
(2)满二叉树
这个是特殊完全二叉树,它指的是每层结点数都达到最大值,并且结点个数等于(2^k)-1,k指的是层数
2.3二叉树的性质
(1)若根结点的层数为1时,一颗非空二叉树的第i层总共有(2^i-1)个节点,i>0
(2)根结点二叉树深度为1,则深度为k的二叉树最大结点个数是(2^k)- 1
(3)度为0的结点比度为2的结点多1个
它的推导过程:可知每一棵树都是由度为0的结点加上度为n的结点所构成的,如n0+n1+n2 = N,又因为一颗有N个结点的树,有N-1条边,所以N-1 = n1 + 2*n2,结合二式化简得,n0 = n2+1
(4)n个结点完全二叉树得深度k为log(n+1)【log以2为底】
它得推导过程是根据(2)进行逆推得到的
(5)对于有n个结点的完全二叉树,从上到下,从左到右对所有结点从0开始编号,那么父亲结点i的左子结点是(2*i)+ 1,右子结点是(2*i)+ 2。但如果i是子结点,那么父结点是(i-1)/ 2
2.4二叉树的存储
二叉树的存储分为两种:类似于链表的链式存储和顺序存储
先讲链式存储,它本质上就是一个包含左边地址、右边地址和值的点与另外的点进行连接,像下图:
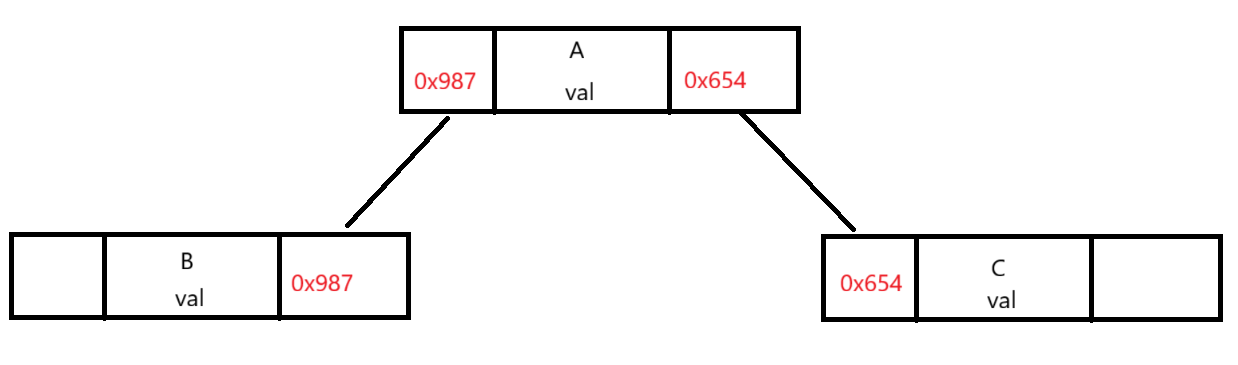
2.5遍历方式
这是一颗二叉树,接下来,我会通过使用不同的方式来进行遍历这一颗二叉树
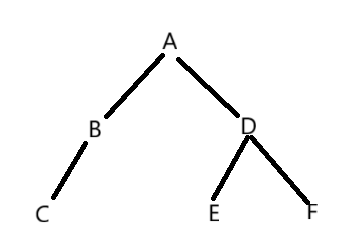
(一)前序遍历
这个的原理是先遍历根,然后到左子树,最后是右子树。所以它的遍历结果是 ABCDEF
(二)中序遍历
这个原理是先遍历左子树,然后再到根,最后是右子树。所以它的遍历结果是 CBAEDF
(三)后序遍历
这个原理是先遍历左子树,然后到右子树,最后是根。所以它的遍历结果是 CBEFDA
2.6二叉树代码构造
(一)构建二叉树
首先,我们先创建一个结点,根据上面我们可以知道一个结点是由val,left,right这三个部分组成的,如下:
public class BinaryTree {static class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}}
}
创建好单个结点后,接下来我们就要把结点进行串起来,串成下面那颗树
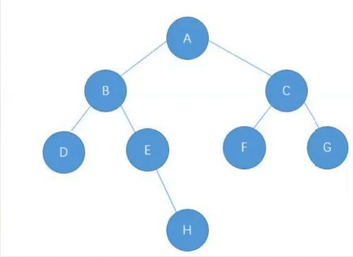
以下是代码的实现:
public TreeNode creatTree(){TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;B.left = D;B.right = E;E.right = H;A.right = C;C.left = F;C.right = G;return A;}(二)遍历二叉树
根据上面遍历的原理,我们可以写出以下代码来进行遍历
前序遍历
//前序遍历public void preOder(TreeNode root){if(root == null){return ;}System.out.print(root.val +" ");preOder(root.left);preOder(root.right);}中序遍历
//中序遍历public void inOder(TreeNode root){if(root == null){return ;}inOder(root.left);System.out.print(root.val + " ");inOder(root.right);}
后序遍历
//后序遍历public void postOder(TreeNode root){if(root == null){return ;}postOder(root.left);postOder(root.right);System.out.println(root.val + " ");}(三)计算树的总共结点
这里能分成两种思路,第一种是通过上面遍历的思路来进行统计。第二种是通过子问题方式,先计算左子树和右子树的个数,最后再加上root结点的个数来进行统计
第一种
//遍历方式
public static int countSize = 0;public void size(TreeNode root){if(root == null){return ;}size(root.left);size(root.right);countSize++;}第二种
//子问题方式public int nodeSize(TreeNode root){if(root == null){return 0;}return nodeSize(root.left) + nodeSize(root.right) + 1;}(四)计算叶子节点
这里也是有两种方法,遍历和子问题方法
第一种
//通过遍历的方法public static int leaveCount = 0;public void leaveSize(TreeNode root){if(root == null){return ;}if(root.left == null && root.right == null){leaveCount++;}leaveSize(root.left);leaveSize(root.right);}第二种
public int getLeaveCount(TreeNode root){if(root == null){return 0;}if(root.left == null && root.right == null){return 1;}return getLeaveCount(root.left) + getLeaveCount(root.right) ;}(五)获得层级结点
这个是用来获得在同一层有多少个结点,以下是代码
public int getLever(TreeNode root,int k){if(root == null){return 0;}if(k == 1){return 1;}return getLever(root.left,k -1 ) + getLever(root.right,k - 1);}(六)求树的高度
我们通过进行递归左数和右树,然后取最大值,以下是代码:
public int getHigh(TreeNode root){if(root == null){return 0;}int ret1 = getHigh(root.left);int ret2 = getHigh(root.right);return Math.max(ret1,ret2) + 1;}(七)寻找对应的元素
这里是通过递归来进行查找元素,原理类似与遍历,只不过多了个判断的条件
public TreeNode Find(TreeNode root,char val){if(root == null){return null;}if(root.val == val){return root;}TreeNode node1 = Find(root.left,val);if(node1 != null){return node1;}TreeNode node2 = Find(root.right,val);if(node2 != null){return node2;}return null;}