每日两道算法(2)
每日两道算法
大数加法
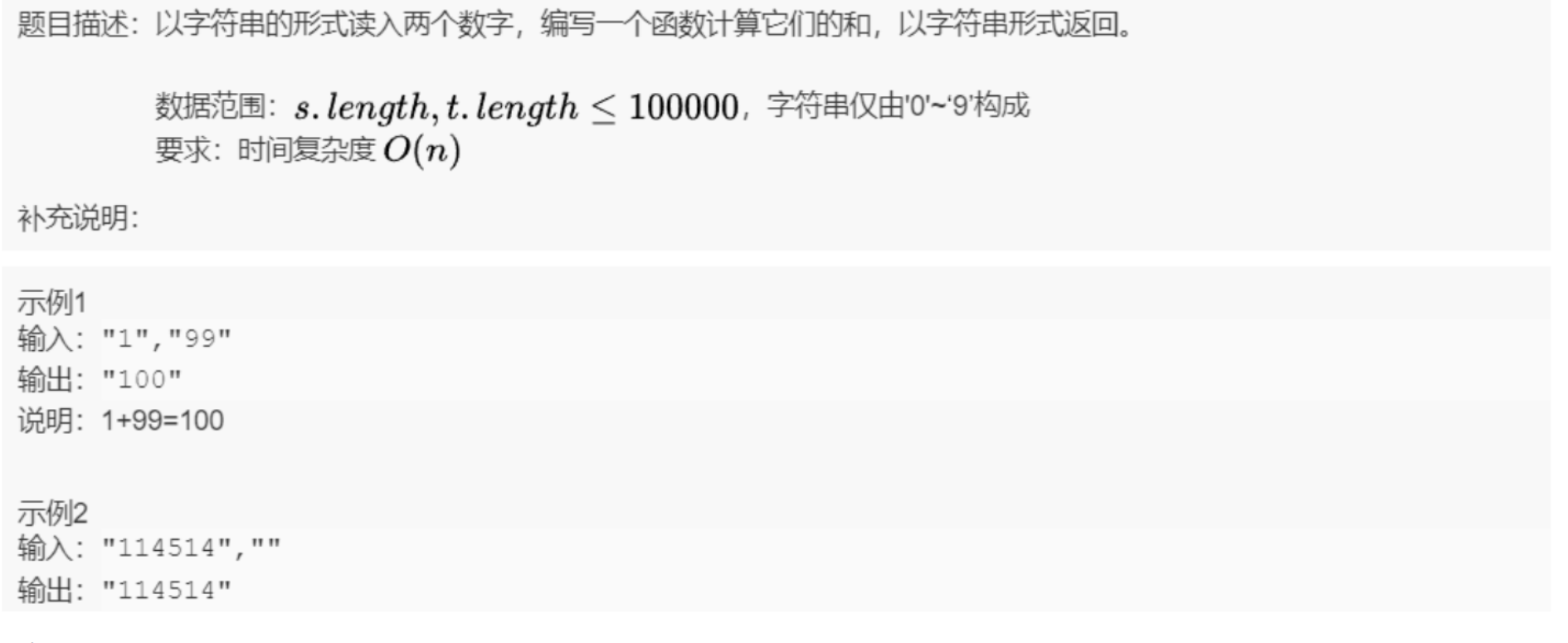
代码如下:
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** 计算两个数之和* @param s string字符串 表示第一个整数* @param t string字符串 表示第二个整数* @return string字符串*/string solve(string s, string t) {// write code herestring ret;int tmp=0;int i=s.size()-1,j=t.size()-1;while(i>=0||j>=0||tmp){if(i>=0)tmp+=s[i--]-'0';if(j>=0)tmp+=t[j--]-'0';ret+='0'+tmp%10;tmp/=10;}reverse(ret.begin(),ret.end());return ret;}
};
不可以。
一、原因分析
在你的代码中,temp变量的作用是存储进位值,它的取值可能是:
- •
0:没有进位 - •
1:有进位(因为最大是 9+9=18,进位最大为1) - •
2、3…9:在多位数连续进位时可能出现,但通常为0或1
循环条件 while(i >= 0 || j >= 0 || temp)的含义是:
- •
i >= 0:s字符串还有数字未处理 - •
j >= 0:t字符串还有数字未处理 - •
temp:还有进位需要处理(等价于temp != 0)
二、如果改成 temp >= 0会怎样?
while(i >= 0 || j >= 0 || temp >= 0) // 错误写法!
问题:temp >= 0在进位处理过程中永远为真,因为:
- •
temp的值来自temp /= 10(整数除法) - •在加法中,
temp始终是非负整数(0, 1, 2, …) - •所以
temp >= 0永远成立
后果:即使字符串都处理完了(i < 0 && j < 0),只要 temp >= 0成立,循环就会无限进行!
三、正确的逻辑验证
当前正确的代码:
while(i >= 0 || j >= 0 || temp) // temp 等价于 temp != 0
{// 处理当前位相加if(i >= 0) temp += s[i--] - '0';if(j >= 0) temp += t[j--] - '0';ret += '0' + temp % 10; // 当前位结果temp /= 10; // 计算进位
}
正常结束条件:
- 1.
i < 0:s字符串处理完 - 2.
j < 0:t字符串处理完 - 3.
temp == 0:进位也处理完
只有这三个条件同时满足,循环才会退出。
四、举例说明
计算 "999" + "1":
初始:i=2, j=0, temp=0
第1轮:个位 9+1=10 → 当前位0,进位1
第2轮:十位 9+0+1=10 → 当前位0,进位1
第3轮:百位 9+0+1=10 → 当前位0,进位1
第4轮:只有进位1 → 当前位1,进位0 ← 这里temp变成0,循环退出
如果写成 temp >= 0,第4轮后 temp=0仍然满足 0 >= 0,循环会继续,产生错误结果。
总结
| 条件 | 含义 | 是否正确 |
|---|---|---|
temp | 还有进位需要处理(temp ≠ 0) | ✅ 正确 |
temp >= 0 | temp是非负数 | ❌ 错误(会导致无限循环) |
temp != 0 | 明确判断是否有进位 | ✅ 等价于原代码 |
所以:保持原代码的 while(i >= 0 || j >= 0 || temp)是正确的,不能改为 temp >= 0。
大数乘法

代码如下:
include <iterator>
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param s string字符串 第一个整数* @param t string字符串 第二个整数* @return string字符串*/string solve(string s, string t) {// write code herereverse(s.begin(),s.end());reverse(t.begin(),t.end());int m=s.size(),n=t.size();vector <int> tmp(m+n);for(int i=0;i<m;i++){for(int j=0;j<n;j++){tmp[i+j]+=(s[i]-'0')*(t[j]-'0');}}int c=0;string ret;for(auto x:tmp){c+=x;ret+='0'+c%10;c/=10;}while(c){ret+='0'+c%10;c/=10;} while(ret.size()>1&&ret.back()=='0') ret.pop_back();reverse(ret.begin(),ret.end());return ret;}
};
好的,这两段代码是处理进位的核心部分,也是这个算法最精妙的地方。我来用最详细的方式拆解它。
第一部分:遍历 tmp数组处理进位
string ret; // 存储最终结果(逆序的)
for(auto x : tmp) // 遍历tmp数组的每一个元素
{c += x; // 步骤1:当前位值 + 上一位的进位ret += '0' + c % 10; // 步骤2:取个位数作为当前位结果c /= 10; // 步骤3:计算新的进位
}
这个循环在做什么?
想象一下手工竖式计算时,我们是从低位到高位逐位计算,同时处理进位。
变量 c的双重作用:
- •既是当前位的累加和(包含当前位值 + 上一位的进位)
- •又是进位存储器
详细步骤分解(用具体例子)
假设经过无进位相乘后,tmp数组是:[15, 22, 13, 4](对应个位、十位、百位、千位)
初始状态:c = 0, ret = ""
第1轮循环(处理个位:tmp[0] = 15)
c += x; // c = 0 + 15 = 15
ret += '0' + c % 10; // 15 % 10 = 5 → ret = "5"
c /= 10; // 15 / 10 = 1(进位1)
结果:个位结果是5,进位1到十位
第2轮循环(处理十位:tmp[1] = 22)
c += x; // c = 1 + 22 = 23(进位1 + 十位值22)
ret += '0' + c % 10; // 23 % 10 = 3 → ret = "53"
c /= 10; // 23 / 10 = 2(进位2到百位)
结果:十位结果是3,进位2到百位
第3轮循环(处理百位:tmp[2] = 13)
c += x; // c = 2 + 13 = 15(进位2 + 百位值13)
ret += '0' + c % 10; // 15 % 10 = 5 → ret = "535"
c /= 10; // 15 / 10 = 1(进位1到千位)
第4轮循环(处理千位:tmp[3] = 4)
c += x; // c = 1 + 4 = 5
ret += '0' + c % 10; // 5 % 10 = 5 → ret = "5355"
c /= 10; // 5 / 10 = 0(无进位)
此时:ret = "5355"(这是逆序的结果),c = 0
第二部分:处理最后的进位
while(c)
{ret += '0' + c % 10; // 将剩余进位转为数字字符c /= 10;
}
什么时候需要这个循环?
当最高位计算后还有进位时。比如计算 999 × 999,最高位会产生进位。
例子:假设最后 c = 3(还有进位3)
第1次循环:ret += '0' + 3 % 10 → ret += '3', c = 3/10 = 0
循环结束
这样就把最后的进位也添加到结果中了。
可视化整个进位处理过程
tmp数组: [15, 22, 13, 4] ← 个位、十位、百位、千位处理过程:
个位: 15 → 当前位5, 进位1
十位: 22 + 1 = 23 → 当前位3, 进位2
百位: 13 + 2 = 15 → 当前位5, 进位1
千位: 4 + 1 = 5 → 当前位5, 进位0结果: "5355"(逆序)
最终逆序: "5535"
总结
| 代码 | 作用 | 数学意义 |
|---|---|---|
c += x | 累加当前位值和进位 | 当前位总和 |
c % 10 | 取个位作为当前位结果 | 当前位数字 |
c /= 10 | 计算新的进位 | 进位值 |
while(c) | 处理最后的进位 | 最高位进位 |
精妙之处:用一个变量 c同时完成了累加和进位存储两个功能,代码非常简洁!
| 作用 | 数学意义 |
| ---------- | -------------------- | ---------- |
| c += x | 累加当前位值和进位 | 当前位总和 |
| c % 10 | 取个位作为当前位结果 | 当前位数字 |
| c /= 10 | 计算新的进位 | 进位值 |
| while(c) | 处理最后的进位 | 最高位进位 |
精妙之处:用一个变量 c同时完成了累加和进位存储两个功能,代码非常简洁!
现在明白这两段进位处理的代码了吗?
