浅谈差分算法--区间变化的上佳策略(C++实现，结合lc经典习题讲解)

        我们开门见山，先抛出一个问题：

        假设你有一个数组，范围0~7，初始化为0，现在要求你进行以下操作：

        (1)在1~4范围上+5；

        (2)在2~6范围上-2；

        一开始我们的思路可能是通过for循环暴力在范围上进行修改，可是如果这样，假设左右区间分别为l,r，每次操作的时间复杂度是O(r-l+1)的线性水平，假设我们有m次操作，那么时间复杂度便是O(n*m)，数据量大了这是不可接受的。而接下来我们要引出的差分算法，可以把这种区间变化操作的时间复杂度降低到常数水平O(1)。这是一种“延迟修改，然后一次性生效”的方式，无需遍历整个区间。

        在介绍差分算法之前，相信朋友们应该对前缀和这个概念并不陌生。这是一种快速求区间累加和的方法，我们建立一个前缀和数组prefix[i]=nums[0]+nums[1]+.....+nums[i]，那么nums[x]=prefix[x]-prefix[x-1]。前缀和是从原数组得到“累积变化”，而差分正好是反过来：
从“变化量”出发，还原原数组。也就是说，可以将差分理解为前缀和的逆运算。因此，我们可以定义差分数组diff：

diff[i]=nums[i]-nums[i-1] i>0;

diff[0]=nums[0]

        实际上，我们只要得到差分数组，就能通过前缀和还原原数组，有点“裂项相消”的感觉：

nums[i]=diff[0]+diff[1]+......+diff[i]

        而差分数组真正的厉害之处在于，假设我们需要对原数组[l,r]区间上进行+v的操作，并不需要取遍历原数组，只需要修改差分数组中的两个位置即可，我觉得核心思想可以用“制造/消除影响”来理解：

diff[l]+=v (从l处开始制造影响)

diff[r+1]-=v (在r+1处消除影响)

        之后在我们通过前缀和还原原数组时，[l,r]区间上都会+v，而其他位置保持不变，整个区间加法就成了时间复杂度只有O(1)的操作！实际上差分记录的不是结果，而是变化。差分是一种“从变化的角度看问题”的思维方式。我们再回过头来看文章开头提出的问题：

        ①首先原数组被初始化为0，那么此时差分数组也全部为0，我们需要在[1,4]范围上+5，此时diff[1]被更新为5，diff[5]被更新为-5，此时差分数组为[0,5,0,0,0,-5,0,0]，根据前缀和还原，原数组被更新为[0,5,5,5,5,0,0,0]。

        ②原数组被更新之后，差分数组随之改变：[0,5,0,0,0,-5,0,0]，我们需要在[2,6]范围上-2，此时diff[2]被更新为-2，diff[7]被更新为2，此时差分数组为[0,5,-2,0,0,-5,0,2]，根据前缀和还原，原数组被更新为[0,5,3,3,3,-2,-2,0]。

一.一维差分

leetcode 1109 航班预订统计

        这道题目其实是一维差分的模板题了，我们大可以把每个航班预定的座位总数视为“原数组”。题设给出的三元组book[i]=[first,last,seats]的含义实际就是原数组在[first,last]区间上加seats即可，思路上确实非常简单。这里给大家分享一个小技巧，就是在建立差分数组时可以在首尾各多补一个0，能够避免一些麻烦的边界讨论问题。我们可以通过下面这段代码大致掌握一维差分问题的大致代码写法：

class Solution {
public:vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {vector<int> diff(n+2);//设置差分数组for(vector<int>&book:bookings){diff[book[0]]+=book[2];diff[book[1]+1]-=book[2];}//加工前缀和for(int i=1;i<cnt.size();i++){diff[i]+=diff[i-1];}vector<int> ans(n);for(int i=0;i<n;i++){ans[i]=diff[i+1];}return ans;}
};

leetcode 1094 拼车

        这道题给出了一个三元组trips[i]=[passengerNums,Start,End]，代表着第i次旅程，有passengerNums个旅客，我们将其从Start处接到，放在End位置，很明显，我们可以把整条路线看成一条“位置线”，把每个旅程都视为子区间，上乘客的过程实际上就是区间的加法操作，于是我们很自然的想到用差分来解决这个问题。实际上这道题的关键判断标准就是车会不会坐满，最后通过前缀和恢复每个位置的乘客人数，只要在任何时刻人数超过 Capacity，就返回 false。示例代码如下：

class Solution {
public:bool carPooling(vector<vector<int>>& trips, int capacity) {vector<int> diff(1001,0);for(vector<int>& trip:trips){diff[trip[1]]+=trip[0];diff[trip[2]]-=trip[0];}int cur=0;for(int i=0;i<diff.size();i++){cur+=diff[i];if(cur>capacity){return false;}}return true;}
};

leetcode 2381 字母移位II

        相信朋友们通过前两道题的练习，通过题目给出的三元组，能够明显地看到这是一道和区间变化相关的题目，那么很自然的联想到用差分来解决这个问题显然不难。但是这道题它不是简单的差分，而是有一点点小小的控制逻辑，即题目中所给出的“前移，后移”操作。不过我们大可把前移视为+1，把后移视为-1；这样主题逻辑实际上和我们前面介绍的其他题目没有什么区别。我们最后再对 diff 做前缀和得到 sum[i]，表示第 i 个字母最终被平移的总次数，这样这种区间变化就一步到位了。在实际写代码的过程中有个关键点就是C++%负数的时候会保留符号，所以我们要先加一个MOD避免产生负数。示例代码如下：

class Solution {const int MOD=26;
public:string shiftingLetters(string s, vector<vector<int>>& shifts) {vector<int> diff(s.size()+2,0);for(vector<int>& shift:shifts){int delta=(shift[2]==1?1:-1);diff[shift[0]]+=delta;diff[shift[1]+1]-=delta;}string ans(s);int sum=0;for(int i=0;i<ans.size();i++){sum += diff[i];int shift = ((ans[i] - 'a') + (sum % MOD) + MOD) % MOD;ans[i] = 'a' + shift;}return ans;}
};

二.二维差分

        通过前文的介绍与题目的练习，相信朋友们已经对差分的思想和方法论有了自己的一些认识。实际上这种区间变化问题不仅存在于一维空间，也存在于更高维度中。我们就来看看在矩阵中如何利用差分的思想解决区间变化问题。和一维一样，二维差分是二维前缀和的逆运算，所以在我们学习二维差分之前，掌握二维前缀和的计算方法是至关重要的。假设我们现在有以下矩阵a[x][y]：

2  -3   5

1   4   7

9   6  -1

        首先在前面题目介绍中，我曾经说过一个点：可以在数组的首尾各补一个0，这样能省去很多的边界讨论。在二维矩阵中也一样，我们在矩阵的0行0列都补上0，之后我们可以构建出前缀和矩阵sum[x][y]，表示从(1,1)到(x,y)这个子矩阵内所有元素的总和，对于上面的矩阵来说前缀和矩阵如下图所示：

2  -1  4

3   4  16

12 19 30

        我们不难总结出二维前缀和的公式，因为左上部分实际上存在重合，所以我们需要减去一次，这实际上就是容斥原理的一种应用，实际上二维前缀和，二维差分的理论核心就是在做容斥原理运算，直观解释就是上方+左方-左上+当前(原矩阵)：

sum[x][y]=a[x][y]+sum[x-1][y]+sum[x][y-1]-sum[x-1][y-1]

        由此我们便通过牺牲一定的空间，把求局部累加和操作的时间复杂度降到O(1)级别。和我们前面介绍的一维差分的问题一样，假设我们有一个矩阵a[x][y]，我们希望让矩阵在(x1,y1)~(x2,y2)范围上都加上v。如果我们采用暴力更新的策略，那么时间复杂度是O((x2-x1+1)*(y2-y1+1))，如果数据量很大这个开销是很难容忍的。从二维前缀和的定义中我们知道，a[i][j] 这个单元格的值，对它右下方所有区域都有影响。我们不如反过来思考，如果希望让矩阵在(x1,y1)~(x2,y2)范围上都加上v，那我只要让二维前缀和的这个区域受到影响。

        与一维差分“制造/消除影响”的大体理念相同，我们在(x1,y1)处先+v，从这里开始制造影响；然后分别在(x2+1,y1)(右边界)和(x1,y2+1)(下边界)处消除影响；最后我们需要把多减的一角(x2+1,y2+1)补回来，即在此处+v。这四个点的加减操作，就是二维差分的本质。我们定义一个差分矩阵diff，于是：

diff[x1][y1]       += v;   // 开始制造影响
diff[x2 + 1][y1]   -= v;   // 在下边界消除
diff[x1][y2 + 1]   -= v;   // 在右边界消除
diff[x2 + 1][y2 + 1] += v; // 左下角被多减一回，要补回来

        最后还原时再对差分矩阵做二维前缀和D[i][j]=diff[i][j]+a[i−1][j]+a[i][j−1]−a[i−1][j−1]得到增量矩阵D，将增量矩阵D与原矩阵相加，就顺利实现了区间的变化操作。这就是二维差分的思路核心。如果朋友们没理解，没关系，可以参考下面示例的变化过程：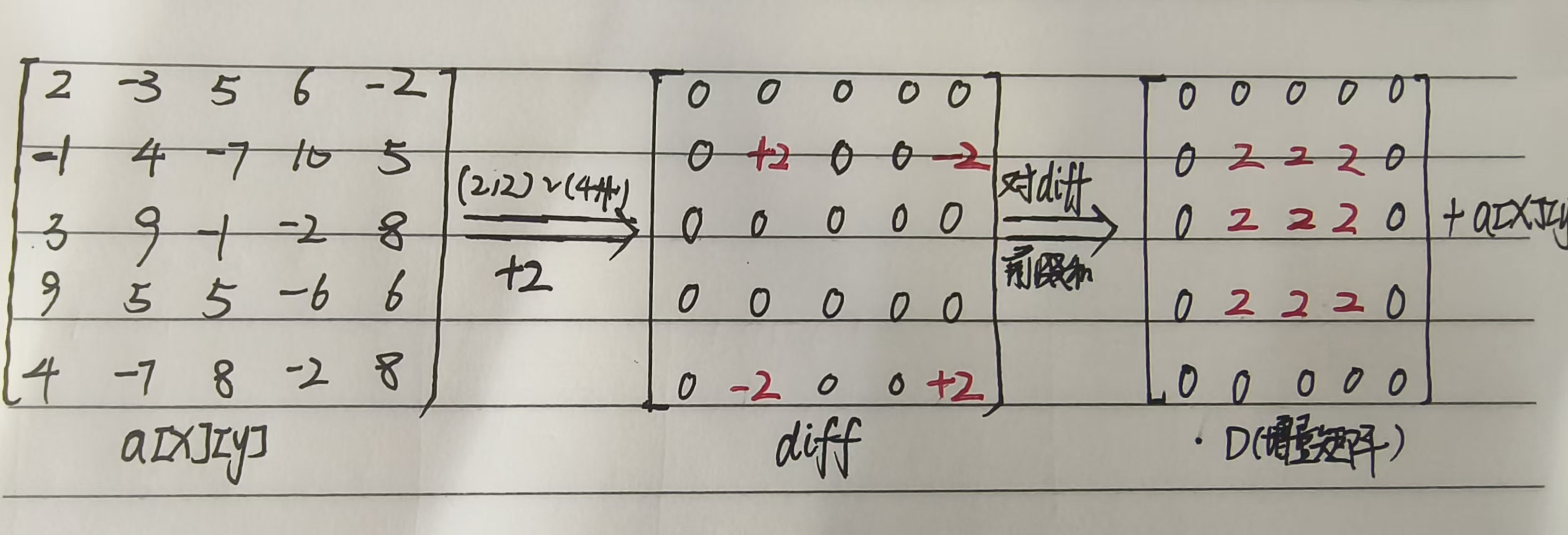

leetcode 2536 子矩阵元素加1

        这道题可以说是二维差分类问题的模板题了。思路上确实没有什么可说的点了，就是简单的在矩阵给定区间范围上进行简单的+1，唯一就是需要注意一下在coding方面的细节，尤其是边界处理我的做法，在下面的code中都有注释供大家参考：

class Solution {
public:void build(vector<vector<int>>& m) {int n = m.size(), c = m[0].size();for (int i = 1; i < n; i++) {       // 注意 i, j 从 1 开始，防止越界for (int j = 1; j < c; j++) {m[i][j] += m[i-1][j] + m[i][j-1] - m[i-1][j-1];}}}// 二维差分更新函数void add(vector<vector<int>>& diff, int a, int b, int c, int d) {diff[a][b] += 1;diff[c + 1][b] -= 1;diff[a][d + 1] -= 1;diff[c + 1][d + 1] += 1;}vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {vector<vector<int>> diff(n + 2, vector<int>(n + 2, 0));// 每个查询执行一次差分更新for (auto& q : queries) {int x1 = q[0] + 1, y1 = q[1] + 1;  int x2 = q[2] + 1, y2 = q[3] + 1;add(diff, x1, y1, x2, y2);}// 对整个矩阵构建前缀和，还原出结果矩阵build(diff);// 输出时去掉外层扩充部分vector<vector<int>> ans(n, vector<int>(n));for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {ans[i-1][j-1] = diff[i][j];}}return ans;}
};

leetcode 2132 用邮票贴满网格图

        这道题可谓是二维差分类问题中的经典了，属于必做的题目，也有一定的难度。我们来结合leetcode官方给出的示例来理解题意：

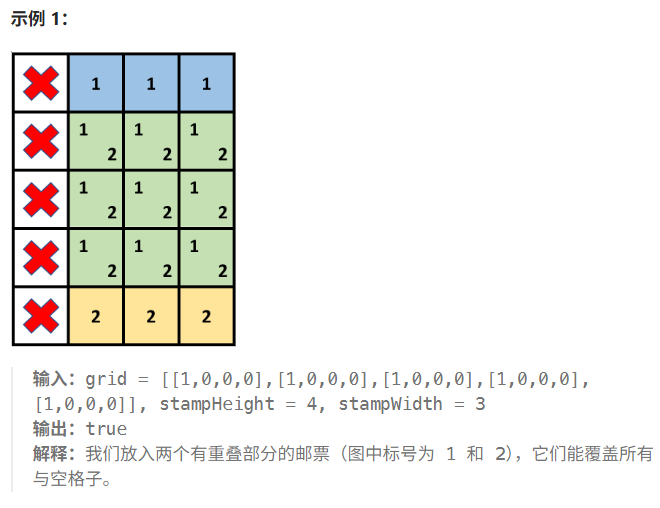
        首先贴邮票这事儿有这么几个规矩：只能贴0不能贴1，且需要把所有0贴满；邮票不能旋转且必须在矩阵内，允许邮票相互重叠，不限定邮票个数。实际上这张“邮票”就限定了一个矩形区域，可能敏感的同学就会反应出来可能是个二维空间上的区间变化问题。对于一个矩形区域，我们首先需要判断是否可以贴邮票，也就是说这个子矩阵范围内是否存在1。我们可以求这个子矩阵的二维前缀和，只要这个前缀和不为0，那么说明这个范围上一定存在1，不能简单粗暴的把邮票贴在这里，这个前缀和操作实际上是非常常见的“区域障碍查询”技巧，值得我们学习。我们不修改原矩阵，如果某个子矩阵上可以贴邮票，我们就在差分矩阵上进行+1的操作。之后利用二维前缀和还原出增量矩阵，与原矩阵进行加和即可还原出“真实的覆盖次数”。最终我们只需遍历矩阵观察是否存在0即可判断出邮票是否贴满，示例代码如下：

class Solution {
public:void build(vector<vector<int>>&m){for(int i=1;i<m.size();i++){for(int j=1;j<m[0].size();j++){m[i][j]+=m[i-1][j]+m[i][j-1]-m[i-1][j-1];}}}void add(vector<vector<int>>& diff,int a,int b,int c,int d){diff[a][b]+=1;diff[c+1][d+1]+=1;diff[c+1][b]-=1;diff[a][d+1]-=1;}int sumRegion(vector<vector<int>>& sum,int a,int b,int c,int d){return sum[c][d]-sum[c][b-1]-sum[a-1][d]+sum[a-1][b-1];}bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {int n=grid.size();int m=grid[0].size();//前缀和数组，查询原始矩阵中某个范围的累加和很快vector<vector<int>> sum(n+1,vector<int>(m+1));for(int i=0;i<n;i++){for(int j=0;j<m;j++){sum[i+1][j+1]=grid[i][j];}}build(sum);//差分数组//当贴邮票的时候，不在原始矩阵里贴，在差分矩阵里贴//原始矩阵里只用来判断能不能贴邮票，不进行修改//每帖一张邮票都在差分矩阵里修改vector<vector<int>> diff(n+2,vector<int>(m+2));for(int a=1,c=a+stampHeight-1;c<=n;a++,c++){for(int b=1,d=b+stampWidth-1;d<=m;b++,d++){//原始矩阵中（a,b）左上角点//根据邮票规格算出右下角点（c,d）//这个区域彻底都是0，那么这个区域可以贴邮票if(sumRegion(sum,a,b,c,d)==0){add(diff,a,b,c,d);}}}build(diff);for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]==0&&diff[i+1][j+1]==0){return false;}}}return true;}
};

leetcode LCP74 最强祝福力场

        如果让我给这道题目给一个标签的话，那毫无疑问绝对是Hard水准。而且这也是一道非常有代表性的题目，具有学习意义。我们来结合leetcode官方给出的示例来理解题意：

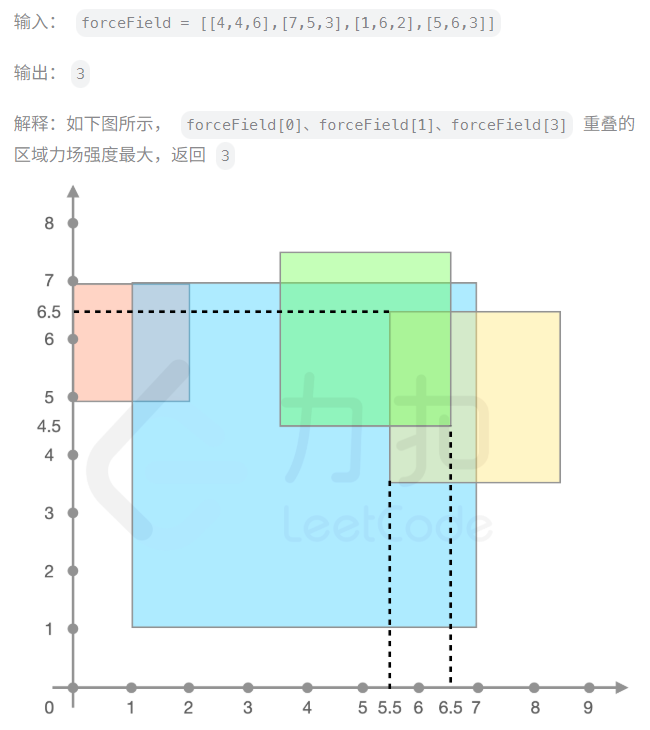
        从特征上来看，这道题目的思路还是非常明确的，就是在区间上叠加变化，很明显可能会采用差分的方法不断更新原数组进行叠加。但是有一些比较值得我们注意和探讨的特殊情况。首先是上面题设中就给出来的一种情况，假设最小划分单位不是整数，而是x.5这样的小数怎么办？我们可以将所有坐标×2，这样坐标之间的相对位置不变，可以使用左移运算<<来实现(常用技巧，位运算运行时间比乘法更快)；其次我们考虑一种极其特殊的情况，假设力场的范围延伸得特别远，比如说几万的量级，难道我们的差分矩阵就要开到几万的数值吗？显然这样的空间开销是难以接受的。实际上每个力场的场强只会在交界区域发生变化，同一个力场中的场强是相同且连续的。实际上，我们最终求的是最大的力场强度，而不是最大力场强度的精确位置。这样我们便引出一种技巧--离散化！

       我们甭管一个力场有多宽，就算它有八万那么宽，只要某个区域内场强没有发生叠加，那八万的效果和1没有区别。关键就在于每个力场的边界，换句话说，只有在力场的边界处，能量值才会发生变化，进入力场会使能量值+1，而离开力场会使能量值-1。我们就在[x+r，x-r]，[y+r，y-r]的区域中更新差分矩阵即可。根据前面的讨论我们已经明确显然我们不能直接开一个二维数组到坐标 10⁹ 或浮点值，实际上我们只需要关心这些边界坐标本身，中间的连续区间不需要展开。也就是说我们只取所有这些关键边界点，排序去重后，把它们“压缩”成连续的整数下标。这种做法既保证了坐标之间的相对顺序，也能极大的节省空间。最后我们只需按照老套路，用二维前缀和进行还原，并记录全局最大场强值，就能求得结果。示例代码如下：

class Solution {
public:// 排序并去重，返回有效长度int Sort(vector<long>& nums) {sort(nums.begin(), nums.end()); // 使用 std::sortint size = 1;for (int i = 1; i < nums.size(); i++) {if (nums[i] != nums[size - 1]) {nums[size++] = nums[i];}}return size;}// 二分查找，返回 v 在有序数组 nums 中的排名（从 1 开始）int rank(vector<long>& nums, long v, int size) {int l = 0, r = size - 1;while (l <= r) {int m = (l + r) / 2;if (nums[m] >= v) {r = m - 1;} else {l = m + 1;}}return l + 1; // 排名从 1 开始}// 二维差分void add(vector<vector<int>>& diff, int a, int b, int c, int d) {diff[a][b] += 1;if (c + 1 < diff.size() && d + 1 < diff[0].size()) diff[c + 1][d + 1] += 1;if (c + 1 < diff.size()) diff[c + 1][b] -= 1;if (d + 1 < diff[0].size()) diff[a][d + 1] -= 1;}int fieldOfGreatestBlessing(vector<vector<int>>& forceField) {int n = forceField.size();// 收集所有 x 和 yvector<long> xs(n << 1);vector<long> ys(n << 1);for (int i = 0, k = 0, p = 0; i < n; i++) {long x = forceField[i][0];long y = forceField[i][1]; long r = forceField[i][2];// 离散化出四个边界xs[k++] = (x << 1) - r; // 左边界xs[k++] = (x << 1) + r; // 右边界ys[p++] = (y << 1) - r; // 下边界ys[p++] = (y << 1) + r; // 上边界}// 排序并去重int sizex = Sort(xs);int sizey = Sort(ys);// 初始化差分数组vector<vector<int>> diff(sizex + 2, vector<int>(sizey + 2, 0));// 遍历每个力场，更新差分数组for (int i = 0; i < n; i++) {long x = forceField[i][0];long y = forceField[i][1];long r = forceField[i][2];int a = rank(xs, (x << 1) - r, sizex);int b = rank(ys, (y << 1) - r, sizey);int c = rank(xs, (x << 1) + r, sizex);int d = rank(ys, (y << 1) + r, sizey);add(diff, a, b, c, d);}// 计算前缀和，找到最大值int ans = 0;for (int i = 1; i < diff.size(); i++) {for (int j = 1; j < diff[0].size(); j++) {diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];ans = max(ans, diff[i][j]);}}return ans;}
};

        通过上面的介绍和题目讲解，相信朋友们能够感受到：差分的核心思想，不在于“加快计算”，而在于抓住变化。它告诉我们：一个区间或一个区域的状态，其实只在“边界”处发生改变，其他地方是平稳的。于是，我们不再对每个点重复操作，而是在起点“制造影响”、在终点“消除影响”，最后通过一次累积（前缀和）把所有变化还原出来。在一维中，差分让区间修改从 O(n)O(n)O(n) 降为 O(1)O(1)O(1)；在二维中，它让矩形区域的批量更新变得轻而易举。当坐标从整数变为浮点或稀疏时，我们进一步引入离散化——不再关注整个连续空间，而是仅关注变化发生的有限边界点。
这样，复杂的连续问题被转化为有限的整数网格问题。差分类的问题也给我们带来了一些启示：不要盯着数据的“静态状态”，而要关注数据的“变化过程”。一旦你能识别“变化在哪里发生”，复杂的问题就会变得简单而优雅。有不当之处还请多多批评指正，我们一起成长！