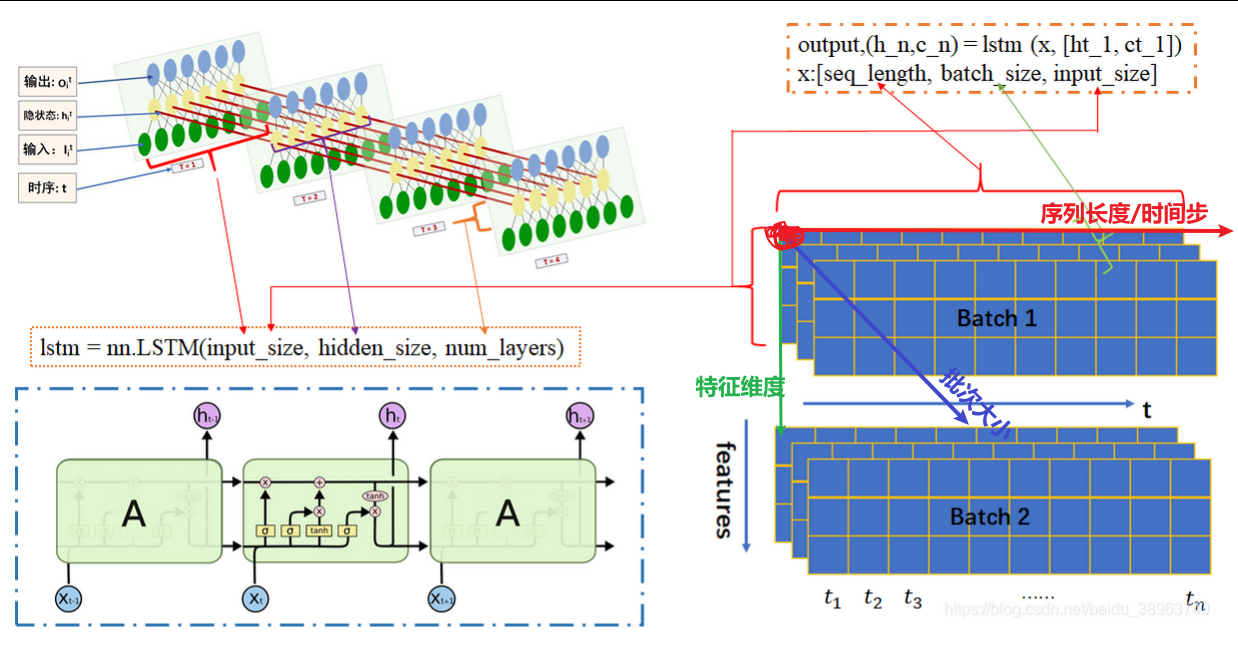
LSTM核心参数与输入输出解读

快速一览表

# 前向传播
output, (hn, cn) = lstm(input, (h0, c0))

我先用一个表格来总结LSTM的核心参数和不同结构下的输出形状：

组件/结构	参数/输出	说明	单层单向示例	多层单向示例	单层双向示例	多层双向示例
核心参数	input_size	输入特征维度	-	-	-	-
	hidden_size	隐藏层特征维度	-	-	-	-
	num_layers	LSTM层数	-	-	-	-
	bidirectional	是否为双向	-	-	-	-
输出 output	形状	（序列长度, 批次大小, 隐藏维度×方向数） （当batch_first=True时批次大小和序列长度位置互换）	(5, 3, 20) （序列5，批次3，隐藏20）	(5, 3, 20) （序列5，批次3，隐藏20）	(5, 3, 40) （序列5，批次3，隐藏40=20x2）	(5, 3, 40) （序列5，批次3，隐藏40=20x2）
	含义	最后一层，所有时间步的隐藏状态	最后一层所有时间步输出	最后一层所有时间步输出	最后一层所有时间步输出，含双向信息	最后一层所有时间步输出，含双向信息
隐藏状态 hn	形状	（层数×方向数, 批次大小, 隐藏维度）	(1, 3, 20) （1层，批次3，隐藏20）	(2, 3, 20) （2层，批次3，隐藏20）	(2, 3, 20) （2方向，批次3，隐藏20）	(4, 3, 20) （4=2层x2方向，批次3，隐藏20）
	含义	所有层的最后一个时间步的隐藏状态	唯一层最后时间步隐藏状态	所有层（此处2层）最后时间步隐藏状态	两个方向最后时间步隐藏状态	所有层及方向最后时间步隐藏状态
细胞状态 cn	形状	（层数×方向数, 批次大小, 隐藏维度）	同hn	同hn	同hn	同hn
	含义	所有层的最后一个时间步的细胞状态（长期记忆）	唯一层最后时间步细胞状态	所有层最后时间步细胞状态	两个方向最后时间步细胞状态	所有层及方向最后时间步细胞状态

下图是我手动推导关于LSTM前向传播的一个图：

LSTM核心参数与输入输出解读

lstm核心参数

在PyTorch中，我们使用torch.nn.LSTM来创建LSTM层，它的核心参数包括：

• input_size：输入数据在每个时间步的特征维度。

• hidden_size：隐藏状态h的特征维度，决定了LSTM的输出能力。

• num_layers：LSTM的层数。层数大于1时，多个LSTM层将堆叠，前一层的输出作为下一层的输入（深层循环神经网络）。

• batch_first：当设置为True时，输入和输出张量的形状为(批次大小, 序列长度, 特征维度)，这更符合常见的习惯。默认为False，即(序列长度, 批次大小, 特征维度)。

• bidirectional：是否使用双向LSTM。双向LSTM会沿着序列的两个方向（正向和反向）分别处理序列，然后将每个时间步两个方向的隐藏状态进行合并（通常是拼接），从而捕获序列的前向和后向信息

输入：(input,(h0,c0))

LSTM的输入主要包括：

• input：序列数据本身。其形状为(序列长度, 批次大小, 输入特征维度)，如果设置了batch_first=True，则为(批次大小, 序列长度, 输入特征维度)

• h0：初始隐藏状态。形状为(层数 * 方向数, 批次大小, 隐藏层维度)。对于单向LSTM，方向数为1；对于双向LSTM，方向数为2。如未提供，默认为零。

• c0：初始细胞状态。形状与h0相同。如未提供，默认为零。

输出：(output(hn,cn))

LSTM的输出包括：

• output：包含最后一层LSTM每个时间步的隐藏状态。其形状为(序列长度, 批次大小, 隐藏层维度 * 方向数)（若batch_first=True则批次大小在前）。对于双向LSTM，每个时间步的输出是正向和反向隐藏状态的拼接，因此特征维度是hidden_size * 2。

• hn：所有层（对于双向LSTM，包含所有方向）在最后一个有效时间步的隐藏状态。形状为(层数 * 方向数, 批次大小, 隐藏层维度)。

• cn：所有层（对于双向LSTM，包含所有方向）在最后一个有效时间步的细胞状态。形状与hn相同。

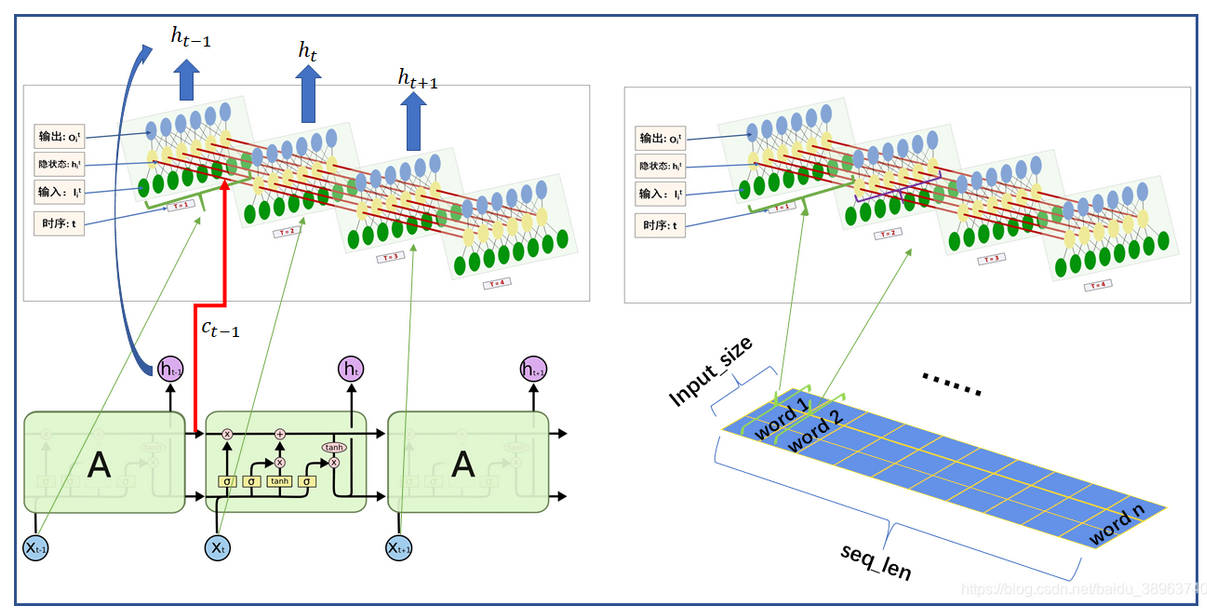
理解output和hn之间的关系很重要：

• 在单向LSTM中，output的最后一个时间步（output[-1]）与hn的最后一层（hn[-1]）是相同的。output包含所有时间步的隐藏状态，而hn是所有层的最后一个时间步的隐藏状态。

• 在双向LSTM中，output的每个时间步都包含了正向和反向的隐藏状态。output的第一个时间步对应反向LSTM的最后一个时间步的隐藏状态（即hn的对应位置），而output的最后一个时间步对应正向LSTM的最后一个时间步的隐藏状态（即hn的对应位置）。

关于output和hn的使用场景：

• 如果你需要每个时间步的输出（例如序列标注任务，如词性标注，每个词都需要输出），那么你应该使用output。

• 如果你只需要整个序列的最终汇总信息（例如序列分类任务，如文本情感分析，整个句子只需要一个分类结果），那么使用hn（通常是最后一层或特定层的最后隐藏状态）是常见且高效的做法。对于双向LSTM，通常会将hn的最后两个隐藏状态（代表正向和反向的最终状态）进行拼接或聚合，以得到整个序列的完整表示。

不同LSTM结构示例

一、处理等长的序列

1.单层单向LSTM

(1)batch_first默认为False

import torch
import torch.nn as nn# 定义参数
input_size = 3   # 每个时间步输入特征维度为3
seq_len = 150       # 序列长度为150
batch_size = 16    # 批次大小为16
hidden_size = 64  # 隐藏层特征维度为64
num_layers = 1    # 一层LSTM
num_directions = 1 # 单向，方向数为1# 创建单层单向LSTM
lstm = nn.LSTM(input_size, hidden_size, num_layers)# 准备输入数据 input(序列长度, 批次大小, 输入特征维度)
input = torch.randn(seq_len, batch_size, input_size)  # (150,16,3)
# 初始化隐藏状态和细胞状态  h0,c0(层数×方向数, 批次大小, 隐藏维度)
h0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)  # (1*1,16,64)
c0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)# 前向传播 output(序列长度, 批次大小, 隐藏维度×方向数)
output, (hn, cn) = lstm(input, (h0, c0))print(f"单层单向LSTM:")
print(f"output shape: {output.shape}") # (150, 16, 64)
print(f"hn shape: {hn.shape}")         # (1, 16, 64)
print(f"cn shape: {cn.shape}")         # (1, 16, 64)
# 验证 output[-1] == hn[-1]
print(torch.allclose(output[-1], hn[-1])) # 应为 True

(2)batch_first设置为True

如果再将batch_first=True, 则

输入input为 (batch_size, seq_len, input_size),

输出output为 (batch_size, seq_len, hidden_dim*num_directions)

# 创建单层单向LSTM (batch_first=True)
lstm = nn.LSTM(input_size, hidden_size, num_layers,batch_first=True)  # 将batch之前，更加符合直观习惯# 准备输入数据 input(批次大小, 序列长度, 输入特征维度)
input = torch.randn(batch_size, seq_len, input_size)  # (16,150,3)
# 初始化隐藏状态和细胞状态 h0,c0(层数×方向数, 批次大小, 隐藏维度)
h0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)  # (1*1,16,64)
c0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)# 前向传播  output(批次大小, 序列长度, 隐藏维度×方向数)
output, (hn, cn) = lstm(input, (h0, c0))print(f"单层单向LSTM:")
print(f"output shape: {output.shape}") # (16, 150, 64)
print(f"hn shape: {hn.shape}")         # (1, 16, 64)
print(f"cn shape: {cn.shape}")         # (1, 16, 64)# 验证 output 的最后一个时间步与 hn 的最后一层相同
print(torch.allclose(output[:, -1, :], hn[-1])) # 应为 True

 总结：【前提：batch_first=True】

output,(hn,cn) = lstm(input,(h0,c0))

    由于

    output(序列长度, 批次大小, 隐藏维度×方向数)：返回最后一层，所有时间步的隐藏状态

    hn(层数×方向数, 批次大小, 隐藏维度)：返回所有层的最后一个时间步的隐藏状态

所以在单层单向LSTM中，输出的最后一个时间步与隐藏状态的最后一层相同，最终取的都是最后一层+最后一个时间步的隐藏状态。即：

    output[:,-1,:] = hn[-1,:,:] = hn[0]

    1.batch_first只会影响input、output的维度,而不会影响h0、c0、hn、cn这些隐藏状态和细胞状态的维度。

2.两层单向LSTM

多层LSTM通过堆叠多个LSTM层来提取更深层的序列特征，上一层的输出作为下一层的输入。

(1)batch_first默认为False

import torch
import torch.nn as nn# 定义参数
input_size = 3   # 每个时间步输入特征维度为3
seq_len = 150       # 序列长度为150
batch_size = 16    # 批次大小为16
hidden_size = 64  # 隐藏层特征维度为64
num_layers = 2    # 两层LSTM
num_directions = 1 # 单向，方向数为1# 创建多层单向LSTM
lstm = nn.LSTM(input_size, hidden_size, num_layers)  # batch_first默认为False# 准备输入数据 input(序列长度, 批次大小, 输入特征维度)
input = torch.randn(seq_len, batch_size, input_size)  # (150,16,3)
# 初始状态 h0,c0(层数×方向数, 批次大小, 隐藏维度)
h0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)  # (2*1,16,64)
c0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)# 前向传播  output(序列长度, 批次大小, 隐藏维度×方向数)
output, (hn, cn) = lstm(input, (h0, c0))print(f"\n多层单向LSTM:")
print(f"output shape: {output.shape}") # (150, 16, 64*1) # 注意：output仍是最后一层的输出
print(f"hn shape: {hn.shape}")         # (2, 16, 64) # 两层最后时间步的隐藏状态
print(f"cn shape: {cn.shape}")         # (2, 16, 64)# 验证 output 的最后一个时间步与 hn 的最后一层相同
print(f"output[-1,:,:] == hn[-1]: {torch.allclose(output[-1,:,:], hn[-1])}")

(2)batch_first设置为True

# 创建多层单向LSTM (batch_first=True)
lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)# 准备输入数据 input(批次大小, 序列长度, 输入特征维度)
input = torch.randn(batch_size, seq_len, input_size)  # (16,150,3)
# 初始化隐藏状态和细胞状态 h0,c0(层数×方向数, 批次大小, 隐藏维度)
h0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)  # (2*1, 16, 20)
c0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)# output(批次大小, 序列长度, 隐藏维度×方向数)
output, (hn, cn) = lstm(input, (h0, c0))print(f"\n多层单向LSTM (batch_first=True):")
print(f"output shape: {output.shape}")  # (16, 150, 64)
print(f"hn shape: {hn.shape}")          # (2, 16, 64)
print(f"cn shape: {cn.shape}")          # (2, 16, 64)# 验证 output 的最后一个时间步与 hn 的最后一层相同
print(f"output[:, -1, :] == hn[-1]: {torch.allclose(output[:, -1, :], hn[-1])}")

总结：【前提：batch_first=True】

output,(hn,cn) = lstm(input,(h0,c0))

    由于

    output(序列长度, 批次大小, 隐藏维度×方向数)：返回最后一层，所有时间步的隐藏状态

    hn(层数×方向数, 批次大小, 隐藏维度)：返回所有层的最后一个时间步的隐藏状态

所以,在多层单向LSTM中,输出的最后一个时间步与隐藏状态的最后一层相同。即：

    output[:,-1,:] = hn[-1,:,:] != hn[0]

    1.lstm层数只会改变h0、c0、hn、cn这些隐藏状态和细胞状态的维度,而不会改变output的维度。

3.单层双向LSTM

双向LSTM通过增加一个从序列末尾向开头处理的反向LSTM，能够同时捕捉前后文信息。

(1)batch_first默认为False

import torch
import torch.nn as nn# 定义参数
input_size = 3   # 每个时间步输入特征维度为3
seq_len = 150       # 序列长度为150
batch_size = 16    # 批次大小为16
hidden_size = 64  # 隐藏层特征维度为64
num_layers = 1  # 1层LSTM
num_directions = 2 # 双向，方向数为2# 创建单层双向LSTM
lstm = nn.LSTM(input_size, hidden_size, num_layers, bidirectional=True)  # 双向LSTM# 准备输入数据 input(序列长度, 批次大小, 输入特征维度)
input = torch.randn(seq_len, batch_size, input_size)  # (150, 16, 3)
# 初始化隐藏状态和细胞状态 h0,c0(层数×方向数, 批次大小, 隐藏维度)
h0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)  # (1*2, 16, 64)
c0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)# 前向传播  output(序列长度, 批次大小, 隐藏维度×方向数)
output, (hn, cn) = lstm(input, (h0, c0))print(f"\n单层双向LSTM:")
print(f"output shape: {output.shape}") # (150, 16, 64*2) 因为是双向LSTM，每个时间步的输出是正向和反向的拼接
print(f"hn shape: {hn.shape}")         # (1*2, 16, 64) 两个方向的最后隐藏状态(前者hn[0,:,:]是正向最后隐藏状态，后者hn[1,:,:]是反向最后隐藏状态)
print(f"cn shape: {cn.shape}")         # (1*2, 16, 64) 两个方向的最后记忆状态# 验证 output 最后一个时间步的前半部分对应正向LSTM的最后隐藏状态，第一个时间步的后半部分对应反向LSTM的最后隐藏状态
print(torch.allclose(output[-1, :, :hidden_size], hn[0])) # 正向最后时间步
print(torch.allclose(output[0, :, hidden_size:], hn[1]))  # 反向最后时间步 (注意是0位置)

(2)batch_first设置为True

# 创建单层双向LSTM (batch_first=True)
lstm = nn.LSTM(input_size, hidden_size, num_layers, bidirectional=True, batch_first=True)  # 将模型的input和output的batch_size参数前置# 准备输入数据 input(批次大小, 序列长度, 输入特征维度)
input = torch.randn(batch_size, seq_len, input_size)  # (16, 150, 3)
# 初始化隐藏状态和细胞状态 h0,c0(层数×方向数, 批次大小, 隐藏维度)
h0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)  # (1*2, 16, 64)
c0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)# 前向传播  output(批次大小, 序列长度, 隐藏维度×方向数) 
output, (hn, cn) = lstm(input, (h0, c0))print(f"\n单层双向LSTM (batch_first=True):")
print(f"output shape: {output.shape}")  # (16, 150, 64*2)
print(f"hn shape: {hn.shape}")          # (1*2, 16, 64)
print(f"cn shape: {cn.shape}")          # (1*2, 16, 64)# 验证双向LSTM的输出关系
# output的最后一个时间步的前半部分 对应 正向LSTM的最后隐藏状态
# output的第一个时间步的后半部分 对应 反向LSTM的最后隐藏状态
print(f"正向验证: {torch.allclose(output[:, -1, :hidden_size], hn[0])}")  # hn[0]是正向LSTM的最后隐藏状态
print(f"反向验证: {torch.allclose(output[:, 0, hidden_size:], hn[1])}")  # hn[1]是反向LSTM的最后隐藏状态

注意：【前提：batch_first = True】

output(序列长度, 批次大小, 隐藏维度×方向数)：双向LSTM，每个时间步的输出是正向和反向的拼接。

    其中，output[:, -1, :hidden_size] 对应 output 最后一个时间步的前半部分，即正向LSTM的最后隐藏状态。

    其中，output[:, 0, hidden_size:] 对应 output 第一个时间步的后半部分，即反向LSTM的最后隐藏状态。

hn(层数×方向数, 批次大小, 隐藏维度)：双向LSTM，需要手动拼接

    前者hn[-2,:,:]是最后一层 正向最后隐藏状态，

    后者hn[-1,:,:]是最后一层 反向最后隐藏状态

    1.lstm层数只会改变h0、c0、hn、cn这些隐藏状态和细胞状态的维度,而不会改变output的维度。

    2.而方向数会改变output+h0、c0、hn、cn的维度

4.多层双向LSTM

多层双向LSTM结合了深度结构和双向处理的优势，能捕捉更复杂的序列依赖关系。

(1)batch_first默认为False

import torch
import torch.nn as nn# 定义参数
input_size = 3   # 每个时间步输入特征维度为3
seq_len = 150       # 序列长度为150
batch_size = 16    # 批次大小为16
hidden_size = 64  # 隐藏层特征维度为64
num_layers = 2  # 2层LSTM
num_directions = 2 # 双向，方向数为2# 创建多层双向LSTM
lstm = nn.LSTM(input_size, hidden_size, num_layers, bidirectional=True)# 准备输入数据 input(序列长度, 批次大小, 输入特征维度)
input = torch.randn(seq_len, batch_size, input_size)  # (150, 16, 3)
# 初始化隐藏状态和细胞状态 h0,c0(层数×方向数, 批次大小, 隐藏维度)
h0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)  # (2*2, 16, 64)
c0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)# 前向传播  output(序列长度, 批次大小, 隐藏维度×方向数)
output, (hn, cn) = lstm(input, (h0, c0))print(f"\n多层双向LSTM:")
print(f"output shape: {output.shape}") # (150, 16, 64*2)
print(f"hn shape: {hn.shape}")         # (2*2, 16, 64) # 2层 * 2方向 = 4
print(f"cn shape: {cn.shape}")         # (2*2, 16, 64) # 验证双向LSTM的输出关系
# output的最后一个时间步的前半部分 对应 正向LSTM的最后隐藏状态
# output的第一个时间步的后半部分 对应 反向LSTM的最后隐藏状态
print("验证双向LSTM的输出关系:")
print("output的最后一个时间步的前半部分 对应 正向LSTM的最后隐藏状态:", torch.allclose(output[-1, :, :hidden_size], hn[-2, :, :]))  # 最后一层正向LSTM的最后隐藏状态 hn[-2, :, :] = hn[2]
print("output的第一个时间步的后半部分 对应 反向LSTM的最后隐藏状态:", torch.allclose(output[0, :, hidden_size:], hn[-1, :, :]))  # 最后一层反向LSTM的最后隐藏状态 hn[-1, :, :] = hn[3]

(2)batch_first设置为True

# 创建多层双向LSTM
lstm = nn.LSTM(input_size, hidden_size, num_layers, bidirectional=True, batch_first=True) # 准备输入数据 input(批次大小,序列长度,输入特征维度)
input = torch.randn(batch_size, seq_len, input_size)  # (16, 150, 3)
# 初始化隐藏状态和细胞状态 h0,c0(层数×方向数, 批次大小, 隐藏维度)
h0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)  # (2*2, 16, 64)
c0 = torch.randn(num_layers * num_directions, batch_size, hidden_size)# 前向传播  output(批次大小, 序列长度, 隐藏维度×方向数)
output, (hn, cn) = lstm(input, (h0, c0))print(f"\n多层双向LSTM (batch_first=True):")
print(f"output shape: {output.shape}")  # (16, 150, 64*2)
print(f"hn shape: {hn.shape}")          # (2*2, 16, 64)
print(f"cn shape: {cn.shape}")          # (2*2, 16, 64)# 验证双向LSTM的输出关系
# 验证双向LSTM的输出是否正确
print("output的最后一个时间步的前半部分 对应 正向LSTM的最后隐藏状态:", torch.allclose(output[:, -1, :hidden_size], hn[-2, :, :]))  # 最后一层正向LSTM的最后隐藏状态 hn[-2, :, :] = hn[2]
print("output的第一个时间步的后半部分 对应 反向LSTM的最后隐藏状态:", torch.allclose(output[:, 0, hidden_size:], hn[-1, :, :]))  # 最后一层反向LSTM的最后隐藏状态 hn[-1, :, :] = hn[3]

总结：

output(批次大小, 序列长度, 隐藏维度×方向数)：无论多少层的双向LSTM，输出的都是最后一层的每个时间步的隐藏状态，且每个时间步的隐藏状态是前向和后向的拼接。

    其中，output[:, -1, :hidden_size] 对应 output 最后一个时间步的前半部分，即正向LSTM的最后隐藏状态。

    其中，output[:, 0, hidden_size:] 对应 output 第一个时间步的后半部分，即反向LSTM的最后隐藏状态。

hn(层数×方向数, 批次大小, 隐藏维度)：双向LSTM，最后一层的正向最后隐藏状态和反向最后隐藏状态需要手动拼接。

   

    其中，hn[-2,:,:] 对应 最后一层 正向最后隐藏状态。

    其中，hn[-1,:,:] 对应 最后一层 反向最后隐藏状态。

例如：由于是两层双向LSTM，所以hn的形状是(层数×方向数, 批次大小, 隐藏维度)，即(2*2, 16, 64)

    其中，hn[0,:,:] 对应 第一层lstm 正向最后隐藏状态。

    其中，hn[1,:,:] 对应 第一层lstm 反向最后隐藏状态。

    其中，hn[2,:,:] 对应 第二层lstm 正向最后隐藏状态。同时也是 最后一层lstm 正向最后隐藏状态，即hn[-2,:,:]

    其中，hn[3,:,:] 对应 第二层lstm 反向最后隐藏状态。同时也是 最后一层lstm 反向最后隐藏状态，即hn[-1,:,:]

所以，可以得出：无论lstm有多少层，都可以通过hn[-2,:,:]和hn[-1,:,:]来获取最后一层lstm的正向最后隐藏状态和反向最后隐藏状态。

    最后一层lstm 正向最后隐藏状态 = hn[-2,:,:] 等价于 output[:, -1, :hidden_size] (前提batch_first=True)

    最后一层lstm 反向最后隐藏状态 = hn[-1,:,:] 等价于 output[:, 0, hidden_size:]

上面的例子都是在处理等长的序列，那么如果序列长度不同，该怎么办？

接下来再加一个条件，即在batch_first=True的条件上，通过nn.utils.rnn.pack_padded_sequence打包来处理变长序列（序列分类任务，无需解包），请分别将4种不同LSTM结构示例代码重新返回一下，注意：每种例子要分别给出两个实现方案（方案一：通过hidden直接取隐藏状态；方案二：通过output取每个序列的最后一个有效输出）

二、处理不等长的序列（batch_first=True）

前提：（batch_first=True + pack_padded_sequence打包序列）

1.单层单向LSTM

基础设置:

import torch
import torch.nn as nn
from torch.nn.utils.rnn import pack_padded_sequence, pad_packed_sequence# 定义参数
input_size = 5  # 输入特征维度
hidden_size = 64  # 隐藏层神经元数量
batch_size = 3  # 批次大小
max_seq_len = 10  # 最大序列长度# 创建变长序列数据(就模拟生成了3条序列，这里就当batch_size=3)
sequences = [torch.randn(8, input_size),  # 长度8torch.randn(9, input_size),  # 长度9torch.randn(10, input_size)   # 长度10
]# 实际长度
lengths = torch.tensor([8, 9, 10], dtype=torch.long)  # 序列长度一般设置长整型(int64)# 填充序列 (batch_first=True)  # pad_sequence返回一个B x T x * 的Tensor，其中T是最长序列的长度。
padded_sequences = torch.nn.utils.rnn.pad_sequence([seq for seq in sequences], batch_first=True, padding_value=0.0
)print(f"填充后序列形状: {padded_sequences.shape}")  # (3, 10, 5)
padded_sequences

方案一：通过hidden取最后一层lstm的 最后一个时间步的隐藏状态

# 创建单层单向LSTM
lstm = nn.LSTM(input_size, hidden_size, num_layers=1, batch_first=True)  # batch_first=True# 按长度降序排序
lengths_sorted, sorted_idx = torch.sort(lengths, descending=True)  # 对序列长度进行降序排序，返回排序后的长度和索引
sequences_sorted = padded_sequences[sorted_idx]  # 使用排序后的索引对填充序列进行排序# 打包序列以处理变长序列
packed_input = pack_padded_sequence(sequences_sorted,  # 按长度降序排序后的序列 形状(3,10,5)lengths_sorted.cpu(),  # 按长度降序排序后的长度 [10,9,8]，注意：如果以tensor形式提供，则必须在CPU上batch_first=True)'''
正常的input(批次大小, 序列长度, 输入特征维度)
打包后的input：是一个PackedSequence对象（注意：所有RNN模块都接受已打包序列作为输入）
PackedSequence对象包含两个主要属性：data：包含所有有效（非填充）元素的张量  形状(8+9+10,5)batch_sizes：每个时间步的有效序列数量  [3, 3, 3, 3, 3, 3, 3, 3, 2, 1] 三维横截面
'''# 前向传播
packed_output, (hn, cn) = lstm(packed_input)  # 如果不给初始状态h0和c0，默认初始状态为0'''
正常的output(批次大小, 序列长度, 隐藏维度×方向数)
打包后的lstm前向传播输出的output：是一个PackedSequence对象
PackedSequence对象包含两个主要属性：data：包含所有有效（非填充）元素的张量  形状(27,64) 64是隐藏维度batch_sizes：每个时间步的有效序列数量  [3, 3, 3, 3, 3, 3, 3, 3, 2, 1] 三维思维但是无论打不打包，hn都是每个序列最后一个有效时间步的隐藏状态，形状为(层数×方向数, 批次大小, 隐藏维度)
'''# hn(层数×方向数, 批次大小, 隐藏维度)
print("单层单向LSTM - 方案一 (通过hidden取隐藏状态):")
print(f"hn shape: {hn.shape}")  # (1*1,3,64)
print(f"取最后一层隐藏状态(还未恢复顺序): {hn[-1].shape}")  # (3, 64)# 恢复原始顺序（根据排序后索引）
_, unsorted_indices = torch.sort(sorted_idx)  # 降序# 取最后一层的隐藏状态，再根据原始索引恢复顺序
final_hidden = hn[-1][unsorted_indices]
print(f"恢复顺序后: {final_hidden.shape}")

方案二：通过 output 取每个序列的最后一个有效输出

# 创建单层单向LSTM（同上）
lstm = nn.LSTM(input_size, hidden_size, num_layers=1, batch_first=True)# 排序和打包（同上）
lengths_sorted, sorted_idx = lengths.sort(descending=True)
sequences_sorted = padded_sequences[sorted_idx]
packed_input = pack_padded_sequence(sequences_sorted, lengths_sorted.cpu(), batch_first=True)# 前向传播（同上）
packed_output, (hn, cn) = lstm(packed_input)  # 如果不给初始状态h0和c0，默认初始状态为0
'''
正常的output(批次大小, 序列长度, 隐藏维度×方向数)
打包后的lstm前向传播输出的output：是一个PackedSequence对象
PackedSequence对象包含两个主要属性：data：包含所有有效（非填充）元素的张量  形状(27,64) 64是隐藏维度batch_sizes：每个时间步的有效序列数量  [3, 3, 3, 3, 3, 3, 3, 3, 2, 1] 三维思维
'''
# 解包：返回填充后的输出张量output、每个序列的实际长度的张量output_lengths
output, output_lengths = pad_packed_sequence(packed_output, batch_first=True)print("单层单向LSTM - 方案二 (通过output取最后一个有效输出):")
print(f"解包后output shape: {output.shape}")  # (3, 10, 64)  output(批次大小, 序列长度, 隐藏维度×方向数)# 手动取每个序列的最后一个有效输出
last_outputs = []
for i, length in enumerate(output_lengths):last_outputs.append(output[i, length-1, :])# stack()函数将列表中的张量按指定维度拼接起来
last_outputs = torch.stack(last_outputs)  # (批次大小, 隐藏维度×方向数)-> (3, 64)# 获取原始顺序（根据排序后索引）
_, unsorted_indices = torch.sort(sorted_idx)# 取最后一层的隐藏状态，再根据原始索引恢复顺序
final_output = last_outputs[unsorted_indices]
print(f"最后一个有效输出: {final_output.shape}")  # (3, 64)# 验证两种方案结果相同
print(f"两种方案结果相同: {torch.allclose(final_hidden, final_output, atol=1e-6)}")

附录：

0.torch.allclose()方法

torch.allclose(input, other, rtol=1e-05, atol=1e-08, equal_nan=False)：用于判断两个张量是否在允许的误差范围内"足够接近"。

参数：

        input: 第一个张量

        other: 第二个张量

        rtol: 相对容差 (relative tolerance)，默认 1e-05

        atol: 绝对容差 (absolute tolerance)，默认 1e-08

        equal_nan: 是否将 NaN 视为相等，默认 False

判断条件：

当满足以下条件时返回 True：

|input - other| ≤ atol + rtol × |other|

为什么不直接使用==进行判断呢？

import torch# 创建两个非常接近的张量
a = torch.tensor([1.0, 2.0, 3.000001])
b = torch.tensor([1.0, 2.0, 3.0])print("直接比较:", a == b)           # tensor([True, True, False])
print("allclose比较:", torch.allclose(a, b))  # True
print("差值:", a - b)                # tensor([0.0000, 0.0000, 0.0000])

torch.allclose(output[-1], hn[-1]) 这行代码：

1. 验证理论：确认单向单层LSTM中最后一个时间步的输出与最终隐藏状态相等

2. 处理精度：避免浮点数计算中的微小精度误差导致验证失败

3. 实用性强：是PyTorch中比较张量相等性的推荐方法

1.torch.sort()操作

torch.sort(input, dim=-1, descending=False, *, stable=False, out=None)：按值对 input 张量沿给定维度进行升序排序。

如果未指定 `dim`，则选择 `input` 的最后一个维度。如果 descending 为 True，则按值降序排序。

如果 stable 为 True，则排序例程将变为稳定排序，保留等价元素的顺序。

    参数：

        input (Tensor) – 输入张量。

        dim (int, optional) – 要沿其排序的维度

        descending (bool, optional) – 控制排序顺序（升序或降序）

    关键字参数：

        stable (bool, optional) – 使排序例程稳定，保证等价元素的顺序得以保留。

        out (tuple, optional) – 可选的输出元组 (Tensor, LongTensor)，可用于作为输出缓冲区

    返回：

        一个 namedtuple，包含 (values, indices)，其中 values 是排序后的值，indices 是原始 input 张量中元素的索引。

注意区分 numpy.argsort()和numpy.sort()！！！

示例：

>>> x = torch.randn(3, 4)  # 3行4列的随机张量
>>> sorted, indices = torch.sort(x)  # 默认按行排序(默认升序),返回排序后的张量和排序后的索引
>>> sorted
tensor([[-0.2162,  0.0608,  0.6719,  2.3332],[-0.5793,  0.0061,  0.6058,  0.9497],[-0.5071,  0.3343,  0.9553,  1.0960]])
>>> indices
tensor([[ 1,  0,  2,  3],[ 3,  1,  0,  2],[ 0,  3,  1,  2]])>>> sorted, indices = torch.sort(x, 0)  # 按列排序(默认升序)
>>> sorted
tensor([[-0.5071, -0.2162,  0.6719, -0.5793],[ 0.0608,  0.0061,  0.9497,  0.3343],[ 0.6058,  0.9553,  1.0960,  2.3332]])
>>> indices
tensor([[ 2,  0,  0,  1],[ 0,  1,  1,  2],[ 1,  2,  2,  0]])

2.使用两次torch.sort()操作恢复原始序列

代码中使用了两次torch.sort()，第一次先对序列长度进行降序排序，返回排序后的长度和索引（实现了对原始序列的降序排序）；

第二次又对排序后的索引进行了排序，返回了排序后索引的排序索引（又将排序后序列恢复为原始序列了）。这个过程到底是怎么实现的？分析如下图：

3.pack_padded_sequence()

pack_padded_sequence(input, lengths, batch_first=False, enforce_sorted=True)：

input 的形状可以是 T x B x * (如果 batch_first 为 False) 或 B x T x * (如果 batch_first 为 True)，其中 T 是最长序列的长度，B 是批次大小，而 * 是任意数量的维度（包括 0）。

对于未排序的序列，请使用 enforce_sorted = False。

如果 enforce_sorted 为 True，序列应该按长度递减排序，即 input[:,0] 应该是最长序列，input[:,B-1] 应该是最短序列。

enforce_sorted = True 仅对 ONNX 导出是必需的。

它是 pad_packed_sequence() 的逆向操作，因此可以使用 pad_packed_sequence() 来恢复 PackedSequence 中打包的底层张量。

参数：

        input (Tensor) – 可变长度序列的填充批次。

        lengths (Tensor 或 list(int)) – 每个批次元素的序列长度列表（如果以 tensor 形式提供，则必须在 CPU 上）。

        batch_first (bool, optional) – 如果为 True，则输入格式为 B x T x *；否则为 T x B x *。默认为 False。

        enforce_sorted (bool, optional) – 如果为 True，则输入应包含按长度递减排序的序列。如果为 False，则输入将无条件排序。默认为 True。

返回：

    一个 PackedSequence 对象

4.PackedSequence对象分析

PackedSequence对象：存储已打包序列的数据和 batch_sizes 列表。所有 RNN 模块都接受已打包序列作为输入。

注意：此类的实例不应手动创建。它们应由 pack_padded_sequence() 等函数实例化。

Batch_sizes 表示批次中每个序列步的元素数量，而不是传递给 pack_padded_sequence() 的可变序列长度。例如，给定数据 abc 和 x，PackedSequence 将包含数据 axbc，其中 batch_sizes=[2,1,1]。

变量：

        data (Tensor) – 包含所有有效（非填充）元素的张量

        batch_sizes (Tensor) – 每个时间步的有效序列数量

        sorted_indices (Tensor, optional) – 包含此 PackedSequence 如何从序列构建的整数张量。

        unsorted_indices (Tensor, optional) – 包含如何恢复具有正确顺序的原始序列的整数张量。

返回类型：

        自我PackedSequence

让我们从调试的视角一步一步分析打包后的效果：

1.假设我们填充后的数据如下所示：

原始三维序列形状: torch.Size([3, 4, 2])
原始序列:
tensor([[[ 1., 10.],[ 2., 20.],[ 3., 30.],[ 4., 40.]],[[ 5., 50.],[ 6., 60.],[ 7., 70.],[ 0.,  0.]],[[ 8., 80.],[ 9., 90.],[ 0.,  0.],[ 0.,  0.]]])
序列长度: tensor([4, 3, 2])

2.排序（按序列长度降序）、并打包后的数据：

排序后序列:
tensor([[[ 1., 10.],[ 2., 20.],[ 3., 30.],[ 4., 40.]],[[ 5., 50.],[ 6., 60.],[ 7., 70.],[ 0.,  0.]],[[ 8., 80.],[ 9., 90.],[ 0.,  0.],[ 0.,  0.]]])
排序后长度: tensor([4, 3, 2])=== PackedSequence对象分析 ===
packed_input.data: tensor([[ 1., 10.],[ 5., 50.],[ 8., 80.],[ 2., 20.],[ 6., 60.],[ 9., 90.],[ 3., 30.],[ 7., 70.],[ 4., 40.]])
packed_input.data形状: torch.Size([9, 2])
packed_input.batch_sizes: tensor([3, 3, 2, 1])

3. 逐步解析三维打包过程

时间步0 (t=0):

• 所有3个序列都有有效数据

• 数据: 序列1的[1,10], 序列2的[5,50], 序列3的[8,80]

• batch_sizes[0] = 3

• data中存储: [[1,10], [5,50], [8,80]]

时间步1 (t=1):

• 所有3个序列都有有效数据

• 数据: 序列1的[2,20], 序列2的[6,60], 序列3的[9,90]

• batch_sizes[1] = 3

• data中存储: [[2,20], [6,60], [9,90]]

时间步2 (t=2):

• 只有前2个序列有有效数据

• 数据: 序列1的[3,30], 序列2的[7,70] (序列3已结束)

• batch_sizes[2] = 2

• data中存储: [[3,30], [7,70]]

时间步3 (t=3):

• 只有第1个序列有有效数据

• 数据: 序列1的[4,40] (其他序列已结束)

• batch_sizes[3] = 1

• data中存储: [[4,40]]

可视化打包过程：

时间步:       0             1             2             3
序列1:    [[1,10]] --> [[2,20]] --> [[3,30]] --> [[4,40]]
序列2:    [[5,50]] --> [[6,60]] --> [[7,70]] --> (结束)
序列3:    [[8,80]] --> [[9,90]] --> (结束)       (结束)打包后的data: 
时间步0: [[1,10], [5,50], [8,80]]    (3个序列)
时间步1: [[2,20], [6,60], [9,90]]    (3个序列)  
时间步2: [[3,30], [7,70]]            (2个序列)
时间步3: [[4,40]]                    (1个序列)batch_sizes: [3, 3, 2, 1]

5.打包、前向传播、解包过程

原始序列数据： lens(5,3,4)

填充后的数据：（3，5，2）->（批次大小，序列长度，特征维度）

排序并打包：

# 按长度降序排序
lengths_sorted, sorted_idx = lengths.sort(descending=True)
sequences_sorted = padded_sequences[sorted_idx]
# 打包序列
packed_input = pack_padded_sequence(sequences_sorted, lengths_sorted.cpu(),  # 需要CPU tensorbatch_first=True
)

LSTM前向传播：

# 创建LSTM
lstm = nn.LSTM(input_size, hidden_size, batch_first=True)
# 前向传播
packed_output, (hn, cn) = lstm(packed_input)

packed_output, (hn, cn)  =  lstm(packed_input)  # 前向传播

假如是 batch_size=True + 单层单向LSTM + 隐藏层维度为64，那么就有：

前向传播后的hn(层数×方向数, 批次大小, 隐藏维度)  --> （1*1，3，64），hn表示：每个序列在最后一个有效时间步的隐藏状态。

• 形状：(1, 3, 64) = (1层, 3个序列, 64维隐藏状态)

• 内容：每个序列在最后一个有效时间步的隐藏状态

• 顺序：按排序后的批次顺序 [序列0, 序列2, 序列1] (因为长度排序后是 [5,4,3])

hn (形状: 1×3×64):
[[ [序列0在时间步4的隐藏状态],  # 形状(64,)[序列2在时间步3的隐藏状态],  # 形状(64,)  [序列1在时间步2的隐藏状态] ] # 形状(64,)
]

正常的output(批次大小, 序列长度, 隐藏维度×方向数)；打包后的lstm前向传播输出的packed_output：是一个PackedSequence对象，packed_output 的含义：

• data: 所有时间步的所有有效输出的扁平化张量，形状(原始序列总长度，特征维度) -> (5+4+3，3)

• batch_sizes: 每个时间步有效的序列数量 -> [3, 3, 3, 2, 1]

解包过程：

output, output_lengths = pad_packed_sequence(packed_output, batch_first=True)

返回一个元组，包含：

填充后的输出张量output，形状为(batch_size, max_length, hidden_size) —> (3，5，64)

一个张量，包含每个序列的实际长度。 len [5，4，3]

注意：解包后的序列顺序与打包前相同（即排序后的顺序，也就是[序列1, 序列3, 序列2]）。我们需要用原始索引恢复顺序。

解包后的优势：

1. 清晰的维度：(batch_size, max_length, hidden_size)

2. 易于索引：output[i, t, :] 直接获取第i个序列在第t个时间步的输出

3. 便于后续处理：可以直接用于其他神经网络层

6.torch.stack() 与 torch.cat()的区别

torch.cat() - 连接 (Concatenate)

• 作用: 在现有维度上连接张量

• 条件: 所有张量在非连接维度上必须形状相同

• 结果: 输出张量的维度数不变

torch.stack() - 堆叠 (Stack)

• 作用: 创建新维度来堆叠张量

• 条件: 所有张量必须完全同形

• 结果: 输出张量的维度数增加1

1.示例数据准备

# 创建几个相同形状的张量
a = torch.tensor([[1, 2, 3],[4, 5, 6]])b = torch.tensor([[7, 8, 9],[10, 11, 12]])c = torch.tensor([[13, 14, 15],[16, 17, 18]])

2.torch.cat() 用法详解

cat() 的维度要求:

3.torch.stack() 用法详解

stack() 的严格形状要求: