【大数据技术03】机器学习与算法
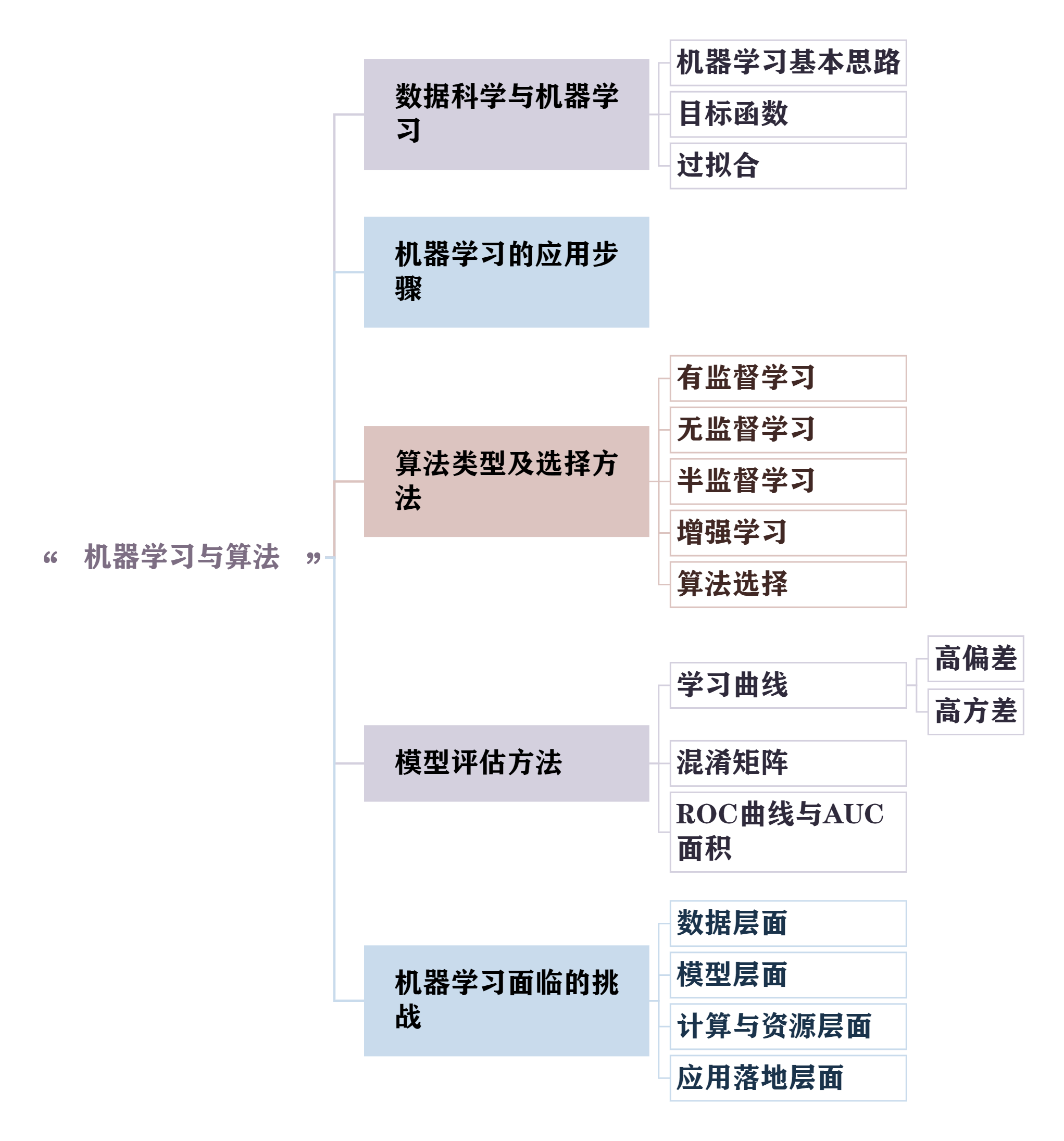
文章目录
- 三.机器学习与算法
- 1.数据科学与机器学习
- 1.1 机器学习的基本思路
- 1.2 目标函数
- 1.3 过/欠拟合
- 2.机器学习的应用步骤
- 3.算法类型与选择方法
- 3.1 有监督学习
- 3.2 无监督学习
- 3.3 半监督学习
- 3.4 增强学习
- 3.5 有监督学习算法和无监督学习算法的分类
- 聚类 --- 无监督+连续型属性
- 分类 --- 有监督+分类型属性
- 回归 --- 有监督 + 连续型属性
- 维度下降 --- 无监督 + 连续型属性
- 关联规则分析 --- 无监督 + 分类型属性
- 3.6 算法选择
- 4.模型评估方法
- 4.1 学习曲线
- (1)高偏差
- (2)高方差
- 4.2 混淆矩阵
- 4.3 ROC曲线与AUC面积
- 5.机器学习面临的挑战
三.机器学习与算法
1.数据科学与机器学习
1.1 机器学习的基本思路
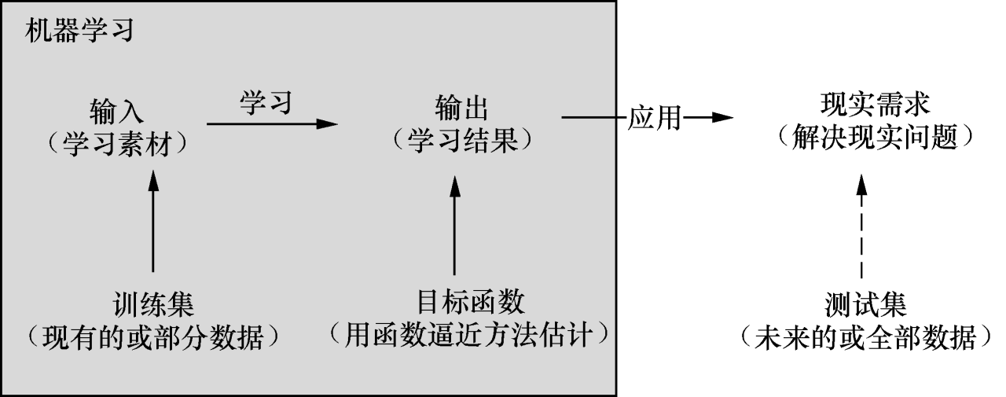
机器学习的基本思路如图所示:
以现有的或部分数据(训练集)作为学习素材(输入),通过特定的学习方法(机器学习算法),让机器学习到(输出)能够处理更多或未来数据的新能力(目标函数)
但是,由于通常在实际工作中很难找到目标函数的精确定义,机器学习中通常采用函数逼近方法进行目标函数估计。
1.2 目标函数
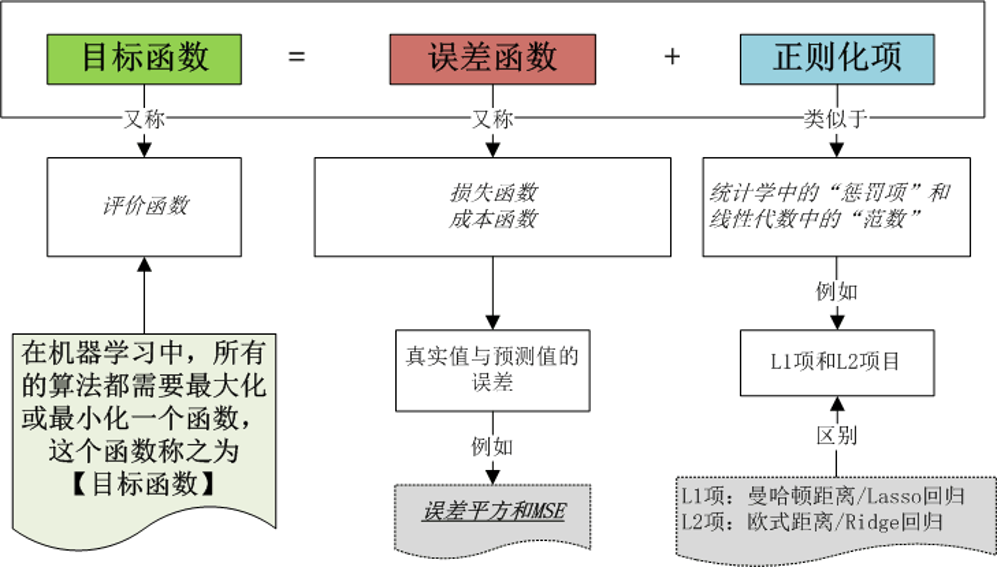
通常,目标函数逼近的思路如图所示,一般采取正则化(Regularization)方法,将目标函数分为“误差函数”和“正则化项”。
1.3 过/欠拟合
过拟合:目标函数在训练集上的拟合性能非常高,而在测试集或者新数据上拟合准确率很低
欠拟合:目标函数在训练集和在测试集或者新数据上拟合准确率都很低
为了防止过拟合现象的出现,机器学习通常采取**“正则化项”。**
常见正则化项有 L1 项(L1 Loss)和 L2 项(L2 Loss),二者的区别在于所涉及的距离计算方法和回归方法不同。
2.机器学习的应用步骤
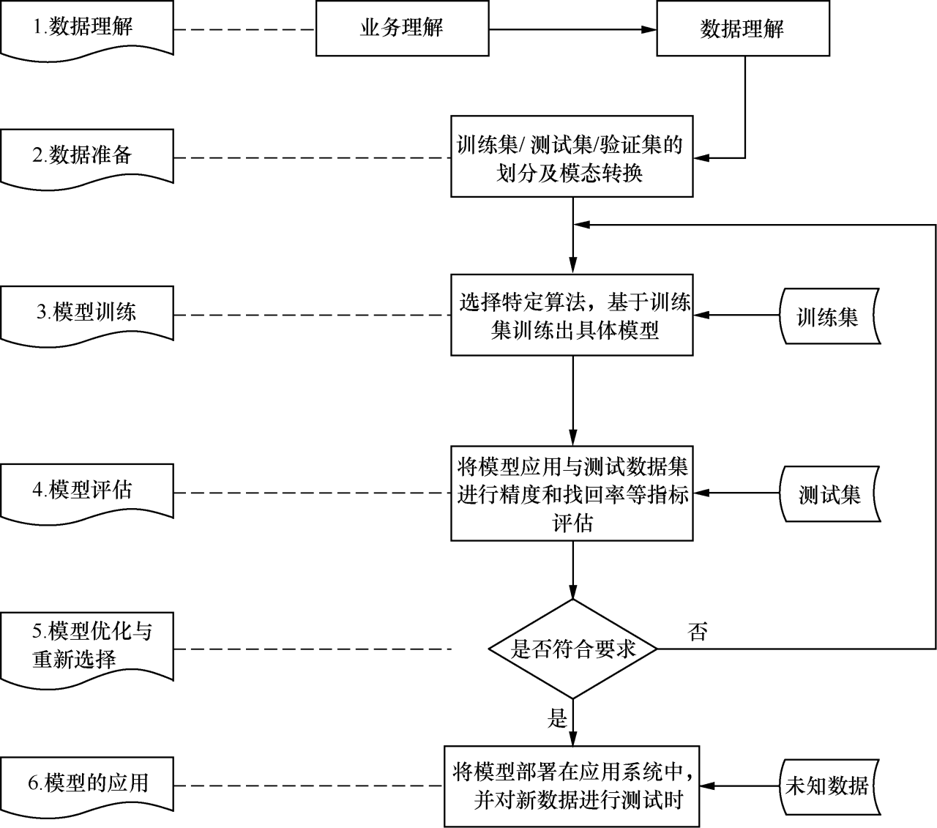
步骤:
- 数据理解
- 数据预处理
- 训练模型
- 模型评估
- 模型优化与重新选择
- 模型应用测试泛化能力
3.算法类型与选择方法
根据学习任务的不同,机器学习算法通常分为有监督学习(Supervised Learning)、 无监督学习(Unsupervised Learning)和半监督学习(Semi-Supervised Leaming),如下图所示。
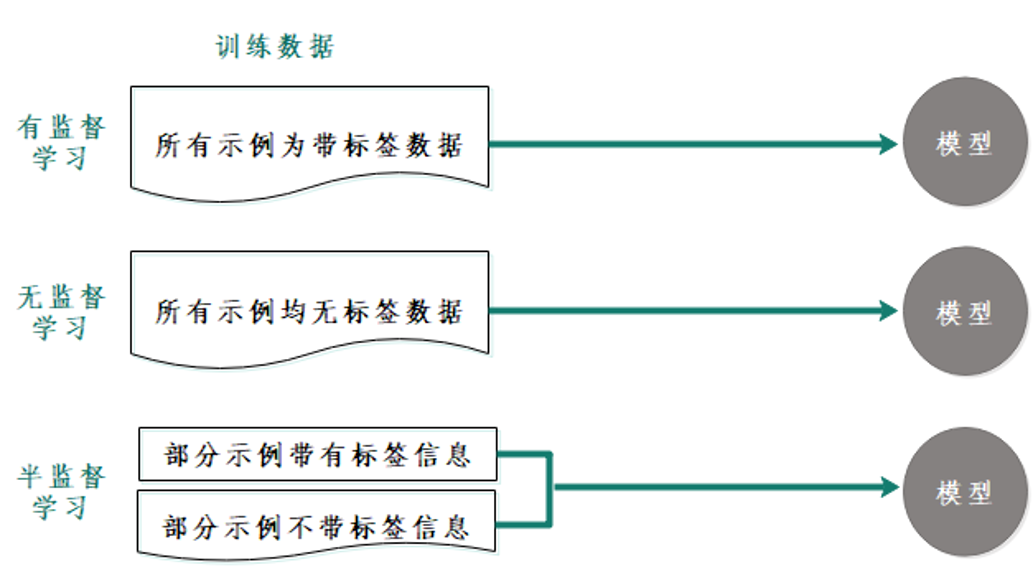
根本区别:数据有没有标签
3.1 有监督学习
有监督学习用已知模式去预测数据, 其使用前提是训练集为带标签数据 (Labeled Data),即训练集中的每个示例(Examples)均带有自己的输出值—标 签(Labels)。
常见的有监督学习算法:
- 最近邻
- 朴素贝叶斯
- 决策树
- 随机森林
- 线性回归
- 支持向量机SVM
- 神经网络分析
3.2 无监督学习
无监督学习常用于从数据中发现未知的模式信息,当训练集中不带标签信息时,通常采用无监督学习算法。
常见的无监督学习算法:
- K-means聚类
- 主成分分析法
- 关联规则分析
3.3 半监督学习
当训练集中的部分样本缺少标签信息时,通常采用半监督学习。
常见的半监督学习算法:
- 半监督分类方法(如生成式方法、判别式方法等)
- 半监督回归方法(如基于差异的方法、基于流形学习的方法)
- 半监督聚类方法(基于距离的方法和大间隔方法)
- 半监督降维方法(如基于类标签的方法和基于成对约束的方法)
- 半监督分类:帮你给 “没标签的样本分类别”(比如给没标 “是否购买” 的用户归类),常用生成式(先猜数据分布,再分类)、判别式(直接找分类边界)等方法;
- 半监督回归:帮你预测 “没标签样本的连续数值”(比如没标 “消费金额” 的用户,预测其可能消费额),常用基于数据差异、或基于数据内在关联(流形学习)的方法;
- 半监督聚类:帮你把 “部分有标签、部分没标签的样本” 分成自然群体(比如部分标了 “偏好品类” 的用户,和没标的用户一起分群),常用算样本距离、或找群体间大间隔的方法;
- 半监督降维:帮你简化 “部分有标签样本” 的特征(比如把用户的 10 个特征减到 3 个,还保留标签信息),常用结合类标签、或样本间约束关系的方法。
3.4 增强学习
主要研究目的:
如何协助自制Agent的学习活动,达到选择最优动作的能力
协助自制 Agent(智能体)学会选最优动作”,其实就是通过增强学习的核心逻辑帮它 “试错、总结、进步”,可以拆成 3 个简单步骤理解,就像教小动物学技能一样:
- **给 Agent 搭 “互动场景”**先明确 Agent 的 “环境”(比如让机器人在仓库里工作,环境就是仓库的布局、货物位置),再定好 Agent 能做的 “动作”(比如机器人能 “前进”“搬货”“转弯”)—— 这是它学习的基础,得先知道 “在什么地方,能做什么”。
- 用 “奖惩信号” 给反馈Agent 做动作后,立刻给它明确的 “奖励” 或 “惩罚”(比如机器人成功把货搬到指定位置,就给个 “正奖励”;撞到货架,就给 “负惩罚”)。这就像教小狗:做对了给零食,做错了轻声制止,让 Agent 知道 “这么做对不对”。
- **让 Agent 在 “试错中积累经验”**Agent 会不断重复 “做动作→收奖惩→调整策略” 的过程:一开始可能乱做动作(比如机器人瞎转悠),但慢慢会发现 “哪种动作能多拿奖励”(比如按 “先找货→再搬→再送” 的顺序做,奖励多),最后就会固定下这套 “能拿到最多奖励” 的动作逻辑 —— 这就是它学会的 “最优动作选择能力”。
增强学习中讨论的Agent 需要具备与环境的交互能力和自治能力,当 Agent 在其环境中做出每个动作时, 施教者会提供奖赏或惩罚信息,以表示结果状态的正确与否。
通常,强化学习任务用马尔科夫决策过程描述,常用的强化学习算法有蒙特卡洛强化学习算法和 Q-Learning 算法。
马尔科夫决策过程(MDP)是一种数学模型
用于刻画在不确定环境中,智能体通过一系列决策最大化长期收益的过程。核心是“马尔科夫性”:下一个状态只依赖当前状态和当前动作,与历史无关
蒙特卡洛强化学习:像 “靠多次试错总结经验”。
比如让智能体反复完成一整轮任务(比如从 “开始找货” 到 “找到货结束” 算一轮),每轮结束后,再回头算 “这轮里每个动作带来的总奖励”—— 比如某轮里 “走 A→B 货架” 最后拿到了 10 分奖励,就记下来 “这个动作好”,下次遇到同样状态优先选。靠多轮 “完整体验” 积累最优动作策略。
Q-Learning:像 “随时记笔记,实时更新经验”。
它会专门记一个 “Q 表”:表格里存着 “在某个状态下,做某个动作能拿到的预期奖励”(比如 “在 A 货架旁,选前进到 B 货架,预期能拿 8 分”)。智能体每做一次动作、拿到奖惩,就立刻更新 Q 表里的数值 —— 不用等一整轮结束,边做边改 “笔记”,更快调整动作选择,慢慢把 Q 表变得更准,最后按 Q 表选 “预期奖励最高” 的动作。
3.5 有监督学习算法和无监督学习算法的分类
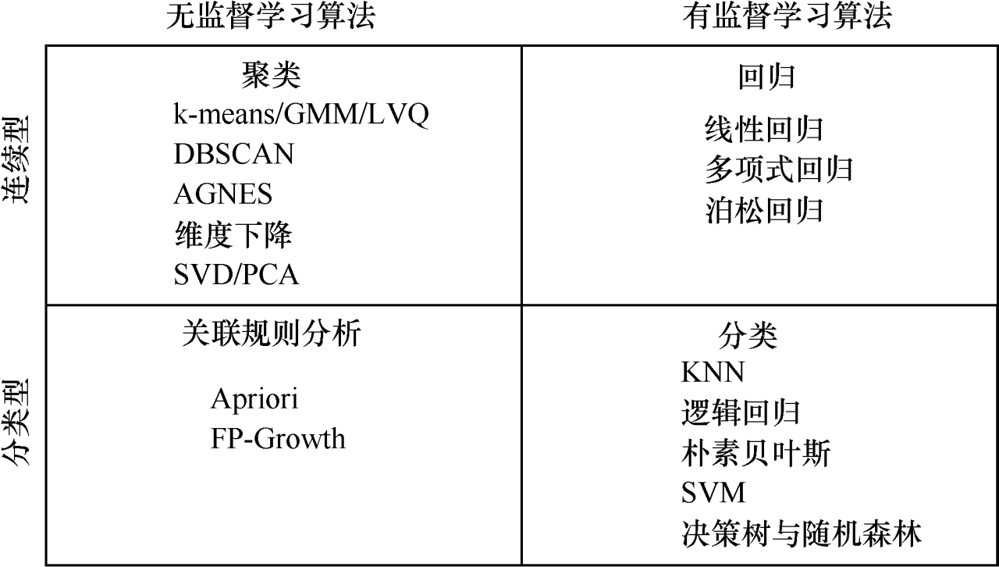
通常,根据属性值是否为连续属性(及是否可以取无限个可能值的属性),将有监督学习算法和无监督学习算法进一步分为四大类,如上图所示。
聚类 — 无监督+连续型属性
- K-means聚类
- 高斯混合聚类(GMM)
- 学习向量量化(LVQ)
- 聚类嵌套(AGNES)
分类 — 有监督+分类型属性
- K近邻(KNN)
- 逻辑回归
- 朴素贝叶斯
- 支持向量机(SVM)
- 决策树
- 随机森林
回归 — 有监督 + 连续型属性
- 线性回归
- 多项式回归
- 泊松回归
- 决策树
- 随机森林
决策树和随机森林既可以解决分类,也可以解决回归类问题
维度下降 — 无监督 + 连续型属性
- 奇异值分解(SVD)
- 主成分分析(PCA)
关联规则分析 — 无监督 + 分类型属性
- Aprori算法
- FP-Growth
3.6 算法选择
在数据科学项目中,算法的选择主要取决于:业务目的、样本和特征的个数、属性值是分类型还是离散型、数据集是否有标签信息等
当然,在实际项目中还需要考虑算法的可解释性(如集成学习算法、深度学习算法等)、是否支持内存计算、训练时间复杂度,以及预测时间复杂度等影响模型应用的具体因素
4.模型评估方法
4.1 学习曲线
学习曲线(Learning Curve)是用来可视化显示模型的“表现力”的一种工具。 学习曲线的横坐标和纵坐标分别为“训练样本数”和“得分”(如准确率或误差等)
通过学习曲线我们可以了解到所训练出的模型中是否存在过拟合或欠拟合现象
看学习曲线时,“一起低” 是欠拟合,“差距大” 是过拟合
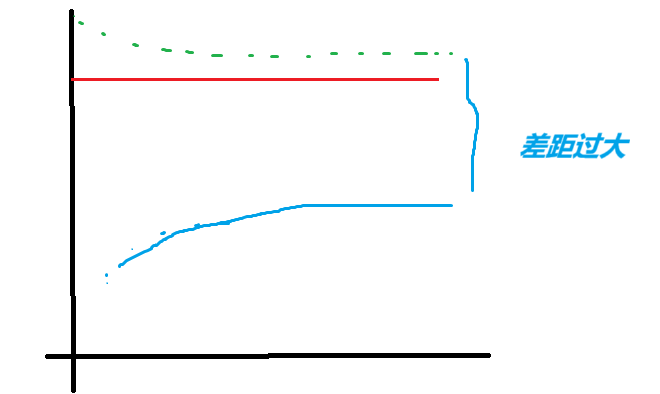
一起低
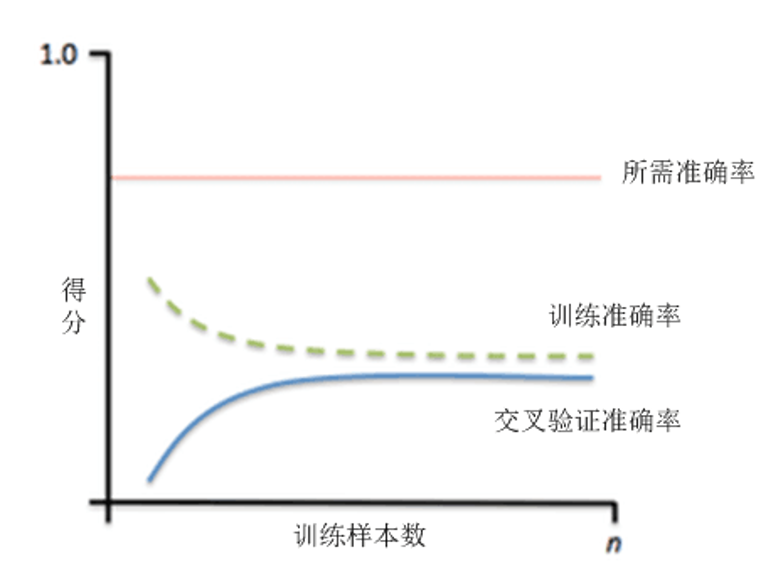
(1)高偏差
随着训练样本数增多,训练准确率和交叉验证准确率趋于收敛,但与所需准确率的偏差很大,如上图所示。
高偏差意味着模型在训练集和交叉验证集上的准确率都很低,很可能存在“欠拟合”现象。
欠拟合原因
- 训练出的模型过于简单
- 所选择的特征属性不能提供充分的信息
(2)高方差
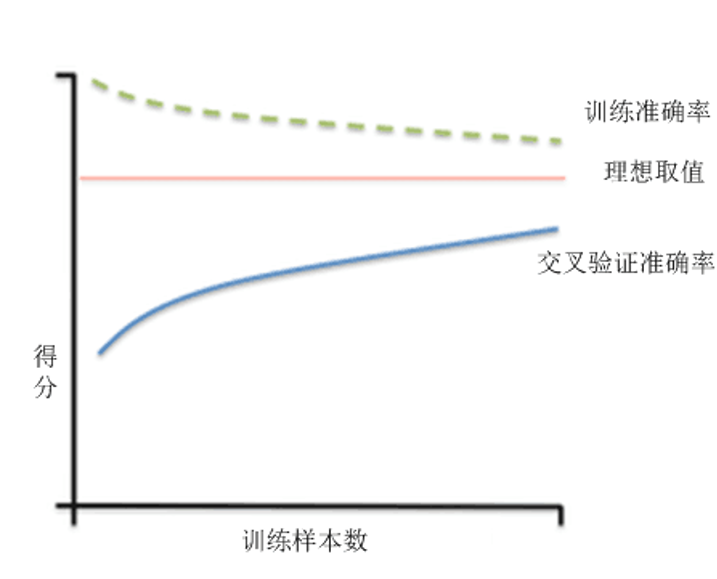
随着训练样本数增多,训练准确率趋于理想取值,但交叉验证准确率低于理想取值,如图所示。
高方差表示对应模型很可能存在“过拟合”现象。
过拟合原因:
- 训练出的模型过于复杂
- 所选择的特征属性太多,但训练样本数量太少
4.2 混淆矩阵
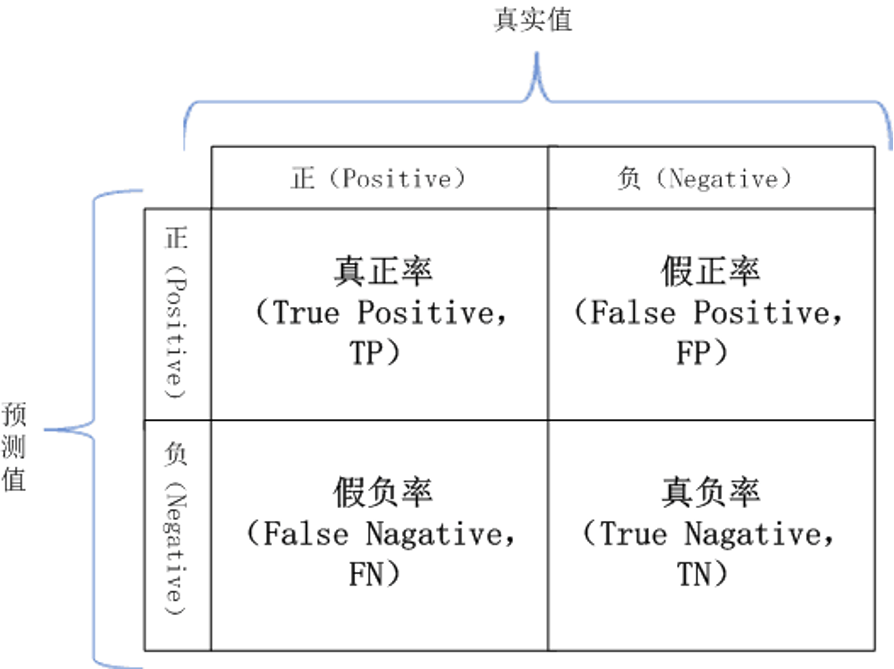
混淆矩阵(Confusion Matrix)是常用于评估有监督学习算法性能的一种工具,是计算精度和召回率等指标以及制作 ROC 曲线的基础,如图所示
其中,用“正例(Positive)”和“负例(Negative)”来表示样本的“类别”;用“真(True)”和“假(False)”来表示“模型预测是否为正确”。
- TP(True Positive):真正例,模型预测是正例,实际上也是正例
- FP(False Positive):假正例。模型预测是正例,但样本实际上是负例
- FN(False Nagative):假负例,模型预测是负例。但样本实际上是正例
- TN(True Nagative):真负例,模型预测是负例,样本实际上也是负例
模型精度(Precision)
在所有判别为正例的结果中,模型正确预测的样例所占的比例
Precision=TP(TP+FP)Precision=\frac{TP}{(TP+FP)} Precision=(TP+FP)TP
模型召回率(Recall)
在所有正例中,模型预测正确的样本所占的比例
Recall=TP(TP+FN)\mathrm{Recall=}\frac{\mathrm{TP}}{(\mathrm{TP+FN})} Recall=(TP+FN)TP
除了模型的精度和召回率,基于混淆矩阵可以定义的模型评估指标还有很多,包括正确率(Accuracy)、错误率(Misclassification/Error Rate)、特异性(Specificity)、 流行程度(Prevalence)等,由于篇幅所限,在此不再逐一详解。
4.3 ROC曲线与AUC面积
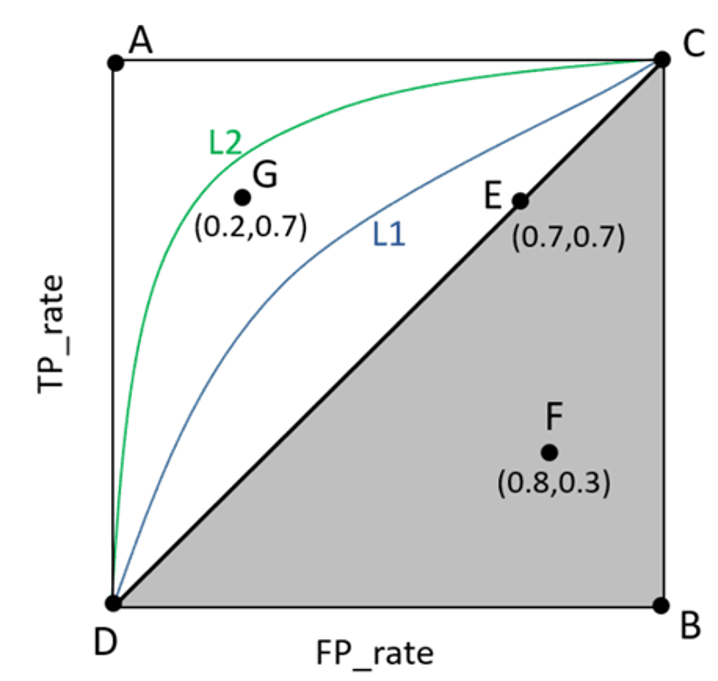
接受者操作特征(Receiver Operating Characteristic,ROC)曲线是以“假正率(FP_ rate)”和“真正率(TP_rate)”分别作为横坐标和纵坐标的曲线。
假正率FPR:模型误判负例为正例的比例
FPR = FP / (FP + TN),FPR 越低,说明模型 “冤枉负例” 的错误越少(比如更少正常邮件被误判为垃圾邮件);
真正率TPR/召回率 :模型正确识别正例的比例,
TPR = TP / (TP + FN),TPR 越高,说明模型 “抓正例” 的能力越强(比如能识别出更多真实垃圾邮件);
通常,人们将 ROC 曲线与“假正率”轴围成的面积称为“曲线之下的区域(Area Under Curve, AUC)面积”。AUC 面积越大,说明模型的性能越好
AUC 是 “ROC 曲线下方的面积”,本质是对 ROC 曲线的量化总结,用 0-1 之间的数值直接衡量模型性能:
- AUC=1:完美模型 → ROC 曲线经过左上角,能 100% 正确识别正例、0% 误判负例(现实中几乎不存在);
- AUC=0.5:随机模型 → ROC 曲线是一条从左下角到右上角的对角线,模型判断和 “抛硬币猜正反” 一样,毫无价值;
- AUC>0.5 且越接近 1:模型性能越好 → 比如 AUC=0.85 的模型,比 AUC=0.7 的模型更能准确区分正例和负例。
5.机器学习面临的挑战
- 算法的可解释性
- 过拟合
- 维度灾难
- 特征工程
- 算法的可扩展性
- 模型集成
数据层面的挑战
- 数据质量问题:实际数据常存在缺失、噪声(错误数据)、冗余(重复无价值信息),直接影响模型学习效果。
- 数据标签难题:有监督学习需要大量带标签数据,而标签标注耗时耗力,且部分场景(如医疗诊断)标签难以精准获取。
- 数据分布差异:训练集与真实应用场景的 “数据分布” 不一致(如训练用城市数据,实际用农村数据),导致模型泛化能力差。
模型层面的挑战
- 过拟合与欠拟合:模型太复杂易 “过拟合”(只适配训练数据,对新数据预测差),太简单易 “欠拟合”(连训练数据都学不好核心规律)。
- 模型可解释性差:部分复杂模型(如深度学习、随机森林)虽预测准确,但内部决策逻辑 “黑箱化”,难以解释 “为什么得出该结果”,限制医疗、金融等敏感场景应用。
- 算法选择与调参难:不同场景适配不同算法,且模型参数(如 k-means 的 k 值、正则化强度)需反复调试,无统一标准。
计算与资源层面的挑战
- 计算成本高:大规模数据或复杂模型(如深层神经网络)训练需大量算力,普通设备难以支撑,且训练时间长。
- 内存与存储压力:海量原始数据和模型参数对存储资源要求高,尤其实时处理场景(如实时推荐)需平衡速度与资源消耗。
应用落地层面的挑战
- 泛化能力不足:模型在训练集表现好,但面对真实环境中的新情况(如突发异常数据、场景变化),预测准确率大幅下降。
- 业务适配性差:模型效果与业务需求脱节(如只追求准确率,却忽略落地时的响应速度、成本控制),难以实际应用。

