定积分的几何应用（一）：平面图形面积计算详解

用数学的语言描述世界，用计算的力量解决问题

定积分是微积分中的核心概念之一，它不仅在数学理论中占有重要地位，更在各个领域的实际问题解决中发挥着巨大作用。本文将重点介绍定积分在几何学中的应用，特别是如何利用定积分计算平面图形的面积。

一、微元法：定积分应用的基础思想

1. 数学定义

微元法是定积分应用的基本方法，其核心思想是"以直代曲"和"无限细分"。当一个量与自变量$x$的变化区间$[a,b]$有关，且满足可加性（即整体量等于各部分量之和）时，我们可以通过微元法将其表示为定积分。

具体来说，如果要求计算的量$I$在区间微元$[x,x+dx]$上的部分量$\Delta I$可以近似表示为$\Delta I\approx f(x)dx$，且误差是比$dx$高阶的无穷小，那么总量$I$就可以表示为定积分$I={\int }_a^{b}f(x)dx$。

2. 手动求解

微元法的应用通常分为三个步骤：

1. 选取积分变量，确定积分区间$[a,b]$
2. 确定微元表达式，在小区间$[x,x+dx]$上找出部分量的近似值$dI=f(x)dx$
3. 积分求解，将微元在区间$[a,b]$上积分$I={\int }_a^{b}f(x)dx$

以曲边梯形为例，我们可以在$[x,x+dx]$上用小矩形面积近似代替小曲边梯形面积，从而得到面积微元$dA=f(x)dx$，整个图形的面积就是$A={\int }_a^{b}f(x)dx$。

3. Python代码

下面是使用Python实现微元法计算曲边梯形面积的示例代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate# 定义函数
def f(x):return x**2 + 1# 微元法计算面积
def area_by_infinitesimal(a, b, n=1000):"""使用微元法计算曲边梯形面积a, b: 积分区间n: 划分的小区间数量"""x = np.linspace(a, b, n+1)dx = (b - a) / narea_elements = f(x[:-1]) * dx  # 每个小微元的面积total_area = np.sum(area_elements)return total_area# 积分区间
a, b = 0, 2# 使用scipy的积分函数验证结果
area_integrate, error = integrate.quad(f, a, b)# 不同的n值
n_values = [10000, 1000000, 10000000]for n in n_values:# 计算面积area = area_by_infinitesimal(a, b, n)print(f"n = {n:>10,}:")print(f"微元法计算的面积: {area:.6f}")print(f"积分函数计算的面积: {area_integrate:.6f}")print(f"绝对误差: {abs(area - area_integrate):.6f}")print()

4. Python代码执行结果

从执行结果可以看出，微元法计算结果与直接积分结果一致，验证了微元法的正确性。当小区间划分越细（n值越大），计算结果越精确。

二、直角坐标系下的平面图形面积

1. 数学定义

在直角坐标系中，由曲线$y=f(x)$，$y=g(x)$（其中$f(x)\ge g(x)$）及直线$x=a$，$x=b$（$a<b$）所围成的平面图形面积为：

$$A={\int }_a^b[f(x)-g(x)]dx$$

如果$f(x)$和$g(x)$的位置关系不确定，则应使用绝对值形式：

$$A={\int }_a^b|f(x)-g(x)|dx$$

2. 手动求解

计算直角坐标系下平面图形面积的一般步骤：

1. 画出图形草图，确定积分变量和积分区间
2. 求交点坐标，解方程$f(x)=g(x)$得到交点横坐标
3. 确定被积函数，根据曲线上下位置关系确定$f(x)-g(x)$或$g(x)-f(x)$
4. 计算定积分，得到图形面积

示例：求由抛物线$y=x^2$及直线$y=3x$所围图形的面积。

解：

1. 求交点：解方程$x^2=3x$，得$x=0$或$x=3$
2. 在区间$[0,3]$上，$3x\ge x^2$
3. 面积公式：$A={\int }_0^3(3x-x^2)dx$
4. 计算积分：$A={\left[\frac{3}{2}{x}^2-\frac{1}{3}{x}^3\right]}_0^3=\frac{27}{2}-9=\frac{9}{2}$

3. Python代码

import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 定义两个函数
def f1(x):return x**2  # y = x^2def f2(x):return 3*x   # y = 3x# 计算交点
def find_intersection(f, g, x_range):x = np.linspace(x_range[0], x_range[1], 1000)diff = f(x) - g(x)intersections = []for i in range(len(diff)-1):if diff[i] * diff[i+1] <= 0:x_root = x[i] - diff[i] * (x[i+1] - x[i]) / (diff[i+1] - diff[i])intersections.append(x_root)return intersections# 计算两条曲线之间的面积
def area_between_curves(f, g, a, b):"""计算函数f(x)和g(x)在区间[a,b]之间的面积"""# 确保f(x) >= g(x)，否则取绝对值area = integrate.quad(lambda x: abs(f(x) - g(x)), a, b)return area# 定义积分区间
x_range = [-1, 4]# 求交点
intersections = find_intersection(f1, f2, x_range)
formatted_intersections = [f"{x:.8f}" for x in intersections]  # 保留8位小数
print(f"交点横坐标: {formatted_intersections}")# 计算面积
area, error = area_between_curves(f1, f2, intersections[0], intersections[1])print(f"两条曲线之间的面积为: {area:.6f}")# 可视化
x = np.linspace(-1, 4, 1000)
y1 = f1(x)
y2 = f2(x)plt.figure(figsize=(10, 6))
plt.plot(x, y1, 'b-', label='$y = x^2$', linewidth=2)
plt.plot(x, y2, 'r-', label='$y = 3x$', linewidth=2)plt.fill_between(x, y1, y2, where=(x >= intersections[0]) & (x <= intersections[1]), alpha=0.3, color='green', label='面积区域')
plt.xlabel('x')
plt.ylabel('y')
plt.title('两条曲线围成的图形面积')
plt.legend()
plt.grid(True)
plt.show()

4. Python代码执行结果

可视化图表将显示两条曲线和它们之间的面积区域，直观展示计算结果。

三、极坐标系下的平面图形面积

1. 数学定义

在极坐标系中，由曲线$r=r(\theta )$及射线$\theta =\alpha$，$\theta =\beta$（$\alpha <\beta$）所围成的平面图形面积为：

$$A=\frac{1}{2}{\int }_{\alpha }^{\beta }{r}^2(\theta )d\theta$$

这一公式的推导基于扇形面积公式$dA=\frac{1}{2}{r}^{2}d\theta$，通过积分将无数个小扇形面积累加得到整个图形面积。

2. 手动求解

极坐标系下计算平面图形面积的步骤：

1. 确定积分变量和积分区间，通常以极角$\theta$为积分变量
2. 写出极径函数$r=r(\theta )$
3. 写出面积微元$dA=\frac{1}{2}{r}^2(\theta )d\theta$
4. 计算定积分，得到图形面积

示例：求心形线$r=a(1+\cos \theta )$（$a>0$）所围图形的面积。

解：

1. 心形线关于极轴对称，只需计算$0\le \theta \le \pi$部分再乘以2
2. 面积公式：$A=2\times \frac{1}{2}{\int }_0^{\pi }[a(1+\cos \theta ){]}^{2}d\theta =a^2{\int }_0^{\pi }(1+2\cos \theta +{\cos }^2\theta )d\theta$
3. 计算积分： ${\int }_0^{\pi }1d\theta =\pi$ ${\int }_0^{\pi }2\cos \theta d\theta =2\sin \theta {|}_0^{\pi }=0$ ${\int }_0^{\pi }{\cos }^2\theta d\theta ={\int }_0^{\pi }\frac{1+\cos 2\theta }{2}d\theta =\frac{\pi }{2}$
4. 总面积：$A=a^2(\pi +0+\frac{\pi }{2})=\frac{3}{2}\pi a^2$

3. Python代码

import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate# 定义极坐标函数
def r(theta, a=1):"""心形线方程"""return a * (1 + np.cos(theta))# 极坐标下的面积计算
def polar_area(r_func, alpha, beta, a=1):"""计算极坐标曲线围成的面积r_func: 极径函数alpha, beta: 积分区间"""# 定义被积函数def integrand(theta):return 0.5 * (r_func(theta, a))**2area, error = integrate.quad(integrand, alpha, beta)return area, error# 计算心形线面积
a = 1
area, error = polar_area(r, 0, 2*np.pi, a)print(f"心形线围成的面积: {area:.6f}")
print(f"理论面积: {1.5 * np.pi * a**2:.6f}")# 可视化心形线
theta = np.linspace(0, 2*np.pi, 1000)
radius = r(theta, a)# 极坐标转直角坐标
x = radius * np.cos(theta)
y = radius * np.sin(theta)plt.figure(figsize=(8, 8))
plt.plot(x, y, 'r-', linewidth=2)
plt.fill(x, y, alpha=0.3, color='red')
plt.title('心形线 $r = 1 + \\cos\\theta$')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.axis('equal')
plt.show()

4. Python代码执行结果

心形线的可视化图形将展示一个典型的心形曲线，帮助我们直观理解极坐标系下的面积计算。

四、参数方程表示的曲线围成的面积

1. 数学定义

当曲线由参数方程$\{\begin{array}{l}x=x(t)\\ y=y(t)\end{array}$（$t\in [\alpha ,\beta ]$）给出时，由该曲线与$x$轴所围成的图形面积为：

$$A={\int }_{\alpha }^{\beta }y(t)x^{\prime }(t)dt$$

这一公式可由直角坐标系下的面积公式通过变量替换得到。

2. 手动求解

参数方程下计算面积的步骤：

1. 确定参数范围$t\in [\alpha ,\beta ]$
2. 写出微分关系$dx=x^{\prime }(t)dt$
3. 代入面积公式$A={\int }_{\alpha }^{\beta }y(t)x^{\prime }(t)dt$
4. 计算定积分

示例：求椭圆$\{\begin{array}{l}x=a\cos t\\ y=b\sin t\end{array}$（$0\le t\le 2\pi$）所围图形的面积。

解：

1. 由于椭圆关于坐标轴对称，只需计算第一象限面积再乘以4
2. 第一象限对应$t\in [0,\frac{\pi }{2}]$
3. $x^{\prime }(t)=-a\sin t$
4. 面积：$A=4{\int }_0^{\frac{\pi }{2}}y(t)x^{\prime }(t)dt=4{\int }_0^{\frac{\pi }{2}}b\sin t\cdot (-a\sin t)dt=-4ab{\int }_0^{\frac{\pi }{2}}{\sin }^{2}tdt$
5. 计算积分：${\int }_0^{\frac{\pi }{2}}{\sin }^{2}tdt={\int }_0^{\frac{\pi }{2}}\frac{1-\cos 2t}{2}dt=\frac{\pi }{4}$
6. 总面积：$A=-4ab\cdot \frac{\pi }{4}=-\pi ab$（取绝对值得$A=\pi ab$）

3. Python代码

import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate# 椭圆的参数方程
def x(t, a=2):return a * np.cos(t)def y(t, b=1):return b * np.sin(t)# 导数函数
def dx_dt(t, a=2):return -a * np.sin(t)# 参数方程下的面积计算
def parametric_area(x, y, dx_dt, alpha, beta, a=2, b=1):"""计算参数方程表示的曲线围成的面积"""def integrand(t):return y(t, b) * dx_dt(t, a)area, error = integrate.quad(integrand, alpha, beta)return abs(area), error  # 取绝对值确保面积为正# 计算椭圆面积
a, b = 2, 1
area, error = parametric_area(x, y, dx_dt, 0, 2*np.pi, a, b)print(f"椭圆面积: {area:.6f}")
print(f"理论面积: {np.pi * a * b:.6f}")# 可视化椭圆
t = np.linspace(0, 2*np.pi, 1000)
x_vals = x(t, a)
y_vals = y(t, b)plt.figure(figsize=(8, 6))
plt.plot(x_vals, y_vals, 'b-', linewidth=2)
plt.fill(x_vals, y_vals, alpha=0.3, color='blue')
plt.title(f'椭圆 $\\frac{{x^2}}{{{a}^2}} + \\frac{{y^2}}{{{b}^2}} = 1$')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.axis('equal')
plt.show()

4. Python代码执行结果

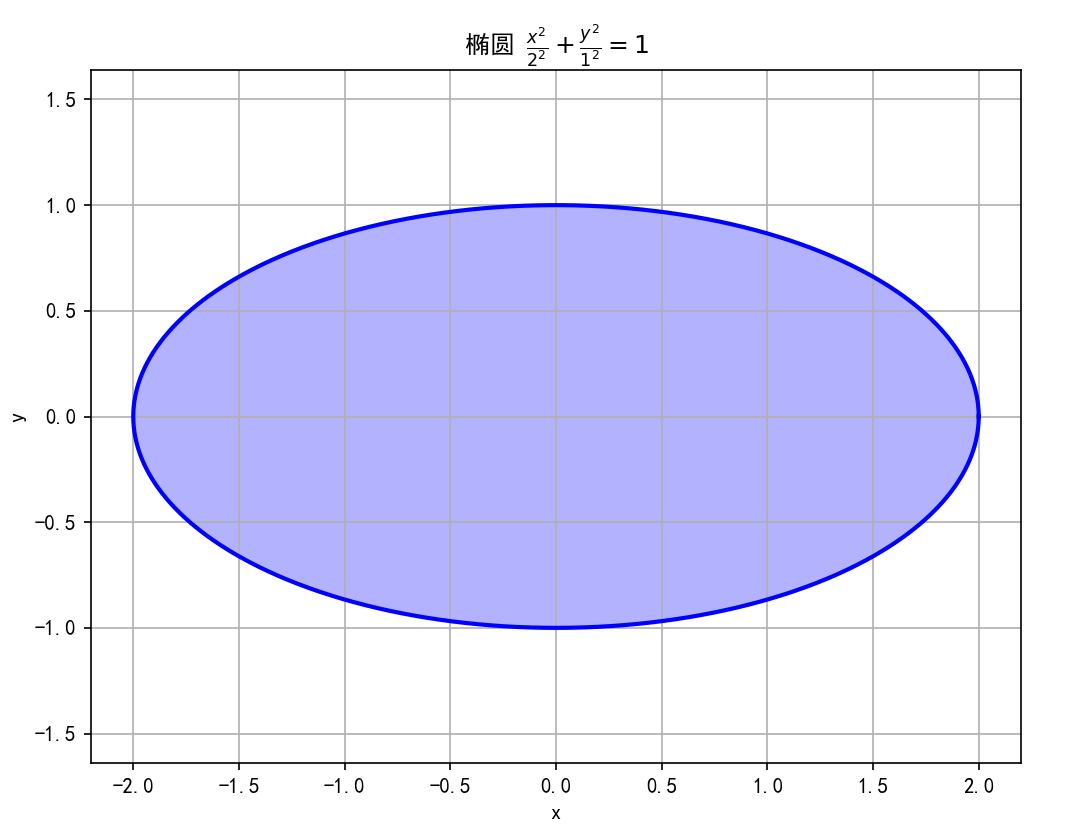
椭圆面积的计算结果与理论值完全一致，验证了参数方程下面积计算方法的正确性。

总结

本文详细介绍了定积分在几何学中的应用，重点讨论了平面图形面积的计算方法。我们通过微元法这一核心思想，分别讲解了直角坐标系、极坐标系和参数方程形式下面积计算的具体步骤。

以下是三种不同情况下面积计算方法的对比：

坐标系	面积公式	应用场景
直角坐标系	$A={\int }_a^b[f(x)-g(x)]dx$	适用于$y$关于$x$的函数关系明确的情况
极坐标系	$A=\frac{1}{2}{\int }_{\alpha }^{\beta }{r}^2(\theta )d\theta$	适用于曲线用极坐标表示更简单的情况
参数方程	$A={\int }_{\alpha }^{\beta }y(t)x^{\prime }(t)dt$	适用于曲线用参数方程表示的情况

掌握这些方法的关键在于理解微元法的思想，并根据具体问题选择合适的积分变量和积分区间。在实际应用中，画出图形草图可以帮助我们更好地理解问题，确定积分上下限和被积函数。

下一篇文章我们将继续探讨定积分在几何学中的其他应用，包括旋转体体积计算、曲线弧长计算等主题。

---

往期精彩回顾：

• 用Python来学微积分35-变上限定积分
• 用Python来学微积分36-牛顿 - 莱布尼茨公式的深度解析

专栏导航目录 《程序员AI之路：从Python起步》完全学习导航

完整代码已开源 ai-learning-path，欢迎Star和Fork！

---

参考资料：

1. 扈志明《微积分》教材

互动邀请：如果你对本章内容有独特的理解或在实际应用中遇到过有趣的问题，欢迎在评论区分享交流！