定积分的几何应用(二):旋转体体积与曲线弧长计算详解
文章目录
- 一、旋转体的体积计算
- 1. 圆盘法(Disk Method)
- 数学定义
- 手动求解
- Python代码
- Python代码执行结果
- 2. 壳层法(Shell Method)
- 数学定义
- 手动求解
- Python代码
- Python代码执行结果
- 二、平面曲线的弧长计算
- 1. 直角坐标方程下的弧长计算
- 数学定义
- 手动求解
- Python代码
- Python代码执行结果
- 2. 参数方程下的弧长计算
- 数学定义
- 手动求解
- Python代码
- Python代码执行结果
- 3. 极坐标方程下的弧长计算
- 数学定义
- 手动求解
- Python代码
- Python代码执行结果
- 三、方法选择与应用技巧
- 旋转体体积计算方法选择
- 曲线弧长计算方法选择
- 总结
从平面到空间,从面积到体积,用微积分探索几何世界的奥秘
在上一篇文章中,我们详细讨论了定积分在平面图形面积计算中的应用。本文将深入探讨定积分在几何学中另外两个重要应用:旋转体体积的计算和曲线弧长的求解。这些内容不仅在数学理论中具有重要意义,在工程、物理和计算机图形学等领域也有广泛应用。
一、旋转体的体积计算
旋转体是指一个平面图形绕该平面内的一条直线(旋转轴)旋转一周而形成的立体图形。计算旋转体体积的主要方法有圆盘法(Disk Method)和壳层法(Shell Method)。
1. 圆盘法(Disk Method)
数学定义
圆盘法适用于平面图形绕坐标轴旋转的情形。设函数 y = f ( x ) y = f(x) y=f(x)在区间 [ a , b ] [a,b] [a,b]上连续且非负,则由曲线 y = f ( x ) y = f(x) y=f(x)、直线 x = a x = a x=a、 x = b x = b x=b及 x x x轴所围成的平面图形绕 x x x轴旋转一周所得的旋转体体积为:
V = π ∫ a b [ f ( x ) ] 2 d x V = \pi \int_a^b [f(x)]^2 dx V=π∫ab[f(x)]2dx
同理,如果曲线由 x = g ( y ) x = g(y) x=g(y)表示,且绕 y y y轴旋转,则体积公式为:
V = π ∫ c d [ g ( y ) ] 2 d y V = \pi \int_c^d [g(y)]^2 dy V=π∫cd[g(y)]2dy
手动求解
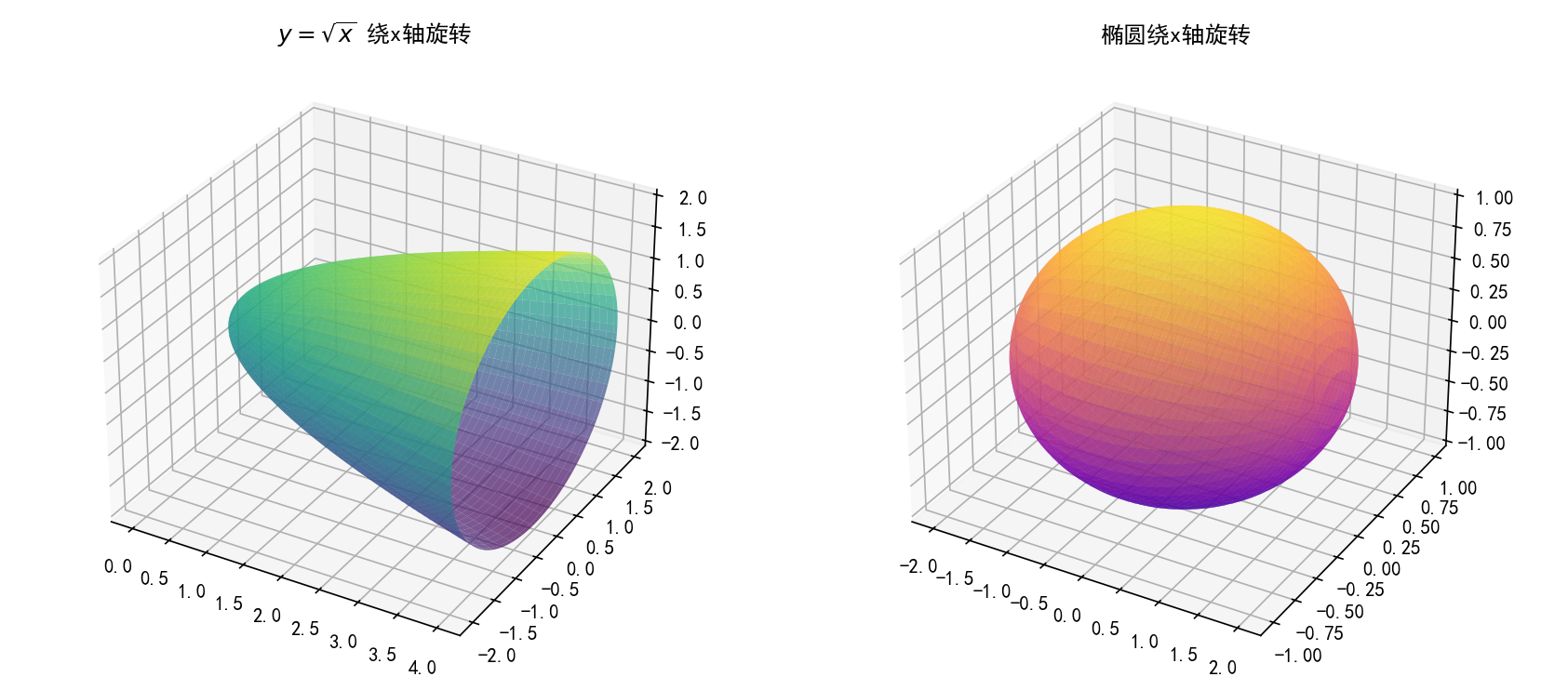
示例1:求由曲线 y = x y = \sqrt{x} y=x在区间 [ 0 , 4 ] [0,4] [0,4]上绕 x x x轴旋转所形成的旋转体体积。
解:
- 确定被积函数: f ( x ) = x f(x) = \sqrt{x} f(x)=x,区间 [ 0 , 4 ] [0,4] [0,4]
- 应用圆盘法公式: V = π ∫ 0 4 ( x ) 2 d x = π ∫ 0 4 x d x V = \pi \int_0^4 (\sqrt{x})^2 dx = \pi \int_0^4 x dx V=π∫04(x)2dx=π∫04xdx
- 计算定积分: ∫ 0 4 x d x = [ x 2 2 ] 0 4 = 16 2 = 8 \int_0^4 x dx = \left[\frac{x^2}{2}\right]_0^4 = \frac{16}{2} = 8 ∫04xdx=[2x2]04=216=8
- 求得体积: V = π × 8 = 8 π V = \pi \times 8 = 8\pi V=π×8=8π
示例2:计算椭圆 x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 a2x2+b2y2=1绕 x x x轴旋转所形成的旋转体(旋转椭球体)体积。
解:
- 将椭圆方程改写为 y = b a a 2 − x 2 y = \frac{b}{a} \sqrt{a^2 - x^2} y=aba2−x2, x ∈ [ − a , a ] x \in [-a,a] x∈[−a,a]
- 由于对称性,只需计算 [ 0 , a ] [0,a] [0,a]区间再乘以2: V = 2 π ∫ 0 a ( b a a 2 − x 2 ) 2 d x = 2 π b 2 a 2 ∫ 0 a ( a 2 − x 2 ) d x V = 2\pi \int_0^a \left(\frac{b}{a} \sqrt{a^2 - x^2}\right)^2 dx = 2\pi \frac{b^2}{a^2} \int_0^a (a^2 - x^2) dx V=2π∫0a(aba2−x2)2dx=2πa2b2∫0a(a2−x2)dx
- 计算积分: ∫ 0 a ( a 2 − x 2 ) d x = [ a 2 x − x 3 3 ] 0 a = a 3 − a 3 3 = 2 3 a 3 \int_0^a (a^2 - x^2) dx = \left[a^2x - \frac{x^3}{3}\right]_0^a = a^3 - \frac{a^3}{3} = \frac{2}{3}a^3 ∫0a(a2−x2)dx=[a2x−3x3]0a=a3−3a3=32a3
- 求得体积: V = 2 π b 2 a 2 × 2 3 a 3 = 4 3 π a b 2 V = 2\pi \frac{b^2}{a^2} \times \frac{2}{3}a^3 = \frac{4}{3}\pi ab^2 V=2πa2b2×32a3=34πab2
Python代码
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate# 圆盘法计算旋转体体积
def disk_method(f, a, b, axis='x'):"""使用圆盘法计算旋转体体积f: 函数a, b: 积分区间axis: 旋转轴,'x'或'y'"""if axis == 'x':# 绕x轴旋转,对x积分volume, error = integrate.quad(lambda x: np.pi * (f(x))**2, a, b)else:# 绕y轴旋转,需要反函数关系# 这里假设f是x关于y的函数volume, error = integrate.quad(lambda y: np.pi * (f(y))**2, a, b)return volume, error# 示例1:y = sqrt(x) 在 [0,4] 上绕x轴旋转
def f1(x):return np.sqrt(x)volume1, error1 = disk_method(f1, 0, 4, 'x')
print(f"旋转体体积1: {volume1:.6f} (理论值: {8*np.pi:.6f})")# 示例2:椭圆绕x轴旋转
a, b = 2, 1 # 椭圆长半轴和短半轴
def ellipse_y(x):return (b/a) * np.sqrt(a**2 - x**2)volume2, error2 = disk_method(ellipse_y, -a, a, 'x')
theoretical_volume = (4/3) * np.pi * a * b**2
print(f"旋转椭球体体积: {volume2:.6f} (理论值: {theoretical_volume:.6f})")# 可视化
fig = plt.figure(figsize=(12, 5))# 第一个子图:y = sqrt(x)
ax1 = fig.add_subplot(121, projection='3d')
x1 = np.linspace(0, 4, 100)
theta = np.linspace(0, 2*np.pi, 100)
X1, Theta = np.meshgrid(x1, theta)
Y1 = f1(X1) * np.cos(Theta)
Z1 = f1(X1) * np.sin(Theta)
ax1.plot_surface(X1, Y1, Z1, alpha=0.7, cmap='viridis')
ax1.set_title(r'$y = \sqrt{x}$ 绕x轴旋转')# 第二个子图:椭圆旋转
ax2 = fig.add_subplot(122, projection='3d')
x2 = np.linspace(-a, a, 100)
X2, Theta2 = np.meshgrid(x2, theta)
Y2 = ellipse_y(X2) * np.cos(Theta2)
Z2 = ellipse_y(X2) * np.sin(Theta2)
ax2.plot_surface(X2, Y2, Z2, alpha=0.7, cmap='plasma')
ax2.set_title('椭圆绕x轴旋转')plt.tight_layout()
plt.show()
Python代码执行结果

2. 壳层法(Shell Method)
数学定义
当旋转轴与积分变量垂直时,壳层法通常更为简便。设函数 y = f ( x ) y = f(x) y=f(x)在区间 [ a , b ] [a,b] [a,b]上连续且非负,则该曲线绕 y y y轴旋转所形成的旋转体体积为:
V = 2 π ∫ a b x f ( x ) d x V = 2\pi \int_a^b x f(x) dx V=2π∫abxf(x)dx
同理,如果曲线由 x = g ( y ) x = g(y) x=g(y)表示,且绕 x x x轴旋转,则体积公式为:
V = 2 π ∫ c d y g ( y ) d y V = 2\pi \int_c^d y g(y) dy V=2π∫cdyg(y)dy
手动求解
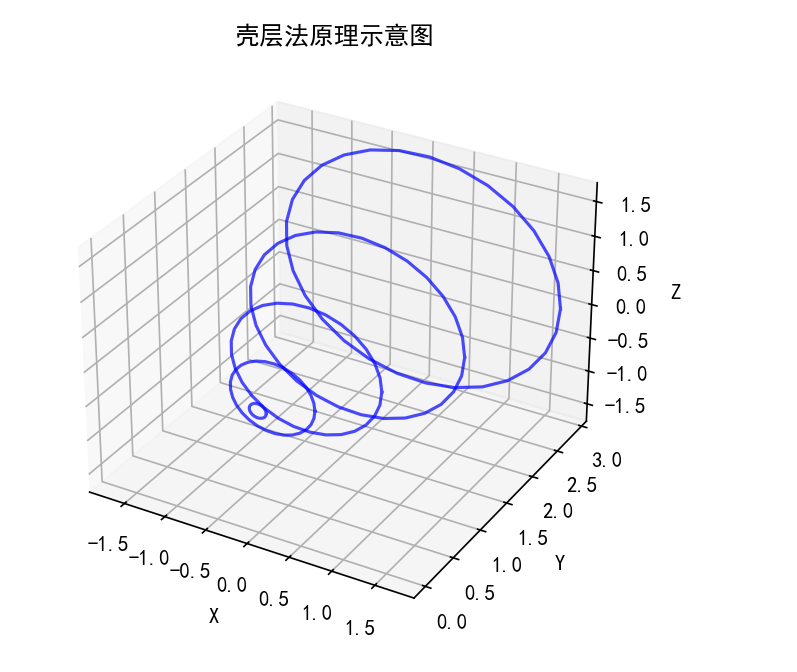
示例:求曲线 y = x 2 y = x^2 y=x2在区间 [ 0 , 2 ] [0,2] [0,2]上绕 y y y轴旋转所形成的旋转体体积。
解:
- 确定被积函数: f ( x ) = x 2 f(x) = x^2 f(x)=x2,区间 [ 0 , 2 ] [0,2] [0,2]
- 应用壳层法公式: V = 2 π ∫ 0 2 x ⋅ x 2 d x = 2 π ∫ 0 2 x 3 d x V = 2\pi \int_0^2 x \cdot x^2 dx = 2\pi \int_0^2 x^3 dx V=2π∫02x⋅x2dx=2π∫02x3dx
- 计算定积分: ∫ 0 2 x 3 d x = [ x 4 4 ] 0 2 = 16 4 = 4 \int_0^2 x^3 dx = \left[\frac{x^4}{4}\right]_0^2 = \frac{16}{4} = 4 ∫02x3dx=[4x4]02=416=4
- 求得体积: V = 2 π × 4 = 8 π V = 2\pi \times 4 = 8\pi V=2π×4=8π
验证(圆盘法): 将函数改写为 x = y x = \sqrt{y} x=y, y ∈ [ 0 , 4 ] y \in [0,4] y∈[0,4],则: V = π ∫ 0 4 ( y ) 2 d y = π ∫ 0 4 y d y = π [ y 2 2 ] 0 4 = π × 8 = 8 π V = \pi \int_0^4 (\sqrt{y})^2 dy = \pi \int_0^4 y dy = \pi \left[\frac{y^2}{2}\right]_0^4 = \pi \times 8 = 8\pi V=π∫04(y)2dy=π∫04ydy=π[2y2]04=π×8=8π 两种方法结果一致。
Python代码
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate# 壳层法计算旋转体体积
def shell_method(f, a, b, axis='y'):"""使用壳层法计算旋转体体积f: 函数a, b: 积分区间axis: 旋转轴,'y'表示绕y轴旋转,'x'表示绕x轴旋转"""if axis == 'y':# 绕y轴旋转,对x积分volume, error = integrate.quad(lambda x: 2 * np.pi * x * f(x), a, b)else:# 绕x轴旋转,对y积分# 这里假设f是x关于y的函数volume, error = integrate.quad(lambda y: 2 * np.pi * y * f(y), a, b)return volume, error# 示例:y = x^2 在 [0,2] 上绕y轴旋转
def f2(x):return x**2volume_shell, error_shell = shell_method(f2, 0, 2, 'y')# 使用圆盘法验证
def inverse_f2(y):return np.sqrt(y) # x = sqrt(y)volume_disk, error_disk = integrate.quad(lambda y: np.pi * (inverse_f2(y))**2, 0, 4)print(f"壳层法计算的体积: {volume_shell:.6f}")
print(f"圆盘法计算的体积: {volume_disk:.6f}")
print(f"理论值: {8*np.pi:.6f}")# 可视化壳层法原理
x = np.linspace(0.1, 2, 20) # 避免x=0
theta = np.linspace(0, 2*np.pi, 50)fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection='3d')# 绘制几个代表性的圆柱壳
for i, xi in enumerate(x[::4]): # 每隔4个取一个点theta_i = np.linspace(0, 2*np.pi, 30)y_i = f2(xi) * np.ones_like(theta_i)x_i = xi * np.cos(theta_i)z_i = xi * np.sin(theta_i)ax.plot(x_i, y_i, z_i, 'b-', alpha=0.7)ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('壳层法原理示意图')plt.show()
Python代码执行结果

二、平面曲线的弧长计算
计算平面曲线的弧长是定积分的另一重要几何应用。根据曲线方程的不同形式,弧长计算公式也有所不同。
1. 直角坐标方程下的弧长计算
数学定义
设曲线 C C C由方程 y = f ( x ) y = f(x) y=f(x)给出,且 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上具有一阶连续导数,则曲线 C C C从 x = a x = a x=a到 x = b x = b x=b的弧长为:
L = ∫ a b 1 + [ f ′ ( x ) ] 2 d x L = \int_a^b \sqrt{1 + [f'(x)]^2} dx L=∫ab1+[f′(x)]2dx
这一公式的推导基于微分三角形思想:弧长微元 d s = ( d x ) 2 + ( d y ) 2 = 1 + ( d y d x ) 2 d x ds = \sqrt{(dx)^2 + (dy)^2} = \sqrt{1 + \left(\frac{dy}{dx}\right)^2} dx ds=(dx)2+(dy)2=1+(dxdy)2dx。
手动求解
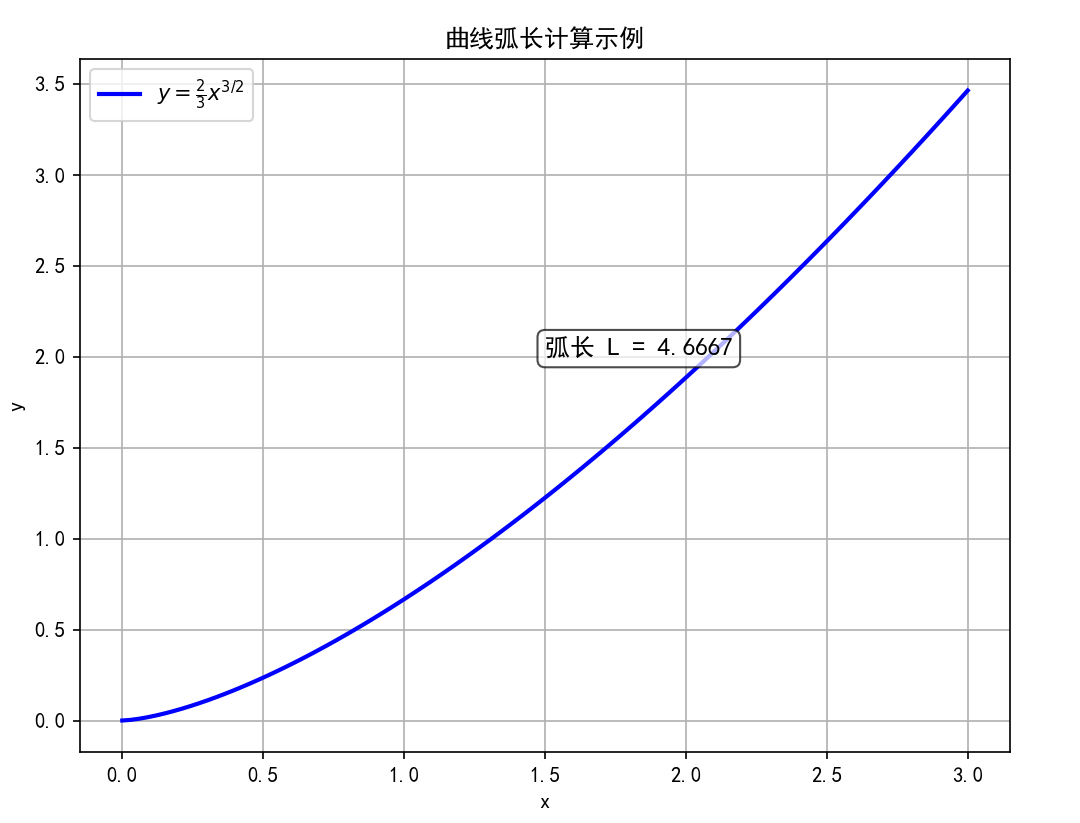
示例:求曲线 y = 2 3 x 3 / 2 y = \frac{2}{3}x^{3/2} y=32x3/2在区间 [ 0 , 3 ] [0,3] [0,3]上的弧长。
解:
- 求导数: f ′ ( x ) = 2 3 ⋅ 3 2 x 1 / 2 = x f'(x) = \frac{2}{3} \cdot \frac{3}{2} x^{1/2} = \sqrt{x} f′(x)=32⋅23x1/2=x
- 构造被积函数: 1 + [ f ′ ( x ) ] 2 = 1 + x \sqrt{1 + [f'(x)]^2} = \sqrt{1 + x} 1+[f′(x)]2=1+x
- 计算弧长: L = ∫ 0 3 1 + x d x L = \int_0^3 \sqrt{1 + x} dx L=∫031+xdx
- 计算积分:令 u = 1 + x u = 1 + x u=1+x,则 d u = d x du = dx du=dx,当 x = 0 x=0 x=0时 u = 1 u=1 u=1, x = 3 x=3 x=3时 u = 4 u=4 u=4 L = ∫ 1 4 u d u = [ 2 3 u 3 / 2 ] 1 4 = 2 3 ( 8 − 1 ) = 14 3 L = \int_1^4 \sqrt{u} du = \left[\frac{2}{3}u^{3/2}\right]_1^4 = \frac{2}{3}(8 - 1) = \frac{14}{3} L=∫14udu=[32u3/2]14=32(8−1)=314
Python代码
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate# 直角坐标下弧长计算
def arc_length_cartesian(f, f_prime, a, b):"""计算直角坐标系下曲线的弧长f: 函数f_prime: 函数的导数a, b: 积分区间"""def integrand(x):return np.sqrt(1 + f_prime(x)**2)length, error = integrate.quad(integrand, a, b)return length, error# 示例:y = (2/3)x^(3/2) 在 [0,3] 上的弧长
def f3(x):return (2/3) * x**(3/2)def f3_prime(x):return np.sqrt(x)length1, error1 = arc_length_cartesian(f3, f3_prime, 0, 3)
print(f"曲线弧长: {length1:.6f} (理论值: {14/3:.6f})")# 可视化曲线
x = np.linspace(0, 3, 100)
y = f3(x)plt.figure(figsize=(8, 6))
plt.plot(x, y, 'b-', linewidth=2, label='$y = \\frac{2}{3}x^{3/2}$')
plt.xlabel('x')
plt.ylabel('y')
plt.title('曲线弧长计算示例')
plt.grid(True)
plt.legend()# 标注弧长
plt.text(1.5, 2, f'弧长 L = {length1:.4f}', fontsize=12, bbox=dict(boxstyle="round,pad=0.3", facecolor="white", alpha=0.7))plt.show()
Python代码执行结果

2. 参数方程下的弧长计算
数学定义
若曲线由参数方程 { x = x ( t ) y = y ( t ) \begin{cases} x = x(t) \\ y = y(t) \end{cases} {x=x(t)y=y(t)( t ∈ [ α , β ] t \in [\alpha, \beta] t∈[α,β])给出,且 x ( t ) x(t) x(t)和 y ( t ) y(t) y(t)在 [ α , β ] [\alpha, \beta] [α,β]上具有连续导数,则弧长公式为:
L = ∫ α β ( d x d t ) 2 + ( d y d t ) 2 d t L = \int_{\alpha}^{\beta} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} dt L=∫αβ(dtdx)2+(dtdy)2dt
手动求解
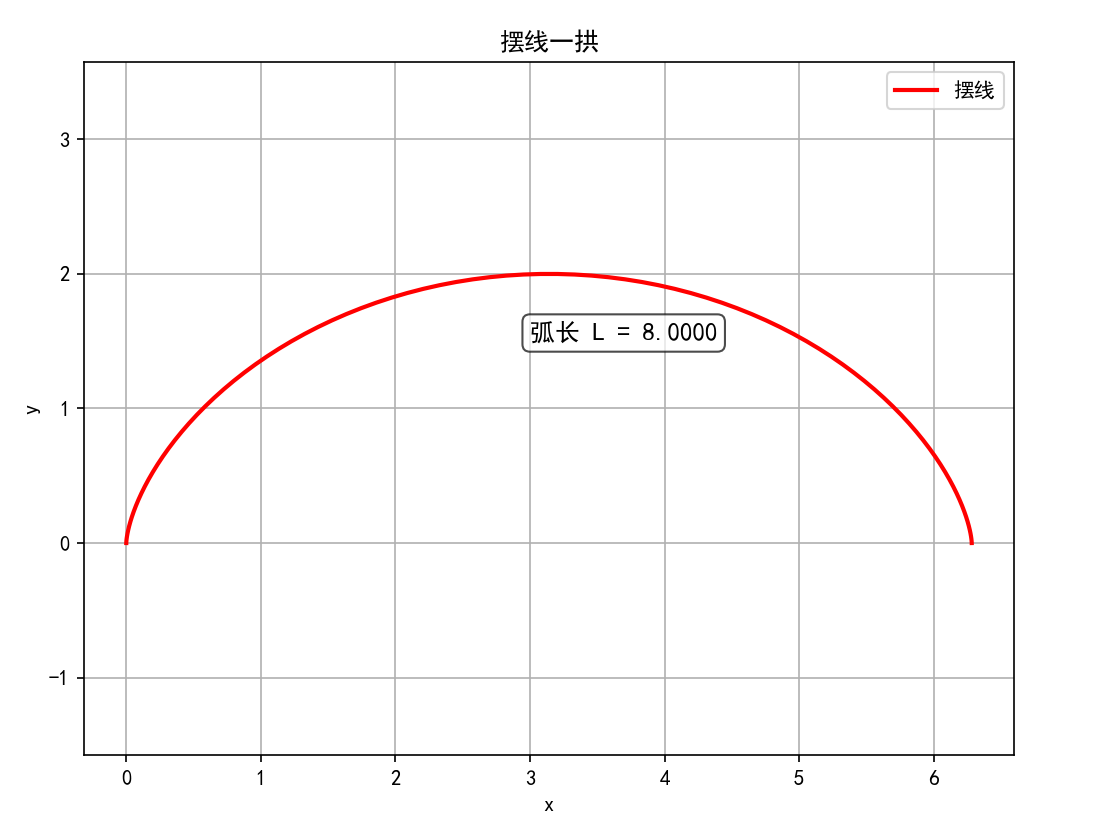
示例:计算摆线 { x = a ( θ − sin θ ) y = a ( 1 − cos θ ) \begin{cases} x = a(\theta - \sin\theta) \\ y = a(1 - \cos\theta) \end{cases} {x=a(θ−sinθ)y=a(1−cosθ)的一拱( 0 ≤ θ ≤ 2 π 0 \leq \theta \leq 2\pi 0≤θ≤2π)的长度。
解:
- 求导数: d x d θ = a ( 1 − cos θ ) \frac{dx}{d\theta} = a(1 - \cos\theta) dθdx=a(1−cosθ), d y d θ = a sin θ \frac{dy}{d\theta} = a\sin\theta dθdy=asinθ
- 构造被积函数: ( d x d θ ) 2 + ( d y d θ ) 2 = a 2 ( 1 − cos θ ) 2 + a 2 sin 2 θ \sqrt{\left(\frac{dx}{d\theta}\right)^2 + \left(\frac{dy}{d\theta}\right)^2} = \sqrt{a^2(1 - \cos\theta)^2 + a^2\sin^2\theta} (dθdx)2+(dθdy)2=a2(1−cosθ)2+a2sin2θ = a 1 − 2 cos θ + cos 2 θ + sin 2 θ = a 2 − 2 cos θ = a\sqrt{1 - 2\cos\theta + \cos^2\theta + \sin^2\theta} = a\sqrt{2 - 2\cos\theta} =a1−2cosθ+cos2θ+sin2θ=a2−2cosθ = a 4 sin 2 ( θ / 2 ) = 2 a ∣ sin ( θ / 2 ) ∣ = a\sqrt{4\sin^2(\theta/2)} = 2a|\sin(\theta/2)| =a4sin2(θ/2)=2a∣sin(θ/2)∣
- 在 [ 0 , 2 π ] [0, 2\pi] [0,2π]上, sin ( θ / 2 ) ≥ 0 \sin(\theta/2) \geq 0 sin(θ/2)≥0,故可去掉绝对值
- 计算弧长: L = ∫ 0 2 π 2 a sin ( θ / 2 ) d θ = 4 a [ − cos ( θ / 2 ) ] 0 2 π = 4 a ( 1 − ( − 1 ) ) = 8 a L = \int_0^{2\pi} 2a\sin(\theta/2) d\theta = 4a\left[-\cos(\theta/2)\right]_0^{2\pi} = 4a(1 - (-1)) = 8a L=∫02π2asin(θ/2)dθ=4a[−cos(θ/2)]02π=4a(1−(−1))=8a
Python代码
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate# 参数方程下弧长计算
def arc_length_parametric(x, y, x_prime, y_prime, alpha, beta):"""计算参数方程下曲线的弧长x, y: 参数函数x_prime, y_prime: 参数的导数alpha, beta: 参数区间"""def integrand(t):return np.sqrt(x_prime(t)**2 + y_prime(t)**2)length, error = integrate.quad(integrand, alpha, beta)return length, error# 示例:摆线一拱的长度
a = 1 # 摆线参数def x_cycloid(theta):return a * (theta - np.sin(theta))def y_cycloid(theta):return a * (1 - np.cos(theta))def x_prime_cycloid(theta):return a * (1 - np.cos(theta))def y_prime_cycloid(theta):return a * np.sin(theta)length_cycloid, error_cycloid = arc_length_parametric(x_cycloid, y_cycloid, x_prime_cycloid, y_prime_cycloid, 0, 2*np.pi)print(f"摆线一拱的长度: {length_cycloid:.6f} (理论值: {8*a:.6f})")# 可视化摆线
theta = np.linspace(0, 2*np.pi, 100)
x_vals = x_cycloid(theta)
y_vals = y_cycloid(theta)plt.figure(figsize=(8, 6))
plt.plot(x_vals, y_vals, 'r-', linewidth=2, label='摆线')
plt.xlabel('x')
plt.ylabel('y')
plt.title('摆线一拱')
plt.grid(True)
plt.axis('equal')
plt.legend()# 标注弧长
plt.text(3, 1.5, f'弧长 L = {length_cycloid:.4f}', fontsize=12, bbox=dict(boxstyle="round,pad=0.3", facecolor="white", alpha=0.7))plt.show()
Python代码执行结果

3. 极坐标方程下的弧长计算
数学定义
若曲线由极坐标方程 r = r ( θ ) r = r(\theta) r=r(θ)( θ ∈ [ α , β ] \theta \in [\alpha, \beta] θ∈[α,β])给出,且 r ( θ ) r(\theta) r(θ)在 [ α , β ] [\alpha, \beta] [α,β]上具有连续导数,则弧长公式为:
L = ∫ α β r 2 ( θ ) + ( d r d θ ) 2 d θ L = \int_{\alpha}^{\beta} \sqrt{r^2(\theta) + \left(\frac{dr}{d\theta}\right)^2} d\theta L=∫αβr2(θ)+(dθdr)2dθ
手动求解
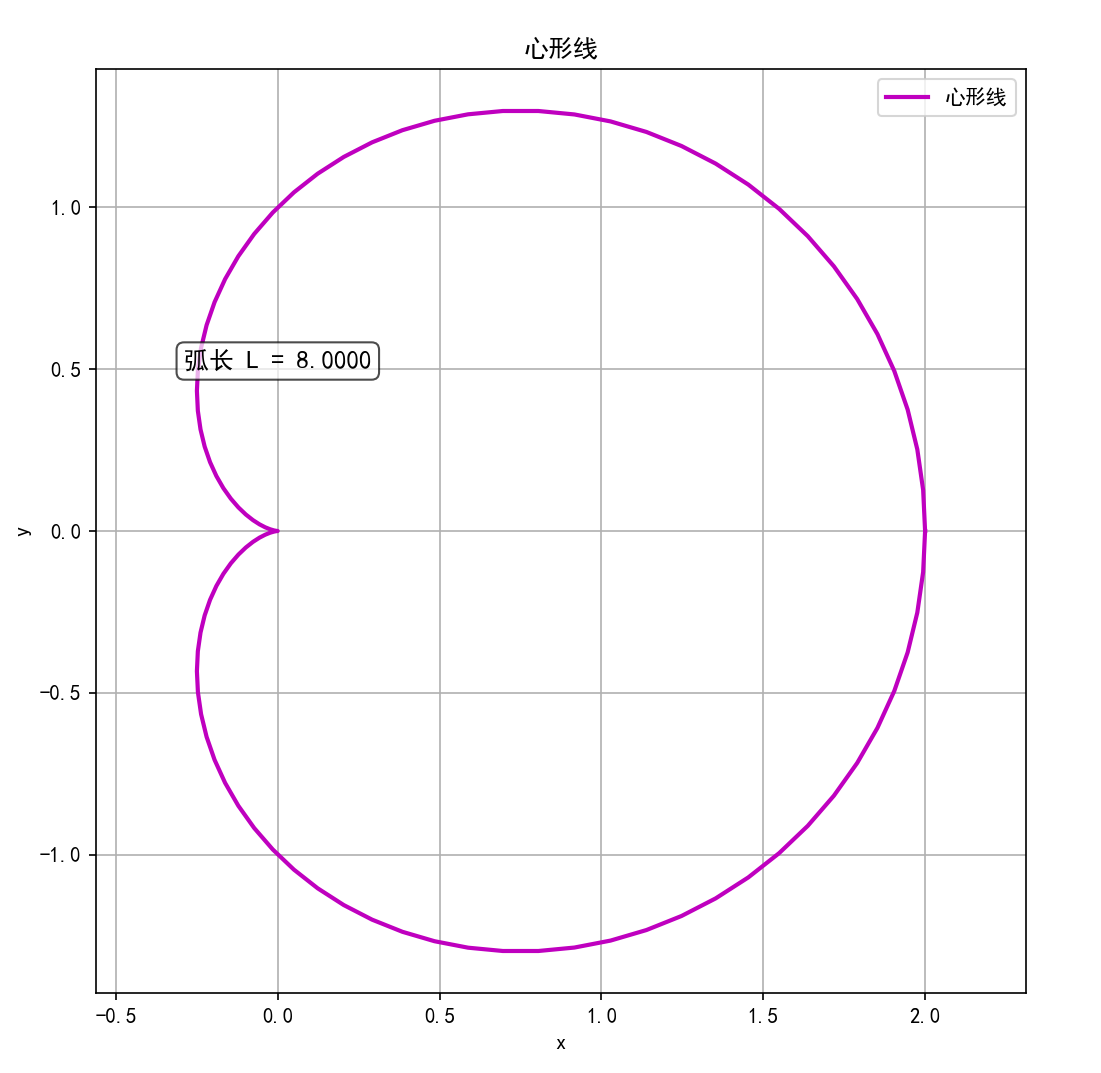
示例:求心形线 r = a ( 1 + cos θ ) r = a(1 + \cos\theta) r=a(1+cosθ)( a > 0 a > 0 a>0, 0 ≤ θ ≤ 2 π 0 \leq \theta \leq 2\pi 0≤θ≤2π)的长度。
解:
- 求导数: d r d θ = − a sin θ \frac{dr}{d\theta} = -a\sin\theta dθdr=−asinθ
- 构造被积函数: r 2 + ( d r d θ ) 2 = a 2 ( 1 + cos θ ) 2 + a 2 sin 2 θ \sqrt{r^2 + \left(\frac{dr}{d\theta}\right)^2} = \sqrt{a^2(1 + \cos\theta)^2 + a^2\sin^2\theta} r2+(dθdr)2=a2(1+cosθ)2+a2sin2θ = a 1 + 2 cos θ + cos 2 θ + sin 2 θ = a 2 + 2 cos θ = a\sqrt{1 + 2\cos\theta + \cos^2\theta + \sin^2\theta} = a\sqrt{2 + 2\cos\theta} =a1+2cosθ+cos2θ+sin2θ=a2+2cosθ = a 4 cos 2 ( θ / 2 ) = 2 a ∣ cos ( θ / 2 ) ∣ = a\sqrt{4\cos^2(\theta/2)} = 2a|\cos(\theta/2)| =a4cos2(θ/2)=2a∣cos(θ/2)∣
- 由于心形线对称,计算 [ 0 , π ] [0, \pi] [0,π]区间再乘以2: L = 2 ∫ 0 π 2 a cos ( θ / 2 ) d θ = 4 a ∫ 0 π cos ( θ / 2 ) d θ L = 2 \int_0^\pi 2a\cos(\theta/2) d\theta = 4a \int_0^\pi \cos(\theta/2) d\theta L=2∫0π2acos(θ/2)dθ=4a∫0πcos(θ/2)dθ
- 计算积分:令 u = θ / 2 u = \theta/2 u=θ/2,则 d u = d θ / 2 du = d\theta/2 du=dθ/2, θ = 0 \theta=0 θ=0时 u = 0 u=0 u=0, θ = π \theta=\pi θ=π时 u = π / 2 u=\pi/2 u=π/2 L = 4 a ∫ 0 π / 2 cos u ⋅ 2 d u = 8 a [ sin u ] 0 π / 2 = 8 a ( 1 − 0 ) = 8 a L = 4a \int_0^{\pi/2} \cos u \cdot 2du = 8a[\sin u]_0^{\pi/2} = 8a(1 - 0) = 8a L=4a∫0π/2cosu⋅2du=8a[sinu]0π/2=8a(1−0)=8a
Python代码
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate# 极坐标下弧长计算
def arc_length_polar(r, r_prime, alpha, beta):"""计算极坐标系下曲线的弧长r: 极径函数r_prime: 极径的导数alpha, beta: 角度区间"""def integrand(theta):return np.sqrt(r(theta)**2 + r_prime(theta)**2)length, error = integrate.quad(integrand, alpha, beta)return length, error# 示例:心形线的长度
a = 1 # 心形线参数def r_cardioid(theta):return a * (1 + np.cos(theta))def r_prime_cardioid(theta):return -a * np.sin(theta)length_cardioid, error_cardioid = arc_length_polar(r_cardioid, r_prime_cardioid, 0, 2*np.pi)print(f"心形线的长度: {length_cardioid:.6f} (理论值: {8*a:.6f})")# 可视化心形线
theta = np.linspace(0, 2*np.pi, 100)
r_vals = r_cardioid(theta)# 极坐标转直角坐标
x_vals = r_vals * np.cos(theta)
y_vals = r_vals * np.sin(theta)plt.figure(figsize=(8, 8))
plt.plot(x_vals, y_vals, 'm-', linewidth=2, label='心形线')
plt.xlabel('x')
plt.ylabel('y')
plt.title('心形线')
plt.grid(True)
plt.axis('equal')
plt.legend()# 标注弧长
plt.text(0, 0.5, f'弧长 L = {length_cardioid:.4f}', fontsize=12, bbox=dict(boxstyle="round,pad=0.3", facecolor="white", alpha=0.7),ha='center')plt.show()
Python代码执行结果

三、方法选择与应用技巧
在实际应用中,正确选择计算方法至关重要。以下是旋转体体积和曲线弧长计算的方法选择指南:
旋转体体积计算方法选择
| 情况 | 推荐方法 | 理由 |
|---|---|---|
| 绕x轴旋转,y=f(x)已知 | 圆盘法 | 直接对x积分,公式简单 |
| 绕y轴旋转,x=g(y)已知 | 圆盘法 | 直接对y积分,公式简单 |
| 绕y轴旋转,y=f(x)已知 | 壳层法 | 避免求反函数,计算更简便 |
| 绕x轴旋转,x=g(y)已知 | 壳层法 | 避免求反函数,计算更简便 |
| 旋转轴不是坐标轴 | 平移坐标轴 | 转化为绕坐标轴旋转的问题 |
曲线弧长计算方法选择
| 曲线表示形式 | 弧长公式 | 适用条件 |
|---|---|---|
| 直角坐标y=f(x) | L = ∫ a b 1 + [ f ′ ( x ) ] 2 d x L = \int_a^b \sqrt{1 + [f'(x)]^2} dx L=∫ab1+[f′(x)]2dx | f’(x)连续 |
| 参数方程x=x(t),y=y(t) | L = ∫ α β [ x ′ ( t ) ] 2 + [ y ′ ( t ) ] 2 d t L = \int_{\alpha}^{\beta} \sqrt{[x'(t)]^2 + [y'(t)]^2} dt L=∫αβ[x′(t)]2+[y′(t)]2dt | x’(t),y’(t)连续 |
| 极坐标r=r(θ) | L = ∫ α β r 2 ( θ ) + [ r ′ ( θ ) ] 2 d θ L = \int_{\alpha}^{\beta} \sqrt{r^2(θ) + [r'(θ)]^2} dθ L=∫αβr2(θ)+[r′(θ)]2dθ | r(θ)连续可导 |
总结
本文详细探讨了定积分在旋转体体积和曲线弧长计算中的应用。通过圆盘法和壳层法,我们可以计算各种旋转体的体积;而根据曲线表示形式的不同,选择适当的弧长公式可以准确求出曲线长度。
这些应用体现了微积分**“化整为零,以直代曲”**的核心思想,通过无限细分和近似替代,将复杂的几何问题转化为可计算的定积分问题。掌握这些方法不仅有助于解决数学问题,也为工程、物理等领域的实际应用提供了重要工具。
在下一篇文章中,我们将继续探讨定积分在物理学中的应用,包括功、质心和转动惯量等问题的计算。
往期精彩回顾:
- 用Python来学微积分35-变上限定积分
- 用Python来学微积分36-牛顿 - 莱布尼茨公式的深度解析
- 定积分的几何应用(一):平面图形面积计算详解
专栏导航目录 《程序员AI之路:从Python起步》完全学习导航
完整代码已开源 ai-learning-path,欢迎Star和Fork!
参考资料:
- 扈志明《微积分》教材
互动邀请:如果你对本章内容有独特的理解或在实际应用中遇到过有趣的问题,欢迎在评论区分享交流!
