高级机器学习作业（二）度量学习 + 稀疏学习 + GMM-EM半监督学习

目录

1. 度量学习

1.1 马氏距离的优势（变换后 协方差矩阵为单位阵）

1.2 协方差不可逆的情形

1.3 马氏距离是否满足距离度量 的四个性质

1.4 联系 PCA和 LDA

2. 特征选择与稀疏学习

2.1 正则化与条件约束

2.2 字典学习与压缩感知

3. 半监督学习 - 高斯混合 - EM - 参数更新公式

---

1. 度量学习

度量学习旨在学习一个适用于某个任务的距离度量，等价于为实现某个距离度量找到合适的特征变换。

马氏距离，标准版 M 为样本协方差的逆，度量学习可看做优化 M。

1.1 马氏距离的优势（变换后 协方差矩阵为单位阵）

可导出-> 去除了变量之间的相关性，并且与量纲无关。

协方差矩阵：维度为特征数量；特征与特征之间的协方差；

协方差矩阵 对称，因为 i 维度对于 j 维度，也等于 j 维度对于 i 维度。

实对称矩阵的性质：

        1. 特征值都是实数；

        2. 不同特征值对应的特征向量正交；

        3. 存在一组完整的、标准正交的特征向量基。

还可推出协方差矩阵半正定：

协方差 也可以写成 中心化减去均值之后  X^T X

      

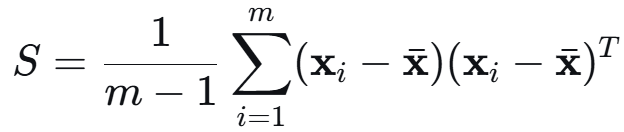
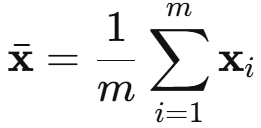
综合上述 实对称 + 半正定的性质，可对协方差矩阵进行正交分解：

还可以进一步，因为特征值非负，可对 D 对角线特征值开根号。

所以标准马氏距离，即为乘以 L^T 空间变换后的距离  X' = XL 。

假设已经中心化  Σ = 1/m X^T X      Σ' = 1/m (XL)^T (XL) = L^T Σ L = I

所以变换后的 X' 对应的协方差矩阵为单位阵。

1.2 协方差不可逆的情形

是否存在某些情况下协方差矩阵不可逆，应该如何应对这个问题？

协方差，即 中心化后的 1/m X^T X；X^T X 可逆 等价于 X列满秩。

证明：左右互推充要性。

右乘 即列变换，列向量（特征）线性相关则 Xv = 0. -> X^T Xv = 0 即不可逆。

所以 X 列满秩，则不存在这样的 v，则 X^X 可逆。

列满秩可能因为：

        样本个数 m 较少；

        或者收集到的样本 特征之间存在线性关系；

解决方法：

        1. 增加样本数量

        2. 使用 PCA 降维减少特征数，选择大特征值重构协方差矩阵

        3. 算伪逆

1.3 马氏距离是否满足距离度量 的四个性质

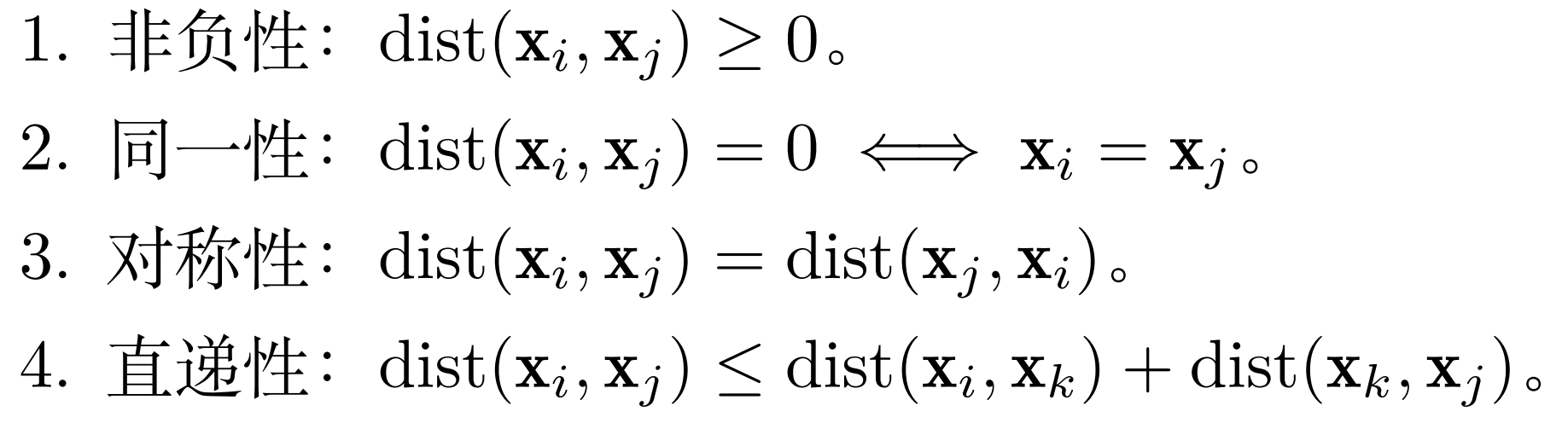
由于半正定 z^T M z ≥ 0，满足非负性。

根据式子定义，i j 对调符合对称性。

当 M 正定时，z^T M z = 0 当且仅当 z = 0 (即 xi = xj) 符合同一性。

但若 M 半正定：

存在 z≠0 满足 z^T M z = 0，不符合同一性。 若 M 的非零特征值数 d' < d，

若前 d'维度相同，后 d-d'维不同，两不同样本的距离也为0。不符合同一性。

4. Cauchy–Schwarz 不等式 -> 直递性&范数三角不等式；

即原来的三角不等式前面的 x 多乘一下 L。

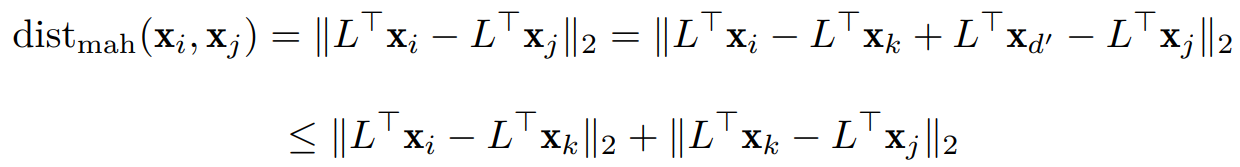
即满足直递性！

1.4 联系 PCA和 LDA

（4）请写出PCA和LDA 对应的马氏距离中的 M。

PCA 的目标： 找到一组正交的投影方向（主成分），使得投影后的数据方差最大。

乘以投影矩阵 W，我们在1中推导 投影矩阵 L。

LDA：最大化类间散度/最小化类内散度（有监督）

类内 Sw 为条件，最大化类间 Sb 投影后方差。

把条件化成类似 PCA 格式的

 记作 a

    又 w = Sw ^(-1/2) a

两把都左乘 Sw^(-1/2) 

这两个都是有投影矩阵 W，即 M = W W^T.

2. 特征选择与稀疏学习

2.1 正则化与条件约束

     

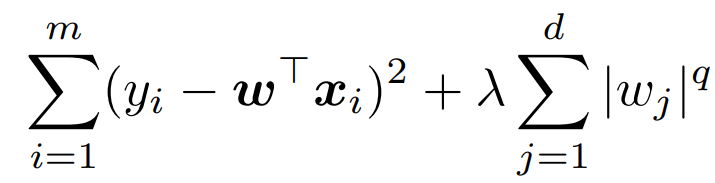
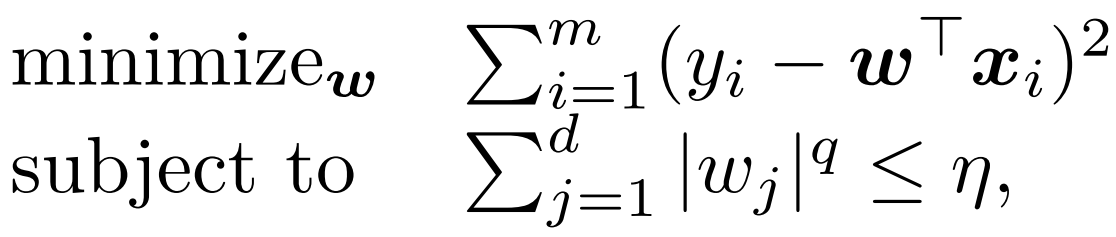
证明左右 正则化与带约束等价。讨论 η 和 正则化系数 λ≥0 之间的联系。

要证等价，即证：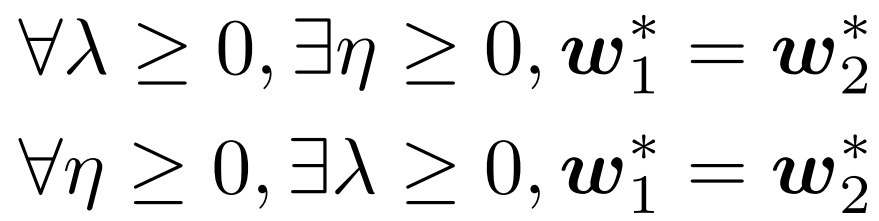

L1对 w 求导，其中 |w|^q 求导还需要引入 符号sign(w)

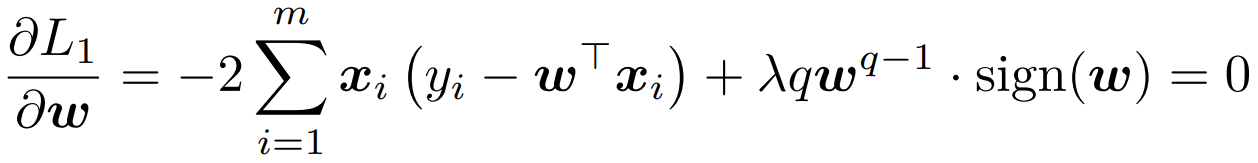
L2 引入拉格朗日函数，并找对应的 KKT条件：

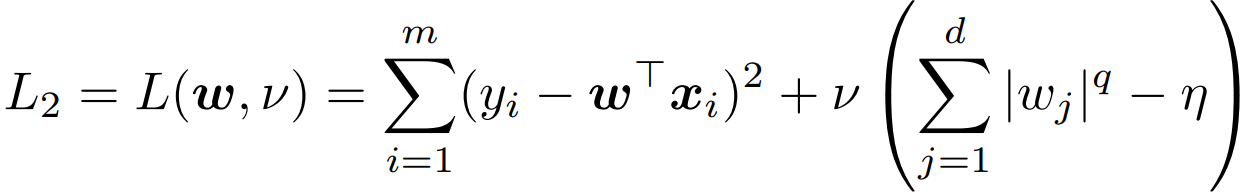
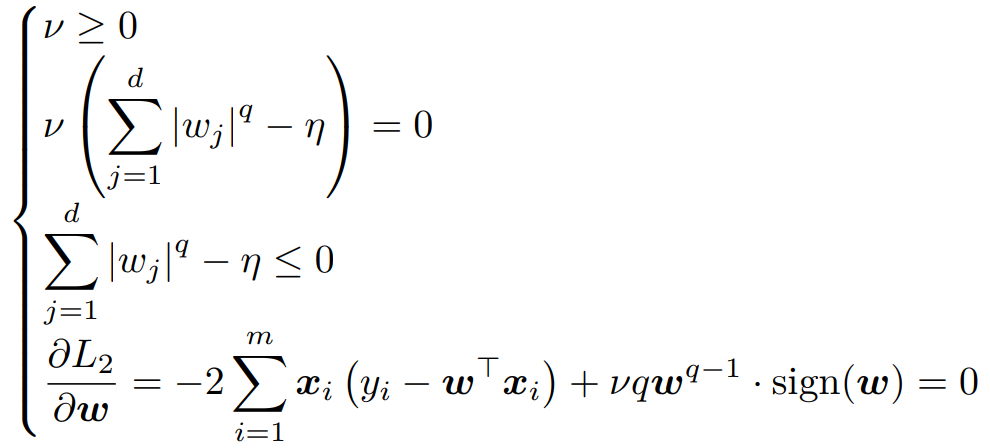
要想 w2* 满足 L1 的导数条件，即取 λ = v；

要想 w1* 满足 L2，即取 

2.2 字典学习与压缩感知

字典学习与压缩感知都有对稀疏性的利用，请你分析两者对稀疏性利用的异同点。

均利用：稀疏表示在提取信号本质特征方面的优势。

字典学习：旨在从给定的训练数据中学习一个字典，使得原始数据可以在该字典下获得 最稀疏的表示。

压缩感知：如何利用信号本身所具有的稀疏性，从部分观测样本中恢复原信号。

3. 半监督学习 - 高斯混合 - EM - 参数更新公式

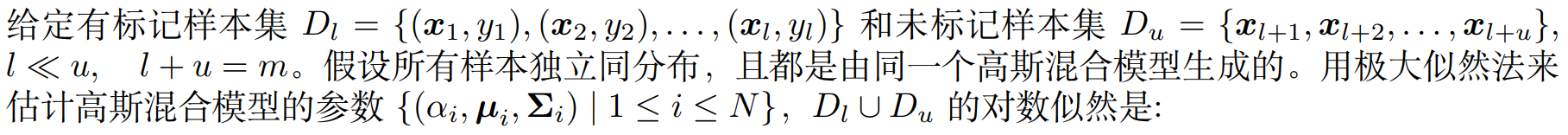
下面两个部分之和：

带标记样本 (x,y) 讨论来自第 i 个分布，为类别 j 的概率。

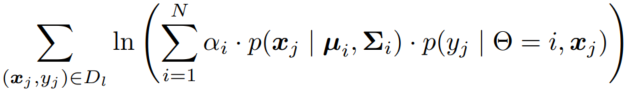
无标记样本 出现的概率（来自各个分布的概率加权和）

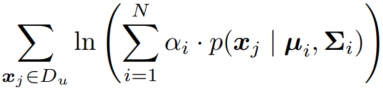
1. 推导 E 步更新公式：根据当前模型参数计算：

未标记样本 xj 属于第 i 个高斯混合成分的概率为：

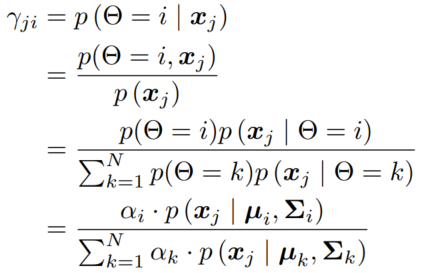
2. 推导 M 步更新公式 μ Σ α：

3.1 M 步 μ 和 Σ 的推导：

多元正态分布形式，以及对 μ 和 Σ 的求导结果：

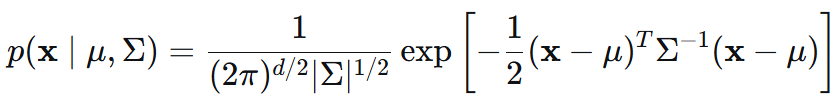
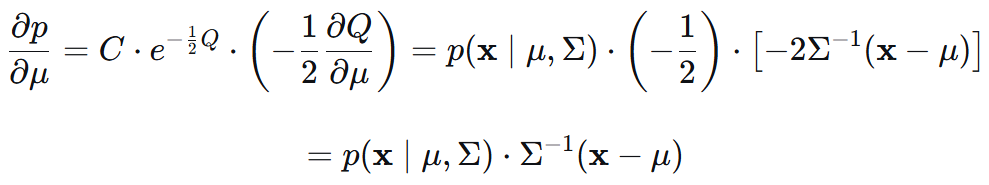
先推对 μ 偏导：

有标签的部分：

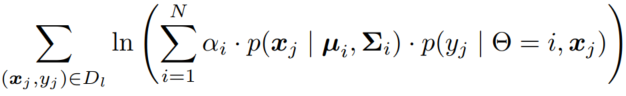
后面那个 在第 i 个分布下的 p 和 μ 无关，和前面的 α一样为常数系数。

单个 μ，里面的求和不需要。

     

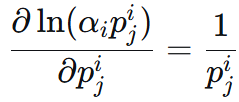
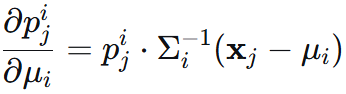
无标签的部分：

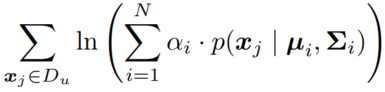
分母是所有类，分子只有第 i 类。（上面那个 分母分子的 p 都是第 i 类，消掉了）

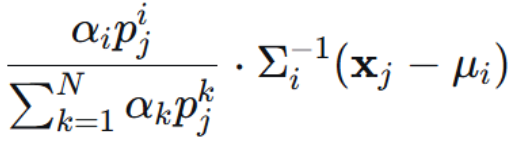
前面这个系数表示 第 j 个样本属于 第 i 个分布的概率，可写作 γji。

再进行样本求和，总体对 μ 和 Σ 求导为如下：

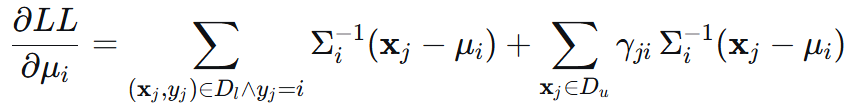
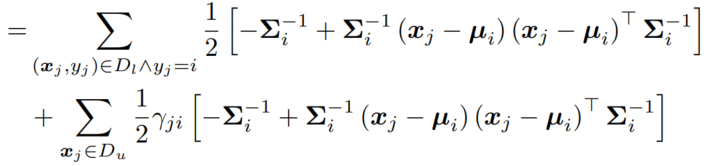
（得出并分析结果）

令导数=0得 μ 和 Σ 为：

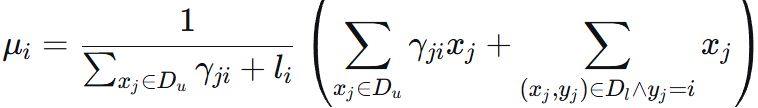
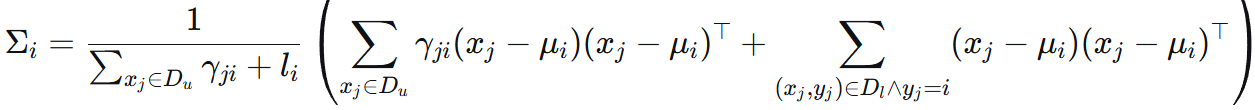
 即为 归属于组件 i 的有效点数。γji 为软分配的权重。

新的均值 μi​ 就是所有被认为属于组件 i 的数据点（包括软分配和硬分配）的加权平均中心。

新的协方差矩阵 Σi 是所有被认为属于组件 i 的数据点（包括软分配和硬分配）的加权平均散布矩阵。

3.2 M 步 权重 α 的推导 -- 凸优化 KKT

α 权重分配，限制和为 1，对于函数 LL。

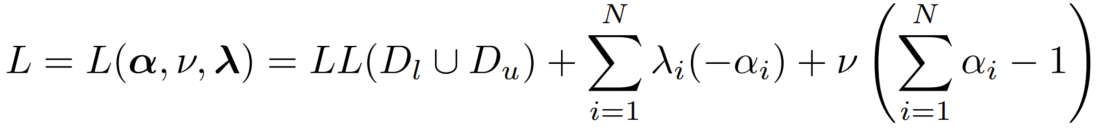
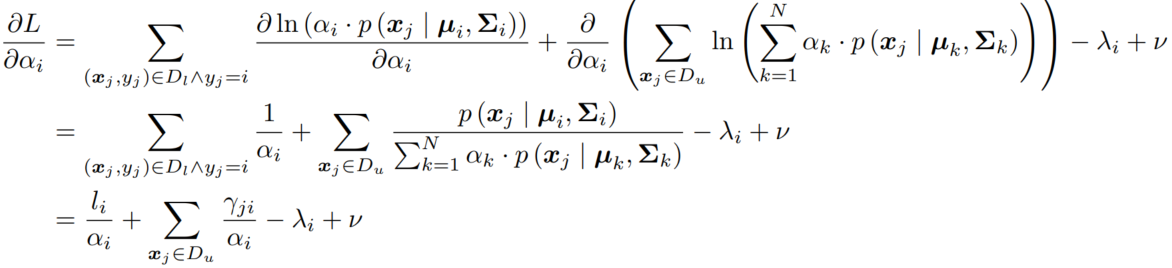
对 KKT 条件进行化简：

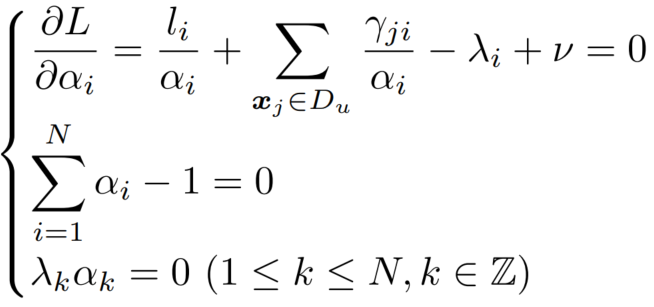
可得最后的更新答案为 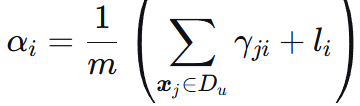 即簇的重要性占比。

可以理解为：【所有数据（有标签 + 无标签）中，归属于簇 i 的“有效点数”的总和】/ 总点数