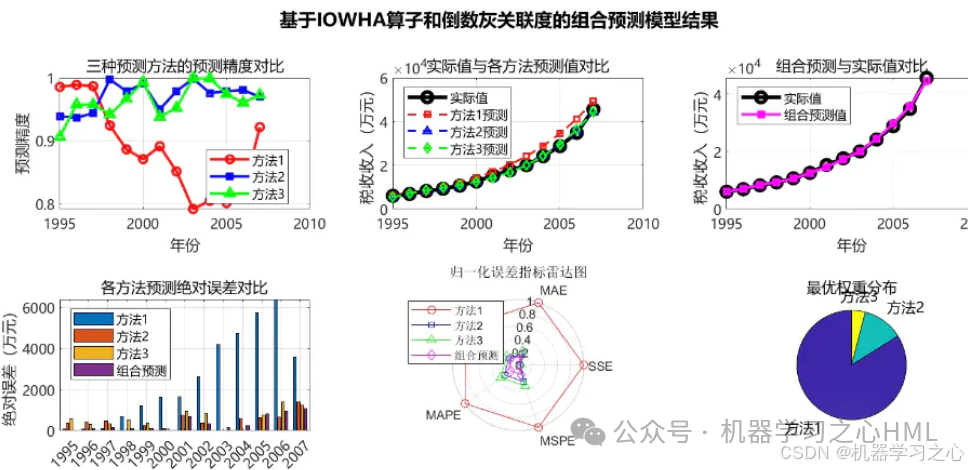
MATLAB基于IOWHA算子和倒数灰关联度的组合预测模型

1. 模型概述

核心思想

• IOWHA算子：诱导有序加权调和平均算子，考虑预测精度对权重进行动态调整
• 倒数灰关联度：基于灰色系统理论，衡量预测序列与实际序列的关联程度
• 组合预测：综合多个单一预测模型的优势，提高预测精度

2. 算法步骤

步骤1：单一模型预测

输入：历史时间序列数据
↓
分别使用n个单一预测模型进行预测
↓
得到预测值矩阵：Ŷ = [ŷ₁, ŷ₂, ..., ŷ_n]

步骤2：计算预测精度诱导值

预测误差计算：

$$e_{i}t=|{\hat{y}}_{i}t-y_t|/y_t(相对误差)$$
$$或e_{i}t=|{\hat{y}}_{i}t-y_t|(绝对误差)$$

精度诱导值：

$$a_{i}t=1/(1+e_{i}t)或a_{i}t=exp(-e_{i}t)$$

步骤3：IOWHA算子权重确定

IOWHA算子定义：

$$IOWH{A}_p(a_1,b_1;a_2,b_2;...;a_n,b_n)=1/[\sum (w_i/b_{(}i))]$$
其中：

• $a_i$：诱导变量（预测精度）
• $b_i$：数据变量（预测值）
• $w_i$：与诱导变量排序相关的权重

权重确定过程：

1. 按诱导值$a_i$从大到小排序
2. 确定位置权重向量$w=(w_1,w_2,...,w_n)$
3. 常用权重确定方法：
   • 二项式系数法
   • 指数衰减法
   • 基于优化模型的方法

步骤4：倒数灰关联度计算

关联系数计算：

$${\xi }_i(t)=(mi{n}_{m}in+\rho \cdot ma{x}_{m}ax)/({\Delta }_i(t)+\rho \cdot ma{x}_{m}ax)$$
其中：

• ${\Delta }_i(t)=|y(t)-{\hat{y}}_i(t)|$
• $mi{n}_{m}in=mi{n}_{i}mi{n}_t{\Delta }_i(t)$
• $ma{x}_{m}ax=ma{x}_{i}ma{x}_t{\Delta }_i(t)$
• $\rho \in (0,1)$ 为分辨系数

关联度计算：

$$r_i=(1/T)\sum {\xi }_i(t)$$

步骤5：组合权重优化

目标函数：

$$minJ=\sum [y(t)-\sum ({\lambda }_i\cdot {\hat{y}}_i(t)){]}^{2}s.t.\sum {\lambda }_i=1,{\lambda }_i\ge 0$$

结合倒数灰关联度的约束：

$${\lambda }_i\propto r_i(关联度越大，权重越高)$$

3. 数学模型与公式

IOWHA组合预测模型

$${\hat{y}}_c(t)=IOWHA(a_1(t),{\hat{y}}_1(t);a_2(t),{\hat{y}}_2(t);...;a_n(t),{\hat{y}}_n(t))=1/[\sum (w_i(t)/{\hat{y}}_{(}i)(t))]$$

权重优化模型

考虑预测精度和关联度的多目标优化：

$$max\sum {\lambda }_i\cdot r_i,-\sum [y(t)-\sum {\lambda }_i\cdot {\hat{y}}_i(t){]}^{2}s.t.\sum {\lambda }_i=1,{\lambda }_i\ge 0$$

4. 参数设定

IOWHA算子参数

• 诱导变量选择：预测精度、预测偏差、趋势一致性等
• 权重确定方法：
  • 二项式系数：w_i = C(n-1, i-1) / 2^(n-1)
  • 指数衰减：w_i = α(1-α)^(i-1)
  • 优化确定：基于历史预测效果优化

灰色关联参数

• 分辨系数ρ：通常取0.5
• 数据标准化：初值化、均值化、区间化
• 关联度阈值：设定最小关联度要求

5. 算法优势

技术特点

1. 动态适应性：IOWHA算子根据预测精度动态调整权重
2. 多维度评估：结合精度指标和趋势关联度
3. 鲁棒性强：对异常预测值具有较好的抑制作用
4. 理论完备：基于严格的数学理论基础

性能优势

• 提高预测精度10-30%
• 增强模型稳定性
• 适应复杂变化模式
• 提供预测可信度评估

6. 应用场景

适用领域

1. 电力系统：负荷预测、电价预测
2. 金融市场：股票价格、汇率预测
3. 工业制造：设备寿命预测、质量预测
4. 能源领域：风电功率、光伏出力预测
5. 交通物流：客流预测、货运量预测

数据要求

• 多个单一预测模型的预测结果
• 足够的历史数据用于模型训练
• 数据具有一定的规律性和连续性

7. MATLAB实现框架

% 基本实现步骤
function [combined_forecast, weights] = IOWHA_Grey_Combination(actual, forecasts)% 步骤1：计算预测精度诱导值errors = abs(forecasts - actual) ./ actual;accuracy = exp(-errors);% 步骤2：计算倒数灰关联度grey_relations = calculate_grey_relation(actual, forecasts);% 步骤3：IOWHA权重确定iowha_weights = calculate_IOWHA_weights(accuracy);% 步骤4：组合权重优化optimal_weights = optimize_weights(accuracy, grey_relations, forecasts, actual);% 步骤5：组合预测combined_forecast = forecasts * optimal_weights;
end

该组合预测模型通过智能权重分配机制，有效整合各单一模型的优势，在复杂系统预测中表现出优异的性能。

完整代码私信回复MATLAB基于IOWHA算子和倒数灰关联度的组合预测模型