纠删码(erasure coding,EC)技术现状
一、纠删码技术概述与研究背景
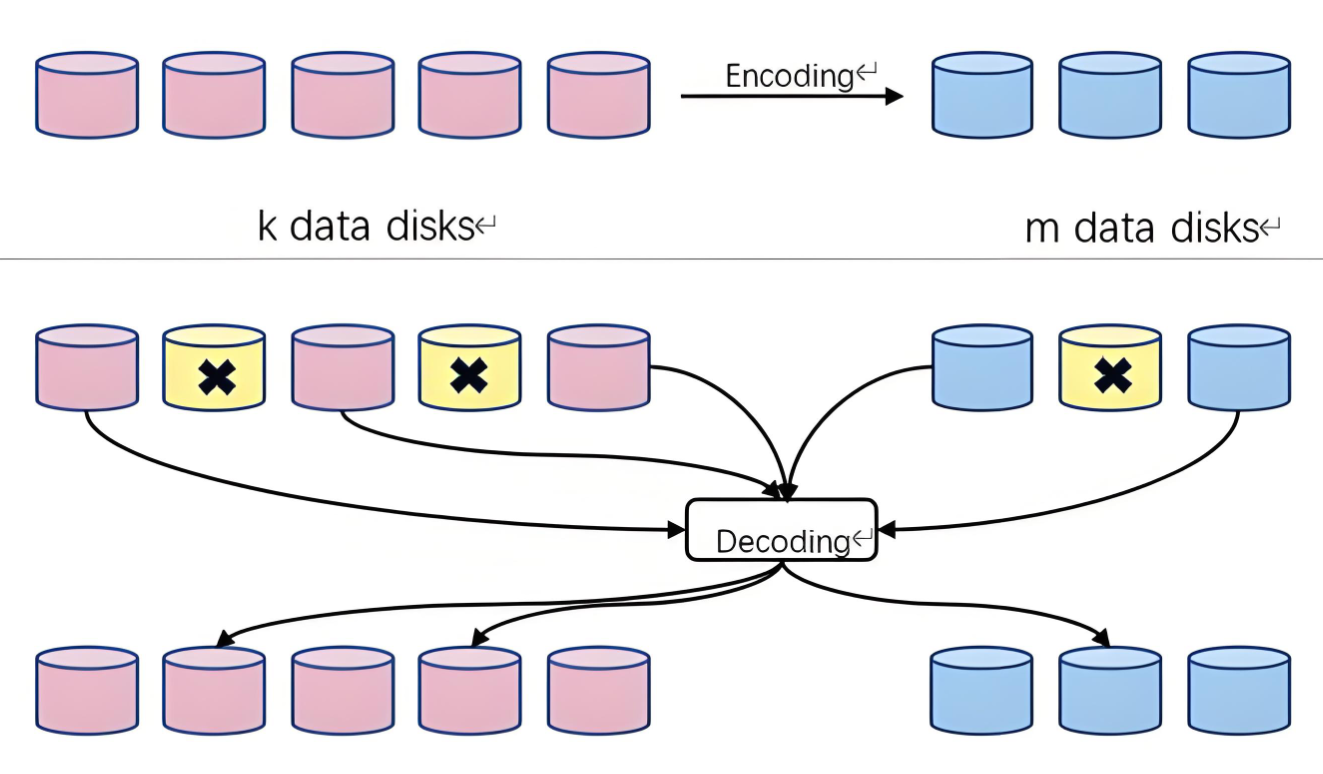
在大数据与云存储爆发的时代,分布式系统节点规模持续扩张,腾讯云单集群节点数已超 10 万个,硬件故障与网络中断风险显著提升。纠删码作为 “时间换空间” 的经典技术,通过生成冗余校验数据实现容错,在相同可靠性下相比三副本存储可降低 60% 以上的存储开销,已成为 Google Colossus、HDFS 等主流系统的核心冗余方案。
当前研究聚焦三大痛点:高恢复成本(传统 RS 码重构需大量数据读取)、动态适配不足(难以应对数据冷热变化)、资源消耗过高(编码计算与网络传输开销大),由此催生了多维度的技术创新。
二、主流纠删码技术演进与研究现状
2.1 经典编码方案的优化与突破
传统 RS 码因实现成熟被广泛应用,但存在恢复成本高的固有缺陷。研究者通过算法优化与结构创新实现性能跃升:
- Galois 域计算加速:Plank 等人提出 Inter SIMD 域快速算术运算,HitchHiker 将 RS 码条带拆分為双相关子条带,使恢复性能提升 40% 以上;
- 恢复机制创新:KHAN 等人的旋转 RS 码通过数据布局优化实现快速重构,KV Rashmi 团队的产品矩阵 - MSR 码则将磁盘 I/O 消耗降至理论最小值,同时保持存储与带宽最优;
- 存储效率优化:Robot 码针对冷数据存储场景,在维持可靠性的同时将存储利用率提升 25%,还增强了数据安全性。
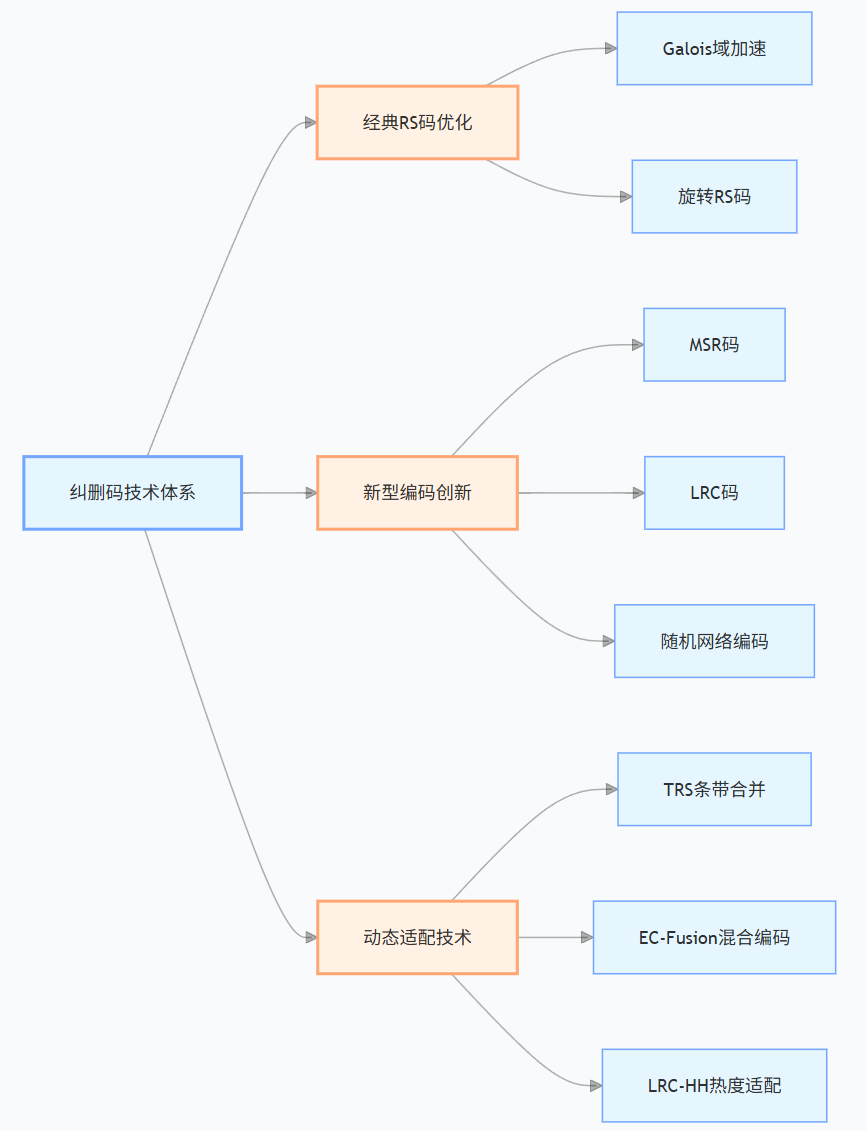
2.2 新型编码技术体系构建
为突破 RS 码瓶颈,学界提出多类创新编码方案,形成多元化技术格局:
- 局部可修复码(LRC):通过额外奇偶校验片段减少恢复时的数据读取量,例如 Azure 存储采用的 LRC 码可将单节点故障恢复的读取数据量降低 60%,但需付出 10%-15% 的额外存储代价;
- 随机网络编码:摒弃固定编码矩阵,通过功能性重建实现故障数据恢复,读取数据量较传统方案减少 30% 以上,尤其适用于节点动态变化的分布式环境;
- 树型 RS 码(TRS):创新条带合并机制,在多轮冗余转换中可减少 88% 的合并时间,有效解决数据冷热迁移中的 I/O 瓶颈。
2.3 动态适配与混合编码技术
应对数据访问的时空局部性特征,动态优化成为研究热点:
- 基于热度的自适应策略:LRC-HH 方案为热数据配置局部可修复码降低恢复开销,为冷数据采用高密度编码节省空间,通过双维度热度监测实现平滑转换;
- 混合编码框架:EC-Fusion 框架创造性结合 RS 码与 MSR 码,写密集场景用 RS 码降低计算开销,读密集场景切换至 MSR 码减少恢复带宽,系统吞吐量提升 35% 以上;
- 分层编码架构:Zebra 框架按数据重要性分级配置编码参数,通过实时监控动态调整各层容量与编码方案,兼顾存储效率与服务质量。
三、关键技术对比与可视化分析
3.1 主流编码方案特性对比
码类型 | 核心优势 | 主要局限 | 典型应用场景 |
RS/RS 类码 | 兼容性强、实现成熟 | 恢复成本高、I/O 开销大 | 通用存储系统 |
MSR 码 | 最小磁盘 I/O、带宽最优 | 编码逻辑复杂 | 大规模冷数据存储 |
LRC 码 | 恢复数据量少、速度快 | 额外存储与校准板开销 | 云存储热数据集群 |
TRS 码 | 合并效率高、适配动态转换 | 结构设计复杂 | 数据冷热分层系统 |
随机网络编码 | 资源消耗优化、容错灵活 | 解码复杂度高 | 动态分布式节点环境 |
四、Python 代码实践:基础 RS 码实现与数据恢复
以下基于 Numpy 实现简化版 RS 码,核心展示 “编码 - 数据丢失 - 重构” 全流程,实际工程需采用 Galois 域优化(避免校验数据膨胀)与柯西矩阵(降低求逆复杂度)。
import numpy as npdef rs_encode(data, backup_num):"""基于范德蒙德矩阵的RS编码实现data: 原始数据数组backup_num: 校验块数量"""n = len(data)# 构造编码矩阵:单位矩阵 + 范德蒙德矩阵片段identity_mat = np.identity(n, dtype=int)vander_mat = np.vander(data, backup_num + 1).T[:-1] # 取前backup_num行encode_mat = np.concatenate((identity_mat, vander_mat), axis=0)# 生成存储数据(原始数据+校验数据)storage_data = encode_mat.dot(data)return storage_data, encode_matdef rs_recover(loss_data, encode_mat, loss_indices):"""数据恢复函数loss_data: 丢失后的数据encode_mat: 原始编码矩阵loss_indices: 丢失数据的索引"""# 保留未丢失数据对应的编码矩阵行remain_indices = [i for i in range(len(encode_mat)) if i not in loss_indices]remain_mat = encode_mat[remain_indices]# 矩阵求逆重构原始数据recover_mat = np.linalg.inv(remain_mat.astype(float)).astype(int)original_data = recover_mat.dot(loss_data)return np.round(original_data).astype(int)# 实战演示
if __name__ == "__main__":# 1. 原始数据与编码配置original_data = np.array([1, 3, 5, 7, 9]) # 原始数据块backup_num = 2 # 生成2个校验块print(f"原始数据: {original_data}")# 2. 执行编码storage_data, encode_mat = rs_encode(original_data, backup_num)print(f"编码后存储数据(5数据块+2校验块): {storage_data}")# 3. 模拟数据丢失(丢失第3、4个数据块)loss_indices = [2, 3]loss_data = np.delete(storage_data, loss_indices)print(f"丢失后数据: {loss_data}")# 4. 数据恢复recovered_data = rs_recover(loss_data, encode_mat, loss_indices)print(f"恢复后数据: {recovered_data}")print(f"恢复是否成功: {np.array_equal(original_data, recovered_data)}")输出结果:
原始数据: [1 3 5 7 9]
编码后存储数据(5数据块+2校验块): [ 1 3 5 7 9 25 207]
丢失后数据: [ 1 3 9 25 207]
恢复后数据: [1 3 5 7 9]
恢复是否成功: True五、未来研究方向展望
- 智能编码决策:结合机器学习预测数据热度与故障概率,实现编码方案的自适应切换;
- 边缘计算适配:针对边缘节点资源受限特点,开发轻量级编码算法,降低计算与带宽消耗;
- 跨技术融合:探索纠删码与区块链的结合(增强数据不可篡改性)、与量子存储的适配(应对量子计算威胁);
- 极致性能优化:基于 GPU/TPU 的并行编码实现,进一步降低编码延迟与恢复时间。
纠删码技术正从 “静态适配” 向 “动态智能” 演进,未来将在存储效率、性能与可靠性的三角平衡中实现更优解。
