当前位置：首页 > news >正文

【论文精读】FDGaussian：基于几何感知扩散模型的单图快速高斯溅射 3D 重建

news 2025/10/25 7:10:18

标题：FDGaussian: Fast Gaussian Splatting from Single Image via Geometric-aware Diffusion Model

作者：Qijun Feng, Zhen Xing, Zuxuan Wu, Yu-Gang Jiang

单位：Fudan University, Shanghai, China（中国上海复旦大学）

发表：arXiv preprint arXiv:2403.10242v1 [cs.CV], 15 Mar 2024

论文链接：https://arxiv.org/pdf/2403.10242v1

项目代码：https://qjfeng.net/FDGaussian/

关键词：3D 重建（3D Reconstruction）、高斯溅射（Gaussian Splatting）、扩散模型（Diffusion Model）

在计算机视觉领域，单视图 3D 重建一直是极具挑战性的任务，其核心难点在于如何从单张 2D 图像中挖掘足够的 3D 几何信息，同时保证多视角一致性与重建效率。复旦大学团队提出的FDGaussian框架，创新性地结合几何感知扩散模型与加速高斯溅射技术，为这一难题提供了高效解决方案。

一、研究背景与挑战

单视图 3D 重建旨在从单张 RGB 图像中恢复物体的 3D 几何结构与外观，是虚拟现实（VR）、增强现实（AR）、机器人交互等领域的关键技术。然而，该任务面临三大核心挑战：

信息局限性：单张 2D 图像丢失了深度维度信息，导致 3D 几何推断存在歧义；
表示权衡难题：
- 显式表示（点云、体素、网格）直观且易变形，但难以呈现真实外观；
- 隐式表示（NeRF）可通过神经网络优化建模复杂结构，但渲染时需大量随机采样，耗时且易产生噪声；
多视角一致性与效率矛盾：现有基于 2D 扩散模型的方法（如 Zero-1-to-3）要么存在多视角不一致问题，要么无法高效处理复杂几何结构，且传统高斯溅射（Gaussian Splatting）优化中存在大量冗余操作，影响效率。

为解决上述问题，FDGaussian 提出两阶段框架：先通过几何感知扩散模型生成多视角一致的图像，再利用加速高斯溅射技术完成高质量 3D 重建。

二、相关工作回顾

在深入解读 FDGaussian 之前，需先了解 3D 重建领域的核心技术演进，这是 FDGaussian 创新的基础。

2.1 3D 重建表示方法对比

不同表示方法各有优劣，FDGaussian 的设计正是为了融合各类方法的优势，规避其缺陷：

表示类型	典型方法	优势	劣势
显式表示	点云（PointNet）、体素（VoxNet）、网格（Pixel2Mesh）	直观易懂、支持变形、工业应用成熟	拓扑灵活性差、难以捕捉真实外观细节
隐式表示	SDF/UDF、NeRF	可建模任意拓扑结构、支持数据驱动学习	渲染需大量采样、计算成本高、难实时
混合表示	3D Gaussian Splatting	结合神经网络优化与显式存储，兼顾质量与速度	传统方法忽略高斯间距，存在冗余分裂 / 克隆操作

2.2 基于 2D 扩散模型的 3D 重建

近年来，2D 扩散模型（如 Stable Diffusion）在图像生成领域取得突破，其强大的 3D 世界先验能力被用于辅助 3D 重建。现有工作可分为两类：

逐形状优化（如 DreamFusion）：优化 3D 表示并利用 2D 扩散模型提供梯度指导，但存在优化时间长、“多脸问题”（同一物体不同视角出现多张脸）等缺陷；
单图生成多视角（如 Zero-1-to-3）：无需训练数据即可生成新视角，但多视角一致性差、复杂几何结构建模能力弱。

FDGaussian 正是针对上述方法的不足，提出几何感知与加速优化策略。

三、FDGaussian 核心方法详解

FDGaussian 的两阶段框架（几何感知多视角生成 + 加速高斯重建）环环相扣，每一步都针对具体痛点设计创新模块。整体流程如图 2 所示：

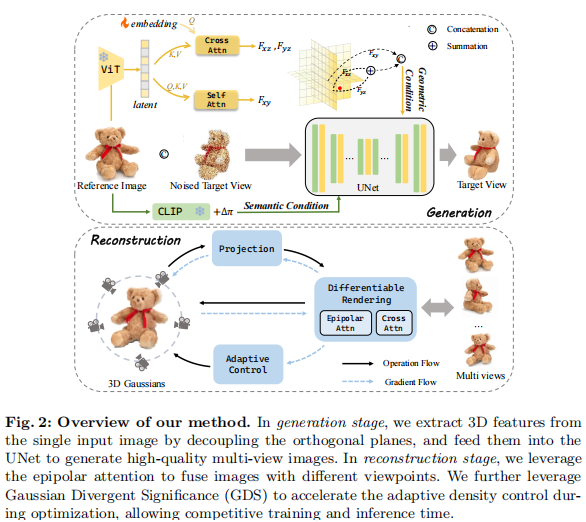
注：左侧为多视角生成阶段（提取几何与语义特征指导扩散模型），右侧为 3D 重建阶段（极线注意力融合多视角 + GDS 加速优化）。

3.1 阶段一：几何感知多视角图像生成

该阶段的目标是生成3D 感知、多视角一致、高保真的图像，核心创新在于 “正交平面分解” 与 “多条件融合”。

3.1.1 几何特征提取：正交平面分解

单张 2D 图像（xy 平面）无法直接提供 3D 信息，FDGaussian 通过正交平面解耦，从 xy 平面中分离出 yz、xz 平面的几何特征，具体步骤如下：

图像编码：使用视觉 Transformer（ViT）对输入图像编码，生成高维 latent 特征 $h$ ，捕捉图像全局相关性；
平面解码：
- xy 平面特征（F_xy）：通过自注意力解码器逆转编码过程，直接从 $h$ 中提取；
- yz/xz 平面特征（F_yz/F_xz）：引入可学习嵌入（Learnable Embedding），通过交叉注意力将 h 转换为正交平面特征，同时保证与 xy 平面的结构对齐；
几何条件融合：将 F_xy、F_yz、F_xz 通过 “拼接 + 求和” 操作组合，形成最终的几何条件 C_geo，公式如下：C_geo = Concat(F_xy, F_yz, F_xz) + Sum(F_xy, F_yz, F_xz)

3.1.2 语义特征与扩散模型优化

为进一步保证生成图像的语义一致性，FDGaussian 引入CLIP 语义条件：

使用 CLIP 图像编码器编码输入参考图，CLIP 文本编码器编码视角变化 Δπ（如 “从上方 30 度观察物体”）；
将两者嵌入拼接，形成语义条件 C_sem = Concat(CLIP_img, CLIP_text(Δπ))。

最终，扩散模型（基于 Stable Diffusion 改进）的输入为 “参考图 + 带噪目标视图 + 几何条件 + 语义条件”，优化目标为最小化去噪误差： $\min _{\theta} \mathbb{E}_{z \sim \mathcal{E}(\mathcal{I}), t, \epsilon \sim \mathcal{N}(0,1)}\left\| \epsilon-\epsilon_{\theta}\left(z_{t}, t, c\left(\mathcal{I}_{r e f}, \Delta \pi\right)\right)\right\| _{2}^{2}$ ，其中， $z_t$ 是 latent 空间带噪特征， $\epsilon_\theta$ 是 UNet 去噪网络， $c(\mathcal{I}_{ref}, \Delta\pi)$ 是融合后的几何 - 语义条件。

3.2 阶段二：加速高斯溅射 3D 重建

传统高斯溅射（Gaussian Splatting）虽兼顾质量与速度，但存在两大问题：1）多视角信息融合不充分；2）优化中存在大量冗余的高斯分裂 / 克隆操作。FDGaussian 通过极线注意力与高斯发散显著性（GDS） 分别解决这两个问题。

3.2.1 高斯溅射基础回顾

3D 高斯溅射用大量 3D 高斯元表示场景，每个高斯元由以下参数定义：

位置 $\mu$ （均值）；
3D 协方差矩阵 $\Sigma$ （通过缩放矩阵 S 与旋转矩阵 R 分解： $\Sigma = R S S^T R^T$ ，保证半正定性）；
颜色 c 与透明度 $\sigma$ 。

渲染时，先将 3D 高斯投影到 2D 图像平面，计算每个像素的高斯贡献，最终通过加权融合得到像素颜色： $\hat{C}=\sum_{i \in N} c_{i} \sigma_{i} \prod_{j=1}^{i-1}(1-\sigma_{j})$ ，其中 N 是覆盖该像素的高斯元集合。

3.2.2 极线注意力：多视角特征融合

传统方法仅用单图初始化高斯，或用普通交叉注意力融合多视角，无法利用视角间的几何约束。FDGaussian 提出极线注意力，基于极线几何缩小特征匹配范围：

极线几何原理：对于视角 s 中的特征点 $p_s$ ，其在视角 t 中的对应点 $p_t$ 必定落在一条固定直线（极线）上，该直线由两视角的相对姿态 $\Delta\pi$ 决定（如图 4 所示）。

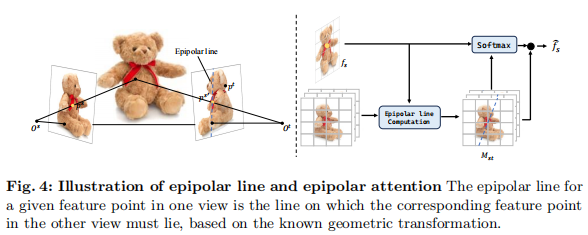
注：极线约束限定了跨视角特征匹配的范围，减少无效计算并提升准确性。

极线注意力计算：
1. 对每个视角 s 的 UNet 中间特征 $f_s$ ，计算其在所有其他视角 t 上的极线集合 $\left \{ l_t \right \}_{t\neq s}$ ；
2. 生成极线权重矩阵 $M_{st}$ ：仅保留极线附近像素的权重，其他位置权重设为 0；
3. 加权融合多视角特征： $\hat{f}_s = \text{Softmax}(M_{st} \cdot f_t)$ ，得到融合后特征用于高斯参数预测。

该机制不仅提升了多视角一致性，还减少了注意力计算量，兼顾准确性与效率。

3.2.3 高斯发散显著性（GDS）：加速优化

传统高斯溅射的分裂 / 克隆操作忽略高斯间距，即使两个高斯元距离极近仍会执行操作，导致大量冗余计算。FDGaussian 提出GDS 指标，衡量高斯元间的 “发散程度”，仅对必要的高斯元执行优化操作：

GDS 定义：结合高斯元的位置差与协方差，量化两者的空间发散程度： $\text{GDS}(G_1, G_2) = \|\mu_1 - \mu_2\|^2 + \text{Tr}\left( \Sigma_1^{-1}\Sigma_2 + \Sigma_2^{-1}\Sigma_1 - 2I \right)$ ，其中 $\mu_1/\mu_2$ 是高斯位置， $\Sigma_1/\Sigma_2$ 是协方差矩阵， $\text{Tr}(\cdot)$ 是矩阵迹。GDS 值越大，说明两个高斯元空间上越分散。
加速策略：
1. 阈值筛选：仅对 “位置梯度> 阈值且 GDS > 阈值” 的高斯元执行分裂 / 克隆；
2. k-NN 简化计算：通过 k 近邻算法找到每个高斯元的最近邻，仅计算这对高斯元的 GDS，将时间复杂度从 $O(N^2)$ 降至 $O(N\log N)$ （N 为高斯元数量）；
3. 协方差分解简化：利用 $\Sigma = R S S^T R^T$ 的对角性与正交性，简化 GDS 中的矩阵运算。

实验表明，GDS 可将优化时间缩短至原来的 1/15，且不损失重建质量。

3.3 损失函数设计

为保证重建图像的结构相似性与感知质量，FDGaussian 采用多损失融合： $\mathcal{L}_{\text{total}} = \lambda_1 \cdot \mathcal{L}_{\text{SSIM}} + \lambda_2 \cdot \mathcal{L}_{\text{LPIPS}}$

$\mathcal{L}_{\text{SSIM}}$ ：结构相似性损失，衡量重建图与真值的结构一致性；
$\mathcal{L}_{\text{LPIPS}}$ ：感知损失，基于预训练 CNN 提取特征，衡量主观视觉质量；
超参数设置： $\lambda_1=0.02$ ， $\lambda_2=0.01$ （通过实验验证的最优值）。

四、实验验证与结果分析

FDGaussian 在Objaverse（800K CAD 模型）与GSO（高质量扫描家居物品）数据集上进行了全面验证，从定量、定性、消融实验三方面证明其优越性。

4.1 实验设置

硬件环境：NVIDIA V100（16GB）GPU；
基线方法：Zero-1-to-3、Realfusion、Consistent-123、Shap-E、DreamGaussian（覆盖隐式 / 显式 / 混合表示方法）；
评价指标：
- 新视角合成（NVS）：PSNR（峰值信噪比，越高越好）、SSIM（结构相似性，越高越好）、LPIPS（感知距离，越低越好）；
- 3D 重建：Chamfer Distance（CD，点云相似度，越低越好）、CLIP 相似度（语义一致性，越高越好）、重建时间（越低越好）。

4.2 定量结果：全面超越基线

4.2.1 新视角合成性能

如表 1 所示，FDGaussian 在两个数据集上的 PSNR、SSIM、LPIPS 均优于所有基线，尤其在 Objaverse 上 PSNR 达到 23.97，比第二名 DreamGaussian 高 2.44，证明其多视角一致性与图像质量优势。

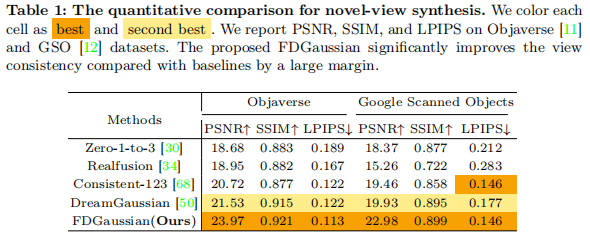
4.2.2 3D 重建性能

如表 2 所示，FDGaussian 在 CD（0.0232）与 CLIP 相似度（80.0）上最优，且重建时间仅 70 秒，远快于 Zero-1-to-3（30 分钟）与 DreamGaussian（2 分钟），实现 “质量与效率双优”。

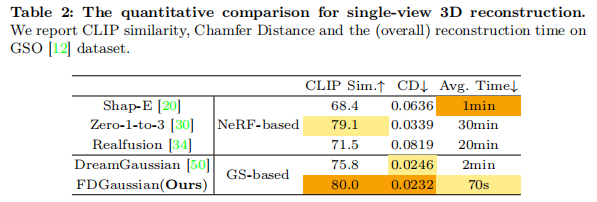
4.3 定性结果：细节与一致性兼顾

4.3.1 新视角合成

如图 3 所示，FDGaussian 生成的近视角与参考图高度一致（几何、语义无偏差），远视角则在保证合理性的同时展现多样性，避免了 “过度一致” 导致的僵硬感。

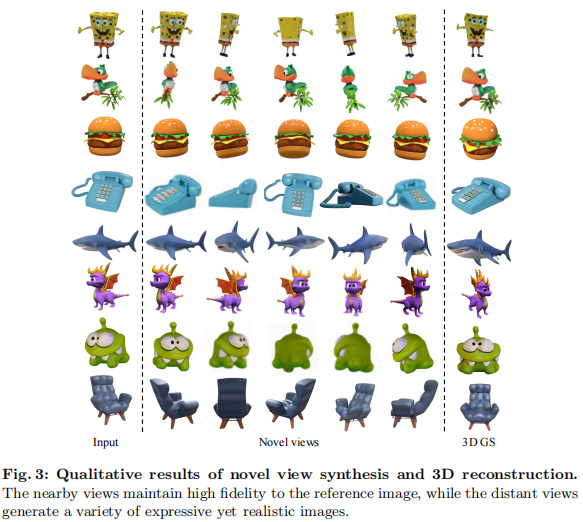
4.3.2 3D 重建对比

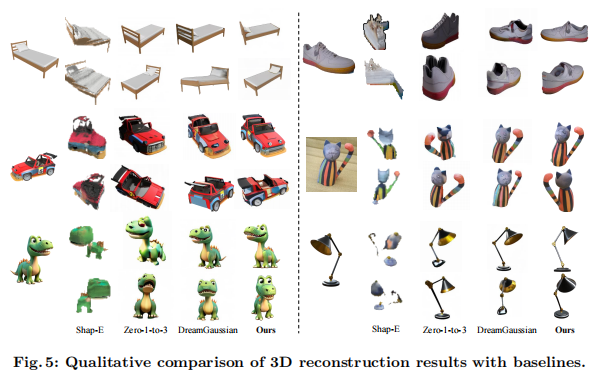
如图 5 所示，对比基线方法，FDGaussian 的优势显著：

Shap-E：易出现几何坍缩，结果模糊；
Zero-1-to-3：多视角不一致（如物体侧面细节错位）；
DreamGaussian：纹理过度平滑，丢失细节；
FDGaussian：几何结构完整、纹理细节清晰、多视角完全一致。

4.4 消融实验：验证核心模块有效性

消融实验针对 FDGaussian 的三大核心模块（正交平面分解、CLIP 语义嵌入、极线注意力、GDS）展开，验证其必要性与贡献。

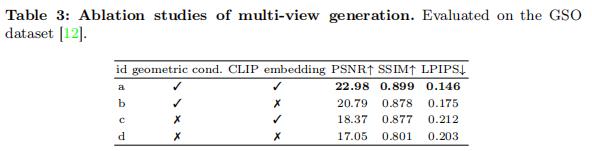
4.4.1 多视角生成模块消融

如表 3 所示，移除 “正交平面分解”（几何条件）后，PSNR 从 22.98 降至 18.37，LPIPS 从 0.146 升至 0.212，证明几何条件是保证多视角一致性的关键；移除 “CLIP 语义嵌入” 也会导致性能下降，说明语义约束可提升图像保真度。

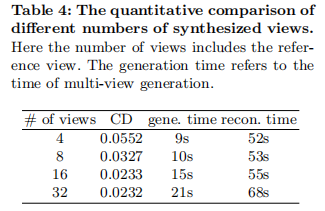
4.4.2 生成视角数量影响

如表 4 所示，随着生成视角数量从 4 增加到 16，CD 从 0.0552 降至 0.0233，重建质量显著提升；但视角数量增至 32 时，CD 仅降至 0.0232，时间却从 70 秒增至 89 秒（生成 21 秒 + 重建 68 秒），证明 16 个视角是 “质量 - 效率” 平衡点。

4.4.3 GDS 加速效果消融

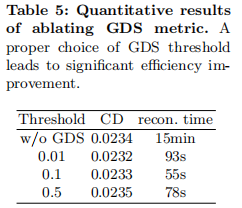
如表 5 所示，不使用 GDS 时，重建时间长达 15 分钟；使用 GDS（阈值 0.1）后，时间缩短至 55 秒，且 CD 仅从 0.0234 升至 0.0233，几乎无质量损失，证明 GDS 的高效性。

4.5 拓展能力：文本到 3D 生成

FDGaussian 可与文本到图像模型（如 DALL-E2、Stable Diffusion）无缝结合，实现 “文本→2D 图像→3D 重建” 的端到端流程。如图 7 所示，即使是 “穿宇航服的熊猫”“90 年代电脑（蒸汽波风格）” 等创意场景，FDGaussian 也能准确捕捉细节，甚至还原遮挡部分的几何结构。