深度学习中的训练流程:从输入到权重更新的完整旅程
文章目录
- 🧠 1. 图解:深度学习训练流程
- 1️⃣ 第一步:输入数据(Input X)
- 2️⃣ 第二步:前向传播(Forward Pass)
- 🔁 数据变换层(Layer)
- 📈 输出预测(Predictions Y')
- 3️⃣ 第三步:计算损失(Loss Function)
- ❌ 对比真实标签(True targets Y)
- 🎯 损失函数(Loss function)
- 📉 损失得分(Loss score)
- 4️⃣ 第四步:优化器更新权重(Weight Update)
- 🔁 优化器(Optimizer)
- 🔍 反向传播(Backward Pass)
- 🔁 权重更新(Weight update)
- 🔄 2. 整体循环:训练的本质
- 🧩 3. 实际应用中的意义
- ✅ 4. 总结
- 📚 5. 结语
深度学习中的训练流程:从输入到权重更新的完整旅程
在深度学习中,模型的学习过程是一个不断迭代优化的过程。本文将以一张经典的神经网络训练流程图为基础,深入浅出地阐述其核心机制——前向传播、损失计算与反向传播。通过理解这一循环,我们可以更好地掌握神经网络是如何“学会”从数据中提取特征并做出准确预测的。
🧠 1. 图解:深度学习训练流程
-
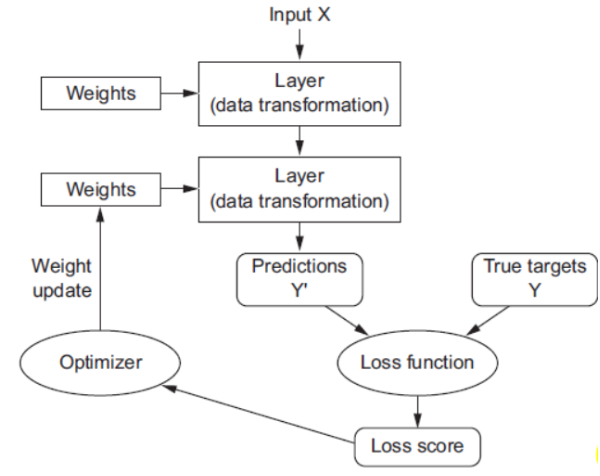
我们来看这张图
-
这个流程图清晰地展示了神经网络训练的核心步骤。接下来,我们将逐一解析每个环节的作用及其相互关系。
1️⃣ 第一步:输入数据(Input X)
-
X 是模型的输入数据,例如图像像素值、文本词向量或传感器读数。
-
这些原始数据被送入神经网络的第一层,作为后续处理的基础。
✅ 示例:如果你正在训练一个手写数字识别模型,那么
X就是 28×28 的灰度图像矩阵。
2️⃣ 第二步:前向传播(Forward Pass)
🔁 数据变换层(Layer)
-
神经网络由多个“层”组成,每一层都对输入进行一次非线性变换。
-
每一层包含一组可学习的参数——权重(Weights) 和偏置(Bias),它们决定了输入如何被转换。
-
变换公式通常为: Output = σ ( W ⋅ X + b ) \text{Output} = \sigma(W \cdot X + b) Output=σ(W⋅X+b)
其中, W W W 是权重矩阵, b b b 是偏置项, σ \sigma σ 是激活函数(如 ReLU、Sigmoid)⚠️ 注意:这里的“Layer”可以是全连接层、卷积层、池化层等,但本质都是对数据的数学变换。
📈 输出预测(Predictions Y’)
-
经过若干层的逐级变换后,最终输出的是模型的预测结果 Y ′ Y' Y′。
-
在分类任务中, Y ′ Y' Y′ 是每个类别的概率分布;在回归任务中,它是连续数值。
✅ 示例:对于 MNIST 分类,$ Y’ $ 是一个长度为 10 的向量,表示该图像属于 0~9 数字的概率。
3️⃣ 第三步:计算损失(Loss Function)
❌ 对比真实标签(True targets Y)
- Y Y Y 是样本的真实标签(Ground Truth),比如正确答案是数字 “7”。
- 我们将预测结果 Y ′ Y' Y′ 与真实标签 Y Y Y 进行比较,衡量两者的差异。
🎯 损失函数(Loss function)
-
损失函数量化了预测错误的程度
💡 损失越小,说明模型预测越接近真实值。
-
常见的损失函数
- 交叉熵损失(Cross-Entropy Loss):用于分类问题
- 均方误差(MSE):用于回归问题
📉 损失得分(Loss score)
-
计算出的损失值称为“损失得分”,它是一个标量(单个数字)。
-
这个分数反映了当前模型表现的好坏,是优化过程的关键信号。
✅ 示例:如果模型把“7”误判为“8”,损失得分会较高;若判断正确,则损失较低。
4️⃣ 第四步:优化器更新权重(Weight Update)
🔁 优化器(Optimizer)
- 优化器根据损失得分来决定如何调整权重。
- 常见的优化器
- SGD(随机梯度下降):随机梯度下降(SGD)是一种优化算法,通过计算损失函数对模型参数的梯度,沿反方向更新权重以最小化误差。与批量梯度下降不同,SGD每次仅用一个样本或小批量数据计算梯度,具有更快的收敛速度和更强的跳出局部最优能力,广泛应用于深度学习模型训练。
- Adam:Adam(Adaptive Moment Estimation)是一种自适应学习率优化算法,结合了动量法和RMSProp的优点。它计算梯度的一阶矩(均值)和二阶矩(未中心化方差)的指数加权平均,自动调整每个参数的学习率,收敛快、稳定性好,广泛用于深度学习模型训练。
- RMSprop:RMSprop(Root Mean Square Propagation)是一种自适应学习率优化算法,通过除以梯度平方的指数加权平均来调整学习率,有效缓解梯度消失或爆炸问题。它使学习率在平坦区域增大、在陡峭区域减小,提升训练稳定性,特别适用于非稳态目标函数,是深度学习中常用的优化方法之一。
🔍 反向传播(Backward Pass)
- 优化器利用反向传播算法计算损失对每个权重的梯度(即变化率)。
- 根据梯度方向和大小,优化器执行更新规则: W new = W old − η ⋅ ∂ Loss ∂ W W_{\text{new}} = W_{\text{old}} - \eta \cdot \frac{\partial \text{Loss}}{\partial W} Wnew=Wold−η⋅∂W∂Loss,其中 η \eta η 是学习率,控制更新步长。
🔁 权重更新(Weight update)
- 更新后的权重会被反馈回网络的各个层,准备下一轮训练。
- 这个过程不断重复,直到模型收敛(损失趋于稳定)。
🔄 2. 整体循环:训练的本质
-
整个流程形成一个闭环:
输入 → 前向传播 → 预测 → 损失计算 → 反向传播 → 权重更新 → 再次输入 -
每一次迭代都让模型更接近最优解。随着训练次数增加,损失逐渐降低,预测能力不断提升。
🧩 3. 实际应用中的意义
- 监督学习:依赖于真实标签 Y Y Y 来指导学习。
- 自动调参:无需人工设定规则,模型通过数据自我学习。
- 泛化能力:经过充分训练后,模型能对未见过的数据做出合理预测。
✅ 4. 总结
-
神经网络通过不断对比预测与真实值之间的差距(损失),并据此调整内部参数(权重),从而逐步提升其预测准确性。
步骤 功能 输入 X 提供原始数据 层(Layer) 对数据进行变换,提取特征 预测 Y’ 模型输出的估计结果 真实标签 Y 正确答案 损失函数 衡量预测误差 损失得分 数量化误差程度 优化器 根据误差调整权重 权重更新 改进模型性能
📚 5. 结语
- 这张看似简单的流程图,实际上蕴含了现代人工智能的核心思想——从数据中学习规律,通过反馈机制持续改进。无论是语音识别、图像生成还是自然语言处理,背后都离不开这种“输入 → 转换 → 损失 → 更新”的基本范式。理解它,你就掌握了深度学习的“心脏跳动”。
