当前位置： 首页 > news >正文

Slotted Aloha

news 2025/10/25 7:08:48

1.论文主要思路

论文地址：Stability and Delay Analysis of Buffered Aloha Networks

一、核心仿真模型与假设

论文的仿真模型是构建其理论分析的基础，其核心是一个离散时间的、基于时隙的仿真系统。

  1. 网络拓扑与节点：
    • 仿真一个包含 n 个节点的网络。
    • 所有节点是同构的，具有相同的参数和行为。
  2. 流量模型：
    • 每个节点都有一个无限大小的缓冲区。
    • 数据包以 伯努利过程 到达每个节点，到达率为 λ。
    • 这意味着在每个时隙开始时，一个节点独立地以概率 λ 产生一个新包。
  3. 队列服务规则：
    • 先进先出。
    • 只有队首包 有资格参与信道竞争。这是“Buffered Aloha”与经典无缓冲区Aloha的关键区别。
  4. 信道访问机制：
    • 时间被划分为时隙，传输在每个时隙开始时进行。
    • 一个HOL包能否传输，取决于它当前的相位 和退避因子 q。
    • 采用 K-指数退避 框架：
      • 一个新成为HOL的包处于相位 0，传输概率为 ( q 0 = 1 ) ( q^0 = 1 ) (q0=1)。
      • 如果传输发生碰撞，则进入下一相位（相位 1），传输概率变为 ( q 1 ) ( q^1 ) (q1)。
      • 以此类推，直到达到截止相位 K。相位 K 的包以概率 ( q K ) ( q^K ) (qK) 传输。
      • 几何重传 是 ( K=1 ) 的特例：所有重传包都以概率 ( q ) 传输。
      • 指数退避 是 ( K=\infty ) 的特例：包可以无限后退，传输概率不断降低。
  5. 碰撞模型：
    • 理想化的：如果在同一个时隙内有超过一个节点传输，则发生碰撞，所有传输的包都失败。
    • 碰撞的包会根据上述规则进入更高的相位（重传状态）。

二、主要仿真指标

论文中明确或隐含地追踪了以下关键性能指标，这些是验证其理论的核心：

  1. 瞬态成功概率 ( p_t )：

    • 定义：到第 ( t ) 个时隙为止，所有HOL包传输尝试中，成功传输的比例。
    • 计算方式： ( p t = 到时隙t为止累计的成功传输次数 到时隙t为止累计的传输尝试次数 ) ( p_t = \frac{\text{到时隙t为止累计的成功传输次数}}{\text{到时隙t为止累计的传输尝试次数}} ) (pt​=到时隙t为止累计的传输尝试次数到时隙t为止累计的成功传输次数​)
    • 目的：这是最重要的观测变量。用于直接观察系统动态：
      • 收敛到期望稳定点 ( p_L )（高吞吐量，稳定）。
      • 还是收敛到非期望稳定点 ( p_A )（低吞吐量，饱和状态）。
      • 验证理论分析中预测的双稳态特性。

  2. 网络吞吐量 ( \hat{\lambda}_{out} )：

    • 定义：长期来看，整个网络平均每时隙成功传输的包数量。
    • 计算方式：在足够长的仿真时间 ( T ) 内， ( λ ^ o u t = 总成功传输包数 T ) ( \hat{\lambda}_{out} = \frac{\text{总成功传输包数}}{T} ) (λ^out​=T总成功传输包数​)。
    • 目的：验证稳定性。论文定义“稳定”为 ( λ ^ o u t = λ ^ = n λ ) ( \hat{\lambda}_{out} = \hat{\lambda} = n\lambda ) (λ^out​=λ^=nλ)。如果吞吐量低于输入率，说明系统不稳定，队列会无限增长。

  3. 访问延迟：

    • 定义：一个包从它成为HOL包的时刻开始，到它被成功传输出去的时刻为止，所经历的时隙数。
    • 观测的统计量：
      • 一阶矩 ( E [ D 0 ] ) ( E[D_0] ) (E[D0​])：平均访问延迟。
      • 二阶矩 ( E [ D 0 2 ] ) ( E[D_0^2] ) (E[D02​])：访问延迟的方差，用于衡量延迟抖动。
    • 目的：
      • 比较不同退避参数下的延迟性能。
      • 验证理论公式（如公式60, 61）的正确性。
      • 揭示指数退避在非期望稳定点 ( p A ) ( p_A ) (pA​) 下的“捕获现象”，表现为二阶矩急剧增大甚至发散（无穷大）。

  4. 系统状态收敛性：

    • 这是一个定性但至关重要的指标。仿真通过观察 ( p t ) ( p_t ) (pt​) 随时间 ( t ) 的变化轨迹，来判断系统最终收敛于哪个稳定点。这直接对应理论分析中的动态方程。

三、仿真运行逻辑与参数扫描

论文的仿真并非只运行一种参数设置，而是进行了系统的参数扫描，以绘制出完整的性能图景：

  1. 验证双稳态：

    • 固定 ( n ), ( λ ^ ) ( \hat{\lambda} ) (λ^), ( K )。
    • 选择不同的退避因子 ( q )，特别是选择在绝对稳定区域 ( S_L ) 内和外的值。
    • 对每个 ( q )，运行仿真，观察 ( p_t ) 的轨迹，看它是收敛到 ( p_L ) 还是 ( p_A )。（对应 图10）

  2. 绘制稳定区域：

    • 固定 ( n ), ( λ ^ ) ( \hat{\lambda} ) (λ^), ( K )。
    • 扫描不同的 ( q ) 值，对于每个 ( q )，测量稳态下的吞吐量 ( λ ^ o u t ) ( \hat{\lambda}_{out} ) (λ^out​)。
    • 将满足 ( λ ^ o u t = λ ^ ) ( \hat{\lambda}_{out} = \hat{\lambda} ) (λ^out​=λ^) 的 ( q ) 范围标记为稳定区域。（对应 图11, 12, 13）

  3. 分析延迟性能：

    • 在稳定区域内，对于每个 ( q )，测量并记录 ( E [ D 0 ] ) ( E[D_0] ) (E[D0​]) 和 ( E [ D 0 2 ] ) ( E[D_0^2]) (E[D02​])。
    • 找到使延迟最小化的最优 ( q )，并与理论公式（如66）进行对比。（对应 图14）

  4. 研究截止相位 ( K ) 的影响：

    • 固定 ( n ), ( λ ^ ) ( \hat{\lambda} ) (λ^), ( q )。
    • 变化 ( K ) 的值（如 1, 2, 4, 8, 16, ∞）。
    • 对每个 ( K )，测量吞吐量和延迟的二阶矩，展示 ( K ) 在稳定性和延迟抖动之间的权衡。（对应 图15）

思考：可以明显看出，虽然本文提到了slotted Aloha，但其实本质上本文提到的是一个加了K退避优化的slotted Aloha变种，所以我们先做基础的slotted Aloha的简单仿真，之后再考虑进行K退避优化

2.我的仿真代码思路（以吞吐量仿真为例）

实现一个基础的、带有固定传输概率的时隙ALOHA协议仿真，核心目标是扫描不同传输概率 q，并测量对应的系统吞吐量和信令开销。

一、核心模型与假设

  1. 网络模型：

    • 节点数量：node_sum 个同构节点。
    • 流量模型：每个节点在每个时隙有独立且相同的概率 lambda 产生一个新包。这是一个伯努利到达过程，总到达率为 Lambda_total = node_sum * lambda。
    • 队列模型：每个节点维护一个队列（代码中用 Node_state_current(:, 2) 表示队列长度）。这是一个缓冲式ALOHA 模型。

  2. 协议机制：

    • 时隙化：时间被划分为等长的时隙，所有传输在时隙开始时同步进行。
    • 传输决策：
      • 只有队列非空的节点才可能传输。
      • 每个这样的节点，独立地以固定概率 q 决定在本时隙是否传输。
      • 这与论文中的 几何重传（K=1） 模型完全一致。节点不记忆碰撞历史，每次传输尝试的概率都是 q。

  3. 碰撞与成功：

    • 如果一个时隙内有且仅有一个节点传输，则传输成功。
    • 如果传输节点数为0（空闲）或大于1（碰撞），则该时隙没有成功传输。
二、仿真流程与逻辑（逐时隙）

仿真核心是一个嵌套循环：外层循环遍历不同的 q 值，内层循环对每个 q 进行 Total_slot 个时隙的模拟。

对于每个时隙 t，执行以下步骤：

  1. 包到达（向量化）：

    • 为所有节点生成随机数，判断本时隙是否有新包到达。
    • 将到达的包加入对应节点的队列。Node_state_current(:, 2) = Node_state_current(:, 2) + arrivals;

  2. 传输决策（向量化）：

    • 找出所有队列非空的节点。has_packet = Node_state_current(:, 2) > 0;
    • 在这些节点中，根据概率 q 决定哪些节点在本时隙尝试传输。should_transmit = has_packet & attempt_prob;
    • 记录尝试传输的节点数 num_attempt_this_slot。

  3. 冲突检测与成功处理：

    • 如果 num_attempt_this_slot == 1，则视为成功传输。
      • 总成功次数 Total_success 加1。
      • 成功节点的队列长度减1。Node_state_current(node_transmit, 2) = max(0, ...) - 1);

  4. 状态重置与指标记录：

    • 信令开销：将本时隙的尝试次数累加到 signaling_count。这反映了系统的冲突水平和控制开销。
    • 重置所有节点的“发送标志位”，为下一个时隙做准备。Node_state_current(:, 1) = 0;
三、关键性能指标

  1. 吞吐量 throughputD_simu：

    • 定义：平均每个时隙成功传输的包数量。
    • 计算：Total_success / Total_slot。
    • 目的：这是最核心的性能指标，用于绘制经典的“吞吐量 vs. 提供负载（或传输概率 q）”曲线，找到使吞吐量最大化的最优 q。

  2. 信令开销 ST：

    • 定义：平均每个时隙发生的传输尝试次数（包括成功的和冲突的）。
    • 计算：signaling_count / Total_slot。
    • 目的：衡量信道竞争的激烈程度和协议效率。过高的 ST 意味着大量能量和资源浪费在冲突上。
四、仿真策略与特点

  1. 参数扫描：

    • 通过外层循环遍历 ACB_bw 数组（即不同的 q 值），系统地研究传输概率对系统性能的影响。

  2. 性能评估：

    • 仿真的最终目标是得到两条曲线：
      • throughputD_simu 随 q 变化的曲线。
      • ST 随 q 变化的曲线。
    • 通过分析这些曲线，可以确定系统的最佳工作点。

  3. 优化技巧：

    • 使用了向量化操作，对所有节点的到达和传输决策进行批量随机数生成和逻辑判断，大大提升了仿真效率。
    • 预生成随机数矩阵（arrival_rand, transmit_rand）是可选的优化，有助于减少循环内的计算开销。

与论文仿真思路的对比

方面我的仿真思路论文中的仿真思路
核心协议几何重传 (K=1)，固定传输概率 qK-指数退避框架，传输概率随碰撞次数变化
关键观测变量无瞬态成功概率 ( p_t )
性能指标吞吐量、信令开销 (ST)吞吐量、平均延迟、延迟二阶矩
分析重点寻找最优固定 q，以最大化吞吐量分析双稳态、稳定区域、延迟抖动与 K 的关系
节点状态队列长度队列长度 + 相位 (0 to K)
动态行为无记忆性，每次尝试概率相同有记忆性，碰撞后退避，传输概率降低

结论

我的仿真代码实现了一个经典且基础的缓冲式时隙ALOHA模型，旨在通过蒙特卡洛仿真验证ALOHA协议的基本特性：

  • 在轻负载下，低 q 可能导致信道利用率不足。
  • 在重负载下，高 q 会导致过多冲突，吞吐量下降。
  • 存在一个最优的 q，使得吞吐量达到最大值。

与论文相比，我的仿真更侧重于协议的“静态”性能评估（扫描q），而论文则深入研究了协议的“动态”行为（收敛性、稳定性）和更复杂的退避机制（K>1）及其对延迟的影响。 如果再进一步研究，可以考虑引入相位（碰撞计数） 和K-指数退避机制，并追踪瞬态成功概率 ( p_t ) 和包延迟的高阶矩。

3.主要仿真思路、结果与分析

吞吐量

跳转到2看吞吐量
代码Main4：

clc;clear;close all;
%% 吞吐量仿真比较：GF vs SAST vs 时隙ALOHAACB_bw_simu = [0.0001,0.001:0.001:0.01];
Lambda_total = 1; % 饱和情况
Node_num = 100;
Total_slot = 2e6;
Node_state = zeros(100,2);% 运行三种协议的仿真
[throughputD_simu1, pt_simu1, ST1] = GF_1(Node_state, ACB_bw_simu, Lambda_total, Total_slot);
[throughputD_simu3, throughputA_simu3, pt_simu3, ST3] = SAST_1(Node_state, ACB_bw_simu, Lambda_total, Total_slot);
[throughputD_simu4, ST4] = slotted_ALOHA(Node_state, ACB_bw_simu, Lambda_total, Total_slot);%% 理论吞吐量分析
ACB_bw_ana = linspace(0, 0.01, 100);
n = Node_num;% GF协议理论吞吐量
throughput1_ana = n .* ACB_bw_ana .* exp(-n .* ACB_bw_ana);% SAST协议理论吞吐量  
nq = n .* ACB_bw_ana;
throughput3_ana = nq ./ (exp(nq) + nq - 1);% 时隙ALOHA理论吞吐量
throughput4_ana = n .* ACB_bw_ana .* exp(-n .* ACB_bw_ana);%% 画图 - 吞吐量比较
figure 
hold on;% 颜色配置
figcol = cell(1,3);
figcol{1} = '#336633';  % GF - 绿色
figcol{2} = '#5C0DAC';  % SAST - 紫色  
figcol{3} = '#FF0000';  % 时隙ALOHA - 红色% 标记形状配置
figshape = cell(1,3);
figshape{1} = '*';
figshape{2} = 'O';
figshape{3} = 'square';linewidth = 1;
markersize = 60;% GF协议
i = 1;
f1 = plot(ACB_bw_ana, throughput1_ana, '-', 'color', figcol{i}, 'LineWidth', linewidth);
s1 = scatter(ACB_bw_simu, throughputD_simu1, markersize, 'MarkerEdgeColor', figcol{i}, ...'Marker', figshape{i}, 'LineWidth', linewidth);% SAST协议
i = 2;
f2 = plot(ACB_bw_ana, throughput3_ana, '--', 'color', figcol{i}, 'LineWidth', linewidth);
s2 = scatter(ACB_bw_simu, throughputD_simu3, markersize, 'MarkerEdgeColor', figcol{i}, ...'Marker', figshape{i}, 'LineWidth', linewidth);% 时隙ALOHA协议
i = 3;
f3 = plot(ACB_bw_ana, throughput4_ana, ':', 'color', figcol{i}, 'LineWidth', linewidth);
s3 = scatter(ACB_bw_simu, throughputD_simu4, markersize, 'MarkerEdgeColor', figcol{i}, ...'Marker', figshape{i}, 'LineWidth', linewidth);hold off;
xlim([0, max(ACB_bw_ana)]);
% 修正字体设置 - 统一使用英文或统一字体
xlabel('Transmission Probability', 'FontName', 'Times New Roman', 'fontsize', 14);
ylabel('Throughput', 'FontName', 'Times New Roman', ...'rotation', 0, 'Horizontalalignment', 'right', 'fontsize', 14);% 或者如果您需要中文标签，可以这样设置：
% xlabel('传输概率', 'FontName', 'SimSun', 'fontsize', 14);
% ylabel('吞吐量', 'FontName', 'SimSun', ...
%     'rotation', 0, 'Horizontalalignment', 'right', 'fontsize', 14);legend([f1, s1, f2, s2, f3, s3], ...{'GF Analysis', 'GF Simulation', 'SAST Analysis', 'SAST Simulation', ...'Slotted ALOHA Analysis', 'Slotted ALOHA Simulation'}, ...'FontName', 'Times New Roman'); % 确保图例也使用相同字体set(gca, 'position', [0.15, 0.15, 0.7, 0.7], 'LineWidth', 0.5, 'fontsize', 14, 'FontName', 'Times New Roman');
set(gcf, 'unit', 'normalized', 'position', [.2, .2, 0.4, 0.45]);
grid on;
box on;save('throughput_comparison.mat');

slotted_ALOHA.m

function [throughputD_simu, ST] = slotted_ALOHA(Node_state, ACB_bw, Lambda_total, Total_slot)
% 时隙ALOHA协议仿真（向量化高速版）[node_sum, ~] = size(Node_state);num_q = max(size(ACB_bw));throughputD_simu = zeros(1, num_q);ST = zeros(1, num_q);lambda_hat = Lambda_total;lambda = lambda_hat / node_sum;  % 每个节点的到达率for k = 1:num_qq = ACB_bw(k);Total_success = 0;signaling_count = 0;% 初始化节点状态: [是否发送, 队列长度]Node_state_current = zeros(node_sum, 2);% 预生成所有时隙所需的随机数（可选，节省时间）% 如果内存允许，可以一次性生成arrival_rand = rand(Total_slot, node_sum);      % 包到达用transmit_rand = rand(Total_slot, node_sum);     % 发送决策用for t = 1:Total_slot% Step 1: 包到达（向量化）arrivals = arrival_rand(t, :)' < lambda;Node_state_current(:, 2) = Node_state_current(:, 2) + arrivals;% Step 2: 传输决策（向量化）has_packet = Node_state_current(:, 2) > 0;attempt_prob = transmit_rand(t, :)' < q;should_transmit = has_packet & attempt_prob;Node_state_current(should_transmit, 1) = 1;num_attempt_this_slot = sum(should_transmit);% Step 3: 冲突检测if num_attempt_this_slot == 1% 成功node_transmit = find(should_transmit, 1);Total_success = Total_success + 1;Node_state_current(node_transmit, 2) = max(0, Node_state_current(node_transmit, 2) - 1);elsenode_transmit = 0;  % 冲突或无传输end% Step 4: 信令开销和状态重置signaling_count = signaling_count + num_attempt_this_slot;Node_state_current(:, 1) = 0;  % 所有节点重置发送标志end% 记录结果throughputD_simu(k) = Total_success / Total_slot;ST(k) = signaling_count / Total_slot;end
end

结果：
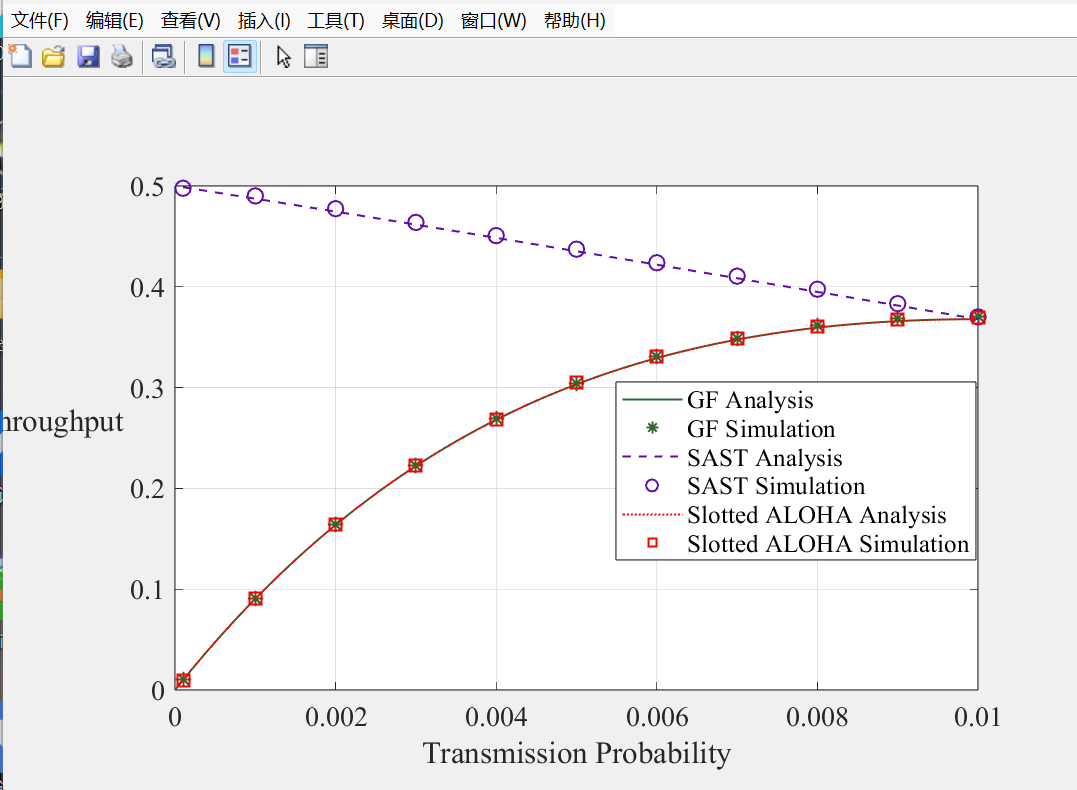
slotted的吞吐量
分析：slottedAloha的吞吐量与给的模板GF差不多，所以可以认为仿真效果很好

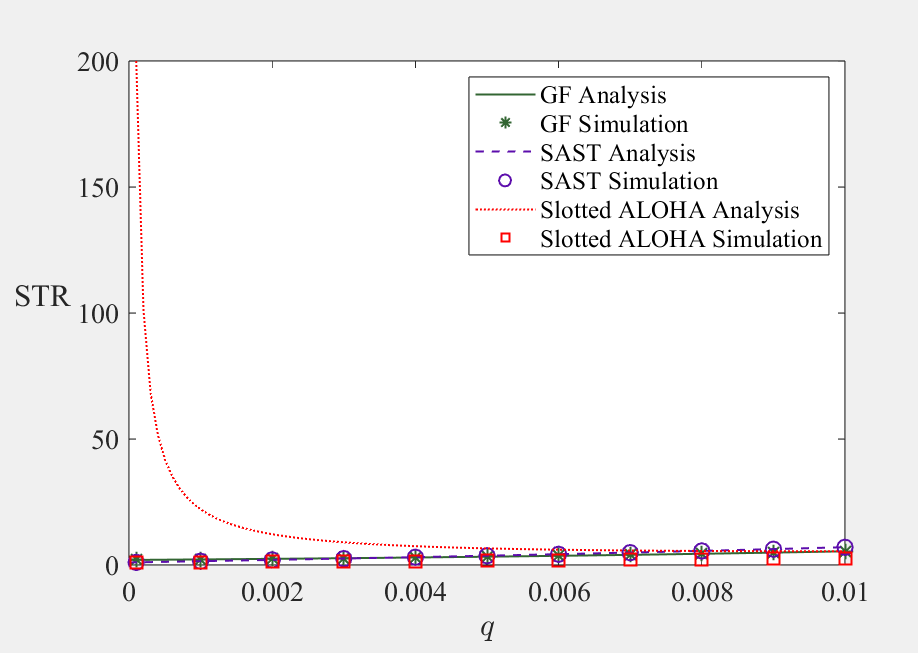
STR

主要思路是比较三种随机接入协议在饱和情况下的信令开销性能。以下是详细分析：

核心目标

比较GF、SAST和时隙ALOHA三种协议的信令传输比(STR)，即每成功传输一个数据包所需的信令开销。

代码结构分析

1. 参数设置

ACB_bw_simu = [0.0001,0.001:0.001:0.01];  % 接入概率范围
Lambda_total = 1;    % 总到达率
Node_num = 100;      % 节点数量
Total_slot = 2e6;    % 总时隙数

2. 仿真执行

调用三个协议的仿真函数：

  • GF协议：GF_1() - 获取吞吐量和信令传输量
  • SAST协议：SAST_1() - 获取吞吐量和信令传输量
  • 时隙ALOHA：slotted_ALOHA() - 获取吞吐量和信令传输量

3. 性能指标计算

计算信令传输比(STR)：

STR = 信令传输量 / 成功传输的数据包数

这个指标反映了协议的效率，值越小说明信令开销越小。

4. 理论分析

为每个协议建立理论模型：

  • GF协议：STR1_ana = 2*exp(Node_num.*ACB_bw_ana)
  • SAST协议：STR3_ana = 2*exp(nq)+2*nq-exp(-nq)
  • 时隙ALOHA：STR4_ana = 2./(Node_num.*ACB_bw_ana.*exp(-Node_num.*ACB_bw_ana))

5. 可视化比较

绘制理论曲线和仿真散点图：

  • 使用不同颜色和标记区分三种协议
  • 理论分析用连续线型，仿真结果用散点标记
  • 设置专业的数据可视化格式

关键特点

  1. 饱和场景：假设系统处于高负载状态
  2. 双验证：同时进行理论分析和仿真验证
  3. 完整对比：从极低概率(0.0001)到较高概率(0.01)全面比较
  4. 标准化指标：使用STR作为统一的比较标准

预期输出

通过图形展示三种协议在不同接入概率下的信令开销性能，验证理论模型的准确性，并为协议选择提供依据。
代码：

clc;clear;close all;
%% 比较三种协议的信令开销（饱和情况下） :仿真 1：GF 3：SAST 4：时隙ALOHAACB_bw_simu=[0.0001,0.001:0.001:0.01];%这里与demo不同，只有20个数据点不够，所以采用这种分类方式，
%极低概率：0.0001（非常保守）
%低概率：0.001-0.005（适度竞争）
%中等概率：0.006-0.01（相对积极）
Lambda_total=1;%总包到达率
Node_num=100;
Total_slot=2e6;
Node_state=zeros(100,2);% 运行三种协议的仿真
[throughputD_simu1,pt_simu1,ST1] = GF_1(Node_state,ACB_bw_simu,Lambda_total,Total_slot);
[throughputD_simu3,throughputA_simu3,pt_simu3,ST3] = SAST_1(Node_state,ACB_bw_simu,Lambda_total,Total_slot);
[throughputD_simu4,ST4] = slotted_ALOHA(Node_state,ACB_bw_simu,Lambda_total,Total_slot);% 计算信令传输比
STR1_simu=ST1./throughputD_simu1;
STR3_simu=ST3./throughputD_simu3;
STR4_simu=ST4./throughputD_simu4;%% 理论分析
ACB_bw_ana=linspace(0,0.01,100);% 原有理论公式
STR1_ana=2*exp(Node_num.*ACB_bw_ana);
nq=Node_num.*ACB_bw_ana;
STR3_ana=2*exp(nq)+2*nq-exp(-nq);% 时隙ALOHA理论公式
STR4_ana = 2 ./ (Node_num .* ACB_bw_ana .* exp(-Node_num .* ACB_bw_ana));save('Main1_saterated_STR');%% 画图 - 饱和的信令开销（包含时隙ALOHA）
figure 
hold on;% 颜色配置
figcol=cell(1,4);
figcol{1}='#336633';  % GF - 绿色
figcol{2}='#5C0DAC';  % SAST - 紫色
figcol{3}='#FF0000';  % 时隙ALOHA - 红色% 标记形状配置
figshape=cell(1,4);
figshape{1}='*';
figshape{2}='O';
figshape{3}='square';
figshape{4}='diamond';linewidth=1;
markersize=60;% GF协议
i=1;
f1=plot(ACB_bw_ana,STR1_ana,'-','color',figcol{i},'LineWidth',linewidth);
s1=scatter(ACB_bw_simu,STR1_simu,markersize,'MarkerEdgeColor',figcol{i},...'Marker',figshape{i},'LineWidth',linewidth);% SAST协议
i=2;
f2=plot(ACB_bw_ana,STR3_ana,'--','color',figcol{i},'LineWidth',linewidth);
s2=scatter(ACB_bw_simu,STR3_simu,markersize,'MarkerEdgeColor',figcol{i},...'Marker',figshape{i},'LineWidth',linewidth);% 时隙ALOHA协议
i=3;
f3=plot(ACB_bw_ana,STR4_ana,':','color',figcol{i},'LineWidth',linewidth);
s3=scatter(ACB_bw_simu,STR4_simu,markersize,'MarkerEdgeColor',figcol{i},...'Marker',figshape{i},'LineWidth',linewidth);hold off;
xlim([0,max(ACB_bw_ana)]);
xlabel('$q$','Interpreter','latex');
ylabel('STR','Interpreter','tex','rotation',0,'Horizontalalignment','right');
legend([f1,s1,f2,s2,f3,s3],{'GF Analysis','GF Simulation','SAST Analysis','SAST Simulation',...'Slotted ALOHA Analysis','Slotted ALOHA Simulation'});
set (gca,'position',[0.15,0.15,0.7,0.7],'LineWidth',0.5,'fontsize',14,'FontName','Times New Roman');
set(gcf,'unit','normalized','position', [.2,.2,0.4,0.45]);
box on

结果：slotted Aloha

http://www.dtcms.com/a/523729.html

相关文章：

  • 「赤兔」Chitu 框架深度解读（六）：剖析 Attention 机制后端实
  • 嵌入式开发中为啥常用do{}while(0)进行宏定义
  • 第六部分：VTK进阶（第172章 vtk-m加速器管线)
  • 矽塔 SA8207 36V输入耐压 高精度可调过流保护与集成智能故障管理 过压过流保护芯片
  • 关键词优化公司网站怎么做网站后台界面
  • 从「Bug 制造机」到「问题解决者」的进化之路
  • 华为新一代鸿蒙操作系统实现与苹果互联
  • 常用 apt 命令及语法（Ubuntu）
  • 华为 AI，建造中的全景图
  • 第二十九篇：动态规划（一）：基础与背包问题
  • 深度学习中的训练流程：从输入到权重更新的完整旅程
  • QT------QPainter::save() 和 QPainter::restore() 的使用方法和作用。
  • http trailer 与 http2
  • 有没有会计做兼职的网站wordpress获取文章
  • 中国人在国外做网站网站代理网站群建设 会议 主持
  • 在Ubuntu Linux安装brew 使用brew安装llama.cpp 运行文心Ernie大模型
  • 基于MATLAB/Simulink的风光储联合系统经M3C接入电网的低电压穿越仿真研究
  • CNCF Kepler与MCP：开启云原生绿色计算的人机协作新纪元
  • 昇腾NPU部署GPT-OSS-20B混合专家模型：从环境配置到性能优化的完整实践指南
  • java8中的‘+‘的使用注意事项
  • 德国莱茵金属公司使用Varjo XR-4创建虚拟现实培训解决方案
  • STM32的GPIOx_ODR，GPIOx_BSRR，GPIOx_BRR寄存器的区别与使用
  • 网站建设指南 菜鸟教程简历模板做的最好的是哪个网站
  • Prometheus + Alertmanager + 钉钉告警
  • 基于 Spring Boot + RabbitMQ 实现应用通信
  • docker一键部署prometheus和grafana
  • 《深入剖析TCP Socket API：从连接到断开的全链路解读》
  • 数据库连接池 HikariCP Spring官方内置连接池 配置简单 以性能与稳定性闻名天下
  • Flink Watermark（水位线）机制详解
  • wordpress wpadmin东莞seo网站建设公司