MTPA算法原理及仿真验证
MTPA算法原理及实现
MTPA 主要解决永磁同步电机在转矩输出与效率、功耗之间的优化平衡。本质是基于凸极电机的磁阻特性，实现 “转矩 - 电流比” 的全局最优，核心解决 “如何用最小的电流产生给定转矩” 的效率优化问题。
电流幅值越小，铜耗越低。MTPA 通过最小化电流，直接降低了电机的能耗。
相同转矩下电流更小，意味着电机可在更低的电流负荷下工作，从而减少发热、缩小体积，提升功率密度（转矩 / 体积比）。
利用磁阻转矩拓展了 “低电流 - 高转矩” 的运行区间，使电机在宽转速范围内保持高效，避免了仅依赖永磁转矩时的电流浪费。
表面式 PMSM（SPMSM）：永磁体贴在转子表面，(L_d = L_q)（隐极特性），此时磁阻转矩为零，转矩仅由永磁转矩产生。这种情况下，产生给定转矩T_e时，(i_q)是唯一变量
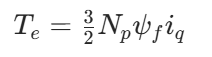
电流幅值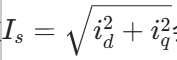
，因此表面式 PMSM 中(i_d = 0)时电流最小。
内置式 PMSM（IPMSM）：永磁体嵌入转子内部，（通常(L_d < L_q)，凸极特性），此时转矩由两部分组成：其中第二项为磁阻转矩，由(L_d)与(L_q)的差异产生
由于(L_d - L_q < 0)，当(i_d为负值（去磁电流）、(i_q)为正值时，磁阻转矩为正值（可辅助产生总转矩）。
对于内置式 PMSM，给定转矩\(T_e\)下，id=0控制时转矩全部由永磁转矩承担
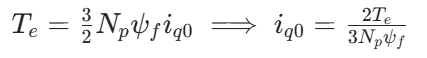
此时电流幅值为Is=Iq0
若引入负的Id，id=-a，则磁阻转矩为正值（辅助发力）
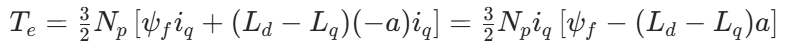
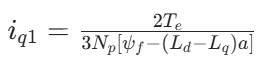
由于Iq1<Iq0
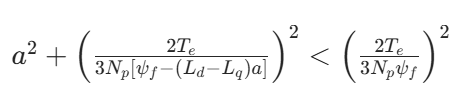
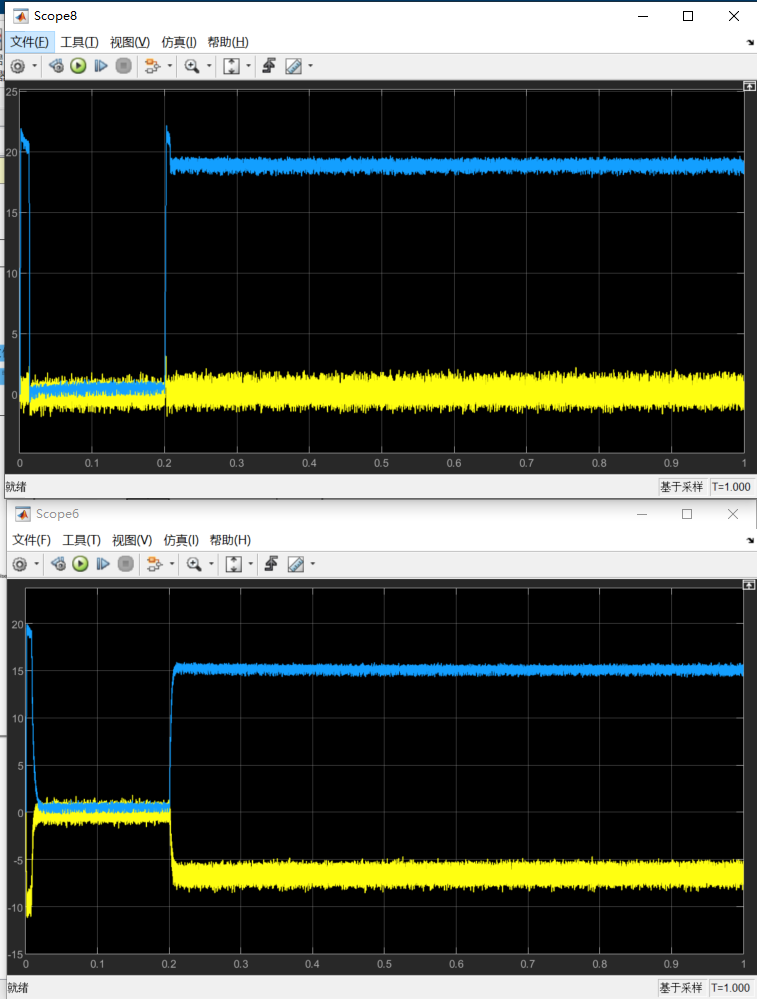
因此，电流幅值对比：MTPA下的Is小于Id=0控制的电流幅值Is
接下来是MTPA具体实现的算法
磁链与转矩方程
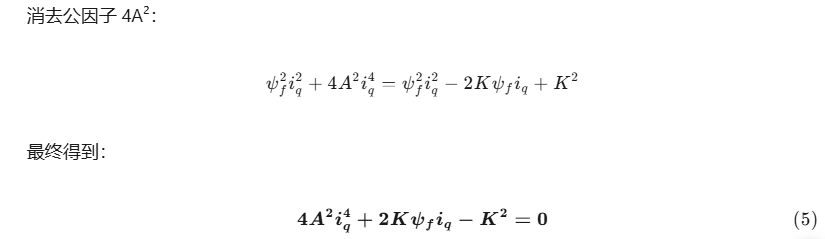
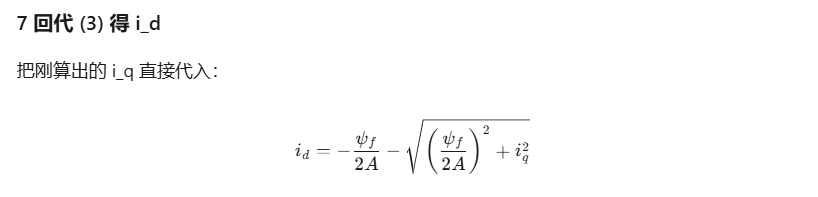
方法总结：
- 用拉格朗日乘子法导出 MTPA 轨迹 (L_d−L_q)(i_q²−i_d²)=ψ_f i_d；
- 把 i_d 用 i_q 表示后代入转矩方程，平方消根号得到 i_q 的二次方程；
- 解二次方程 → 得 i_q，再回代轨迹公式 → 得 i_d，即完成“同样转矩下电流最小”的 MTPA 计算。
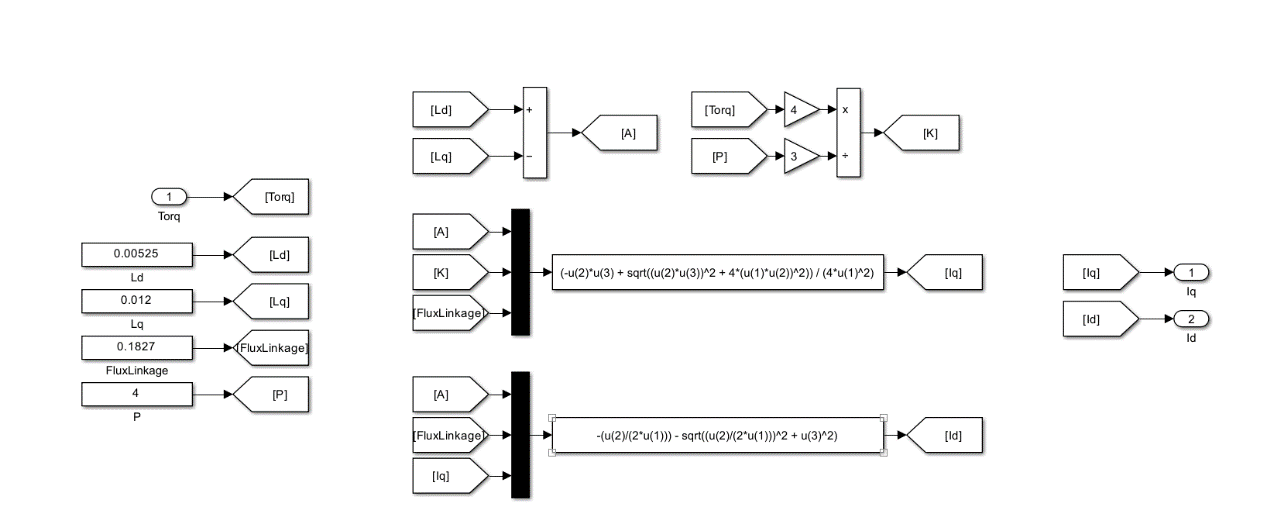
MTPA算法模型搭建：
接入FOC系统
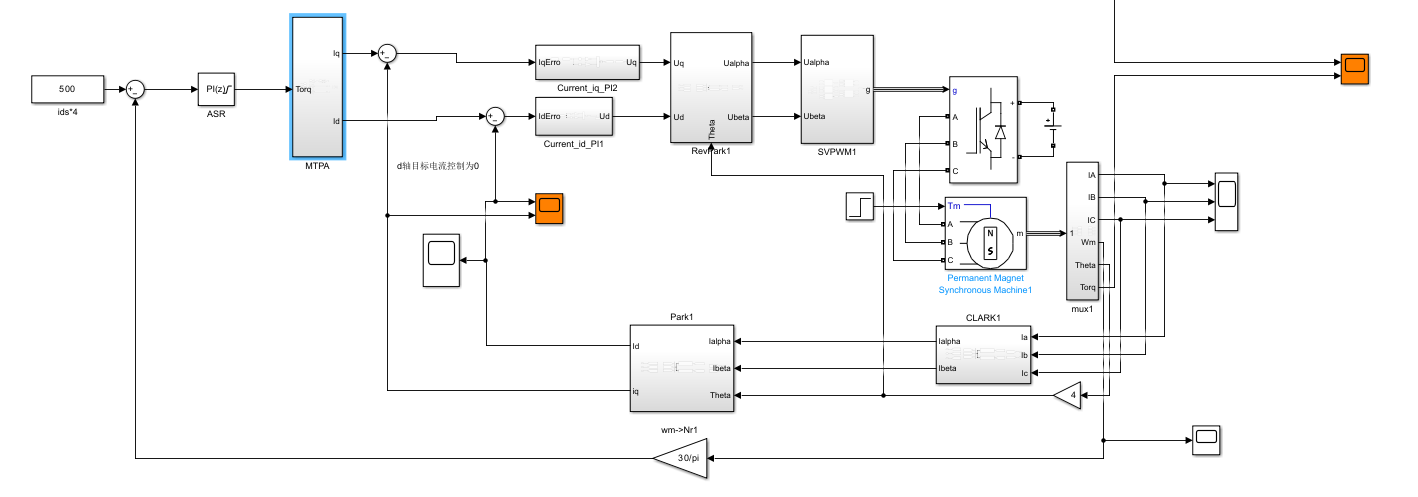
与传统FOC，id=0策略对比
仿真参数
磁链 | 0.1827 |
Ld | 0.00525 |
Lq | 0.012 |
Pn | 4 |
逆变器电压 | 310 |
对比实验：
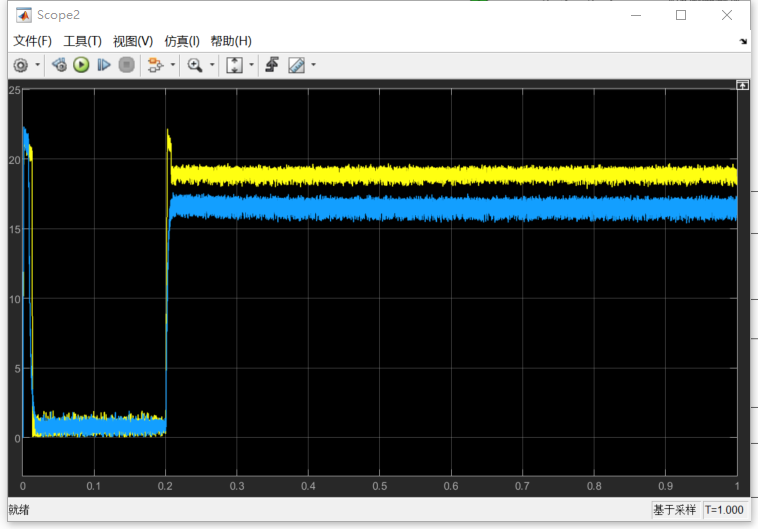
设置目标转速500转、对电机施加阶跃扭矩控制，空载启动，0.2s时刻施加12牛米扭矩。
仿真结果：
电机扭矩
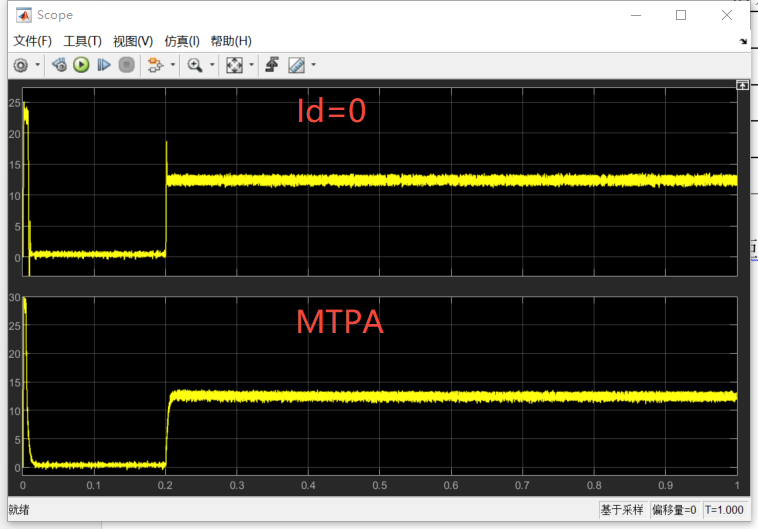
D/Q轴电流曲线
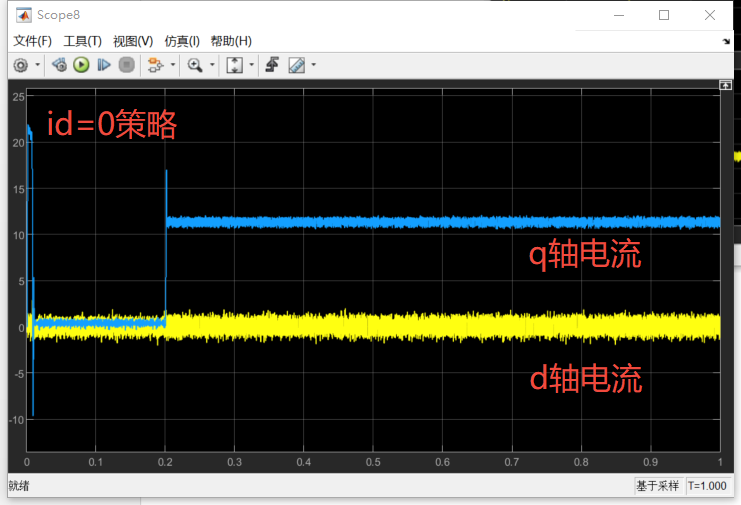
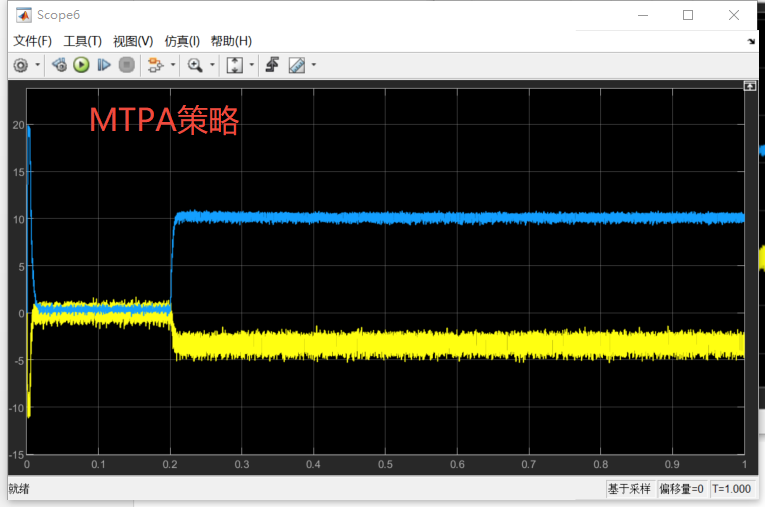
电流幅值比较
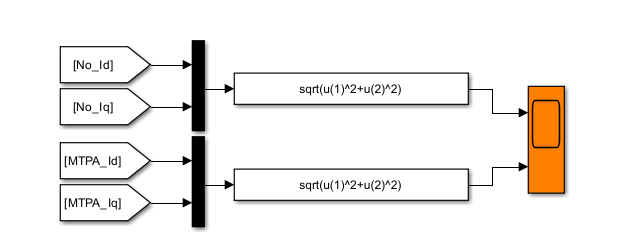
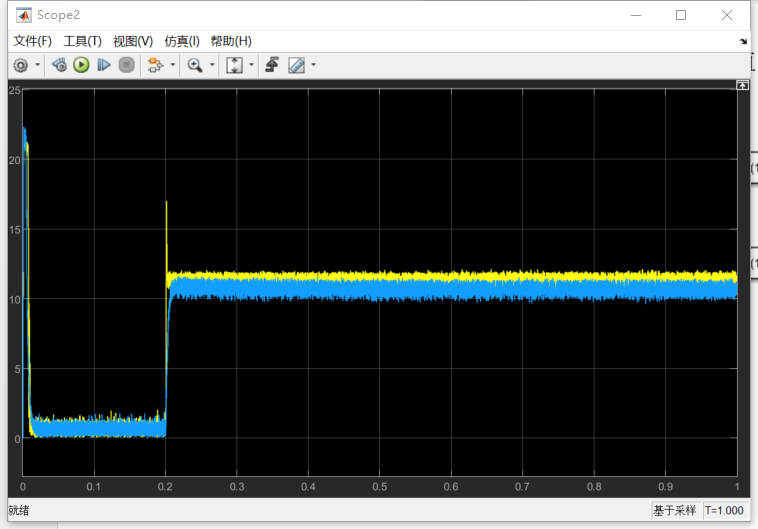
现在，将扭矩阶跃请求调大到20牛米，转速调到800转，此时观察Id=0控制策略和MTPA控制策略的电流幅值情况，就比较清晰明了了。
