【数字逻辑】数字逻辑实验实战:74HC151实现逻辑函数+74HC138搭全加器(附接线步骤+避坑指南)
数字逻辑实验实战:74HC151实现逻辑函数+74HC138搭全加器(附接线步骤+避坑指南)
刚做数字逻辑实验时,我对着74HC151和74HC138这两个芯片犯了难——明明 datasheet 写着“8选1数据选择器”“3-8译码器”,却不知道怎么接线实现逻辑函数,更分不清“选数据”和“译地址”的区别。后来才发现,其实74HC151就是个“带地址的8选1开关”,74HC138是“3位输入转8位输出的翻译器”,跟着步骤拆解,实操其实很简单。今天就把这份实验的解题思路拆成新手友好版,从器件功能到接线实操,再到结果验证,帮你轻松搞定实验。
一、实验先搞懂:核心器件是啥?实验目标是啥?
先明确实验的核心,避免上手就接线导致混乱:
1. 实验目标
- 用 74HC151(8选1数据选择器) 实现逻辑函数
F(A,B,C,D)=Σ(0,2,6,7)(即最小项m0、m2、m6、m7为1,其余为0); - 用 74HC138(3-8线译码器)+ 与非门 实现全加器(输入:被加数Ai、加数Bi、低位进位Ci-1;输出:和Si、高位进位Ci)。
2. 核心器件通俗解释
| 器件 | 通俗功能 | 关键引脚(新手必记) |
|---|---|---|
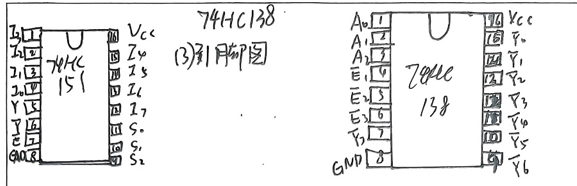
| 74HC151 | 8选1开关:3位地址选1路数据输出 | G(使能端,低电平有效,接GND)、A2-A0(地址端)、D0-D7(数据端)、Y(输出端) |
| 74HC138 | 3-8翻译器:3位输入→对应输出低电平 | G1(使能端1,高电平有效)、G2A/G2B(使能端2,低电平有效,接GND)、A2-A0(地址端)、Y0-Y7(输出端,低电平有效) |
| 与非门 | 全1出0,有0出1(实现“与”的反运算) | 2输入/3输入均可,根据需要选 |
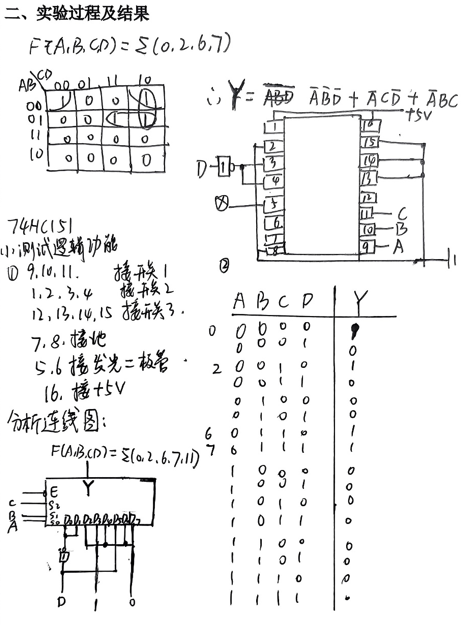
二、第一部分:74HC151实现逻辑函数 F(A,B,C,D)=Σ(0,2,6,7)
这部分的核心是“把4变量逻辑函数,通过74HC138的3位地址端+1位数据端实现”,步骤拆解如下:
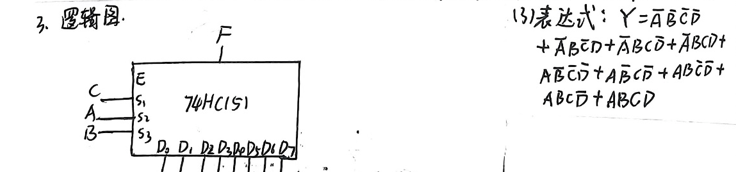
1. 关键思路:4变量→3地址+1数据
74HC151只有3个地址端(A2-A0),但逻辑函数F是4变量(A,B,C,D),所以要“分组”:
选 A,B,C作为地址端(A2=A,A1=B,A0=C),剩下的D作为“数据端的输入”,通过推导确定每个地址对应的D0-D7该接D、0还是1。
2. 推导数据端D0-D7(新手也能看懂的方法)
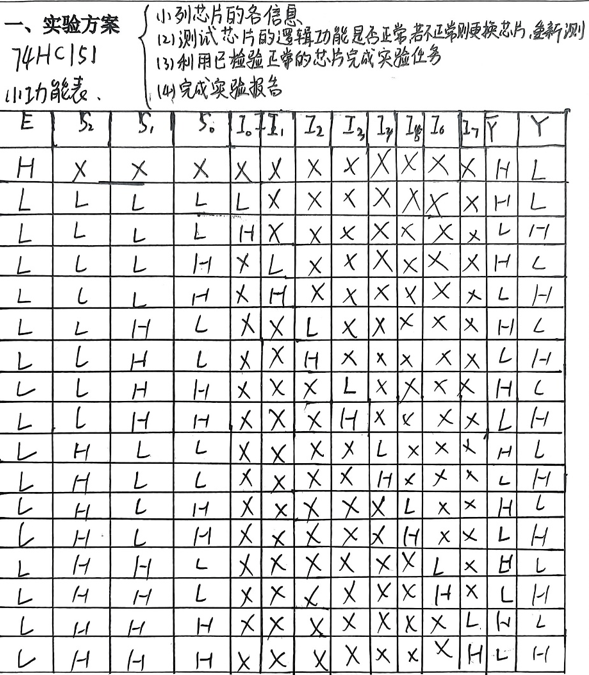
先列逻辑函数F的真值表(只看A,B,C分组,看每组中D取0/1时F的值):
| 地址(A,B,C) | 对应最小项分组 | F的值(根据F=Σ(0,2,6,7)) | Dx该接啥?(Dx是74HC151的数据端) |
|---|---|---|---|
| 000(A2-A0=000) | m0,m8(D=0→m0,D=1→m8) | F(m0)=1,F(m8)=0 → F=¬D | D0=¬D(或接D非端,若没有非门,也可理解为D=0时F=1,D=1时F=0) |
| 001(A2-A0=001) | m1,m9 | F(m1)=0,F(m9)=0 → F=0 | D1=0(接GND) |
| 010(A2-A0=010) | m2,m10 | F(m2)=1,F(m10)=0 → F=¬D | D2=¬D |
| 011(A2-A0=011) | m3,m11 | F(m3)=0,F(m11)=0 → F=0 | D3=0 |
| 100(A2-A0=100) | m4,m12 | F(m4)=0,F(m12)=0 → F=0 | D4=0 |
| 101(A2-A0=101) | m5,m13 | F(m5)=0,F(m13)=0 → F=0 | D5=0 |
| 110(A2-A0=110) | m6,m14 | F(m6)=1,F(m14)=1 → F=1 | D6=1(接VCC) |
| 111(A2-A0=111) | m7,m15 | F(m7)=1,F(m15)=1 → F=1 | D7=1 |
简单说:D0和D2接D的非(或直接根据D的输入对应接线),D6和D7接高电平(VCC),其余D1-D5接低电平(GND)。
3. 实验接线步骤(以仿真软件或面包板为例)
- 电源接线:74HC151的VCC接5V,GND接电源地;
- 使能端:74HC151的G端(引脚15)接GND(必须低电平,芯片才工作);
- 地址端:A2(引脚1)接变量A,A1(引脚2)接变量B,A0(引脚3)接变量C;
- 数据端:D0(引脚4)接¬D,D1(引脚5)接GND,D2(引脚6)接¬D,D3(引脚7)接GND,D4(引脚9)接GND,D5(引脚10)接GND,D6(引脚11)接VCC,D7(引脚12)接VCC;
- 输出端:74HC151的Y端(引脚13)接LED(串个电阻),看LED亮灭判断输出。
4. 结果验证
输入不同的A,B,C,D组合,比如:
- A=0,B=0,C=0,D=0 → F=1(LED亮);
- A=0,B=0,C=0,D=1 → F=0(LED灭);
- A=1,B=1,C=0,D=0 → F=1(LED亮);
只要输出和逻辑函数F的真值表一致,就说明成功。
三、第二部分:74HC138+与非门实现全加器
全加器的核心是“先写出和Si、进位Ci的最小项表达式,再用74HC138的输出(最小项非)+与非门实现”。
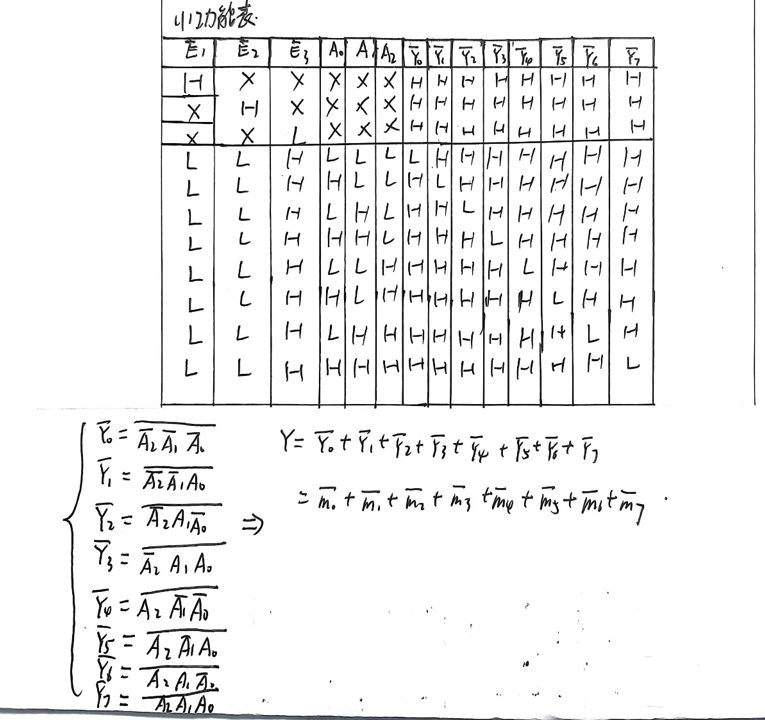
1. 全加器的逻辑表达式(先搞懂原理)
全加器有3个输入(Ai, Bi, Ci-1),2个输出:
- 和Si = Ai⊕Bi⊕Ci-1 → 展开为最小项:
Si=Σ(1,2,4,7)(即当输入为001、010、100、111时,Si=1); - 进位Ci = AiBi + AiCi-1 + BiCi-1 → 展开为最小项:
Ci=Σ(3,5,6,7)(即输入为011、101、110、111时,Ci=1)。
2. 关键思路:74HC138输出→与非门实现“与”
74HC138的输出Y0-Y7是“最小项非”(比如输入000时,Y0=0,对应¬m0;输入001时,Y1=0,对应¬m1)。
而“与非门”的逻辑是:¬(X∧Y∧Z) = ¬X∨¬Y∨¬Z,反过来:X∧Y∧Z = ¬(¬X∧¬Y∧¬Z)。
所以:
- Si=Σ(1,2,4,7) = m1∨m2∨m4∨m7 = ¬(¬m1∧¬m2∧¬m4∧¬m7) → 用4输入与非门,输入接Y1、Y2、Y4、Y7(因为Y1=¬m1,Y2=¬m2…);
- Ci=Σ(3,5,6,7) = m3∨m5∨m6∨m7 = ¬(¬m3∧¬m5∧¬m6∧¬m7) → 用4输入与非门,输入接Y3、Y5、Y6、Y7。
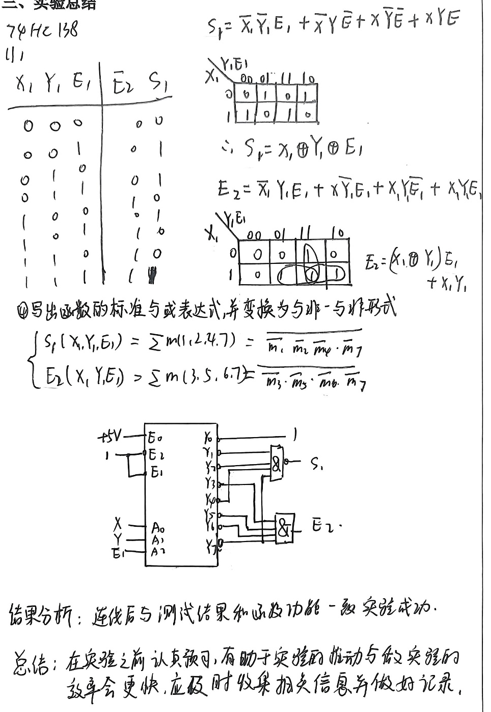
3. 实验接线步骤
- 74HC138电源:VCC接5V,GND接GND;
- 74HC138使能端:G1(引脚6)接VCC,G2A(引脚4)接GND,G2B(引脚5)接GND(必须满足这个组合,芯片才译码);
- 地址端:A2(引脚3)接Ai,A1(引脚2)接Bi,A0(引脚1)接Ci-1;
- 与非门接线:
- Si:4输入与非门的4个输入分别接74HC138的Y1(引脚15)、Y2(引脚14)、Y4(引脚12)、Y7(引脚9),与非门输出接LED;
- Ci:另一个4输入与非门的4个输入分别接74HC138的Y3(引脚13)、Y5(引脚11)、Y6(引脚10)、Y7(引脚9),与非门输出接另一个LED;
4. 结果验证
输入8组Ai, Bi, Ci-1,比如:
- Ai=0, Bi=0, Ci-1=0 → Si=0(LED灭),Ci=0(LED灭);
- Ai=0, Bi=0, Ci-1=1 → Si=1(LED亮),Ci=0(LED灭);
- Ai=1, Bi=1, Ci-1=1 → Si=1(LED亮),Ci=1(LED亮);
输出和全加器真值表一致,就说明成功。

四、新手必看:实验避坑指南
- 74HC151使能端忘接GND:芯片一直不工作,输出始终为高,LED一直灭;
- 74HC138使能端接错:比如G1接GND,芯片不译码,所有输出都为高,与非门输出始终为低;
- 逻辑函数推导时变量对应错:比如把A,B,C接成A0,A1,A2(地址端顺序反了),输出完全混乱,一定要按“A2=A,A1=B,A0=C”接线;
- 与非门输入接错引脚:比如Si接了Y0,Y1,Y2,Y3,而不是Y1,Y2,Y4,Y7,导致输出和预期相反。
五、实验总结
其实组合逻辑电路实验的核心就是“先把逻辑表达式拆成器件能实现的形式”——74HC151靠“地址选数据”实现多变量函数,74HC138靠“译码出最小项非”+与非门实现逻辑运算。只要搞懂器件的“通俗功能”,再一步步推导接线,实验一点都不难。
