【LeetCode】长度最小的子数组
文章目录
- 前言
- 题目描述
- 算法原理
- 代码实现
前言
道友们,今天咱们来做长度最小的子数组!
题目链接:209.长度最小的子数组
题目描述
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 子数组
[numsl, numsl+1, ..., numsr-1,numsr],并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入: target = 7, nums =
[2,3,1,2,4,3]
输出: 2
解释: 子数组[4,3]是该条件下的长度最小的子数组。
示例 2:
输入: target = 4, nums =
[1,4,4]
输出: 1
示例 3:
输入: target = 11, nums =
[1,1,1,1,1,1,1,1]
输出: 0
提示:
1 <= target <= 10^91 <= nums.length <= 10^51 <= nums[i] <= 10^4
算法原理
题目要求其实很简单,让我们在给定的一个含有 n 个正整数的数组中找一个子数组,要求子数组的总和要大于等于给定的目标值 target ,且长度要最小。
解法一:
一般做这种题最简单也是最好想的办法必然是暴力解法,先暴力枚举所有的子数组,再判断找出符合条件的最短的子数组即可。这里还有个可以优化的地方
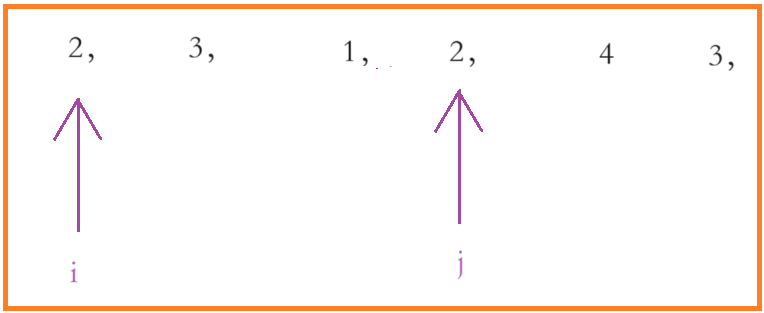
在这张图片里面,i 和 j 所组成的子数组的和是 8,已经大于目标值 target 了,那 j 再往后和 i 组成的数组的和绝对要比 8 大,因为数组中都是正整数、且子数组的长度也要比图片中的长,这是显而易见的。那这个时候我们就可以大胆的把 j 后面所有的情况都舍去,这样可以避免一些不必要的枚举。
总体上,暴力解法的代码逻辑看起来还是比较简单的,不管三七二十一,咱们先写出来再说
class Solution
{
public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size(), ret = INT_MAX;for (int i = 0; i < n; i++){int sum = nums[i];if (sum >= target) return 1;for (int j = i + 1; j < n; j++){ sum += nums[j];if (sum >= target){ret = min(ret, j - i + 1);break;}}}return ret;}
};
在写代码的时候要注意一下,因为我们找的是长度最小的子数组,所以一开始我们初始化的长度要大一点,不然不好判断,这里我们是直接给了整型的最大值 INT_MAX。写完之后咱们提交一下
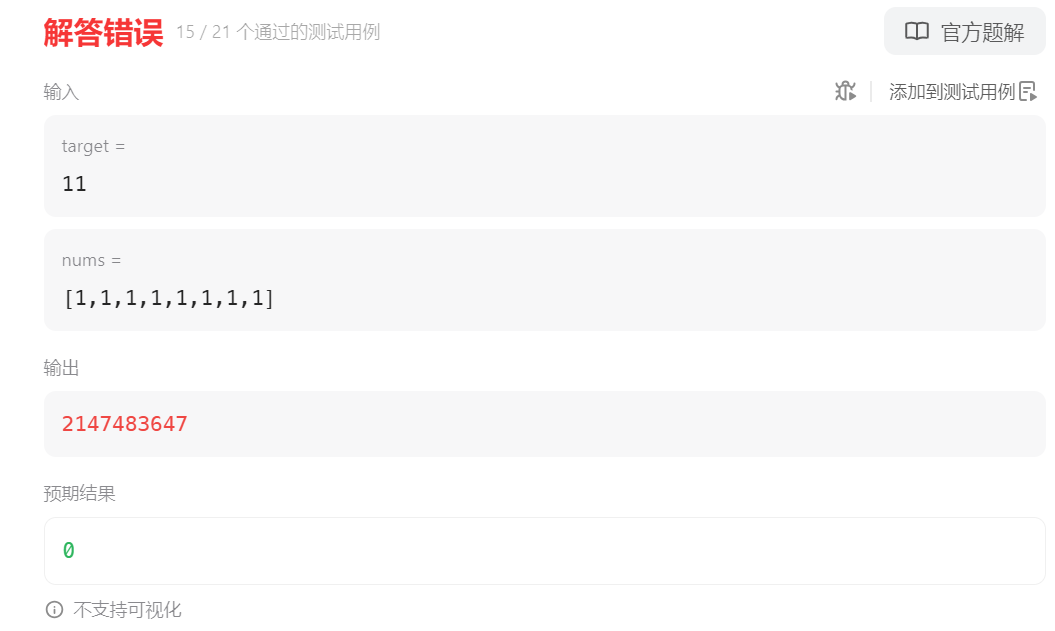
这怎么是解答错误?不应该是超出时间限制吗?咱先看一下出错的用例长啥样子,看完之后就发现问题了,在这个出错的用例中,我们发现没有符合要求的子数组,所以返回了 0,但按照我们的代码逻辑走下去,子数组的和一直小于目标值 target,所以判断条件进不去,最终 ret 返回的还是 INT_MAX,所以我们在最后返回值那里还要特殊判断一下
return ret == INT_MAX ? 0 : ret;
现在应该没什么问题了,我们再提交一下
不出我们所料,这种解法会超出时间限制,那有什么办法能优化一下?
解法二:
还是先来看我们的暴力枚举的方法:
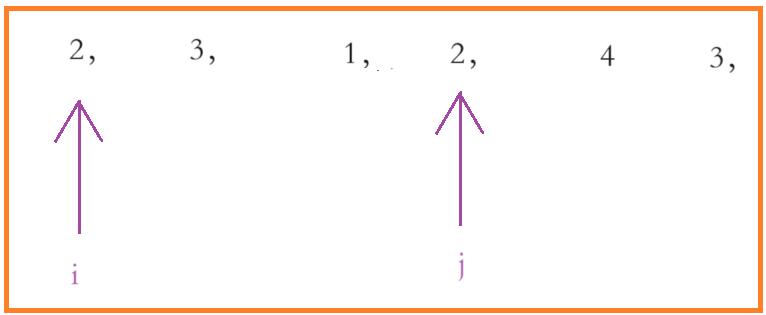
如上图,在暴力枚举那里,我们找到一个子数组的和大于等于目标值 target,我们是直接跳过 j 后面所有的情况,然后让 i++,进行下一次循环,j 又从 i + 1的位置开始枚举所有的子数组,一遍一遍对数组求和。

这里我们就看到,这种方法每次都会重复计算数组的和,那能不能避免这部分重复计算的过程呢?
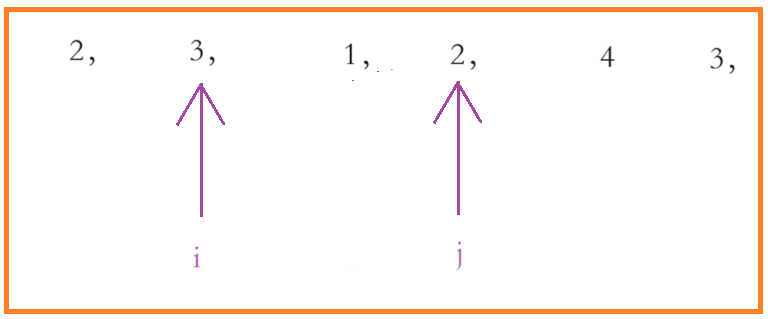
回到刚才,在进行下一次循环的时候,我们保持 j 的位置不变,这个时候如图所示,i 和 j 所在的区间求和,我们是可以直接算出来的:
在原先那个子数组求和的基础上,直接减去刚开始 i 指向的元素就行了,减完之后,我们再让 i 指向下一个元素,这样就不用再一遍一遍的加了
在这个过程中我们发现,维护子数组的两个指针都是不回退的,即两个指针都是同向双指针,就像一个窗口一样在数组上不停地滑动,所以这种方法也叫滑动窗口。
那这个时候我们可能会有一些疑问,如果下一次循环的时候,j 的位置不变,只让 i++,我们怎么确定会不会把真正要找的那个子数组给漏掉?
其实这种情况是不可能发的,我们简单分析一下,以上图为例:
- 如果在 i 和 j 之间出现了我们要找的那个子数组,这意味着子数组的和至少已经等于目标值 target 了。这个时候 j 是断然不会走到现在的位置上的,它只会在当前位置的前面。
- 如果我们要找的那个子数组在 i 和 j 所在区间的左边也是同样的道理
- 如果我们要找的那个子数组在 i 和 j 所在区间的右边,那么这个时候我们就需要循环判断一下,如果大于,我们就让左边出区间,再继续判断,最终一定会找到那个子数组。
分析完了之后,我们来看看这道题怎么用滑动窗口来做?
还是以上面的图为例,其实我们在进行下一次循环的时候,子数组求和之后有两种情况,要么和小于目标值 target,要么和大于等于目标值 target :
- 其实小于的话,很好办,我们就继续让它往下加就行了
- 那如果是大于等于的情况怎么办?
其实也好办,就像刚才分析的那样,循环判断,如果大于等于目标值 target,就让左边的元素出区间,再循环判断、如果小了,那就是第一种情况,直到遍历完整个数组
我们可以以示例 1为例,走一遍这个过程,最后会发现,到右指针出数组的时候,循环就结束了

到这里,这道题的算法原理就终于讲清楚了,说了这么多,下面咱们直接来写代码
代码实现
其实很多时候,做题的思路是好想的,但真正写起代码来,问题就出现了,会有各种各样的问题,像我在写这道题的时候也是被折磨了好久,但是万幸,最后还是写出来了,所以道友们在做题的时候还是不要气馁,毕竟像我这样的人都能写的出来,你们一定行滴!
class Solution
{
public:int minSubArrayLen(int target, vector<int>& nums) {int left = 0, right = 0;int n = nums.size(), sum = 0, len = INT_MAX;while(right < n){sum += nums[right];while (sum >= target){len = min(len, right - left + 1);sum -= nums[left++];}right++;}return len == INT_MAX ? 0 : len;}
};
和暴力解法那里一样,这里也要注意返回值的问题,写完之后我们提交看看
当看到两个大大的通过出来的那一瞬间,我感觉没有什么比这两个字更让我感到亲切了。简单分析一下时间复杂度,我们这里是两个指针遍历一遍数组,最坏的情况是右边的先走到头,然后左边的再走到头,一共走n + n == 2n次,所以时间复杂度还是O(n)。
完!
