图像处理～多尺度边缘检测算法

差量算子（Difference Operator）

差量算子是边缘检测的基础工具，通过计算像素间的灰度差来识别图像中的边缘（灰度变化剧烈的区域）
核心定义：差量算子是一个 “模板”（如 Roberts、Sobel 算子），通过对图像像素进行局部差分运算，输出像素的灰度变化强度。例如：

一阶差分算子 - Roberts 算子

最终边缘强度的计算公式

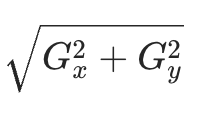
差分模板是实现差分计算的 “工具载体”，计算逻辑是模板的 “运算规则”，二者是 “形式” 与 “内涵” 的关系
模板通过特定的计算逻辑，完成对图像像素的差分运算，从而提取边缘、纹理等特征。

一阶差分算子 - Sobel 算子

Sobel 的标准发音是 /ˈsoʊbəl/（美式音标），中文可简单读作 “索贝尔”

Sobel 算子是图像处理中经典的一阶微分边缘检测算子
核心优势：提取边缘的同时通过 “加权平均” 抑制噪声，对水平和垂直方向的边缘检测效果突出，广泛用于图像边缘提取、特征识别等场景
它通过计算图像灰度值的 “一阶导数”（即灰度变化率）来检测边缘

它通过 3×3 邻域的加权差分，既保留一阶差分 “捕捉灰度变化率” 的核心能力，又通过加权平均抑制噪声
因此比 2×2 一阶差分算子（如 Roberts）应用更广泛

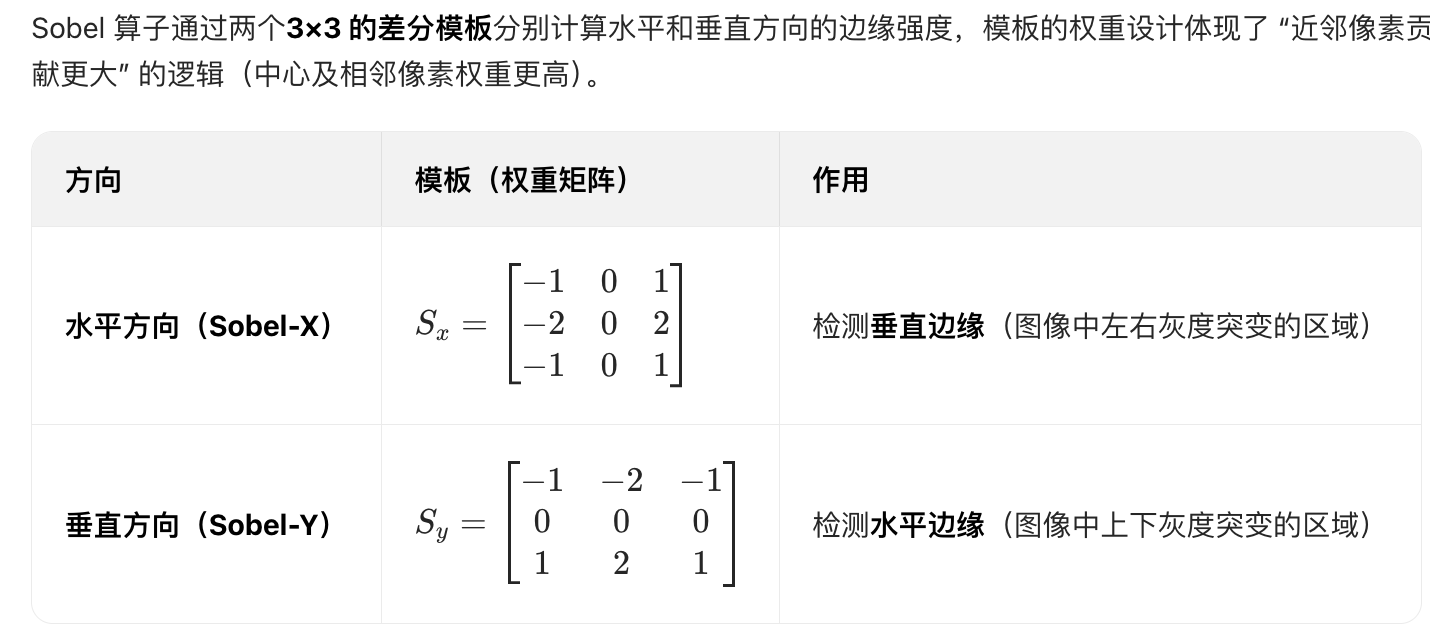
sobel算子的运算：

抗噪声能力强：3×3 邻域的 “加权平均”（中心像素权重为 2，相邻像素为 1）能平滑局部噪声，避免噪声被误判为边缘
边缘定位较准：一阶微分特性能有效捕捉灰度突变的位置，且加权设计让边缘响应更集中，不易出现边缘 “弥散”
方向针对性强：Sobel-X 和 Sobel-Y 模板分别对垂直、水平边缘敏感，可按需单独提取某一方向的边缘

示例：


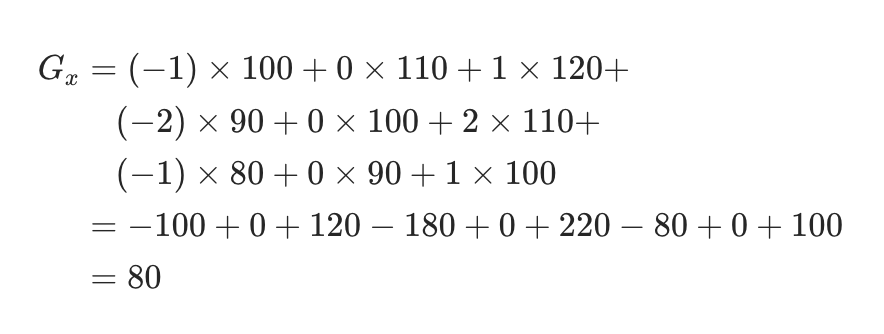
个人理解：相当于 120 - 100，2 * （110 - 90） 、100 - 80，中心及相邻像素权重更高（从左往右权重分别是1、2、1），抑制局部噪声

一阶差分算子和二阶差分算子对比

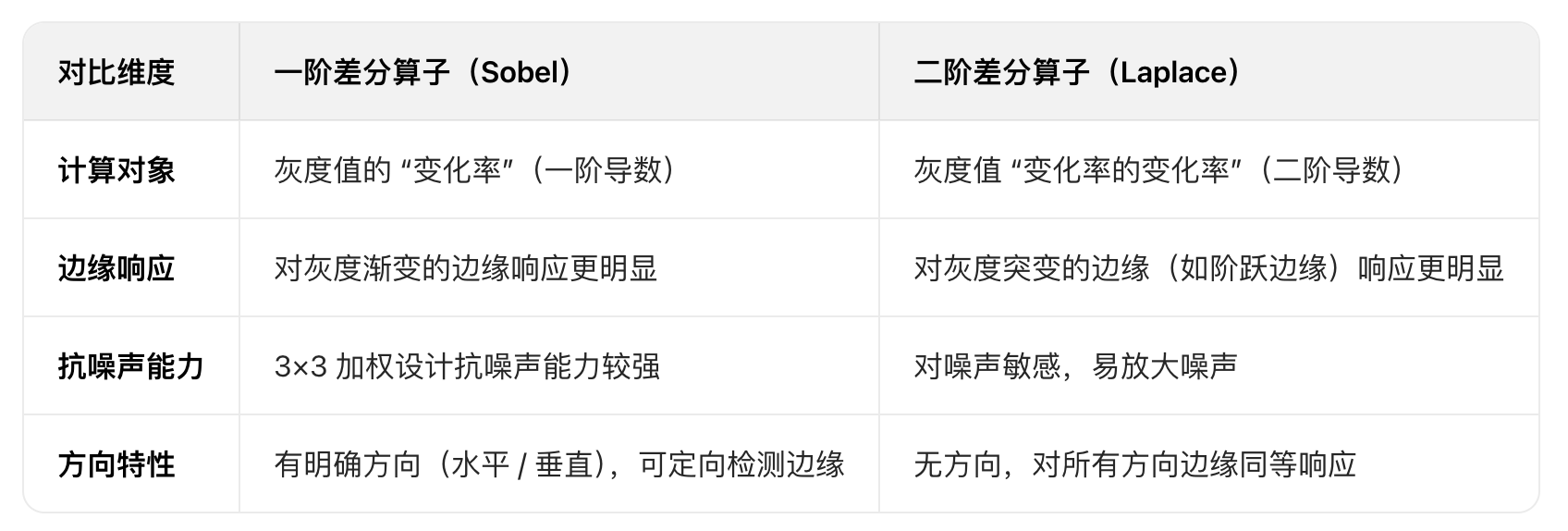
差量函数 - Difference Function

多尺度边缘检测算法

核心是在不同 “尺度”（如不同大小的滤波核、不同分辨率的图像）下提取边缘，以解决单一尺度下边缘检测的局限性
（如小尺度易受噪声干扰、大尺度易丢失细节）
通过构建尺度空间（如高斯金字塔、小波变换的多尺度分解），在多个尺度上分别检测边缘，再综合各尺度的边缘响应

例如：
高斯-拉普拉斯（LoG）多尺度检测：先对图像做不同尺度高斯模糊，再用拉普拉斯算子检测边缘，小尺度捕捉细边缘，大尺度捕捉粗边缘
小波变换多尺度检测：通过小波分解将图像分为高频（细节）和低频（概貌）子带，在不同子带（对应不同尺度）中提取边缘

优势：
能同时保留细边缘（如纹理、小物体轮廓）和粗边缘（如大物体轮廓、场景结构），避免单一尺度下 “要么噪点多、要么细节丢” 的问题
应用：高精度图像分析（如医学图像的多组织边缘提取）、场景理解（如自动驾驶中同时识别车道线细边缘和车辆粗轮廓）

多尺度边缘融合算法

在多尺度边缘检测的基础上，将不同尺度的边缘信息整合为统一的边缘图，解决多尺度边缘 “如何取舍、如何互补” 的问题

通过 “权重分配” 或 “特征投票” 的方式，融合各尺度的边缘响应。常见策略包括：

• 基于置信度的融合：给不同尺度的边缘响应赋予 “置信权重”（如小尺度边缘易受噪声影响，权重低；大尺度边缘更稳定，权重高），再加权求和得到最终边缘。
• 基于梯度的融合：计算各尺度边缘的梯度幅值和方向，选择 “梯度最显著、方向最一致” 的边缘作为最终边缘。
• 基于学习的融合：用深度学习模型（如 U-Net、EdgeCNN）直接学习 “多尺度边缘到融合边缘” 的映射关系，端到端输出最优边缘图

优势：输出的边缘图既包含细粒度细节，又具备全局一致性，解决了多尺度边缘 “碎片化、冗余化” 的问题
应用：图像增强（如老照片修复中的边缘补全）、目标识别（如同时识别小零件的细边缘和大设备的粗边缘，提升识别精度）

多尺度边缘检测和融合的关联与区别

对比维度 多尺度边缘检测算法 多尺度边缘融合算法
核心任务 从不同尺度 “提取” 边缘 将多尺度边缘 “整合” 为统一边缘图
技术逻辑 尺度空间构建 + 单尺度边缘检测 多尺度边缘评估 + 权重/投票融合
输出形式 多个尺度的边缘图（如小尺度边缘图、大尺度边缘图） 单一的融合边缘图
典型工具链 LoG 金字塔、小波分解 置信度加权、梯度投票、深度学习模型

以城市街景图像的边缘分析为例：

• 多尺度边缘检测：
  小尺度提取 “交通标志的细边缘、行人轮廓的细节”，大尺度提取 “建筑轮廓、道路结构的粗边缘”，得到多个尺度的边缘图
• 多尺度边缘融合：
  给小尺度边缘（易受噪声干扰）分配低权重，大尺度边缘（更稳定）分配高权重，再融合出 “既清晰又完整” 的街景边缘图，用于后续的道路分割、目标追踪等任务

多尺度边缘检测是 “分解问题”—— 在不同尺度下分别提取边缘
多尺度边缘融合是 “解决问题”—— 将分解的边缘信息整合为更优的结果

附录

边缘的成因

• Surface Normal Discontinuity（表面不连续）
  指物体表面的朝向突然改变。如图中药瓶的 “瓶盖顶部” 和 “瓶身侧面” 朝向不同，一个向上、一个向外，这种表面方向的突变会在图像中形成边缘。
• Depth Discontinuity（深度不连续）
  指物体在空间深度上的突变。例如药瓶的边缘是 “前景药瓶” 和 “背景空间” 的分界，深度从药瓶的 “近” 突然变为背景的 “远”，这种深度跳变会在图像中产生边缘。
• Surface Color Discontinuity（表面颜色不连续）
  指物体表面颜色或灰度的突然变化。图中药瓶上的 “AOT” 文字与瓶身颜色不同，这种颜色差异会在图像中形成明显的边缘。
• Illumination Discontinuity（光照不连续）
  指光照条件的突变（如阴影、高光的边界）。例如药瓶表面的阴影边缘，或光线照射导致的明暗突变，这些光照变化会在图像中产生边缘。

discontinuity ˌdɪsˌkɒntɪˈnjuːəti 不连续；中断；间断性；断绝
illumination ɪˌluːmɪˈneɪʃn 光亮，照明；启迪，阐明；<英>彩灯，灯饰；（旧时书上通常用手工绘制的）彩饰，彩图

灰度突变的边缘（Step Edge）

灰度突变的边缘又称 “阶跃边缘”，是最典型的边缘类型
核心特征：边缘两侧的灰度值在极短距离内发生剧烈跳变，从一个稳定灰度值 “瞬间” 过渡到另一个稳定灰度值
视觉表现：边缘轮廓清晰、锐利，过渡区域极窄（通常只有 1-2 个像素宽度）
示例效果：黑白文字的边缘（黑色字体到白色背景的跳变）、纯色物体与背景的边界（如红色苹果放在白色桌面上的边缘）

数学特性：
从灰度变化率（一阶导数）来看，突变边缘的一阶导数在边缘位置会出现尖锐的峰值（对应 “瞬间跳变”）
从二阶导数来看，会出现 “正峰 + 负峰” 的脉冲对（对应 “跳变的起始和结束”）

检测适配：
适合用二阶差分算子（如 Laplace 算子）检测，因为二阶导数对 “突变” 的响应更敏感
一阶算子（如 Sobel）也能检测，但对 “突变” 的定位精度略逊于二阶算子

示例：

灰度渐变的边缘（Ramp Edge）

灰度渐变的边缘又称 “斜坡边缘”，核心特征是边缘两侧的灰度值不是瞬间跳变，而是通过一个 “过渡区域” 缓慢变化，从一侧灰度值逐渐过渡到另一侧灰度值。
视觉表现：边缘轮廓柔和、模糊，过渡区域有明显的宽度（通常超过 2 个像素）。
示例：阳光下物体的阴影边缘（从亮到暗有渐变过渡带）、渐变色背景的边界（如从浅蓝色到深蓝色的渐变区域）、低分辨率图像中的边缘（像素模糊导致过渡变宽）。
数学特性：从灰度变化率来看，渐变边缘的一阶导数在 “过渡区域” 会形成一个平缓的波峰（对应 “缓慢变化”），波峰宽度与过渡区域宽度一致；二阶导数则会出现 “负峰 + 正峰” 的平缓波形（对应 “变化率的上升和下降”）。
检测适配：适合用一阶差分算子（如 Sobel、Prewitt 算子）检测，因为一阶算子对 “变化率” 的捕捉更稳定，能有效提取渐变区域的整体边缘；二阶算子对渐变边缘的响应较弱，易因过渡平缓导致边缘 “断裂”。

高斯金字塔

一种多尺度图像表示方法，通过对图像进行高斯平滑（模糊）和下采样，生成一系列分辨率逐渐降低的图像层级，形成 “金字塔” 结构
（底层为高分辨率原图，顶层为低分辨率概貌）

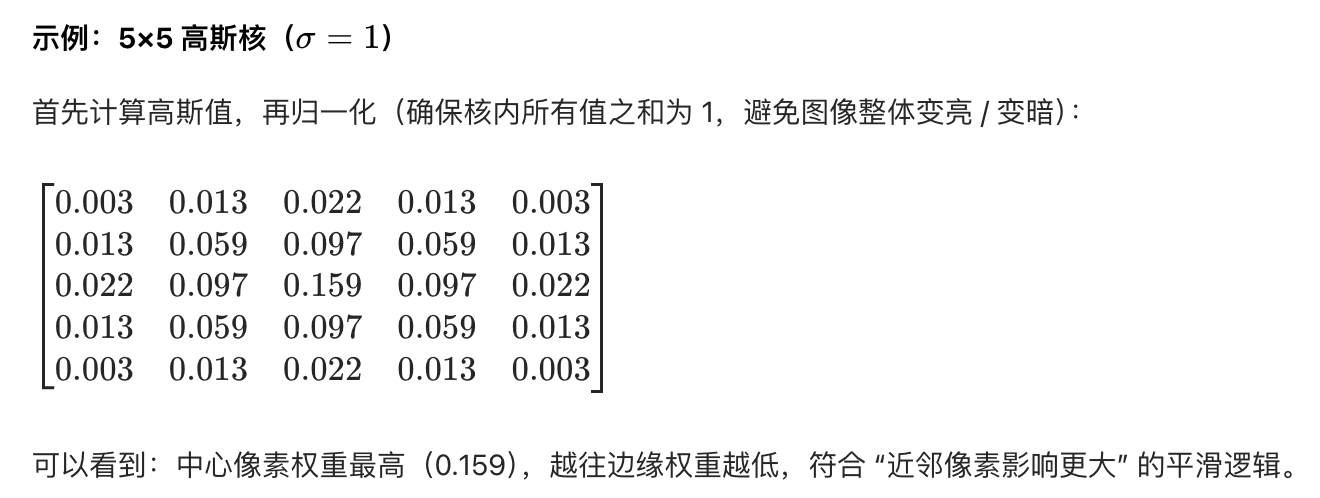
步骤 1：高斯平滑
对图像应用高斯滤波器（如 5×5 高斯核），抑制高频噪声和细节，使图像更平滑

步骤 2：下采样
对平滑后的图像每隔一个像素采样一次（删除偶数行和列），图像尺寸减半
重复上述两步，即可生成多层高斯金字塔

核心特性
多尺度覆盖：不同层级对应不同尺度的图像特征（高层捕捉大结构，低层保留细节）
抗混叠性：高斯平滑先于下采样，避免了直接降采样导致的 “锯齿” 或 “伪影”

典型应用
多尺度特征提取：如 SIFT 算法通过高斯金字塔检测不同大小的物体特征
图像压缩与融合：仅存储低分辨率层和差分信息，实现高效压缩；或在不同层级融合图像，实现无缝拼接

小波变换的多尺度分解

小波变换的多尺度分解是将信号（或图像）分解为不同尺度的频带分量，通过 “伸缩 - 平移” 的小波基函数，同时在时域和频域实现局部化分析，克服傅里叶变换 “全局化” 的缺陷

二维离散小波变换（DWT）原理
对图像进行多尺度分解时，每一层会将图像分为 4 个子带：
LL 子带：低频分量（图像的概貌，分辨率降低）
LH 子带：水平高频分量（垂直边缘信息）
HL 子带：垂直高频分量（水平边缘信息）
HH 子带：对角高频分量（斜向边缘和细节）
对 LL 子带重复上述分解，可得到多层小波金字塔

效果

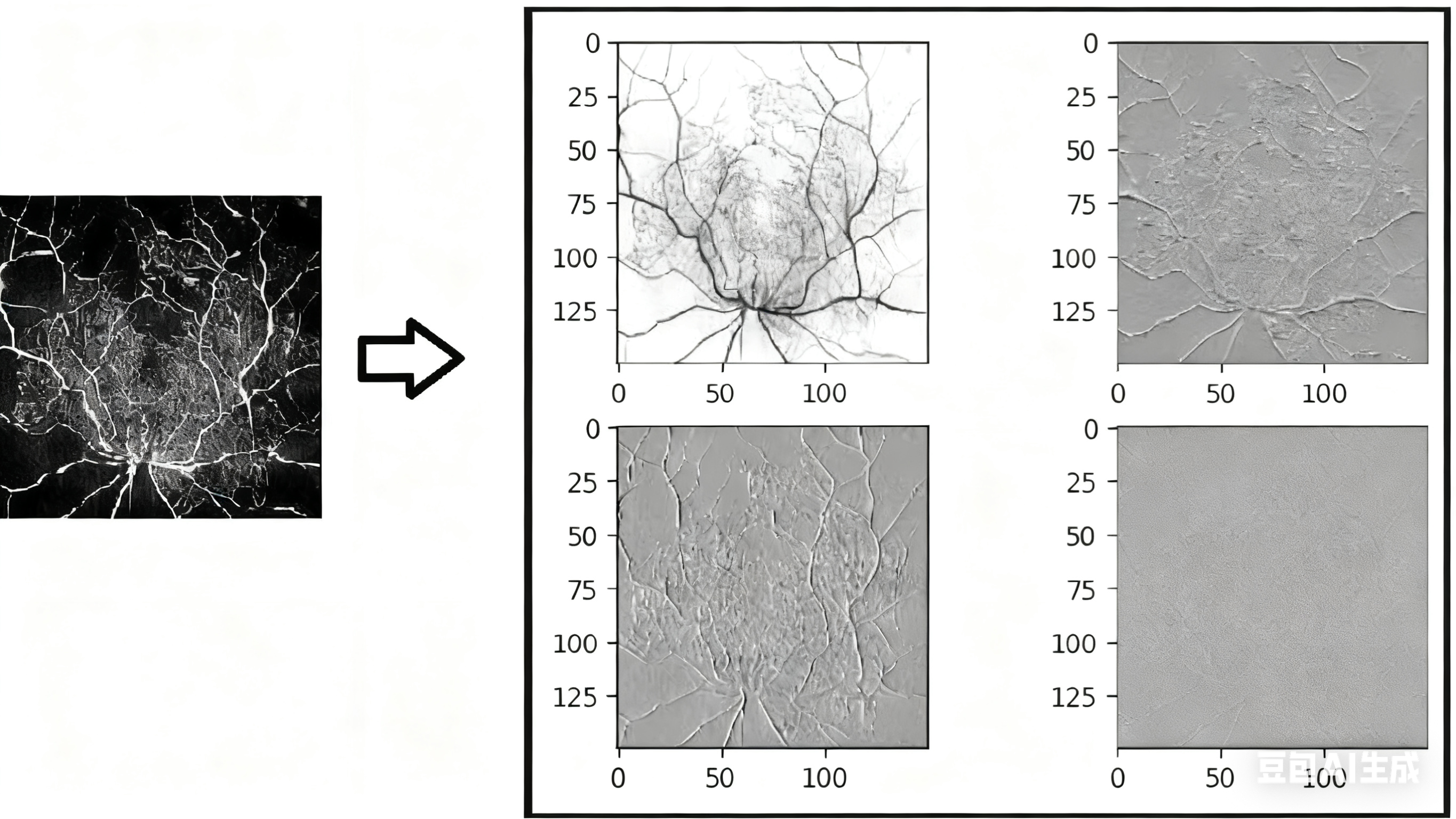
核心特性
时频局部化：小尺度（高频）对应时域的精细细节，大尺度（低频）对应时域的全局结构
稀疏表示：自然图像的小波系数多集中在低频和少量高频，适合压缩和降噪

典型应用
图像压缩：如 JPEG2000 标准基于小波变换，通过量化和编码高频子带实现高效压缩
多尺度边缘检测：不同子带对应不同方向和尺度的边缘，可用于纹理分析、目标识别

高斯金字塔和小波变换的多尺度分解的区别

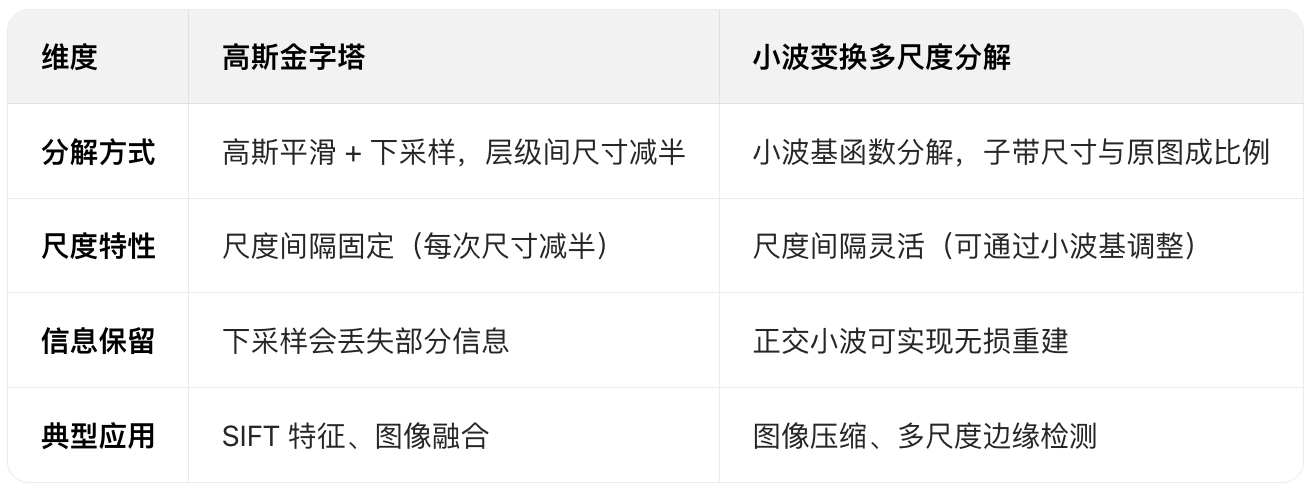
张量积 - Tensor Product

一维尺度函数（Scaling Function）

一维小波函数（Wavelet Function）

φ和ψ

φ：是希腊字母表的第二十一位字母，标准发音为 /ˈfaɪə/（美式音标），中文通常读作 “斐” 或 “菲”
ψ：是希腊字母表的第二十三位字母，标准发音为 /saɪ/（美式音标），中文通常读作 “赛”

二维小波基元的具体计算

Diagonal daɪˈæɡən(ə)l 对角线的，对角的；斜的，斜线的；沿斜线运动的；斜线，斜纹；（几何学中的）对角线；矩阵对角线元素

张量积如何实现 “方向敏感性”
通过张量积构造的二维基元，本质是分离 x 和 y 方向的特征响应：
若某一方向用 “平滑的尺度函数”，则该方向的变化被抑制；
若某一方向用 “敏感的小波函数”，则该方向的变化被放大。
这种 “分离性” 使得 3 个小波函数能分别聚焦于垂直、水平、斜向的边缘
这正是小波变换能 “多方向提取特征” 的数学根源，也是它比高斯金字塔（无方向区分）更适合边缘检测的关键。