当前位置：首页 > news >正文

递归-50.Pow(x,n)-力扣(LeetCode)

news 2025/10/20 7:29:42

个人主页：1白天的黑夜1-CSDN博客

专栏：力扣刷题录_1白天的黑夜1的博客-CSDN博客、企鹅程序员：Linux 系统与网络编程_1白天的黑夜1的博客-CSDN博客

一、题目解析

二、算法原理

解法1：暴力循环->时间复杂度：超时

解法2：快速幂->时间复杂度：O(log n)

如何编写递归代码？

1、重复子问题->函数头

2、只关心某一个子问题做什么->函数体

3、递归函数的出口

细节问题

1、观察题目条件可知n有正也有负

2、n次方数的负数转正可能会溢出

根据编写思路和细节问题，去编写尝试代码，提升自己的代码能力，题目链接如下

三、代码示例

四、递归展开图

看到最后，如果对您有所帮助，还请点赞、收藏和关注一键三连，在未来还会继续带来优秀的内容，感谢观看，我们下期再见！

一、题目解析

二、算法原理

解法1：暴力循环->时间复杂度：超时

例如2的3次方，可以写作2*2*2，可以一直乘下去，但根据题目提供n的取值范围，很明显是会超时的。

解法2：快速幂->时间复杂度：O(log n)

这里快速幂有两种，一种用循环涉及到二进制，另一种则是博客的主题-递归。

快速幂的思想是假如我要求3的16次方，我会先求出3的8次方，3^8*3^8=3^16，但我得知道3的8次方是多少，所以我又先求出3的4次方，3^4*3^4=3^8，同理去求3的平方，3^2*3^2=3^4，去求3的1次方，最后去求3的0次方，便完成了3的16次方计算。

如果求的奇数次方呢？比如3的15次方，那就先求3的7次方，3^7*3^7*3=3^15，同理向下细分求解。

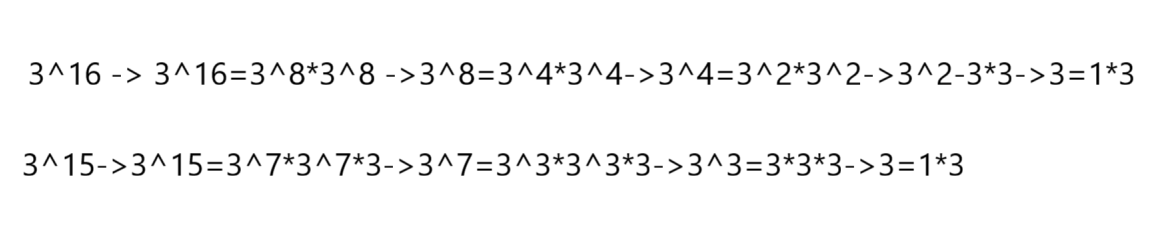
如何编写递归代码？

1、重复子问题->函数头

我们的重复子问题就是计算某一个数的几次方，并且需要返回值。所以需要两个参数，一个接收底数，一个接收次方数，返回类型为double，因为底数可以是小数。可以直接用题目给的函数头。

2、只关心某一个子问题做什么->函数体

由于次方有奇有偶，所以需要判断一下，通过一个变量接收递归函数的返回值，然后根据奇偶将其结果返回。

3、递归函数的出口

当传入的次方数为0时，直接返回1即可

细节问题

1、观察题目条件可知n有正也有负

例如3^-2=1/3^2，为了保证结果为double类型的，需要将其写为1.0/3^2，在函数体中多加入一个判断条件

2、n次方数的负数转正可能会溢出

例如-2^31变为正数时，int存不下，int最大为2^31-1，所以需要一个long或long long类型的变量存储，然后对long或long long类型的变量变为正数。

根据编写思路和细节问题，去编写尝试代码，提升自己的代码能力，题目链接如下

50. Pow(x, n) - 力扣（LeetCode）

三、代码示例

class Solution {
public:double myPow(double x, int n){if(x==1) return 1;if(n == 0) return 1;double tmp = 0.0;if(n>0){tmp = myPow(x,n/2);return n%2 == 0 ? tmp*tmp : tmp*tmp*x;}else{long long nn = n;nn = -nn;tmp = myPow(x,nn/2);return n%2 == 0 ? 1.0/(tmp*tmp) : 1.0/(tmp*tmp*x);}}
};