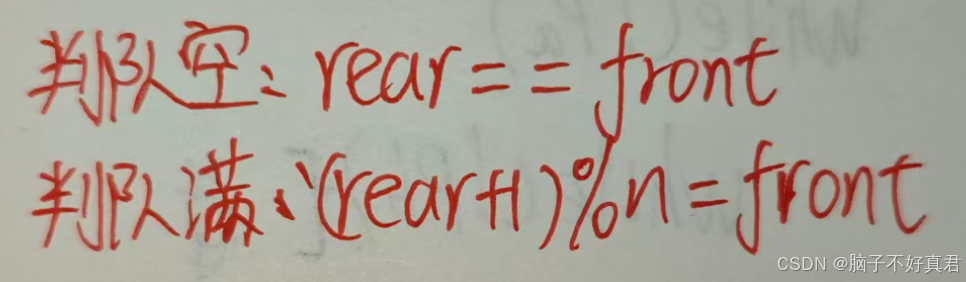第三章 栈和队列——课后习题解练【数据结构(c语言版 第2版)】
第三章 栈和队列
1.选择题
(1)(2)(3)(4)
答案:CCDA
(5)
(6)(7)(8)
答案:DAB
(9)
(10)(11)(12)
答案:DDD
(13)
(14)
答案:C
(15)
答案:B.终止条件和递归部分
2.算法设计题
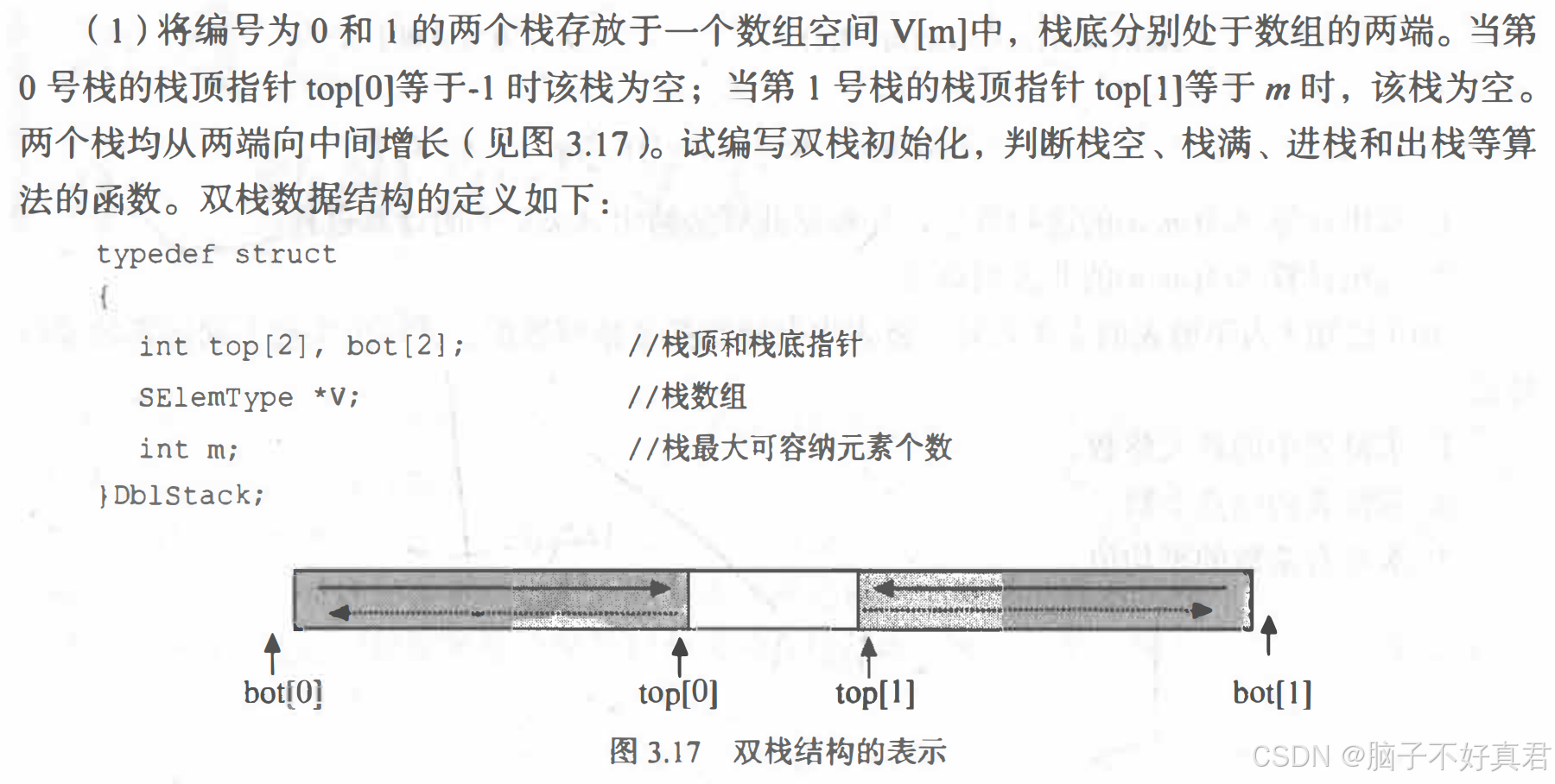
(1)
双栈初始化函数
// 双栈初始化 int InitDblStack(DblStack *S, int maxsize) {S->v = (SElemType *)malloc(sizeof(SElemType) * maxsize);if (!S->v) {return 0; // 内存分配失败}S->m = maxsize;// 0号栈:从数组左端向右增长S->bot[0] = 0;S->top[0] = -1; // 栈空条件:top[0] == -1// 1号栈:从数组右端向左增长S->bot[1] = maxsize - 1;S->top[1] = maxsize; // 栈空条件:top[1] == mreturn 1; // 初始化成功 }判断栈空函数
// 判断栈是否为空 int StackEmpty(DblStack *S, int i) {if (i == 0) {return S->top[0] == -1; // 0号栈空} else if (i == 1) {return S->top[1] == S->m; // 1号栈空}return -1; // 栈编号错误 }判断栈满函数
// 判断栈是否满(两栈相遇) int StackFull(DblStack *S) {return S->top[0] + 1 == S->top[1]; // 两栈顶指针相邻 }进栈函数
// 元素进栈 int Push(DblStack *S, int i, SElemType x) {if (StackFull(S)) {return 0; // 栈满,进栈失败}if (i == 0) { // 0号栈进栈S->top[0]++; // 栈顶指针右移S->v[S->top[0]] = x; // 存入元素} else if (i == 1) { // 1号栈进栈S->top[1]--; // 栈顶指针左移S->v[S->top[1]] = x; // 存入元素} else {return 0; // 栈编号错误}return 1; // 进栈成功 }出栈函数
// 元素出栈 int Pop(DblStack *S, int i, SElemType *x) {if (StackEmpty(S, i)) {return 0; // 栈空,出栈失败}if (i == 0) { // 0号栈出栈*x = S->v[S->top[0]]; // 取出元素S->top[0]--; // 栈顶指针左移} else if (i == 1) { // 1号栈出栈*x = S->v[S->top[1]]; // 取出元素S->top[1]++; // 栈顶指针右移} else {return 0; // 栈编号错误}return 1; // 出栈成功 }
(2)
// 定义顺序栈的存储结构 #define StackSize 100 // 预分配的栈空间最多为100个元素 typedef char DataType; // 栈元素的数据类型为字符typedef struct {DataType data[StackSize]; // 栈的存储数组int top; // 栈顶指针 } SeqStack;// 函数功能:判断字符向量是否为回文 // 参数说明:bunch - 待判断的字符串指针 // 返回值:1表示是回文,0表示不是回文 int IsHuiwen(char *bunch) {SeqStack s; // 定义顺序栈int i, len; // i:循环计数器,len:字符串长度char temp; // 临时变量,用于存储出栈的字符// 初始化栈InitStack(&s);// 获取字符串长度len = strlen(t);// 将字符串的前半部分字符入栈// 例如:"abcdcba" -> 前3个字符"abc"入栈for (i = 0; i < len / 2; i++) {Push(&s, bunch[i]);}// 处理奇数长度字符串的中间字符// 如果长度为奇数,从中间字符的下一个开始比较// 如果长度为偶数,直接从后半部分开始比较if (len % 2 == 0) {i = len / 2; // 偶数长度:从中间开始比较} else {i = len / 2 + 1; // 奇数长度:跳过中间字符}// 依次弹出栈中字符与字符串后半部分比较while (!EmptyStack(&s)) {temp = Pop(&s); // 弹出栈顶字符// 比较弹出的字符与字符串对应位置的字符if (temp != bunch[i]) {return 0; // 发现不匹配,不是回文} else {i++; // 继续比较下一个字符}}// 所有字符都匹配,是回文return 1; }
(7)
循环队列结构定义
#define MAXSIZE 100 // 队列最大容量typedef struct {int *Q; // 存放队列元素的数组int front; // 队头指针int rear; // 队尾指针 int tag; // 队列状态标志:0-空,1-满int m; // 队列实际容量 } CycleQueue;队列初始化函数
// 判断队列是否为空 // 空队列条件:front == rear 且 tag == 0 int QueueEmpty(CycleQueue *cq) {return (cq->front == cq->rear) && (cq->tag == 0); }// 判断队列是否已满 // 满队列条件:front == rear 且 tag == 1 int QueueFull(CycleQueue *cq) {return (cq->front == cq->rear) && (cq->tag == 1); }插入算法(enqueue)
// 元素入队算法 // 参数:cq - 队列指针,x - 要插入的元素 // 返回值:1-成功,0-失败(队列已满) int enqueue(CycleQueue *cq, int x) {// 检查队列是否已满if (QueueFull(cq)) {printf("队列已满,无法插入元素 %d\n", x);return 0;}// 在队尾插入元素cq->Q[cq->rear] = x;// 队尾指针循环后移cq->rear = (cq->rear + 1) % cq->m;// 插入元素后,队列肯定不空,设置tag=1cq->tag = 1;printf("元素 %d 入队成功\n", x);return 1; }删除算法(dequeue)
// 元素出队算法 // 参数:cq - 队列指针,x - 用于返回出队元素的指针 // 返回值:1-成功,0-失败(队列为空) int dequeue(CycleQueue *cq, int *x) {// 检查队列是否为空if (QueueEmpty(cq)) {printf("队列为空,无法删除元素\n");return 0;}// 保存队头元素*x = cq->Q[cq->front];// 队头指针循环后移cq->front = (cq->front + 1) % cq->m;// 删除元素后,队列肯定不满,设置tag=0cq->tag = 0;printf("元素 %d 出队成功\n", *x);return 1; }