当前位置：首页 > news >正文

AI人工智能-深度学习的基本原理-第二周（小白）

news 2025/10/20 7:30:29

数学基础

线性代数

标量

一个标量就是一个单独的数

向量

一个向量是一列数
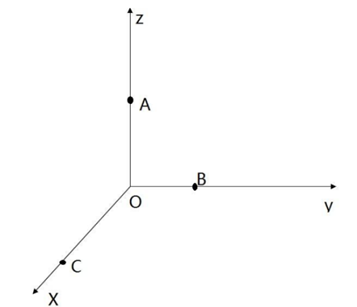
可以把向量看做空间中的几个点，每个元素是不同坐标轴上的坐标
向量中有几个数，就叫几维向量
如4维向量：[1,2,3,4]

向量的运算

注意：以下都需要维度相同

向量加和：A + B = B + A
例子：[1, 2] + [3, 4] = [4, 6]
向量的内积：A * B = B * A
例子：[1, 2] * [3, 4] = 1 * 3 + 2 * 4 = 11
向量夹角余弦
$\cos \Theta$ = A * B / |A| $\cdot$ |B|
向量的模：|A| = $\sqrt{x1^2 + x2^2+...+xn^2}$

矩阵

是一个二维数组，矩阵中的每个值是一个标量，可以通过行号和列号进行索引。

$\begin{bmatrix} 1 &2 \\ 3& 4 \end{bmatrix}$ 2 * 2的矩阵， $\begin{bmatrix} 1 & 3\\ 2& 4\\ 3& 5 \end{bmatrix}$ 3 * 2的矩阵

矩阵的运算

矩阵加法（需要维度相同）

$\begin{bmatrix} 1 & 2\\ 3& 4 \end{bmatrix} +\begin{bmatrix} 4 &2 \\ 3&1 \end{bmatrix} =\begin{bmatrix} 5 &4 \\ 6&5 \end{bmatrix}$

矩阵乘法（不满足交换律）

A * B != B * A
当左矩阵A的列数等于右矩阵B的行数，A与B可以相乘
M*N矩阵乘以N*P的矩阵得到M*P的矩阵，A ∈ $R^{M*N}$ * B ∈ $R^{N*P}$ = C∈ $R^{M*P}$ （R代表的是实数集）

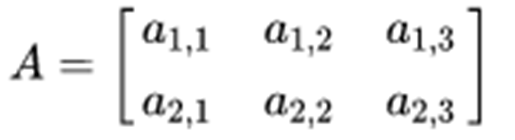
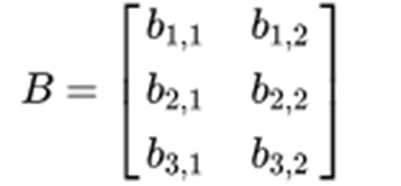
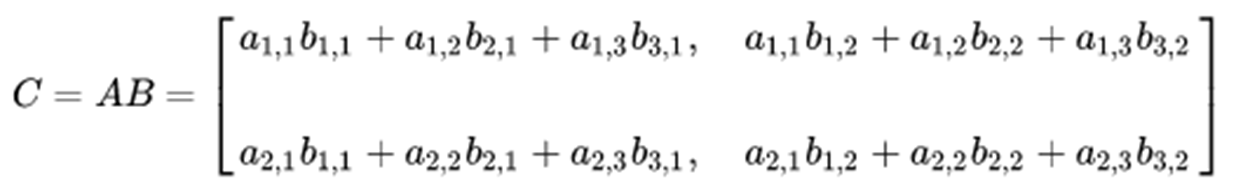
符合分配律
A *(B + C) = A*B + A*C
符合结合律
A * (B * C) = (A*B)*C

矩阵点乘

注意：两矩阵必须形状一致

同位相乘，得到的维度也没有变

$\begin{bmatrix} 1 &2 \\ 3&4 \end{bmatrix}\cdot \begin{bmatrix} 1 &2 \\ 0&-1 \end{bmatrix}= \begin{bmatrix} 1 &4 \\ 0 & -4 \end{bmatrix}$

常见的矩阵操作

矩阵转置（行列互换transpose）

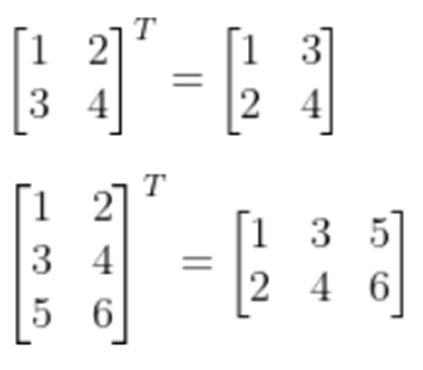
向量<==>矩阵

[1,2,3,4] ---reshape 2*2--> $\begin{bmatrix} 1 &2 \\ 3&4 \end{bmatrix}$

$\begin{bmatrix} 1 &2 \\ 3&4 \\ 5&6 \end{bmatrix}$ ---flatten---> [1,2,3,4,5,6]

张量（tensor）

通俗的说：将三个2*2的矩阵排列在一起，就可以称为一个3*2*2的张量，将4个3*2*2的张量排列在一起，就可以称为4*3*2*2的张量

是神经网络训练中最为常见的数据形式。

所有的输入，输出，中间结果，几乎都是以张量的形式存在。

张量的常见操作

x

x.shape = 2 * 2 * 2

x.transpose(1,2)

x.shape = 2*2*2

作用

transpose()用于交换张量的两个指定维度。

特点

交换维度：只改变维度的顺序
不改变数据存储：与view类似，返回视图而非副本
可以交换任意两个维度：比简单的转置更灵活

语法

tensor.transpose(dim0, dim1)

import torch# 创建一个3×4的张量
x = torch.tensor([[1, 2, 3, 4],[5, 6, 7, 8],[9, 10, 11, 12]])
print("原始形状:", x.shape)  # torch.Size([3, 4])# 交换第0维和第1维（行和列交换）
x_t = x.transpose(0, 1)
print("转置后形状:", x_t.shape)  # torch.Size([4, 3])
print(x_t)
# tensor([[ 1,  5,  9],
#         [ 2,  6, 10],
#         [ 3,  7, 11],
#         [ 4,  8, 12]])# 对于3D张量
x_3d = torch.randn(2, 3, 4)
print("3D原始形状:", x_3d.shape)  # torch.Size([2, 3, 4])# 交换第0维和第2维
x_3d_t = x_3d.transpose(0, 2)
print("交换后形状:", x_3d_t.shape)  # torch.Size([4, 3, 2])

x.view(4,2)

x.shape = 4*2

view()用于改变张量的形状（shape），但不改变张量中的数据本身，只改变数据的"视图"。

特点

不改变数据存储：只改变数据的解释方式
要求元素总数不变：新形状的元素数量必须与原形状相同
返回共享存储的视图：修改view后的张量会影响原始张量

语法

tensor.view(*shape)

import torch# 原始张量
x = torch.arange(12)  # [0, 1, 2, ..., 11]
print("原始张量:", x.shape)  # torch.Size([12])# 改变形状
x_2d = x.view(3, 4)
print("2D视图:", x_2d.shape)  # torch.Size([3, 4])
print(x_2d)
# tensor([[ 0,  1,  2,  3],
#         [ 4,  5,  6,  7],
#         [ 8,  9, 10, 11]])# 再改变形状
x_3d = x.view(2, 3, 2)
print("3D视图:", x_3d.shape)  # torch.Size([2, 3, 2])# 使用-1自动计算维度大小
auto_shape = x.view(3, -1)  # -1会被自动计算为4
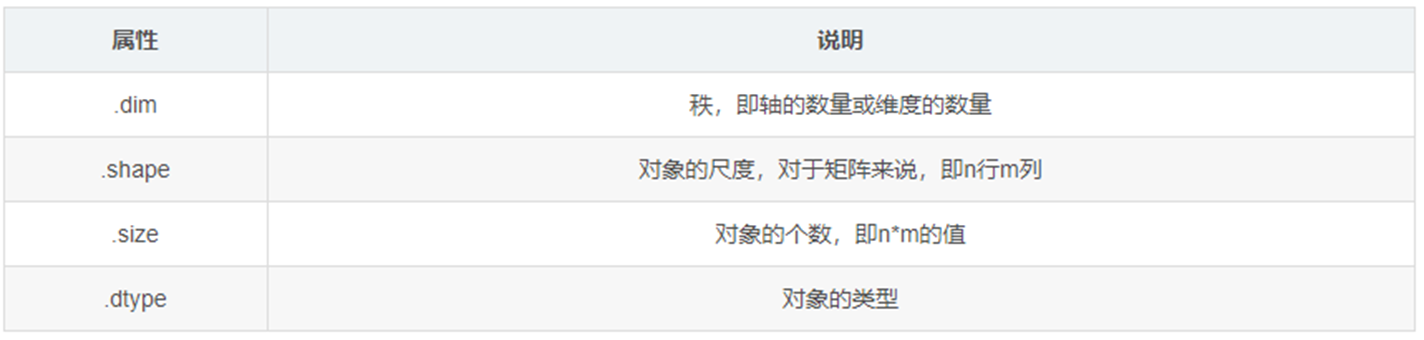
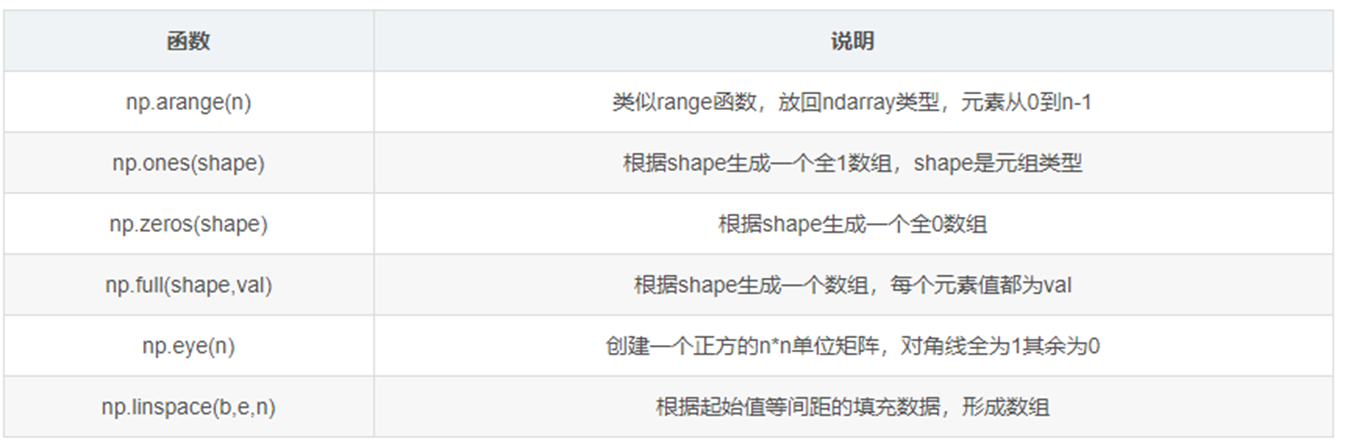
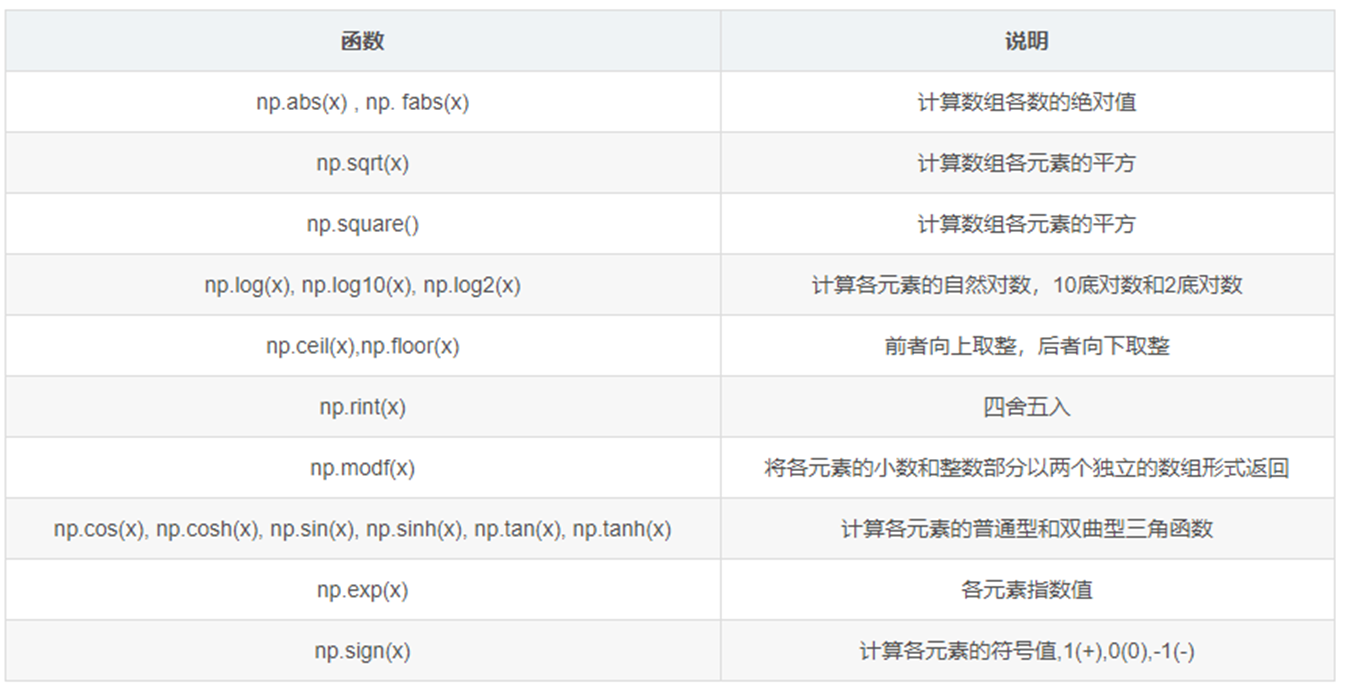
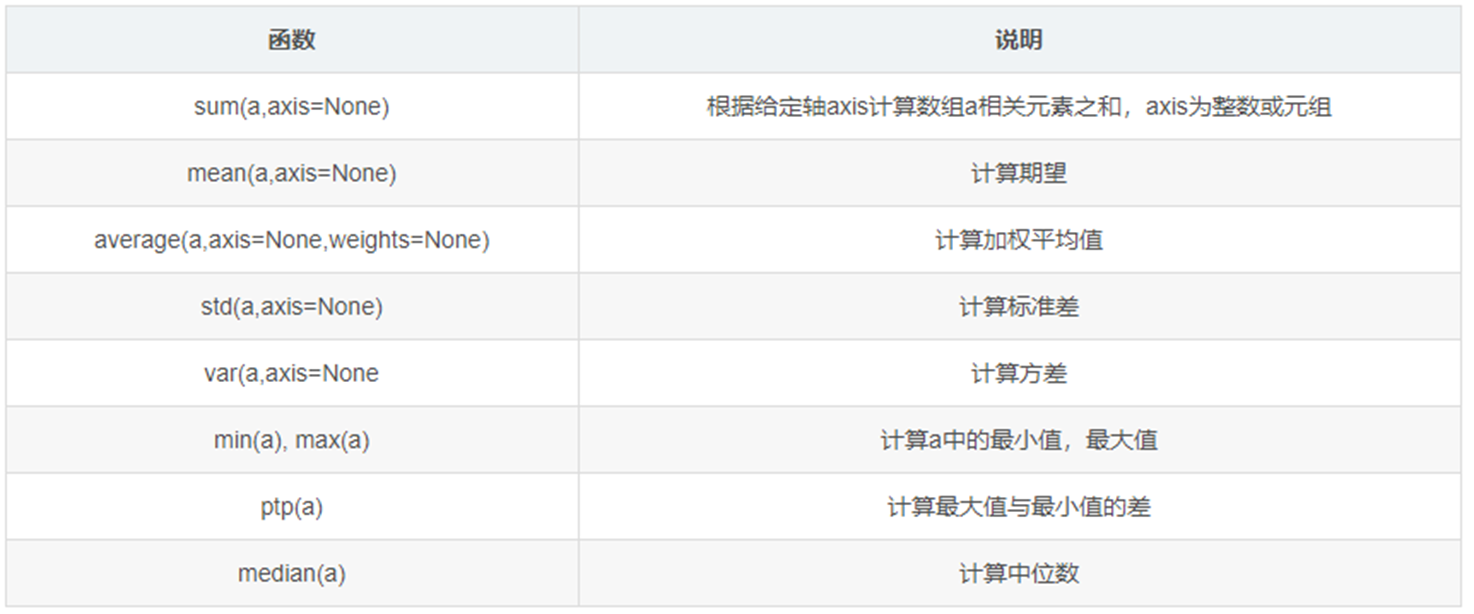
print("自动计算:", auto_shape.shape)  # torch.Size([3, 4])