常见的位运算的总结
左移:<< :每左移 1 位右侧补 1 个 0,移出去的数字舍去。
右移:>> :每右移 1 位,舍弃最右侧的位,最左侧补 0(正数场景)。(负数则在最左侧补1)
按位取反:~
按位与:&(有0则0)
按位或:|(有1则1)
按位异或:^(相同为0,相异为1)
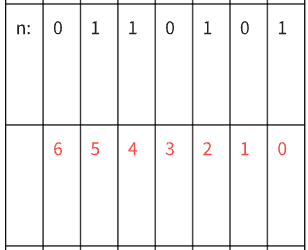
给定一个数n,确定它的二进制表示中的第x位是0还是1
如上图所示,第二行的数字就表示这个数字的第x位。
解决办法:
(n>>x)&1
上述运算式的结果是0,则第x位是0,反之则为1。
将一个数n的二进制表示的第x位修改成1
解决办法:
n=n|(1<<x)
我们以把上图中的数n的第3位修改为1为例来讲解:
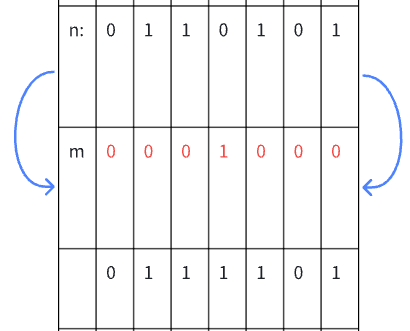
由于我们只想把第x位修改为1,同时要保持其他位上的数字不变。
所以我们可以让n|m,因为|的规则是有1则1。而由于m这个数字除了第x位是1之外,其他位上的数字都是0,这样就可保证第x位在经过运算之后一定是1。
而其他位上的数字在运算过后的结果是几,就取决于原来该位上的数字是多少了。
现在的问题是m这个数如何获得,其实也很简单:m=1<<x
综上所述,这个问题的解决办法就是:n=n|(1<<x)
将一个数n的二进制表示的第x位修改成0
解决办法:
n=n&(~(1<<x))
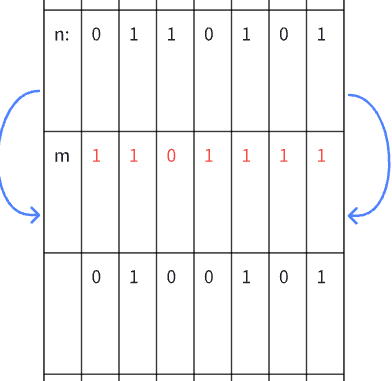
我们以把n的第4位修改为0为例。
我们只需要让n&m,就可以得到这个结果。
这是由于&的运算规则是有0则0,然而m的第x为恰好是0,这就可以保证当n&m的时候,这一位的结果肯定是0。
而其他位的结果是多少就有n原来那个数位上是多少来决定了。
而m=~(1<<x)。
所以这个问题的解决办法就是n=n&(~(1<<x))
提取一个数(n)二进制表示中最右侧的1
解决办法:
n&(-n)
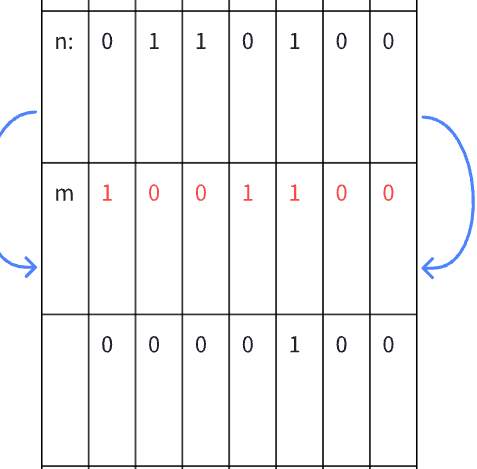
上图中的m就是-n,由此可见-n就是把n的最右侧的1左边的区域全部都按位取反。
这样再进行&操作的时候,最右侧的1左边的区域的数字就都变成了0。
这样经过&运算之后,我们就可以提取出来n的最右侧的1了。
消除一个数(n)二进制表示中最右侧的1
解决办法:
n&(n-1)
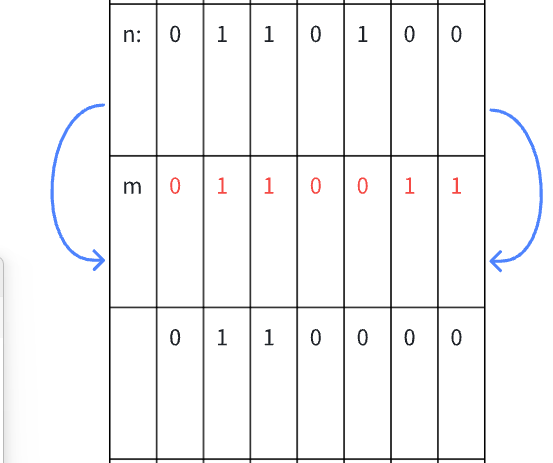
由此可见m(n-1)就是把n的最右侧的1的右边的区域(包括这个1)全部按位取反
这样再进行&运算之后,就可以把最右侧的1消除掉。
异或(^)运算的运算律
- a^0=a
- a^a=0
- a^b^c=a^(b^c)
运用这个运算律我们可以解决LeetCode上编号为136和260这两个题。
