Differential evolution with collective ensemble learning

Differential evolution with collective ensemble learning（基于集体集成学习的差分进化算法）

ABSTRACT（摘要）

多种搜索策略的集成学习已被证明能有效提升差分进化（DE）在全局优化中的性能。在现有的集成学习方法中，每个目标解的后代是根据所考虑问题的优化需求，从策略池中选择其中一个策略生成的。然而，由于后代的遗传物质通常来源于单一策略，不同策略的优势无法被同时用于优化具有不同属性的决策变量。为了解决这个问题，本文提出了集体集成学习（CEL）范式，该范式融合了多种策略的优势来生成一个后代。CEL主要包括组件分解（CD）和组件集成（CI）机制。CD机制考虑维度级的进化状态，将目标解以及由不同生成策略产生的候选解分别划分为开发性（exploitative）和探索性（explorative）组件。接着，实施CI机制，根据在组件级别执行的子相似度（sub-similarity）测量，集成适当的组件以形成后代。通过与基线方法、各个独立机制、现有集成学习方法以及几种先进的DE变体进行性能比较，CEL的有效性和优势得到了验证和讨论。

关键词: 差分进化；策略自适应；集成学习；变量特征；全局优化

---

1. 引言（Introduction）

差分进化（Differential Evolution, DE）[1]已被证明是解决各类优化问题时最具竞争力的进化算法（EAs）之一。在过去的二十年中，因其解决不同类型问题的通用性和简洁性，DE得到了广泛的研究[2-4]。DE包含四个组成部分：初始化、变异、交叉和选择。首先，在搜索空间中随机生成初始种群。随后，在变异过程中通过差分向量向种群引入扰动，接着进行交叉过程以产生试验向量（即后代）。最后，执行选择操作以筛选出更好的解进入下一代。生成有前途的后代和选择后代都对DE的性能有显著影响。因此，研究人员致力于改进生成方法[5-11]、调整控制参数[12-14]以及优化选择策略[15]。其中，生成方法，主要是DE变异策略，得到了广泛研究，以期更好地采样出有前途的后代。

根据无免费午餐（No Free Lunch, NFL）定理[16]，没有单一的优化算法能够高效处理所有类型的优化问题。因此，源自机器学习的集成学习（Ensemble Learning, EL）被引入，旨在为优化器提供更广泛的适应性，并已被证明是提高DE性能的有效工具。现有的将EL与DE相结合的方法可以从不同角度进行分类[5]。考虑到每个目标解所产生的候选解数量，这些方法可分为竞争特征集成（competitiveness-featured）和平等特征集成（equality-featured）两种范式。

在竞争特征集成中，多种变异策略竞争只为每个目标生成一个候选解，该候选解自然成为其后代。目前已开发出许多竞争机制，例如基于记忆的[17]、基于概率的[18-21]、基于多种群的[22]、基于适应度的[23]、基于阶段的[24]以及基于状态的[25,26]机制等。不同的是，在平等特征集成中，使用多种策略为每个目标解生成多个候选解，然后通过某些规则从中确定一个作为后代。目前已开发出几种选择规则，包括适应度比较[27]、廉价代理模型（Cheap Surrogate Model, CSM）[28]、低估模型（Underestimation Model, UM）[29]以及同时考虑目标和决策空间的相似性选择（Similarity Selection, SS）规则[30]。平等特征集成与竞争特征集成的显著区别在于，平等特征集成允许所有策略有平等的机会为同一个目标解生成候选解。然而，与竞争特征集成类似，平等特征集成中的最终后代仍然是由单一策略生成的。因此，我们在本文中将其统称为单一集成学习（Single Ensemble Learning, SEL） 方法，这类方法未探索候选解之间通过信息交换来形成潜在更优解的可能性。候选解之间的信息交换可以将不同策略的优势融合到一个后代中，这对于解决变量性质差异显著的问题（如混合函数[31]）或变量间收敛程度不同的问题是有益的。

基于这些考虑，本文提出了集体集成学习（Collective Ensemble Learning, CEL） 范式，该范式包含三个机制：组件分解、组件集成和基于马氏距离的相似性度量。首先，在组件分解中，根据进化状态将每个目标解中的变量分类为收敛目标组件和多样性目标组件。随后，每个组件利用多种策略生成子候选解。其次，在组件集成中，执行子相似性选择（Sub-similarity Selection, SubS）规则，通过计算子候选解与对应组件的相似度来衡量其局部开发性和探索性特征。最后，来自不同候选解的组件被集体组合以形成后代。通过组件分解，可以将收敛程度不同的变量分开并独立进行优化，这使得搜索更加有效。此外，组件集成融合了不同策略的优势。为了更准确地度量相似性，提出了基于马氏距离（Mahalanobis Distance, MaD）的子相似性计算方​​法，该方法解决了因变量尺度不同而导致的度量误差问题，并提高了相似性选择的预测准确性。本文的动机和贡献可总结如下：

（1）与现有的SEL范式不同，提出的CEL范式通过一种集体机制生成每个后代，该机制集体地组合了由不同策略生成的多个候选解中的子组件。

（2）提出的组件分解机制将一个优化问题分解为子问题，并根据其自身特征更有效地处理它们。提出的组件集成机制根据子相似性选择规则充分利用候选解中的遗传材料，丰富了后代的生成方式。

（3）为了减少复杂场景下相似性度量的误差并提高预测精度，引入了基于马氏距离的候选选择方法。

（4）CEL表现出显著优于其他SEL方法的性能。其底层机制也通过全面的实验进行了研究和解释。

本文其余部分组织如下。第2节简要介绍了经典的DE算法并回顾了相关工作。第3节详细描述了提出的CEL范式。第4节展示了全面的实验以验证所提出方法，而第5节对本文进行了总结。

---

2. 背景（Background）

2.1 差分进化 (Differential Evolution)

在差分进化（DE）中，每一代都会执行三个遗传操作：变异、交叉和选择，以进化一个目标种群 XG={x→1,G,x→2,G,...,x→NP,G}\mathbf{X}_{G}=\{\overrightarrow{x}_{1,G},\overrightarrow{x}_{2,G},..., \overrightarrow{x}_{NP,G}\}XG​={x1,G​,x2,G​,...,xNP,G​}，该种群包含 NP 个 D 维个体。

在优化开始之前，在 $G=0$ 时，通过均匀采样在整个搜索空间中生成初始种群。

DE的变异 (DE’s mutation): 随后，在变异阶段，一个基向量（base vector）与至少一个差分向量（differential vector）相结合。以下列出了几种常用的变异策略：

DE/rand/1:
$${\overrightarrow{v}}_{i,G}={\overrightarrow{x}}_{r_1,G}+F({\overrightarrow{x}}_{r_2,G}-{\overrightarrow{x}}_{r_3,G})\text{\hspace{1em}(1)}$$

DE/best/1:
$${\overrightarrow{v}}_{i,G}={\overrightarrow{x}}_{best,G}+F({\overrightarrow{x}}_{r_1,G}-{\overrightarrow{x}}_{r_2,G})\text{\hspace{1em}(2)}$$

DE/rand/2:
$${\overrightarrow{v}}_{i,G}={\overrightarrow{x}}_{r_1,G}+F({\overrightarrow{x}}_{r_2,G}-{\overrightarrow{x}}_{r_3,G})+F({\overrightarrow{x}}_{r_4,G}-{\overrightarrow{x}}_{r_5,G})\text{\hspace{1em}(3)}$$

DE/best/2:
$${\overrightarrow{v}}_{i,G}={\overrightarrow{x}}_{best,G}+F({\overrightarrow{x}}_{r_1,G}-{\overrightarrow{x}}_{r_2,G})+F({\overrightarrow{x}}_{r_3,G}-{\overrightarrow{x}}_{r_4,G})\text{\hspace{1em}(4)}$$

其中 $r_1$, $r_2$, $r_3$,$r_4$ 和 $r_5$ 是从 [1, NP] 中选出的互不相同的随机整数，并且不等于 $i$。${\overrightarrow{x}}_{best,G}$ 和 $F$ 分别表示当前种群中的最佳个体和一个在 (0, 1] 范围内的缩放参数。

DE的交叉 (DE’s crossover): 变异之后，在每个变异向量 ${\overrightarrow{v}}_{i,G}$ 和相应的目标向量 ${\overrightarrow{x}}_{i,G}$ 之间进行交叉操作，以获得试验向量 ${\overrightarrow{u}}_{i,G}$。二项式交叉（binomial crossover）如下所示：

$$u_{i,jG}=\{\begin{array}{ll}{v}_{ij,G}& \text{if }ran{d}_j(0,1)\le CR\text{ or }j=j_{rand}\\ x_{ij,G}& \text{otherwise}\end{array}\text{\hspace{1em}(5)}$$

其中 $ran{d}_j$ (0,1) 表示一个从 (0,1) 区间生成的随机实数，$j_{rand}$ 是一个在 [1, D] 范围内随机选择的整数，$CR$ 是一个在 [0,1] 范围内的交叉参数。

DE的选择 (DE’s selection): 比较每对 ${\overrightarrow{u}}_{i,G}$ 和 ${\overrightarrow{x}}_{i,G}$ 的适应度，只有当后代的适应度更小（针对最小化问题）或至少相等时，它才会被接受进入下一代，如下所示：

$${\overrightarrow{x}}_{i,G+1}=\{\begin{array}{ll}{\overrightarrow{u}}_{i,G}& \text{if }f({\overrightarrow{u}}_{i,G})\le f({\overrightarrow{x}}_{i,G})\\ {\overrightarrow{x}}_{i,G}& \text{otherwise}\end{array}\text{\hspace{1em}(6)}$$

2.2 面向DE的竞争特征与平等特征集成范式 (Competitiveness-featured and equality-featured ensemble paradigms for DE)

自问世以来，DE因其简单的结构和高效的性能，吸引了科学和工程领域研究人员的广泛关注[2]。DE拥有许多可选的变异策略以及可调整的控制参数 $F$ 和 $CR$，这使得它可以灵活地调整进化方向和进化规模。在过去的二十年中，策略利用和参数控制得到了广泛研究。关于组合不同策略的方式，现有研究可分为以下两类。

1. 竞争特征集成 (Competitiveness-featured Ensemble)

在此类别中，多种策略竞争只为每个目标解生成一个候选解（该候选解也就是后代）。这可以通过策略自适应（strategy adaptation）或基于观察的策略分配（observation-based strategy allocation）来实现。

策略自适应旨在更好地在不同的进化阶段利用合适的变异策略。相关技术包括自适应算子选择（Adaptive Operator Selection, AOS），例如概率匹配（Probability Matching, PM）[32]、自适应追求（Adaptive Pursuit, AP）[32]和多臂赌博机（Multi-Armed Bandit, MAB）[33]；SaDE [17]中基于成功-失败历史的策略自适应；EPSDE [18]中基于集成的策略自适应；SaM [34]中受参数控制方法启发的策略自适应；ZEPDE [35]中基于分区的策略自适应；MPEDE [22]中基于多种群的多策略集成；HIDIE [36]中基于历史和启发式的策略自适应；以及FaDE [37]中策略的显式自适应。PM和AP都属于基于概率的策略分配方案，它们调整每个变异策略的概率以匹配其奖励分布。在PM中，策略池中的每个变异策略都不会被忽略，而AP则通过一个称为学习率的超参数来调整“赢家通吃”策略的贪婪水平。SaDE [17]根据先前经验获得的概率，从策略池中选择合适的变异策略。在EPSDE [18]中，多种策略池和多组控制参数共存，以竞争后代的生成。SaM [34]引入了一个策略参数，通过参数自适应方法从策略池中选择合适的策略。ZEPDE [35]使变异策略适应进化阶段，考虑到在早期过程应倡导探索，而在后期则需要更多开发。在MPEDE [22]中，每隔一定代数后，更多的计算资源会被分配给由三个指示子种群确定的更优变异策略。在HIDIE [36]中，结合了整个种群的历史成功经验和个体的当前状态来为每个解调整变异策略。在[37]中，FaDE将整个进化过程分为两部分，即SCSS阶段和自适应世代。前者用于检测探索和开发的需求，从而指导后者的策略自适应。在[38]中，三种高效的DE变体分别在三个小的指示种群上执行，经过一定代数后，奖励的子种群被分配给表现最好的优化器。[39]中提出的基于投票机制的集成框架利用了几种约束处理技术，并将它们视为投票者来评估每对解，从而找出更好的一个。在[40]中，不同的解排序方法被结合到基于通用投票机制的集成框架中来选择潜在的解。更多的投票被分配给最有效的解排序方法，而对较差的方法则进行惩罚。

基于观察的策略分配根据从决策空间和目标空间获得的观察结果来调整后代生成方法。相关研究包括大量基于适应度的方法[23, 41, 42, 43, 44, 45, 46]。在[23]中，IDE根据个体的适应度排名为其分配不同的变异策略。[41]中的ETI-DE对优等解和劣等解分别采用了基于事件触发的脉冲式变异控制。Cui等人提出的MPADE [42]根据适应度将整个种群分成三个小规模的子群，并对这三个子群使用不同的策略。[43]中的多层竞争合作DE根据适应度分配计算资源。[44]中基于邻域的自适应DE利用个体邻域的适应度在开发和探索之间进行权衡。基于从包含多种变异策略的策略池中获得的观察结果来选择合适策略的方法也受到青睐[45, 46]。在[45]中，适应度改进作为从策略池中选择变异策略的指导原则。在[46]中，策略池由三种变异策略组成，在考虑适应度的情况下，会为每个小规模子群中的个体选择其中一种策略。

2.平等特征集成 (Equality-featured Ensemble)

与上述方法（其中只有最合适的策略有机会为每个目标解生成后代）显著不同，基于平等的集成方法平等对待所有策略。具体来说，它使用多种策略为每个目标解采样多个候选解，然后筛选出一个作为后代。因此，每种策略都获得了生成候选解的机会。一个经典代表是CoDE算法[27]，该算法使用三对变异策略和控制参数来采样三个候选解，并选择最适应的候选解作为后代。在基于廉价代理模型（CSM）的DE [28]中，使用多种策略生成多个候选解，最终后代的选择由基于Parzen窗的密度估计控制。在基于低估的多变异（UM）方法[29]中，选择候选解的规则是一种低估（underestimation），其中采用候选解与中心（即所有候选解的均值）之间的距离来构建廉价的抽象凸低估模型。在选择候选解与相似性选择（SCSS）[30]方法中，为每个目标解生成两个候选解，最终候选解的确定由基于欧几里得度量的相似性选择（SS）规则给出，其中优等的目标向量选择更近的候选解，而劣等的目标向量偏好更远的候选解。在[47]中，两种分别从逻辑上局部最适应个体和随机选择的优等解学习到的精英引导变异策略被同时应用于创建两个候选解。适应度较小的解被视为最终后代。在[48]中，通过两组变异和交叉算子产生两个试验向量，并根据适应度选择较优者作为最终的试验向量。

---

3. 提出的方法（Proposed method）

从第2节可以看出，集成学习已成功应用于DE。为了融合不同策略的优势，已经开发了各种集成机制。每个目标解的后代都是由策略池中被认为适合生成有前途后代的其中一个策略孕育产生的。然而，集体集成（collective ensemble）——即集体地组合来自不同策略的遗传材料以生成后代——在文献中尚未得到充分探索。由于策略的优势被组合到单个后代中，这种方法的特点在于维度级（dimension-level） 的集成，并且它可能更恰当地满足不同变量的搜索需求。基于这些考虑并为填补这一空白，本文提出了集体集成学习（CEL）。其新颖性在图1中描绘并描述如下。图1(a)展示了单一集成学习（SEL） 方法论，这在现有的多策略DE中广泛存在。在这种方法论中，每个目标解的后代由其中一种策略产生。而在图1(b)所示的提出的CEL方法论中，每个目标解被划分为多个组件（components）。每个组件利用（多种）策略生成子后代（sub-offspring）。每个目标解的最终后代是这些子后代的集体组合（collective combination）。CEL包含组件分解（CD） 和组件集成（CI） 两个核心机制，以下小节将分别详细描述。

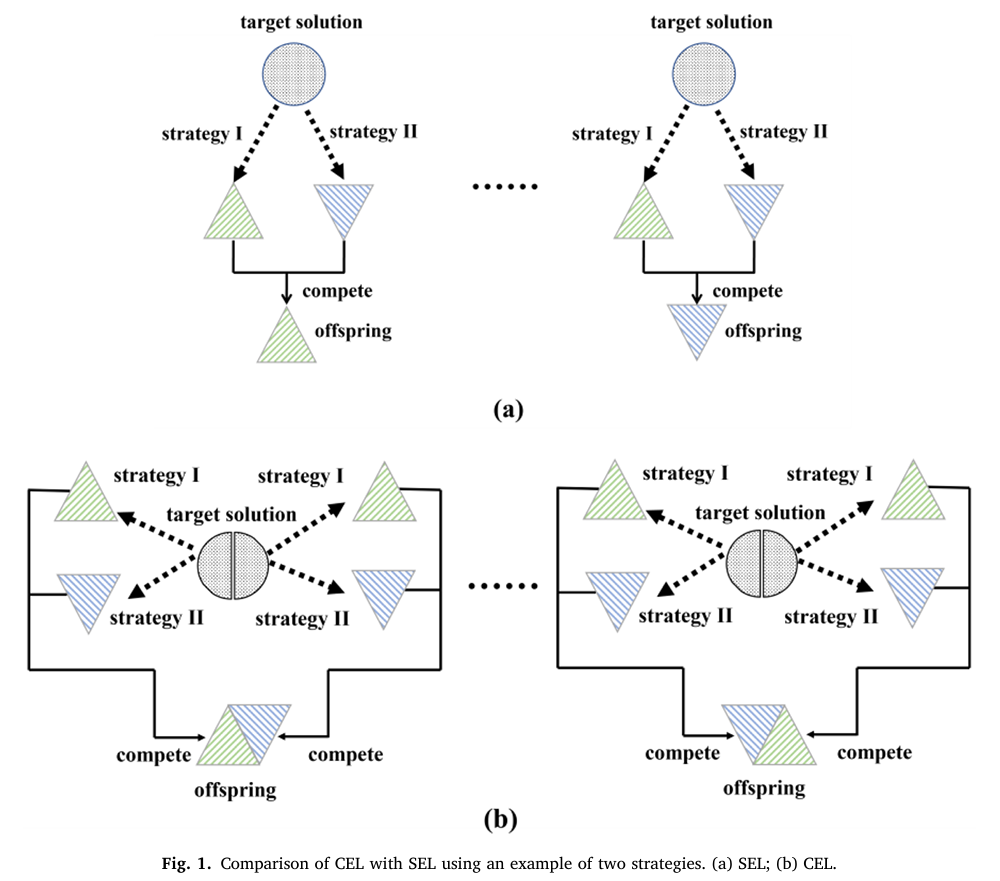
图1: 使用两种策略的例子比较CEL与SEL。(a) SEL; (b) CEL.

3.1 组件分解 (Component Decomposition)

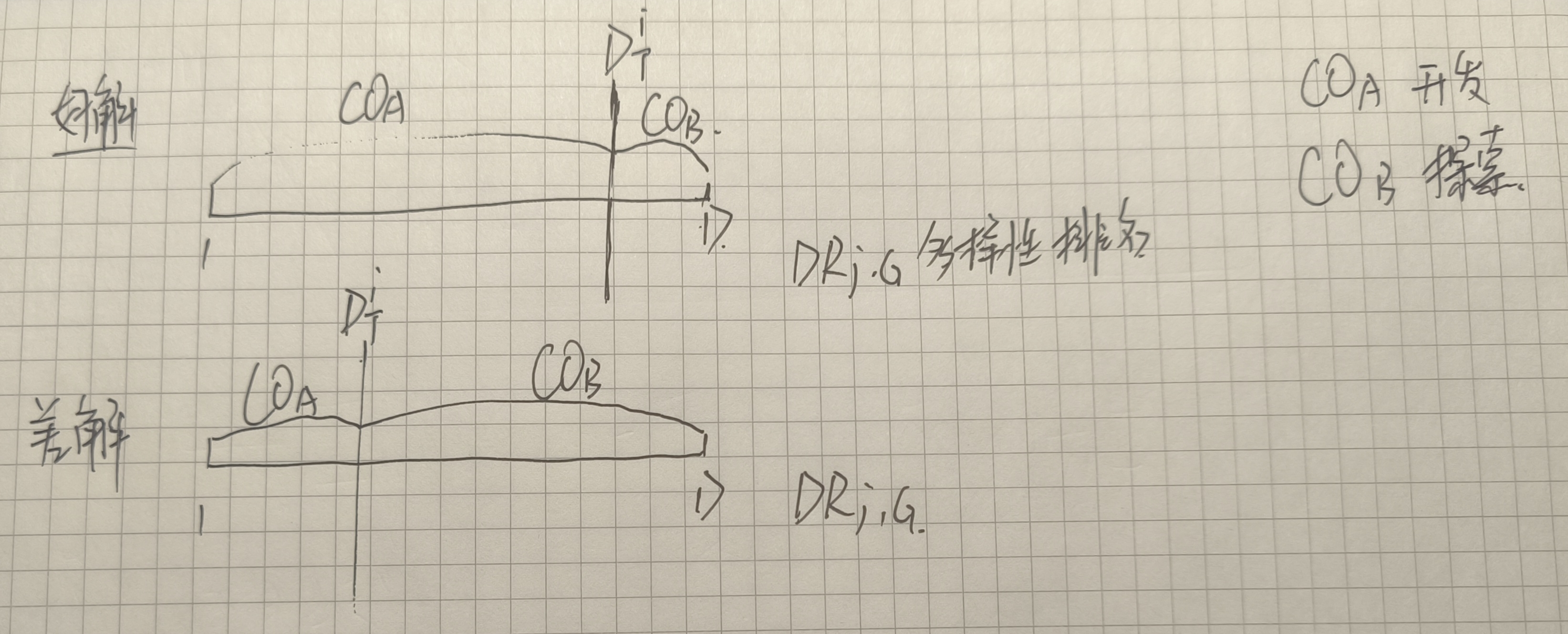
为了结合不同策略的潜在好处，对于每个目标解，CD首先使用多种策略生成多个候选解，以提供更多的遗传材料。随后，考虑到在优化过程中，当变量具有显著不同的特征时，某些变量可能收敛相对较快，而其他变量则收敛较慢，将这种差异整合到后代的生成中是合理的。为此，目标解的整个 D 个变量及其通过不同策略获得的候选解的相应变量，被分别划分为一个开发性组件（exploitative component）（记为 $C{O}_A$）和一个探索性组件（explorative component）（记为 $C{O}_B$），分别由快速收敛和慢速收敛的变量组成。为了有效对变量进行分组，我们在每一代跟踪每个变量的多样性（diversity），其计算如下：

$$d_{j,G}=\frac{1}{NP}{\sum }_{i=1}^{NP}{\left(x_{i,j,G}-{\bar{x}}_{j,G}\right)}^2\text{\hspace{1em}(7)}$$

其中 ${\bar{x}}_{j,G}=\frac{1}{NP}{\sum }_{i=1}^{NP}{x}_{i,j,G}$ 是第 j 个变量的中心。$d_{j,G}$越小，变量的多样性越小。接着，将 dj,G{j=1,2,...,D}d_{j,G} \{j=1, 2, ..., D\}dj,G​{j=1,2,...,D} 按升序排序，并分配多样性排名 $D{R}_{j,G}$，从 $1$ 到 $D$，其中 $\mathbf{D}{\mathbf{R}}_{\mathbf{j},\mathbf{G}}=1$ 表示多样性最小，$\mathbf{D}{\mathbf{R}}_{\mathbf{j},\mathbf{G}}=\mathbf{D}$ 表示多样性最大。

利用 $D{R}_{j,G}$，第 i 个目标解及其相应的候选解分别被划分为两个组件：$C{O}_A$ 包含 $D{R}_{j,G}\le D_T^i$ 的变量，$C{O}_B$ 包含 $D{R}_{j,G}>D_T^i$ 的变量。$D_T^i$ 是第 i 个目标解的阈值，设置为：

$$D_T^i=\text{ceil}((1-rank(i)/NP)\times D)\text{\hspace{1em}(8)}$$

其中 $rank(i)$ 是第 i 个目标解的适应度排名，$rank(i)=1$ 和 $rank(i)=NP$ 分别表示最适应和最差的解，$\text{ceil}(\cdot )$ 表示向上取整函数。根据公式(8)，较适应和较差的解分别与较大和较小的 $D_T^i$ 值相关联。对于较适应的解，较大的 $D_T^i$ 值将鼓励更多低多样性维度进行收敛（开发），而对于较差的解，较小的 $D_T^i$ 值将鼓励更多高多样性维度以维持多样性（探索）。

3.2 组件集成 (Component Integration)

生成候选解后，衡量它们的潜力至关重要。在组件集成中，首先在目标解（当前解）和候选解之间执行相似性计算，以识别其局部开发性和探索性属性。在此，遵循组件划分，在目标解和每个候选解的对应组件之间执行子相似性（Sub-similarity, SubS） 计算。图2展示了一个包含两个候选解的例子。首先使用两种策略为每个目标解 ${\mathbf{X}}_{\mathbf{i}}$ 生成两个候选解 ${C1}_i$ 和 ${C2}_i$ 。然后，根据第3.1节（组件分解）的程序，将 ${\mathbf{X}}_{\mathbf{i}}$、${C1}_i$ 和 ${C2}_i$ 的变量划分为开发性组件（A）和探索性组件（B）。接着，执行 ${\mathbf{X}}_{\mathbf{i}}$与候选解之间每个对应组件的相似性计算。因此，这被称为子相似性计算。最后，利用计算出的子相似度 $subs{1}^A,subs{2}^A,subs{1}^B,subs{2}^B$，确定最终后代的组件来自哪个候选解。有四种可能的组件集成方式：全部来自 ${C1}_i$，全部来自 ${C2}_i$，以及 ${C1}_i$和 ${C2}_i$组件的集体组合。可以看出，与将所有决策变量视为一个整体并执行整体相似性计算不同，子相似性计算是在每个组件内部执行的。

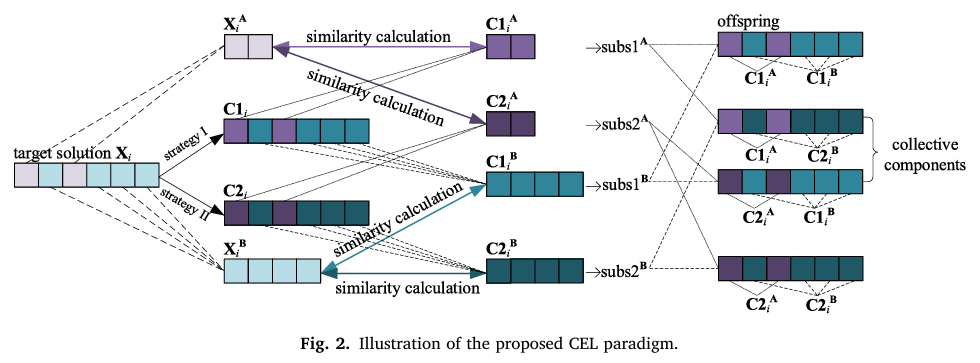
图2: 提出的CEL范式的示意图。

3.3 基于马氏距离的相似性度量 (Mahalanobis distance-based similarity)

为了更准确地度量相似性，采用了马氏距离（Mahalanobis Distance, MaD）（我们前期工作[49]中已初步研究）。马氏距离在分布背景下测量点之间的距离，其定义为：

$$Ma{D}_{1,2}=\sqrt{{\left({\overrightarrow{x}}_1-{\overrightarrow{x}}_2\right)}^{T}Co{v}^{-1}\left({\overrightarrow{x}}_1-{\overrightarrow{x}}_2\right)}\text{\hspace{1em}(9)}$$

其中 ${\overrightarrow{x}}_1$ 和 ${\overrightarrow{x}}_2$ 是两个待测点，$\mathbf{Cov}$ 是种群的协方差矩阵，根据公式(10)计算，

$${\mathbf{Cov}}_{j,k}=\frac{1}{NP-1}\sum _{i=1}^{NP}(x_{i,j,G}-{\bar{x}}_{j,G})(x_{i,k,G}-{\bar{x}}_{k,G})\text{\hspace{1em}(10)}$$

其中 ${\mathbf{Cov}}_{j,k}$ 表示第 j 维和第 k 维之间的协方差，${\bar{x}}_{j,G}=\frac{1}{NP}{\sum }_{i=1}^{NP}{x}_{i,j,G}$ 和 ${\bar{x}}_{k,G}=\frac{1}{NP}{\sum }_{i=1}^{NP}{x}_{i,k,G}$ 分别是第 j 维和第 k 维的中心。${\mathbf{Cov}}^{-1}$ 是协方差矩阵 $\mathbf{Cov}$ 的逆矩阵。

与欧几里得距离（EuD）相比，MaD解决了EuD中因维度尺度不同和忽略维度相关性而导致的测量误差问题。维度尺度差异可能出现在任何类型的函数中，无论是单峰还是多峰。而在混合函数（hybrid functions）中，这种现象可能更明显，因为变量来自具有显著不同特征的基本函数，因此变量的分布也不同。图3展示了一个二维例子在候选选择过程中根据EuD和MaD度量得到的结果。在EuD度量下，候选解C1（红点）比候选解C2（绿点）更接近目标解P8（蓝方块）；而在MaD度量下，情况正好相反。因此，当为P8确定更近的候选解时，EuD选择C1，而MaD选择更服从种群分布的C2。

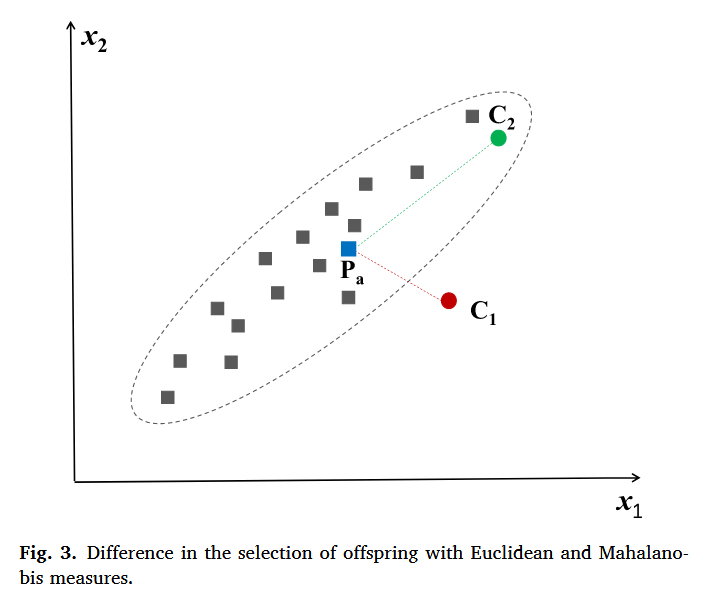
图3: 使用欧几里得和马氏距离度量选择后代的差异。

为了实证说明对性能的影响，图4显示了基于EuD和MaD的候选选择方法在二维移位旋转弯曲雪茄函数（2-D shifted and rotated bent cigar function，CEC2017测试集[31]中的F1）上获得的最终种群。在这两种算法中，选择两个候选解中更接近目标解的那个作为后代。从图4可以观察到，基于MaD的方法获得了收敛更好的种群（最佳适应度小于1E-10），而基于EuD的方法收敛较慢，种群更具多样性（最佳适应度大于1E-6）。此外，图5绘制了基于MaD和EuD的方法在29个50维CEC2017函数上取得的平均预测精度（PA）。PA用于衡量从候选解中成功选择最适应解的概率，其定义为

$$PA=NS/TN\text{\hspace{1em}(11)}$$

其中 TN 是选择候选解的总试验次数，NS 是成功选择最适应候选解的试验次数。从图5可见，在包括F1, F3, F4, F11–F16, F18, F19, F25, F27–F30在内的16个函数上，MaD实现了显著高于EuD的PA；而在其余函数上，两种方法表现相似。考虑函数类型，不仅在混合函数上，在单峰函数F1和F3、简单多峰函数F4以及组合函数F25和F27–F30上，都可以观察到PA的改进。

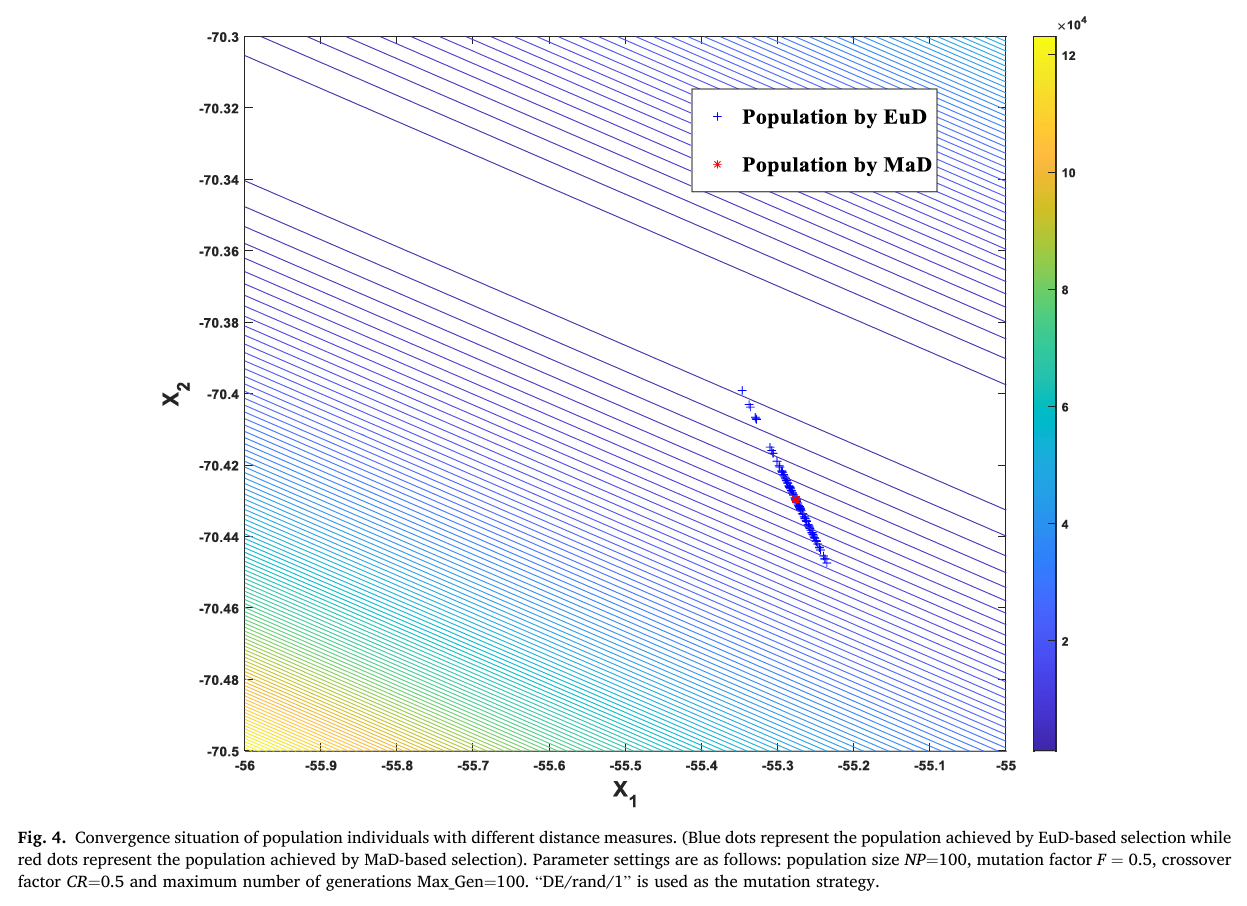
图4: 使用不同距离度量的种群个体收敛情况。（蓝点代表基于EuD选择获得的种群，红点代表基于MaD选择获得的种群）。参数设置如下：种群大小 $NP$=100，变异因子 $F=0.5$，交叉因子 $CR=0.5$，最大代数 Max_Gen=100。使用“DE/rand/1”作为变异策略。
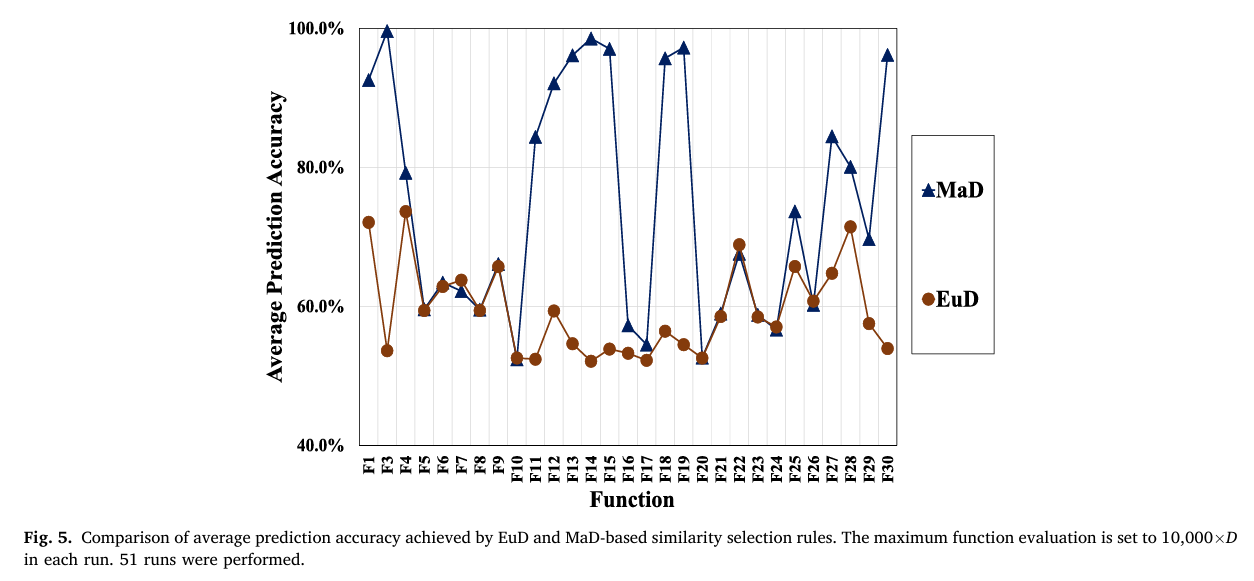图5: 基于欧几里得和马氏距离的相似性选择规则所达到的平均预测精度比较。每次运行的最大函数评估次数设置为10,000$\times D$。进行了51次运行。

3.4 CEL的整体实现 (Overall implementation of CEL)

结合上述CD、CI和MaD机制，算法1展示了每代CEL的整体实现（以两个候选解为例）。输入包括当前种群 $X_G$ 和适应度排名 $rank$。输出是最终的后代 $U_G$，它将进一步用于DE选择（即公式(6)）。

• 在算法1中，第1行获取当前种群 $X_G$ 在维度级别上的多样性及多样性排名，这作为将变量分解为分别具有开发和探索特性的两个组件的指导。
• 由于使用了基于MaD的相似性，第2行计算协方差矩阵 $\mathbf{Cov}$ 及其逆矩阵。利用逆矩阵，可以获得组件中变量之间的关系，用于马氏距离计算。
• CD机制的核心在于第4-7行。对于每个解，第4行通过不同的生成程序（包括变异（例如公式(1)-(4)）和交叉操作（公式(5)）产生两个候选解 ${C1}_{i,G}$ 和 ${C2}_{i,G}$。第5行根据多样性排名 $DR$ 和阈值 $D_T^i$ 确定包含在开发性和探索性组件中的维度。根据前述分解规则，将 ${\mathbf{X}}_{i,G}$ 及其两个候选解 ${C1}_{i,G}$ 和 ${C2}_{i,G}$ 分别分离为两个子解 $({\mathbf{X}}_{i,G}^A,{\mathbf{X}}_{i,G}^B)$, $({C1}_{i,G}^A,{C1}_{i,G}^B)$ 和 $({C2}_{i,G}^A,{C2}_{i,G}^B)$。
• 第7-14行对应于CI机制的核心。具体来说，首先根据第7行（其中 $rand(0,1)$ 是(0,1)内的均匀分布随机数）识别每个目标解是否为优等解（superior）。第8和9行计算每个优等目标解与相应候选解在每个组件内的子相似性，然后选择最近的子候选解用于局部开发；而第11和12行对劣等目标解（inferior）执行操作，选择最远的子候选解用于探索。最后，第14行将两个子候选解组合为一个整体。注意，对优等解的相似性计算是马氏度量（MaD），这更精确，并用于提高预测精度（第8和9行）。而对于劣等解，则采用欧几里得距离（EuD）以维持种群多样性（第11和12行）。

算法1: CEL范式。

3.5 CEL的优势 (Benefits of CEL)

基于上述CEL的新特性，其潜在优势讨论并强调如下。

首先，由于CEL的动机是并专注于变量特征，我们首先考虑混合函数（HyF），其中决策变量具有显著不同的特征。在HyF的构建中，几个子向量（每个来自一个相应的基本函数）被组合形成决策向量。HyF的函数适应度计算为所有基本函数适应度的总和。为作说明，图6显示了来自CEC2017测试套件[31]的30维混合函数F11和F12的决策向量组成，该图从MATLAB代码“input_data”文件夹下的“shuffle_data.txt”文件获取。从图6可以看出，F11由Zakharov函数、Rosenbrock函数和Rastrigin函数分别由6、12和12个变量组成，而F12由高条件椭圆函数、改进的Schwefel函数和弯曲雪茄函数分别由9、9和12个变量构造。利用这种特征，可以通过对变量进行分类并同时且独立地优化它们来提高优化效率。前一个分类操作旨在根据不同的特征（即收敛相对较快或较慢）对变量进行分组，从而将整个问题划分为两个截然不同的子问题，而后一个操作则独立地优化这两个子问题。这两个操作分别由CD和CI机制完成。在CD中，通过比较变量的相对多样性来捕获变量特征；而在CI中，执行SubS以实现独立优化。

其次，对于非混合函数，类似地，在所有变量中，有些可能收敛相对较快，而其他则较慢。利用SubS，通常相互冲突的收敛性和多样性维持任务被分别分配给两个组件。

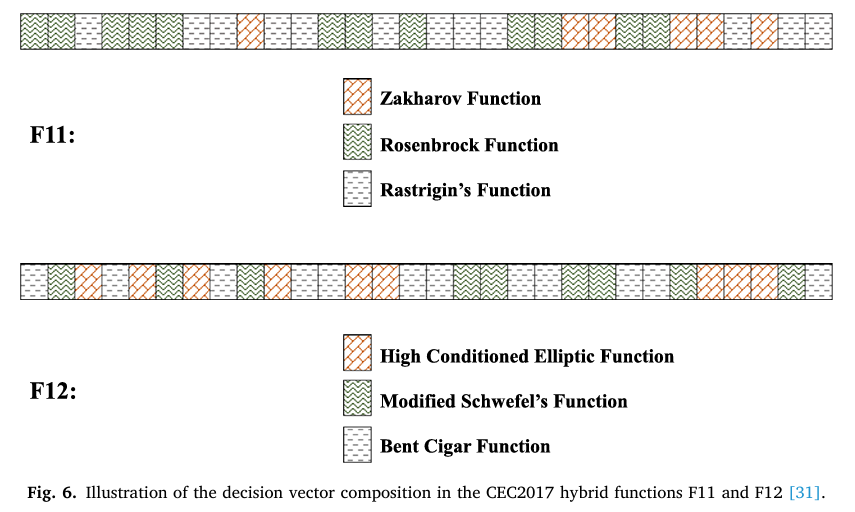
图6: CEC2017混合函数F11和F12中决策向量组成的示意图[31]。

3.6 CEL的新颖性 (Novelty of CEL)

根据以上描述，我们在此强调CEL范式的新颖性和贡献。

（1）如第2.2节所述，在现有工作中，尽管考虑了多种策略，但在竞争特征和平等特征集成范式中，每个后代都是由单一策略生成的。然而，在CEL中，后代可以来源于由不同策略生成的不同组件的组合。这使得能够为每个组件应用合适的策略，从而同时充分利用各种策略的优点。

（2）变量分解在合作协同进化方法[50,51]中被广泛用于处理大规模优化问题，该方法考虑变量间的相互作用将变量分解到不同的组中。然而，在CEL中，CD机制关注的是当前种群中每个维度的分布，而不是变量间的相互作用，并根据每个维度的多样性将变量分解为开发性和探索性组件，这与合作协同进化中的分解方法不同。（见图6下方的文字说明，此处意指CD的分解依据不同）。此外，通过考虑维度的多样性，也可以确定维度的开发和探索任务，这通常在合作协同进化中是无法实现的。

---

4. 实验仿真（Simulation）

在本节中，通过在CEC2017 [31]测试套件（包含29个具有各种数学特征的最小化函数，例如单峰、多峰、混合和组合函数）上进行的全面实验，研究所提出的CEL方法的有效性。为了比较性能，我们采用解误差值 $SE$，定义为 $f(x)-f(x^{\ast })$，其中 $f(x^{\ast })$ 是最优函数值，$f(x)$ 是在 $10^4\times D$ 次函数评估后获得的最小误差值。对于每个比较算法，执行51次独立试验，并采用5%显著性水平的Wilcoxon符号秩检验[52][57]来比较这51组结果。符号“+”、“=”和“-”分别表示基于CEL的算法性能显著优于（即赢，W）、相似于（即平，T）或差于（即输，L）被比较算法。所有算法均在MATLAB中编码，并在配备Intel Core i7-9700 CPU @ 3.00 GHz、16 GB内存和Windows 10操作系统的PC上运行。

4.1 CEL 对比 SEL-based DE

为了验证CEL的有效性，我们首先将其应用于一个基线算法EaDE（显式自适应DE）[35]，该算法的性能显著优于几种先进的DE算法，如L-SHADE [53]、SCSS-L-SHADE [30] 和 JSO [54]。EaDE基于SEL，其中后代由其中一种策略生成。因此，比较CEL-EaDE和EaDE可以清晰地揭示CEL和SEL之间的性能差异。在30维、50维和100维函数上的比较结果如表1所示。

表1：基于51次独立运行的CEL-EaDE与EaDE在CEC2017基准测试集（30维、50维及100维）上的性能比较

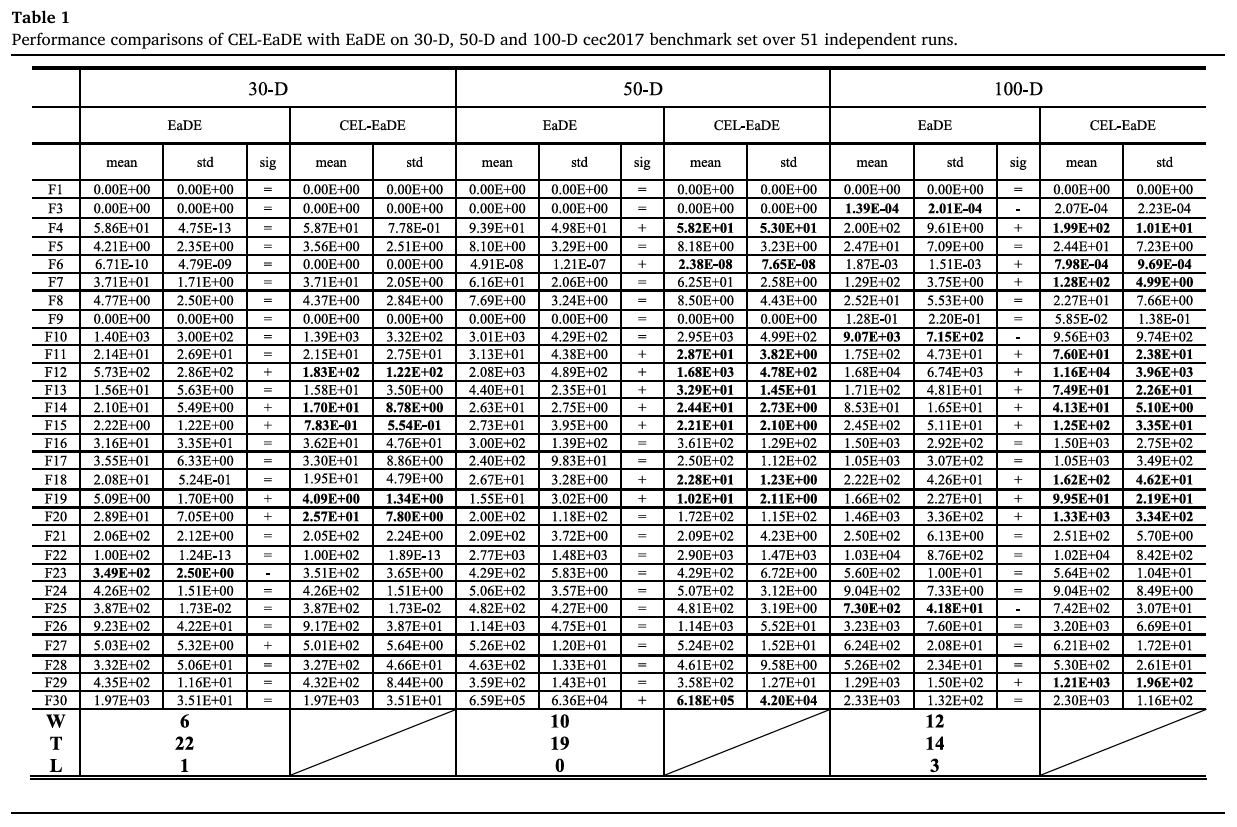
从表1中观察到以下情况：

1. CEL-EaDE在30维、50维和100维案例中的性能均优于EaDE，分别赢了6、10、12次，输了1、0、3次。对于更高维度的问题，其有效性更为显著；
2. 从表1来看，性能提升主要归功于混合函数F11-F20。具体来说，在30维案例中，CEL在五个函数（F12, F14, F15, F19, F20）上提升了性能，并在其余五个函数上性能相当。在50维案例中，CEL在七个函数（F11-F15, F18, F19）上提供了更好的性能，并在其余三个函数上性能相似。在100维函数上也可以观察到类似的优势，在八个函数（F11-F15, F18-F20）上性能更好，在两个函数（F16, F17）上性能相似；
3. 对于单峰和简单多峰函数F1, F3和F4-F10，CEL在五个案例（50-D F4, 50-D F6, 100-D F4, 100-D F6, 100-D F7）中获胜，在两个案例（100-D F3, 100-D F10）中失败。对于组合函数F21-F30，CEL在三个函数（30-D F27, 50-D F30, 100-D F29）上表现更优，在两个函数（30-D F23, 100-D F25）上表现较差。

总体而言，与EaDE相比，CEL-EaDE在混合函数上显示出显著优势，并在其他类型的函数上具有竞争力。

4.2 CEL 对比 先进的 SEL 方法

通过与以下先进的SEL方法进行比较，进一步证明了CEL的性能：

• Meval：对于每个目标解，使用函数评估来评估候选解，并选择最适应的一个作为后代；
• CSM：对于每个目标解，通过廉价代理模型（Cheap Surrogate Model）[28]从候选解中确定后代；
• UM：对于每个目标解，通过低估模型（Underestimation Model）[29]从候选解中确定后代；

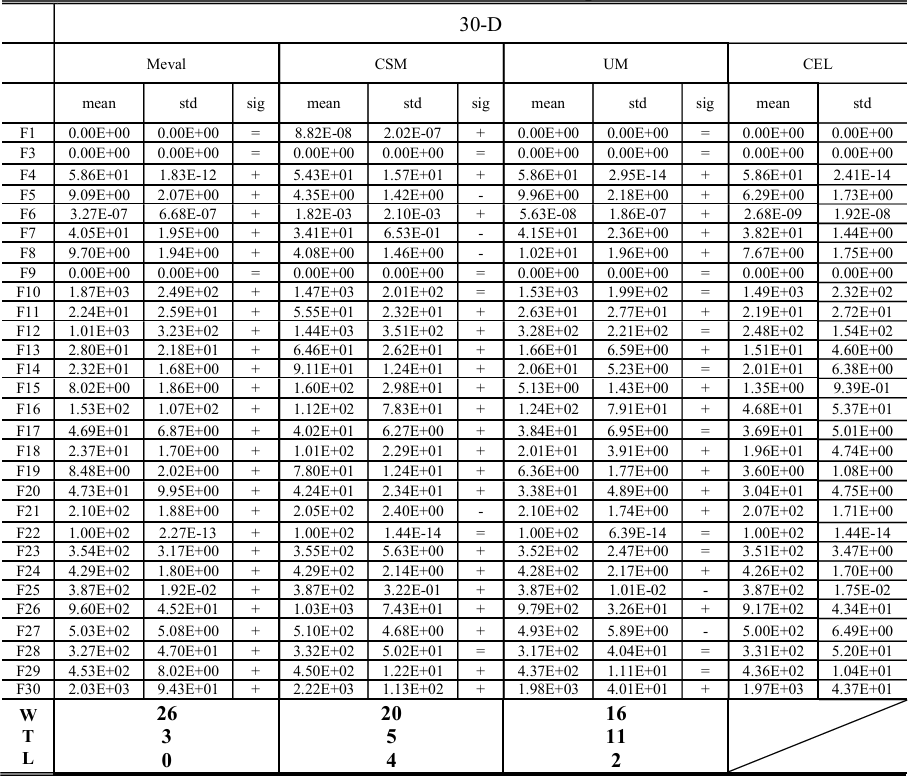
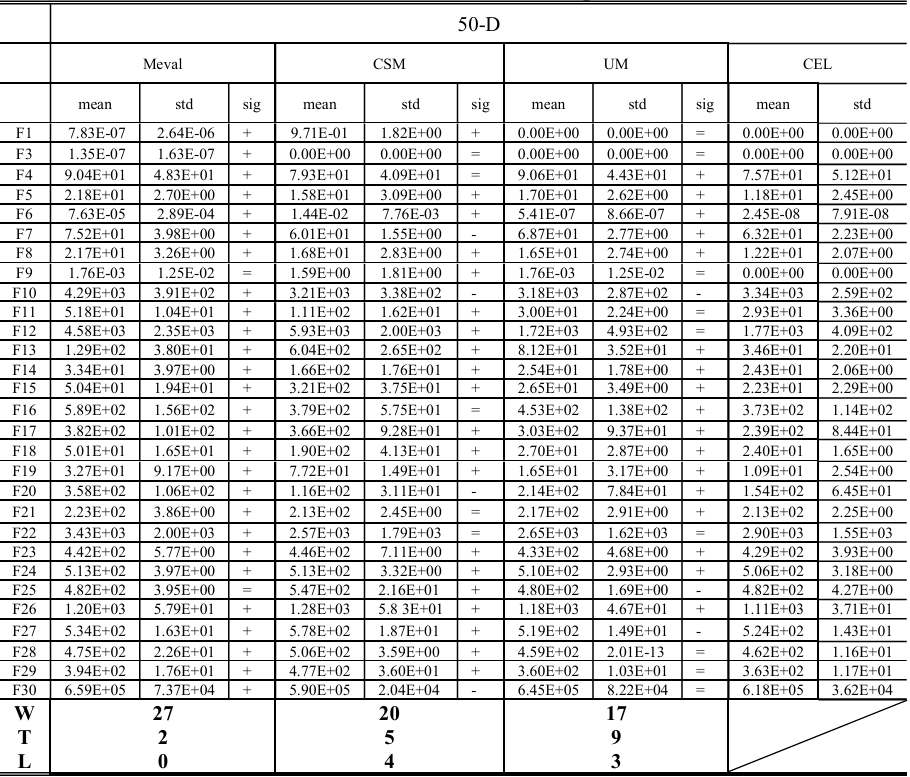
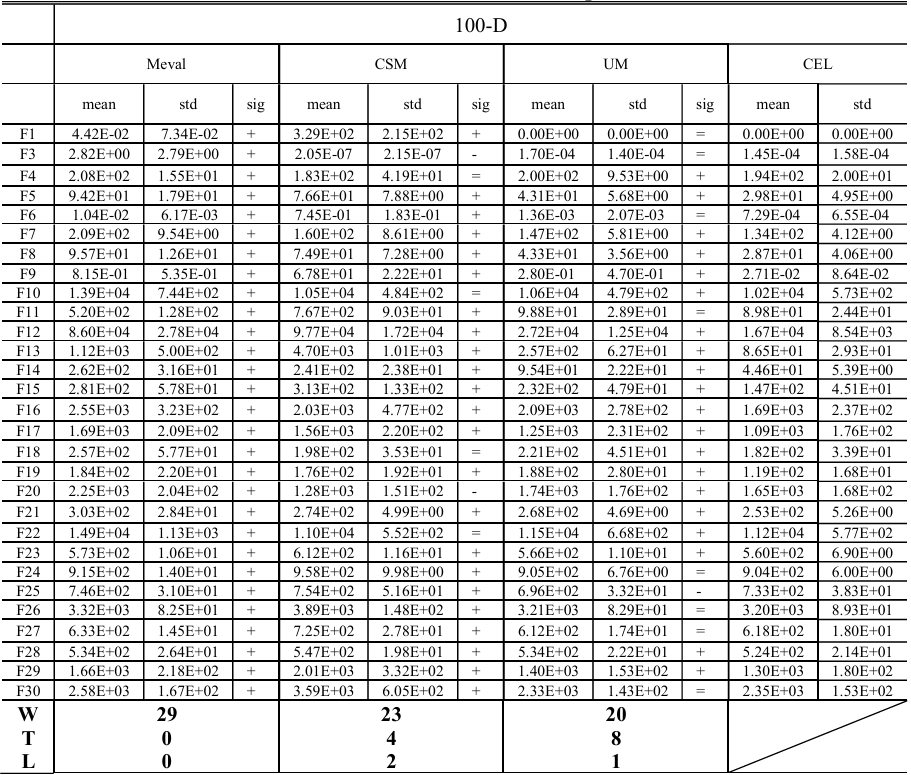
Meval和CSM不需要特定的参数设置，而UM中支持向量的斜率控制参数 $C$ 根据原始文献设置为10,000。所有比较方法和CEL都在L-SHADE [53]上实现。CEL与Meval、CSM和UM的性能比较在 补充文件（Supplementary materials） 的表S1中给出，并在表2中进行了总结。与Meval相比，CEL在30维、50维和100维函数上分别赢了26、27和29个案例，没有输掉任何案例。与CSM相比，CEL在总共87个案例中的63个案例中表现更好，在10个案例中表现较差（包括30维的F5, F7, F8, F21；50维的F7, F10, F20, F30；100维的F3, F20）。相对于UM，CEL在53个案例中具有优势，在6个案例中失利。具体来说，UM更适合解决30维和50维的F27、50维的F10、30维、50维和100维的F25，而CEL在大多数其他案例中表现更好。

表2：在30维、50维和100维CEC2017基准问题上与基于SEL方法的比较结果。

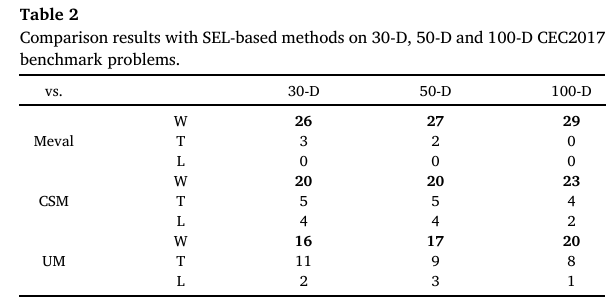
为了展示整体性能，图7绘制了所有比较方法在所有考虑函数上针对归一化解误差（NSE）的经验累积分布函数（ECDF）图。ECDF的定义在补充文件中提供。较大的ECDF值对应更好的性能。从图7可以观察到，对于所有的NSE值，CEL获得的ECDF曲线始终位于Meval和CSM之上。与UM相比，当NSE小于0.83时，CEL 始终更好，而当NSE大于0.83时，两者性能相似。

图7：CEL与其他比较方法（Meval, CSM, UM）所达到的ECDF。

4.3 时间复杂度比较 (Comparison of time complexity)

多样性计算和多样性排名的时间复杂度分别为 $O(NP\ast D)$ 和 $O(D\ast {\log }_{2}D)$。因此，SubS的开销是 $O(D\ast (NP+{\log }_{2}D))$。关于MaD，计算协方差矩阵和逆矩阵的复杂度分别为 $O(NP\ast D^2)$ 和 $O(D^3)$。因此，MaD的开销是 $O((NP+D)\ast D^2)$。因此，当NP设置为D的倍数时，基于CEL的DE在每一代的时间复杂度为 $O(D^3)$，这高于Meval的 $O(D^2)$。而与CSM和UM相比，由于它们在每一代的复杂度为 $O(N{P}^2\ast D)$ [28, 29]，当NP显著大于D时，CSM和UM的复杂度高于CEL。当NP小于D时，CEL的复杂度更高。

为了实验研究时间复杂度，采用了[31]中建议的方法，如下所述。

$T_0$ 是计算以下测试程序所需的时间：

for i = 1:1,000,000
x = 0.55 + (double) i;
x = x + x; x = x/2; x = x*x; x=sqrt(x); x=log(x); x=exp(x);
x = x/(x + 2);
end

$T_1$ 是在F18上进行200,000次函数评估所需的时间。$T_2$ 是一个算法使用200,000次评估解决F18五次运行的平均时间。$(T_2-T_1)/T_0$ 衡量了算法的复杂度。本实验考虑了30维和100维问题。

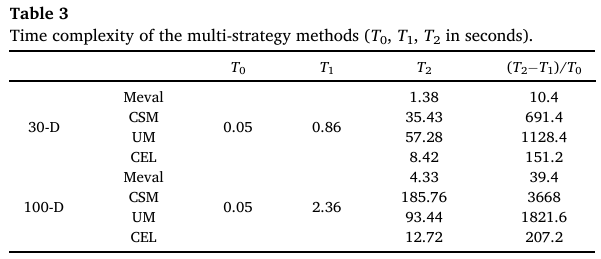
表3显示了第4.2节中算法的实验结果，从中可以看出，在30维和100维案例中，Meval的复杂度最低，在30维案例中依次是CEL、CSM和UM，在100维案例中依次是CEL、UM和CSM。

表3：多策略方法的时间复杂度（$T_0$, $T_1$, $T_2$ 单位为秒）。

4.4 CEL 用于改进先进的 DEs (CEL for advancing state-of-the-art DEs)

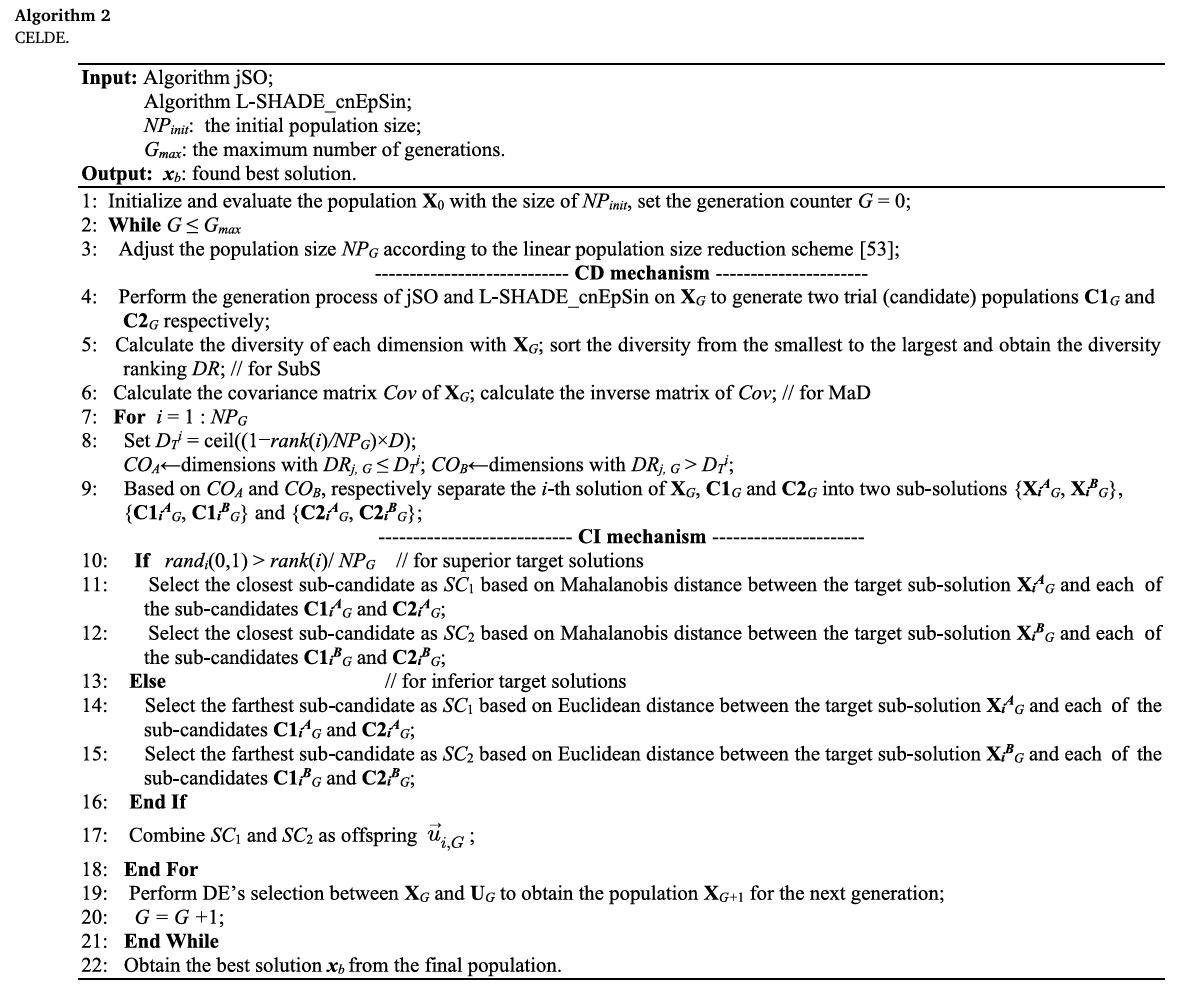
研究CEL对具有不同优势的先进DEs的贡献也很有意义。为此，将CEC2017竞赛中表现顶级的DEs——L-SHADE_cnEpSin [55] 和 JSO [54]——视为基线，得到的变体命名为CELDE。遵循CEL的过程（算法1），CELDE的伪代码如算法2所示。

算法2：CELDE

从表4可以看出，CELDE的性能优于基线DEs。更具体地说，与L-SHADE_cnEpSin相比，CELDE在50个函数上表现出优势，在8个函数上存在劣势。相对于JSO，CELDE在48个案例中表现更优，在3个案例中表现较差。考虑到函数类型，CELDE在两个基线的简单多峰、混合和组合函数上表现更优，在单峰函数上性能相当。关于维度，可以观察到CELDE的优越性对于更高维函数更为显著。

表4：CELDE与基线在30维、50维和100维CEC2017基准集上经过51次独立运行的性能比较。

为了进一步证明CELDE的性能，考虑了其他六个先进的DEs。它们是：PaDE [13]（一种具有新参数自适应机制的改进L-SHADE算法）；EBL-SHADE [21]（一种具有新变异策略的增强L-SHADE算法）；EaDE [37]；L-SHADE-RSP [56]（一种增强的JSO算法，是CEC2018竞赛中排名第一的DE）；EJADE [48]（一种具有两种交叉策略的改进JADE算法）；以及DTDE [15]（一种基于域变换的DE变体）。比较算法的参数设置根据原始文献进行设置。

从表5所示的比较结果来看，CELDE在总体上优于大多数竞争对手。具体来说，在30维案例中，与PaDE、EBL-SHADE、EaDE、L-SHADE-RSP和EJADE相比，“赢/输”（W/L）指标分别为“12/7”、“9/7”、“9/5”、“12/6”和“17/5”。与DTDE相比，CELDE在8个函数上表现更好，但在10个函数上失利。CELDE的性能优势在50维和100维案例中更为显著，相对于PaDE、EBL-SHADE、EaDE、L-SHADE-RSP、EJADE和DTDE的“W/L”分别变为“41/6”、“42/9”、“36/8”、“30/7”、“49/2”和“28/25”。

表5：CELDE与六个先进DE在30维、50维和100维CEC2017基准集上经过51次独立运行的性能比较。



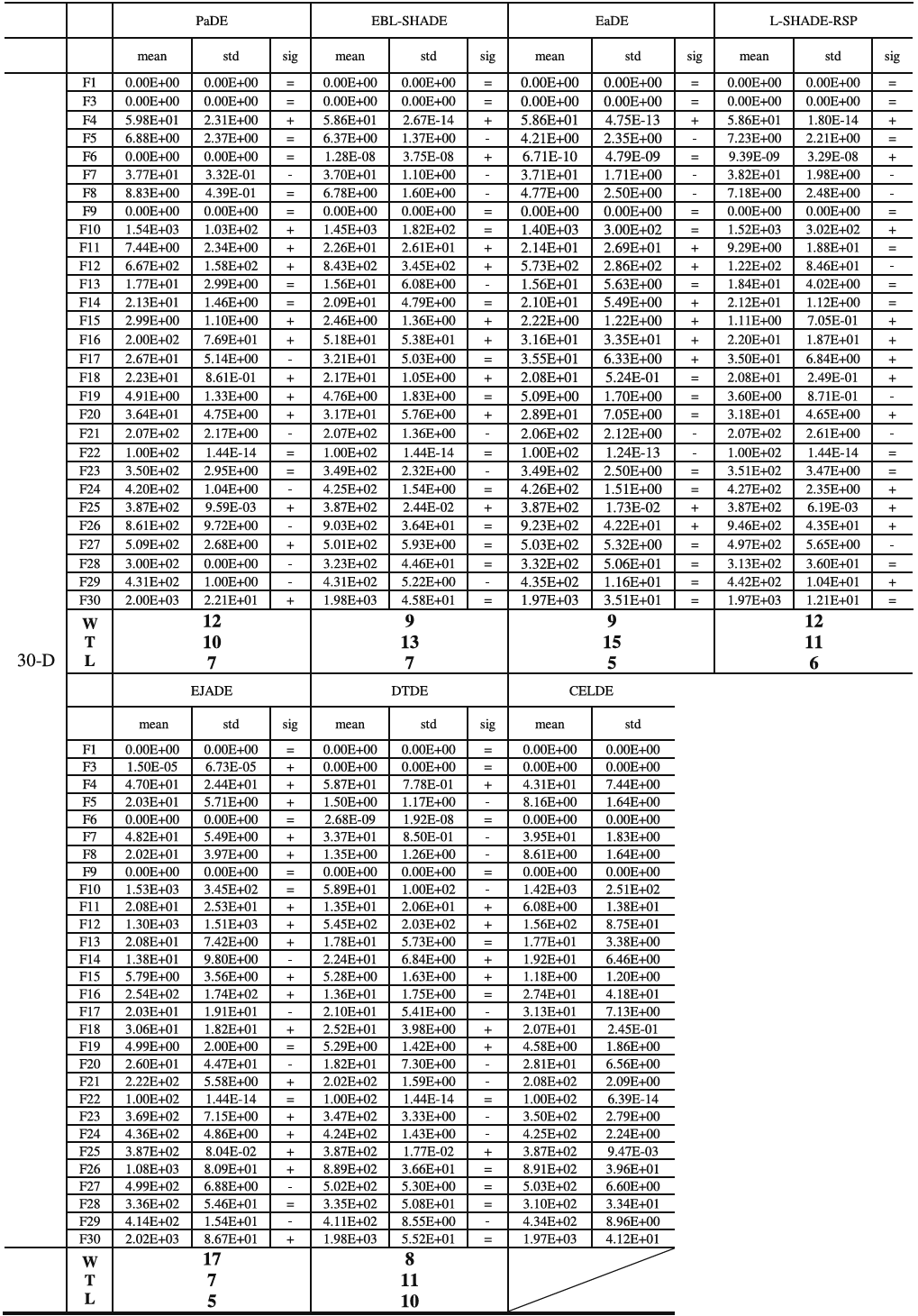
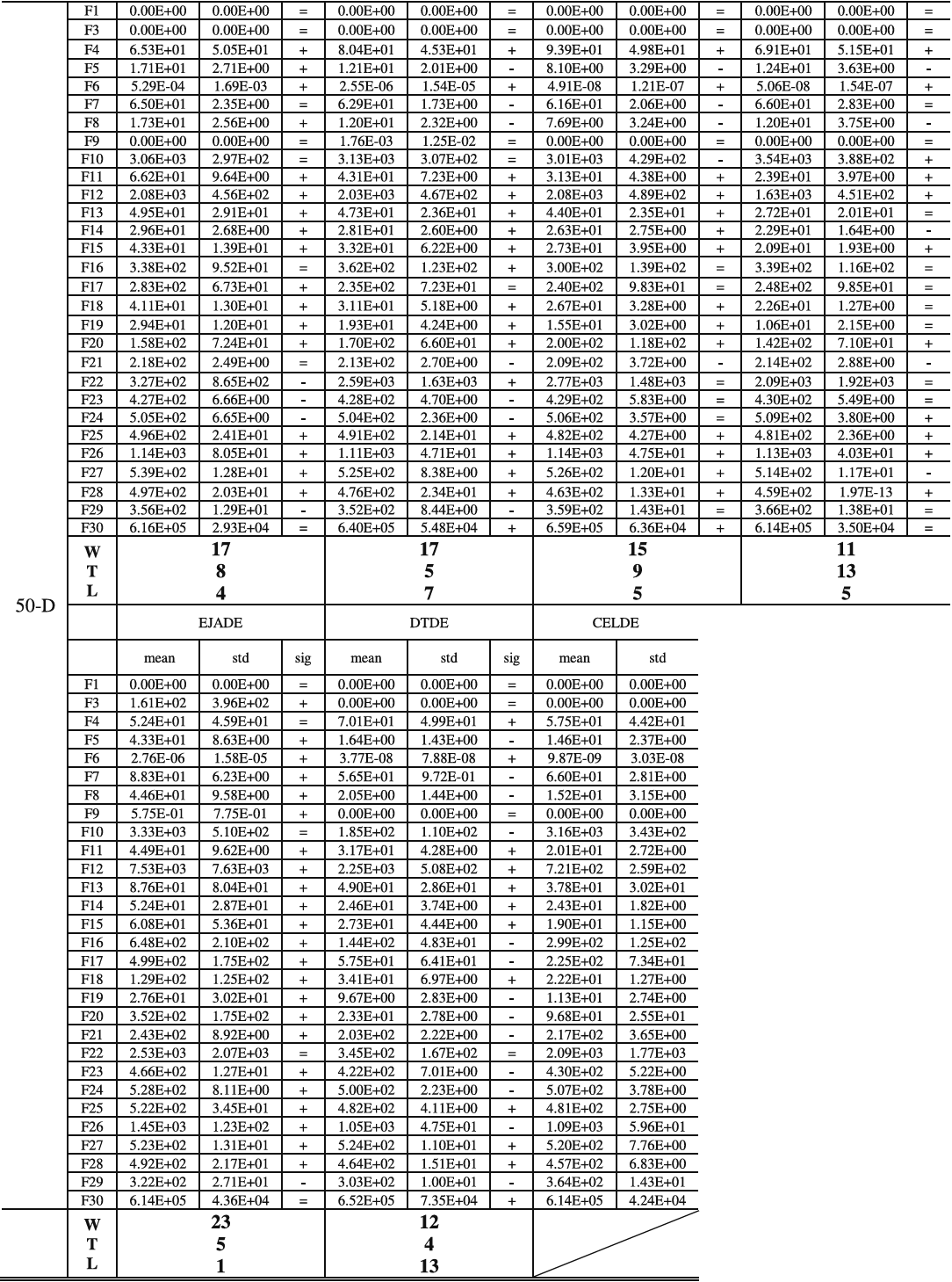
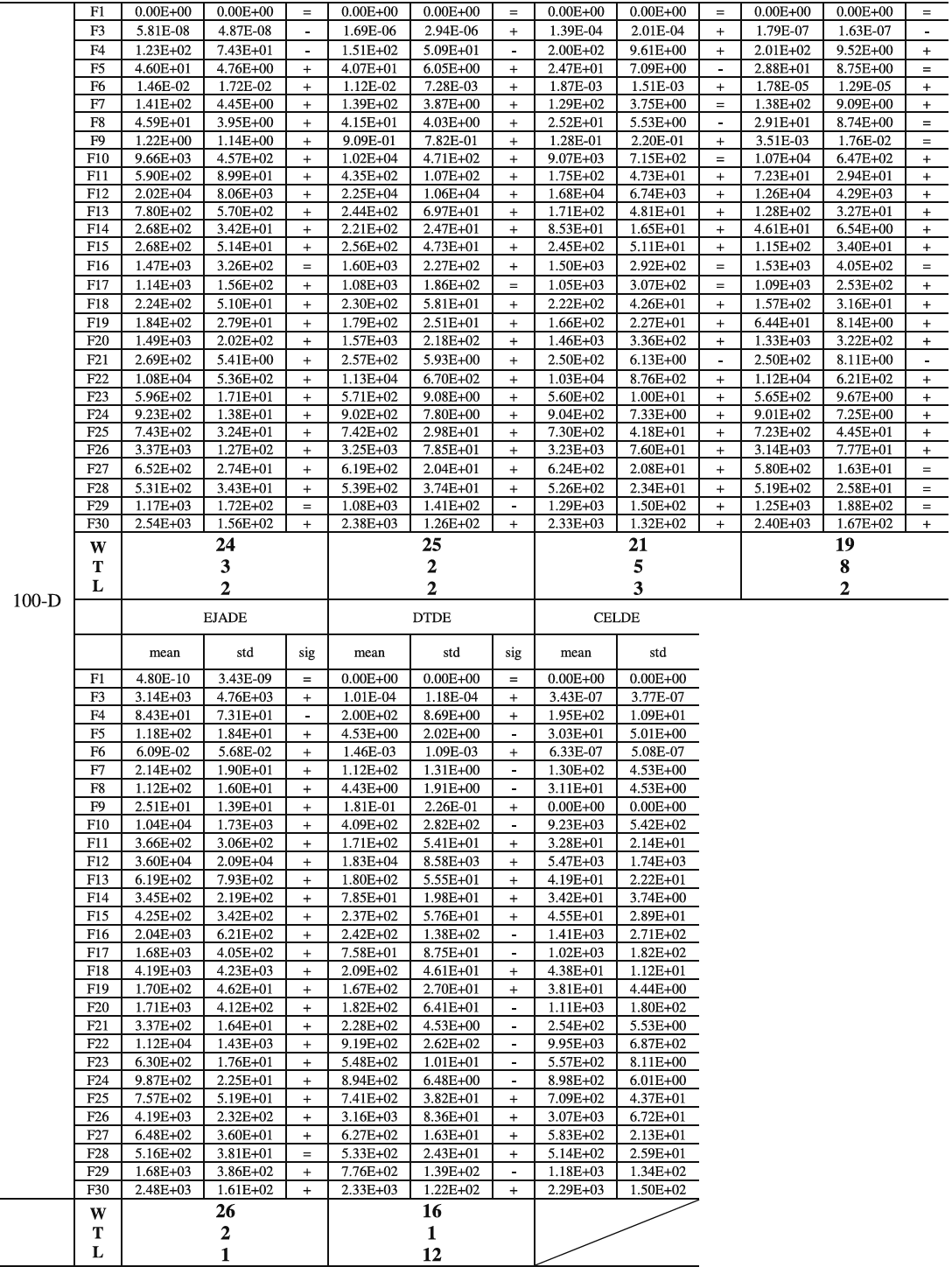
为了得出统计结论，表6显示了多问题Wilcoxon检验结果，从中可以看出CELDE在统计上优于L-SHADE_cnEpSin、JSO、PaDE、EBL-SHADE、EaDE、L-SHADE-RSP和EJADE。而与DTDE性能相当。图8显示了整体性能排名，其中CELDE取得了最佳的排名值3.32。可以观察到，原始基线，即L-SHADE_cnEpSin和JSO，性能差于L-SHADE-RSP和DTDE。而通过CEL，CELDE的排名值小于L-SHADE-RSP和DTDE。这证实了所提出的CEL方法的贡献。

表6：根据多问题Wilcoxon检验的CELDE与先进DEs的整体性能比较。

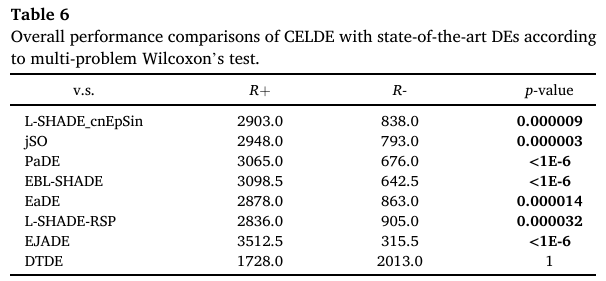
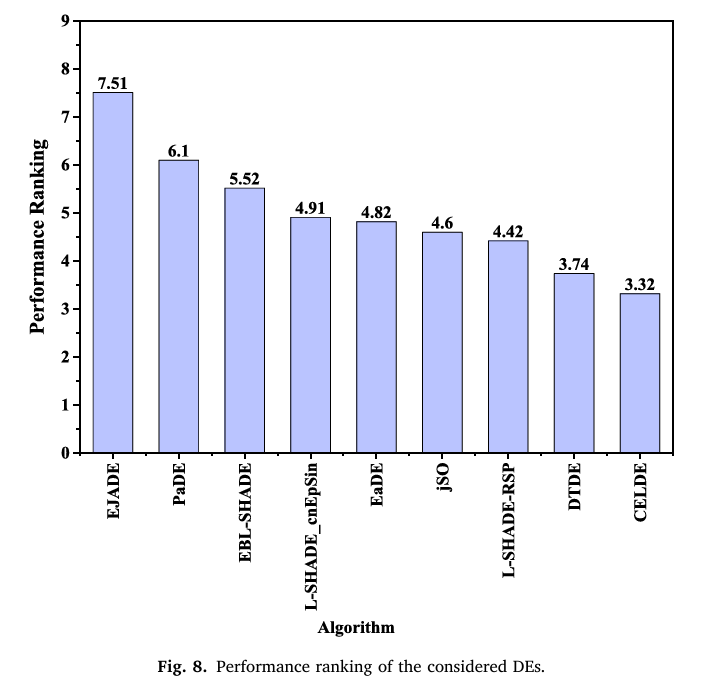
图8：所考虑DE的性能排名。

4.5 CEL 中各机制的益处 (Benefit of the mechanisms in CEL)

CEL的特点是子相似性（SubS）选择规则和基于马氏距离（MaD）的相似性选择。为了评估每个单独机制对性能提升的贡献，构建了以下两个仅包含单一机制的变体：

• wo-SubS：该变体通过停用SubS但保留MaD来构建（“wo”表示“without”）。具体来说，在个体级别执行相似性选择（SS），并选择其中一个单一的候选解。
• wo-MaD：该变体保留SubS，但将马氏度量替换为欧几里得度量。

除了上述差异，所有其他设置与CEL保持相同。性能比较在补充文件的表S2和表S3中显示，比较结果汇总在表7中。

表7：在30维、50维和100维CEC2017基准问题上与单一机制变体的比较结果。

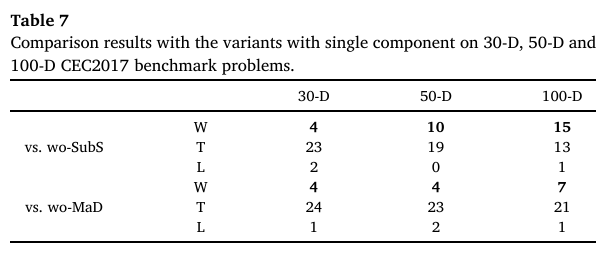
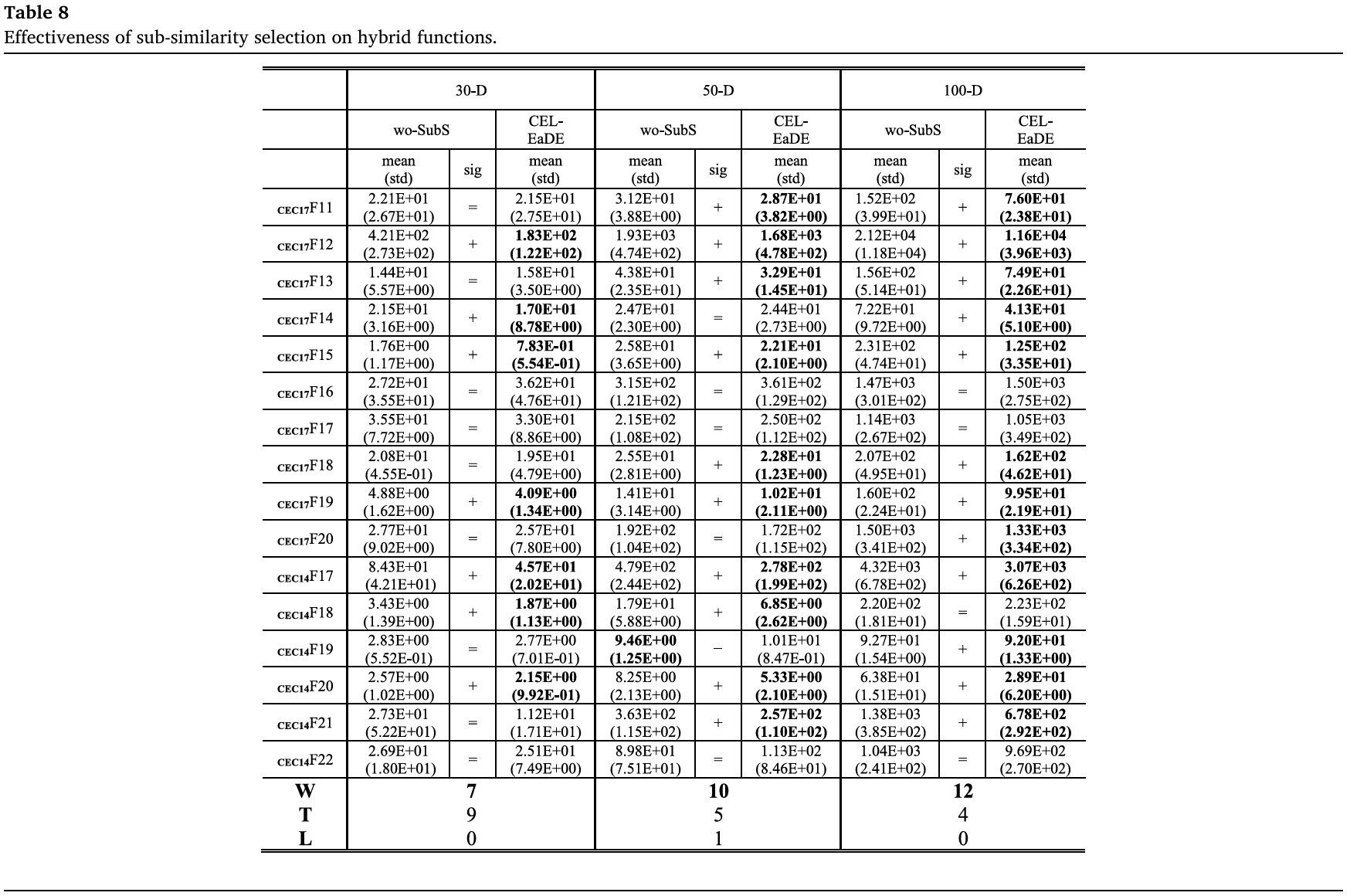
(1) 与 wo-SubS 的比较：从表7可以看出，在所有的30维、50维和100维案例中，CEL-EaDE的性能始终优于wo-SubS，“赢/输”（W/L）指标分别为“4/2”、“10/0”和“15/1”。更具体地说，从表S2可以看出，在30维案例中，SubS在四个混合函数F12、F14、F15和F19上改善了性能，在两个组合函数F23和F25上表现较差，而在单峰和简单多峰函数上性能相似。在50维案例中，SubS在混合函数、单峰和简单多峰函数以及组合函数上分别提升了6个（F11-F13, F15, F18, F19）、2个（F4, F6）和2个（F21, F27）案例的性能，没有在任何案例上失利。在100维函数上，SubS在混合函数上的优势更为显著，在八个函数（F11-F15, F18-F20）上都有改进。在简单多峰函数上，SubS在F4、F6、F7和F9上取得了更好的性能。而在组合函数上，SubS在F26、F28和F30上更优，在F21上较差。总体而言，SubS在混合函数上的性能符合预期。此外，随着维度的增加，其优势更为显著，这表明SubS更适合解决多变量问题。除了CEC2017混合函数，表8还进一步展示了在六个CEC2014 [58]混合函数F17-F22上的性能。在这些函数上也可以观察到类似的性能提升。考虑到所有48个混合函数案例，SubS在29个案例中表现更优，仅在1个案例中表现较差。

表8：子相似性选择在混合函数上的有效性。

为了深入了解优化过程，我们在每一代分别使用SubS和SS来选择它们对应的后代，并比较两个后代的适应度。“SubS (S)”表示由SubS为优等目标解选择的后代适应度优于由SS选择的后代的总次数，而“SS (S)”表示由SS为优等目标解选择的后代适应度优于由SubS选择的后代的总次数。“SubS (I)”和“SS (I)”是类似的定义，针对劣等目标解的后代。图9显示了在29个50维CEC2017函数上这些指标的对比。一方面，比较SubS (S)和SS (S)，可以观察到在除F1、F4和F25之外的26个函数上，SubS (S)大于或相当于SS(S)，这意味着对于优等目标解，SubS比SS更能生成有希望的后代。此外，可以发现在混合函数F11-F15、F18和F19上的优势更为显著，这与表8中显示的性能优势高度相关。另一方面，比较SubS (I)和SS (I)，在大多数函数上SubS (I)小于SS (I)。由于较小的值会探索更多的搜索区域，这表明与SS相比，SubS鼓励对劣等目标解进行更多的探索。总之，与SS相比，在大多数考虑的函数上，SubS增强了对优等解的开发，同时保持了对劣等解的多样性。

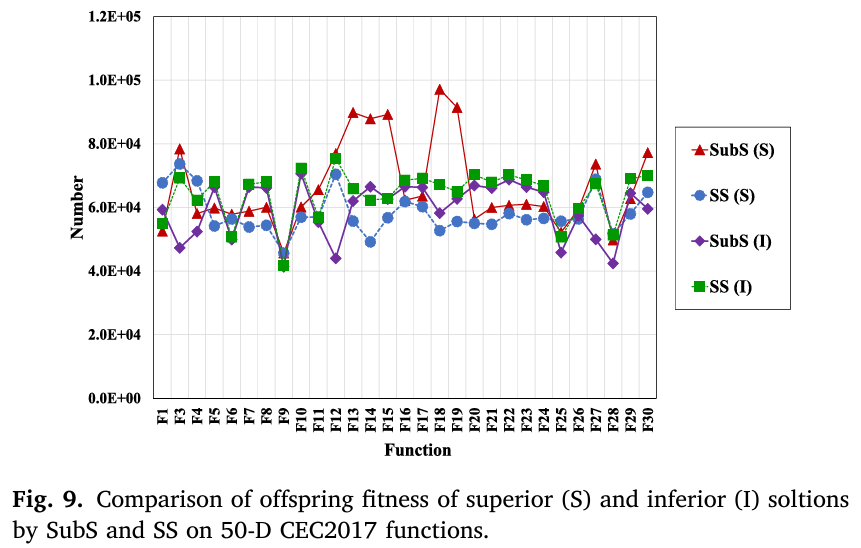
图9：在50维CEC2017函数上，通过SubS和SS选择的优等(S)和劣等(I)解的后代适应度比较。

(2) 与 wo-MaD 的比较：从表7可以看出，在30维、50维和100维函数上，MaD分别在4、4、7个案例中表现出比EuD更好的性能，分别在1、2、1个案例中表现较差。从表S3可以看出，大部分改进（共13个案例 = 3(30维) + 3(50维) + 7(100维)）发生在混合函数上。

为了深入了解优化过程，我们在每一代分别使用MaD和EuD独立确定后代，并比较它们的适应度。图10显示了在29个50维CEC2017函数上MaD和EuD的对比，其中“MaD”表示由MaD选择的后代适应度优于由EuD选择的后代的总次数，而“EuD”表示由EuD选择的后代适应度优于由MaD选择的后代的总次数。从图10可以证实，MaD在所有考虑的函数上都获得了比EuD更多的适应度更优的后代数量，这意味着它能更好地预测候选解的适应度优越性。

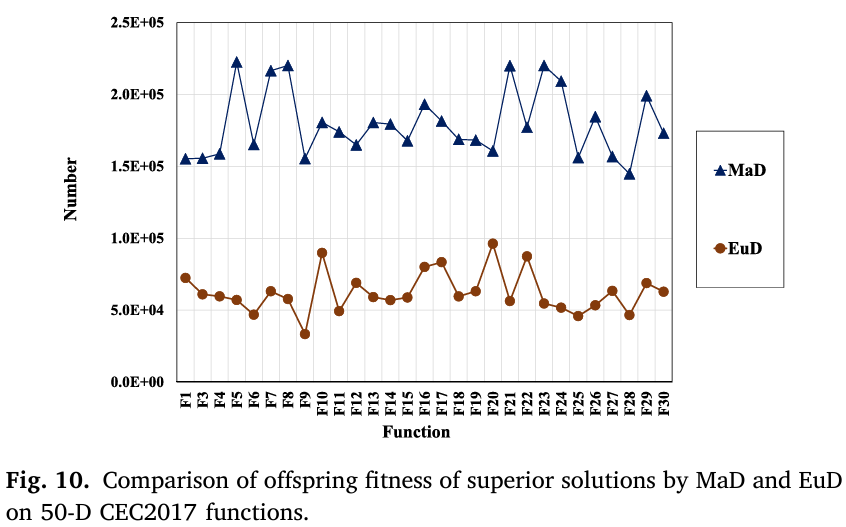
图10：在50维CEC2017函数上，由MaD和EuD选择的更优后代数量对比。

4.6 组件分解中多样性排名的有效性 (Effectiveness of the diversity ranking in component decomposition)

在组件分解中，整个决策向量根据每一代的多样性排名进行划分。构建了Variant-Random变体来验证利用变量多样性排名进行分组的有效性。为此，在Variant-Random中，决策变量在每一代随机排序。

补充文件的表S4呈现了比较结果。通过与Variant-Random的比较（“赢/输”指标为“8/0”），证实了利用变量多样性度量进行分组的有效性。改进主要体现在混合函数上，有六个案例（包括F12-F15, F18和F19）。此外，它还在简单多峰函数F4和组合函数F30上提升了性能。这些改进的根本原因在于多样性的排序过程将变量按顺序排列。为了提供实验证据，我们记录了每一代每个维度的多样性排名 $DR$ （$DR=d_{j,G}$），最终得到每个维度在整个进化过程中的平均 $DR$（记为 $aDR$）。$aDR$ 进一步按升序排序，其中 ranking = 1 和 ranking = $D$ 分别表示整体最小和最大的多样性。使用CEL-EaDE在30维F11-F20上进行了实验，维度的整体多样性排名如图11所示。从该图中观察到以下几点：

1. 当包含一个单峰函数作为基本函数时，相应维度的多样性排名远小于多峰函数。例如包括F11中的单峰Zakharov函数，F12、F14和F18中的单峰高条件椭圆函数，F12、F13、F15和F19中的单峰弯曲雪茄函数，F18中的单峰Discus函数。
2. 同一基本函数在不同混合函数中的多样性排名可能显著不同。例如，改进的Schwefel函数在F17中具有小的多样性排名值，而在F12中具有大的值。Rosenbrock函数在F16中具有小的多样性排名值，而在F15中具有大的值。这取决于基本函数之间的相对难度。
3. 多样性排名操作清楚地区分了来自不同基本函数的变量。例如，在包含四个基本函数的F16上，根据多样性升序的分组顺序是：Rosenbrock函数 → HGBat函数 → 改进的Schwefel函数 → 扩展的Schaffer F6函数。在F20上，尽管有多达六个基本函数，多样性顺序也很清晰：Happycat函数 → 改进的Schwefel函数 → Katsuura函数 → Rastrigin函数 → Schaffer的F7函数 → Ackley函数。
4. 一些多峰函数，如Schaffer和Ackley， consistently产生大的多样性排名，例如在F14、F16-F18和F20上。

对于CEC2014混合函数F17-F22，也可以得出类似的结论，如图12所示。

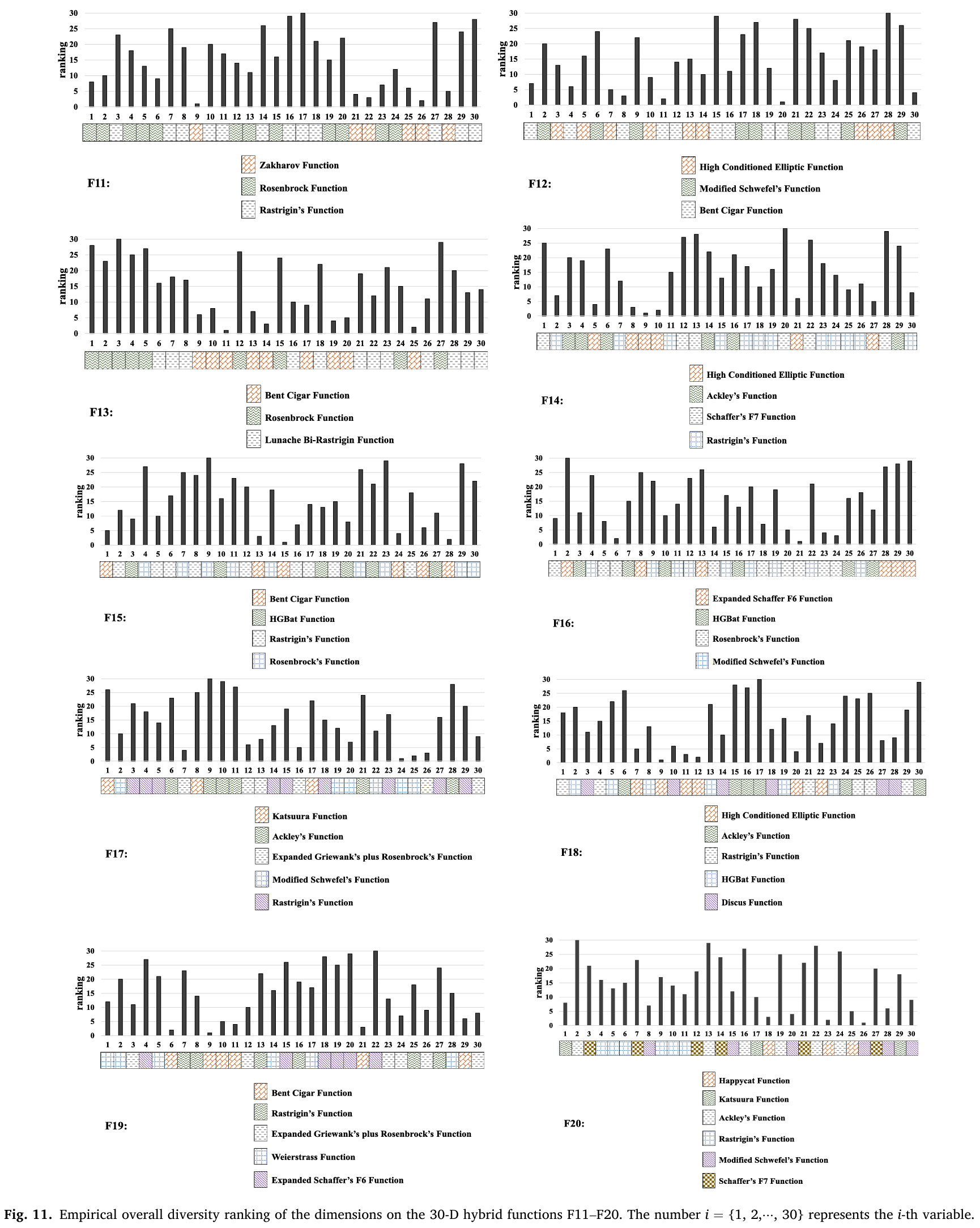
图11：在30维混合函数F11-F20上维度的经验整体多样性排名。数字 i = {1, 2,…, 30} 代表第 i 个变量。

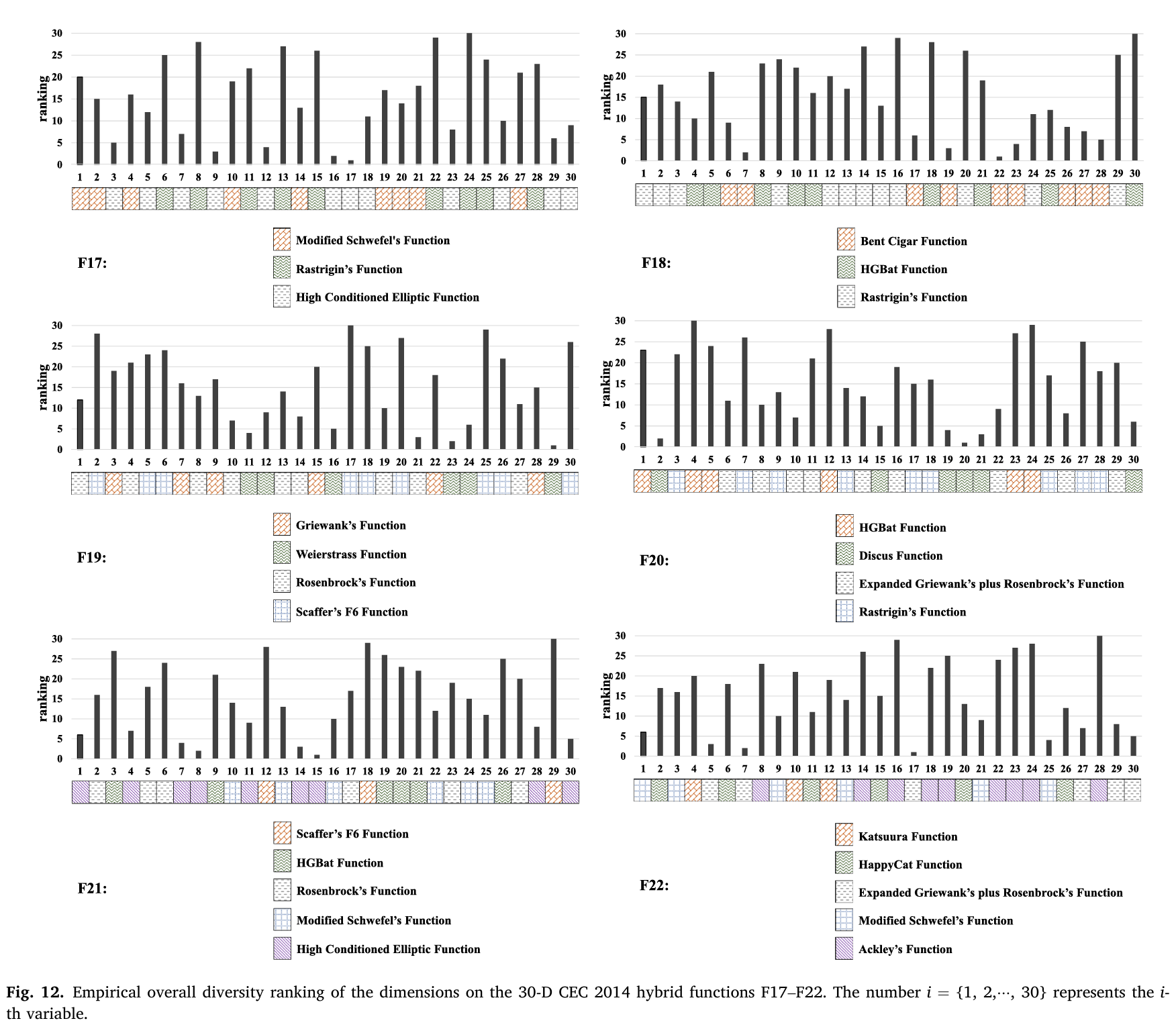
图12：在30维CEC2014混合函数F17-F22上维度的经验整体多样性排名。数字 i={1,2,…,30}i = \{1, 2, \ldots, 30\}i={1,2,…,30} 代表第 $i$ 个变量。

---

5. 结论

本文中，我们提出了一种称为集体集成学习（CEL） 的范式，用于全局优化。在CEL的组件分解（CD） 中，通过多样性排名（diversity ranking） 操作将决策向量分类为开发性组件和探索性组件。接着，在组件集成（CI） 中，执行子相似性（sub-similarity） 计算，以在目标解与由多种策略生成的候选解之间的每个组件内部进行，从而选择合适的组件。CEL中的最终后代是来自候选解的组件的集体整合（collective integration）。为了进一步改进用于衡量局部开发性和探索性特征的相似性度量，对优等解执行了基于马氏距离（Mahalanobis distance） 的相似性选择，以提高预测精度。所提出的CEL将优化问题分解为两个子问题，并根据其各自的特征分别且同时地对它们进行优化。

通过实验验证了CEL的有效性以及每个独立机制的贡献。性能提升的深层原因也通过实证研究得以揭示和解释。正如实验所证实的那样，CEL的性能优于几种现有的SEL方法。CELDE显著改进了基线DEs，并在统计上优于几种先进的DEs。

关于未来的工作，CEL可能会扩展到其他类型的进化算法（EAs）。此外，其在解决其他类型优化问题方面的有效性，例如多目标优化、多模态优化和约束优化[59, 60, 61]，也需要进一步研究。

• PaDE的代码可从 https://sites.google.com/view/zhengyumeng 获取；
• EBL-SHADE的代码可从 https://sites.google.com/view/optimization-project/files 获取；
• JSO, L-SHADE_cnEpSin 和 L-SHADE-RSP的代码可从 https://github.com/P-N-Suganthan 获取；
• EaDE 和 DTDE的代码可从 https://zszhomepage.github.io 获取。

---

补充材料（Supplementary materials）

ECDF的定义（DEFINITION OF ECDF）

示例：如果算法 A 的 ECDF 在 $x=3$ 时达到 $0.8$，表示 $80\%$ 的实验中，其 $NSE\le 0.3$；若算法 B 在相同 $x$ 处只有 0.5，则说明 A 更优。

表S1

表S1 CEL与基于SEL的方法在30维、50维和100维CEC2017基准测试集上51次独立运行的性能比较

---

参考文献

[1] R. Storn, K. Price, Differential evolution–A simple and efficient heuristic for global optimization over continuous spaces, J. Global. Optim. 11 (1997) 341–359.
[2] S. Das, S.S. Mullick, P.N. Suganthan, Recent advances in differential evolution—An updated survey, Swarm. Evol. Comput. 27 (2016) 1–30.
[3] R.D. Al-Dabbagh, F. Neri, N. Idris, M.S. Baba, Algorithm design issues in adaptive differential evolution: Review and taxonomy, Swarm. Evol. Comput. 43 (2018) 284–311.
[4] K.R. Opara, J. Arabasb, Differential evolution: A survey of theoretical analyses, Swarm. Evol. Comput. 44 (2019) 546–558.
[5] G. Wu, R. Mallipeddi, P.N. Suganthan, Ensemble strategies for population-based optimization algorithms – A survey, Swarm. Evol. Comput. 44 (2019) 695–711.
[6] J. Zhang, A.C. Sanderson, JADE: Adaptive differential evolution with optional external archive, IEEE Trans. Evol. Comput. 13 (2009) 945–958.
[7] M. Yang, et al., Differential evolution with auto-enhanced population diversity, IEEE Trans. Cybernet. 45 (2015) 302–315.
[8] G. Li, Q. Zhang, Z. Wang, Evolutionary competitive multitasking optimization, IEEE Trans. Evolut. Comput. 26 (2022) 278–289.
[9] L.M. Zheng, S.X. Zhang, K.S. Tang, S.Y. Zheng, Differential evolution powered by collective information, Inf. Sci. 399 (2017) 13–29.
[10] Y.T. Li, T. Han, X.F. Wang, H. Zhou, S.Q. Tang, MjSO: A modified differential evolution with a probability selection mechanism and a directed mutation strategy, Swarm Evol. Comput. 78 (2023) 101294.
[11] X.-G. Zhou, C.-X. Peng, J. Liu, Y. Zhang, G.-J. Zhang, Underestimation-assisted global-local cooperative differential evolution and the application to protein structure prediction, IEEE Trans. Evol. Comput. 24 (2020) 536–550.
[12] R. Tanabe, A. Fukunaga, Reviewing and benchmarking parameter control methods in differential evolution, IEEE Trans. Cybernet. 50 (2020) 1170–1184.
[13] Z. Meng, J.-S. Pan, K.-K. Tseng, PaDE: An enhanced differential evolution algorithm with novel control parameter adaptation schemes for numerical optimization, Knowl. Based Syst. 168 (2019) 80–99.
[14] J. Sun, X. Liu, T. Ba ̈ck, Z. Xu, Learning adaptive differential evolution algorithm from optimization experiences by policy gradient, IEEE Trans. Evol. Comput. 25 (2021) 666–680.
[15] S.X. Zhang, Y.N. Wen, Y.H. Liu, L.M. Zheng, S.Y. Zheng, Differential evolution with domain transform, IEEE Trans. Evol. Comput. 27 (2023) 1440–1455.
[16] D.H. Wolpert, W.G. Macready, No free lunch theorems for optimization, IEEE Trans. Evol. Comput. 1 (1997) 67–82.
[17] A.K. Qin, V.L. Huang, P.N. Suganthan, Differential evolution algorithm with strategy adaptation for global numerical optimization, IEEE Trans. Evol. Comput. 13 (2009) 398–417.
[18] R. Mallipeddi, P. Suganthan, Q. Pan, M. Tasgetiren, Differential evolution algorithm with ensemble of parameters and mutation strategies, Appl. Soft. Comput. 11 (2011) 1679–1696.
[19] Z.-Z. Liu, et al., An adaptive framework to tune the coordinate systems in natureinspired optimization algorithms, IEEE Trans. Cybernet. 49 (2018) 1403–1416. [20] S. Gao, Y. Yu, Y. Wang, J. Wang, J. Cheng, M. Zhou, Chaotic local search-based differential evolution algorithms for optimization, IEEE Trans. Syst., Man, Cybern., Syst 51 (2021) 3954–3967.
[21] A.W. Mohamed, A.A. Hadi, K.M. Jambi, Novel mutation strategy for enhancing SHADE and LSHADE algorithms for global numerical optimization, Swarm. Evol. Comput. 50 (2019) 100455.
[22] G. Wu, Mallipeddi R, P.N. Suganthan, et al., Differential evolution with multipopulation based ensemble of mutation strategies, Inf. Sci. 329 (2016) 329–345. [23] L. Tang, Y. Dong, J. Liu, Differential evolution with an individual-dependent mechanism, IEEE Trans. Evol. Comput. 19 (2015) 560–574.
[24] S.X. Zhang, S.Y. Zheng, L.M. Zheng, An efficient multiple variants coordination framework for differential evolution, IEEE Trans. Cybernet. 47 (2017) 2780–2793.
[25] A. Ghosh, S. Das, A. Das, L. Gao, Reusing the past difference vectors in differential evolution—A simple but significant improvement, IEEE Trans. Cybernet. 50 (2020) 4821–4834.
[26] Z.H. Zhan, Z.J. Wang, H. Jin, et al., Adaptive distributed differential evolution, IEEE Trans. Cybernet. 11 (2020) 4633–4647.
[27] Y. Wang, Z. Cai, Q. Zhang, Differential evolution with composite trial vector generation strategies and control parameters, IEEE Trans. Evol. Comput. 15 (2011) 55–66.
[28] W. Gong, A. Zhou, Z. Cai, A multi-operator search strategy based on cheap surrogate models for evolutionary optimization, IEEE Trans. Evol. Comput. 19 (2015) 746–758.
[29] X. Zhou, G. Zhang, Differential evolution with underestimation-based multimutation strategy, IEEE Trans. Cybernet. 49 (2018) 1353–1364.
[30] S.X. Zhang, W.S. Chan, Z.K. Peng, S.Y. Zheng, K.S. Tang, Selective-candidate framework with similarity selection rule for evolutionary optimization, Swarm Evol. Comput. 56 (2020) 100696.
[31] N.H. Awad, M.Z. Ali, J.J. Liang, B.Y. Qu, P.N. Suganthan, Problem Definitions and Evaluation Criteria For the CEC 2017 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization, Nanyang Technol. Univ., Singapore, 2016. Nov.
[32] W. Gong, A ́. Fialho, Z. Cai, H. Li, Adaptive strategy selection in differential evolution for numerical optimization: An empirical study, Inf. Sci. 181 (2011) 5364–5386.
[33] D. Thierens, Adaptive strategies for operator allocation, in: Parameter Setting in Evolutionary Algorithms, 54, Springer, Berlin Heidelberg, 2007, pp. 77–90.
[34] W. Gong, Z. Cai, C.X. Ling, H. Li, Enhanced differential evolution with adaptive strategies for numerical optimization, IEEE Trans. Syst., Man, Cybern., Cybern 41 (2011) 397–413.
[35] Q. Fan, X. Yan, Self-adaptive differential evolution algorithm with zoning evolution of control parameters and adaptive mutation strategies, IEEE Trans. Cybern. 46 (2016) 219–232.
[36] X.-F. Liu, et al., Historical and heuristic-based adaptive differential evolution, IEEE Trans. Syst., Man, Cybern., Syst 49 (2018) 2623–2635.
[37] S.X. Zhang, W.S. Chan, K.S. Tang, S.Y. Zheng, Adaptive strategy in differential evolution via explicit exploitation and exploration controls, Appl. Soft. Comput. 107 (2021) 107494.
[38] G. Wu, X. Shen, H. Li, et al., Ensemble of differential evolution variants, Inf. Sci. 423 (2018) 172–186.
[39] G. Wu, X. Wen, L. Wang, W. Pedrycz, P.N. Suganthan, A voting-mechanism-based ensemble framework for constraint handling techniques, IEEE Trans. Evolut. Comput. 26 (2022) 646–660.
[40] W. Qiu, J. Zhu, G. Wu, H. Chen, W. Pedrycz, P.N. Suganthan, Ensemble manyobjective optimization algorithm based on voting mechanism, IEEE Trans. Syst., Man, Cybernet.: Syst 52 (2022) 1716–1730.
[41] W. Du, et al., Differential evolution with event-triggered impulsive control, IEEE Trans. Cybernet. 47 (2017) 244–257.
[42] L. Cui, G. Li, Q. Lin, J. Chen, N. Lu, Adaptive differential evolution algorithm with novel mutation strategies in multiple sub-populations, Comput. Oper. Res. 67 (2016) 155–173.
[43] S.X. Zhang, L.M. Zheng, K.S. Tang, S.Y. Zheng, W.S. Chan, Multi-layer competitivecooperative framework for performance enhancement of differential evolution, Inf. Sci. 482 (2019) 86–104.
[44] M. Tian, X. Gao, Differential evolution with neighborhood-based adaptive evolution mechanism for numerical optimization, Inf. Sci. 478 (2019) 422–448.
[45] L. Tian, Z. Li, X. Yan, High-performance differential evolution algorithm guided by information from individuals with potential, Appl. Soft. Comput. 95 (2020) 106531.
[46] X. Xia, et al., A fitness-based adaptive differential evolution algorithm, Inf. Sci. 549 (2021) 116–141.