java-代码随想录第63天|拓扑排序、117. 软件构建、dijkstra(朴素版)、47. 参加科学大会
目录
拓扑排序
117. 软件构建
dijkstra(朴素版)
47. 参加科学大会
学习链接:代码随想录
拓扑排序
拓扑排序的应用场景
大学排课,例如 先上A课,才能上B课,上了B课才能上C课,上了A课才能上D课,等等一系列这样的依赖顺序。 问给规划出一条 完整的上课顺序。
拓扑排序在文件处理上也有应用,我们在做项目安装文件包的时候,经常发现 复杂的文件依赖关系, A依赖B,B依赖C,B依赖D,C依赖E 等等。
如果给出一条线性的依赖顺序来下载这些文件呢?
如果上面的依赖关系是一百对呢,一千对甚至上万个依赖关系,这些依赖关系中可能还有循环依赖,你如何发现循环依赖呢,又如果排出线性顺序呢。
所以 拓扑排序就是专门解决这类问题的。
概括来说,给出一个 有向图,把这个有向图转成线性的排序 就叫拓扑排序。
当然拓扑排序也要检测这个有向图 是否有环,即存在循环依赖的情况,因为这种情况是不能做线性排序的。
所以拓扑排序也是图论中判断有向无环图的常用方法。
实现
拓扑排序指的是一种 解决问题的大体思路, 而具体算法,可能是广搜也可能是深搜。
实现拓扑排序的算法有两种:卡恩算法(BFS)和DFS
拓扑排序的过程,其实就两步:
找到入度为0 的节点,加入结果集
将该节点从图中移除
循环以上两步,直到 所有节点都在图中被移除了。
结果集的顺序,就是我们想要的拓扑排序顺序 (结果集里顺序可能不唯一)
117. 软件构建
题目描述
某个大型软件项目的构建系统拥有 N 个文件,文件编号从 0 到 N - 1,在这些文件中,某些文件依赖于其他文件的内容,这意味着如果文件 A 依赖于文件 B,则必须在处理文件 A 之前处理文件 B (0 <= A, B <= N - 1)。请编写一个算法,用于确定文件处理的顺序。
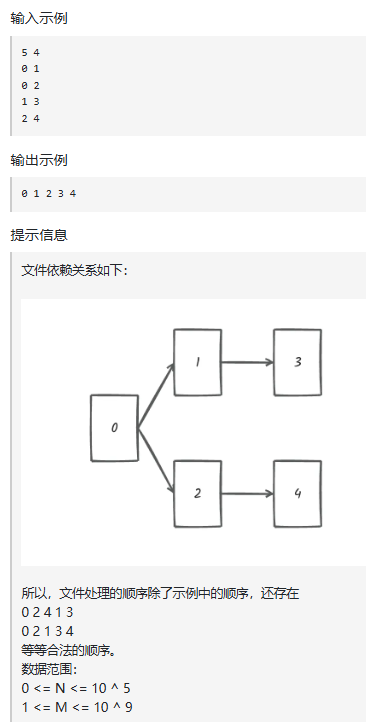
输入描述
第一行输入两个正整数 N, M。表示 N 个文件之间拥有 M 条依赖关系。
后续 M 行,每行两个正整数 S 和 T,表示 T 文件依赖于 S 文件。
输出描述
输出共一行,如果能处理成功,则输出文件顺序,用空格隔开。
如果不能成功处理(相互依赖),则输出 -1。
import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();List<List<Integer>> umap = new ArrayList<>(); // 记录文件依赖关系int[] inDegree = new int[n]; // 记录每个文件的入度for (int i = 0; i < n; i++)umap.add(new ArrayList<>());for (int i = 0; i < m; i++) {int s = scanner.nextInt();int t = scanner.nextInt();umap.get(s).add(t); // 记录s指向哪些文件inDegree[t]++; // t的入度加一}Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < n; i++) {if (inDegree[i] == 0) {// 入度为0的文件,可以作为开头,先加入队列queue.add(i);}}List<Integer> result = new ArrayList<>();// 拓扑排序while (!queue.isEmpty()) {int cur = queue.poll(); // 当前选中的文件result.add(cur);for (int file : umap.get(cur)) {inDegree[file]--; // cur的指向的文件入度-1if (inDegree[file] == 0) {queue.add(file);}}}if (result.size() == n) {for (int i = 0; i < result.size(); i++) {System.out.print(result.get(i));if (i < result.size() - 1) {System.out.print(" ");}}} else {System.out.println(-1);}}
}dijkstra(朴素版)
本题就是求最短路,最短路是图论中的经典问题即:给出一个有向图,一个起点,一个终点,问起点到终点的最短路径。
dijkstra算法:在有权图(权值非负数)中求从起点到其他节点的最短路径算法。
需要注意两点:
dijkstra 算法可以同时求 起点到所有节点的最短路径
权值不能为负数
dijkstra 算法 同样是贪心的思路,不断寻找距离 源点最近的没有访问过的节点。
这里我也给出 dijkstra三部曲:
第一步,选源点到哪个节点近且该节点未被访问过
第二步,该最近节点被标记访问过
第三步,更新非访问节点到源点的距离(即更新minDist数组)
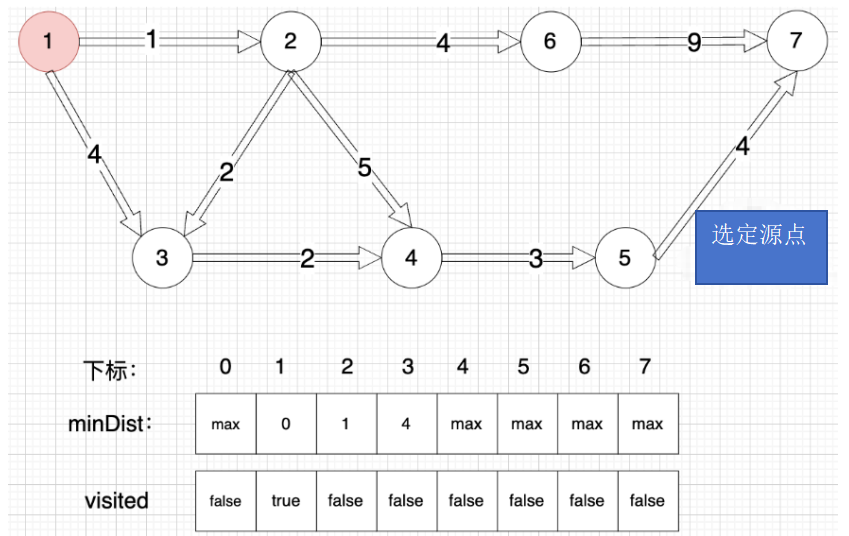
在dijkstra算法中,同样有一个数组很重要,起名为:minDist。
minDist数组 用来记录 每一个节点距离源点的最小距离。
47. 参加科学大会
题目描述
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。
小明的起点是第一个车站,终点是最后一个车站。然而,途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素(如天气变化)等不同,这些因素都会影响每条路径的通行时间。
小明希望能选择一条花费时间最少的路线,以确保他能够尽快到达目的地。
输入描述
第一行包含两个正整数,第一个正整数 N 表示一共有 N 个公共汽车站,第二个正整数 M 表示有 M 条公路。
接下来为 M 行,每行包括三个整数,S、E 和 V,代表了从 S 车站可以单向直达 E 车站,并且需要花费 V 单位的时间。
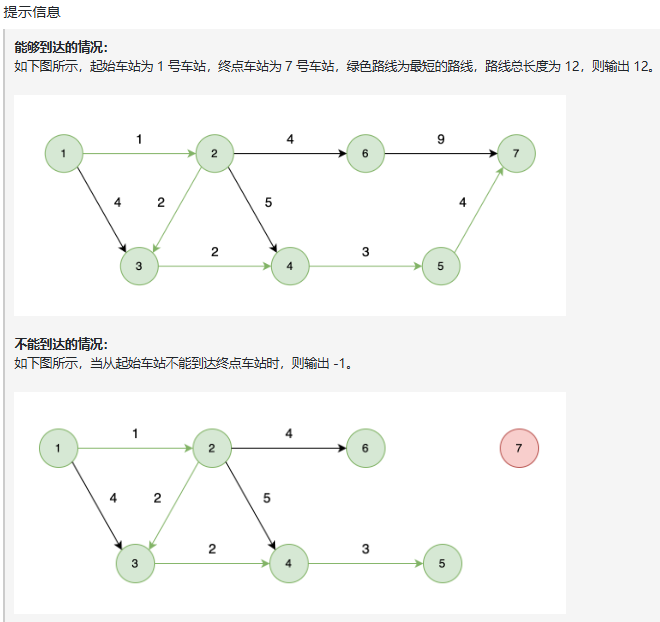
输出描述
输出一个整数,代表小明从起点到终点所花费的最小时间。

import java.util.Arrays;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();int[][] grid = new int[n + 1][n + 1];for (int i = 0; i <= n; i++) {Arrays.fill(grid[i], Integer.MAX_VALUE);}for (int i = 0; i < m; i++) {int p1 = scanner.nextInt();int p2 = scanner.nextInt();int val = scanner.nextInt();grid[p1][p2] = val;}int start = 1;int end = n;// 存储从源点到每个节点的最短距离int[] minDist = new int[n + 1];Arrays.fill(minDist, Integer.MAX_VALUE);// 记录顶点是否被访问过boolean[] visited = new boolean[n + 1];minDist[start] = 0; // 起始点到自身的距离为0for (int i = 1; i <= n; i++) { // 遍历所有节点int minVal = Integer.MAX_VALUE;int cur = 1;// 1、选距离源点最近且未访问过的节点for (int v = 1; v <= n; ++v) {if (!visited[v] && minDist[v] < minVal) {minVal = minDist[v];cur = v;}}visited[cur] = true; // 2、标记该节点已被访问// 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)for (int v = 1; v <= n; v++) {if (!visited[v] && grid[cur][v] != Integer.MAX_VALUE && minDist[cur] + grid[cur][v] < minDist[v]) {minDist[v] = minDist[cur] + grid[cur][v];}}}if (minDist[end] == Integer.MAX_VALUE) {System.out.println(-1); // 不能到达终点} else {System.out.println(minDist[end]); // 到达终点最短路径}}
}