【深度学习计算机视觉】10：转置卷积

【作者主页】Francek Chen
【专栏介绍】$\lceil$PyTorch深度学习$\rfloor$ 深度学习 (DL, Deep Learning) 特指基于深层神经网络模型和方法的机器学习。它是在统计机器学习、人工神经网络等算法模型基础上，结合当代大数据和大算力的发展而发展出来的。深度学习最重要的技术特征是具有自动提取特征的能力。神经网络算法、算力和数据是开展深度学习的三要素。深度学习在计算机视觉、自然语言处理、多模态数据分析、科学探索等领域都取得了很多成果。本专栏介绍基于PyTorch的深度学习算法实现。
【GitCode】专栏资源保存在我的GitCode仓库：https://gitcode.com/Morse_Chen/PyTorch_deep_learning。

---

  到目前为止，我们所见到的卷积神经网络层，例如卷积层和汇聚层，通常会减少下采样输入图像的空间维度（高和宽）。然而如果输入和输出图像的空间维度相同，在以像素级分类的语义分割中将会很方便。例如，输出像素所处的通道维可以保有输入像素在同一位置上的分类结果。

  为了实现这一点，尤其是在空间维度被卷积神经网络层缩小后，我们可以使用另一种类型的卷积神经网络层，它可以增加上采样中间层特征图的空间维度。本节将介绍转置卷积（transposed convolution），用于逆转下采样导致的空间尺寸减小。

import torch
from torch import nn
from d2l import torch as d2l

一、基本操作

  让我们暂时忽略通道，从基本的转置卷积开始，设步幅为1且没有填充。假设我们有一个$n_h\times n_w$的输入张量和一个$k_h\times k_w$的卷积核。以步幅为1滑动卷积核窗口，每行$n_w$次，每列$n_h$次，共产生$n_h{n}_w$个中间结果。每个中间结果都是一个$(n_h+k_h-1)\times (n_w+k_w-1)$的张量，初始化为0。为了计算每个中间张量，输入张量中的每个元素都要乘以卷积核，从而使所得的$k_h\times k_w$张量替换中间张量的一部分。请注意，每个中间张量被替换部分的位置与输入张量中元素的位置相对应。最后，所有中间结果相加以获得最终结果。

  例如，图1解释了如何为$2\times 2$的输入张量计算卷积核为$2\times 2$的转置卷积。

图1 卷积核为2×2的转置卷积。阴影部分是中间张量的一部分，也是用于计算的输入和卷积核张量元素。

  我们可以对输入矩阵X和卷积核矩阵K实现基本的转置卷积运算trans_conv。

def trans_conv(X, K):h, w = K.shapeY = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))for i in range(X.shape[0]):for j in range(X.shape[1]):Y[i: i + h, j: j + w] += X[i, j] * Kreturn Y

  与通过卷积核“减少”输入元素的常规卷积相比，转置卷积通过卷积核“广播”输入元素，从而产生大于输入的输出。我们可以通过图1来构建输入张量X和卷积核张量K从而验证上述实现输出。此实现是基本的二维转置卷积运算。

X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
trans_conv(X, K)

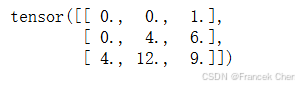
  或者，当输入X和卷积核K都是四维张量时，我们可以使用高级API获得相同的结果。

X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
tconv(X)

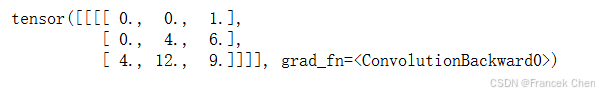
二、填充、步幅和多通道

  与常规卷积不同，在转置卷积中，填充被应用于的输出（常规卷积将填充应用于输入）。例如，当将高和宽两侧的填充数指定为1时，转置卷积的输出中将删除第一和最后的行与列。

tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=1, bias=False)
tconv.weight.data = K
tconv(X)

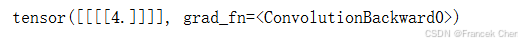
  在转置卷积中，步幅被指定为中间结果（输出），而不是输入。使用图1中相同输入和卷积核张量，将步幅从1更改为2会增加中间张量的高和权重，因此输出张量在图2中。

图2 卷积核为2×2，步幅为2的转置卷积。阴影部分是中间张量的一部分，也是用于计算的输入和卷积核张量元素

  以下代码可以验证图2中步幅为2的转置卷积的输出。

tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
tconv.weight.data = K
tconv(X)

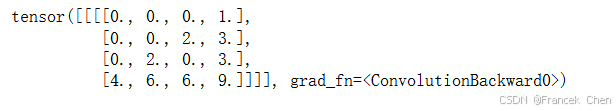
  对于多个输入和输出通道，转置卷积与常规卷积以相同方式运作。假设输入有$c_i$个通道，且转置卷积为每个输入通道分配了一个$k_h\times k_w$的卷积核张量。当指定多个输出通道时，每个输出通道将有一个$c_i\times k_h\times k_w$的卷积核。

  同样，如果我们将$\mathsf{X}$代入卷积层$f$来输出$\mathsf{Y}=f(\mathsf{X})$，并创建一个与$f$具有相同的超参数、但输出通道数量是$\mathsf{X}$中通道数的转置卷积层$g$，那么$g(Y)$的形状将与$\mathsf{X}$相同。下面的示例可以解释这一点。

X = torch.rand(size=(1, 10, 16, 16))
conv = nn.Conv2d(10, 20, kernel_size=5, padding=2, stride=3)
tconv = nn.ConvTranspose2d(20, 10, kernel_size=5, padding=2, stride=3)
tconv(conv(X)).shape == X.shape

三、与矩阵变换的联系

  转置卷积为何以矩阵变换命名呢？让我们首先看看如何使用矩阵乘法来实现卷积。在下面的示例中，我们定义了一个$3\times 3$的输入X和$2\times 2$卷积核K，然后使用corr2d函数计算卷积输出Y。

X = torch.arange(9.0).reshape(3, 3)
K = torch.tensor([[1.0, 2.0], [3.0, 4.0]])
Y = d2l.corr2d(X, K)
Y

  接下来，我们将卷积核K重写为包含大量0的稀疏权重矩阵W。权重矩阵的形状是（$4$，$9$），其中非0元素来自卷积核K。

def kernel2matrix(K):k, W = torch.zeros(5), torch.zeros((4, 9))k[:2], k[3:5] = K[0, :], K[1, :]W[0, :5], W[1, 1:6], W[2, 3:8], W[3, 4:] = k, k, k, kreturn WW = kernel2matrix(K)
W

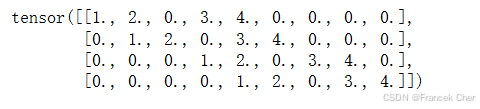
  逐行连结输入X，获得了一个长度为9的矢量。然后，W的矩阵乘法和向量化的X给出了一个长度为4的向量。重塑它之后，可以获得与上面的原始卷积操作所得相同的结果Y：我们刚刚使用矩阵乘法实现了卷积。

Y == torch.matmul(W, X.reshape(-1)).reshape(2, 2)

  同样，我们可以使用矩阵乘法来实现转置卷积。在下面的示例中，我们将上面的常规卷积$2\times 2$的输出Y作为转置卷积的输入。想要通过矩阵相乘来实现它，我们只需要将权重矩阵W的形状转置为$(9,4)$。

Z = trans_conv(Y, K)
Z == torch.matmul(W.T, Y.reshape(-1)).reshape(3, 3)

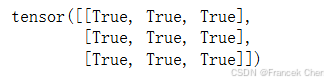
  抽象来看，给定输入向量$\mathbf{x}$和权重矩阵$\mathbf{W}$，卷积的前向传播函数可以通过将其输入与权重矩阵相乘并输出向量$\mathbf{y}=\mathbf{Wx}$来实现。由于反向传播遵循链式法则和${\nabla }_{\mathbf{x}}\mathbf{y}={\mathbf{W}}^{\top }$，卷积的反向传播函数可以通过将其输入与转置的权重矩阵${\mathbf{W}}^{\top }$相乘来实现。因此，转置卷积层能够交换卷积层的正向传播函数和反向传播函数：它的正向传播和反向传播函数将输入向量分别与${\mathbf{W}}^{\top }$和$\mathbf{W}$相乘。

小结

• 与通过卷积核减少输入元素的常规卷积相反，转置卷积通过卷积核广播输入元素，从而产生形状大于输入的输出。
• 如果我们将$\mathsf{X}$输入卷积层$f$来获得输出$\mathsf{Y}=f(\mathsf{X})$并创造一个与$f$有相同的超参数、但输出通道数是$\mathsf{X}$中通道数的转置卷积层$g$，那么$g(Y)$的形状将与$\mathsf{X}$相同。
• 我们可以使用矩阵乘法来实现卷积。转置卷积层能够交换卷积层的正向传播函数和反向传播函数。