信号 | 基本描述 / 分类 / 运算
注:本文为 “信号描述 ” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
信号的描述
一、信号的多维度描述
信号可从物理、数学和形态三个维度进行定义,各维度描述既相互独立又相互关联,共同构成对信号的完整认知。
(一)物理描述
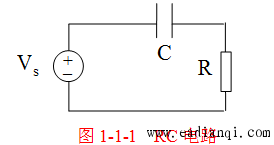
从物理本质上看,信号是信息寄寓的变化形式,其物理描述对应信号的物理量,即信号的具体名称。例如:在RC电路中,电流信号与电压信号均为信号的物理描述。
(二)数学描述
从数学角度出发,信号是一个或多个变量的函数。变量的个数决定了信号的维度:
- 单变量函数对应一维信号(如语音信号,以时间为变量);
- 双变量函数对应二维信号(如黑白图像,以平面空间位置为变量)。
(三)形态描述
从形态表现上,信号以波形或图像的形式呈现,可直观反映信号的变化规律,帮助建立对信号的主观认知。例如:
-
语音信号表现为声压随时间变化的一维波形;
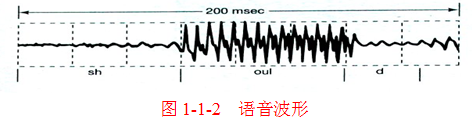
-
黑白照片表现为亮度随空间位置(x,y)变化的二维图像。

二、信号的分类
在信号与系统分析中,根据信号的时间函数特性,可将信号分为以下三类:
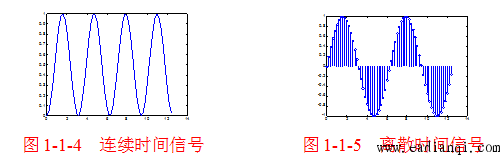
(一)连续时间信号与离散时间信号
两类信号的区别在于自变量的取值方式,具体定义与表示如下表所示:
| 信号类型 | 定义 | 自变量特性 | 表示符号 |
|---|---|---|---|
| 连续时间信号 | 自变量可在连续区间内任意取值的信号 | 自变量 ttt 为连续变量(取值范围通常为 (−∞,+∞)(-\infty,+\infty)(−∞,+∞)) | x(t)x(t)x(t) |
| 离散时间信号 | 自变量仅在一组离散值上取值的信号 | 自变量 nnn 为整数(取值范围通常为 {…,−2,−1,0,1,2,…}\{\dots,-2,-1,0,1,2,\dots\}{…,−2,−1,0,1,2,…}) | x[n]x[n]x[n] |
(二)能量信号与功率信号
能量信号与功率信号的划分基于信号的能量和平均功率定义,需分别针对连续时间信号与离散时间信号进行计算。
1. 连续时间信号 x(t)x(t)x(t) 的能量与平均功率
- 能量 E∞E_{\infty}E∞:信号在无限时间区间内的能量总和,定义为:
E∞=limT→∞∫−TT∣x(t)∣2dtE_{\infty} = \lim_{T \to \infty} \int_{-T}^{T} |x(t)|^2 dt E∞=T→∞lim∫−TT∣x(t)∣2dt - 平均功率 P∞P_{\infty}P∞:信号在无限时间区间内的平均功率,定义为:
P∞=limT→∞12T∫−TT∣x(t)∣2dtP_{\infty} = \lim_{T \to \infty} \frac{1}{2T} \int_{-T}^{T} |x(t)|^2 dt P∞=T→∞lim2T1∫−TT∣x(t)∣2dt
2. 离散时间信号 x[n]x[n]x[n] 的能量与平均功率
- 能量 EEE:信号在无限离散时间点上的能量总和,定义为:
E=limN→∞∑n=−NN∣x[n]∣2E = \lim_{N \to \infty} \sum_{n=-N}^{N} |x[n]|^2 E=N→∞limn=−N∑N∣x[n]∣2 - 平均功率 PPP:信号在无限离散时间点上的平均功率,定义为:
P=limN→∞12N+1∑n=−NN∣x[n]∣2P = \lim_{N \to \infty} \frac{1}{2N+1} \sum_{n=-N}^{N} |x[n]|^2 P=N→∞lim2N+11n=−N∑N∣x[n]∣2
3. 信号类型判定
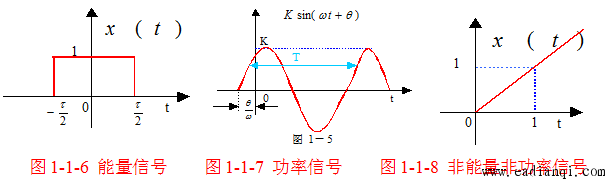
- 能量信号:当 T→∞T \to \inftyT→∞(或 N→∞N \to \inftyN→∞)时,能量 EEE 为有限值,平均功率 P=0P = 0P=0;
- 功率信号:当 T→∞T \to \inftyT→∞(或 N→∞N \to \inftyN→∞)时,能量 E→∞E \to \inftyE→∞,平均功率 PPP 为有限值;
- 非能量非功率信号:既不满足能量信号条件,也不满足功率信号条件的信号(如脉冲信号、斜坡信号)。
(三)周期信号与非周期信号
周期信号是指信号波形随时间(或离散时间点)周期性重复的信号,非周期信号则无重复规律。
1. 连续时间周期信号
- 定义:若存在非零常数 T0T_0T0(称为基波周期),使得对所有 ttt 均满足:
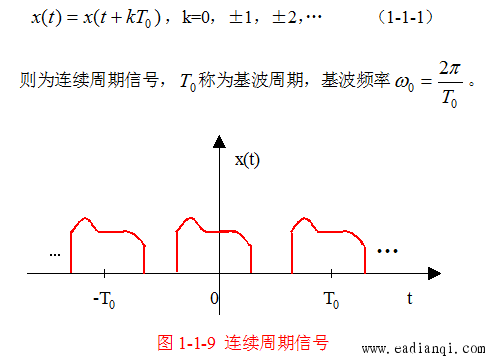
x(t)=x(t+kT0),k=0,±1,±2,…x(t) = x(t + kT_0), \quad k = 0, \pm1, \pm2, \dots x(t)=x(t+kT0),k=0,±1,±2,…
则称 x(t)x(t)x(t) 为连续时间周期信号。 - 基波频率:与基波周期对应的角频率,定义为 ω0=2πT0\omega_0 = \frac{2\pi}{T_0}ω0=T02π;
- 典型示例:sin(ω0t)\sin(\omega_0 t)sin(ω0t)、cos(ω0t)\cos(\omega_0 t)cos(ω0t) 等正弦信号。
2. 离散时间周期信号
- 定义:若存在正整数 N0N_0N0(称为基波周期),使得对所有 nnn 均满足:
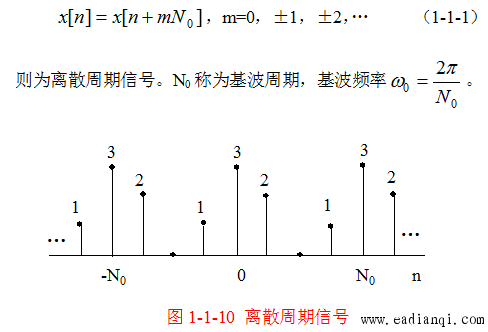
x[n]=x[n+mN0],m=0,±1,±2,…x[n] = x[n + mN_0], \quad m = 0, \pm1, \pm2, \dots x[n]=x[n+mN0],m=0,±1,±2,…
则称 x[n]x[n]x[n] 为离散时间周期信号。 - 基波频率:与基波周期对应的角频率,定义为 ω0=2πN0\omega_0 = \frac{2\pi}{N_0}ω0=N02π。
3. 组合信号的周期性判定
组合信号(如 f1(t)+f2(t)f_1(t) + f_2(t)f1(t)+f2(t) 或 f1[n]+f2[n]f_1[n] + f_2[n]f1[n]+f2[n])的周期性需根据各分量信号的周期判断:
- 连续时间组合信号:设 f1(t)f_1(t)f1(t) 的基波周期为 T1T_1T1,f2(t)f_2(t)f2(t) 的基波周期为 T2T_2T2。若 T1T2=n1n2\frac{T_1}{T_2} = \frac{n_1}{n_2}T2T1=n2n1(n1,n2n_1, n_2n1,n2 为互质正整数),则组合信号为周期信号,其基波周期为 T0=LCM(T1,T2)=n2T1=n1T2T_0 = \text{LCM}(T_1, T_2) = n_2T_1 = n_1T_2T0=LCM(T1,T2)=n2T1=n1T2;若 T1T2\frac{T_1}{T_2}T2T1 为无理数,则组合信号为非周期信号。
- 离散时间组合信号:设 f1[n]f_1[n]f1[n] 的基波周期为 N1N_1N1,f2[n]f_2[n]f2[n] 的基波周期为 N2N_2N2,则组合信号一定为周期信号,其基波周期为 N0=LCM(N1,N2)N_0 = \text{LCM}(N_1, N_2)N0=LCM(N1,N2)(LCM\text{LCM}LCM 表示最小公倍数)。
三、信号的基本时域变换
信号的时域变换包括时移、反射、尺度变换,变换仅改变信号的时域位置或形态,不改变信号的本质特性。
(一)时移
时移是指信号沿时间轴(或离散时间轴)平移,信号的波形与幅度保持不变。
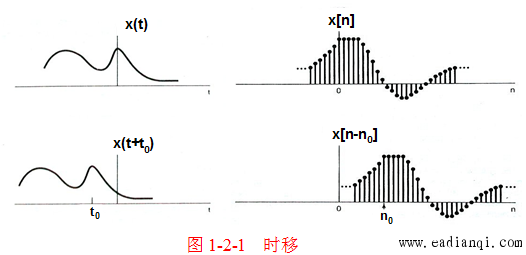
1. 连续时间信号的时移
- 变换形式:x(t−t0)x(t - t_0)x(t−t0)(t0t_0t0 为时移量);
- 时移规律:
- 当 t0>0t_0 > 0t0>0 时,信号 x(t)x(t)x(t) 沿时间轴右移(延时);
- 当 t0<0t_0 < 0t0<0 时,信号 x(t)x(t)x(t) 沿时间轴左移(超前)(可表示为 x(t+∣t0∣)x(t + |t_0|)x(t+∣t0∣))。
2. 离散时间信号的时移
- 变换形式:x[n−m]x[n - m]x[n−m](mmm 为时移量,且 mmm 为整数);
- 时移规律:
- 当 m>0m > 0m>0 时,信号 x[n]x[n]x[n] 沿离散时间轴右移(延时);
- 当 m<0m < 0m<0 时,信号 x[n]x[n]x[n] 沿离散时间轴左移(超前)(可表示为 x[n+∣m∣]x[n + |m|]x[n+∣m∣])。
(二)反射
反射是指信号以时间轴原点(或离散时间轴原点)为对称轴进行反转,信号的波形形态保持不变,仅左右方向反转。
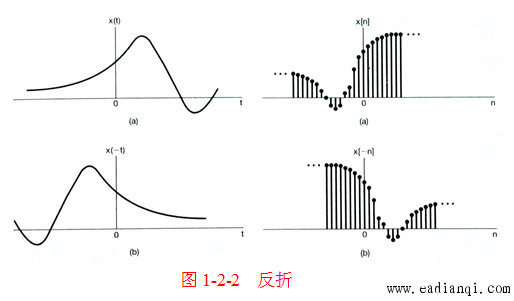
1. 连续时间信号的反射
- 变换形式:x(−t)x(-t)x(−t);
- 变换规律:将 x(t)x(t)x(t) 以 t=0t = 0t=0 的纵轴为对称轴进行反折。
2. 离散时间信号的反射
- 变换形式:x[−n]x[-n]x[−n];
- 变换规律:将 x[n]x[n]x[n] 以 n=0n = 0n=0 的纵轴为对称轴进行反折。
(三)尺度变换
尺度变换是指信号沿时间轴(或离散时间轴)进行压缩或扩展,改变信号的时域宽度,需注意离散信号的尺度变换存在采样点丢失问题。
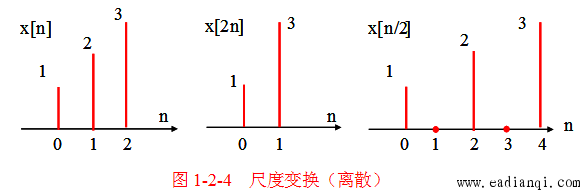
1. 连续时间信号的尺度变换
- 变换形式:x(at)x(at)x(at)(aaa 为尺度因子);
- 变换规律:
- 当 a>1a > 1a>1 时,信号 x(t)x(t)x(t) 沿时间轴压缩(时域宽度减小);
- 当 0<a<10 < a < 10<a<1 时,信号 x(t)x(t)x(t) 沿时间轴扩展(时域宽度增大);
- 当 a<0a < 0a<0 时,信号 x(t)x(t)x(t) 先反射(因负号),再按 ∣a∣|a|∣a∣ 进行压缩或扩展。
2. 离散时间信号的尺度变换
- 变换形式:x[an]x[an]x[an](aaa 为正整数尺度因子);
- 变换规律:
- 当 a>1a > 1a>1 时,信号 x[n]x[n]x[n] 沿离散时间轴压缩,但会丢失非 aaa 整数倍的采样点,无法从压缩后的信号恢复原信号;
- 当 a=1ka = \frac{1}{k}a=k1(kkk 为正整数)时,信号 x[n]x[n]x[n] 沿离散时间轴扩展,需在原采样点之间插入零值(或插值)以保持信号形态。
3. 综合变换公式
时移、反射、尺度变换的综合表达式可统一表示为:
- 正向尺度与平移:x(at±b)=x[a(t±ba)]x(at \pm b) = x\left[a\left(t \pm \frac{b}{a}\right)\right]x(at±b)=x[a(t±ab)];
- 反向尺度与平移:x(−at±b)=x[−a(t∓ba)]x(-at \pm b) = x\left[-a\left(t \mp \frac{b}{a}\right)\right]x(−at±b)=x[−a(t∓ab)]。
变换顺序建议:对时间变量 ttt(或 nnn)进行变换时,建议按“尺度变换→反射→时移”的顺序操作,可避免因顺序混乱导致的错误(在卷积运算中需注意“先反射再时移”的特殊场景)。
(四)变换示例
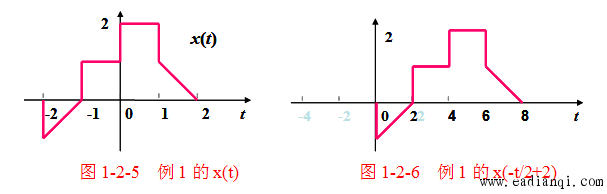
已知 x(t)x(t)x(t) 的波形如图 1-2-5 所示(波形范围:t∈[−1,1]t \in [-1,1]t∈[−1,1],幅度为 2),需绘制 x(−12t+1)x\left(-\frac{1}{2}t + 1\right)x(−21t+1) 的波形,步骤如下:
- 尺度变换:对 x(t)x(t)x(t) 进行扩展(尺度因子 a=12a = \frac{1}{2}a=21),得到 x(12t)x\left(\frac{1}{2}t\right)x(21t)(时域宽度从 222 扩展为 444,范围 t∈[−2,2]t \in [-2,2]t∈[−2,2]);
- 反射变换:对 x(12t)x\left(\frac{1}{2}t\right)x(21t) 进行反射,得到 x(−12t)x\left(-\frac{1}{2}t\right)x(−21t)(波形以 t=0t = 0t=0 为轴反转,范围仍为 t∈[−2,2]t \in [-2,2]t∈[−2,2]);
- 时移变换:对 x(−12t)x\left(-\frac{1}{2}t\right)x(−21t) 右移 222 个单位(因 −12t+1=−12(t−2)-\frac{1}{2}t + 1 = -\frac{1}{2}(t - 2)−21t+1=−21(t−2)),得到 x(−12(t−2))=x(−12t+1)x\left(-\frac{1}{2}(t - 2)\right) = x\left(-\frac{1}{2}t + 1\right)x(−21(t−2))=x(−21t+1)(最终范围 t∈[0,4]t \in [0,4]t∈[0,4])。
四、信号的奇偶分解
任意信号均可分解为偶分量(Even Component)与奇分量(Odd Component)之和,且分解满足唯一性;同时,信号的能量等于其偶分量能量与奇分量能量之和(能量守恒)。
(一)连续时间信号的奇偶分解
-
分解公式:
x(t)=xe(t)+xo(t)x(t) = x_e(t) + x_o(t) x(t)=xe(t)+xo(t)
其中:- 偶分量 xe(t)x_e(t)xe(t)(满足 xe(−t)=xe(t)x_e(-t) = x_e(t)xe(−t)=xe(t)):
xe(t)=12[x(t)+x(−t)]x_e(t) = \frac{1}{2}\left[x(t) + x(-t)\right] xe(t)=21[x(t)+x(−t)] - 奇分量 xo(t)x_o(t)xo(t)(满足 xo(−t)=−xo(t)x_o(-t) = -x_o(t)xo(−t)=−xo(t)):
xo(t)=12[x(t)−x(−t)]x_o(t) = \frac{1}{2}\left[x(t) - x(-t)\right] xo(t)=21[x(t)−x(−t)]
- 偶分量 xe(t)x_e(t)xe(t)(满足 xe(−t)=xe(t)x_e(-t) = x_e(t)xe(−t)=xe(t)):
-
能量关系:
∫−∞∞x2(t)dt=∫−∞∞xe2(t)dt+∫−∞∞xo2(t)dt\int_{-\infty}^{\infty} x^2(t) dt = \int_{-\infty}^{\infty} x_e^2(t) dt + \int_{-\infty}^{\infty} x_o^2(t) dt ∫−∞∞x2(t)dt=∫−∞∞xe2(t)dt+∫−∞∞xo2(t)dt
(二)离散时间信号的奇偶分解
-
分解公式:
x[n]=xe[n]+xo[n]x[n] = x_e[n] + x_o[n] x[n]=xe[n]+xo[n]
其中:- 偶分量 xe[n]x_e[n]xe[n](满足 xe[−n]=xe[n]x_e[-n] = x_e[n]xe[−n]=xe[n]):
xe[n]=12[x[n]+x[−n]]x_e[n] = \frac{1}{2}\left[x[n] + x[-n]\right] xe[n]=21[x[n]+x[−n]] - 奇分量 xo[n]x_o[n]xo[n](满足 xo[−n]=−xo[n]x_o[-n] = -x_o[n]xo[−n]=−xo[n]):
xo[n]=12[x[n]−x[−n]]x_o[n] = \frac{1}{2}\left[x[n] - x[-n]\right] xo[n]=21[x[n]−x[−n]]
- 偶分量 xe[n]x_e[n]xe[n](满足 xe[−n]=xe[n]x_e[-n] = x_e[n]xe[−n]=xe[n]):
-
能量关系:
∑k=−∞∞x2[k]=∑k=−∞∞xe2[k]+∑k=−∞∞xo2[k]\sum_{k=-\infty}^{\infty} x^2[k] = \sum_{k=-\infty}^{\infty} x_e^2[k] + \sum_{k=-\infty}^{\infty} x_o^2[k] k=−∞∑∞x2[k]=k=−∞∑∞xe2[k]+k=−∞∑∞xo2[k]
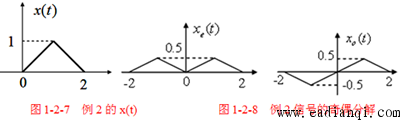
(三)分解示例
已知 x(t)x(t)x(t) 的波形如图 1-2-7 所示(波形:t∈[0,2]t \in [0,2]t∈[0,2] 时 x(t)=tx(t) = tx(t)=t,其余时刻 x(t)=0x(t) = 0x(t)=0),求其偶分量 xe(t)x_e(t)xe(t) 与奇分量 xo(t)x_o(t)xo(t):
- 计算 x(−t)x(-t)x(−t):t∈[−2,0]t \in [-2,0]t∈[−2,0] 时 x(−t)=−tx(-t) = -tx(−t)=−t,其余时刻 x(−t)=0x(-t) = 0x(−t)=0;
- 偶分量 xe(t)=12[x(t)+x(−t)]x_e(t) = \frac{1}{2}\left[x(t) + x(-t)\right]xe(t)=21[x(t)+x(−t)]:t∈[0,2]t \in [0,2]t∈[0,2] 时 xe(t)=t2x_e(t) = \frac{t}{2}xe(t)=2t,t∈[−2,0]t \in [-2,0]t∈[−2,0] 时 xe(t)=−t2x_e(t) = -\frac{t}{2}xe(t)=−2t,其余时刻 xe(t)=0x_e(t) = 0xe(t)=0;
- 奇分量 xo(t)=12[x(t)−x(−t)]x_o(t) = \frac{1}{2}\left[x(t) - x(-t)\right]xo(t)=21[x(t)−x(−t)]:t∈[0,2]t \in [0,2]t∈[0,2] 时 xo(t)=t2x_o(t) = \frac{t}{2}xo(t)=2t,t∈[−2,0]t \in [-2,0]t∈[−2,0] 时 xo(t)=t2x_o(t) = \frac{t}{2}xo(t)=2t,其余时刻 xo(t)=0x_o(t) = 0xo(t)=0。
五、信号的基本运算
信号的基本运算包括加减、相乘、微分(仅连续信号)、积分(仅连续信号),运算均在对应时间点(或时间段)上进行。
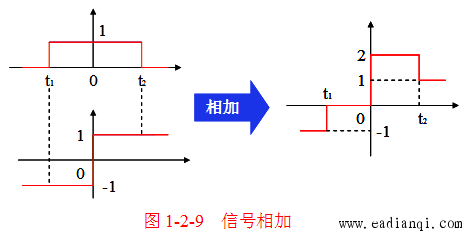
(一)加减运算
- 定义:两个信号在同一时间点(或离散时间点)的幅度值相加或相减;
- 连续时间信号:x(t)=x1(t)±x2(t)x(t) = x_1(t) \pm x_2(t)x(t)=x1(t)±x2(t);
- 离散时间信号:x[n]=x1[n]±x2[n]x[n] = x_1[n] \pm x_2[n]x[n]=x1[n]±x2[n];
- 运算规则:对所有 ttt(或 nnn),逐点计算 x1x_1x1 与 x2x_2x2 的幅度代数和。
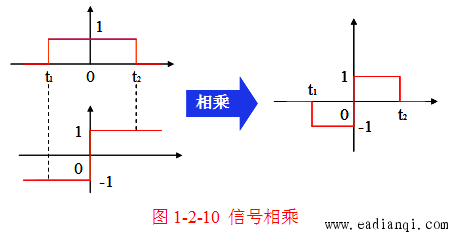
(二)相乘运算
- 定义:两个信号在同一时间点(或离散时间点)的幅度值相乘;
- 连续时间信号:x(t)=x1(t)⋅x2(t)x(t) = x_1(t) \cdot x_2(t)x(t)=x1(t)⋅x2(t);
- 离散时间信号:x[n]=x1[n]⋅x2[n]x[n] = x_1[n] \cdot x_2[n]x[n]=x1[n]⋅x2[n];
- 运算规则:对所有 ttt(或 nnn),逐点计算 x1x_1x1 与 x2x_2x2 的幅度乘积(典型应用:信号调制)。
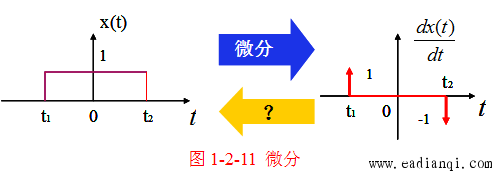
(三)微分运算(仅连续时间信号)
- 定义:信号对时间的一阶导数,反映信号幅度随时间的变化率;
- 定义式:y(t)=dx(t)dt=x(1)(t)y(t) = \frac{dx(t)}{dt} = x^{(1)}(t)y(t)=dtdx(t)=x(1)(t);
- 关键特性:在信号的间断点处,微分结果为冲激信号,冲激强度等于间断点处的幅度跳变值(例如:若 x(t)x(t)x(t) 在 t=t0t = t_0t=t0 处从 AAA 跳变到 BBB,则 dx(t)dt\frac{dx(t)}{dt}dtdx(t) 在 t=t0t = t_0t=t0 处包含强度为 B−AB - AB−A 的冲激)。
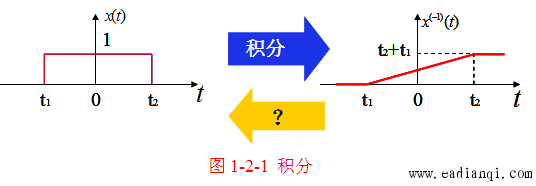
(四)积分运算(仅连续时间信号)
- 定义:信号从 −∞-\infty−∞ 到当前时刻 ttt 的定积分,反映信号幅度随时间的累积效应;
- 定义式:y(t)=∫−∞tx(τ)dτ=x(−1)(t)y(t) = \int_{-\infty}^{t} x(\tau) d\tau = x^{(-1)}(t)y(t)=∫−∞tx(τ)dτ=x(−1)(t);
- 关键特性:分段积分时,需考虑前一段积分结果对当前积分的影响(即积分具有“记忆性”),积分后的信号波形比原信号更平滑(可抑制高频噪声)。
六、连续时间典型信号
连续时间典型信号包括复指数信号、正弦信号,二者通过欧拉公式建立关联,是信号与系统分析的基础信号。
复指数信号是最常用的信号,其表示式为:
x(t)=Ceatx(t) = Ce^{at}x(t)=Ceat,
其中 CCC 和 aaa 一般为复数,C=α+jβC = \alpha + j\betaC=α+jβ,a=σ+jωa = \sigma + j\omegaa=σ+jω。
连续实指数信号
若 CCC 和 aaa 为实数,则为实指数信号,波形如图 1-3-1 所示。
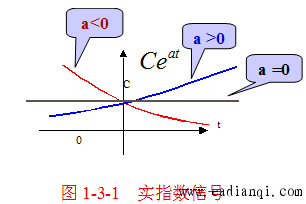
- 当 a<0a < 0a<0 时,信号衰减。
- 当 a>0a > 0a>0 时,信号增长。
连续虚指数信号
令 a=−jω0a = -j\omega_0a=−jω0,则有 x(t)=ejω0tx(t) = e^{j\omega_0 t}x(t)=ejω0t
例:证明连续虚指数信号是周期信号。
证明:若存在 TTT,使得 ejω0(t+T)=ejω0te^{j\omega_0(t+T)} = e^{j\omega_0 t}ejω0(t+T)=ejω0t 对所有 ttt 成立,则 x(t)x(t)x(t) 是周期的。为此必须有 ejω0T=1e^{j\omega_0 T} = 1ejω0T=1
当 T=2πω0T = \frac{2\pi}{\omega_0}T=ω02π 时,对所有 ttt 都满足 x(t)=x(t+T)x(t) = x(t+T)x(t)=x(t+T),因此 x(t)x(t)x(t) 是周期信号。
欧拉公式(Euler’s Relation)
ejωt=cos(ωt)+jsin(ωt)e^{j\omega t} = \cos(\omega t) + j\sin(\omega t)ejωt=cos(ωt)+jsin(ωt)
由此可得:
cos(ωt)=ejωt+e−jωt2\cos(\omega t) = \frac{e^{j\omega t} + e^{-j\omega t}}{2}cos(ωt)=2ejωt+e−jωt
sin(ωt)=ejωt−e−jωt2j\sin(\omega t) = \frac{e^{j\omega t} - e^{-j\omega t}}{2j}sin(ωt)=2jejωt−e−jωt
ej(ωt+ϕ)=cos(ωt+ϕ)+jsin(ωt+ϕ)e^{j(\omega t + \phi)} = \cos(\omega t + \phi) + j\sin(\omega t + \phi)ej(ωt+ϕ)=cos(ωt+ϕ)+jsin(ωt+ϕ)
取实部则得到余弦信号:
x(t)=Acos(ωt+ϕ)x(t) = A\cos(\omega t + \phi)x(t)=Acos(ωt+ϕ)
余弦信号是信号与系统分析中经常要用到的一类典型信号,如图 1-3-2 所示。
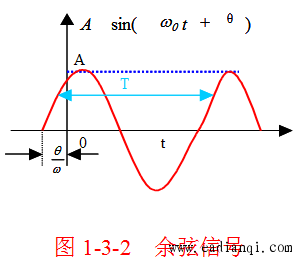
余弦信号具有以下性质:
- ω\omegaω 越大,振荡频率越高。
- 对任何 ω\omegaω,都是周期的。
连续周期复指数信号
连续周期复指数信号具有两个性质:
- 基波频率相同。
- 周期信号都可以分解为成谐波关系的正弦信号的线性组合,即傅立叶级数表示。
一个成谐波关系的复指数信号的集合:一组基波频率是某一正频率 ω0\omega_0ω0 的整数倍的周期复指数信号:
xk(t)=ejkω0tx_k(t) = e^{jk\omega_0 t}xk(t)=ejkω0t
其中 k=0,±1,±2,…k = 0, \pm1, \pm2, \ldotsk=0,±1,±2,…。基波频率 ωk=kω0\omega_k = k\omega_0ωk=kω0,基波周期 Tk=T0∣k∣T_k = \frac{T_0}{|k|}Tk=∣k∣T0,它们有一个公共周期 T0T_0T0。
一般复指数信号
一般复指数信号可以通过实指数信号和周期复指数信号来表示:
x(t)=Ceatx(t) = Ce^{at}x(t)=Ceat
其中 a=σ+jωa = \sigma + j\omegaa=σ+jω,C=∣C∣ejθC = |C|e^{j\theta}C=∣C∣ejθ。
则有:
x(t)=∣C∣e(σ+jω)t=∣C∣eσtej(ωt+θ)x(t) = |C|e^{(\sigma + j\omega)t} = |C|e^{\sigma t}e^{j(\omega t + \theta)}x(t)=∣C∣e(σ+jω)t=∣C∣eσtej(ωt+θ)
一般复指数信号可以看成是实指数信号 eσte^{\sigma t}eσt 和周期复指数信号 ejωte^{j\omega t}ejωt 相乘的结果。它包含了这两个信号的基本特性:参数 ω\omegaω 反映了振荡信号的变化频率,而参数 σ\sigmaσ 则反映了振荡信号峰值的变化趋势,用包络线 ∣C∣eσt|C|e^{\sigma t}∣C∣eσt 来描述信号峰值的变化趋势,如图 1-3-3 所示。
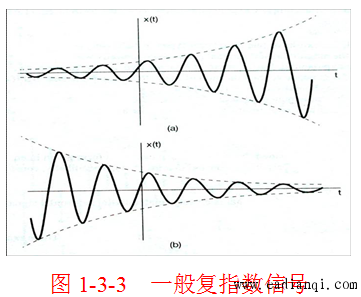
- 当 σ>0\sigma > 0σ>0 时,是幅度增长的正弦信号。
- 当 σ<0\sigma < 0σ<0 时,是幅度衰减的正弦信号。
七、离散时间典型信号
离散时间典型信号包括复指数序列、正弦序列、单位脉冲序列、单位阶跃序列,其特性与连续时间信号既有相似性,也存在本质差异(如离散信号的频率周期性)。
(一)复指数序列
复指数序列是离散时间信号的基础形式,常用两种表达式表示,需注意其频率的周期性特性。
1. 基本形式
- 形式 1(常用):x[n]=Cαnx[n] = C \alpha^nx[n]=Cαn(CCC 为复振幅,α\alphaα 为复底数);
- 形式 2(与连续对应):x[n]=Ceβnx[n] = C e^{\beta n}x[n]=Ceβn(β\betaβ 为复频率,α=eβ\alpha = e^{\beta}α=eβ)。
2. 实指数序列
当 CCC 与 α\alphaα 均为实数时,x[n]=∣C∣αnx[n] = |C| \alpha^nx[n]=∣C∣αn,根据 α\alphaα 的取值分为四种情况:
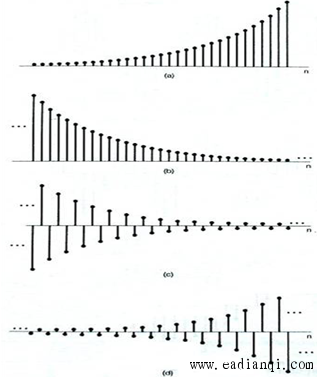
- α>1\alpha > 1α>1:序列幅度随 nnn 指数增长;
- 0<α<10 < \alpha < 10<α<1:序列幅度随 nnn 指数衰减;
- −1<α<0-1 < \alpha < 0−1<α<0:序列幅度随 nnn 指数衰减,且正负交替;
- α<−1\alpha < -1α<−1:序列幅度随 nnn 指数增长,且正负交替。
3. 周期特性
离散时间复指数序列 ejω0ne^{j\omega_0 n}ejω0n 具有独特的频率周期性:
ej(ω0+2kπ)n=ej2kπn⋅ejω0n=ejω0n,k=0,±1,±2,…e^{j(\omega_0 + 2k\pi)n} = e^{j2k\pi n} \cdot e^{j\omega_0 n} = e^{j\omega_0 n}, \quad k = 0, \pm1, \pm2, \dots ej(ω0+2kπ)n=ej2kπn⋅ejω0n=ejω0n,k=0,±1,±2,…
即:频率相差 2π2\pi2π 整数倍的离散复指数序列完全相同,因此离散信号的有效频率范围为 [−π,π][-\pi, \pi][−π,π] 或 [0,2π][0, 2\pi][0,2π]。
4. 周期性判定
离散时间复指数序列 ejω0ne^{j\omega_0 n}ejω0n 为周期序列的充要条件是:存在正整数 NNN(周期),使得对所有 nnn 满足 ejω0(n+N)=ejω0ne^{j\omega_0(n + N)} = e^{j\omega_0 n}ejω0(n+N)=ejω0n,即:
ejω0N=1⟹ω0N=2mπ(m为正整数)e^{j\omega_0 N} = 1 \implies \omega_0 N = 2m\pi \quad (m 为正整数) ejω0N=1⟹ω0N=2mπ(m为正整数)
整理得:ω02π=mN\frac{\omega_0}{2\pi} = \frac{m}{N}2πω0=Nm(即 ω02π\frac{\omega_0}{2\pi}2πω0 为有理数)。此时:
- 基波频率:ω0′=2πN=ω0m\omega_0' = \frac{2\pi}{N} = \frac{\omega_0}{m}ω0′=N2π=mω0;
- 基波周期:N0=2mπω0N_0 = \frac{2m\pi}{\omega_0}N0=ω02mπ(取最小正整数)。
(二)正弦序列
正弦序列由复指数序列的实部或虚部得到,其频率特性与离散复指数序列一致。
1. 基本形式
x[n]=Acos(ω0n+ϕ)x[n] = A \cos(\omega_0 n + \phi) x[n]=Acos(ω0n+ϕ)
其中:
- AAA 为振幅;
- ω0\omega_0ω0 为角频率(单位:rad),有效范围 [−π,π][-\pi, \pi][−π,π];
- ϕ\phiϕ 为初相位(单位:rad)。
2. 频率特性
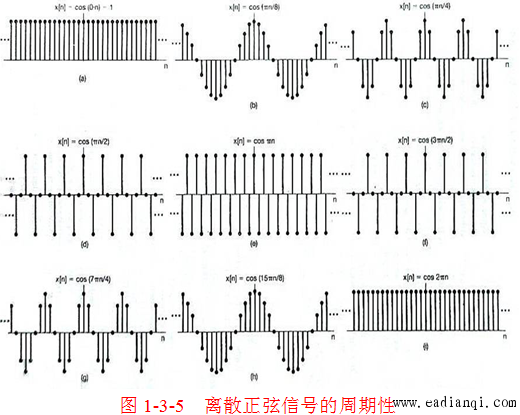
离散正弦序列的包络频率随 ω0\omega_0ω0 的变化规律如下:
- 当 ω0=0\omega_0 = 0ω0=0 或 ω0=2kπ\omega_0 = 2k\piω0=2kπ(kkk 为整数)时,x[n]=Acos(ϕ)x[n] = A \cos(\phi)x[n]=Acos(ϕ)(直流序列,包络频率最低);
- 当 ω0\omega_0ω0 从 000 增至 π\piπ 时,包络频率逐渐增高;
- 当 ω0=π\omega_0 = \piω0=π 时,x[n]=Acos(πn+ϕ)=A(−1)ncos(ϕ)x[n] = A \cos(\pi n + \phi) = A(-1)^n \cos(\phi)x[n]=Acos(πn+ϕ)=A(−1)ncos(ϕ)(包络频率最高);
- 当 ω0\omega_0ω0 从 π\piπ 增至 2π2\pi2π 时,包络频率逐渐降低,最终回到直流序列。
重要结论:离散正弦序列的最高包络频率为 π\piπ。
(三)连续与离散正弦信号对比
| 特性 | 连续时间正弦信号 cos(ω0t)\cos(\omega_0 t)cos(ω0t) | 离散时间正弦序列 cos(ω0n)\cos(\omega_0 n)cos(ω0n) |
|---|---|---|
| 振荡频率 | ω0\omega_0ω0 不同,信号不同 | 频率相差 2π2\pi2π 整数倍,信号相同 |
| 周期性 | 对任意 ω0≠0\omega_0 \neq 0ω0=0 均为周期信号 | 仅当 ω02π=mN\large\frac{\omega_0}{2\pi} = \frac{m}{N}2πω0=Nm(m,Nm,Nm,N 为正整数)时为周期序列 |
| 基波频率 | ω0\omega_0ω0 | ω0m\frac{\omega_0}{m}mω0(mmm 为最简分数分子) |
| 基波周期 | T0=2πω0T_0 = \frac{2\pi}{\omega_0}T0=ω02π(ω0≠0\omega_0 \neq 0ω0=0) | N0=2mπω0N_0 = \frac{2m\pi}{\omega_0}N0=ω02mπ(ω0≠0\omega_0 \neq 0ω0=0,取最小正整数) |
(四)单位脉冲序列
单位脉冲序列(又称单位样值序列)是离散时间信号中最基本的信号,具有“采样”特性。
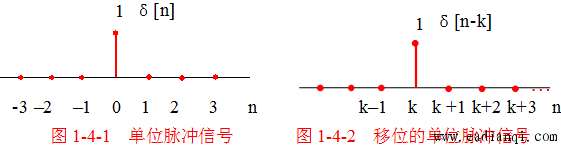
1. 脉冲信号
δ[n]={1n=00n≠0\delta[n] = \begin{cases} 1 & n = 0 \\ 0 & n \neq 0 \end{cases} δ[n]={10n=0n=0
2. 移位脉冲信号
移位 kkk 个单位的单位脉冲序列:
δ[n−k]={1n=k0n≠k\delta[n - k] = \begin{cases} 1 & n = k \\ 0 & n \neq k \end{cases} δ[n−k]={10n=kn=k
其中:
- 当 k>0k > 0k>0 时,序列右移 kkk 个单位;
- 当 k<0k < 0k<0 时,序列左移 ∣k∣|k|∣k∣ 个单位。
3. 采样性质
单位脉冲序列可提取信号在特定离散时间点的幅度值(采样):
- 采样 n=0n = 0n=0 处幅度:x[n]δ[n]=x[0]δ[n]x[n] \delta[n] = x[0] \delta[n]x[n]δ[n]=x[0]δ[n];
- 采样 n=n0n = n_0n=n0 处幅度:x[n]δ[n−n0]=x[n0]δ[n−n0]x[n] \delta[n - n_0] = x[n_0] \delta[n - n_0]x[n]δ[n−n0]=x[n0]δ[n−n0]。
(五)单位阶跃序列
单位阶跃序列可由单位脉冲序列累加得到,常用于表示信号的“起始”特性。
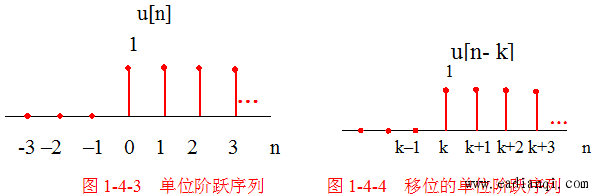
1. 阶跃序列
u[n]={1n≥00n<0u[n] = \begin{cases} 1 & n \geq 0 \\ 0 & n < 0 \end{cases} u[n]={10n≥0n<0
2. 移位阶跃序列
移位 kkk 个单位的单位阶跃序列:
u[n−k]={1n≥k0n<ku[n - k] = \begin{cases} 1 & n \geq k \\ 0 & n < k \end{cases} u[n−k]={10n≥kn<k
其中:
- 当 k>0k > 0k>0 时,序列右移 kkk 个单位;
- 当 k<0k < 0k<0 时,序列左移 ∣k∣|k|∣k∣ 个单位。
3. 单位脉冲序列与单位阶跃序列的关系
-
差分关系:单位脉冲序列是单位阶跃序列的一阶后向差分:
δ[n]=u[n]−u[n−1]\delta[n] = u[n] - u[n - 1] δ[n]=u[n]−u[n−1] -
累加关系:单位阶跃序列是单位脉冲序列从 −∞-\infty−∞ 到 nnn 的累加:
u[n]=∑m=−∞nδ[m]u[n] = \sum_{m=-\infty}^{n} \delta[m] u[n]=m=−∞∑nδ[m]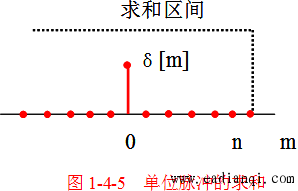
单位脉冲序列的采样性质: -
信号在 n=0n = 0n=0 时的采样:
x[n]δ[n]=x[0]δ[n]x[n] \delta[n] = x[0] \delta[n] x[n]δ[n]=x[0]δ[n] -
信号在 n=n0n = n_0n=n0 时的采样:
x[n]δ[n−n0]=x[n0]δ[n−n0]x[n] \delta[n - n_0] = x[n_0] \delta[n - n_0] x[n]δ[n−n0]=x[n0]δ[n−n0]
八、信号运算与变换的工程应用
在信号与系统的工程实践中,前述信号的运算、变换及典型信号模型并非孤立存在,而是广泛应用于通信、控制、图像处理等领域,以下结合文档中核心概念补充其应用逻辑:
(一)信号时移与尺度变换的应用
- 通信系统中的信号同步:在数字通信接收端,需通过时移操作(调整 t0t_0t0 或 mmm)对齐接收信号与本地参考信号的时间基准,避免因传输时延导致的码间串扰。例如,对离散接收序列 x[n−m]x[n - m]x[n−m] 调整 mmm 值,使接收码元与本地采样时钟同步。
- 语音信号的变速播放:语音信号本质是声压随时间变化的连续信号 x(t)x(t)x(t),通过尺度变换 x(at)x(at)x(at) 可实现变速:当 a>1a > 1a>1 时,信号时域压缩,播放速度加快(音调升高);当 0<a<10 < a < 10<a<1 时,信号时域扩展,播放速度减慢(音调降低),且需通过插值处理避免离散信号压缩时的采样点丢失问题。
(二)能量信号与功率信号的工程判定
在通信系统设计中,需根据信号的能量/功率特性选择传输方案:
- 能量信号(如脉冲信号):能量集中在有限时间内,适合短距离、突发式传输(如雷达探测信号),需重点关注信号的峰值能量以避免传输链路过载;
- 功率信号(如正弦载波信号):功率有限但能量无限,适合长距离、持续式传输(如广播电台的载波信号),需重点控制信号的平均功率以满足频谱规范和设备功耗要求;
- 非能量非功率信号(如斜坡信号)因能量和功率均无界,实际工程中需通过截断处理转化为能量信号后使用。
(三)周期信号的谐波分解与信号传输
根据文档中“周期信号可分解为成谐波关系的正弦信号线性组合”的结论,在通信与信号处理中可实现:
- 信号调制:将低频基带信号(如语音信号)与高频正弦载波信号相乘,本质是利用正弦信号的周期性和谐波特性,将基带信号频谱搬移至高频频段,以适应无线信道的传输特性(如射频信号传输需符合特定频段的频谱规划);
- 频谱分析:通过傅里叶级数分解,可获取周期信号的各次谐波分量(基波频率 ω0\omega_0ω0 的整数倍),进而分析信号的频谱结构,为滤波器设计提供依据(如通过滤除高次谐波实现信号降噪)。
(四)单位脉冲序列的采样应用
离散单位脉冲序列 δ[n]\delta[n]δ[n] 的采样特性是数字信号处理的基础:
- 信号采样:在模数转换(ADC)过程中,连续时间信号 x(t)x(t)x(t) 与周期性脉冲序列(由 δ[n]\delta[n]δ[n] 扩展得到)相乘,得到离散序列 x[n]=x(nTs)x[n] = x(nT_s)x[n]=x(nTs)(TsT_sTs 为采样周期),且需满足奈奎斯特采样定理(采样频率 fs=1/Tsf_s = 1/T_sfs=1/Ts 大于信号最高频率的2倍),避免频谱混叠;
- 系统建模:在离散系统分析中,单位脉冲序列 δ[n]\delta[n]δ[n] 可作为“测试信号”,通过测量系统对 δ[n]\delta[n]δ[n] 的响应(单位脉冲响应 h[n]h[n]h[n]),利用卷积运算求解系统对任意输入信号的响应,简化系统设计与分析流程。
(五)信号奇偶分解的噪声抑制
信号的奇偶分解特性可用于噪声抑制:实际采集的信号常包含偶对称噪声(如直流偏移)和奇对称噪声(如差分干扰),通过分解得到偶分量 xe(t)x_e(t)xe(t) 和奇分量 xo(t)x_o(t)xo(t),可针对性滤除某类噪声。例如,在生物医学信号(如心电图信号)处理中,通过提取偶分量可去除因电极接触不良导致的奇对称干扰,提升信号质量。
九、小结:信号类型 / 运算公式
连续信号能量
E∞=limT→∞∫−TT∣x(t)∣2dtE_{\infty} = \lim_{T \to \infty} \int_{-T}^{T} |x(t)|^2 \, dtE∞=T→∞lim∫−TT∣x(t)∣2dt
ttt 是连续时间变量;TTT 是积分时间区间。
离散信号能量
E=limN→∞∑n=−NN∣x[n]∣2E = \lim_{N \to \infty} \sum_{n=-N}^{N} |x[n]|^2E=N→∞limn=−N∑N∣x[n]∣2
nnn 是离散时间变量(整数);NNN 是求和区间边界。
连续周期信号
x(t)=x(t+kT0)(k=0,±1,…)x(t) = x(t + kT_0) \quad (k = 0, \pm1, \dots)x(t)=x(t+kT0)(k=0,±1,…)
T0T_0T0 是基波周期;ω0=2π/T0\omega_0 = 2\pi/T_0ω0=2π/T0 是基波频率。
离散周期信号
x[n]=x[n+mN0](m=0,±1,…)x[n] = x[n + mN_0] \quad (m = 0, \pm1, \dots)x[n]=x[n+mN0](m=0,±1,…)
N0N_0N0 是基波周期;ω0=2π/N0\omega_0 = 2\pi/N_0ω0=2π/N0 是基波频率。
连续信号奇偶分解
xe(t)=12[x(t)+x(−t)]x_e(t) = \frac{1}{2}[x(t) + x(-t)]xe(t)=21[x(t)+x(−t)]
xo(t)=12[x(t)−x(−t)]x_o(t) = \frac{1}{2}[x(t) - x(-t)]xo(t)=21[x(t)−x(−t)]
xe(t)x_e(t)xe(t) 是偶分量;xo(t)x_o(t)xo(t) 是奇分量。
离散信号奇偶分解
xe[n]=12[x[n]+x[−n]]x_e[n] = \frac{1}{2}[x[n] + x[-n]]xe[n]=21[x[n]+x[−n]]
xo[n]=12[x[n]−x[−n]]x_o[n] = \frac{1}{2}[x[n] - x[-n]]xo[n]=21[x[n]−x[−n]]
xe[n]x_e[n]xe[n] 是偶分量;xo[n]x_o[n]xo[n] 是奇分量。
复指数信号(连续)
x(t)=Ce(r+jω0)tx(t) = C e^{(r + j\omega_0)t}x(t)=Ce(r+jω0)t
CCC 是复振幅;rrr 是衰减/增长系数;ω0\omega_0ω0 是角频率。
复指数序列(离散)
x[n]=Cαn或x[n]=Ceβnx[n] = C \alpha^n \quad \text{或} \quad x[n] = C e^{\beta n}x[n]=Cαn或x[n]=Ceβn
CCC 是复振幅;α=eβ\alpha = e^{\beta}α=eβ 是复底数;β\betaβ 是复频率。
单位脉冲序列
δ[n]={1n=00n≠0\delta[n] = \begin{cases} 1 & n = 0 \\ 0 & n \neq 0 \end{cases}δ[n]={10n=0n=0
仅在 n=0n = 0n=0 处取值为1,其余时刻为0。
单位阶跃序列
u[n]={1n≥00n<0u[n] = \begin{cases} 1 & n \geq 0 \\ 0 & n < 0 \end{cases}u[n]={10n≥0n<0
仅在 n≥0n \geq 0n≥0 处取值为 1,其余时刻为 0。
符号规范说明:
- 连续时间信号用圆括号表示(如 x(t)x(t)x(t)),离散时间信号用方括号表示(如 x[n]x[n]x[n]),避免混淆;
- 角频率 ω0\omega_0ω0 单位为 rad(离散)或 rad/s(连续),周期 T0T_0T0(连续)单位为 s,N0N_0N0(离散)为无量纲整数;
- 复指数信号中的幅度 ∣C∣|C|∣C∣、初相位 θ\thetaθ 均为实数,确保物理意义明确(幅度非负,相位范围为 [−π,π][-\pi, \pi][−π,π])。
via:
- 信号的描述
https://www.eadianqi.com/zc/xinhaoyuxitong/4274.html - 信号的分类
https://www.eadianqi.com/zc/xinhaoyuxitong/4275.html - 信号的时移
https://www.eadianqi.com/zc/xinhaoyuxitong/4276.html - 信号的反射
https://www.eadianqi.com/zc/xinhaoyuxitong/4277.html - 信号的尺度变换
https://www.eadianqi.com/zc/xinhaoyuxitong/4278.html - 信号的奇偶分解
https://www.eadianqi.com/zc/xinhaoyuxitong/4279.html - 信号的加减运算
https://www.eadianqi.com/zc/xinhaoyuxitong/4280.html - 信号的相乘运算
https://www.eadianqi.com/zc/xinhaoyuxitong/4281.html - 信号的微分运算
https://www.eadianqi.com/zc/xinhaoyuxitong/4282.html - 信号的积分运算
https://www.eadianqi.com/zc/xinhaoyuxitong/4283.html - 连续指数信号与正弦信号
https://www.eadianqi.com/zc/xinhaoyuxitong/4284.html - 离散时间复指数信号与正弦信号
https://www.eadianqi.com/zc/xinhaoyuxitong/4285.html - 离散的单位脉冲信号与阶跃信号
https://www.eadianqi.com/zc/xinhaoyuxitong/4286.html
