《强化学习数学原理》学习笔记10——策略迭代

策略迭代（Policy Iteration）算法是另一个求解最优策略的算法。

一、策略迭代的核心思想

策略迭代算法主要包含两个关键步骤，循环执行这两个步骤，直到得到最优策略。

（一）策略评估（Policy Evaluation）

对于当前的策略 ${\pi }_k$，计算每个状态的价值 $v_{{\pi }_k}$。这一步的目的是衡量上一次迭代得到的策略 ${\pi }_k$。此时要用到贝尔曼期望方程：

$$v_{{\pi }_k}=r_{{\pi }_k}+\gamma P_{{\pi }_k}{v}_{{\pi }_k}\text{\hspace{1em}(1)}$$

其中，${\pi }_k$ 是上一次迭代得到的策略，$v_{{\pi }_k}$ 是该策略对应的状态值，$r_{{\pi }_k}$ 和 $P_{{\pi }_k}$ 通过系统模型得到。

（二）策略改进（Policy Improvement）

这一步基于策略评估结果改进策略，从而得到新策略。具体而言，在第一步中计算出 $v_{{\pi }_k}$ 后，就能通过下式得到一个新策略 ${\pi }_{k+1}$：

$${\pi }_{k+1}=\arg \underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}_{{\pi }_k})\text{\hspace{1em}(2)}$$

在对算法有了上述描述后，自然会引出三个问题：

• 在策略评估步骤中，如何求解状态价值 $v_{{\pi }_k}$？
• 在策略改进步骤中，为何新策略 ${\pi }_{k+1}$ 比 ${\pi }_k$ 更好？
• 该算法为何最终能收敛到最优策略？

接下来我们逐一回答这些问题。

1、策略评估步骤中如何计算状态价值 $v_{{\pi }_k}$？

有两种求解式 (1) 中贝尔曼方程的方法，现在简要记录一下。

第一种是闭式解：
$$v_{{\pi }_k}=(I-\gamma P_{{\pi }_k}{)}^{-1}{r}_{{\pi }_k}\text{\hspace{1em}(3)}$$
这种闭式解对理论分析很有用，但实际实现效率不高，因为计算矩阵的逆需要借助其他数值算法。

第二种是易于实现的迭代算法：
$$v_{{\pi }_k}^{(j+1)}=r_{{\pi }_k}+\gamma P_{{\pi }_k}{v}_{{\pi }_k}^{(j)},j=0,1,2,\dots \text{\hspace{1em}(4)}$$

其中 $v_{{\pi }_k}^{(j)}$ 表示对 $v_{{\pi }_k}$ 的第 $j$ 次估计值。从任意初始猜测 $v_{{\pi }_k}^{(0)}$ 开始，当 $j\to \infty$ 时，能保证 $v_{{\pi }_k}^{(j)}\to v_{{\pi }_k}$ ，这也是迭代算法的理论基础。

也就是说，在策略迭代过程中（式（1）），嵌入了另一种迭代算法（式 (4)）。理论上，这种嵌入的迭代算法需要无限步（即 $j\to \infty$）才能收敛到真实的状态价值 $v_{{\pi }_k}$，但这在实际中是不可能实现的。在实际应用中，当满足某个准则时，迭代过程就会终止。例如，终止准则可以是 $\Vert v_{{\pi }_k}^{(j+1)}-v_{{\pi }_k}^{(j)}\Vert$ 小于预先指定的阈值，或者 $j$ 超过预先指定的值。如果不进行无限次迭代，我们只能得到 $v_{{\pi }_k}$ 的一个不精确值，而这个值会被用于后续的策略改进步骤。这会造成问题吗？答案是否定的。这在学习截断策略迭代算法中会清楚原因，此处不做进一步说明。

2、策略改进步骤中，为何 ${\pi }_{k+1}$ 比 ${\pi }_k$ 更好？

策略改进步骤能够改进给定的策略，如下所示。

定理 1（策略改进）：如果 ${\pi }_{k+1}=\arg {\max }_{\pi }(r_{\pi }+\gamma P_{\pi }{v}_{{\pi }_k})$，那么 $v_{{\pi }_{k+1}}\ge v_{{\pi }_k}$。

这里，$v_{{\pi }_{k+1}}\ge v_{{\pi }_k}$ 意味着对于所有状态 $s$，都有 $v_{{\pi }_{k+1}}(s)\ge v_{{\pi }_k}(s)$。这个定理的证明如下。

定理 1 的证明
由于 $v_{{\pi }_{k+1}}$ 和 $v_{{\pi }_k}$ 都是状态价值，它们满足贝尔曼方程：
$$\{\begin{array}{l}{v}_{{\pi }_{k+1}}=r_{{\pi }_{k+1}}+\gamma P_{{\pi }_{k+1}}{v}_{{\pi }_{k+1}}\\ v_{{\pi }_k}=r_{{\pi }_k}+\gamma P_{{\pi }_k}{v}_{{\pi }_k}\end{array}\text{\hspace{1em}(5)}$$

因为 ${\pi }_{k+1}=\arg {\max }_{\pi }(r_{\pi }+\gamma P_{\pi }{v}_{{\pi }_k})$，所以我们知道：
$$r_{{\pi }_{k+1}}+\gamma P_{{\pi }_{k+1}}{v}_{{\pi }_k}\ge r_{{\pi }_k}+\gamma P_{{\pi }_k}{v}_{{\pi }_k}\text{\hspace{1em}(6)}$$

由此可得：
$$\begin{array}{rl}{v}_{{\pi }_k}-v_{{\pi }_{k+1}}& =(r_{{\pi }_k}+\gamma P_{{\pi }_k}{v}_{{\pi }_k})-(r_{{\pi }_{k+1}}+\gamma P_{{\pi }_{k+1}}{v}_{{\pi }_{k+1}})\\ & \le (r_{{\pi }_{k+1}}+\gamma P_{{\pi }_{k+1}}{v}_{{\pi }_k})-(r_{{\pi }_{k+1}}+\gamma P_{{\pi }_{k+1}}{v}_{{\pi }_{k+1}})\\ & \le \gamma P_{{\pi }_{k+1}}(v_{{\pi }_k}-v_{{\pi }_{k+1}})\end{array}\text{\hspace{1em}(7)}$$

反复调用式（7）可得：
$$\begin{array}{rl}{v}_{{\pi }_k}-v_{{\pi }_{k+1}}& \le {\gamma }^2{P}_{{\pi }_{k+1}}^2(v_{{\pi }_k}-v_{{\pi }_{k+1}})\le \cdots \le {\gamma }^n{P}_{{\pi }_{k+1}}^n(v_{{\pi }_k}-v_{{\pi }_{k+1}})\\ & \le \underset{n\to \infty }{\lim }{\gamma }^n{P}_{{\pi }_{k+1}}^n(v_{{\pi }_k}-v_{{\pi }_{k+1}})=0\end{array}\text{\hspace{1em}(8)}$$

这个极限成立是因为当 $n\to \infty$ 时，${\gamma }^n\to 0$，并且对于任意 $n$，$P_{{\pi }_{k+1}}^n$ 是一个非负的随机矩阵。这里，随机矩阵指的是所有行的和都等于 1 的非负矩阵。所以， $v_{{\pi }_k}-v_{{\pi }_{k+1}}\le 0$，证明策略 ${\pi }_{k+1}$ 要优于 ${\pi }_k$。

3、该算法为何最终能收敛到最优策略？

策略迭代算法会生成两个序列，一个是策略序列{π0,π1,…,πk,… }\{\pi_0, \pi_1, \dots, \pi_k, \dots\}{π0​,π1​,…,πk​,…}，另一个是状态价值序列{vπ0,vπ1,…,vπk,… }\{v_{\pi_0}, v_{\pi_1}, \dots, v_{\pi_k}, \dots\}{vπ0​​,vπ1​​,…,vπk​​,…}。

假设$v^{\ast }$是最优状态价值，根据引理 1，我们知道对于所有的$k$，都有$v_{{\pi }_k}\le v^{\ast }$。又因为策略是不断改进的，所以状态价值序列满足$v_{{\pi }_0}\le v_{{\pi }_1}\le v_{{\pi }_2}\le \cdots \le v_{{\pi }_k}\le \cdots \le v^{\ast }$。

因此，$v_{{\pi }_k}$是一个非递减且有上界（$v^{\ast }$）的序列，根据单调收敛定理，当 $k\to \infty$ 时，$v_{{\pi }_k}$会收敛到一个常数，记为$v_{\infty }$。

定理 2（策略迭代的收敛性）：由策略迭代算法生成的状态价值序列 {vπk}k=0∞\{v_{\pi_k}\}_{k=0}^{\infty}{vπk​​}k=0∞​ 会收敛到最优状态价值 $v^{\ast }$。因此，策略序列 {πk}k=0∞\{\pi_k\}_{k=0}^{\infty}{πk​}k=0∞​ 会收敛到一个最优策略。

下面是该定理的证明：

定理 2 的证明
证明的思路是展示策略迭代算法比价值迭代算法收敛得更快。

具体来说，为了证明{vπk}k=0∞\{v_{\pi_k}\}_{k=0}^{\infty}{vπk​​}k=0∞​的收敛性，我们引入另一个由下式生成的序列{vk}k=0∞\{v_k\}_{k=0}^{\infty}{vk​}k=0∞​：
$$v_{k+1}=f(v_k)=\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}_k)\text{\hspace{1em}(9)}$$

这个迭代算法是值迭代算法。我们已经知道，对于任意初始值 $v_0$，$v_k$ 会收敛到 $v^{\ast }$。

对于 $k=0$ ，我们总能找到一个 $v_0$ ，使得对于任何 ${\pi }_0$，都有 $v_{{\pi }_0}\ge v_0$。

接下来，我们通过归纳法证明对于所有的$k$，都有$v_k\le v_{{\pi }_k}\le v^{\ast }$。

对于$k\ge 0$，假设$v_{{\pi }_k}\ge v_k$。

对于$k+1$，我们有：
$$\begin{array}{rl}{v}_{{\pi }_{k+1}}-v_{k+1}& =(r_{{\pi }_{k+1}}+\gamma P_{{\pi }_{k+1}}{v}_{{\pi }_{k+1}})-\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}_k)\\ & \ge (r_{{\pi }_{k+1}}+\gamma P_{{\pi }_{k+1}}{v}_{{\pi }_k})-\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}_k)\\ & \text{（因为根据引理 1，}{v}_{{\pi }_{k+1}}\ge v_{{\pi }_k}\text{，且}{P}_{{\pi }_{k+1}}\ge 0\text{）}\\ & =(r_{{\pi }_{k+1}}+\gamma P_{{\pi }_{k+1}}{v}_{{\pi }_k})-(r_{{\pi }_k^{\prime }}+\gamma P_{{\pi }_k^{\prime }}{v}_k)\\ & \text{（假设}{\pi }_k^{\prime }=\arg \underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}_k)\text{）}\\ & \ge (r_{{\pi }_k^{\prime }}+\gamma P_{{\pi }_k^{\prime }}{v}_{{\pi }_k})-(r_{{\pi }_k^{\prime }}+\gamma P_{{\pi }_k^{\prime }}{v}_k)\\ & \text{（因为}{\pi }_{k+1}=\arg \underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}_{{\pi }_k})\text{）}\\ & =\gamma P_{{\pi }_k^{\prime }}(v_{{\pi }_k}-v_k)\end{array}\text{\hspace{1em}(10)}$$

由于$v_{{\pi }_k}-v_k\ge 0$，且$P_{{\pi }_k^{\prime }}$是非负的，所以$P_{{\pi }_k^{\prime }}(v_{{\pi }_k}-v_k)\ge 0$，因此$v_{{\pi }_{k+1}}-v_{k+1}\ge 0$。

因此，我们可以通过归纳法证明，对于任何$k\ge 0$，都有$v_k\le v_{{\pi }_k}\le v^{\ast }$。由于$v_k$收敛到$v^{\ast }$，所以$v_{{\pi }_k}$也会收敛到$v^{\ast }$。

这个证明不仅展示了策略迭代算法的收敛性，还揭示了策略迭代和价值迭代算法之间的关系。大致来说，如果两种算法都从相同的初始猜测开始，由于策略评估步骤中嵌入了额外的迭代，策略迭代会比价值迭代收敛得更快。

二、策略迭代的元素形式与实现

为了实现策略迭代算法，我们需要研究它的元素形式（Elementwise form）。

（一）策略评估的元素形式

首先，策略评估步骤是从 $v_{{\pi }_k}=r_{{\pi }_k}+\gamma P_{{\pi }_k}{v}_{{\pi }_k}$ 中求解 $v_{{\pi }_k}$，所用到的迭代算法如式（4）所示，其元素形式为：
$$v_{{\pi }_k}^{(j+1)}(s)=\sum _a{\pi }_k(a|s)\left(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v_{{\pi }_k}^{(j)}(s^{\prime })\right),s\in \mathcal{S}\text{\hspace{1em}(11)}$$
其中 $j=0,1,2,\dots$。这里，$v_{{\pi }_k}^{(j)}(s)$ 表示在策略 ${\pi }_k$ 下，对状态 $s$ 的价值的第 $j$ 次迭代估计值。从每个状态 $s$ 的任意初始猜测 $v_{{\pi }_k}^{(0)}(s)$ 开始，随着迭代进行，$v_{{\pi }_k}^{(j)}(s)$ 会逐渐收敛到策略 ${\pi }_k$ 下状态 $s$ 的真实价值 $v_{{\pi }_k}(s)$。

（二）策略改进的元素形式

其次，策略改进步骤是求解 ${\pi }_{k+1}=\arg {\max }_{\pi }(r_{\pi }+\gamma P_{\pi }{v}_{{\pi }_k})$，该方程的元素形式为：
$${\pi }_{k+1}(s)=\arg \underset{\pi }{\max }\sum _a\pi (a|s)\underset{q_{{\pi }_k}(s,a)}{\underbrace{\left(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v_{{\pi }_k}(s^{\prime })\right)}},s\in \mathcal{S}\text{\hspace{1em}(12)}$$
其中 $q_{{\pi }_k}(s,a)$ 是策略 ${\pi }_k$ 下的动作价值（action value）。令 $a_k^{\ast }(s)=\arg {\max }_a{q}_{{\pi }_k}(s,a)$，那么贪心最优策略为：
$${\pi }_{k+1}(a|s)=\{\begin{array}{ll}1,& a=a_k^{\ast }(s),\\ 0,& a\ne a_k^{\ast }(s)\end{array}\text{\hspace{1em}(13)}$$
这意味着，在状态 $s$ 下，新策略 ${\pi }_{k+1}$ 会确定性地选择能使动作价值 $q_{{\pi }_k}(s,a)$ 最大的动作 $a_k^{\ast }(s)$，而对其他动作的选择概率为 $0$。
算法流程的伪代码如下所示：

三、策略迭代的示例说明

为了更直观地理解策略迭代算法的执行过程，我们来看一个简单示例。

（一）示例背景

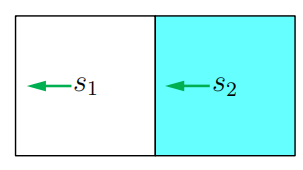
考虑如图所示的简单示例，存在两个状态，有三个可能的动作：A={aℓ,a0,ar}\mathcal{A} = \{a_{\ell}, a_0, a_r\}A={aℓ​,a0​,ar​}，分别代表向左移动、保持不变和向右移动。奖励设置为 $r_{\text{boundary}}=-1$，$r_{\text{target}}=1$，折扣率 $\gamma =0.9$。

（二）算法分步实现

我们逐步展示策略迭代算法的实现过程。当 $k=0$ 时，从上图所示的初始策略开始，这个策略并不好，因为它没有朝着目标区域移动。接下来展示如何应用策略迭代算法得到最优策略。

1、策略评估步骤

首先，在策略评估步骤中，需要求解贝尔曼方程：
$$\{\begin{array}{l}{v}_{{\pi }_0}(s_1)=-1+\gamma v_{{\pi }_0}(s_1)\\ v_{{\pi }_0}(s_2)=0+\gamma v_{{\pi }_0}(s_1)\end{array}\text{\hspace{1em}(14)}$$
由于方程简单，可以手动求解得到：
$$v_{{\pi }_0}(s_1)=-10,v_{{\pi }_0}(s_2)=-9\text{\hspace{1em}(15)}$$
在实际中，也可以用式 (4) 的迭代算法求解。例如，选择初始状态价值 $v_{{\pi }_0}^{(0)}(s_1)=v_{{\pi }_0}^{(0)}(s_2)=0$，根据式 (4) 有：
$$\{\begin{array}{l}{v}_{{\pi }_0}^{(1)}(s_1)=-1+\gamma v_{{\pi }_0}^{(0)}(s_1)=-1\\ v_{{\pi }_0}^{(1)}(s_2)=0+\gamma v_{{\pi }_0}^{(0)}(s_1)=0\end{array}\text{\hspace{1em}(16)}$$
$$\{\begin{array}{l}{v}_{{\pi }_0}^{(2)}(s_1)=-1+\gamma v_{{\pi }_0}^{(1)}(s_1)=-1.9\\ v_{{\pi }_0}^{(2)}(s_2)=0+\gamma v_{{\pi }_0}^{(1)}(s_1)=-0.9\end{array}\text{\hspace{1em}(17)}$$
$$\{\begin{array}{l}{v}_{{\pi }_0}^{(3)}(s_1)=-1+\gamma v_{{\pi }_0}^{(2)}(s_1)=-2.71\\ v_{{\pi }_0}^{(3)}(s_2)=0+\gamma v_{{\pi }_0}^{(2)}(s_1)=-1.71\end{array}\text{\hspace{1em}(18)}$$
$⋮$
随着迭代次数增加，可观察到趋势：$v_{{\pi }_0}^{(j)}(s_1)\to v_{{\pi }_0}(s_1)=-10$，$v_{{\pi }_0}^{(j)}(s_2)\to v_{{\pi }_0}(s_2)=-9$。

2、策略改进步骤

其次，在策略改进步骤中，关键是计算每个状态 - 动作对的 $q_{{\pi }_0}(s,a)$，可通过下表演示该过程：

表 1：图 4.3 示例中 $q_{{\pi }_k}(s,a)$ 的表达式

$q_{{\pi }_k}(s,a)$	$a_{\ell }$	$a_0$	$a_r$
$s_1$	$-1+\gamma v_{{\pi }_k}(s_1)$	$0+\gamma v_{{\pi }_k}(s_1)$	$1+\gamma v_{{\pi }_k}(s_2)$
$s_2$	$0+\gamma v_{{\pi }_k}(s_1)$	$1+\gamma v_{{\pi }_k}(s_2)$	$-1+\gamma v_{{\pi }_k}(s_2)$

将之前策略评估步骤得到的 $v_{{\pi }_0}(s_1)=-10$，$v_{{\pi }_0}(s_2)=-9$ 代入上表：

表 2：$k=0$ 时 $q_{{\pi }_k}(s,a)$ 的值

$q_{{\pi }_0}(s,a)$	$a_{\ell }$	$a_0$	$a_r$
$s_1$	$-10$	$-9$	$-7.1$
$s_2$	$-9$	$-7.1$	$-9.1$

通过寻找 $q_{{\pi }_0}$ 的最大值，得到改进后的策略 ${\pi }_1$：
$${\pi }_1(a_r|s_1)=1,{\pi }_1(a_0|s_2)=1$$
这个策略如下图所示，显然是最优的：

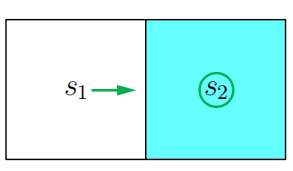
上述过程表明，在这个简单示例中，单次迭代就足以找到最优策略。对于更复杂的示例，则需要更多次迭代。

在策略的演变过程中，还存在以下两个规律：

• 首先，如果我们观察策略的演变过程，会发现一个有趣的规律：靠近目标区域的状态会比远离目标的状态更早找到最优策略。只有当靠近目标的状态先找到通往目标的轨迹，更远的状态才能找到途经这些靠近目标的状态以抵达目标的轨迹。
• 其次，状态价值的空间分布呈现出一个有趣的规律：距离目标更近的状态具有更大的状态价值。这种规律的原因在于，从更远的状态出发的智能体必须经过很多步才能获得正奖励，而这样的奖励会被严重折扣，因此相对较小。