数据结构与算法:合集1.0版
文章目录
- 引入:
- 第一章 绪论
- 1.1、数据结构的研究内容
- 1.1.1、数据结构的核心
- 1.1.2、什么是数据结构?
- 数值计算
- 非数据计算。
- 例1、学生学籍管理系统
- 例2 人机对弈问题。井字棋
- 例3、地图导航——求最短路径(最快路径)
- 1.2、基本概念和术语
- 1.2.1、数据、数据元素、数据项和数据对象
- 数据元素
- 数据项
- 数据、数据元素、数据项三者之间的关系:
- 数据对象
- 数据元素、数据对象与数之间的关系
- 1.2.2、数据结构(Data Structure)
- 数据结构
- 数据结构包括以下三个方面的内容:
- 数据结构的两个层次
- 逻辑结构
- 物理结构(存储结构)
- 逻辑结构与存储结构的关系
- 逻辑结构的种类
- 划分方法一
- 划分方式二——四类基本逻辑结构
- 存储结构的种类(四种基本的存储结构)
- 顺序存储结构:
- 链式存储结构:
- 索引存储结构:
- 散列存储结构:
- 1.2.3、抽象类型和抽象数据类型
- 引入概念:
- 数据类型(Data Type)
- 抽象数据类型(Abstract Data Type,ADT)
- 概念小结:(1.1-1.2内容总结)
- 1.3、抽象数据类型的表现与实现
- 1.3.1、抽象数据类型的表现
- 1.3.2、抽象数据类型的实现
- 1.4、算法和算法分析
- 1.4.1、算法的定义:
- 1.4.2、算法的描述:
- 1.4.3、算法与程序:
- 1.4.4、算法特性:
- 1.4.5、算法设计的要求:
- 1.4.6、算法分析:
- 1.4.7、算法时间效率的度量
- 1.4.8、算法时间复杂度定义
- 1.4.9、分析算法算法时间的基本方法
- 1.4.10、算法时间复杂度分析(例题)todo
- 1.4.11、算法时间复杂度计算
- 1.4.12、算法时间效率的比较
- 1.4.13、渐进空间复杂度
- 1.4.14、算法空间复杂分析例题todo
- 1.4.15、设计好算法的过程
- 第二章 线性表
- 2.1、线性表的定义和特点
- 2.1.1、引入概念:
- 2.1.2、线性表(Linear List):
- 2.1.3、线性表的逻辑特征:
- 2.2、案例引入todo
- 2.2.1、一元多项式的运算:
- 2.2.2、稀疏多项式的运算
- 2.2.3、图书管理系统
- 2.3、线性表的类型定义
- 2.3.1、线性表的类型定义
- 2.3.2、基本操作(一)
- 2.3.3、基本操作(二)
- 2.3.4、基本操作(三)
- 2.3.5、基本操作(四)
- 2.3.6、基本操作(五)
- 2.3.7、基本操作(六)
- 2.4、线性表的顺序表示和实现
- 2.4.1、线性表的顺序存储表示
- 2.4.2、线性顺序结构的图示:
- 2.4.3、多项式的顺序存储结构类型定义
- 2.4.4、补充:类C语言有关操作
- 2.4.4.1、补充:元素类型说明
- 2.4.4.2、补充:数组定义
- 2.4.4.3、补充:C语言的内存动态分配
- 2.4.4.4、补充:C++的动态存储分配
- 2.4.4.5、补充:C++中的参数传递
- 2.4.4.5.1、值传递:
- 2.4.4.5.2、传地址:
- 2.4.4.5.2.1、传地址方式——指针变量作为参数
- 2.4.4.5.2.2、传地址方式——数组名作为参数
- 2.4.4.5.2.2、传地址方式——引用类型作为参数(C++)
- 2.4.4.5.2.3、引用类型做形参的三点说明
- 2.4、线性表的顺序表示和实现
- 2.4.1、线性表的顺序存储表示
- 2.4.1.1、预备内容
- 2.4.1.2、顺序表示意图
- 2.4.2、顺序表基本操作的实现3
- 2.4.2.1、线性表的基本操作
- 2.4.2.2、操作算法中用到的预定义常量和类型
- 2.4.2.3、【算法2.1 】线性表L的初始化(参数用引用)
- 2.4.2.4、线性表L的销毁和清空。
- 2.4.2.5、求线性表L的长度和判断其是否为空。
- 2.4.2.6、【算法2.2 】顺序表中的取值(根据位置i获取相应数据元素的内容)
- 2.4.3、线性表的顺序表示和实现4
- 2.4.3.1、顺序表上的查找操作
- 2.4.3.2、【算法2.3 】顺序表中的查找
- 2.4.3.3、【算法2.3 】顺序表中的查找算法分析
- 2.4.3.4、平均查找长度ALS(Average Search Length):
- 2.4.4、线性表的顺序表示和实现5
- 2.4.4.1、顺序表的插入思路
- 插入位置在最后
- 插入位置在中间
- 插入位置在最前面
- 插入异常的两种情况:
- **总结:**
- 2.4.4.2、顺序表的插入的算法实现
- 2.4.4.3、顺序表的插入的算法分析(主要看时间效率)
- 2.4.5、线性表的顺序表示和实现6
- 2.4.5.1、顺序表的插删除思路
- 删除位置在最后
- 删除位置在中间
- 删除位置在最前面
- 总结
- 2.4.5.2、顺序表的算法实现
- 2.4.5.2、顺序表的算法分析
- 2.4.5、小结(2.4内容总结)
- 2.5-I、链式最基本的表示和实现——单链表
- 2.5.1、知识回顾以及引入链式:
- 2.5.2、两个经典案例
- 2.5.3、与链式存储有关的术语和示意图
- 2.5.4、讨论
- 2.5.5、知识回顾
- 2.5.6、单链表的定义和表示
- 2.5.7、单链表基本操作的实现
- 2.5.7.1、【单链表的初始化(算法2.6)】(带头结点的单链表)
- 2.5.7.2、【补充单链表的几个常用简单算法】
- 2.5.7.2.1、算法1:判断链表是否为空:
- 2.5.7.2.2、算法2:单链表的销毁:链表销毁后不存在。
- 2.5.7.2.3、算法3:清空单链表
- 2.5.7.2.4、算法4:求单链表的表长
- 2.5.8、单链表的基本操作的实现
- 2.5.8.1、算法1:取值——取单链表中第i个元素的内容
- 2.5.8.2、算法2:查找——取单链表中第i个元素的内容
- 2.5.8.2.1、按值查找
- 2.5.8.2.2、按值查找
- 2.5.8.3、算法3:插入——在第i个结点前插入值为e的新节点
- 2.5.8.4、算法4:删除——删除第i个结点
- 2.5.8.5、算法5:单链表的建立
- 2.5.8.5.1、头插法——元素插入在链表头部,也叫前插法。
- 2.5.8.5.2、尾插法——元素插入在链表尾部,也叫尾插法todo
- 2.5-II、链式其他形式的表示和实现——循环链表、双链表
- 2.5.1、循环链表
- 2.5.2、带尾指针的循环链表的合并
- 2.5.3、双向链表
- 2.5.4、算法1:双向链表的插入
- 2.5.5、算法2:双向链表的删除
- 2.5.6、单链表、循环链表和双链表的时间效率比较
- 2.6、顺序表的和链式表的比较
- 先总结链式表的优缺点
- 接着是顺序表和链表的比较
- 2.7、线性表的应用
- 2.7.1、线性表、有序表的合并————表示
- 2.7.2、线性表、有序表的合并————实现
- 2.8、案例分析与实现
- 第三章 栈和队列
- 3.1、栈和队列的定义和特点
- 3.1.1、普通线性表的插入和删除操作
- 3.1.2、栈的应用——后进先出
- 3.1.3、队列常见应用
- 3.1.4、栈的定义和特点
- 栈的相关概念
- 栈的示意图
- 总结:
- 3.1.5、队列的定义和特点
- 3.2、案例引入
- 3.2.1、案例3.1:进制转换
- 3.2.2、案例3.2:括号匹配
- 3.2.3、案例3.3:表达式求值
- 3.2.4、案例3.4:舞伴问题
- 3.3、栈的表示和操作的实现
- 3.3.1、栈的抽象数据类型的类型定义
- 3.3.2、顺序栈的表示
- 3.3.3、顺序栈的实现——涉及栈的相关操作
- 3.3.4、链栈的表示
- 3.3.5、链栈的实现
- 3.4、栈与递归
- 3.4.1、递归
- 3.5、队列的表示和操作的实现
- 3.5.1、队列的表示和实现
- 3.5.3、链式队列表示和实现
- 第四章 串 、数组和广义表
- 4.1、串的定义及其术语
- 4.2、案例引入
- 4.3、串的类型定义、存储结构及其运算、
- 4.3.1、串的类型定义、存储结构
- 4.3.2、串的模式匹配算法——最常用
- 4.3.2.1、Brute-Force简称BF算法,亦称简单匹配算法。采用穷举法的思路。
- 4.3.2.2、KMP(Knuth Morris Pratt)算法
- 4.4、数组
- 4.4.1、基本概念
- 4.4.2、如何定义数组的抽象数据类型及其操作
- 4.4.3、数组的顺序存储
- 4.4.4、特殊矩阵的压缩存储
- 4.4.4.1、对称矩阵:
- 4.4.4.2、三角矩阵:
- 4.4.4.3、对角矩阵(带状矩阵):
- 4.4.4.4、稀疏矩阵:
- 4.5、广义表
- 4.5.1、广义表的定义
- 4.5.2、广义表的性质
- 4.5.3、广义表与线性表的区别?
- 4.5.4、广义表的基本运算
- 4.6、案例分析与实现
- 第五章 树和二叉树
- 5.1、树和二叉树的定义
- 5.1.1、树的定义
- 5.1.2、树的基本术语
- 5.1.2、线性结构和树结构的区别
- 5.1.2、二叉树的定义
- 5.2、案例引入
- 5.3、树和二叉树的抽象数据类型定义
- 5.4、二叉树的性质和存储结构
- 5.4.1、两种特殊形式的二叉树
- 5.4.1.1、满二叉树
- 5.4.1.2、完全二叉树(Complete binary tree)
- 5.4.2-a、二叉树顺序存储结构
- 5.4.2.1、二叉树的顺序存储缺点:
- 5.4.2-b、二叉树链式存储结构
- 5.4.2-c、三叉链表——二叉树链表的扩展
- 5.5、遍历二叉树和线索二叉树
- 5.5.1、遍历二叉树
- 1、遍历二叉树算法描述
- 2、先、中、后序遍历二叉树的练习。
- 3、遍历的算法实现——先序,中序和后序遍历
- 4、遍历算法的分析
- 5、遍历二叉树的非递归算法——以中序为例
- 6、二叉树的层次遍历及其算法实现
- (1)二叉树的层次遍历
- (2)二叉树的算法实现
- 7、二叉树遍历算法的应用
- 二叉树的建立
- 复制二叉树
- 计算二叉树的深度
- 计算二叉树结点总数
- 计算二叉树叶子结点数(补充)
- 5.5.2、线索二叉树
- 5.6、树和森林
- 5.6.1、常见的树的结构
- 1、双亲表示法
- 2、孩子链表
- 3、孩子兄弟表示法(二叉树表示法,二叉树链表表示法)
- 5.6.2、树、森林与二叉树的转换
- 1、树转换成二叉树
- 2、二叉树转换成树——逆序操作
- 3、森林转化二叉树(二叉树与多棵树之间的关系)
- 4、二叉树转化森林
- 5.6.3、树与森林的遍历
- 1、树的遍历(三种方式)
- 2、森林的遍历
- 5.7 、哈夫曼树及其应用
- 5.7.1 、哈夫曼树的基本概念
- 5.7.2 、哈夫曼树的构造算法
- 1、哈夫曼算法(构造哈夫曼树的方法):口诀+详细步骤描述
- 2、哈夫曼树构造算法的实现
- 5.7.3 、哈夫曼编码
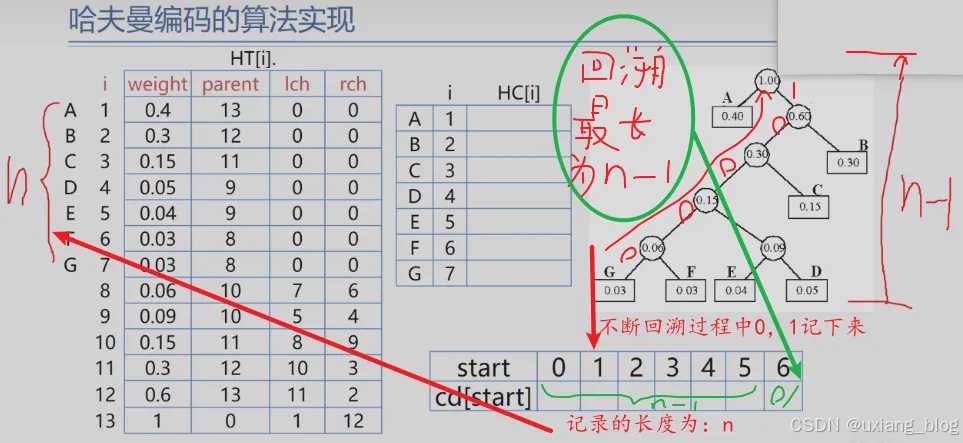
- 5.7.4 、哈夫曼编码的算法实现
- 5.7.5 、哈夫曼编码的应用举例
- 第六章 图
- 6.1、图的定义和基本术语
- 6.1.1、图的定义和术语
- 6.2、案例引入
- 6.2.1、六度空间理论
- 6.2.2、六度空间理论验证:
- 6.3、图的类型定义
- 6.4、图的存储结构
- 6.4.1、邻接矩阵
- 数组(邻接矩阵)表示法 todo
- 无向图的邻接矩阵表示法
- 有向图的邻接矩阵表示法
- 网(即有权图)的邻接矩阵表示法
- 邻接矩阵的存储表示:用两个数组分别存储顶点表和邻接矩阵
- 采用邻接矩阵表示创建无向网
- 邻接矩阵——有什么好处?
- 邻接矩阵——有什么不好?
- 6.4.2、链接表
- 邻接表的表示法(链式)
- 无向图
- 有向图
- 图的邻接表存储表示:
- 邻接表操作举例说明:
- 采用邻接表表示法创建无向网
- 6.4.3、十字链表和邻接多重表
- 1、十字链表——用于有向图
- 2、邻接多重表——用于无向图的另一种链式存储结构
- 6.5、图的遍历
- 6.5.1、遍历定义:
- 1、深度优先遍历(DFS)——一路走到黑,无路可走了往前退一步。
- 2、广度优先搜素(BFS - Breadth_First Search)
- DFS与BFS算法效率比较
- 6.6、图的应用
- 6.6.1、最小生成树
- 构成最小生成树方法一:普里姆(Prim)算法
- 构成最小生成树方法二:克鲁斯卡尔(Kruskal)算法。
- 两种算法比较:
- 6.6.2、最短路径
- Dijkstra(迪杰斯特拉)算法——单源最短路径
- Floyd(佛洛伊德)算法——所有顶点间的最短路径
- 6.6.3、扩扑排序
- 6.6.4、关键路径
- 6.7、案例分析与实现
- 第七章 查找
- 7.1、查找的基本概念
- 7.2、线性表的查找
- 7.2.1、顺寻查找(线性查找)
- 7.2.2、折半查找(二分或对分查找)
- 查找过程:
- 折半查找算法:(非递归算法)
- 折半查找——递归算法
- 折半查找的性能分析——判定树
- 折半查找的性能分析——ASL
- 7.2.3、分块查找
- 分块查找(索引顺序查找)todo
- 分块查找性能分析
- 分块查找优缺点
- 查找方法比较
- 7.3、树表的查找
- 7.3.1、二叉排序树
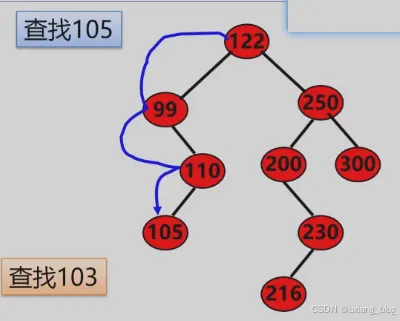
- 二叉树排序树的操作——查找
- 算法:二叉排序树的递归查找
- 二叉排序树的操作——插入
- 二叉排序树的操作——生成
- 二叉排序树的操作——删除
- 7.3.2、平衡二叉树
- 1、平衡二叉树的定义
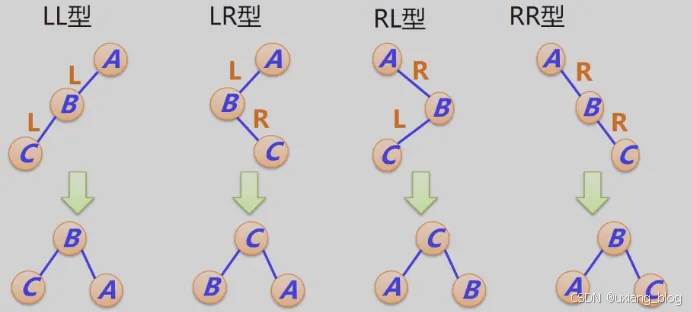
- 2、失衡二叉排序树的分析与调整
- 7.3.3、B-树
- 7.3.4、B+树
- 7.4、散列表的查找
- 7.4.1、散列表的基本概念
- 7.4.2、散列表的若干术语
- 7.4.3、散列函数的构造方法
- 7.4.4、散列表的查找
- 第八章 排序
- 8.1、基本概念和排序方法概述
- 8.1.1、概述
- 8.1.2、排序方法的分类
- 按存储介质可分为:
- 按比较器个数排序可分为:
- 按辅助空间可分为:
- 按稳定性可分为:
- 按自然性可分为:
- 8.1.3、学习内容
- 按排序依据原则
- 按排序所需工作量
- 8.2、插入排序
- 基本思想:
- 基本操作:有序插入
- 插入位置图示
- 8.2.1、直接插入排序:todo
- 直接插入排序———算法描述
- 直接插入排序——性能分析
- 8.2.2、折半插入排序
- 折半插入排序——算法描述
- 折半插入排序——算法分析todo
- 8.2.3、希尔排序
- 希尔排序————算法描述
- 希尔排序————算法分析
- 8.3、交换排序
- 1、冒泡排序——基于简单交换思想
- 冒泡排序算法分析
- 2、改进的交换排序——快速排序
- 快速排序算法分析:
- 8.4、选择排序
- 1、简单选择排序
- 简单选择排序算法分析
- 2、堆排序
- 筛选过程的算法描述为:
- 堆排序算法如下:
- 8.5、归并排序
- 8.6、基数排序
- 8.7、外部排序(略)
- 8.8、综合比较
- 1、各种排序方法比较
- 2、各种排序方法的综合比较
- 时间性能
- 空间性能
- 排序方法的稳定性能
- 关于“排序方法的时间复杂度的下限”
本文根据87师兄[B站up]同意转载于王卓老师的《数据结构与算法》课程历经10周写成,近期发布在CSDN上,里面有些加入了自己的理解[多为引用部分],不免有些错误,有错误之处可以在评论区指出,根据自己时间修改。此处整理成合文,省却一章章翻阅,方便查阅。
说明:引用部分是说明补充内容;红色字体为引出问题;紫色字体为专业术语或者重要部分;黑色粗体为文章结构所需。10.25.2025完结。
引入:
凭借一句话获得图灵奖的Pascal语言之父——Nicaklaus Wirth,让他获得图灵奖的这句话就是他提出的著名公式: “程序=数据结构+算法”,这个公式展示了程序的本质。
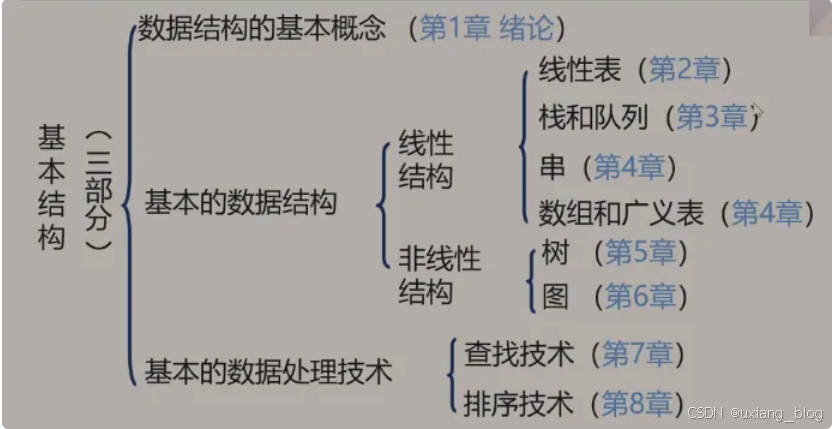
课程知识结构体系——这门课程是什么?
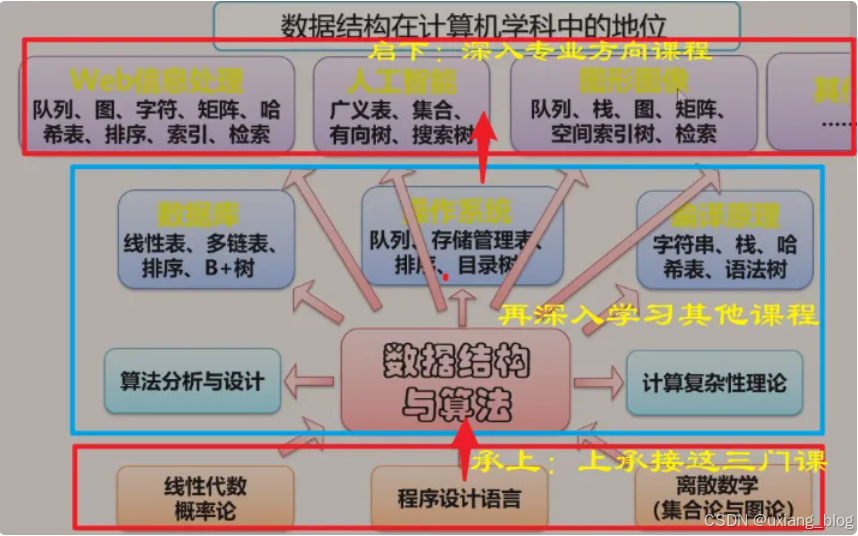
数据结构的重要性——这门课程重要吗?
数据结构是计算机软件相关专业的专业基础课。
在教学计划种的地位:核心、承上启下的课程。
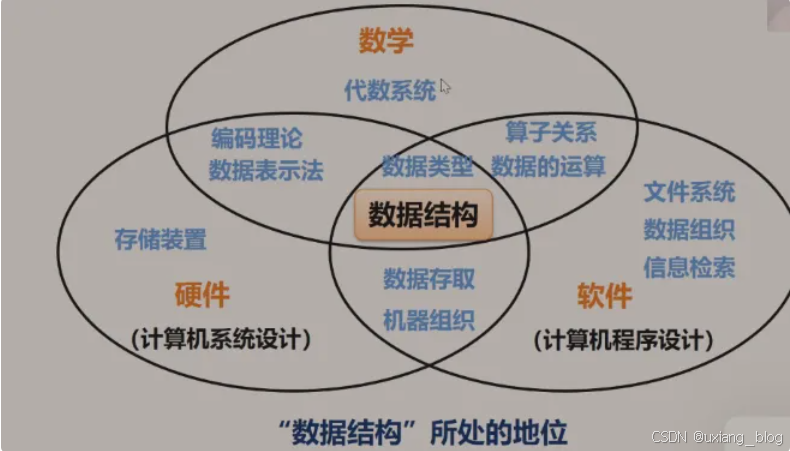
数据结构是介于数学、计算机硬件和计算软件三者之间的一门核心课程。
类似于武术中的“练功”科目:“练武不练功,到头一场空”
考研:必考专业课,四门专业课,共150分,《数据结构和算法》占45分(更有很多多学校只考数据结构和算法)。
找工作:面试时最主要核心内容。
第一章 绪论
1.1、数据结构的研究内容
1.1.1、数据结构的核心
怎么定义数据结构的?总括的一个过程
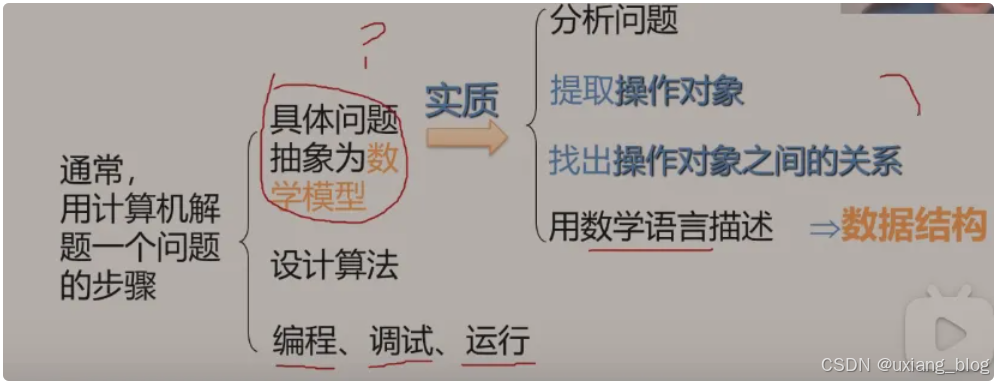
1.1.2、什么是数据结构?
从历史阶段数据结构的实际例子当中引入数据结构的概念
数值计算
早期,计算机主要用于数值计算。
例1、求解梁架结构中的应力。
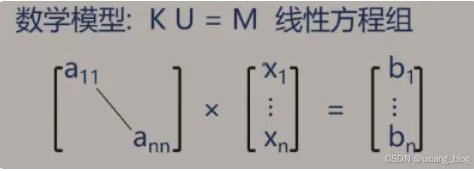
例2、预报人口增长情况。
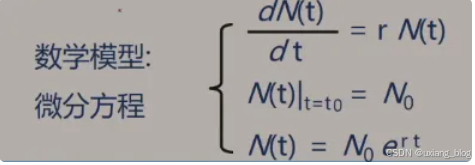
首先,分析问题、提取操作对象。然后,找出操作对象之间的关系,用数学语言加以描述,建立相应的数学方程。最后,求解数学方程:高斯消元法、有限元法、差分法。。。。
特点:数据元素间的关系简单,计算复杂。
——————————————————————————————————————————————
非数据计算。
随着计算机应用领域的扩展,计算机被越来越多地用于非数据计算。
例1、学生学籍管理系统
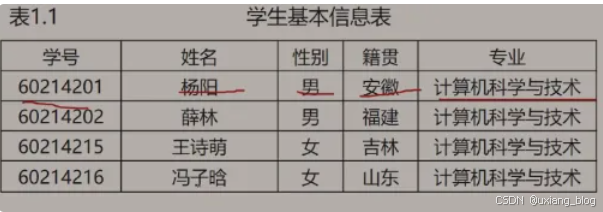
操作对象:每位学生的信息(学号、姓名、性别、籍贯,专业等)。
操作算法:查询、插入、修改、删除等。
操作对象之间的关系:线性关系
数据结构:线性数据结构、线性表。
类似的的还有图书管理系统、人事管理系统、仓库管理系统、通讯录等。
操作对象:若干行数据记录。
操作算法:查询、插入、修改、删除等。
操作对象之间的关系:线性关系
数据结构:线性数据结构、线性表。
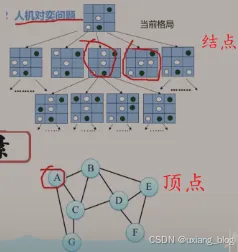
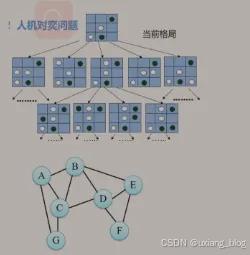
例2 人机对弈问题。井字棋
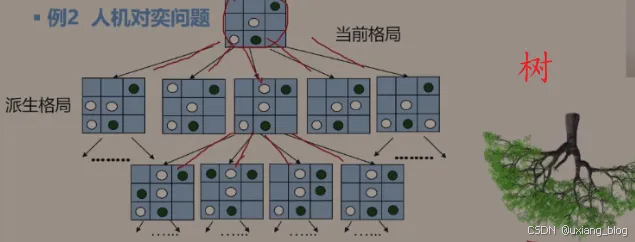
之所以能对弈:策略已经输入计算机,可以根据当前棋盘格局,来预测棋局发展趋势,甚至最后结局。
计算机的操作对象:各种棋局状态,即描述棋盘的格局信息。
计算机的算法:走棋,即选择一种策略使棋局状态发生变化(由一个格局派生出另一个格局)。
操作对象之间的关系:非线性关系、树。 另一个树的例子。
文件系统的系统结构图
磁盘根目录下有很多子目录以及文件,每个子目录里游可以包含多个子目录以及文件,但每个字目录只有一个父目录,依此类推。
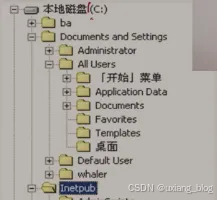
本问题是一种典型的树型结构问题,数据与数据成一对多的关系,是一种典型的非线性关系结构——树形结构。
例3、地图导航——求最短路径(最快路径)
引出图的概念
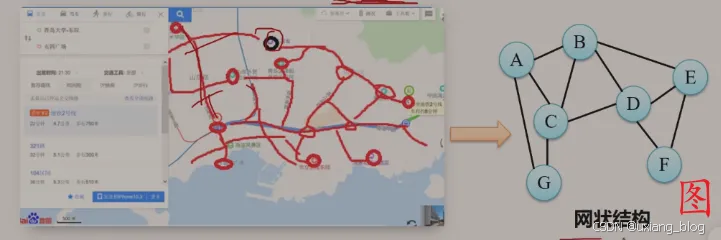
综上所述
这些问题的共性是都无法用数学的公式或方程来描述,是一些 "非数值计算”的程序设计问题。
描述非数值计算问题的数学模型不是数学方程,而是诸如表、树和图之类的具有逻辑关系的数据。
数据结构是一门研究非数值计算的程序设计中计算机的操作对象以及他们之间的关系和操作的学科。
要想有效地使用计算机,就必须学习数据结构。
1.2、基本概念和术语
1.2.1、数据、数据元素、数据项和数据对象

数据
是能够输入计算机能被计算机处理的各种符号的集合
● 信息的载体
● 是对客观事实符号化的表示
● 能够被计算机识别、储存和加工
包括:
● 数值型的数据:整数、实数等。
● 非数值型的数据:文字、图像、图形、声音等。
数据元素
是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。
也称为元素,或称为记录、结点或顶点。
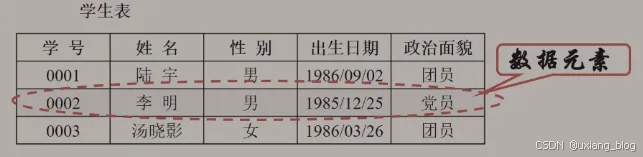
数据项
构成数据元素的不可分割的最小单位。
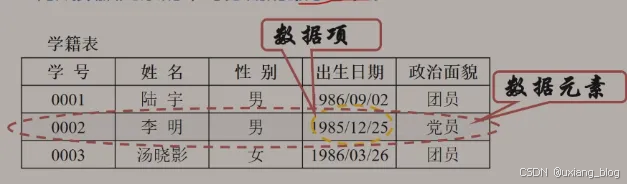
数据、数据元素、数据项三者之间的关系:
数据>数据元素>数据项
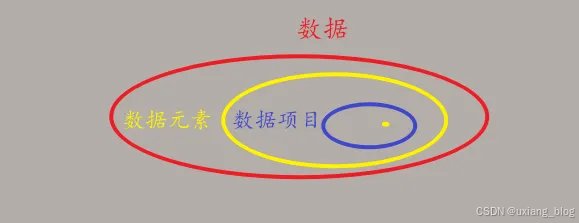
数据对象
是性质相同的数据元素的集合,是数据的一个子集。

数据元素、数据对象与数之间的关系
数据元素与数据的关系:是集合的个体
数据元素与数据的关系:集合的子集
1.2.2、数据结构(Data Structure)
数据结构
数据元素不是孤立存在的,他们之间存在着某种关系,数据元素相互之间的关系称为结构。
是指相互之间存在一种或多种特定关系的数据元素集合。
或者说,数据结构是带结构的数据元素的集合。
数据结构包括以下三个方面的内容:
1、数据元素之间的逻辑关系,也成为逻辑关系。
2、数据元素及其关系在计算机内存中的表示(又称为映像),称为数据的物理结构或者数据的储存结构。
3、数据的运算和实现,即对数据元素可以施加的操作以及着些操作在相应的储存结构上的实现。
数据结构的两个层次
逻辑结构
● 描述数据元素之间的逻辑关系
● 与数据的存储无关,独立于计算
● 是从具体问题抽象出的数学模型
物理结构(存储结构)
● 数据元素及其关系在计算机存储器中的结构(存储方式)
● 是数据结构在计算机中的表示
逻辑结构与存储结构的关系
● 存储结构是逻辑关系的映像与元素本身的映像。
● 逻辑结构是数据结构的抽象,存储结构是数据结构的实现。
● 两者综合起来建立了数据元素之间的结构关系。
逻辑结构的种类
划分方法一
1、线性结构:有且只有一个开始和一个终端节点,并且所有结点都最多只有一个直接前趋和一个直接后继。 例如:线性表、战队列、串。
2、非线性结构:一个结点可能有多个直接前趋和直接后继。 例如:树、 图。
划分方式二——四类基本逻辑结构
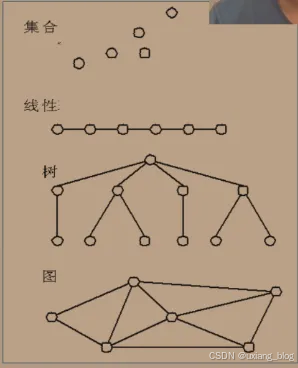
1、集合结构:结构中的数据元素之间除了同属于一个集合的关系外,无任何其他关系。
2、线性结构:结构中的数据元素之间存在着一对一的线性关系。
3、树形结构:结构中的数据元素之间存在着一对多的层次关系。
4、图状结构或网状结构:结构中的数据元素之间存在着多对多的任意关系。
存储结构的种类(四种基本的存储结构)

顺序存储结构:
● 用一组连续的存储单元依此存储数据元素,数据元素之间的逻辑关系由元素的存储位置来表示。
● C语言中用数组来实顺序存储结构

注解:在前面的元素就存储在前面(比如bat在前面就存在前面),在后面的元素存储在后面(比如eat在后面就存在后面),中间的就存在中间。
链式存储结构:
● 用一组任意的存储单元存储数据元素,数据元素之间的逻辑关系用指针来表示。
● C语言中用指针来实现链式存储结构。
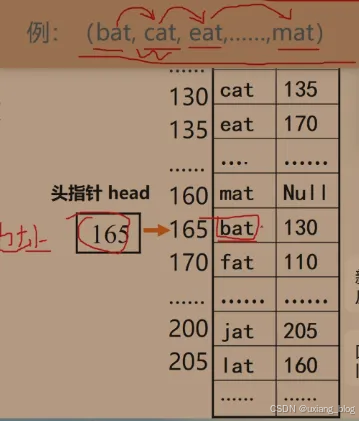
注解:怎么保证就是访问的时候就是以(bat、cat、eat,…,mat)这样的呢?存储的时候既存储了前一个元素本身,又存储了下一个元素的地址,这样访问的时候就能保证是(bat、cat、eat,…,mat)这样的,而不是其他样子了。前一个的值+下一个值的地址体会这样的思想,能够把这个和那个区分开来,尤其是在所含元素相同的情况下。
索引存储结构:
● 在存储结点信息的同时,还建立附加的索引表。
● 索引表中的每一项称为一个索引项,
● 索引项的一般形式是:(关键字,地址)
● 关键字是能唯一标识一个结点的哪些数据项。
● 若每个结点在索引表中都有一个索引项,则该索引表称之为稠密索引(Dense Index)。若一组结点在索引表中只对应一个索引项,则该索引表称为为稀疏索引(Sparse Index)。
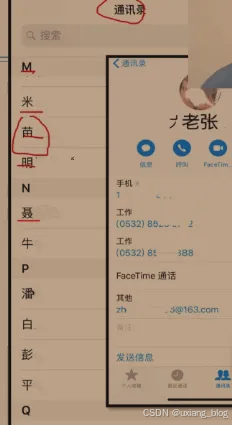
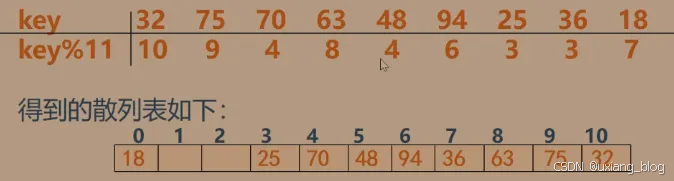
散列存储结构:
● 根据结点的关键字直接计算出该结点的存储地址。
1.2.3、抽象类型和抽象数据类型
引入概念:
● 在使用高级程序设计语言编写程序时,必须对程序中出现的每个变量、常量或表达式,明确说明他们所属的数据类型。

● 一些最基本的数据结构可以使用数据类型来实现,如数组、字符串等;
● 而另一些常用的数据结构,如栈、队列、树、图等,不能直接用数据类型来表示。
● 高级语言中的数据类型明显地或隐含地规定了在程序执行期间的变量和表达中所有可能的取值范围,以及在这些数值范围上所允许进行的操作。

● 数据类型的作用:约束变量和常量的取值范围和约束变量和常量的操作。
数据类型(Data Type)
● 定义:数据类型是一组性质相同的值的集合以及定义这个值集合上的一组操作的总称。

抽象数据类型(Abstract Data Type,ADT)
抽象:抽象是从众多的事物中抽取出共同的、本质性的特征,而舍弃其非本质的特征的过程。具体地说,抽象就是人们在实践的基础上,对于丰富的感性材料通过去粗取精、去伪存真、由此及彼、由表及里的加工制作,形成概念、判断、推理等思维形式,以反映事物的本质和规律的方法。
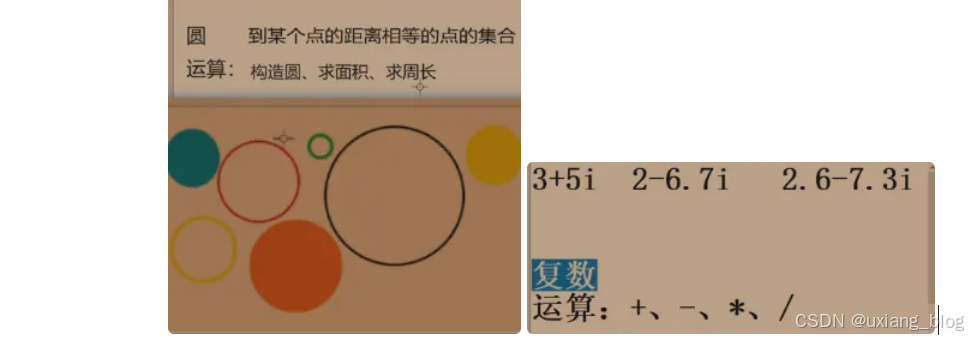
定义:抽象数据类型是指一个数学模型以及定义在此数学模型上的一组操作。包括:以下三部分
● 由用户定义,从问题抽象出数据模型(逻辑结构)
● 还包括定义早期数据模型上的一组抽象运算(相关操作)
● 不考虑计算机内的具体存储结构与运算的具体实现算法。
形式定义:(比较严谨的定义)

定义格式:

其中:数据对象、数据关系的定义用伪代码描述。基本操作的定义格式为:

基本操作定义格式说明:
参数表:赋值参数 只为操作提供输入值。引用参数 以&打头,除课提供输入值外,还将返回操作结构。
初始条件:描述操作执行之前数据结构和参数应满足的条件,若部满足,则操作失败,并返回相应出错信息。若初始条件为空,则省之。
操作结果:说明操作正常完成之后,数据结构的变化状况和应返回的结果。
抽象数据类型(ADT)定义的举例:Circle的定义

问题描述:在高级语言中,没有复数类型,但是可以借助已有的数据类型解决复述类型的问题。

Complex抽象数据类型的基本操作:

概念小结:(1.1-1.2内容总结)
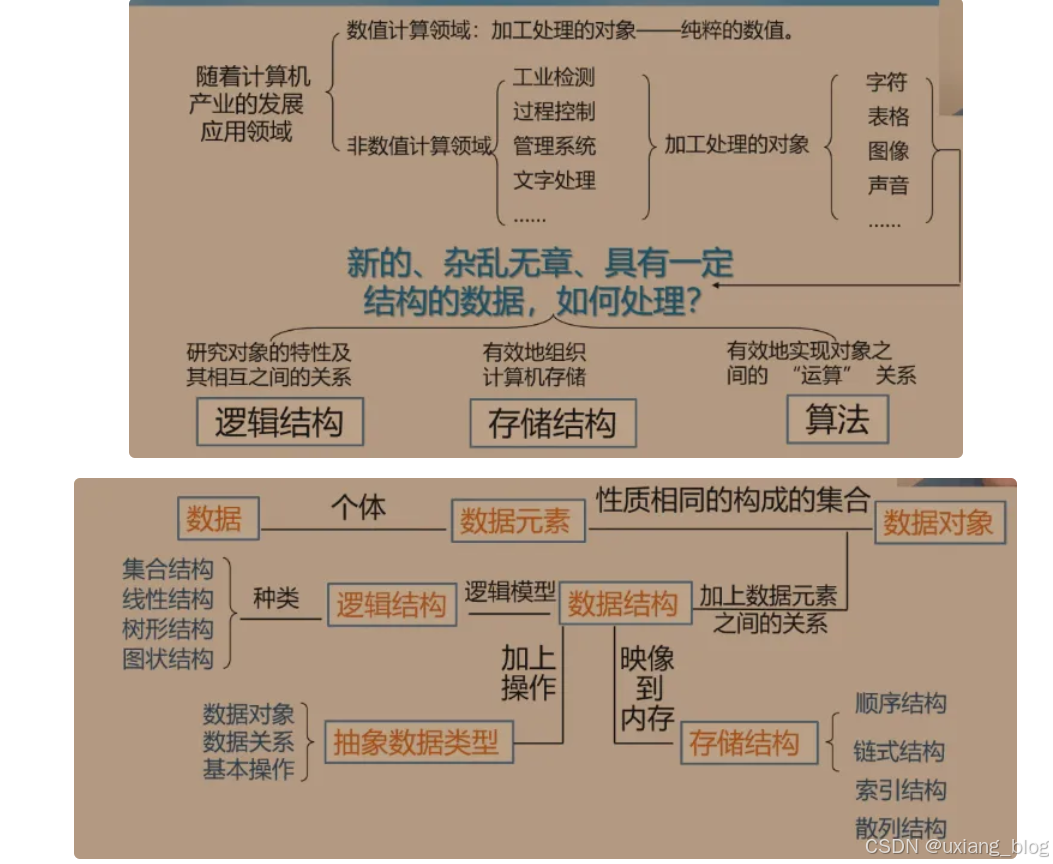
1.3、抽象数据类型的表现与实现
1.3.1、抽象数据类型的表现
抽象数据类型怎么定义呢?它有它的固定格式。

一个问题抽象为要给抽象数据类型后,仅是形式上的抽象定义,还没有达到问题解决得目的,要实现这个目标,就要把抽象的变成具体的,即抽象数据类型在计算机上实现,变成一个能用的具体的数据类型。
1.3.2、抽象数据类型的实现
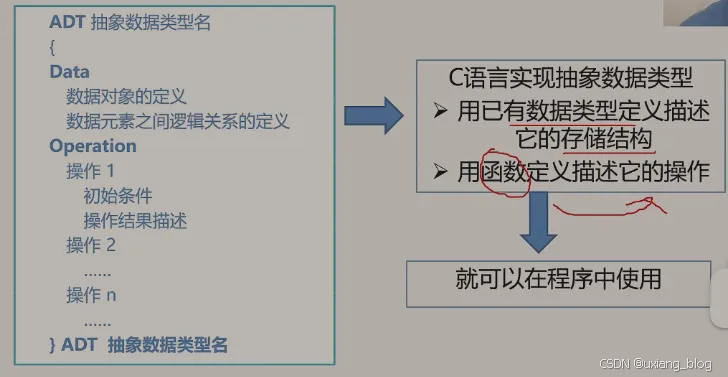
抽象数据类型可以通过固有的数据类型(如整形、实型、字符型等)来表示和实现。即利用处理器中已存在的数据类型来说说明新的结构,用已经实现的操作来组合新的操作。
注:在本课程的学习过程中,我们使用的类C语言(介于伪码和C语言之间)作为描述工具。其描述见教材P10-11。但是上机时要用具体语言实现,如C或C++等。

例如:抽象数据类型“复数”的实现

注:
| Complex是我们定义的一个结构类型 带*:指针变量,它是指向Complex类型的指针。 不带*:Complex类型的普通变量。 |
求下列表达式的值

注解:add(z1,z2,z3):意思式把复数z1和复数z2相加后的值放到z3里面。后面multiply()同理。
1.4、算法和算法分析

1.4.1、算法的定义:
对于特定的问题求解方法和步骤的一种描述,它式指令的有限序列。其中每个指令表示一个或多个操作。

——————————————————————————————————————————————
1.4.2、算法的描述:
自然语言:英语、中文

流程图:传统流程图、NS流程图
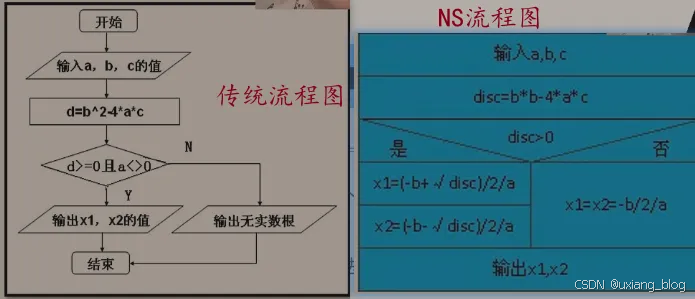
伪代码:类语言:类C语言
程序代码:C语言程序、Java语言程序…
——————————————————————————————————————————————
1.4.3、算法与程序:
算法:是解决问题的一种方法或一个过程,考虑如何将输入转换成输出,一个问题可以有多种算法。
程序:是用某种程序设计语言对算法的具体操作。

——————————————————————————————————————————————
1.4.4、算法特性:
一个算法必须具备以下5个重要特性。
● 有穷性:一个算法必须总是在执行有穷步之后结束,且每一步都在有穷时间内完成。
● 确定性:算法中的每一条指令必须有确切的含义,没有二义性,在任何条件下,只有唯一的一条执行路径,即对于相同的输入只能得到相同的输出。
● 可行性:算法是可执行的,算法描述的操作可以通过已经实现的基本操作执行有限次来实现。
● 输入:一个算法有零个或多个输入。
● 输出:一个算法有一个或多个输出。
——————————————————————————————————————————————
1.4.5、算法设计的要求:
● 正确性(Correctness)

● 可读性(Readability):站在人阅读交流的角度制定的要求

● 健壮性(Robustness)

● 高效性(Efficiency)

对于同一个问题,可以有许多不同的算法。究竟如何来评价这些算法的优劣程序呢?———————算法分析
1.4.6、算法分析:
算法分析的目的是看算法实际是否可行,并在同一问题存在多的算法时可进行性能上的比较,以便从中挑选出比较优的算法。
一个好的算法首先要具备正确性、然后时健壮性、可读性、在几个方面都满足的情况下,主要考虑算法的效率,通过算法的效率高低来评判不同算法的优劣程度。算法效率考虑以下2个方面:
● 时间效率:指的时算法所耗的时间;
● 空间效率:指的时算法执行过程所耗费的村春空间。
有时候两者存在矛盾,这个要视具体情况综合评定。
——————————————————————————————————————————————
1.4.7、算法时间效率的度量
算法时间效率可以依据该算法编制的程序在计算机上执行所消耗的时间来度量。有以下2种度量方法。
事后统计:将算法实现,测算其时间和空间的开销。其缺点是:编写程序实现算法将花费较多的时间和精力;所得实验结果依赖于计算机的软硬件等环境因素,掩盖算法本身的优劣。
事前分析:对算法所消耗资源的一种估算方法。
事前分析方法:
一个算法的运行时间是指一个算法在计算机上运行所消耗的时间大致可以等于计算机执行一种简单的操作(如赋值、比较、移动等)所需要的时间与算法种进行的简单操作次数乘积。简单概括为以下公式。
| 算法运行时间=一个简单操作所需的时间x简单操作次数 |
每条语句执行一次所需要的时间,一般是随机器而异的。取决于机器的指令性能、速度以及编译的代码质量。是由机器本身软硬件环决定的,它于算法无关。所以,我们可以假设执行每条语句所需要的时间均为单位时间。此时对算法的运行时间的讨论就可以转换为讨论算法中所有语句的执行次数,即频度之和了。这就可以独立于不同机器的软硬件环境分析算法的实际爱你性能了。
——简化来讲,每条语句执行一次所需要时间由计算机软硬件决定,它与算法无关,所以就把其时间化为单位时间“1”来看,所以上面公式就为“算法运行时间=每条语句频度x1,看算法运行时间就看每条语句频度就行了。
例如:两个nxn矩阵相乘的算法可描述为:
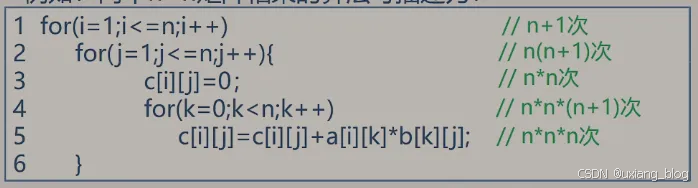
我们把算法所耗费的是时间定义为该算法每条语句的频度之和,则上述算法的时间消耗T(n)为:
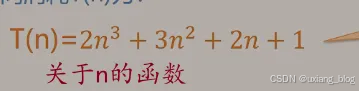
为了便于比较不同算法的时间效率,我们仅比较它们的数量级,数量级越大的越不好。

若某个辅助函数f(n),使得当n趋近于+∞时,T(n)/f(n)的极限值为不等于0的常数,则称f(n)是T(n)的同量级函数。记作T(n)=O(f(n)),称为O(f(n))为算法的渐进时间复杂度(O是数量级的符号),简称时间复杂度。
对于求解矩阵相乘问题,算法耗费时间:
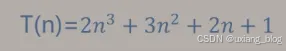
n ->∞时,T(n)/n3 ->2,这表示n充分大时,T(n)与n3n^3n3是同阶或同数量,引入大“O”记号,则T(n)可记作:
T(n)=O(n3)T(n) = O(n^3)T(n)=O(n3)
这个公式就是求解矩阵相乘问题的算法渐进时间复杂度。
一般情况下,不必计算所有操作的执行次数,而只考虑算法中的基本操作执行的次数,它就是规模n的某个函数,用T(n)T(n)T(n)表示。
1.4.8、算法时间复杂度定义
算法中基本语句重复执行的次数是问题规模n的某个函数f(n),算法的时间量度记作:T(n)=O(f(n))T(n) = O(f(n))T(n)=O(f(n))
T(n)=O(f(n))T(n) = O(f(n))T(n)=O(f(n))表示随着n的增大,算法执行的时间的增长率和f(n)的增长率相同,称为渐进时间复杂度。
基本语句重复执行的次数:
(1)算法中重复执行次数和算法中执行时间成正比的语句。
(2)对算法运行时间的贡献最大。
(3)执行次数最多。
问题规模n:n越大算法的执行时间越长
(1)排列:n为记录数
(2)矩阵:n为矩阵的阶数
(3)多项式:n为多项式的项数
(4)集合:n为元素个数
(5)树:n为数的结点个数
(6)图:n为图的顶点数或边数

1.4.9、分析算法算法时间的基本方法
定理1:若F(n)=amnm+...+a1n1+a0F(n) = a_mn^m + ... +a_1n^1 + a_0F(n)=amnm+...+a1n1+a0是m次多项式,则T(n)= O(nmn^mnm)。忽略所有的低次幂和最高次幂系数,体现出增长率的含义。
1、找出语句频度最大的那条语句作为基本语句。
2、计算基本语句的频度得到问题规模n的某个函数f(n)。
3、取其数量级用符号“O"表示。
例如:todo没有理解

1.4.10、算法时间复杂度分析(例题)todo


1.4.11、算法时间复杂度计算
请注意:有的情况下,算法中基本操作执行的次数还随问题输入输入数据集不同而不同。
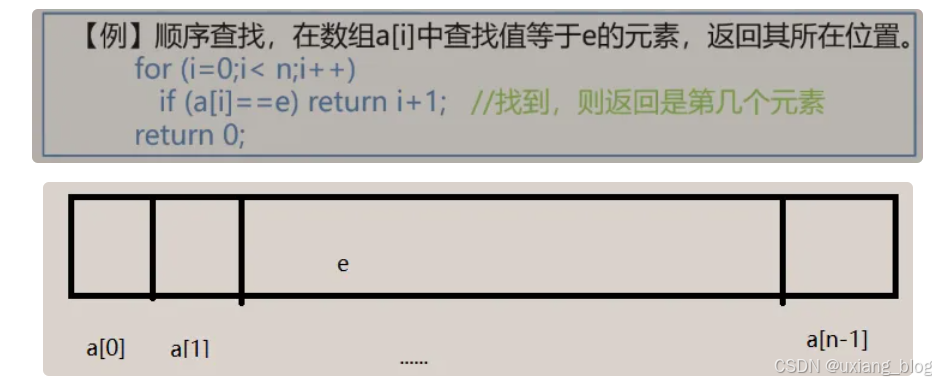
最好的情况:1次。最坏的情况:n。平均时间复杂度为:O(n)。
最坏时间复杂度:指在最坏的情况下,算法的时间复杂度。
平均时间复杂度:指在所有可能输入实例在等概率出现的情况下,算法的期望运行时间。
最好时间复杂度:指在最好情况下,算法时间复杂度。
一般总是考虑在最坏的情况下的时间复杂度,以保证算法你运行时间不会比它更长。
对于复杂的算法,可以将它分成几个容易估算的部分,然后利用大O加法法则和乘法法则,计算算法的时间复杂度:
加法法则:
T(n)=T1(n)+T2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))T(n) = T1(n) + T2(n) = O(f(n)) + O(g(n)) = O(max(f(n),g(n)))T(n)=T1(n)+T2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))
乘法法则:
T(n)=T1(n)∗T2(n)=O(f(n))∗O(g(n))=O(f(n)∗g(n))T(n) = T1(n) * T2(n) = O(f(n)) * O(g(n)) = O(f(n)*g(n))T(n)=T1(n)∗T2(n)=O(f(n))∗O(g(n))=O(f(n)∗g(n))
1.4.12、算法时间效率的比较
当n取得很大时,指数时间算法和多项式时间算法在所需时间上非常悬殊。
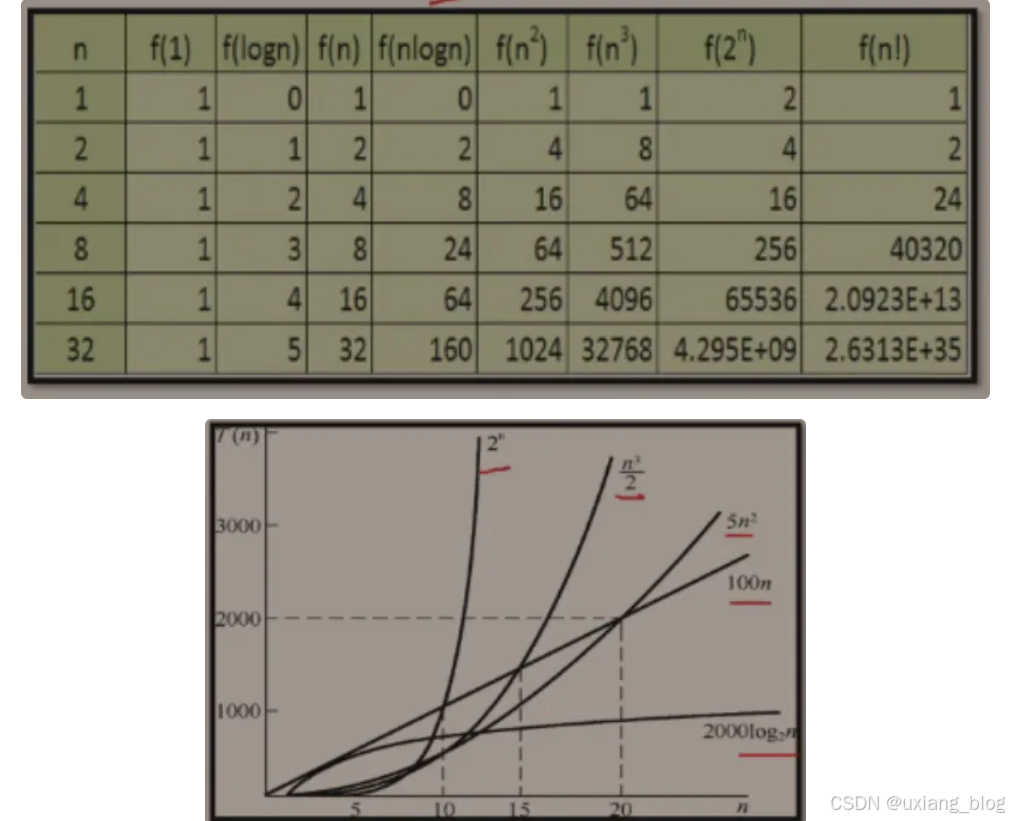
时间复杂度T(n)按数量递增顺序为:

1.4.13、渐进空间复杂度
空间复杂度:计算你所需存储空间的度量,记作:S(n)=O(f(n))S(n) = O(f(n))S(n)=O(f(n))
其中n为问题的规模(或大小)。
算法本身要占据的空间,输入/输出,指令,常数,变量等
算法要使用的辅助空间。
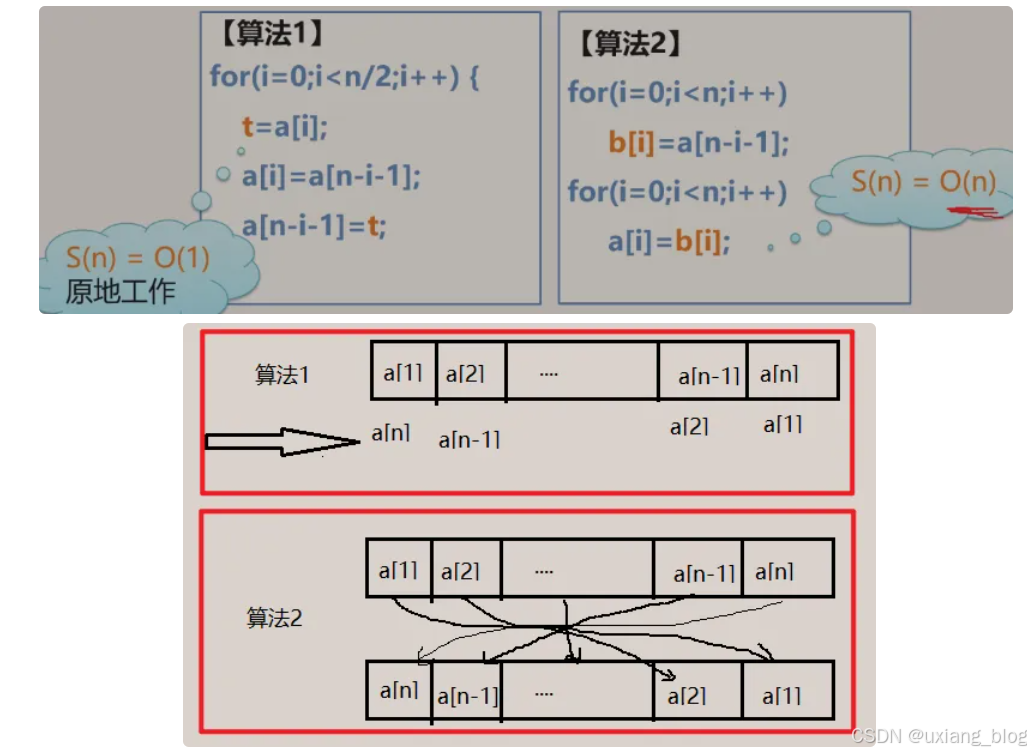
1.4.14、算法空间复杂分析例题todo
例:将一个数组a中的n个数逆序存放到原数组中。
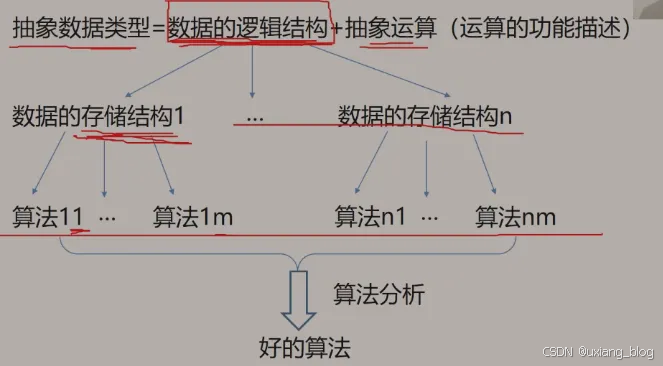
1.4.15、设计好算法的过程
第二章 线性表
知识回顾

2.1、线性表的定义和特点
2.1.1、引入概念:
线性表是具有相同特性的数据元素的一个有限序列。涉及到的概念有:起始结点(线性起点)、终端结点(线性终点)、数据元素、下标、空表、直接前趋、直接后继。
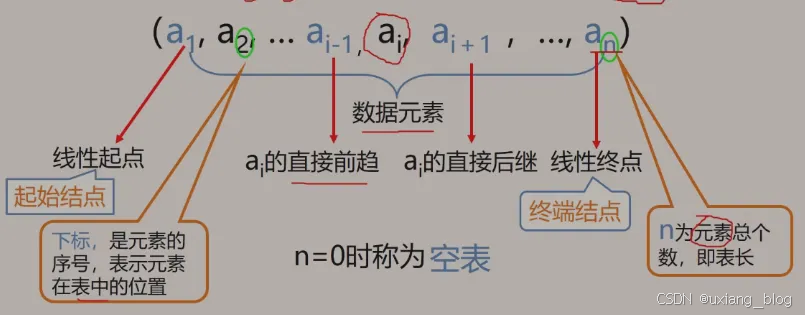
2.1.2、线性表(Linear List):
由n(n>=0)个元素的(结点)a1,a2,...,ana_1,a_2,...,a_na1,a2,...,an组成的有限序列。
● 其中数据元素的个数n定义为表的长度。
● 当n=0时称为空表,注意列表是从a1a_1a1开始的。
● 将非空的线性表(n>0)记作:(a1,a2,...,ana_1,a_2,...,a_na1,a2,...,an)
● 这里的数据元素ai(1<=i<=n)a_i(1<=i<=n)ai(1<=i<=n)只是一个抽象的符号,其具体含义在不同的情况下可以不同,见下例。
例1 :分析26个英文字母组成的英文表。
(A、B、C、...、ZA、B、C、...、ZA、B、C、...、Z)此英文表中数据元素都是字母,元素间关系是线性。
例2 :分析学生情况登记表
例3 :某单位历年拥有计算机的数量(6、17、28、50、92、188)
例4 :12星座(白羊、金牛、双子、巨蟹、狮子、处女、天秤、天蝎、射手、魔蝎、水瓶、双鱼)
总结:同一线性表中的元素必定具有相同特性,数据元素间的关系是线性关系。
2.1.3、线性表的逻辑特征:
从上例子可看出线性表的逻辑特征是:
● 在非空的线性表,有且仅有一个开始结点a1a_1a1,它没有一个直接前趋,而且仅有一个直接后继a2a_2a2;
● 有且仅有要给终端结点an,它没有直接后继,而仅有一个直接前趋aaan-1;
● 其余的内容结点ai(2<=i<=n−1)a_i(2<=i<=n-1)ai(2<=i<=n−1)都是有且仅有一个直接前趋aaan-1和一个直接后继aaai+1;
总结:线性表是一种典型的线性结构。
2.2、案例引入todo
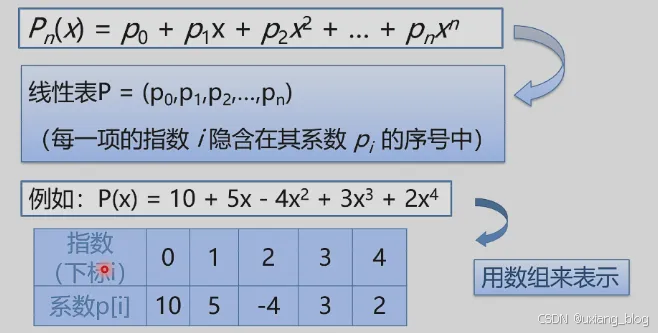
2.2.1、一元多项式的运算:
一元多项式的运算:实现两个多项式加、减、乘运算

但是有些多项式并不是每一个项都有,如果按照前面这种存储方式,就会浪费很大的存储空间,那这样的多项式该怎么表示呢?特例——稀疏多项式
**
2.2.2、稀疏多项式的运算
稀疏多项式的表示:解决方法式是再引入一个指标,在前面只用系数的基础上,加上一个指数这个指标描述,就能进行它们之间的运算了。用(系数,指数)表示
稀疏多项式的运算:

第一步:稀疏多项式中提取系数和指数两个指标
线性表A=((7,0),(3,1),(9,8),(5,17))
线性表B=((8,1),(22,7),(-9,8))
第二步:
创建一个新数组c
分别从头遍历比较a和b的每一项
遵循规则:
● 指数相同:对应系数相加,若其和不为0,则在C中增加一个新项。
● 指数不相同:则将指数比较小的项复制到c中
一个多项式已遍历完毕时,将另一个剩余项一次复制到c中即可。
但数组c多大合适呢?分配多了浪费空间(比如按照多项式的和定义,线性表A有4项,线性表B有3项,共计7项,这些为0的项不占空间,就浪费空间),分配少了又怕装不下。 ——解决方法如下。

顺序存储结构存在问题:存储空间分配不灵活,运算的空间复杂度高。——>使用链式存储结构
多项式相加的优化——链式存储结构
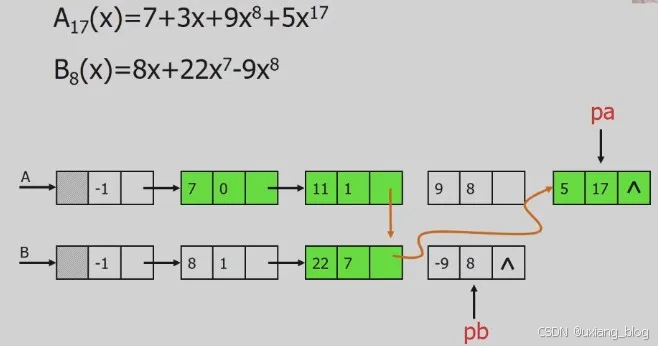
2.2.3、图书管理系统
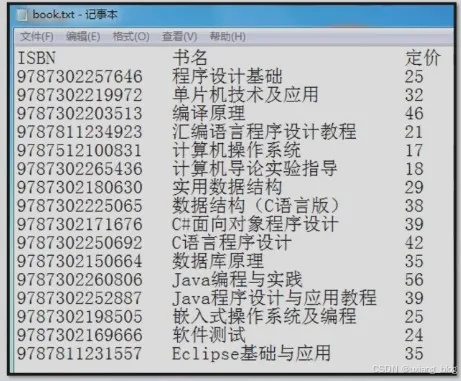
需要的功能:(1)查找 (2)插入 (3)删除 (4)修改 (5)排序 (6)计数
那么这些需要的功能怎么实现呢?也可以使用线性表来实现。
把图书表抽象为线性表,表中的每本图书抽象线性表中的数据元素。
怎么存储它呢?可以用顺序存储方式,也就是数组存储方式,也可以使用链式存储方式。但是那种存储方式比较好
呢?
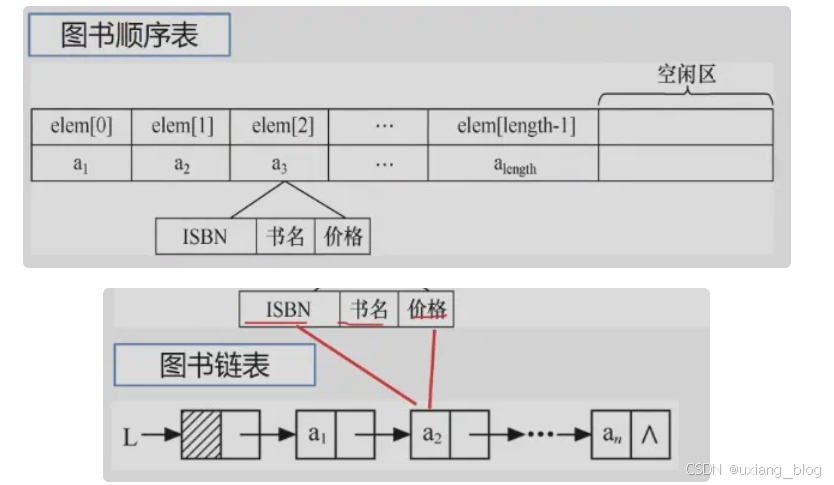
● 选择适当的存储结构
● 实现此存储结构上的基本操作
● 利用基本操作完成功能
这样的图书信息管理系统可以这样处理,那么相类似的也可以,比如,教师管理系统,员工管理系统,商品管理系统等等。
总结:(以上三个案例的总结2.2.1-3)
● 线性表中数据元素的类型可以为简单类型,也可以为复杂类型。
● 许多实际应用问题所设计的基本操作有很大相似性,不应为每个具体应用单独编写程序。
● 从具体应用中抽象出共性的逻辑结构和基本操作(抽象数据类型),然后实现其存储结构和基本操作
2.3、线性表的类型定义
2.3.1、线性表的类型定义
抽象数据类型线性表的定义如下:

2.3.2、基本操作(一)
1、初始化线性表 InitLIst(&L) (Initialization List)
操作结果:构造一个空的线性表L。
2、销毁线性表 DestroyList(&L)
初始条件:线性表L已经存在。
操作结果:销毁线性表L。(从内存中)
3、清除线性表 ClearList(&L)
初始条件:线性表L已经存在
操作结果:将线性表L重置为空表。(内存中线性表本身还存在,但是表中没有元素)
2.3.3、基本操作(二)
4、判断线性表是否为空 ListEmpty(L)
初始条件:线性表L已经存在。
操作结果:若线性表L为空(n=0),则返回TURE;否则返回为FALSE。
5、求线性表的长度 ListLength(L)
初始条件:线性表L已经存在。
操作结果:返回线性表L中的数据元素个数。
2.3.4、基本操作(三)
6、获取线性表中的元素 GetElem(L,i,&e);
初始条件:线性表L已经存在,1<= i <= ListLength(L)。
操作结果:用e返回线性表L中的第i个数据元素的值。
7、查找定位线性表中元素 LocateElem(L,e,compare())
初始条件:线性表L已经存在,compare()是数据元素判定函数。(compare()可判定这个元素x(x>e,x<e,x=e等等)取决于实际情况)
操作结果:返回L中第1个与e满足compare()的数据元素的位序。这样的数据元素不存在则返回值为0。
2.3.5、基本操作(四)
8、求线性表L中一个元素的前趋 PriorElem(L,cur_e,&pre_e)
初始条件:线性表L已经存在。
操作结果:若cur_e是线性表L的数据元素,且不是第一个,则pre_e返回它的前趋,否则操作失败,pre_e无意义。
9、求线性表L中一个元素的后继 NextElem(L,cur_e,&next_e)
初始条件:线性表L已经存在。
操作结果:若cur_e 是线性表L的数据元素,且不是第最后一个,则用next_e返回它的后继,否则操作失败,next_e无意义。
2.3.6、基本操作(五)
10、线性表中插入一个元素 ListInsert(&L,i,e)
初始条件:线性表L已经存在,1<=i<= ListLength(L) +1。(可以插在第一个位置,即i=1,也可以插入到最后一个位置,即n+1)。
操作结果:在L的第i个位置之前插入新的数据元素e,L的长度加一。
插入元素e之前(长度为n):(a1,a2,...,a(a_1,a_2,...,a(a1,a2,...,ai-1,ai,...,an)a_i,...,a_n)ai,...,an)
插入元素e之后(长度为n+1):(a1,a2,...,a(a_1,a_2,...,a(a1,a2,...,ai-1,e,ai,...,an)a_i,...,a_n)ai,...,an)
2.3.7、基本操作(六)
11、删除线性表中的一个元素 ListDelete(&L,i,&e)
初始条件:线性表L已经存在,1<= i <= ListLenght(L)。
操作结果:删除线性表L的第i个数据元素,并用e返回其值,线性表L的长度减一。
删除前(长度为n):(a1,a2,...,a(a_1,a_2,...,a(a1,a2,...,ai-1ai,aa_i,aai,ai+1,...,an),...,a_n),...,an)
删除后(长度n-1):(a1,a2,...,a(a_1,a_2,...,a(a1,a2,...,ai-1,a,a,ai+1,...,an),...,a_n),...,an)
12、遍历(访问)线性表中每个元素 (&L,visited())
初始条件:线性表L已经存在
操作结果:依此对线性表中每个元素调用visited()。不管是干什么,是删除也好,插入也罢,但是要对线性表中的每个元素都要一个挨一个操作一遍。
总结:
以上所提及的运算是逻辑结构上定义的运算。只是给出这些运算的功能是“做什么”,至于“如何做”等实现细节,只有待确定了存储结构之后才考虑。
后续课程中将学习线性表的存储及在才存储结构上各种操作的实现。
2.4、线性表的顺序表示和实现
2.4.1、线性表的顺序存储表示
线性表的顺序表示又称顺序存储结构或顺序映像。
顺序存储定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。
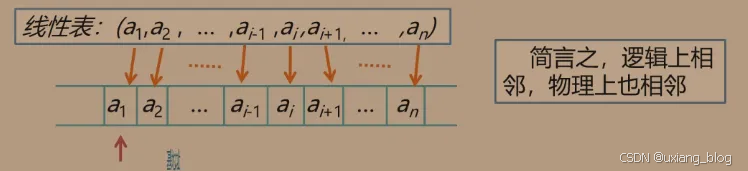
线性表的第1个数据元素a1a_1a1的存储位置,称作为线性表的起始位置或基地址。
顺序存储结构:
例如:线性表(1,2,3,5,6)的存储结构:

线性表顺序存储结构占用一片连续的存储空间。知道某个元素的存储位置就可以计算其他元素的存储位置。
顺序表中元素存储位置的计算:

如果每个元素占8个存储单元,ai存储位置是2000单元,则ai+1存储位置是? 2008单元
假设线性表的每个元素需占l个存储单元,则第i+1个数据元素的存储位置和第i个元素的存储位置之间满足关系:
LOC(ai+1) = LOC(ai) + l
由此,所有数据元素的存储位置均可由第一个数据元素的存储位置得到:
LOC(ai) = LOC(a1) + (i-1) * l (LOC(a1)为基地址)
2.4.2、线性顺序结构的图示:
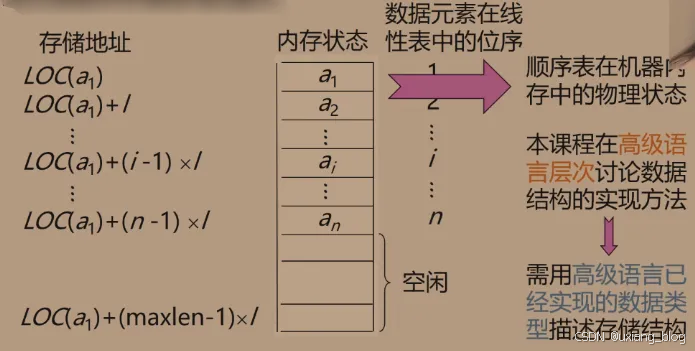
顺序表的特点:以物理位置相邻表示逻辑关系。任一元素均可随机存取。(优点)

一维数组的定义方式:类型说明符 数组名[常量表达式]
说明:常量表达式中可以包含常量和符号常量,不能包含变量。即C语言中不允许对数组的大小动态定义。
此时就存在一个矛盾:需要线性表长可变(删除),但是数组长度不可动态定义。这时候该怎么办呢?———>用一个变量表示顺序表的的长度属性。定义模板如下:

2.4.3、多项式的顺序存储结构类型定义

怎么样定义这个线性表呢?定义例子如下:


2.4.4、补充:类C语言有关操作
2.4.4.1、补充:元素类型说明
顺序表类型定义

ElemType是什么?它代表的是线性表中元素的类型,这个元素的类型是什么类型,它就指什么类型的。如果里面存放的是‘a’,‘b’,'c’那ElemType就是Char类型;如果数组存放的是多项式系数,而系数是小数,那ElemType就是float类型。根据处理的问题具体情况而修改。如果不想修改,另一个办法是事先把这个类型定义一下。如下:

2.4.4.2、补充:数组定义

数组静态分配的我们知道,但是碰到数组动态分配的这种定义的方法就不太了解了?
第一种(左)数组的存储空间是静态分布的,我们定义在那儿定义数组之后,那里所占的空间就确定了,data[MaxSize]里面存放的是什么呢?是data[0]首元素的地址,也就是这个数组的的首地址或者基地址。既然里面是存放地址的,那第二种(右)数组可以用指针变量来定义,当这样定义之后,那么这样的数组有多大呢?我们就可以用内存动态分配的函数来分配内存,我们用有这样的一个顺序表类型,再用这样的顺序类型定义了一个变量L。

这个L就是我们的顺序表了,这个L就有两个成员,一个是ElemType *data,用来存放顺序表中的元素,还有一个就是L.length,存放我们当前的顺序表当中的个数。那怎么为这个动态的数组分配空间呢?我们就可以利用这样的分配函数就可以分配空间了。
2.4.4.3、补充:C语言的内存动态分配

malloc(m)函数,开辟m字节长度的地址空间,并返回这段空间的首地址。
注解:即老师说的,听了能够对概念有所启发的内容,但是这部分内容往往有些冗余,可能一个词语反复说好多遍,而且因为写笔记的人往往听力有些问题,再加上一些自己的理解不到位,有些笔记甚至是错误的,但这是值得的。
注解:通俗来讲,就是分配内存的,它的参数m要求是一个整数,也就是分配空间的字节数,总共需要多少个字节,所以要求参数是一个整数。
sizeof(x)运算,计算变量x的长度。
注解:sizeof(x)MaxSize这里面分配了多少个字节呢?我们要放MaxSize个元素,这个MaxSize可能是100,也可能是1000,根据需要。那么其中一个元素需要多大的空间呢?假设一个元素是8个字节,那么sizeof(ElemType)就写成8,sizeof(ElemType)MaxSize=1008=800,就写800。但是每个都需要我们算出来那就非常麻烦,所以有一个计算字节大小的运算,那就是sizeof(ElemType),sizeof(ElemType)可以计算一个变量,或者是计算一个类型,这个括号里面的参数ElemType既可以是类型,也可以是变量。如果这个类型是字符char型那么这里sizeof(ElemType)便是1,如果是整型int,在32位操作系统当中就是4个字节。就这样sizeof(ElemType)可以通过自己来计算。
注解:假设sizeof(ElemType)MaxSize=1008=800字节的空间,那么这800字节存什么东西,存200个整数,还是100实数呢?还是存系数,指数呢?到底是怎么划分?分成200个小空间,还是100个小空间?就要依靠前面的(ElemType)来解决,是怎么划分的,是通过类型划分的,如果是char,一个元素1个字节,就划分为800/1=800个空间;如果是int,一个元素4个字节,就划分为800/4=200个空间。号是什么意思?是一个指针,要放到这个数组当中【L.data=(ElemType)malloc(sizeof(ElemType)MaxSize)】,数组【L.data】这个元素是什么东西呢?是首元素的地址【看前面定义ElemType data】,所以要转换成这个类型的指针,(ElemType)此出的"()"是强制类型转换。如果(int)那就强制转换成int,如果是(int)那就是强制转成指向整型的指针。这样就活得了后面一整大片【(ElemType*)malloc(sizeof(ElemType)*MaxSize)】的基地址,知道了基地址就可以对后面的元素操作了。
free§函数,释放指针p所指变量的存储空间,即彻底删除一个变量。
注解:这里讲得是分配内存,如果后面不需要了就可以释放掉,释放内存空间呢?用的就是free§函数。
使用这些动态分配函数的时候,要知道这些函数在哪里,就在<stdlib.h>,所以需要加载上上头文件:<stdlib.h>
2.4.4.4、补充:C++的动态存储分配
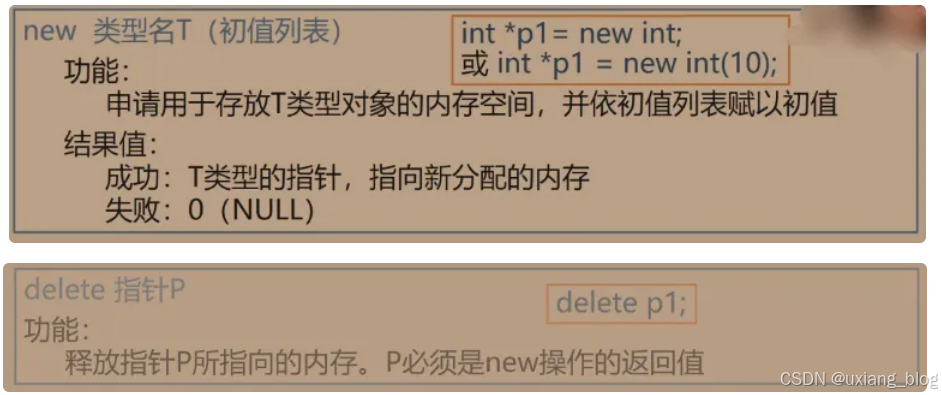
有时候也会借助C++语法,为什么?C++的语法可以让我们的算法写得更简短。有的同学会说好不容易把C的写法搞懂了,又怎么开始用C++的啦,这个遵循的原则是怎么方便怎么来,只要能够描述把算法描述清楚即可,也是C++的使得算法更简洁的这个优点,有些算法会用C++来表示。
2.4.4.5、补充:C++中的参数传递
函数调用时传送给形参表的实参必须与形参三个一致(类型、个数、顺序)
参数传递有两种方式
值传递(参数为整形、实型、字符型等)
传地址
● 参数为指针变量
● 参数为引用类型(重点了解这个)
● 参数为数组名
2.4.4.5.1、值传递:
把实参的值传送给函数局部工作区相应的副本中,函数使用这个副本执行必要的功能。函数修改的时副本的值,实参的值不变。
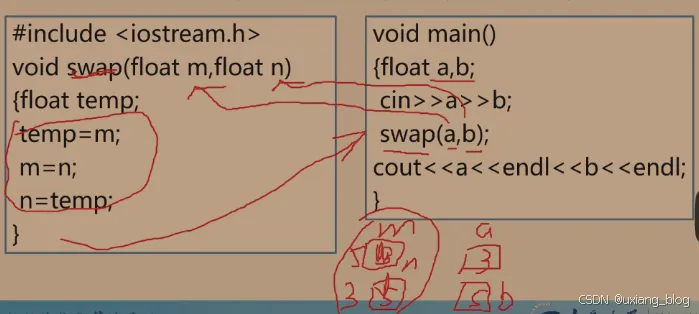
注解:float a,b;定义了两个值,作为实参,在swap(a,b)中调用过程中,将a传递给m,b传递给n,然后在被调用的函数中【也就是左边声明下面的那一块】m和n调换了各自的值,被调用完后,m和n的值就被释放了,然后返回到调用的地方继续执行,a和b的值没有发生任何变化。传递的是值,形参和实参各用各的空间。比如a=3,b=5,在swap(a,b)传递过程中,实参a的值传递给了形参m,m=3,实参b的值传递给了形参n,n=5,然后在void swap(float m,float n)中m和n发生值发生了交换,m=5,n=3,但当被调用函数void swap(float m,float n)结束了,返回到释放得地方的时候,被调用函数释放掉了,a和b没有任何变化。这就是传值,形参发生改变,实参值不会改变。
2.4.4.5.2、传地址:
2.4.4.5.2.1、传地址方式——指针变量作为参数
1、形参变化影响实参
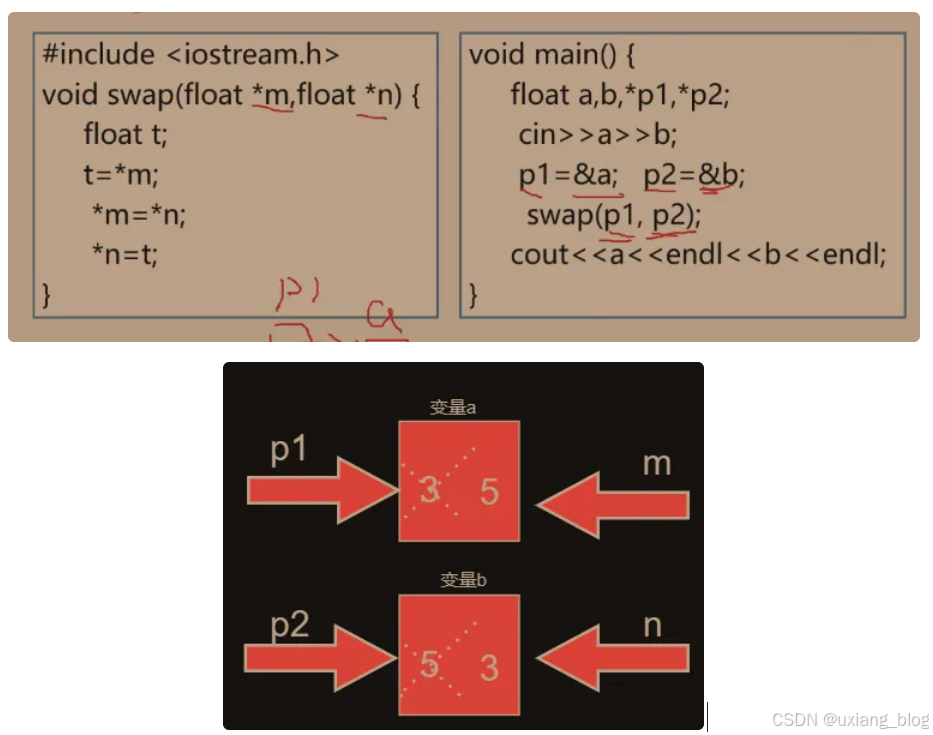
注解:定义了两个指针p1和p2,p1指向a,p2指向b作为实参传递。假设a里面存放3,b里面存放5。p1存放的是的a的地址,p2存放的是b的地址,用箭头表示指向它。现在调用函数swap(p1,p2),void swap(float *m,float *n),指针m指向的也是a,指针n指向的也是b。*m表示指针变量的内容,这个函数中变量a和变量b交换了值,交换完毕了,形参m,n释放没有了,返回到调用的地方,a,b输出的时候有无变化呢?我们说是变化了。
2、形参变化不影响实参?

注解:相比形参变化影响实参的,不同点在哪里呢?void swap(float *m,float *n){}里面多了一个临时变量float t。给t赋值的不是m,而是m本身,m存放的是什么呢?m存放的是a的地址,所以t存放的时候的时候也是a的地址,这样过来就对a,b没什么影响。
2.4.4.5.2.2、传地址方式——数组名作为参数
传递的是数组的首地址
对形参数组所作的任何改变都将反应到实参数组中

注解:char a[10] = “hello”;主函数中定义了一个字符数组,存放了5个字符串,调用子函数sub(a),将数组名作为参数传递实际上就是传递了数组的首地址,那么就可以写成void sub(char b[]){}的形式,注意char []里面不能有大小,或者用*b表示,都可以,对形参b[]= “world”;操作也就是对a[10]操作,释放完后就返回到调用出,此时输出的a就发生了变化。
例:用数组做函数的参数,求10个整数的最大数

2.4.4.5.2.2、传地址方式——引用类型作为参数(C++)
什么是应用???
引用:它用来给一个对象提供一个替代的名字。

int i =5;定义了一个i,但是int &j=i,j引用了i,所以操作j就和操作i是一样的,它就是一个i的代名词,i改变时j也跟着改变,i一开始是5,后来是7,所以j也跟着i变成7啦。从另一个角度理解,&j是地址,它和i的地址是一样的,所以它们公用的是同一个空间。

注解:m,a公用要给空间,n,b公用一个空间,所以对m,n的操作实际上就是对a,b的操作,这种操作比之前的操作数组的容易,公用同一个空间,所以形参不比产生新的空间。
2.4.4.5.2.3、引用类型做形参的三点说明
1、传递引用给函数与传递指针的效果是一样的,形参变化实参也发生变化。
2、引用类型作形参,在内存中并没有产生实参的副本,它直接对实参操作;而一般变量作为参数,形参与实参就占用不同的存储单元,所以形参变量的值是实参变量的副本。因此,当参数传递的数据较大时,引用比用一般变量传递参数的时间和空间效率都好。
3、指针参数虽然也能达到与使用引用的效果,但在被调函数中需要重复是使用“*指针变量名”的形式进行运算,这很容易产生错误且程序的阅读性较差;另一方面,在主调函数的调用点处,必须用变量的地址作为实参。
2.4、线性表的顺序表示和实现
2.4.1、线性表的顺序存储表示
2.4.1.1、预备内容
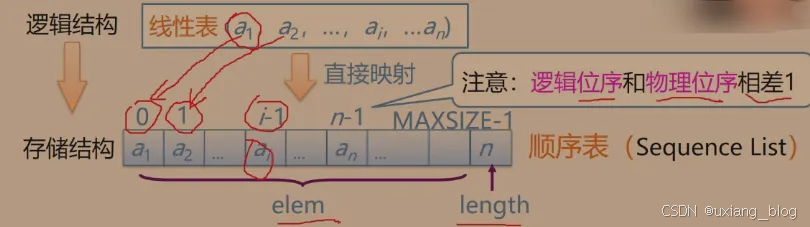
注解:将逻辑上相邻的元素存储在物理位置上也相邻的元素,这种直接映射过去的方式就是顺序表,在高级语言里实用数组实现的。线性表中的元素不是固定的,经常要插入元素个数增加,删除元素个数减小,怎么定义数组的大小呢?解决办法就是定义一个比较大的数组,不用的就空着,但这样的话怎么知道元素的个数呢?就需要额外需要一个变量length来记录这个表中元素的个数。也就是需要表达线性表的存储就需要2个部分,一部分呢是一个数组,另一部分是一个整数,两部分放到一起表示一个顺序表。(Sequence List)。逻辑位序和物理位序是相差1的,逻辑上存储是从1开始的,而在物理存储上元素位数是从0开始的,所以逻辑位序比物理位序大1。

2.4.1.2、顺序表示意图
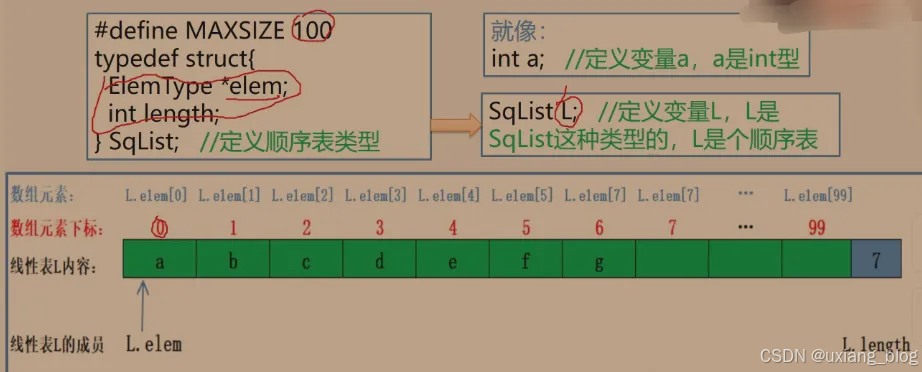
注:理解好这个示意图之后接下来的算法就比较简单了。我们定义了一个顺序表类型,定义类型之后才会对这顺序表分配空间,就和int a;一样,定义了a的类型之后,内存就会给这个变量开辟一个变量名字为a的空间。Sqlist L;这个定义了之后就可以对顺序表进行操作了。定义了这样一个类型的变量L,就会被分配空间。这样的空间是怎么样子的呢?有俩部分组成,首先是一个数组ElemType *elem;有100个元素,就可以往里面存储了,第二个是一个整数,用来记录这个数组中元素的个数的。具体来操作该怎么做呢?整个绿色+蓝色的就是顺序表L,那我们要操作绿色即数组这一块,可以用下标来表示它,L.elem[0]就是下标为0的第一个元素,L.elem[99]下标为99的第100个元素。那我们就可以操作它。比如增加一个元素,就要修改线性表L的成员L.ength。这便是操作线性表L的方法。如果是指针型的,那可以用L->elem L->length。
2.4.2、顺序表基本操作的实现3
2.4.2.1、线性表的基本操作

2.4.2.2、操作算法中用到的预定义常量和类型

注解:操作算法中有一些预定常量和类型,比如OK返回的是什么?如果没有这些上机就会报错,也不知道怎么回事?,TRUE, FALSE这些到底返回的是什么,需要去看看。还有返回值是那种类型int or char 需要定义一下。
2.4.2.3、【算法2.1 】线性表L的初始化(参数用引用)
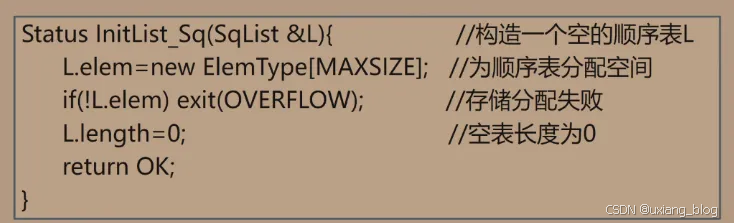
注解:第一个算法是线性表的初始化,我们这个参数用得是应用型的,也就是我们调用这个函数完成线性表的初始化,那么这个主调函数也就自动获得了咱们这个形参,我们对形参进行操作也就是对实参进行操作。操作名字是inistList初始化线性表,这个不是普通的线性表,是顺序表也就是Sq,它的操作对象是什么呢?你给我一个线性表L,我构造好线性表L,通过引用型&L就返回了,最前面是返回的状态值Status,如果构造好了就返回OK,return OK;那么怎么构造的呢?给L动态分配空间,new ElemType[MAXSZIE];获取元素中的地址L.elm = ,刚分配好空间线性表里面一个元素也没有,所以L.ength = 0。一般情况下有数组分配空间和元素长度这两部分就够了,那么中间if(!L.elem)=exit(OVERFLOW);是干什么的,这是一种异常处理,分配内存的时候,空间分配太小了,那存储就会发生错误,死机了或者是不出结果了,或是其他的错误,我们要避免这种情况,如果里面没有内容,也就是分配失败,退出的时候就返回OVERFLOW这个值,OVERFLOW返回的是-2,成功了就返回 Ok-1,我们根据返回的结果进行后续的操作。这样一个空的顺序便构造好,可以往里面写内容了。
2.4.2.4、线性表L的销毁和清空。

注解:所谓销毁线性表,就是线性表所占的空间释放掉,让空间回归内存。直接用C++语法删除掉,但前提是得有,所以加了一个if判断语句。

注解:清空的意思是线性表仍在,但是我要告诉计算机我这里面没有元素了,以将L.length = 0的形式告诉计算机。
2.4.2.5、求线性表L的长度和判断其是否为空。

注解:就是我们需要知道线性表中到底有多少个元素。GetLength获取长度,然后返回线性表的L.length成员。
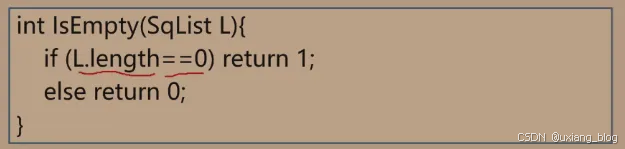
注解:只需判断一下L.length是否为0,如果是0那就是没有元素,也就是空的。
2.4.2.6、【算法2.2 】顺序表中的取值(根据位置i获取相应数据元素的内容)

注解:这个算法是取i的值,我们十多a1存在下标为0的位置,a2 存在下标为1的位置,ai存在下标为i-1的位置,所以我们直接把下标为[i-1]的取出来放到e里面就行了。(e = Lelem[i-1]);痛过引用型返回,但是不能直接返回,需要判断一下其位置是否合理性,如果你给了我一个负数或者超过n-1的,那么就说这些没有元素,所以要判断一下,给个返回值告诉一下。这个的算法复杂度是多少呀?这些都执行一次,执行10000次,只要不发生变化,那就是常量阶,即O(1)。
2.4.3、线性表的顺序表示和实现4
2.4.3.1、顺序表上的查找操作

按值查找:
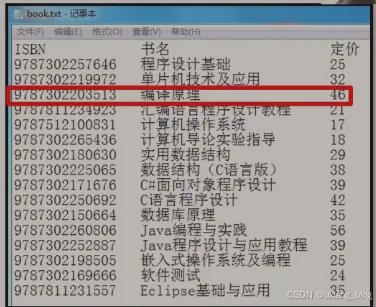
例如:在图书表中,按照给定书号进行查找,确定是否存在该图书。如果存在:输出的第几个元素。如果不存在,输出0。
2.4.3.2、【算法2.3 】顺序表中的查找
在线性表L中查找与指定值e相同的数据元素位置。
从表的一端开始,逐个进行记录的关键字和给定值的比较。找到,返回该元素的位置序号,未找到,返回0。

注解:给定线性表L,(SqList L),给定元素e(ElemType e),从这个线性表中查找,怎么查找呢?从存储位置下标为0的元素开始查找(i=0),看是否与e一样,一样就返回逻辑序号(存储序号是从0开始的,逻辑序号是从1开始的,所以逻辑序号=存储序号+1),如果不一样,那么i++,进行下一次循环,如果一样返回e的位置,如果在存储序号(0,L.length)范围里面仍旧没有找到,就return 0不再执行了。接下来就分析一下这个算法的复杂度,算法的复杂度要分析时间效率和空间效率,重点分析时间效率,时间效率是用渐进复杂度分析的,它是怎么计算的呢?分三个步骤,(1)找到执行次数最多的语句,(2)看它到底执行多少次(3)表示成O(x)的形式。见2.4.3.3
还有另一种算法,这里就不介绍了。

2.4.3.3、【算法2.3 】顺序表中的查找算法分析
因为查找算法的基本操作为:将记录的关键字同给定值进行比较。
基本操作: L.elem[i] == e

注解:这个线性表中存储了7个元素,所以L.length=7,比如查找元素是a,则e=‘a’,那么第一次查找用得是L.elem[0]的值和查找的值a进行比较,结果只需第一查找就找到了,那么就返回i+1(此时i=0,i+1=1),代表是这个表中的第一个元素,这个时候就比较了1次。假设查找值是b,则e=‘b’,那么进行第一次查找用的L.elem[0]的值和查找的值b进行比较,第一次没有找到,那么i++进行下一次循环,第二次用的是L.elem[1]与查找值b进行比较,这次找到了,就返回i+1(此时i=1,i+1=2),代表是这个表中的第二个元素,c,d,e,f,g亦是如此。那平均查找几次呢?那每个元素都找一遍。比较次数:e=a,1次;e=b,2次;e=c,3次,…,e=g,7次;平均下来(1+2+3+…+7)/7=4。那么这个顺序查找衡量需要查找多少次呢,就需要引入一个描述词——平均比较次数(即平均查找长度)来衡量。
总结:L.elem[i] == e,此处e就是查找值,要查找之前使其具体化,L.elem[i]指针执向的内存中的值,当找到查找值e时,i也就随之确定了,此时i是存储序号,但我们要看的是表L中的序号,也就是逻辑序号,此时根据逻辑序号与存储序号的关系,返回i+1就得到了逻辑序号了。
2.4.3.4、平均查找长度ALS(Average Search Length):
为确定记录在表中的位置,需要与给定值进行比较的关键字的个数的期望值叫做查找算法的平均查找长度。
对含有n个记录的表,查找成功时:
ALS=∑i=0nPiCiALS=\sum_{i=0}^n {P_iC_i}ALS=∑i=0nPiCi
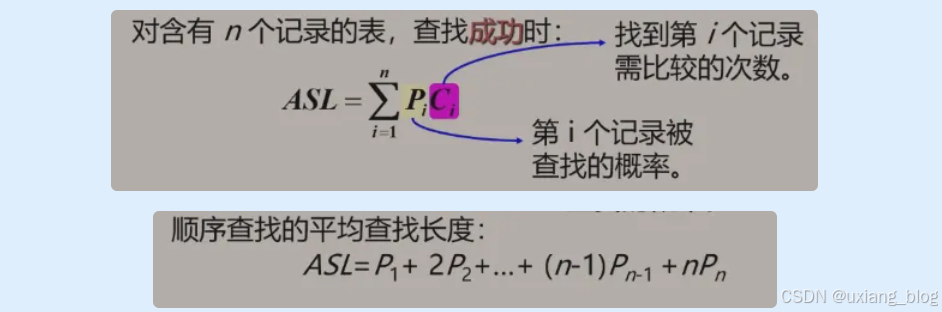
注解:从平均查找长度角度看上一个问题就是(1+2+3+…+7)/7=4,换一种角度来表示11/7+21/7+…+7*1/7=4。这里是n是7个的时候。

注解:假设Pi=1/n,则ASL=1P1 +2P2+…+(n-1)P(n-1)+nP(n)=1/n*(1+2+…+(n-1)+n)=1/n*[n(n-1)]/2=(n+1)/2

2.4.4、线性表的顺序表示和实现5
2.4.4.1、顺序表的插入思路

顺序表的插入:

插入不同的位置的算法演示:(L.length下面三种情况都会先赋值7,只介绍L.elem[]的变化)
插入位置在最后

注解:比如插入元素g,那么就为L.elem[6]的位置赋值。
插入位置在中间
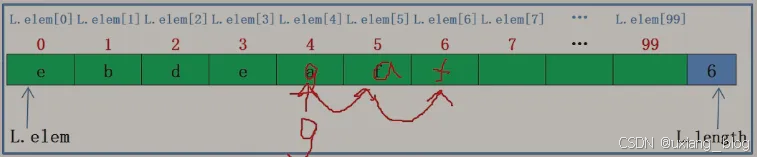
注解:比如把元素放到L.elem[4]的位置,那么就把f搬到L.elem[6],把a搬到L.elem[5],此时把L.elem[4]的位置腾出来了,然后给L.elem[4]赋值即可。
插入位置在最前面
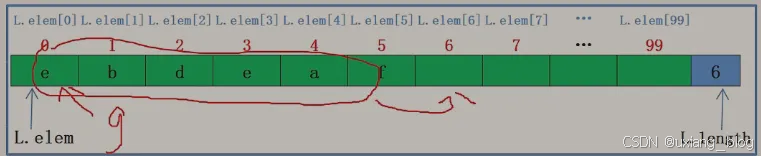
注解:比如把g插入到L.elem[0],就需要把圈出来的元素往后面移动,具体移动规则,从圈出的元素最后一个f开始,从L.elem[5]移动到L.elem[6],然后是a从L.elem[4]移动到L.elem[5],依此如是,就会把L.elem[0]的位置腾出来,然后给L.elem[0]赋值完成。
插入异常的两种情况:
第一、比如插入L.elem[0]位置前面。
第二、比如插入上面数组已经存满,但要插入到L.elem[100]位置,此种情况为溢出。
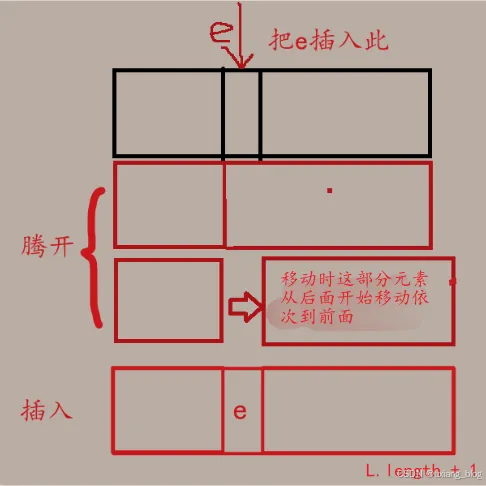
总结:
插入表的插入运算是指在表的第i(1<=i<=n+1)个位置,插入新结点e,使长度为n的线性表(a1,a2,…,ai-1,ai,…,an)变成长度为n+1的线性表(a1,…,ai-1,e,ai,…,an)
算法思想:
(1)、判断插入位置i是否合法。
(2)、判断顺序表的存储空间是否已满,若已满返回ERROR。
(3)、将n至第i位的元素依此向后移动一个位置,空出第i个位置。
(4)、将要插入的新元素e放到第i个位置。
(5)、表长加1,插入成功返回OK。
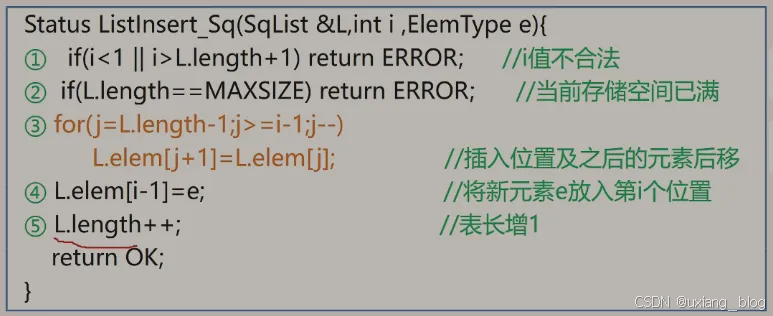
2.4.4.2、顺序表的插入的算法实现
2.4.4.3、顺序表的插入的算法分析(主要看时间效率)
算法时间主要耗费在移动元素上
● 若插入在尾结点之后,则根本无需移动(特别快);
● 若插入在首接结点之前,则表种元素全部后移(特别慢);
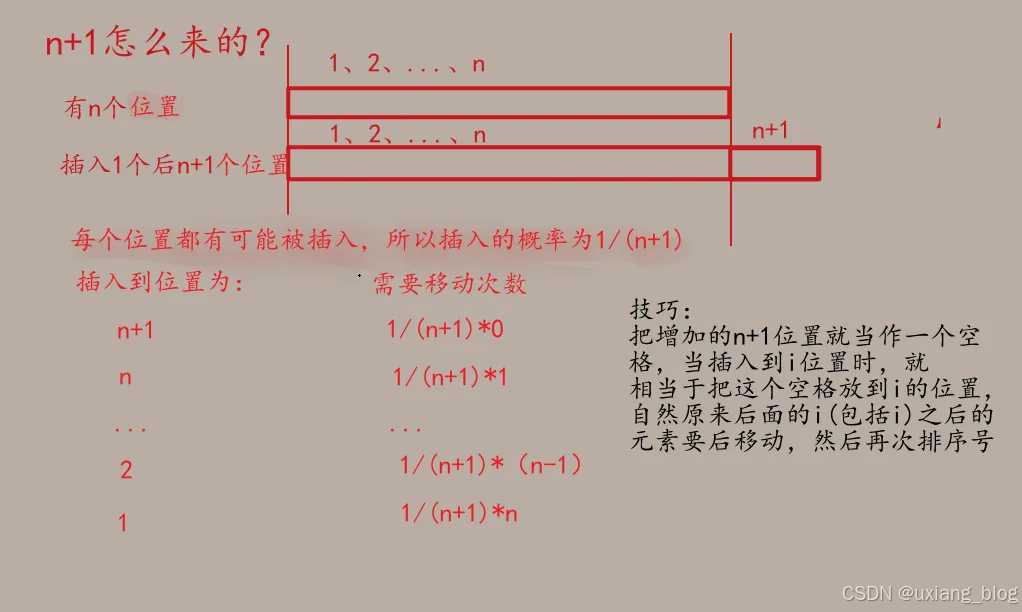
● 若要考率在各种位置插入(n+1可能)的平均移动次数,该如:
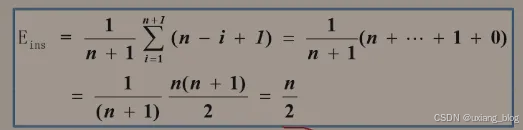
● 顺序表插入算法的平均时间复杂度O(n)。
注解:自己理解
2.4.5、线性表的顺序表示和实现6

2.4.5.1、顺序表的插删除思路
顺序表的删除:

删除不同的位置的算法演示:(L.length下面三种情况都会赋值5,只介绍主要的变化——L.elem[]的变化)
删除位置在最后
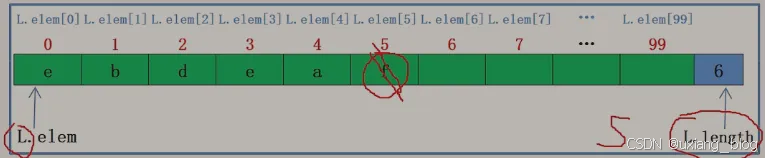
注解:比如删除最末的f,直接将L.elem[5]删除,L.length-1。
删除位置在中间
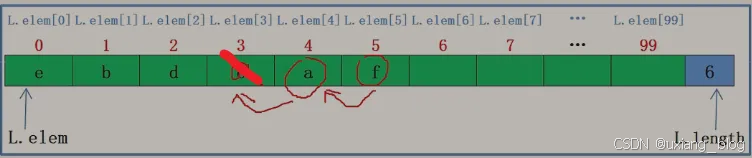
注解:比如将L.elem[3]上的e删除,则后面从a开始移动,接着f,从前到后的顺序。
删除位置在最前面
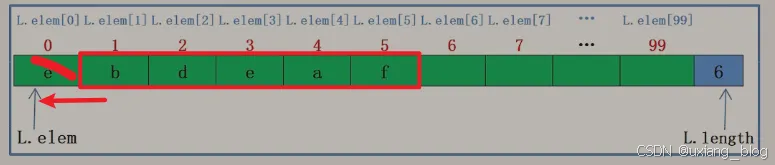
总结
线性表的删除运算是将表的第i(1<=i<=n)个结点删除使得长度为n的线性表(a1,…,ai-1,ai,ai+1,…,an),变长度为n-1的线性表a1,…,ai-1,ai+1,…,an
算法思想:
(1)判断删除位置i是否合法(合法值为1<=i<=n)。
(2)将欲删除的元素保留在e中。
(3)将第i+1至第n位的元素依此向前移动一个位置。
(4)表长减一,删除成功返回OK。
2.4.5.2、顺序表的算法实现

2.4.5.2、顺序表的算法分析
算法时间主要消耗在移动元素的操作上
● 若删除尾结点,则根本无需移动(特别快);
● 若删除首结点,则表中n-1个元素全部前移(特别慢);
● 若考虑在各种位置的删除(共n中可能)的平均次数,该如何计算?
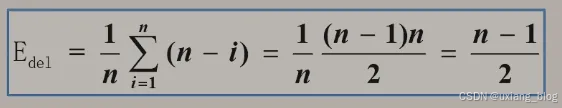
注解:
● 顺序表删除算法的平均时间复杂度O(n)。
2.4.5、小结(2.4内容总结)
顺序表(线性表的顺序存储结构)的特点
(1)利用数据元素的存储位置表示线性表中相邻数据元素之间的前后关系,即线性表的逻辑结构与存储结构一致。
(2)在访问线性表时,可以快速地计算出任何一个数据元素的存储地址。因此可以粗略地认为,访问每个元素所花时间相等。
——这种存取元素的方法被称为随机存取法。
顺序表的基本操作

顺序表的操作算法分析:
● 时间复杂度
○ 查找、插入、删除算法的平均复杂度为O(n)
● 空间复杂度
○ 显然,顺序表操作算法的复杂度S(n)=O(1)(没有占用辅助空间)
顺序表的优缺点:
优点
● 存储密度大(结点本身所占存储量/结点结构所占存储量)
● 可以随机存取表中任一元素
缺点——>解决方法:链表
● 在插入、删除某一元素时,需要移动大量元素
● 浪费存储空间
● 属于静态存储形式[数组],数据元素的个数不能自由扩充。
——————————引入链表
2.5-I、链式最基本的表示和实现——单链表
2.5.1、知识回顾以及引入链式:
顺序表的特点:以物理位置相邻表示逻辑关系。
顺序表的优点:任一元素均可随机存取。
顺序表的缺点:进行插入和删除操作时,需移动大量的元素。存储空间不灵活。
由于顺序表固有的缺点,存储空间不灵活,存储多了浪费,少了又容易溢出,为了解决该问题,链式存储结构应用而生,如下:
链式存储结构:
● 结点字存储器中的位置时任意的,及逻辑上相邻的数据元素在物理上不一定相邻。
线性表的链式表示又称为非顺序映像或链式映像。
那怎么存储的呢?
● 用一组物理位置任意的存储单元来存放线性表的数据元素。
● 这组存储单元即可以是连续的,也可以是不连续的,甚至是零散分布在内存中的任意位置上的。
● 链表中元素的逻辑次序和物理次序不一定相同。
2.5.2、两个经典案例
例如:线性表:(赵、钱、孙、李、周、吴、郑、王)
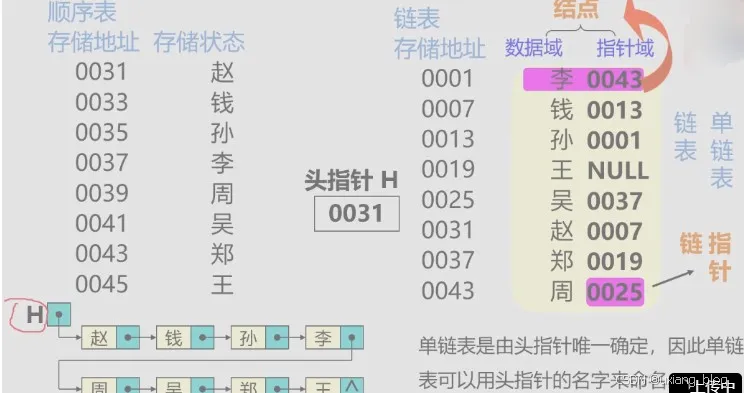
例如:26个英文小写字母表的链式存储结构
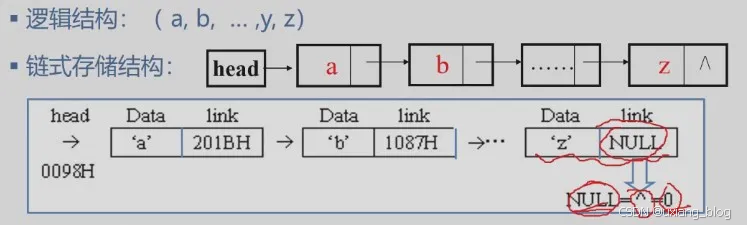
各结点由两个域组成:
● 数据域:存储元素数值数据
● 指针域:存储直接后继结点的位置
2.5.3、与链式存储有关的术语和示意图
1、结点:数据元素的存储映像。由数据域和指针两部分组成
数据域+ 指针域名
2、链表:n个结点由指针链组成一个链表。它是线性表的链式映像,称为线性表的链式存储结构。
示意图:
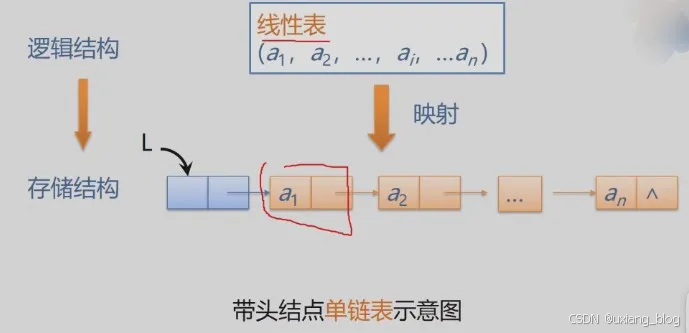
注解:^表示NULL的意思。
3、单链表、双链表和循环链表:
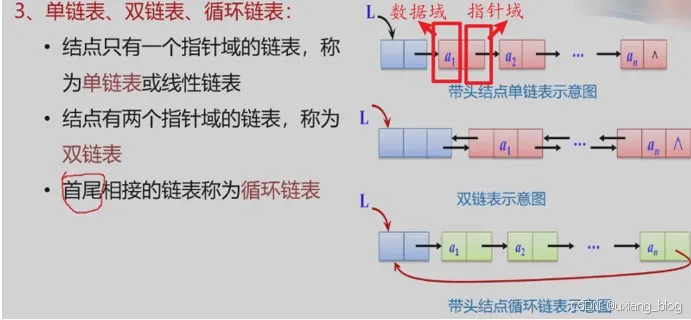
注解:单链表只有一个指针域,用来存储下一个元素的地址,双链表以数据域为中心,有一前一后两个指针域,前指针域用来存储前趋元素的地址,后指针域用来存储后继元素的地址。循环链表中是单链表的的改变,最后一个元素的指针域由原来的存储为NULL变为用来存储的是第一个元素的地址,使其首位相接,谓循环链表。
4、头指针、头结点和首结点:
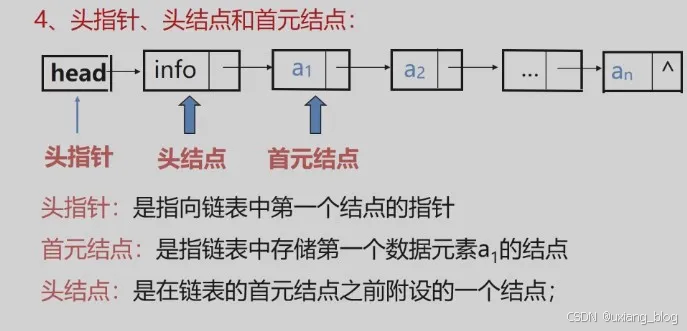
上面例子中的链表的存储结构示意图有以下两种形式:
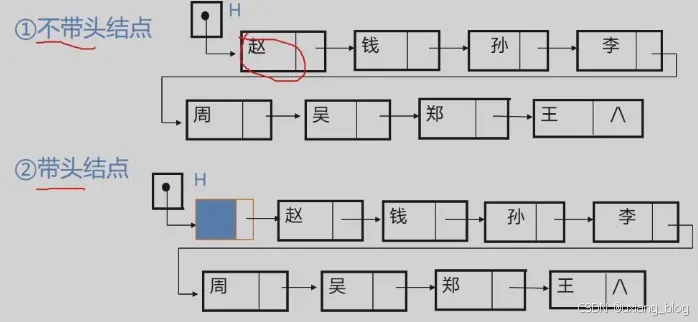
2.5.4、讨论
讨论1、如何表示空表?
● 无头结点时,头指针为空时表示空表
● 有头结点时,当头结点的指针域为空的时表示为空表
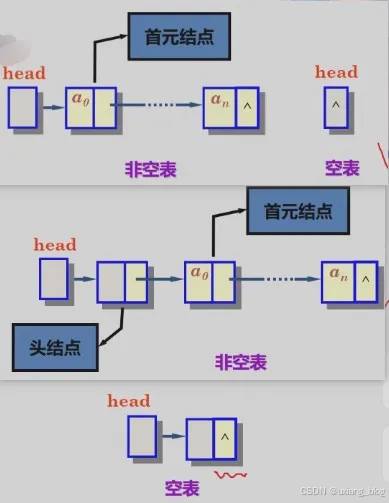
讨论2、在链表中设置头结点有什么好处?
● 1、便于首元结点的处理。首元姐结点的地址保存在头结点的指针域中,所以·在链表的第一个位置上的操作和其他位置一致,无须进行特殊处理;
● 2、便于空表的和非空表的统一处理。无论链表是否为空,头指针都是指向头结点的非空指针,因此空表和非空表的处理也就统一了。
讨论3:头结点的数据域内装的是什么?
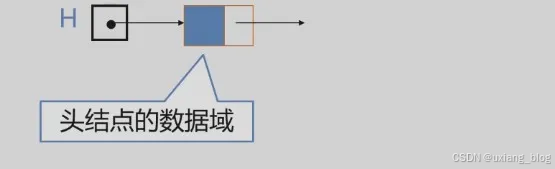
头结点的数据域可以为空,也可以存放线性表长度等附加信息,但此结点不能计入链表长度值。
链表的(链式存储结构)的特点
(1)、结点在存储器中的位置手机任意的,即逻辑上相邻的数据元素在物理上不一定相邻。
(2)、访问时只能通过头指针进入链表,并通过每个结点的指针域依次向后顺序扫描其余结点,所以寻找第一个结点和最后一个结点所花费的时间不等。——这种存取元素的方法叫做顺序存取法。

2.5.5、知识回顾
线性表的链式存储结构
● 线性表中数据元素(结点)在存储中的位置是任意的,即逻辑上相邻的数据元素在物理位置上不一定相邻。
● 结点

● 链表 n个结点由指针链组成一个链表。 链表是顺序存取的。
○ 单链表:每个结点只有一个指针域。
○ 双链表:每个结点有两个指针域
○ 循环链表:链表结点首尾相连。
2.5.6、单链表的定义和表示
带头指针的单链表:
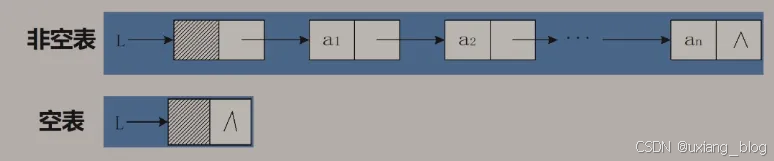
单链表是由表头唯一确定,因此单链表可以用头指针的名字来命名。若头指针名是L,则把链表称为表L。
单链表的存储结构
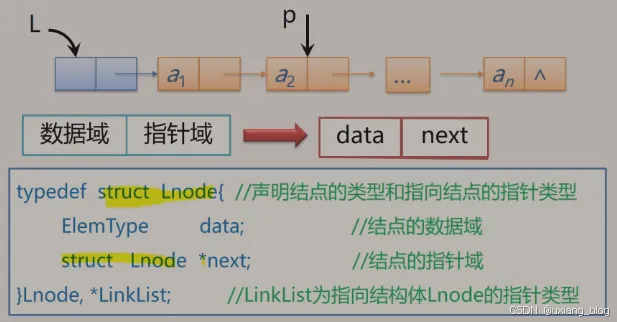
注解:这里的data类型统称为ElemType,具体是什么类型,是int还是float,都视具体情况确定。
struct Lnode用自己定义自己,这种属于嵌套类型的定义。struct Lnode({}里面的)是什么样的类型呢?是指包括两个成员(ElemType data和struct Lnode next)的struct Lnode{}这种类型指针去。前面的typedef给这部分重新起了一个名字。
Lnode, LinkList;//Lnode,结点,比如图中a,对a结点操作就是a.
data,a.next。定义这种指向结点的指针类型可以用p(把LinkList具体化了)或者Lnode, *LinkList也可以用Lnode *L,LinkList L表示。
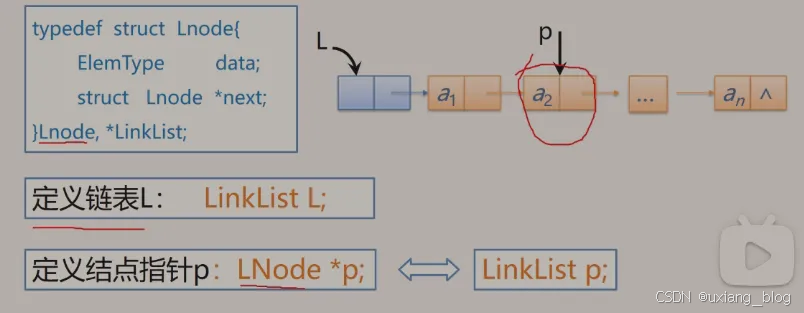
注解:要操作一个单链表L就用LinkList L;要定义一个指针变量,这个指针变量是指向某一个结点的,那就用LNode *p来表示,p本来就指针,所以也可以用 LinkList p;来表示。
通常来说,定义指向头结点的指针,它就代表整个列表,常用LinkList L;来定义,而不是用LNode *L;指向这个结点的指针,虽然也对,但是不建议这么定义。指向结点的指针呢?通常用LNode *p来表示,而不用LinkList p;
例如,存储学生学号、姓名、成绩的单链表结点类型定义如下:

注解:*next指针——>指向那种类型的变量?struct student next?——>指向具有这4个成员Struct student{ char num[8]; char name[8]; int score; struct student *next}这种类型。
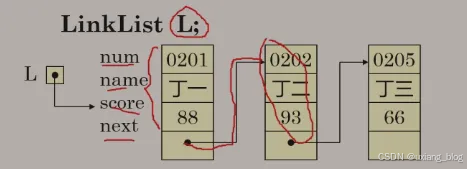
注解:首先它有三个数据域,存储num、和name、score,还有一个指针域,next,是那种类型的呢?指向后面(0202,丁二,93, .)它自己这种类型,然后定义一个指向这个表的指针,LinkList L,让L指向第一个元素。
但是这种方式不大常用,为了统一链表的操作,通常如下定义:
将数据项单独定义成一个结构类型ElemType,然后直接用这个结构类型直接定义一个数据域data,这样就和前面的操作统一了,就方便操作。
2.5.7、单链表基本操作的实现
2.5.7.1、【单链表的初始化(算法2.6)】(带头结点的单链表)
● 即构造一个如图的空表

算法步骤
● (1)生成新结点作头结点,用头指针L指向头结点。
● (2)将头结点的指针域置空。
算法描述
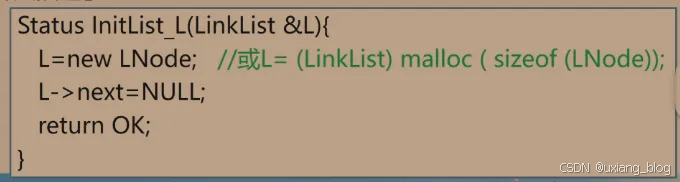
注解:C++:L = new LNode;//这句的含义是把new的结点的地址赋予给L。或C: L= (LinkListA)malloc (sizeof(LNode));//此句的意思是,malloc()从内存中找到一个这么大空间sizeof(LNode),然后经过(LinkList)转换成指向结点的指针的空间的地址赋予给L。
L是一个指针变量,怎么操作它所指的结点的指针域呢?——。
L->next = NULL;//将L所指的结点的指针域置空。
ruturn OK;//返回OK结束。
2.5.7.2、【补充单链表的几个常用简单算法】
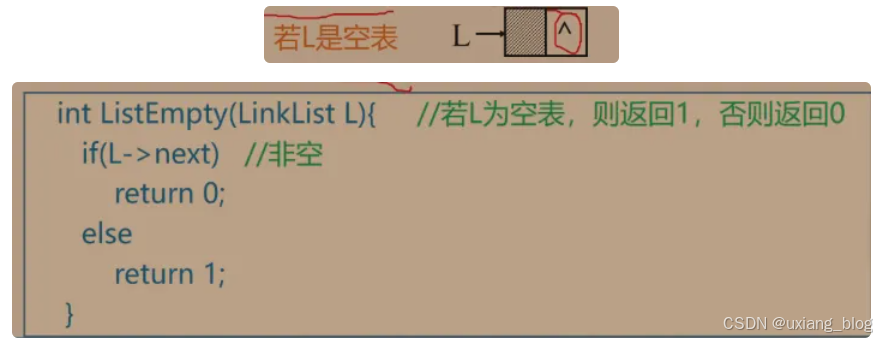
2.5.7.2.1、算法1:判断链表是否为空:
空表:链表中无元素,称为空链表(头指针和头结点仍然存在)
算法实现:判断头结点指针域是否为空
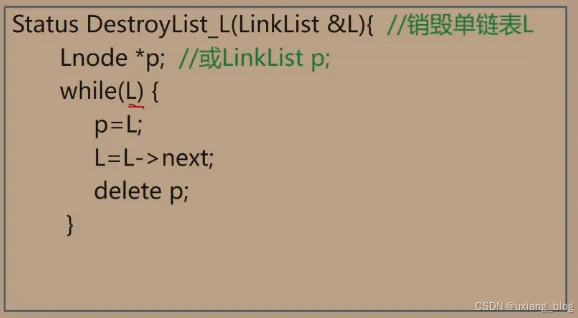
2.5.7.2.2、算法2:单链表的销毁:链表销毁后不存在。
算法步骤:从头指针开始,依此释放所有结点。
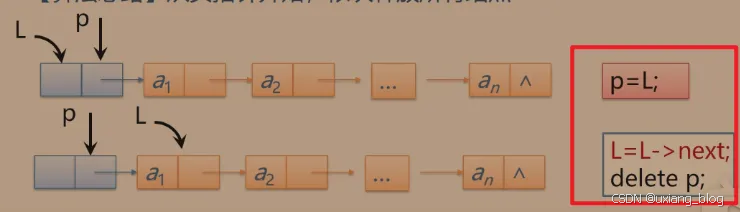
注解:怎么操作呢?还需要一个另为一个指针变量(如p),用来操作结点。操作指针变量p,将它指向头结点L,然后把结点L释放掉(也指删掉)。怎么把一个变量(这里具体化是指针变量p)指向头结点(此处具体化指头结点L)呢?我们把这个空间的(这里指的是头结点的空间)地址赋值给这个变量,比如p = &a;如此则有p=L;便代表指针变量p指向头结点L了,接着便可以把这个结点删掉了,但不能直接删掉,因为删掉之后下一个结点的地址也随之被删掉了,我们的办法是先将L移动到下一个结点的位置(由链表的性质,头结点是由数据域+指针域组成的,而头结点的指针域存放着后继结点的地址,所以可以利用头结点所存的地址移动到下一个结点,即L=L->next;),然后删除前一个结点,依此类推,就释放掉了整个单链表。释放的具体操作是,C++:delete p; C:free(p)。注意两组搭配:
● C++:new 对应删除 deletep;
● C: malloca()函数 对应删除 free§;
但是问题来了,依此类推下去什么时候结束呢?我们直到最后一个an的结点数据域中是,意思是空,所以见到这个标志(,NULL,空)则说明该结束了,即L = L->NULL 。结束条件:L == NULL,循环条件:L! = NULL,非空也可简单表示成:L
算法描述:
2.5.7.2.3、算法3:清空单链表
链表仍存在,但链表中无元素,成为空链表(头指针和头结点仍然在)
算法步骤:依此释放所有结点,并将头结点指针域设置为空。
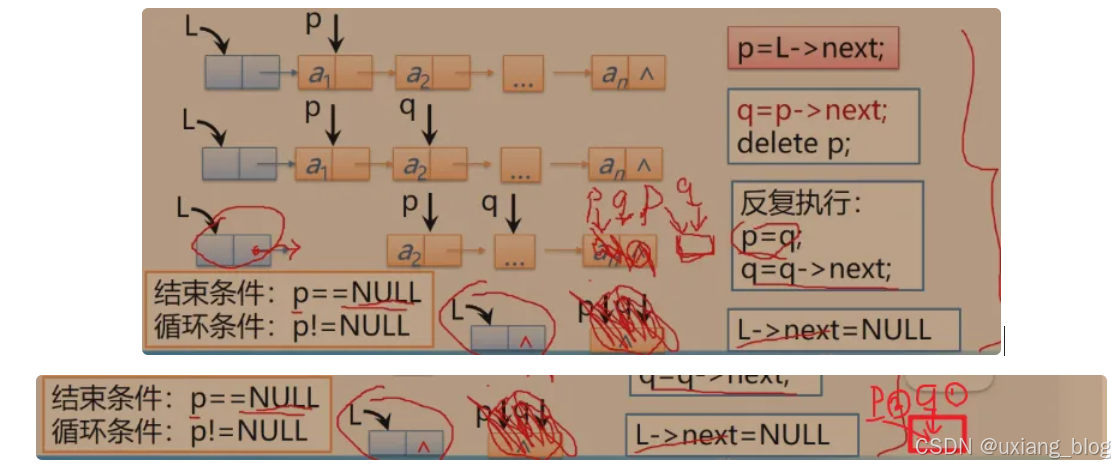
注解:比如现在有一个列表L,我们把链表清除,从第一个元素开始,依此清除,最后将头节点指针域置为空,就结束了。那我们说从头元结点开始,那怎么获取第一个结点的地址呢?第一个结点的地址在首元结点的next域(应该是指针域),L->next,获得即首元结点(存放第一个元素的结点)的地址,然后把它赋值给指针p,即L= L->next。上一次做销毁操作的是时候连头结点一块都销毁了,那我们怎么让指针指向头结点呢?头指针里面就存在头结点的地址,直接把头结点L赋值给p,即p=L。点单链表中最长用的操作,p= L->next (首元结点),和 p=L(头结点)是常用的操作。在清空链表时,是从清空首元结点开始的,并不像销毁单链表那样所有结点都删除,而且还有最后给头结点置空,所以清空链表中独有的操作是,有指针变量p来精进行操作(删除动作),另为一个变量q来记录下一结点的地址。先由q记录下一结点的地址q=p->next;然后用指针变量p删除前面一个结点,接着再由记录变量q告诉指针变量p接下来要删除哪一个结点,即p=q;,随后记录变量q便跳到下下个结点去记录q=q->next;依此往复,(如果p=q和q=q->next互换顺序,那么两个变量同时指向同一个结点,没法删除)。
那什么时候结束呢?将头结点的指针域设置为空就可以。
算法描述:

2.5.7.2.4、算法4:求单链表的表长
算法思路:从首元结点开始,依此计数所有结点
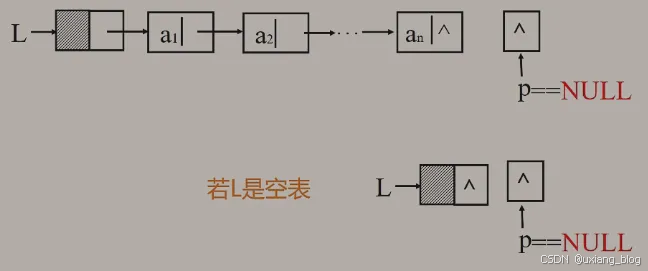
注解:现在我们数出单链表中有多少个元素。从首元结点开始,依此计数所有结点。怎么从首元结点开始呢?首元结点的地址存在于头结点的next域存着,则需要把头结点next域赋值给指针即可,即p = L -> next(i=1,ai);然后看一下这个结点是不是空的,是空的就不再往下面数了。怎么解决从首元结点移动下一个结点的呢?根据单链表的性质,首元结点的next域是存着下一个结点的地址的,则选要把它的next域赋值给指针即可,p = p -> next;其他移动情况也是同理,直到指针为NULL为止。若是空表则需要使得指针p所指结点为空,则需要将头指针L赋值给p,即p = L。
算法实现:

2.5.8、单链表的基本操作的实现
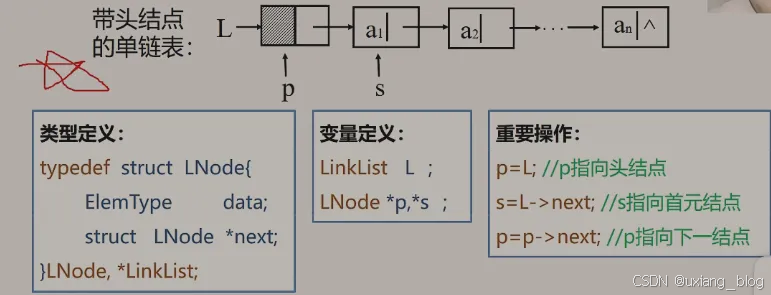
知识回顾:(下图内容非常重要是需要记住的内容)
注解:
类型定义部分:链表当中每个结点需要存储数据元素,除了存储数据元素本身,还需要存储下一个元素的地址,所以它的结点类型是由两个成员变量,一个存储数据元素的data,和另一个存储地址next的指针,由这个两个成员变量组成的这种结构类型struct LNode{},然后同typedef 重新把它们定义成了结构类型名LNode和LinkList,一个是这种类型的结点LNode,另一个是指向这种结点的指针类型。
变量定义部分:那么我们就可以利用它们两个去定义我们需要的结点和指针。LinkList本身就是指针型,所以L前面无需加*号,指向结点的类型需要加✳号,*p,*s。
重要操作部分:
p=L;//p指向头结点
s= L ->next;//s指向首元结点
p=p -> next;//p指向下一个结点
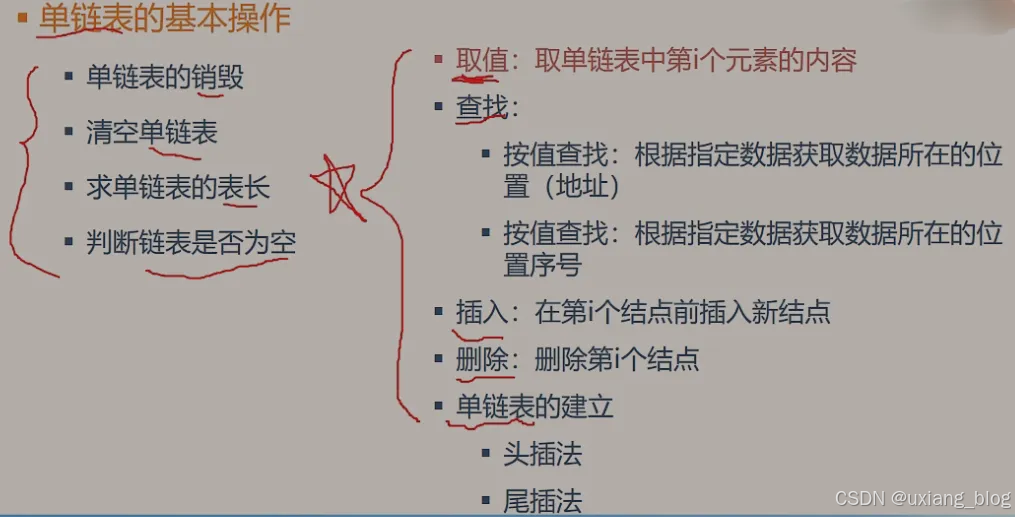
之前学习了单链表的基本操作:
● 单链表的销毁
● 清空单链表
● 求单链表的表长
● 判断链表是否为空
接下来要学习的是:——非常重要
● 取值:取单链表中第i个元素的内容
● 查找:
○ 按址查找:根据指定数据获取数据所在的位置(地址)
○ 按值查找:根据指定数据获取数据所在的位置序号
● 插入:在第i个结点前插入新节点
● 删除:删除第i个结点
● 单链表的建立
○ 头插法
○ 尾插法
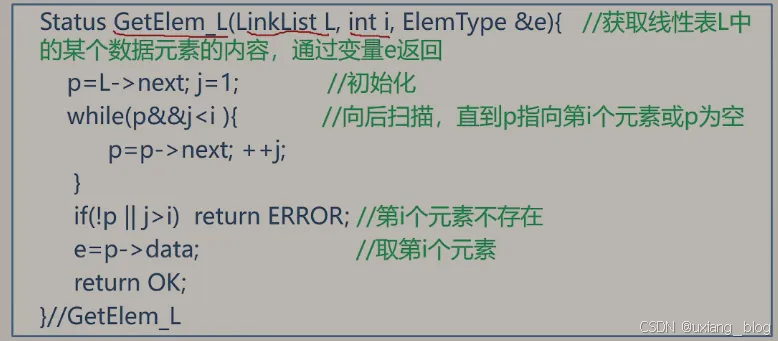
2.5.8.1、算法1:取值——取单链表中第i个元素的内容
思考:顺序表里如何找到第i个元素?L->elem[i-1] ——随机存储

注解:引入一个变量j来记录序号,从首元结点开始,即定义首元结点j=1,然后随着指针逐个往下走,依此逐个将j增加。有3种情况。
● 要是查找元素i不合法:比如i=-1,或者0,那么这样的数找不到,为了方便,链表中查找是根据逻辑顺序从1开始的,如果要查从-1,0这样不存在的,是不合法的,也会返回相应的ERROR。
● 如果查找元素i在范围内:比如i=3,则根据查找就会找到相应的数据 30。
● 如果查找元素i不在范围内:比如i=15,而实际上该单链表只能存储j=6个元素,所以超出范围后,就会返回NULL。
算法实现:
算法步骤:
● 1、从第1个结点(L->next)顺序扫描,用指针p扫描指向当前扫描到的结点,p初值p = p->next。
● 2、j 做计数器,累计当前扫描过的结点数,j初值为1;
● 3、当p指向扫描到的下一个结点时;计数器j加1。
● 4、当 j == i 时,p所指的结点就是要找的第i个结点。
算法描述:
2.5.8.2、算法2:查找——取单链表中第i个元素的内容
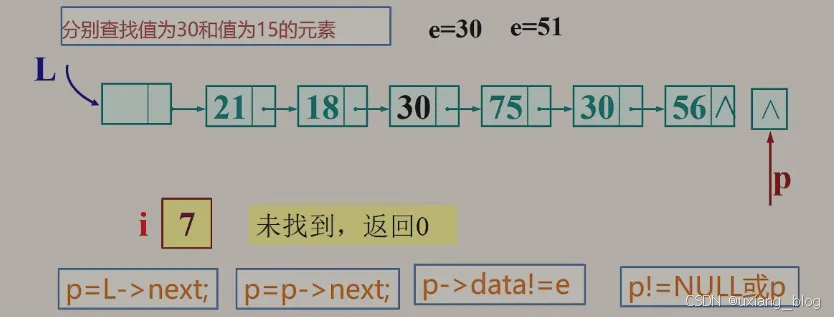
2.5.8.2.1、按值查找
按值查找:根据指定数据获取数据所在的位置(地址)。如果找到了就返回当前的位置(地址)p(比如:30),如果要返回第几个那就返回计数器的值(本例子结合上面的图是i的值)。

2.5.8.2.2、按值查找

2.5.8.3、算法3:插入——在第i个结点前插入值为e的新节点
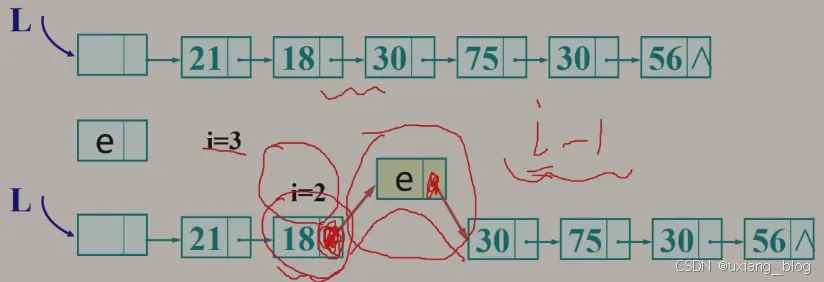
算法步骤:
● 1、首先找到ai-1的存储位置p。
● 2、生成一个数据域为e的新节点s。
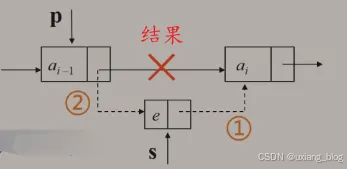
● 3、插入新结点:
○ (1)、新结点的指针域指向结点 ai:s->next = p -> next;
○ (2)、结点ai-1的指针域指向新节点:p -> next = s;
思考:步骤(1)和(2)能互换吗?先执行(2)后执行(1),可否?
注解:不可以,会丢失ai的地址。原来ai-1里面存储着ai的地址,互换之后就会丢失ai的地址,效果上面想当于砍断了ai-1和ai,在ai-1处接了一个s而已,如果在看砍断之前先用一个指针q记录下ai的地址,然后再砍断之后把q所记录ai的地址续在s上,这是可以的。
算法描述:

注解:需要掌握3点:
● 1、如果插入的?
● 2、怎么找到i-1个结点?
● 3、非法插入?怎么保证插入在i结点?
2.5.8.4、算法4:删除——删除第i个结点
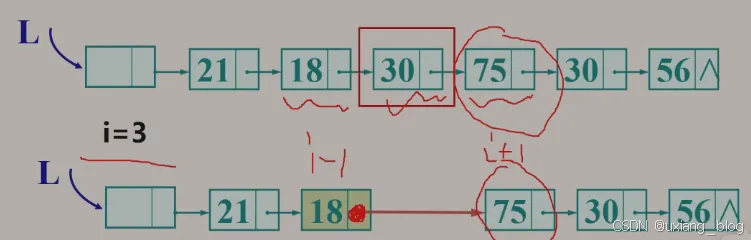
算法步骤:
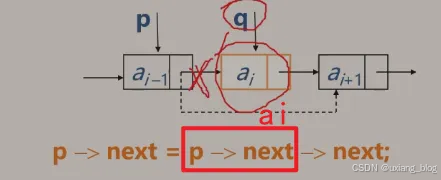
● 1、首先找到ai-1的存储位置p,保存要删除的ai的值。
● 2、令p -> next 指向ai+1。
● 释放结点ai的空间。
算法描述:

总结:算法2-5的时间效率分析:
单链表的查找、插入、删除算法时间效率分析
1、查找:因线性表只能顺序存取,即在查找时要从头指针找起,查找时间复杂度为O(n)。
2、插入和删除:
● 因线性链表不需要移动元素,只要修改指针,一般情况下时间复杂度为 O(1)。
● 但是,如果要在单链表中进行前插或删除操作,由于要从头查找前趋结点,所耗时间复杂度为O(n)。
2.5.8.5、算法5:单链表的建立
2.5.8.5.1、头插法——元素插入在链表头部,也叫前插法。
算法步骤:
● 1、从一个空表开始,重复读入数据;
● 2、生成新结点,将读入数据存放到新节点的数据域中
● 3、从最后一个结点开始,依此将各个结点插入到表的前端。
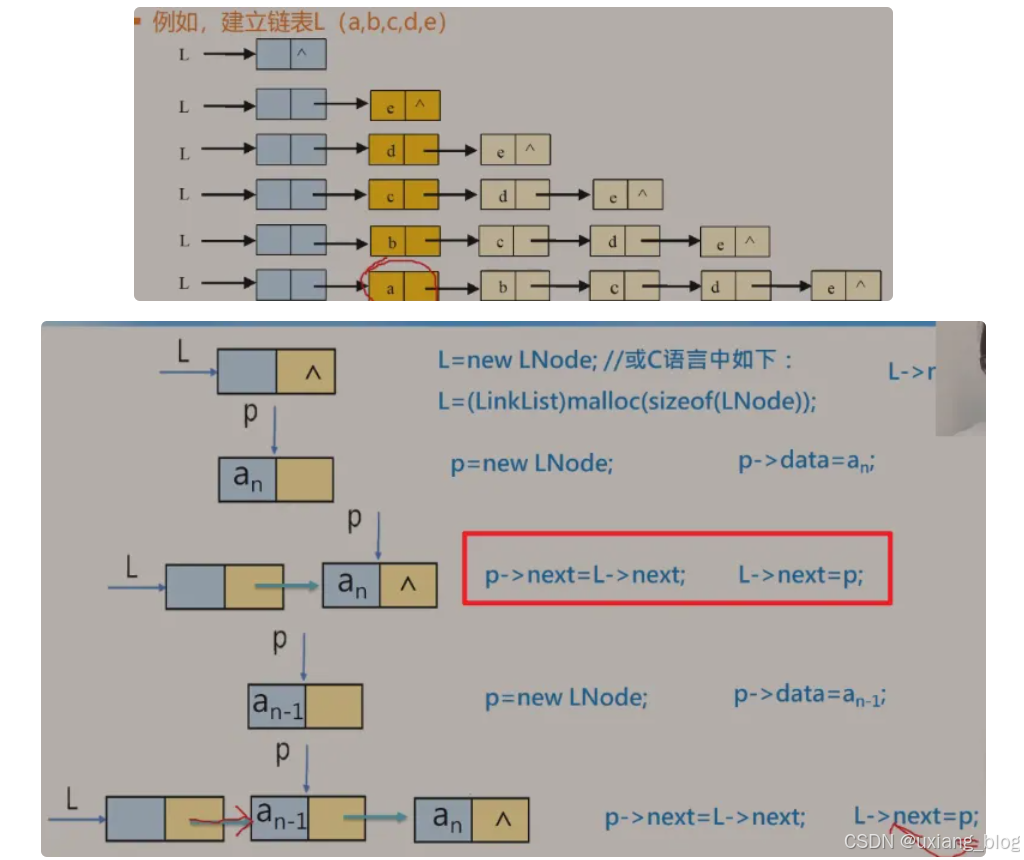
注解:p->next = L ->next; //把头结点的next中的NULL转换到新节点next中
L -> next = p;//然后再把新结点p赋值给头结点的next,就把新节点接到头结点L后面了。
后面接法如此重复。
算法描述:

2.5.8.5.2、尾插法——元素插入在链表尾部,也叫尾插法todo
算法步骤:
● 1、从一个空表L开始,将新结点逐个插入到链表的尾部,尾指针r指向链表的尾结点。
● 2、初始时,r同L均指向头结点。每读入一个数据元素则申请一个新结点,将新结点插入到尾结点后,r指向新结点。
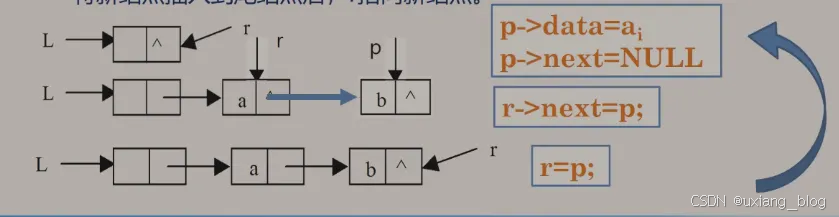
算法描述

2.5-II、链式其他形式的表示和实现——循环链表、双链表
2.5.1、循环链表
循环链表:是一种头尾相接的链表(即:表中最后i一个结点的指针域指向头结点,整个链表形成一个环)。
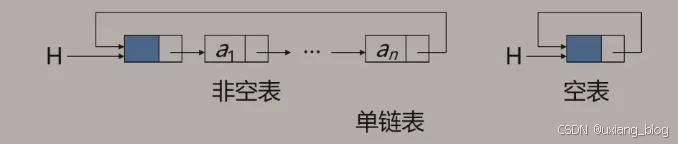
注解:单链表中最后一个结点之后再无其他结点自然最后一个结点的指针域中为空,但在循环链表中,最后一个结点的指针域不为空,它存储的是头结点的地址。这样有什么好处呢?相比单链表,在循环链表中,到最后一个结点后还可以向下继续寻找头结点,继而其他结点。循环结点的空表怎么表示?其头结点存储的是自身的地址(或者头结点的指针域指向自身)。那循环链表中怎么知道到最后一个一个结点an呢?
优点:从表中任一结点出发均可找到表中其他结点。
————————那循环链表中怎么知道到最后一个一个结点an呢?
最后结点an的确认:由于循环链表中没有NULL指针,故涉及遍历操作时,其终止条件就不再像非循环链表那样判断p或p->next是否为空,而是判断他们是否等于头指针。

经常首尾操作,循环链表的选择:————为什么要选带尾指针的循环链表?

2.5.2、带尾指针的循环链表的合并
带尾指针循环链表的合并(将Tb合并再Ta之后)
注解:整个链表是怎么表示的呢?带头指针的链表表示时只需要一个头指针的地址就能代表整个链表,当然也就暗示默认知道这个头指针的地址了,当然带尾指针的链表也是同理,即Ta就知道an的地址,知道这个原理就能理解下面分析过程了。
算法步骤:
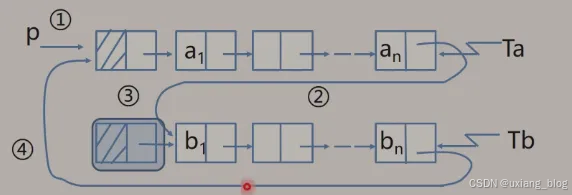
分析有哪些操作?
- p存表头结点 p = Ta -> next;
- Tb表头(首元结点,而非头结点)连接头Ta的表尾 Ta-> next = Tb -> next -> next;
- 释放Tb表头结点 delete Tb -> next;
- 修改指针 Tb -> next = p;
算法描述:

2.5.3、双向链表
为什么要讨论双向链表?——因为单链表的某些缺陷,使得人们开始设计最优化的方案。

单链表中的结点——>有指示后继的指针域——>找后继结点方便;即:查找某结点的后继结点的执行时间尾O(1)。——>无指示前趋的指针域——>找前趋结点难:从表头出发查找,即:查找某结点的前趋结点的执行时间为O(n)。可用双向链表来克服这种单链表的这种缺点。
注解:简单来说,因为单链表的属性,一个结点=数据域+下一个结点的地址,这样的结构使得查找一个结点下一个结点容易,但是查找该结点上一个结点就很难,得从头结点开始查起。双向链表企图解决基于容易查找后继结点的优点上,又容易查找前驱结点的方法。
双向链表:在单链表的每个结点里面再增加一个指向其直接前趋的指针域prior,这样链表中就形成了有两个方向不同的链,故称为双向链表。
双向链表的结构定义:
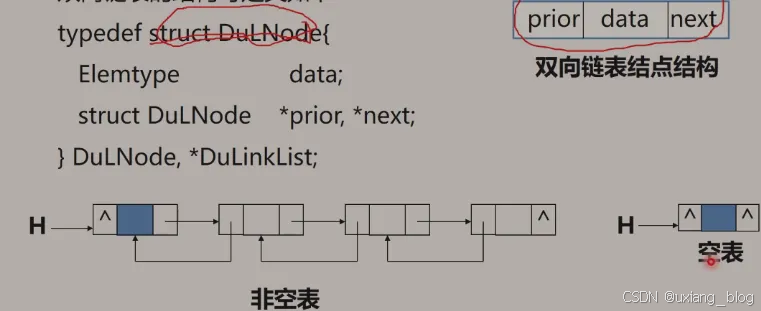
按照研究但单链表的方法,双链表也可以有循环链表,如下:
双向循环链表:
和单链的循环链表类似,双向链表也可以有循环表
● 让头结点的前驱指针指向链表的最后一个结点
● 让最后一个结点的后继指针指向头结点。

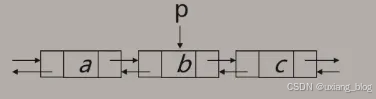
那么问题来了,我们知道单链表中是一个数据域+指针域,这个指针域指向下一个结点(也是存储着下一个结点的地址),但在双向链表中,这种 “指针域+ 数据域 + 指针域” 结构中,怎么规范一个结点两个指针域的问题?(实现功能,简单易懂)?———————————即一个结点的后继结点是下一个结点的前驱结点。
双向链表结构的对称性(设指针p指向某一结点):
p -> prior ->next = p = p -> next -> prior
在双链表中有哪些操作(如:ListLength 、GetElem等),因仅涉及一个方向的指针,故它们的算法与线性链表的相同。但在插入、删除时,则需同时修改两个方向上的指针,两者的操作的时间复杂度均为O(n)。
2.5.4、算法1:双向链表的插入
算法步骤:
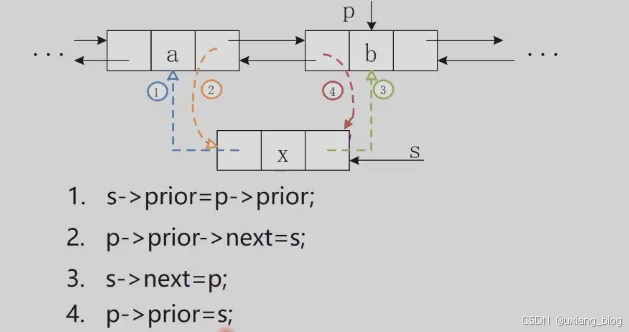
算法描述:
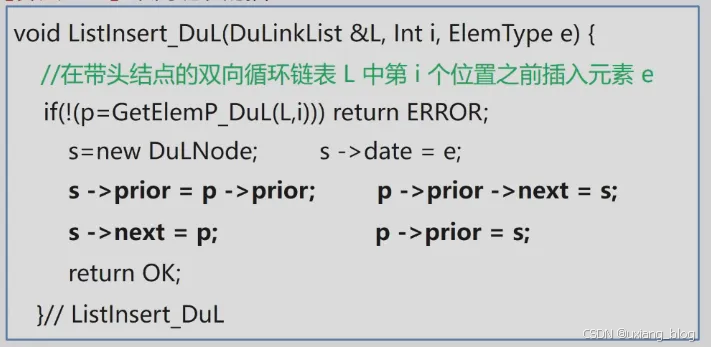
注解:if(!(p = GetElemP_DuL(L,i))) return ERROR;//在链表L中找到i赋值给p,即p指向i个结点,如果这是时候给到i的位置不合理,是非法的(体现在!上),那就返回错误。
2.5.5、算法2:双向链表的删除
算法步骤:
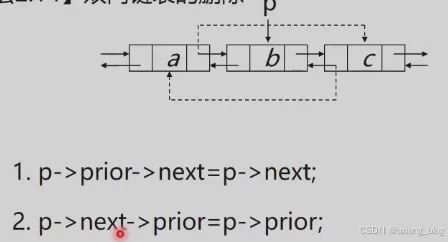
注解:已知p结点位置,用p来操作,
● 1、需将a结点(p->prior)的next域存储上c结点的地址(c的地址存在于指针p的next域中);
● 2、需将c结点(p->next)的前驱prior存储上a结点的地址(a的地址存在于指针p的前驱中);。
算法描述:

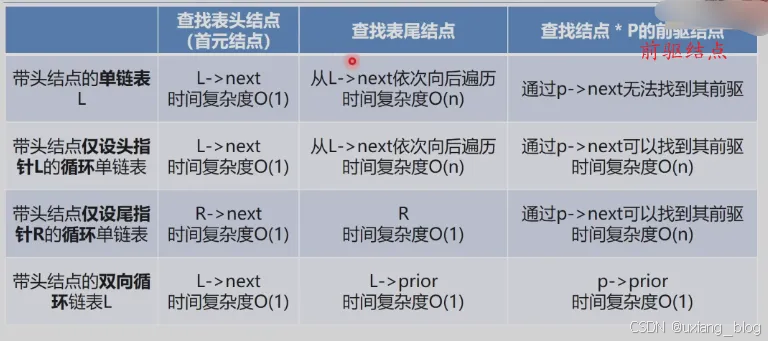
2.5.6、单链表、循环链表和双链表的时间效率比较
2.6、顺序表的和链式表的比较
先总结链式表的优缺点
● 链式存储结构的优点:
○ 结点空间可以动态申请和释放:
○ 数据元素的逻辑次序依靠结点的指针来指示,插入和删除时不需要移动数据元素。
● 链式存储结构的缺点:
○ 存储密度小,每个结点的指针域需额外占用存储空间。当每个结点的数据域所占字节不多时,指针域所占存储空间的比重显得很大。
○ 链式存储结构是非随机存取结构。对任一结点的操作都要从头指针依指针链查找到该结点,这增加了算法的复杂度。
存储密度:是指结点数据本身所占的存储量和整个结点结构中所占的存储量之比,
即:存储密度=结点数据本身占用的空间结点占用的空间总量存储密度 = \frac{结点数据本身占用的空间}{结点占用的空间总量}存储密度=结点占用的空间总量结点数据本身占用的空间

一般地,存储密度越大,存储空间的利用率就越高。显然,顺序表的存储密度为1(100%),而链表的存储密度小于1。
接着是顺序表和链表的比较
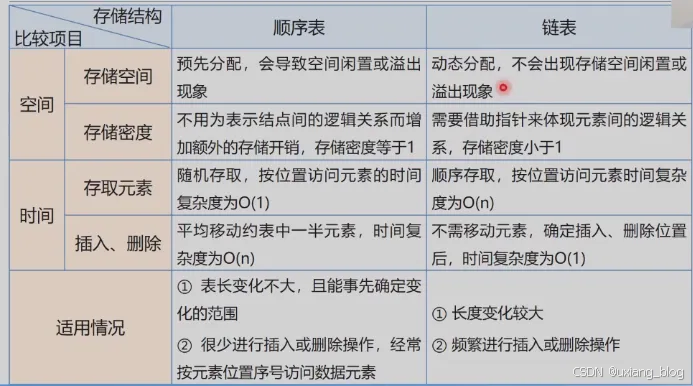
————————2.7介绍线性表的典型应用,2.8介绍2.2案例引入 中案例如何解决
2.7、线性表的应用
2.7.1、线性表、有序表的合并————表示
线性表的合并:
● 问题描述:假设利用两个线性表La和Lb分别表示两个集合A和集合B,现要求一个新的集合A=A∪B。

● 算法步骤:依此取出b中的每个元素,执行以下操作:
○ 1、在La中查找每个元素
○ 2、如果找不到,则将其插入La的最后
● 算法描述

算法的时间复杂度是:O(ListLength(La)*ListLength(Lb))
有序表的合并:
● 问题描述:已知线性表La和Lb中的数据元素按值非递减(不是严格递减,有的值相等)有序排列,现要求将La和Lb归并为一个新的线性表Lc,且Lc中的数据元素仍然按值非递减有序排列。

● 算法步骤:
○ 1、创建一个空表Lc
○ 2、依此从La或Lb中“摘取”,元素较小的结点插入到Lc表的最后,直到其中一个表变空为止
○ 3、继续将La或Lb其中一个表的剩余结点插入在Lc表的最后
2.7.2、线性表、有序表的合并————实现
【算法2.16】有序表合并——用顺序表实现
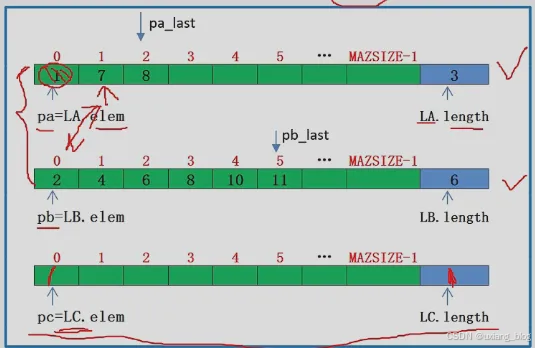
算法描述:

todo没有理解

算法的时间复杂度是:O(ListLength(La)+ListLength(Lb))
算法的空间复杂度是:O(ListLength(La)+ListLength(Lb))
【算法2.17】有序表合并——用链表表实现
用La的头结点作为Lc的头结点
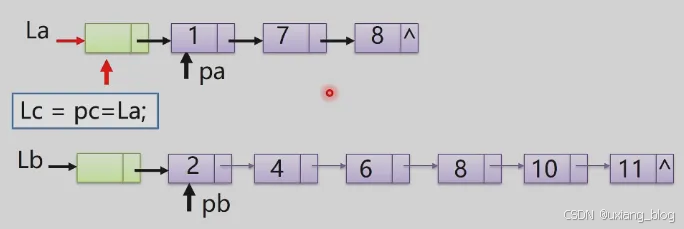
注解:用La的头结点作为Lc的头结点,Lc=pc=La;将La的头结点赋值给Lc,再指定三个指针变量来操作列表中的结点,La列表中用pa操作,Lb列表中用pb操作,Lc列表中用pc操作。
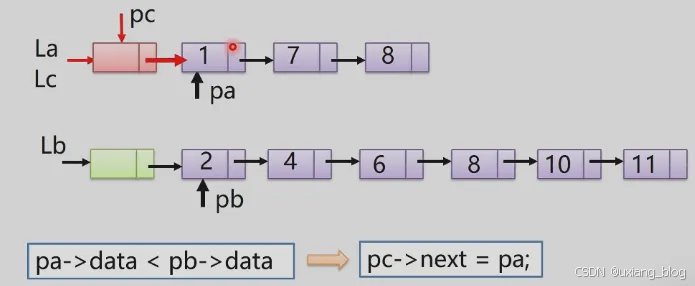
注解:先看一下当前结点pa和pb所指的那个比较小,因为pa的数据域data小于pb的数据域,则把pa接在Lc列表中,即pc -> next = pa;然后pc的指针指向1所在的结点(图示如下),pa又指向La列表中下一个结点(图示如下)。
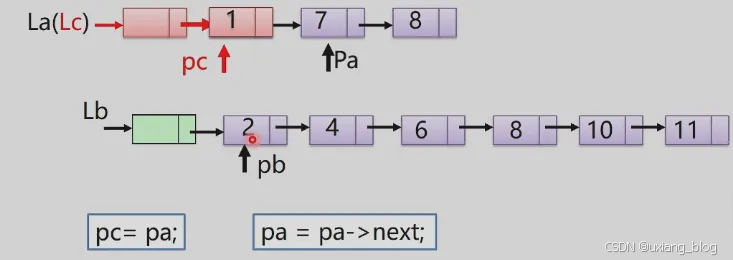
注解:接着是La列表中pa指针所指的第二结点(7所在地方),和Lb列表中pb所指的首元结点(2所在的地方)进行比较,因为7大于2,所以1后面接下来的是比较小2,作为Lc列表中的第二个结点,随后Lb中首元结点已经接上使用完了,pb指针指向下一个结点(示图如下),依此类推。
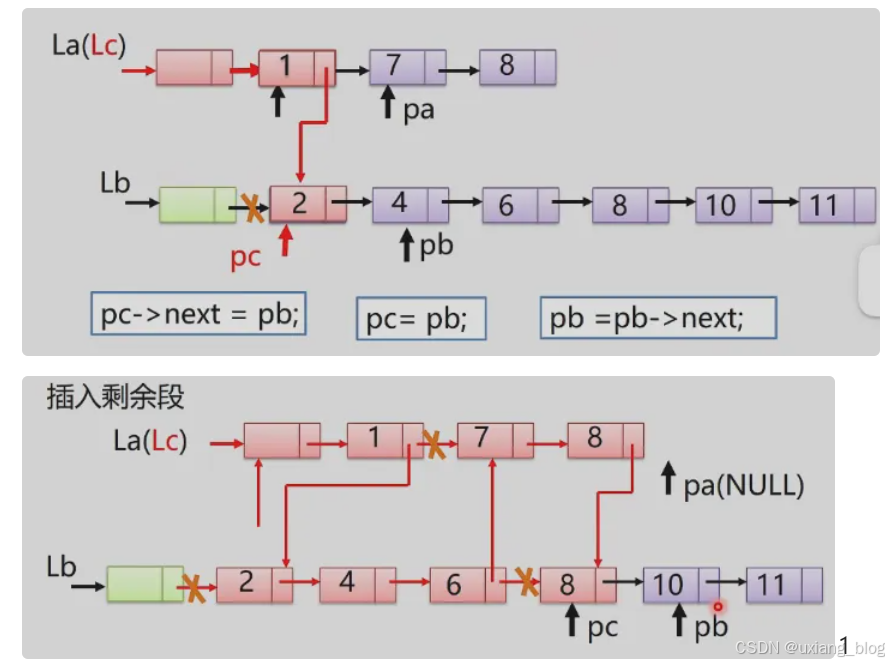
注解:La列表的长度小于Lb列表的长度,所以直到La表中完毕(pa为NULL),就会直接把Lb列表中剩余的元素接上,这样就形成了Lc列表了(图示如下)。
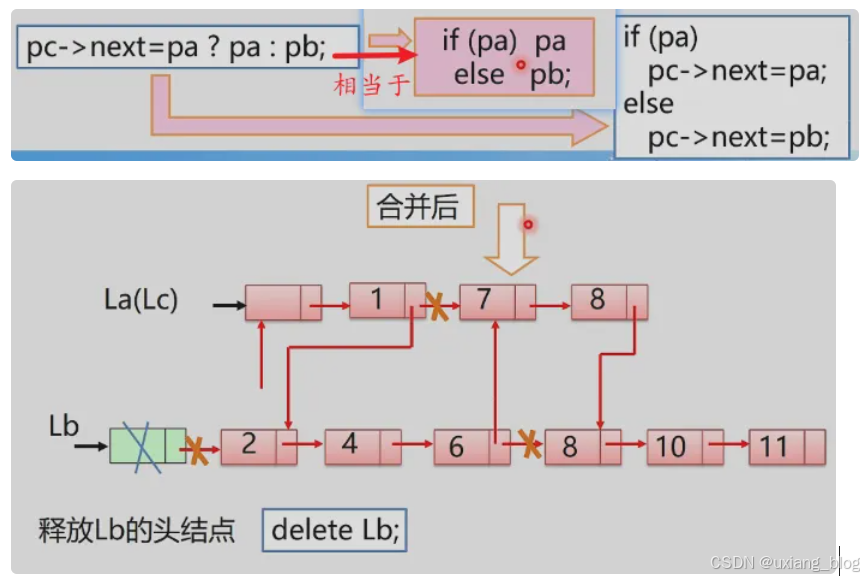
注解:最后把列表Lb的头结点释放掉就完成,完整的算法描述如下:
算法描述:
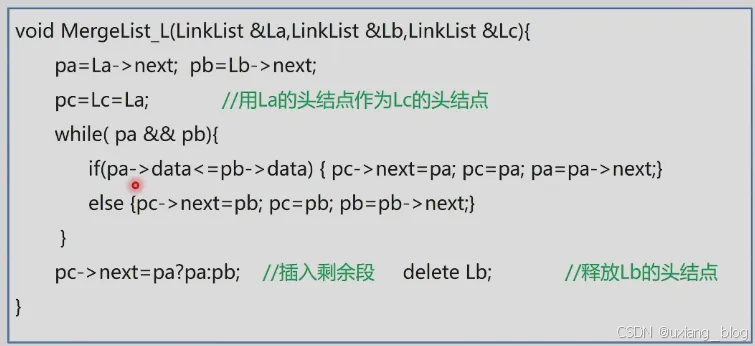
算法的时间复杂度是:O(ListLength(La)+ListLength(Lb))
算法的空间复杂度是:O(1)
注解:在生成Lc列表中(即La列表和Lb列表合并),直接在列表La和列表Lb上操作,没有涉及额外的空间,所以空间复杂度为1(在原来的空间上就表示1)。
2.8、案例分析与实现
【案例2.1】一元多项式的运算:实现两个多项式加、减、乘运算
实现两个多项式相加运算:

【案例2.2】:稀疏多项式的运算
多项式非零项的数组表示

多项式非零项的数组实现
线性表A=((7,0),(3,1),(9,8),(5,17))
线性表B=((8,1),(22,7),(-9,8))
算法步骤:
● 创建一个新数组c
● 分别从头遍历比较a和b的每一项
○ 指数相同,对应系数相加,若其和不为零,则在c中增加一个新项
○ 指数不相同,则将指数较小的项复制到c中
● 一个多项式已遍历完毕时,将另一个剩余项依次复制到c中即可
c多大合适呢?——————————若a是n这么大,b为m大,那么c为m+n,最小为多少呢,为0。还得新建一个数组c存储,来一个新空间,空间上也比较浪费,如何解决?
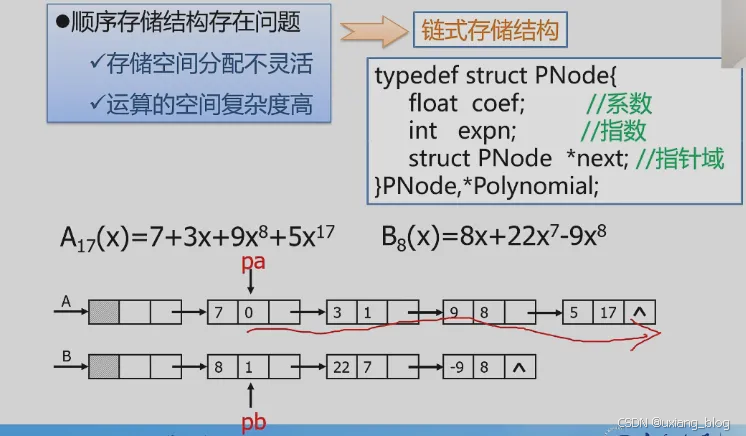
多项式创建——【算法步骤】
(1)创建要一个只有头结点的空链表。
(2)根据多项式的项的个数,循环n次执行以下操作:
● 生成一个新结点s;
● 输入多项式当前项的系数和指数赋给新结点s的数据域;
● 设置一前驱指针pre,用于指向待找到的第一个大于输入项指数的结点的前驱,pre初值指向头结点;
● 指针q初始化,指向首元结点;
● 循环链向下逐个比较链表中当前结点与输入项指数,找到第一个大于输入项指数的结点q;
● 将输入项结点s插入到结点*q之前。
多项式创建——【算法描述】:

多项式相加————【算法分析】:
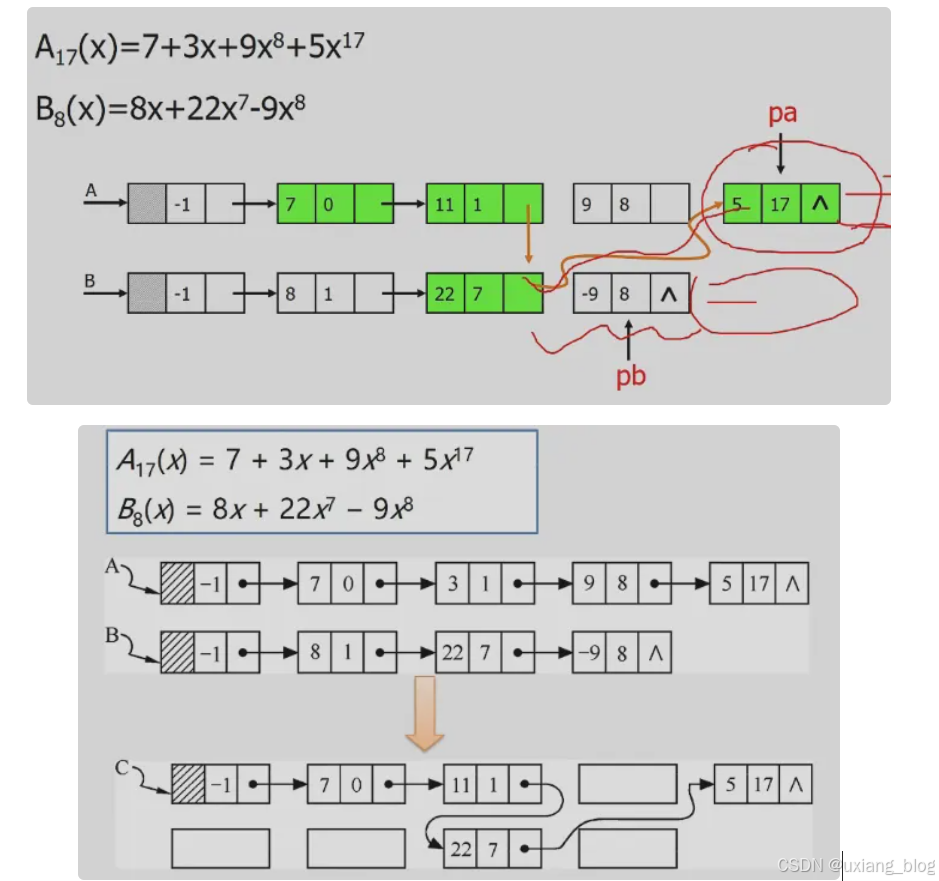
多项式相加————【算法步骤】:
1、指针p1和p2初始化,分别指向pa和pb的首元结点。
2、p3指向和多项式的当前结点,初值为pa的头结点。
3、当指针p1和p2均未达到相应表尾时,则循环比较p1和p2所指结点对应的指数值(p1->expn与p2->expn),有下列3种情况:
● 当p1->expn==p2->expn时,则将两个结点中的系数相加
○ 若和不为0,则修改p1所指结点的系数值,同时删除p2所指结点
○ 若和为0,则删除p1和p2所指结点;
● 当p1->expnexpn时,则应摘取p1所指结点插入到“和多项式”l链表中去;
● 当p1->expn>p2->expn时,则应摘取p2所指结点插入到“和多项式”l链表中去。
4、将非空多项的剩余段插入p3所指结点之后。
5、释放pb的头结点。
【案例2.3 】:图书信息管理系统
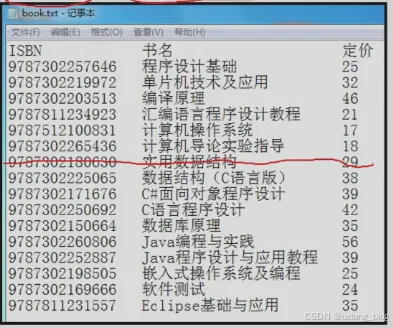
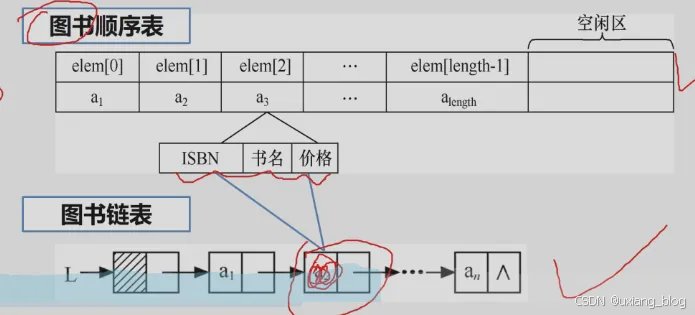
注解:图书管理系统完成一些对图书的管理操作,比如说按照书名查询,有没有《Java入门到放弃》的书,比如说要删除一本叫做《使用数据结构》的书,还有修改书名,等等一系列增删改查操作,这些问题呢?就是从问题当中抽象出数据模型,是线性表,先后顺序的逻辑关系。此线性表中的每个元素呢都是复杂元素,每个数据元素都包含书号书名定价三个数据项,咱们这些问题怎么实现呢?即可以用顺序表也可以用链表实现,而其表中的数据域data存储着ISBN 书名 价格。
注解:用顺序表?还是链表?到底用那种呢?如果表中的书的变化不大,很少做删除,插入操作,而且经常需要通过序号去查找一本书籍,那么便用顺序表,因为顺序表的逻辑顺序和存储顺序一致。如果表中书的变化非常大,经常要删除,插入操作,那就用链式结构。接下来这两种表如何定义?

第三章 栈和队列
3.1、栈和队列的定义和特点
栈和队列是两种常用的、重要的数据结构
栈和队列是限定插入和删除只能在表的“端点”进行的线性表
● 栈和队列是线性表的子集(是插入和删除位置受限的线性表)
3.1.1、普通线性表的插入和删除操作
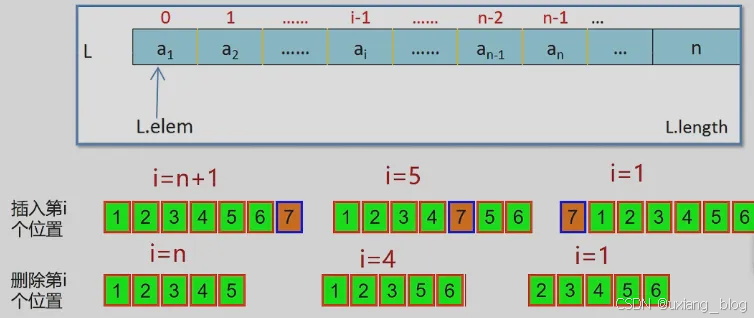
注解:
插入的位置可以在所有元素的之后,所有元素之后不需要移动元素,也可以在某个中间的位置插入,那么这个位置之后所有的元素都需要依此后移,等元素插入进去;也可以插入到第一个位置,如果插入到第一个位置,则所有的元素都需要后移动。
删除的位置如果在最后一个位置,则无需移动其他元素,只需要将最后一个元素删除即可;如果删除中间的元素,删除之后,则需要将后面的元素依此前移;如果删除第一个元素,则其后面的元素都需要前移。

注解:线性表呢?插入的时候可以在i个位置上来插入,插入的位置范围是(1,n+1)(1<= i <= n +1)。删除的时候可以在i个位置上删除,删除的位置范围是(1,n)(1<= i <= n)。栈和队列呢,就不能在任意的位置上删除了,我们规定它只能到表的端点,其中栈呢?插入的时候只能插入到表尾,也就是n+1位置,在删除的时候也只能删除最后一个第n元素。例子如下:

3.1.2、栈的应用——后进先出
由于栈的操作具有后进先出的固有特性,使得栈成为程序设计中有用工具。另外,如果问题求解的过程具有“后进先出”的天然特性的话,则求解的算法中也必然需要利用“栈”。
● 数据转换
● 表达式求值
● 括号匹配的检验
● 八皇后问题
● 行编辑程序
● 函数调用
● 迷宫求解
● 递归调用的实现
注解:那么队列呢?队列也是对表的端点操作,插入的时候限定插入在表尾,删除的的时候限定只能删除第一个元素。

3.1.3、队列常见应用
由于队列的操作具有先进先出的特性,使得队列成为程序设计中解决类似排队问题的有用工具。
● 脱机打印输出:按申请的先后顺序依此输出。
● 多用户系统中,多个用户排成队,分时地循环使用CPU和主存。
● 按用户的优先级排成多个队,每个优先级一个队列。
● 实时控制系统中,信号按接受的先后顺序依此处理。
● 网络电文传输,按到达的时间先后顺序依次进行。
3.1.4、栈的定义和特点
栈(stack)——是一个特殊的线性表,是限定仅在一端(通常是表尾)进行插入和删除操作的线性表。又称后进先出(Last In First Out)的线性表,简称LIDFO结构。
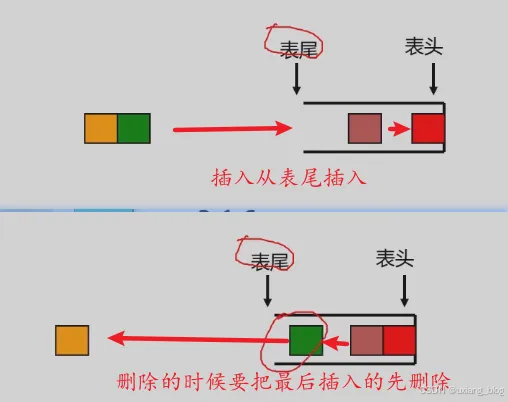
栈的相关概念
栈是仅在表尾进行插入、删除操作的线性表。
表尾(即an端)称为栈顶Top;表头(即a1端)称为栈底Base

插入元素到栈顶(即表尾)的操作,称为入栈。
从栈顶(即表尾)删除最后一个元素的操作,称为出栈。

栈的示意图
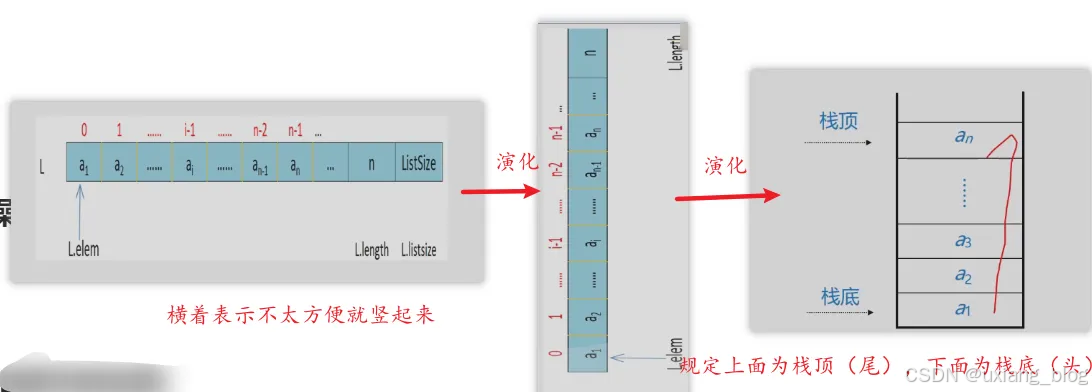
入栈的示意图:
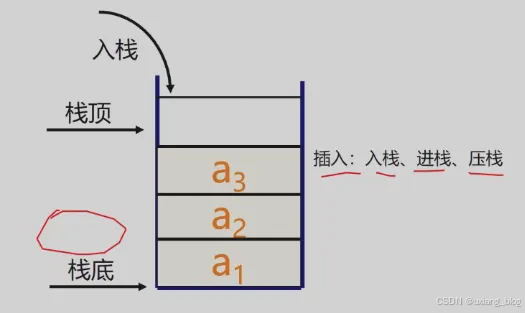
出栈的示意图
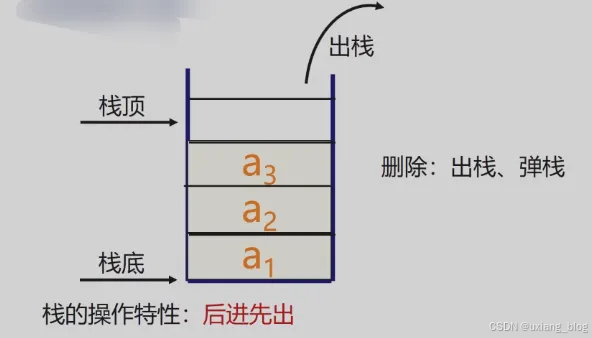
思考:
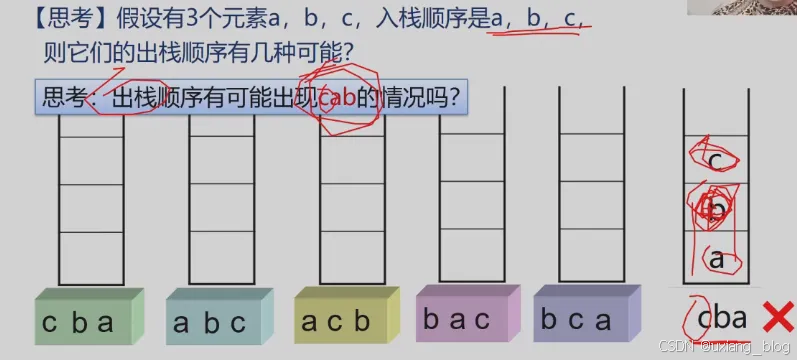
总结:
栈的相关概念:
● 1、定义:限定只能在表的一端进行插入和删除运算的线性表(只能在栈顶操作)
● 2、逻辑结构:与同线性表相同,仍为一对一关系
● 3、存储结构:用顺序栈或链栈存储均可,但以顺序栈更常见
● 4、运算结构:只能在栈顶运算,且访问结点时依照后进先出(LIFO)的原则
● 5、实现方式:关键时编写入栈和出栈函数,具体实现依顺序栈或链栈的不同而不同。
栈与一般线性表有什么不同
● 栈与一般线性表的区别:仅在运算滚则不同。

3.1.5、队列的定义和特点
队列(queue)是一种先进先出(Frist In Frist Out----FIFO)的线性表。在表一端插入(表尾),在另一端(表头)删除
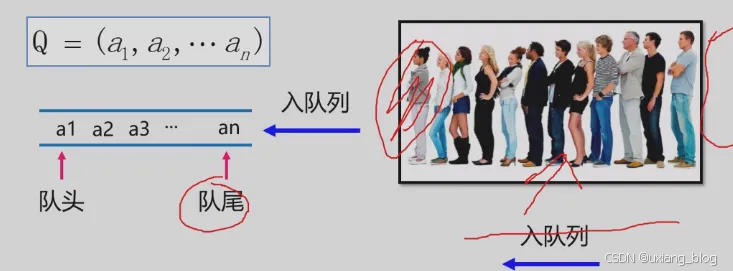
总结:
队列的相关概念
● 1、定义:只能在表的一端进行插入运算,在表的另一端进行删除运算的线性表(头删尾插)
● 2、逻辑结构:与线性表相同,仍为一对一关系。
● 3、存储结构:顺序队或链队,以循环顺序队列更常见。
● 4、运算规则:只能在队首和队尾运算,且访问结点时依照先进先出(FIFO)的原则
● 5、实现方式:关键是掌握入队和出队操作,具体是实现依顺序队或链队的不同而不同。
3.2、案例引入

3.2.1、案例3.1:进制转换
十进制整数N向其他进制数d(二,八,十六)的转换是计算机实现计算的基本问题
转换法则:除以d倒取余
该转换法则对应于一个简单算法原理:
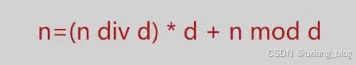
其中:div 为整除运算,mod为求余运算
例如:把十进制数159转换成八进制数。
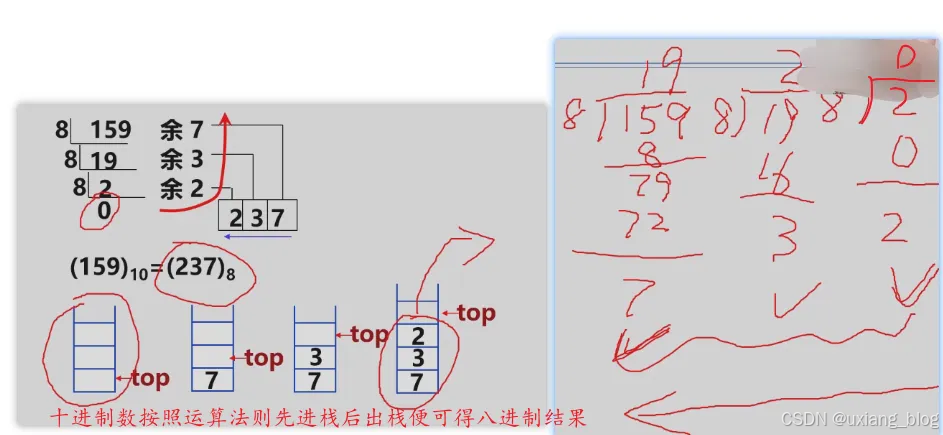
3.2.2、案例3.2:括号匹配
假设表达式中允许包含两种括号:圆括号和方括号
其嵌套的顺序随意,即:
● 1、( [ ] ( ) ) 或[ ( [ ] [ ] ) ]为正确格式
● 2、[ ( ] ) 为错误格式
● 3、( [ ( ) )或(()[ ] )为错误格式
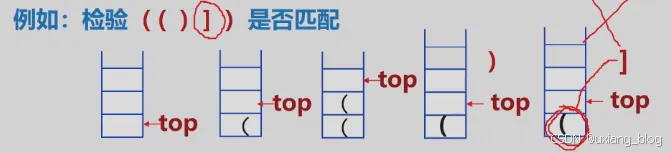
注解:先将第一个圆括号左半部分入栈,接着是第二个圆括号左半部分,到第三个的时候是圆括号的右半部分,这时候第三个和第二个匹配完成便出栈,接着是第四个方括号右半部分,这时候又和第一个圆括号左半部分,发现匹配不成功。这个也是利用了栈的性质,先入栈的后匹配,后入栈的先匹配。这时候可以判断括号是否匹配,格式是否正确,有没有出现交叉的情况。
3.2.3、案例3.3:表达式求值
表达式求值是程序设计语言编译中一个最基本的问题,它的是实现也需要用栈。
这里介绍的算法是由运算符优先级运算顺序的对表达式求值算法。
————算符优先算法。
表达式的组成
● 操作数(operand):常数、变量。
● 运算符(operator):算数运算符、关系运算符和逻辑运算符。
● 界限符(delimiter):左右括弧和表达式结束符。
任何一个算术表达式都由操作数(常量、变量)、算数运算符(+、-、*、/)和界限符(括号、表达式结束符‘#’、虚设的表达式起始符 ‘#’ )组成。后两者统称为算符。

为了实现表达式求值。需要设置两个栈:
一个是算符栈OPTR,用于寄存运算符。
另一个称为操作数栈OPND,用于寄存运算数和运算结果。
求值的处理过程是自左至右扫描表达式的每一个字符
● 当扫描的是运算数,则将其压入栈OPND,
● 当扫描到的是运算符时
○ 若这个运算符比OPTR栈顶运算符的优先级高,则入OPTR,继续向后处理
○ 若这个运算符比OPTR栈顶运算符优先级低,则从OPND栈中弹出两个运算数, OPTR中弹出栈顶运算符进行运算,并将运算结构压入栈OPND。
● 继续处理当前字符,直到遇到结束符为止。
——这个过程比较复杂,这里大概了解,后面会详细介绍。
3.2.4、案例3.4:舞伴问题
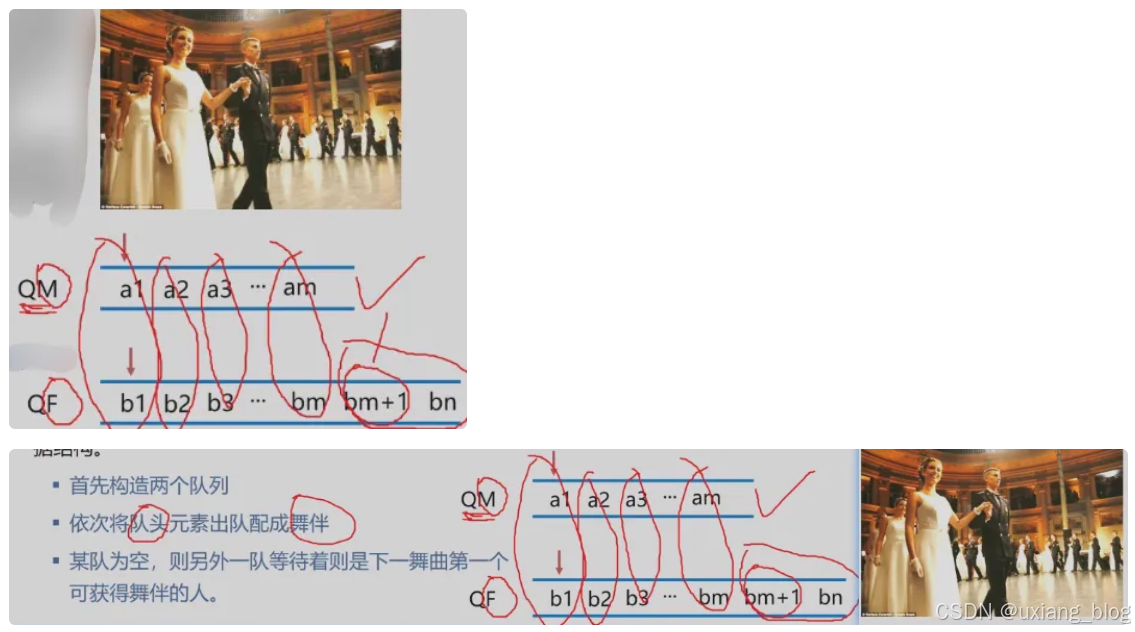
假设在舞会上,男士和女士各自排成一队。误舞会开始时,依此从男队和女队的队头开始各出一人配成舞伴。如果两队初始人数不相同,则较长的那一队中为配队者等待下一轮舞曲。现要求写一算法模拟上述舞伴配对问题。
显然,先入队的男士或女士先出对配成舞伴。因此该问题具有典型的先进先出特性,可以用队列作为算法的数据结构。
3.3、栈的表示和操作的实现
3.3.1、栈的抽象数据类型的类型定义
ADT Stack {数据对象:D = { ai | ai ∈ ElemSet, i = 1,2,...,n,n >= 0 }数据关系: R1 = { < ai- 1, ai >| ai - 1, ai ∈ D,i =2,...,n } 约定an端为栈顶,a1端为栈底。 基本操作:初始化、进栈、出栈、取栈顶元素等
} ADT Stack
InitStack(&S) 初始化操作
操作结果:构造一个空栈S。
DestroyStack(&S) 销毁栈操作
初始条件:栈 S 已存在。
操作结果: 栈 S已被销毁。
StackEmpty(S) 判定 S 是否为空栈
初始条件: 栈 S 已存在。
操作结果: 若栈S为空栈,则返回TRUE,否则FALSE
StackLength(S) 求栈的长度
初始条件:栈 S 已存在。
操作结果: 返回 S 的元素个数, 即栈的长度。
GetTop(S,&e) 取栈顶元素
初始条件: 栈 S 已存在且非空。
操作结果: 用e 返回S 的栈顶元素。
ClearStack(&S) 栈置空操作
初始条件:栈 S 已存在。
操作结果: 栈 S 清为空栈。
Push(&S,e) 入栈操作
初始条件: 栈S已存在。
操作结果: 插入元素e为新的栈顶元素。
Pop(&S,&e) 出栈操作
初始条件: 栈 S 已存在且非空。
操作结果: 删除S的栈顶元素an,并用e返回其值。
3.3.2、顺序栈的表示
由于栈本身就是线性表,于是栈也有顺序存储和链式存储两种实现方式。
● 栈的顺序存储——顺序栈
● 栈的链式存储——链栈
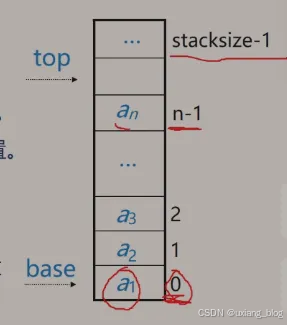
存储方式:同一般线性表的顺序存储结构完全相同,利用一组地址连续的存储单元依此连续的存储单元依此存放栈底到栈顶的数据元素。栈底一般在低地址端。
● 附设top指针,指示栈顶元素在顺序栈中的位置。
● 零设base指针,指示栈底元素在顺序栈中的位置。但是,为了操作方便,通常top指示真正的栈顶元素之上的下标地址。
● 另外,用stacksize 表示栈可使用的最大容量
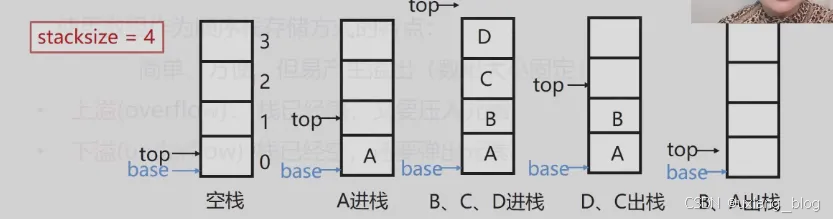
注解:这里认识一下栈的各种情况:这个栈最多能放4个元素,即stacksize = 4;空栈:最左边的是空栈,什么是空栈呢?空栈就是top指针和base执政都指向0,它两个的值是一样的,即base == top;入栈:什么是入栈呢?就本例而言就是往这个初始化为0,最大容量为4的栈里面放入放元素,当A元素扔进去后这个top指针就会向上走一步指向下标为1的位置,这就是说栈里面有一个元素了,同理,其他元素也是如此,直到放到第三个的图示情况,D放满这个栈的最大容量后,这个top指针指向下标为4的位置,这时候还能插入元素吗,是怎么判断的呢?这便是利用top与base的差值为最大容量判断的,只要 top - base等于最大容量stacksize了,就不能往里面插元素了,要是继续扔元素(上溢)该怎么处理呢?处理办法如下:
栈满时的处理办法:
1、报错,返回操作系统。
2、分配更大的空间,作为栈的存储空间,将原栈的内容移入新栈。但是这个办法比较费时,尤其是元素比较多的时候,不到万不得已不要用。
出栈():有入栈就会出栈,情况和入栈差不多,就是把元素从这个栈顶部(栈顶)到栈底部(栈底)依此取出来,取一个,top指针向下移动一个,直到top再次等base就没有元素可以取了,要是还想取,这行为那就叫做下溢。
使用数组作为顺序栈存储方式的特点:
简单、方便、但容易产生溢出(数组大小固定)
● 上溢(overflow):栈已经满,又要压入元素
● 下溢(underflow):栈已经空,还要弹出元素
注:上溢是一种错误,使问题的处理无法处理进行;而下溢一般认为是一种结束条件,即问题处理结束。
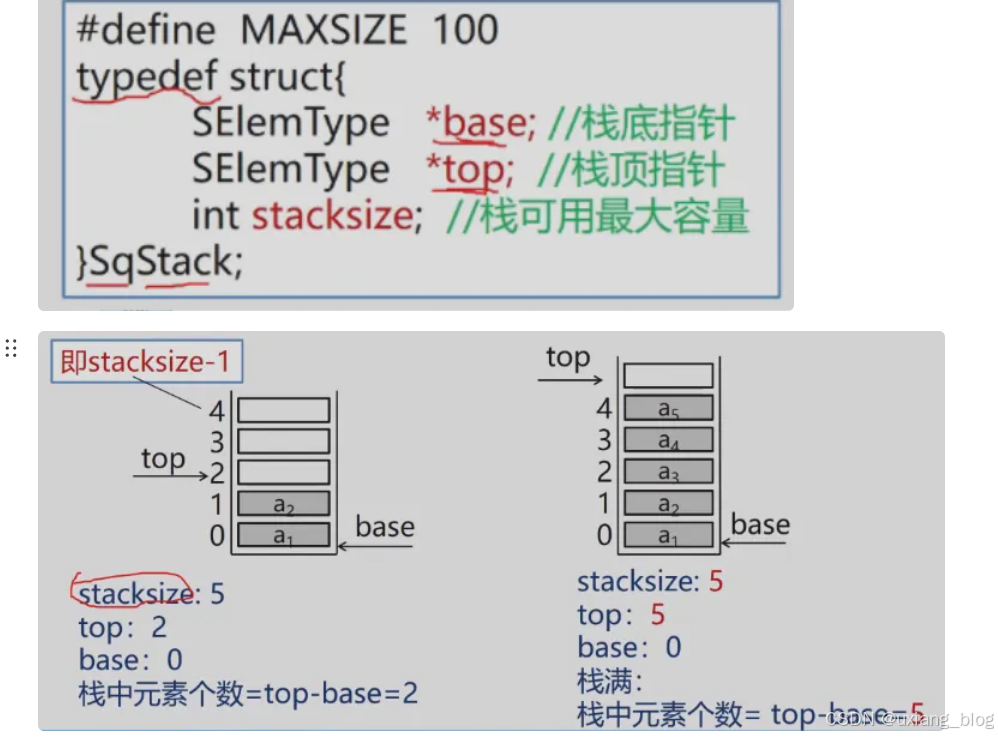
注解:此处表示stacksize是用下标整数相减的,但是能用指针相减吗?可以,两个指针的相减实质是它们之间的差值,而且它们的差值与用整数相减的效果是一样的,则可以使用指针相减代替整数相减,而且这里的指针可以用定义成int类型,这也是没有问题的,但前提条件是这里的指针是同一个数组里面的。
3.3.3、顺序栈的实现——涉及栈的相关操作
【算法3.1】顺序栈的初始化
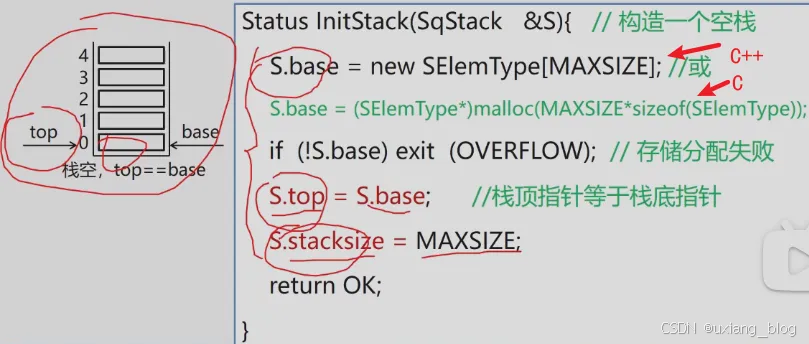
顺序栈判断是否为空

注解:top指针和base指针是否相等。
求顺序栈的长度
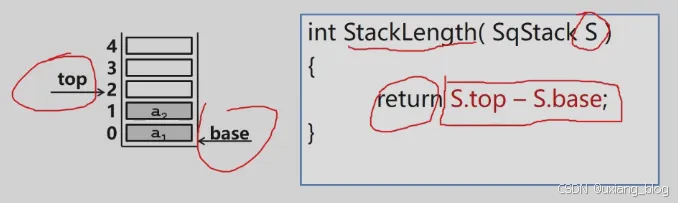
注解:两个指针之差,top指针减去base。
清空顺序栈
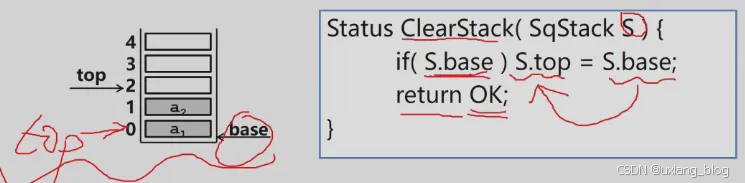
注解:清空顺序栈,是清空顺序栈的内容,如果栈中有元素,那就把base指针赋值给top指针,使得top指针和base指针相同,它们之间没有空间去存储元素,这样就清空顺序栈了。
销毁顺序栈
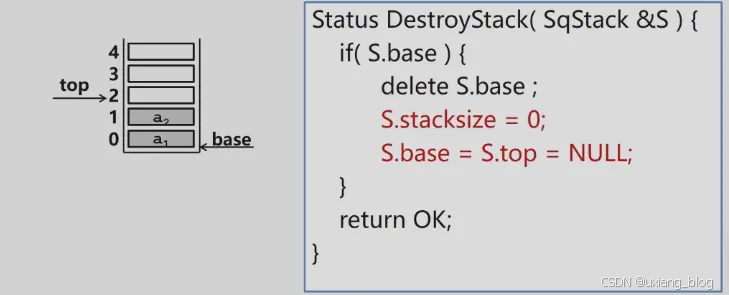
注解:实质是销毁空间,释放到内存池当中去了。这样顺序表里面不仅是里没有内容了,而且这栈本身也没有了。delete S.base是数组回归内存,和其下2句是把这个DestroyStack结构设置为空了。
【算法3.2】顺序栈的入栈
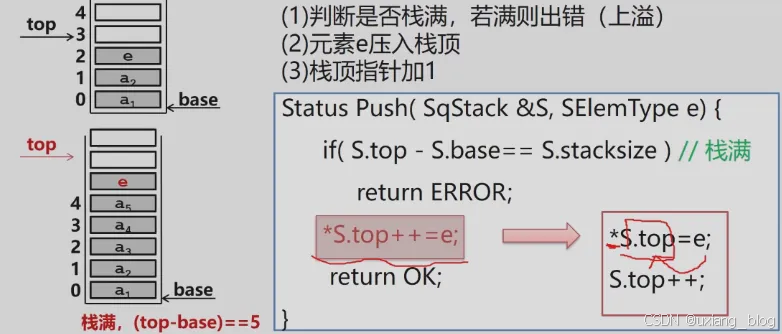
注解:入栈就是把元素存进去,每存进一个元素,栈里面就多了一个元素,top指针就向上移动一个位置,总结为第一存元素,其次top指针上移两个步骤。但是如果top指针已经满了呢?再往里面存就存不进去了,要想确保入栈这个操作正常进行,需要在存取元素前先要有个判断才行,满了就不再往里面存了。S.top,这里“”的意思是代表指针当前所指的那那块空间进行操作。的运算级比++高,所以先执行S.top=e;后执行S.top++这个可以合成一句:*S.top ++ = e;
【算法3.3】顺序栈的出栈

注解:关于出栈有2个问题,最核心的操作是当元素取出的是时候top指针会随着元素的减少会下移。另为一个问题是怎么判断什么时候停止的问题,在取出的过程一定会元素取完的时候,这时候top指针会和base指针同时指向0,即 S.top == S.base,所以依此为信号可以做一个判断操作。
3.3.4、链栈的表示
链栈是运算受限的单链表,只能在链表头部进行操作。
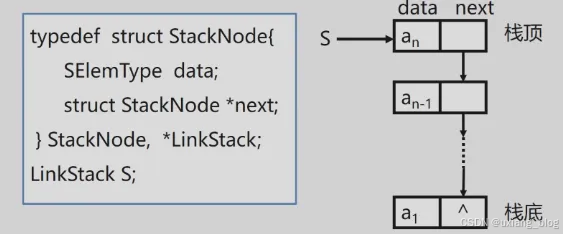
注解:也是定义一个结构类型,这个结构类型呢,叫做栈的结点(struct StackNode),每个结点包含一个数据域(data)和一个指针域(next),其中数据域是存放栈中元素的,所以它是栈里头的类型;指针域是指向下一个元素的,所以它指向的类型也是这样(struct StackNod)的一个结构类型,所以仍然用结构类型定义这个指针,这种叫做自己定义自己的方式叫做嵌套类型。我们定义这样的类型struct StackNode{ }就叫做结点类型StackNode,然后再用这个类型定义一个指向这样结点的指针类型*LinkStack,然后用大写字母S代表这个栈。
注意:链栈中指针的方向。
● 链表的头指针就是栈顶
● 不需要头结点
● 基本不存在栈满的情况
● 空栈相当于头指针指向空
● 插入和删除仅在栈顶处执行
3.3.5、链栈的实现
【算法3.5】链栈的初始化

【补充算法】判断链栈是否为空
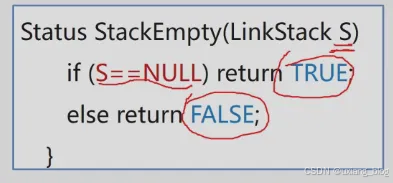
【算法3.6】链栈的入栈
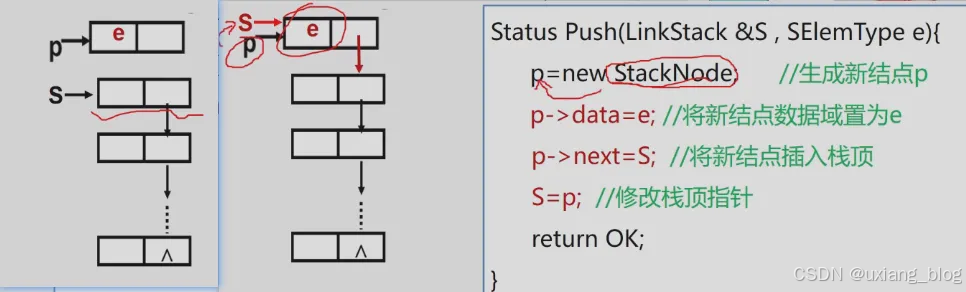
【算法3.7】链栈的出栈
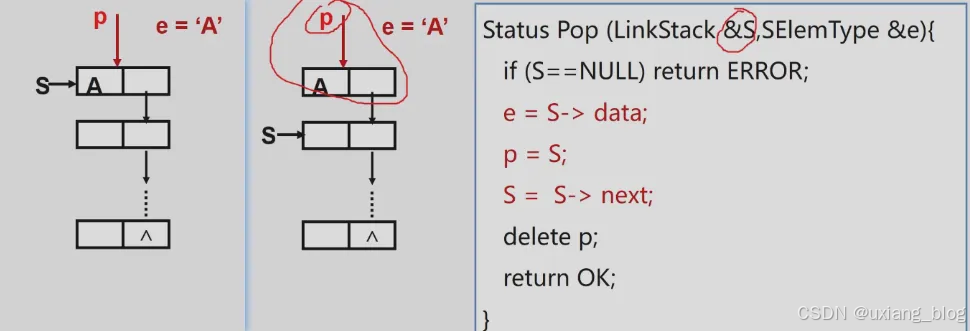
【算法3.8】取栈顶元素
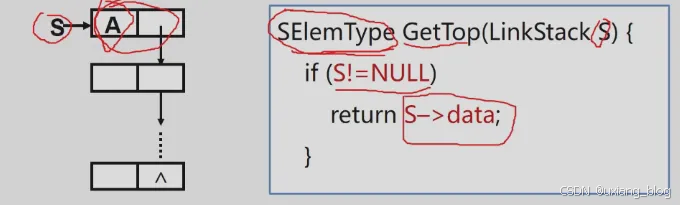
3.4、栈与递归
3.4.1、递归
递归的定义:
● 若一个对象部分地包含它自己,或用它自己给自己定义 ,则称这个对象是递归的;
● 若一个过程直接地或间接地调用自己,则称这个过程是递归的过程。

以下三种情况常常用到递归方法
● 递归定义的数学函数
● 具有递归特性的数据结构
● 可递归求解的问题
举例

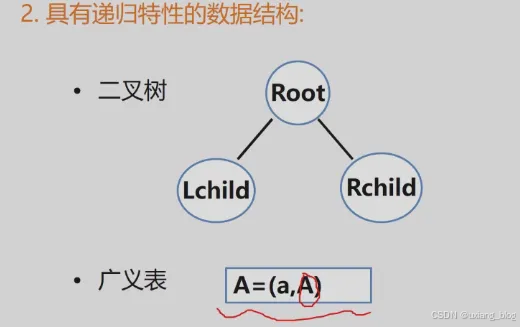
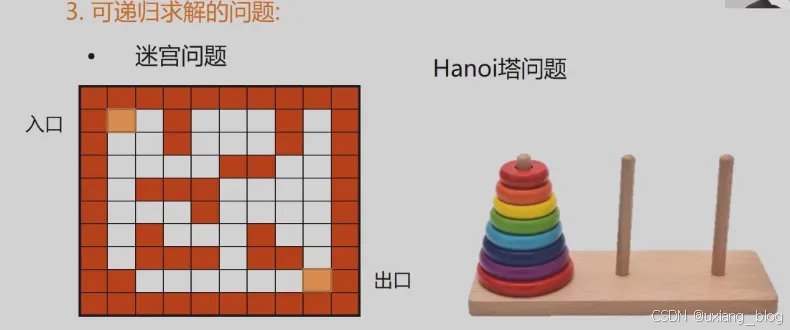
递归问题————用分治法求解
分治法:对于一个较为复杂的问题,能够分解成几个相对简单的且解法相同或类似的子问题来求解
必备的三个条件:
● 1、能将一个问题转变成一个新问题,而新问题与原问题的解法相同或类同,不同的仅是处理的对象,且这些处理对象是变化有规律的
● 2、可以通过上述转化而使问题简化
● 3、必须有一个明确的递归出口,或称递归的边界
分治法求解递归问题算法的一般形式:
Void p(参数表){if (递归结束条件) 可直接求解步骤; ----基本项else p(较小的参数); -----归纳项
}
例如:
Long Fact(long n){if(n == 0){return 1;//基本项}else {return n*Fact(n-1);//归纳项}
}
**函数调用过程**
调用前,系统完成:
(1)将实参,返回地址等传递给被调用函数
(2)为被调用函数的局部变量分配存储区
(3)将控制转移到被调用函数的入口
调用后,系统完成:
(1)保存被调用函数的计算结果
(2)释放被调用函数的数据区
(3)依照被调用函数保存的返回地址将控制转移到调用函数
当多个函数构成嵌套调用时:类似于栈

求解阶乘n!的过程:todo

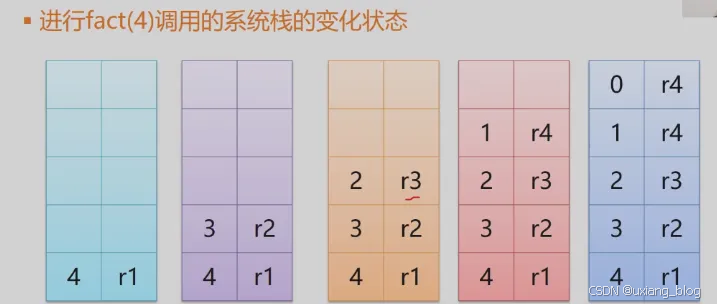
递归函数调用的实现
| “层次” | 主函数 | 0层 |
| 第一次调用 | 1层 | |
| … | … | |
| 第i次调用 | i层 |
”递归工作栈“——递归程序运行期间使用的数据存储区
”工作记录“——>实在参数、局部变量、返回地址
递归的优缺点:
● 优点:结构清晰,程序易读
● 缺点:每次调用的要成成工作记录,保存状态信息,入栈;返回时要出栈,恢复状态信息。时间开销大。
所以程序来说我们愿意用递归,从时间效率来说是比较差的,如果有时候对时间效率比较高的时候我们就要把递归变成非递归,方法如下(简单了解):
● 方法一:尾递归、单向递归——>循环结构
● 方法二:自用栈模拟系统运行时栈
尾递归——>循环结构

单向递归——>循环结构
虽然有一处以上的递归调用语句的参数只和主调函数有关,相互之间参数无关,并且这些递归调用语句处于算法的最后。

借助栈改写递归
● 递归程序在执行时需要系统提供栈来实现
● 仿照递归算法执行过程中递归工作栈的状态变化可写出相应的非递归程序
● 改写后的非递归算法与原来的递归算法相比,结构不够清晰,可读性较差,有的还需要经过一系列优化
3.5、队列的表示和操作的实现
3.5.1、队列的表示和实现
队列示意图
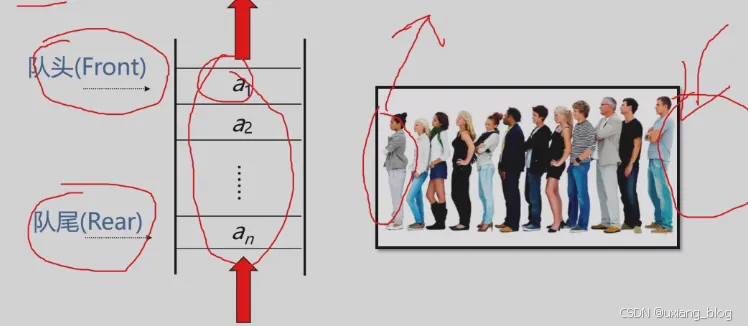
相关术语
● 队列(Queue)是仅在表尾进行插入操作,在表头进行删除操作的线性表。
● 表为即an端,称为队尾;表头即a1端,称为队头。
● 插入元素称为入队;删除元素称为出队。
● 队列的存储结构为链式或顺序队(常用循环循序队)
● 它是一种先进先出(FIFO)的线性表。
队列的相关概念

队列的常见应用

队列的抽象数据类型定义

● 队列的物理存储可以用顺序结构,也可以用链式存储结构。相应地,队列的存储方式也分为两种,即顺序队列和链式队列。
● 队列的顺序表示——用一组数组base[MAXQSIZE]
3.5.2、顺序队列表示和实现

#define MAXQSIZE 100 //最大队列长度
Typedef struct {QElemType *base; //初始化的动态分配存储空间int front; //头指针int rear; //尾指针
}SqQueue;
对空、入队、出队、溢出
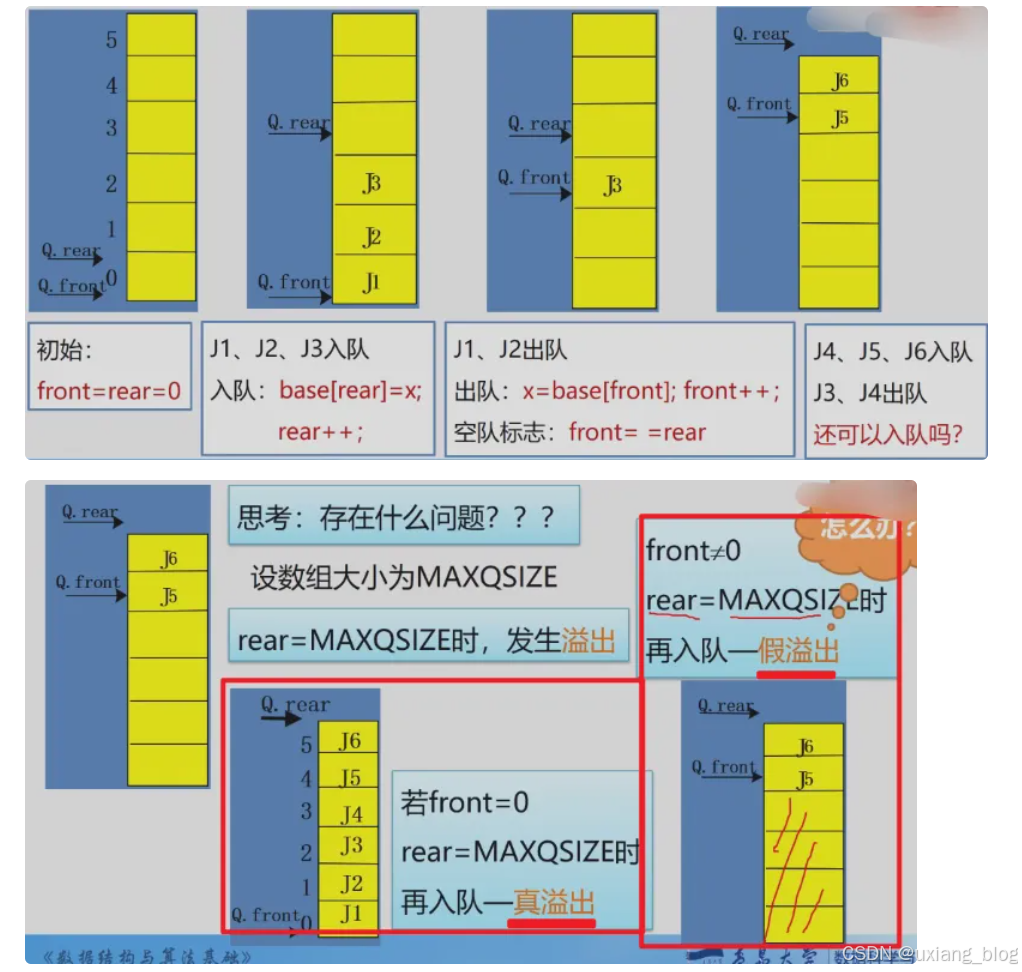
怎么解决假溢出问题呢?————引入循环队列(模运算,取余运算)
● 1、将队中元素依次向对头方向移动。缺点:浪费时间。每移动一次,队中元素都要移动。
● 2、将队空间设想成一个循环的表,即分配给队列的m个存储单元,可以循环使用,当rear为maxqsize时,若向量的开始端空着,有可以从头使用空着的空间。当front 为maxqsize时,也是一样的。
循环队列:当base[0]接在base[MAXQSIZE -1]之后,若rear +1 == M,则令rear = 0;
● 实现方法:利用模(mod,C语言中:%)运算
● 插入元素:Q.base[Q.rear] = x; Q.rear = (Q.rear +1)% MAXQSIZE;
● 删除元素;x = Q.base[s.front] Q.front = (Q.front +1)% MAXQSIZE
● 循环队列:循环使用队列分配的存储空间。
怎么判断队空和队满的问题?
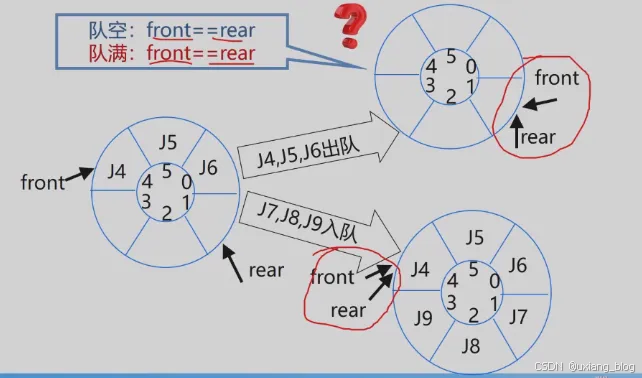
我们知道不管是队空还是队满的时候,其头指针front 和尾指针rear均指在一块区域,那么怎么区分队空和队满呢?
解决方案:
● 1、另外设一个标志以区别队空、队满
● 2、另设一个变量,记录元素个数
● 3、少用一个元素空间。
循环队列解决队满时判断方法——少用一个元素空间
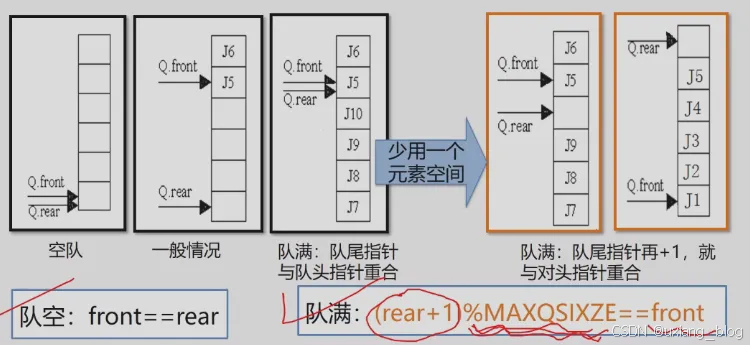
循环队列的操作
● 队列的初始化

Status InitQueue( SqQueue & Q){Q.base = new QEleType[MAXQSIZE] //分配数组去空间,为什么这里是一个指针呢?因为数组元素的首地址就是一个指针//c语言: Q.base = (QElemType*)malloc(MAXQSIZE*sizeof(QElemType));if(!Q.base) exit(OVERFLOW); //存储分配失败Q.front = Q.rear = 0; //头指针尾指针为0,队列为空return OK;
}
● 求队列的长度
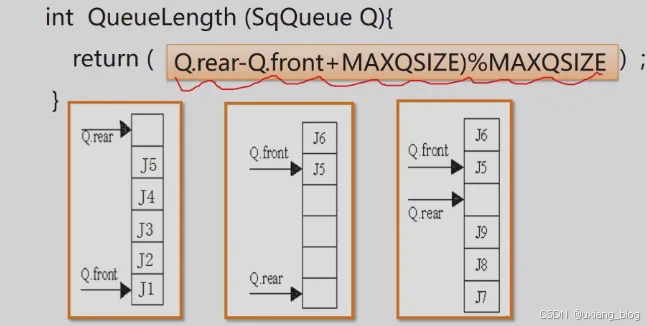
int QueueLength (SqQueue Q){return ((Q.rear - Q.front + MAXQSIZE) % MAXQSIZE);
}
● 循环队列入队
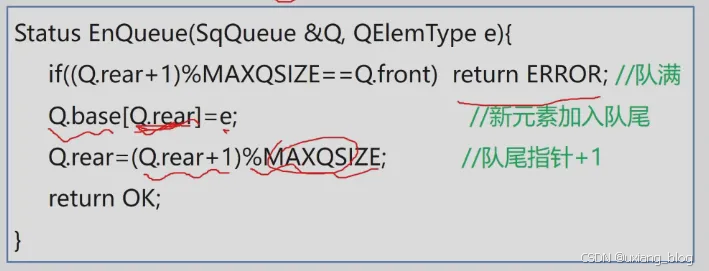
Status EnQueue(SqQueue & Q,QElemType e){if((Q.rear + 1)% MAXQSIZE == Q.front)return ERROR; //队满Q.base[Q.rear] = e; //新元素加入队尾Q.rear = (Q.rear + 1) % MAXQSIZE; //队尾指针 +1return OK;
}
● 循环队列的出队
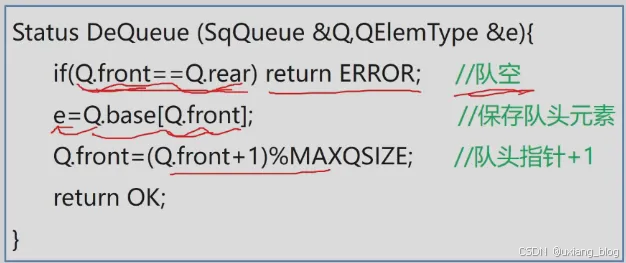
Status DeQueue()SqQueue&Q,QEleType & e){if(Q.front == Q.rear) return ERROR; //队空e = Q.base[Q.front]; //保存队头元素Q.front = (Q.front + 1)%MAXQSIZE; //队头指针+1return OK;
}
3.5.3、链式队列表示和实现
若用户无法估计所用队列的长度,则宜采用链式队列

链队列的类型定义

#define MAXQSIZE 100 //最大队列长度
typedef struct Qnode {QElemType data;stuct Qnode *next;
}QNode,*QuenePtr;typedef struct{QuenePtr front; //队头指针QuenePtr rear; //队尾指针
}LinkQueue;
链队列运算指针变化状况
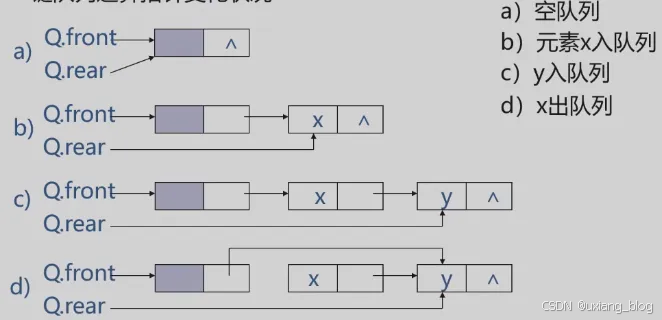
链队列的操作——链队列初始化(算法3.16)
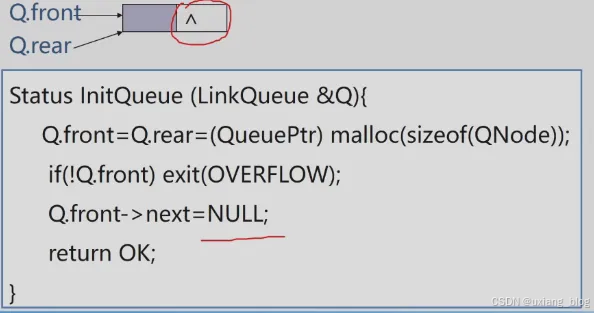
Status InitQueue (LinkQueue & Q){Q.front = Q.rear = (QueuePtr) malloc(sizeof(QNode));if(!Q.front)exit(OVERFLOW);Q.front->next = NULL;return OK;
}
链队列的操作——销毁链队列(算法3.16)
算法思想:从队头结点开始,依次释放所有结点
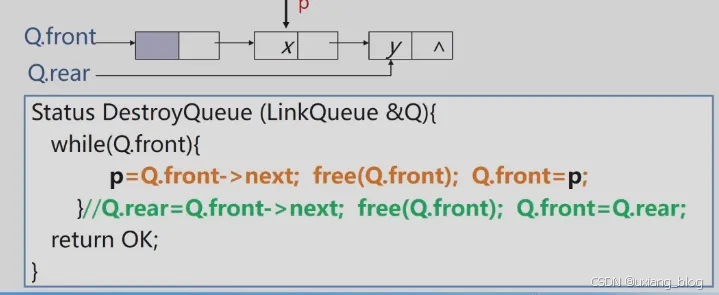
Status DestroyQueue (LinkQueue &Q){while(Q.front){p = Q.front -> next; free(Q.front); Q.front = p;//可以写成Q.rear = Q.front -> next; free(Q.front); Q.front = Q.rear;}return OK;
}
链队列的操作——将元素e入队(算法3.17)
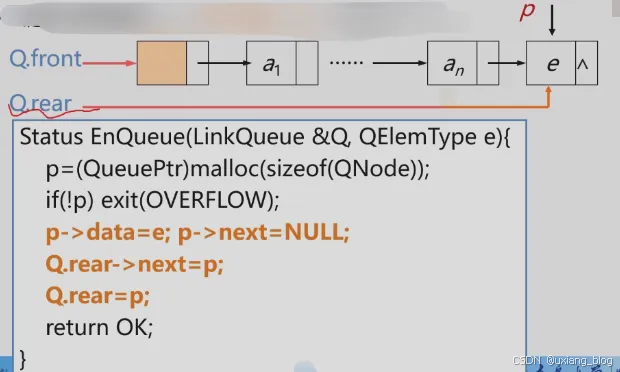
Status EnQueue(LinkQueue & Q, QElemType e){p = (QueuePtr)malloc(sizeof(QNode));if(!p) exit(OVERFLOW);p -> data = e; p -> next = NULL;Q.rear -> next = p;Q.rear = p;return OK;
}
链队列的操作——链队列出队(算法3.18)
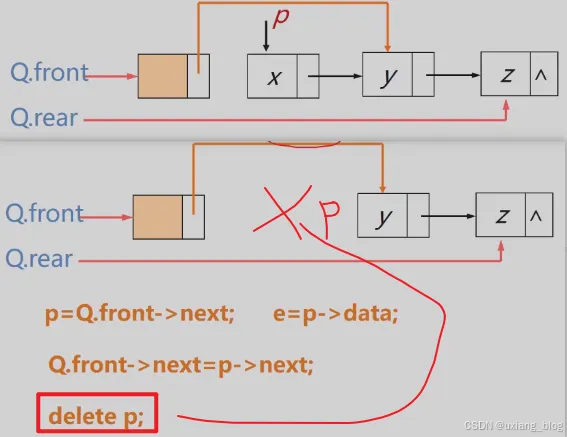
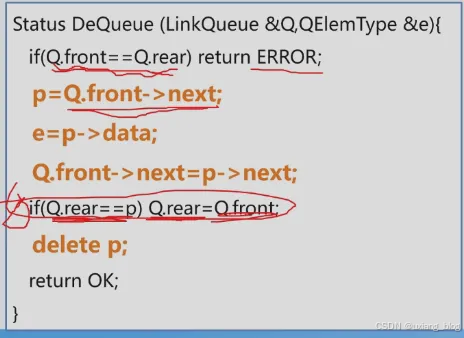
Status DeQueue( LinkQueue & Q, QElemType & e){if( Q.front == Q.rear ) return ERROR;p = Q.front -> next;e = p -> data;Q.front -> next = p -> next;if( Q.rear == p ) Q.rear = Q.front;delete p;return OK;
}
链队列的操作——求链队列的队头元素(算法3.19)

Status GetHead( LinkQueue Q, QElemType & e){if( Q.front == Q.rear ) return ERROR;e = Q.front -> next -> data;return OK;
}
第四章 串 、数组和广义表
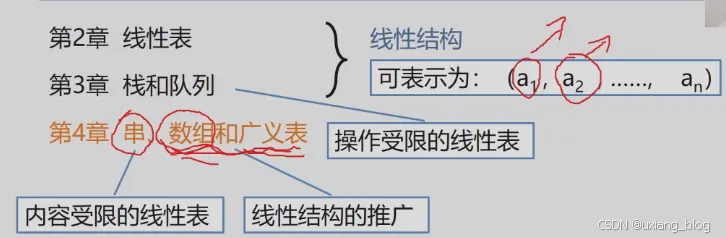
4.1、串的定义及其术语
串(Sring)-----零个或多个任意字符组成的有限序列。
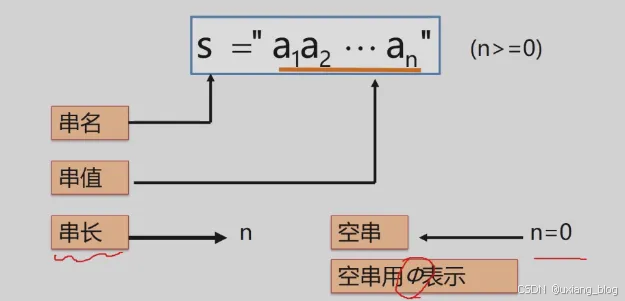
子串:一个串中任意个连续字符组成的子序列(含空串)称为该串的子串。真字串是指不包含自身的所有字串。

主串:包含子串中的串相应地称为主串。
字符位置:字符在序列中的序号为该字符在串中的位置
子串位置:子串第一个字符在主串中的位置
空格串:由一个或多个空格组成的串,与空串不同。
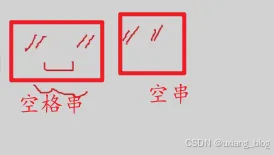

串相等:当且仅当两个串的长度相等并且各个对应位置的字符都相同时,这两个串才是相等的。所有的空串都是相等的。

4.2、案例引入
串的应用非常广泛,计算机上的非数值处理的对象大部分是字符串数据,例如:文字编辑、符号处理、各种信息处理系统等等。
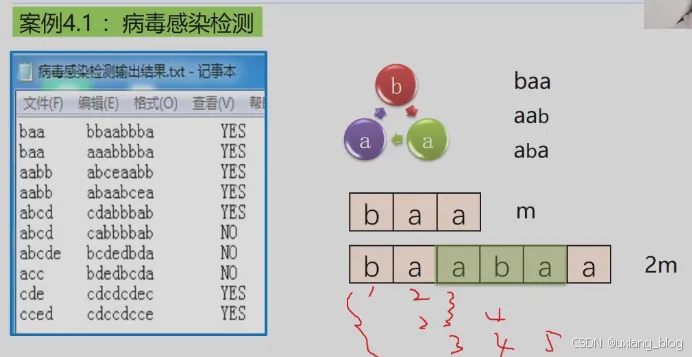
案例4.1:病毒感染检测
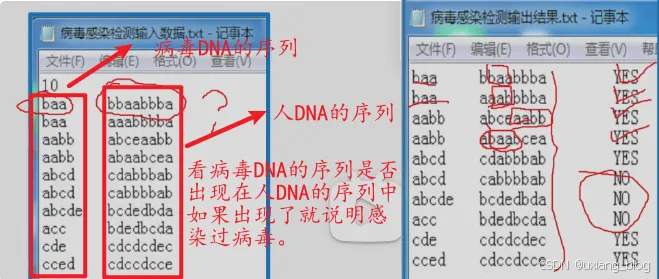
研究者将人的DNA和病毒DNA均表示成由一些字母组成的字符串序列。然后加测病毒DNA序列是否在患者的DNA序列中出现过,如果出现过,则此人感染了该病毒,否则没有感染。
例如:假设病毒的DNA序列为baa,患者1的DNA序列为aaabbba,则感染,患者者2的DNA序列为babbba,则未感染。(为什么呢?注意:人的DNA序列是线性的,而病毒的DNA序列是环装的,则baa,aab,aba均是病毒序列)
4.3、串的类型定义、存储结构及其运算、
4.3.1、串的类型定义、存储结构
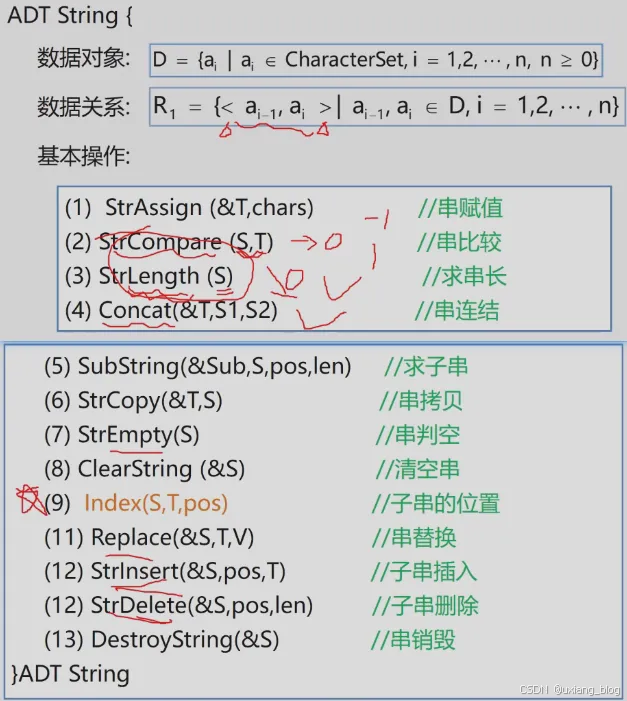
串中元素逻辑关系与线性表的相同,串可以采用与线性表相同的存储结构。
| 顺序串 | 链串 | |
| 逻辑结构 | 串 | 串 |
| 存储结构 | 顺序存储结构 | 链式存储结构 |
串的顺序存储结构:只要看一下存储结构的位置就知道逻辑结构中谁先谁后。

#define MAXLEN 255
typedef struct{char ch[MAXLEN + 1]; //存储串的一组数组int length; //串的当前长度
}SString;
注解:这里为什么MAXLEN +1;前面定义MAXLEN是255,则MAXLEN +1实际就是256,我们知道数组的下标是从0开始的,[0]~[255]一共由256个元素,但是为了某种算法的方便我们不采取数组下标从0开始,而是使得它从1开始。
串的链式存储结构:链的存储结构并不一定是连续的,根据指针把所存元素拉扯在一起。
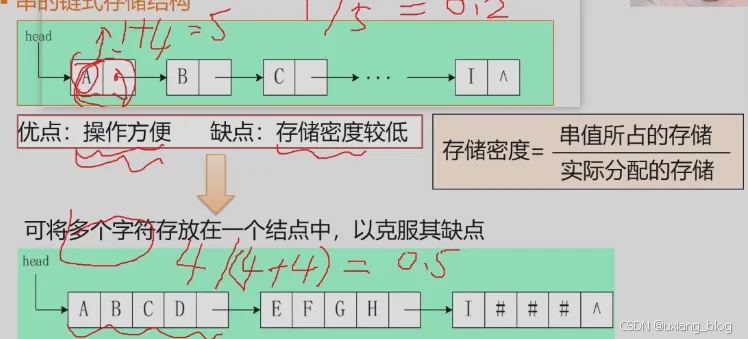
注解:1+4:一个字符串本身的存储大小的1个字节+一个指针所占的4个字节(假设)。4+4 :4个字符串本身的存储大小4个字节 + 一个指针所占的的4个字节。随着这个块所存放的元素增多,这个存储密度就会越来越大。
串的链式存储结构——块链结构

#define CHUNKSIZE 80 //块的大小可由用户定义
typedef struct Chunk{char ch[CHUNKSIZE];struct Chunk *next;
}Chunk;typedef struct{Chunk *head, *tail; //串的头指针和尾指针int curlen; //串的当前长度}LString; //字符串的块链结构
总结:在实际应用中,串的顺序存储结构与链式存储结构中,顺序存储结构用的很多,在串这块中很少用到删除和插入,最多的操做就是匹配运算和查找运算等,这个时候用顺序存储结构会更加方便,所以后面我们会基于顺序存储结构,即顺序串来讲解。————————————后面基于顺序串讲
4.3.2、串的模式匹配算法——最常用
算法目的:确定主串中所含子串(模式串)第一次出现的位置(定位)。
算法应用:搜索引擎、拼写检查、语言翻译、数据压缩
算法种类:
● BF算法(Brute-Force,暴力算法又称古典的、经典的、朴素的、穷举的)
● KMP算法(特点:速度快)
4.3.2.1、Brute-Force简称BF算法,亦称简单匹配算法。采用穷举法的思路。

算法思路:是从S的每一个字符开始依次与T的字符进行匹配。
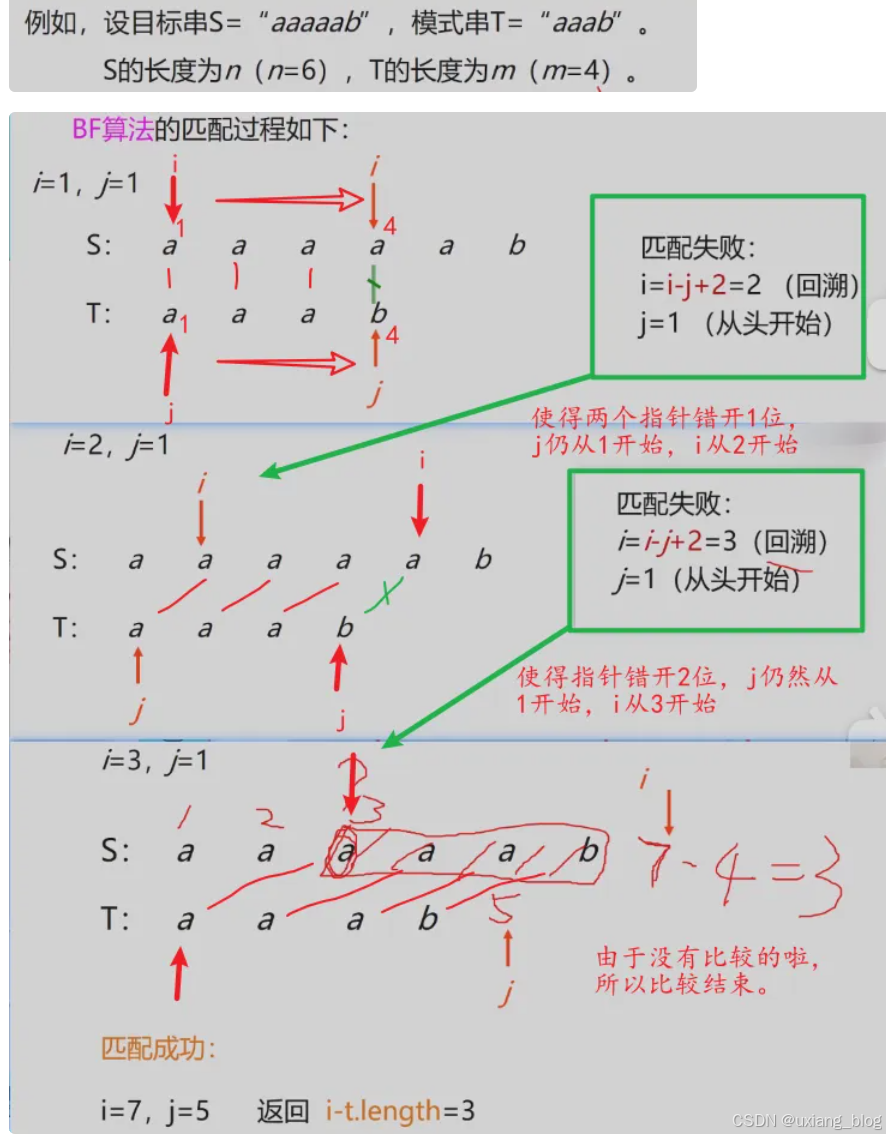
BF算法设计思想:
Index(S,T,pos)
——>将主串的第pos个字符和模式串的第一个字符比较——>(1)若相等,继续逐个比较后续字符;(2)若不等,从主串的下一个字串起,重新与模式串的第一个字符比较。——>(1)直到主串的一个连续字符序列与模式串相等。返回值为S中与T匹配的子序列第一个字符的序号,即匹配成功。(2)否则,匹配失败,返回值 0
BF算法描述——todo

注解:这个是从主串的头(1的位置)开始查找的,但如果从中间的某个位置开始,就需要增加一个参数pos来控制这个变量。这个算法如下:

BF算法时间复杂度
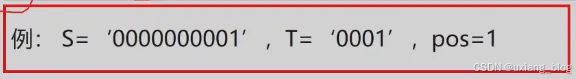
若n为主串长度,m为子串长度,最坏情况是(1)主串前面n-m个位置都部分匹配到子串的最后一位,即这n-m位各比较了m次,最后m位也个比较了1次。
总次数为:(n - m)m + m = (n - m + 1)* m
若m<<n,则算法复杂度O(n*m)。
4.3.2.2、KMP(Knuth Morris Pratt)算法
KMP算法是D.E.Knuth、J.H.Morris和V.R.Pratt共同 提出的,简称KMP算法。该算法较BF算法有较大改进,从而使得算法效率有了某种程度的提高。
KMP算法设计思想
利用已经部分匹配的结果而加快模式串的滑动速度?且主串S的指针i不必回溯!可提速到O(n+m)!
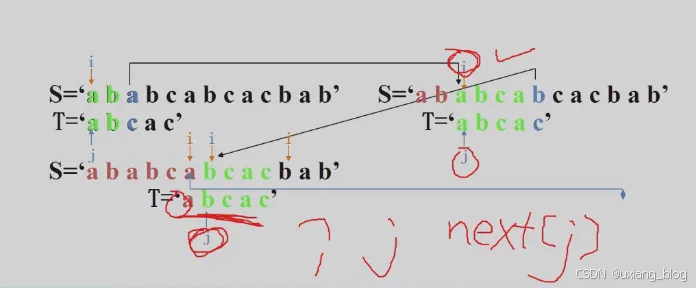
由此可指,i的有规律可循,但是j是怎么个规律呢?j要去的下一个位置我们用一个数组next[j]来存,那next[j]是怎么算得呢?为此,定义next[j]函数,表明当模式中得第j个字符与主串相应字符“失配”时,在模式中需要重新和主串中该字符进行比较得字符的位置。todo:不明白
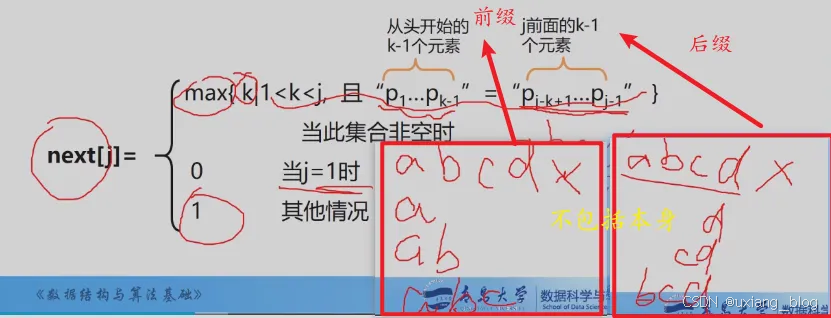
例如:



注解:
特殊情况需要next函数的改进:

修正的值用nextval来存。
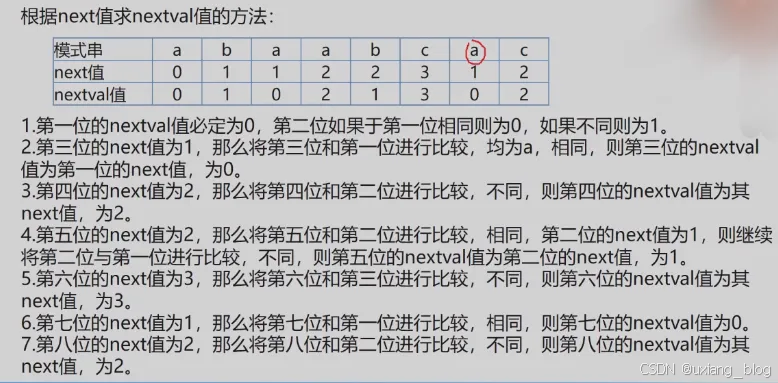

这个修正的算法非常复杂,无需研究,只要能看懂上面的表格,并且会用这个算法就行了。
4.4、数组
4.4.1、基本概念
数组:按一定格式排列起来的,具有相同类型的数据元素集合。
一维数组:若线性表中的数据元素为非结构的简单元素,则称为一维数组。
一维数组的逻辑结构:线性结构。定常的线性表。
声明格式: 数据类型 变量名称[长度];
二维数组:若一维数组中的数据元素又是一维数组结构,则称为二维数组。
二维数组的逻辑结构:
| 看成:非线性结构 | 每一个数据元素既在一个行表中,又在一个列表中。 |
| 看成:线性结构,定长 | 的线性表 该线性表的每个数据元素也是一个定长的线性表。 |

声明格式:数据类型 变量名称 [行数][列数]

在C语言中,一个二维数组类型也是可以定义为一维数组类型(其分量类型为一维数组类型),即:
typedef elemtype array2[m][n];
等价于:
typedef elemtype array1[n];
typedef arry1 array2[m];
三维度数组:若二维数组中的元素又是一个一维数组,则称为三维数组。
…
n维数组:若n-1维数组中的元素又是一个一维数组结构,则称作n维数组。
结论:线性表结构是数组结构的一个特例,而数组结构又是线性表结构的扩展。
数组特点:结构固定 ——定义后,维数和维界不再改变。
数组基本操作:除了结构的初始化和销毁之外,只有取元素和修改元素值的操 作。
4.4.2、如何定义数组的抽象数据类型及其操作
n维度数组的抽象数据类型


基本操作:

4.4.3、数组的顺序存储

注意:数组可以是多维的,但存储数据元素内存单元地址是一维的,因此,在存储数组结构之前,需要解决将多维关系映射到一维关系的问题。
一维度数组:


二维数组:
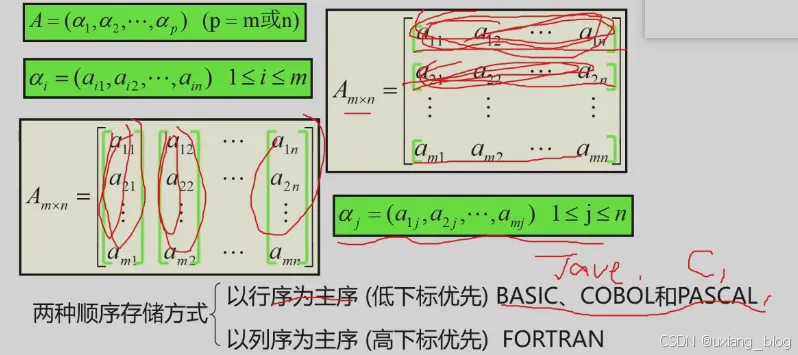
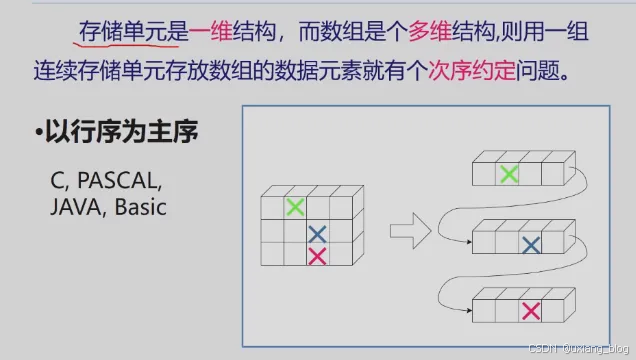
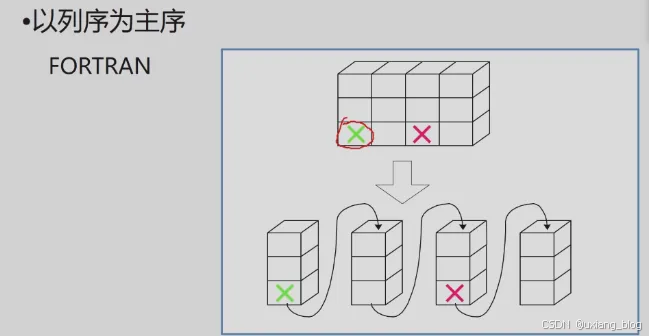
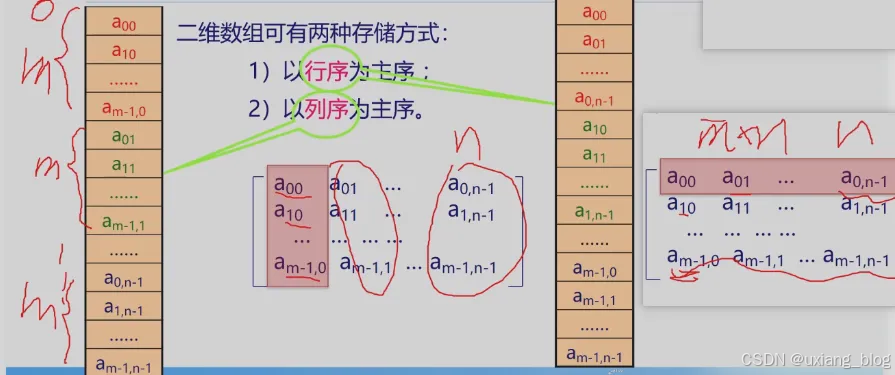
计算二维当中某一个元素的位置

计算三维中某个元素的位置
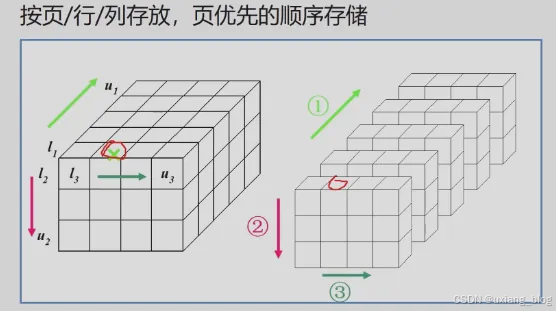

n维数组中某个元素的位置:

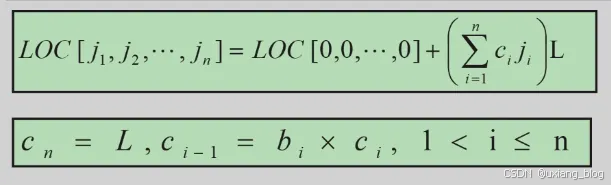
如何计算,例子如下:


4.4.4、特殊矩阵的压缩存储
矩阵:一个由m*n个元素排成的m行n列的表。

矩阵的常规存储:将矩阵描述为一个二维数组。
矩阵的常规存储特点:可以对其元素进行随机存储;矩阵运算非常简单;存储密度为1。
不适宜常规存储的矩阵:值相同的元素很多且呈某种规律分布;零元素多。
矩阵的压缩存储:为多个相同的非零元素只分配一个存储空间;对零元素不分配空间。
1、什么是压缩存储?
若多个数据元素的值都相同,则分配一个元素值得存储空间,且零元素不占存储空间。
2、什么样的矩阵能够压缩?
一些特殊矩阵,如:对称矩阵,对角矩阵,三角矩阵,稀疏矩阵等。
3、什么叫做稀疏矩阵?
矩阵中非零元素的个数较少(一般小于5%)
4.4.4.1、对称矩阵:
特点:在n*n的矩阵a中,满足如下性质:
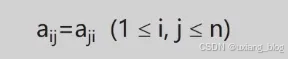
存储方法:只存储下(或者上)三角(包括主对角线)的数据元素。共占用n*(n + 1)/2个元素空间。

但是随即出现一个问题,那就是aij存到哪里去了?如果修改这个值,我们怎么知道修改的值在哪里呢?——————————所以需要找到它,怎么找到它呢?
对称矩阵的存储结构:
对称矩阵上下三角中的元素数均为:n(n + 1)/2,可以以行序为主序将元素放在一个一维数组Sa[n(n + 1)/2]中
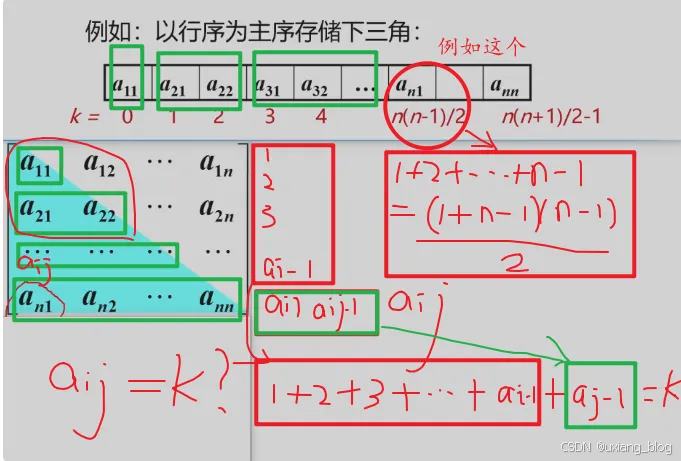
4.4.4.2、三角矩阵:
特点:对角线以下(或者以上)的数据元素(不包括对角线)全部为常数C。

存储方法:重复元素c共享一个元素存储空间,共占用n(n+1)/2 + 1个元素空间: sa[1…n(n + 1)/2 + 1],此处1为常数c的。

4.4.4.3、对角矩阵(带状矩阵):
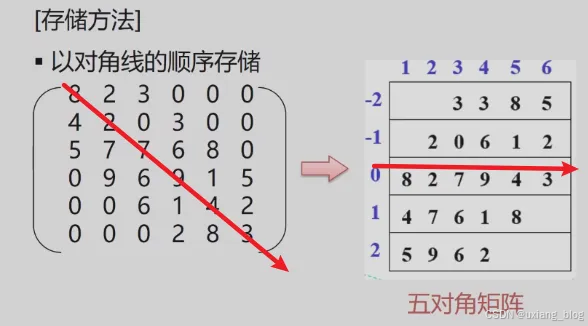
特点:在n*n的方阵中,所有非零元素都集中在以对角线为中心的带状区域中,区域外的值全为0,则称为对角矩阵。常见的有三对角矩阵、五对角矩阵、七对角矩阵等。
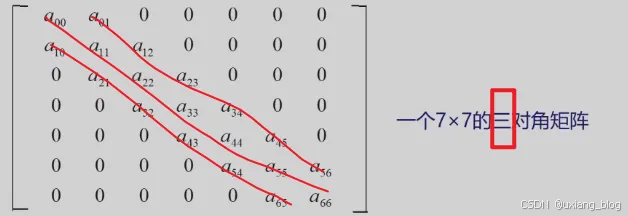
例如:
4.4.4.4、稀疏矩阵:
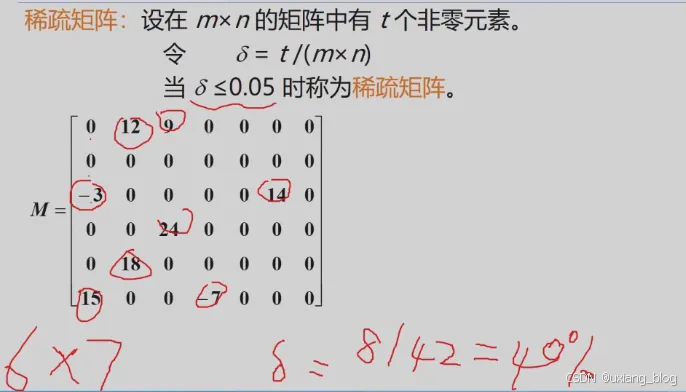
注解:在存储密度约4%,还远远没有达到稀疏的程度,就上面例子视觉上看着已经非常浪费空间了,如果达到稀疏了那浪费将非常严重,怎么解决这个稀疏数组浪费空间的问题?——三元组法(i,j,aij)唯一确定矩阵的一个非零元素。

压缩存储原则:存各非零元的值、行列位置和矩阵的行列数。三元组的不同表示方法可决定稀疏矩阵不同的压缩存储方法。
三元组顺序表——稀疏矩阵存储的一种方法
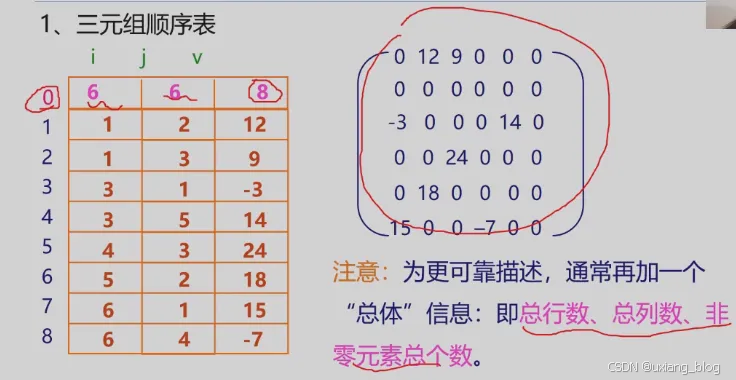
例如:试还原出下列三元组所表示的稀疏矩阵。
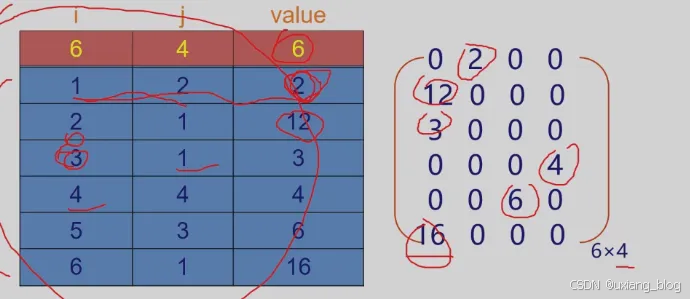
三元组顺序表又称有序的双下标法。
三元组顺序表的优点:非零元在表中按行序存储,因此便于进行依行顺序处理的矩阵运算。
三元组顺序表的缺点:不能随机存取。若按行号存取某一行中的非非零元,则需从头开始进行查找。
十字链表——稀疏矩阵的链式存储的另一种结构
● 优点:它能够灵活地插入因运算二产生的新的非零元素,删除因运算而产生的新的零元素,实现矩阵的各种运算。
● 在十字链表中,矩阵的每一个非零元素用一个结点表示,该结点除了(row,col,value)以外,还有两个域:
○ right:用于链接同一行中的下一个非零元素;
○ down:用于链接同一列中的下一个非零元素。
● 十字链表中结点的结构示意图:

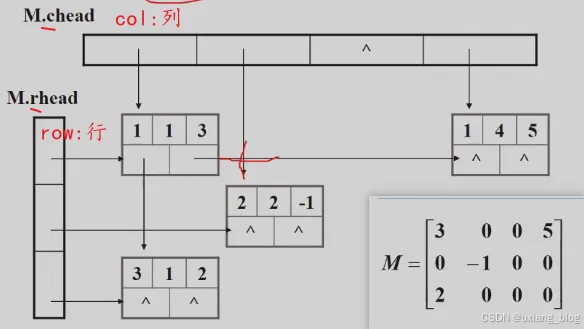
例如:试还原出下列十字链表所表示的稀疏矩阵。
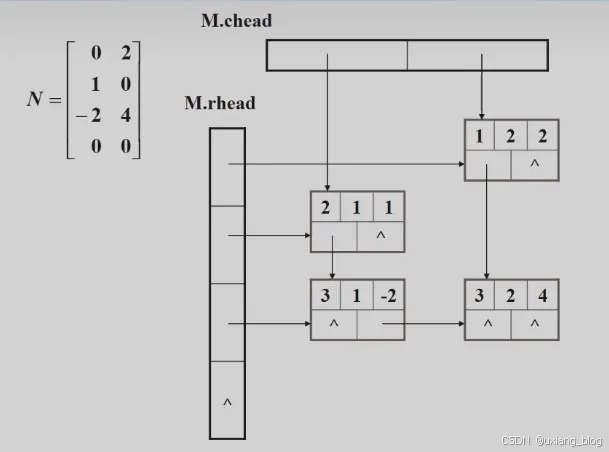
4.5、广义表
4.5.1、广义表的定义
广义表(又称列表Lists)是n>=0个元素a0,a1,...,a_0,a1,...,a0,a1,...,an-1的有限序列,其中每一个ai或者是原子,或者是一个广义表。
例如中国举办的国际足球邀请赛,参赛队名单可表示如下:

在这个表中,叙利亚队应该排在法国队伍后面,但未能参加,成为空表。国家队,山东鲁能,广州恒大均为东道主的参赛队参加,构成一个小的线性表,成为原线表的一个数据元素。这种扩宽了的线性表就是广义表。
● 广义表通常记作:LS =(a1,a2,…,an),其中:LS为表名,n为表的长度,每一个ai为表的元素。
● 习惯上,一般用大写字母表示广义表,小写字母表示原子。
● 表头:若LS非空(n>=1),则其第一个元素a1就是表头。记作head(LS) = a1。== 注意==:表头可以是原子,也可以示子表。
● 表尾:除表头之外的其他元素组成的表。记作tail(LS) = (a2,…, an)。注意:表尾不是最后一个元素,而是一个子表。
例如:

4.5.2、广义表的性质
1、广义表中的数据元素有相对次序;一个直接前驱和一个直接后继。
2、广义表的长度定义为最外层所包含元素的个数;

3、广义表的深度定义为该广义表展开后所含括号的重数;

4、广义表可以为其他广义表共享;
如:广义表B就共享A。在B中不必列出A的值,而是通过名称来引用,B=(A)。
5、广义表可以是一个递归的表。
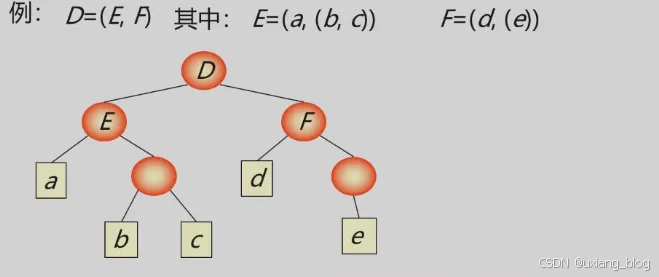
如:F = (a,F) = (a,(a,(a,(a,…))))。注意:递归表的深度示无穷值,长度示有限值。
6、广义表示多层次结构,广义表的元素可以是单元素,亦可以是子表,而子表的元素还看了一是子表,…。
可以用图形形象地表示。
4.5.3、广义表与线性表的区别?
广义表可以看成是线性表的推广,线性表是广义表的特例。
广义表的结构相当灵活,在某种前提下,它可以兼容线性表、数组、树和有向图等各种常用的数据结构。
当二维数组的每行(或每列)作为子表处理时,二维数组即为一个广义表。
另为,树和用向图也可以用广义表来表示。
由于广义表不仅集中了线性表、数组、树和有向图等常见数据结构的特点,而且可有效地利用存储空间,因此在计算机的许多应用领域都有成功使用广义表的实例。
4.5.4、广义表的基本运算
1、求表头GetHead(L):非空广义表的第一个元素,可以是一个单一原子,也可以是一个子表。
2、求表尾GetTail(L):非空广义表除去表头一外其他元素构成的表。表尾一定时一个表。
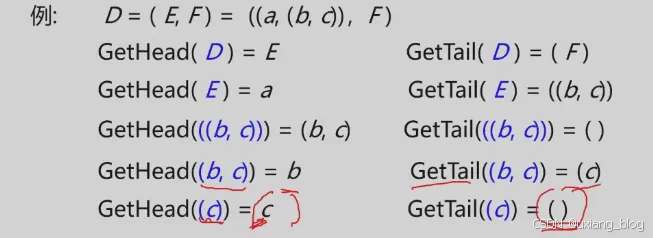
4.6、案例分析与实现
案例分析
● 因为患者的DNA和病毒DNA均是由一些字母组成的字符串序列,要检测某种病毒的DNA序列是否在患者的DNA序列中出现过,实际上就是字符串的模式匹配问题。
● 可以利用BF算法,也可以利用更高效的KMP算法。
● 但与一般的模式匹配问题不同的是,此案例中病毒的DNA序列是环状的。
● 这样需要对传统的BF算法或KMP算法·进行改进。
案例实现
● 对于每一个待检测的任务,假设病毒DNA序列的长度是m,因为病毒DNA序列是环状的,为了线性取到每个可行的长度为m的模式串,可将存储病毒DNA序列的字符串长度扩大为2m,将病毒DNA序列连续存储2次。
● 然后循环m次,依次取得每个长度为m的环状字符串,将此串做为模式串,将人的DNA序列作为主串,调用BF算法进行模式匹配。
● 只要匹配成功,即可中止循环,表明该人感染了对应的病毒;否则循环m次结束循环时,可通过BF算法的返回值判断该人是否感染了对应的病毒。
第五章 树和二叉树


5.1、树和二叉树的定义
5.1.1、树的定义
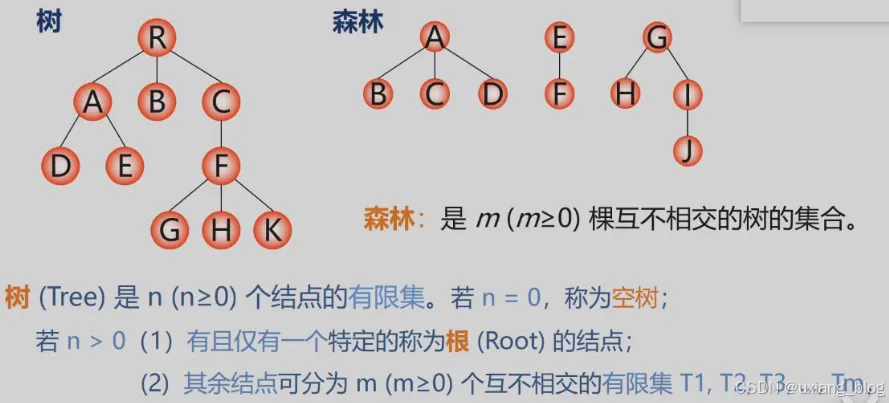
树(Tree)是n(n>=0)个结点的有限集。
● 若n = 0,则称为空树;
● 若n > 0,则它满足如下两个条件:
○ (1)、有且仅有一个特定的称为根(Root)的结点;
○ (2)、其余结点可以分为m(m >= 0)个互不相交的有限集T1,T2,T3…,Tm,其中每一个集合本身又是一个棵树,并称为根的子树(SubTree)。
树是n个结点的有限集,显然,树的定义是一个递归的定义。
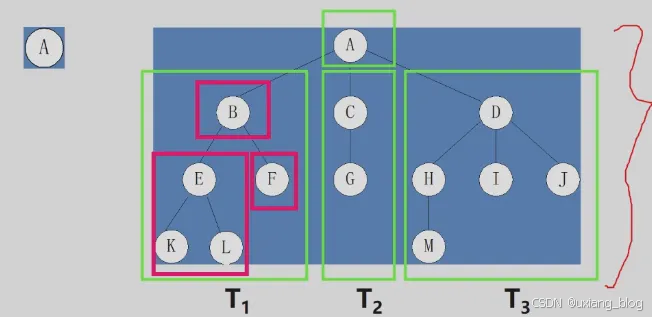
树的其他表示方式
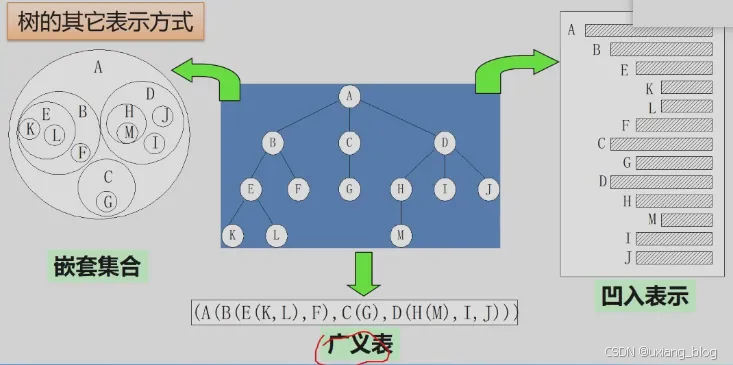
5.1.2、树的基本术语
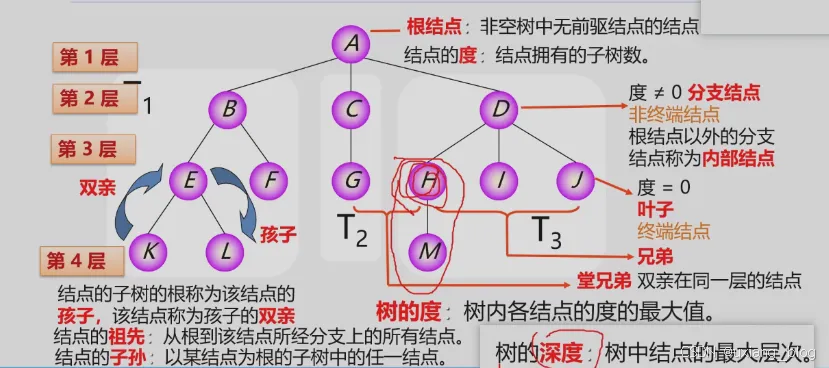
————————-----------上下关系
根结点:非空书中无前驱结点的结点。
结点的度:结点拥有的子树数。
● 度 != 0,非终端结点,分支结点。
● 度 = 0,叫做==终端结点==,也叫叶子。
● 根结点以外的分支结点称为内部结点。
树的度:树内各结点的度的最大值。
结点的子树的根称为该结点的孩子,该结点称为孩子的双亲。
————————————水平关系
兄弟:有共同的双亲的结点,就是兄弟结点。比如HIJ有共同的双亲D。H,I,J相互为兄弟。
堂兄弟:他们没有共同的双亲,但是他们的双亲都在同一层结点。比如G和H就是堂兄弟,从根结点(记为第一层)开始,它们的双亲,G的双亲C,H的双亲D,都在第2层。
结点的祖先:从根结点到该结点所经分支上的所有结点。比如M,从M开始:M——>H——>D——>A,到根结点结束,这条线中,H,D,A都是M的祖先,包括它的双亲H。
结点的子孙:以某结点为根的子树中的任一结点。比如A,从A开始:A——>D——>H——>M,到根结点结束,这条线中,H,D,M都是A的子孙。
树的深度:树中结点的最大层次。也叫做树的高度,本文中树的深度为第4层。
注解:
● 树的度:a有3个分支,b有2个分支,c有1个分支,d有3个分支,…,里面分支最多的就是3,所以3是这个树的度。
● 内部结点:a是根结点,所以剔除掉,剩下的所有结点就是内部结点。
● 双亲和孩子:比如A结点生出BCD三个分支,所以A结点是BCD的双亲,BCD结点是A的孩子。
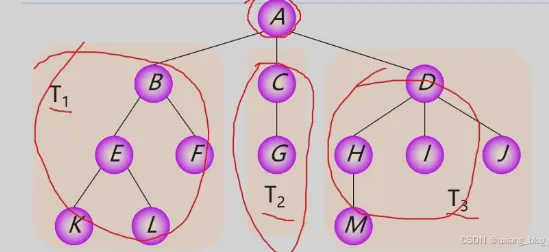
有序树:树中结点的各子树从左到右有次序(最左边的为第一个孩子)。比如A下面三个分支B所在的T1,C所在T2,D所在的T3,必须按照T1为左,T2为中,T3为右的顺序,这就是有序树。
无序树:树中结点的各子树无次序。
森林:是m(m >= 0)棵互不相交的树的集合。把根结点删除树就变成了森林。一棵树可以看成是一个特殊的森林。给森另种的子树加上一个双亲结点,森林就变成了树。
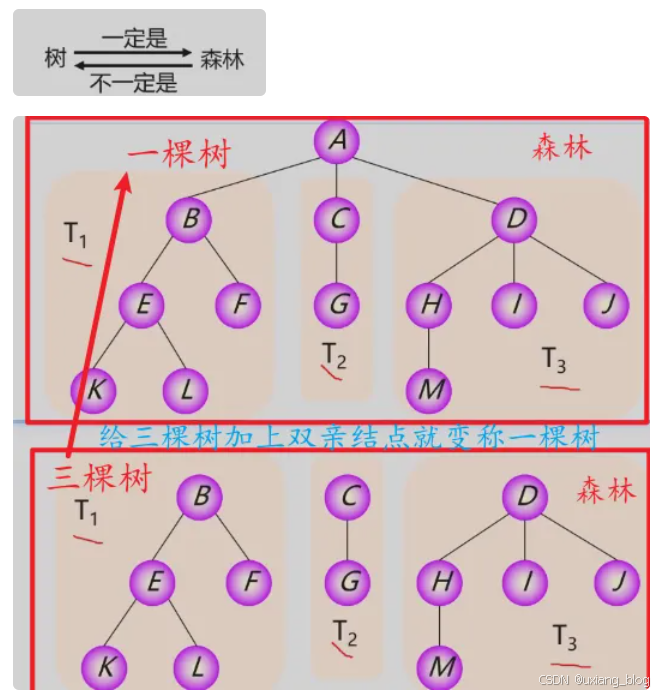
5.1.2、线性结构和树结构的区别
| 线性结构 | 树结构 |
| 第一个数据元素 无前驱 | 根结点(只有一个) 无双亲 |
| 最后一个数据元素 无后继 | 叶子结点(可以有多个)无孩子 |
| 其他数据元素 一个前驱一个后继 | 一个双亲,多个孩子 |
| 一对一 | 一对多 |
5.1.2、二叉树的定义
为何要重点研究每结点最多只有两个“叉”的树?
● 二叉树的结构最简单,规律性最强;
● 可以证明,所有树能转换为唯一对应的二叉树,不失一般性。
普通树(多叉树)若不转换成为二叉树,则运算很难实现
二叉树在树结构的应用中起着非常重要的作用,因为对二叉树的许多操作算法简单,而任何树都可以与二叉树相互转换,这样就解决了树的存储结构以其运算中存在的复杂性。
二叉树是n(n >= 0)个结点的有限集,它或者是空集(n = 0),或者由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成。
特点
1、每个结点最多有俩孩子(二叉树中不存在大于2的结点:0,1,2)
2、子树有左右之分,其次序不能颠倒。
3、二叉树可以是空集合,根可以有空的左子树或空的右子树。
注意:
二叉树不是树的特殊情况,它们是两个概念。
二叉树结点的子树要区分左子树和右子树,即使只有一棵子树也要区分,说明它是左子树,还是右子树。
树当结点只有一个孩子时,就无须区分它时左还是右的次序。因此二者时不同的。这是二叉树与树的最主要的差别。
(也就是二叉树每个结点位置或者说次序都是固定的,可以是空,但是不可以说它没有位置,而树的结点位置是相对于别的结点来说的,没有别的结点时,它就无所谓左右了)
思考:
具有3个结点的二叉树可能有几种不同的形态?普通树呢?
二叉树有5种形态:
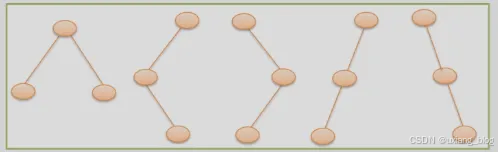
而树有2种状态:
二叉树的5种基本形态
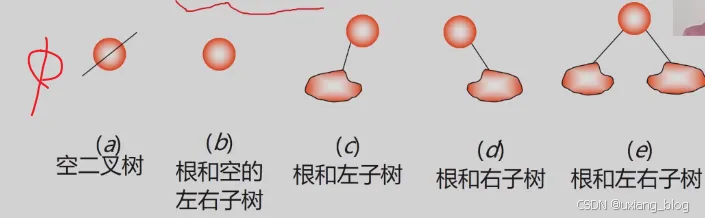
注意:虽然二叉树于与树概念不同,但是有关树的基本术语对二叉树都适用。
5.2、案例引入
案例1:数据压缩问题
将数据文件转换成由0、1组成的二进制串,称之为编码。
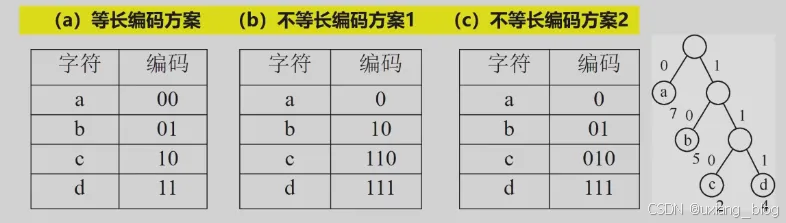
案例2:利用二叉树求解表达式的值
以二叉树表示表达式的递归定义如下:
(1)若表达式为数或简单变量,则相应二叉树中仅有一个根结点,其数据域存放该表达式信息;
(2)若表示式为“第一操作数 运算符 第二操作数”的形式,则相应的二叉树中以左子树表示第一操作数,右子树表示第二操作数,根结点的数据域存放运算符(若为一元运算,则左子树为空),其中,操作数本身又为表达式。
5.3、树和二叉树的抽象数据类型定义
二叉树的抽象数据类型定义

ADT BinaryTree{数据对象D: D是具有相同特性的数据元素的集合数据关系R:若D = Ø,则R = Ø;若D != Ø,则R = {H};H是如下二元关系:(1)root 唯一 //关于根的说明(2) Dj∩Dk = Ø //关于子树不相交的说明(3)... //关于数据元素的说明(4) ... //关于左子树和右子树的说明基本操作P: //至少有20个
}ADT BinaryTree
最常用的基本操作

CreateBiTree(&T,definition)初始条件:defeinition 给出二叉树T的定义。操作结构:按definiton构造二叉树T。
PreOrderTraverse(T)初始条件: 而叉树T存在。操作结果: 先遍历T,对每个结点访问一次。
InOrderTraverse(T)初始条件: 二叉树T存在。操作结构: 中序遍历T,对每个结点访问一次。
PostOrderTraverse(T)初始条件:二叉树T存在。操作结构: 后遍历T,对每个结点访问一次。
5.4、二叉树的性质和存储结构
性质一:在二叉树的第i层至多有2i-1个结点(i >= 1)。
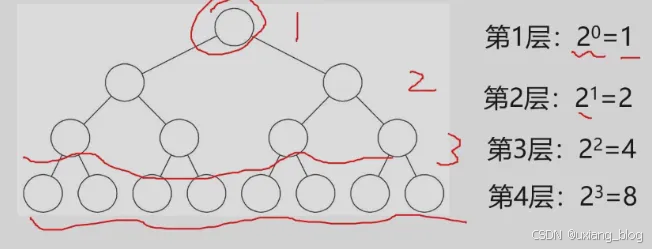
证:采用归纳证明此性质。
归纳基:当i = 1 时,只有一个根结点,2i-1 = 20 = 1,命题成立。
归纳假设: 设对于所有的j(1<= j < i),命题成立, 即第j层至多有2j-1 个结点。那么可以证明j = i 时命题也成立。
归纳证明: 由归纳假设可知,第 i - 1 层上至多有 2i-2 个结点。由于二叉树每个结点的度最大为2,故在第i层上最达结点为第i - 1 层上最大结点的2倍,即:2* 2i-2 = 2 i-1。证毕。
提问:第i层至少有_个结点? 1个。
性质二: 深度为k的二叉树至多有2k - 1 个结点(k >= 1)。
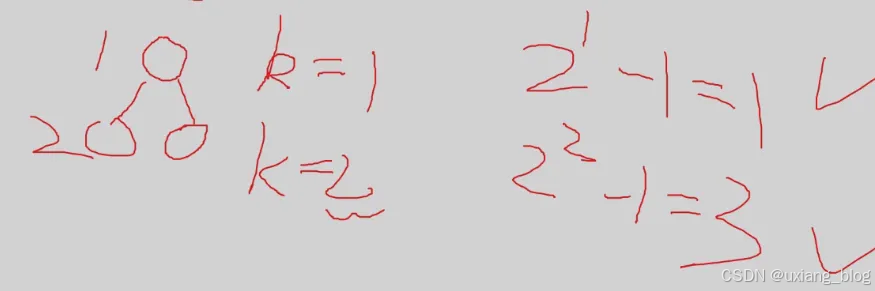

提问:深度为k时至少有_个结点? k个
性质三:对于一棵二叉树T,如果其叶子树为n0, 度为2的结点树为n2,则n0 = n2 + 1。
直观上看
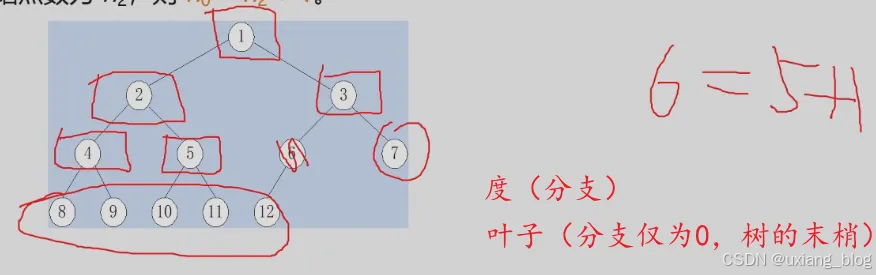
证明过程——从引入边的角度证明
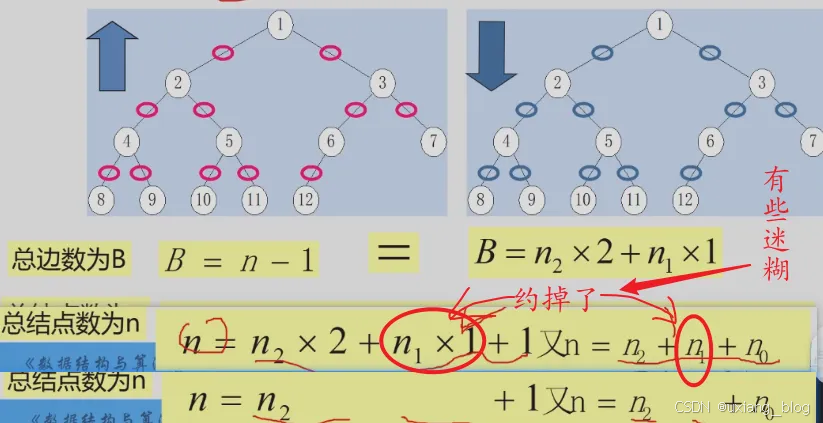
注解:性质三结论不重要,重要的是2种分析边和结点关系的方式,
这个性质怎么证明它呢?从分支个数来,先从下往上看,每个结点到它的双亲结点都有一个分支(边),只有根结点没有(从下往上看,根结点没有双亲结点,所有说只有根结点没有边),记所有结点为n,则产生的边数为n-1;从上往下看,度为2的结点产生2条边,度为1的结点产生1条边,叶子结点没有边,度为2的结点记作n2,度为1的结点记作n1,所有种类的结点加起来就是所得边数:n22 + n11 + n0 * 1。
5.4.1、两种特殊形式的二叉树

5.4.1.1、满二叉树
定义:一棵深度为k且有2k-1 个结点的二叉树称为满二叉树。
特点:
● 1、每一层上的结点数都是最大结点树(即每层都满),
● 2、叶子节点全部在最底层
对满二叉树结点位置编号
● 编号规则: 从根结点开始,自上而下,自左而右。
● 每一个结点位置都有元素。
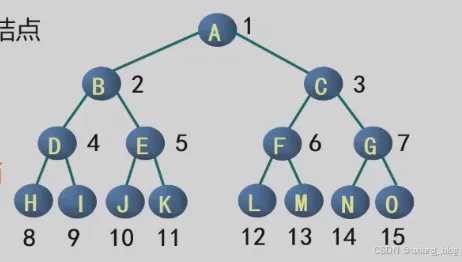
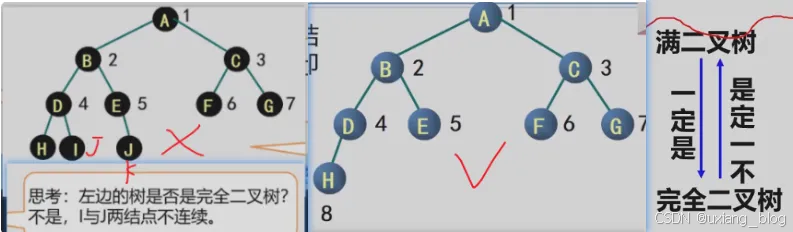
思考:下面的二叉树是满二叉树吗?
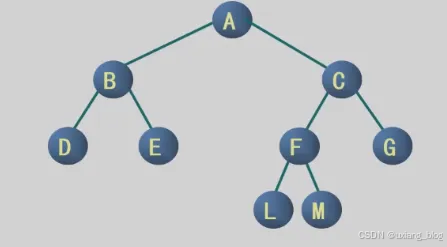
不是,从以下角度分析。
从满二叉树定义来看:一棵深度为k且有2k-1 个结点的二叉树称为满二叉树。此二叉树深度为4,但是实际结点(9个)少于定义要求结点(24-1=15个),所以此不为满二叉树。
从满二叉树特点来看:
1、每一层上的结点数都是最大结点树(即每层都满),此二叉树第一层(20)1个,满足,第二层(21)2个满足,第三层(22) ,实际为2个不满足。
2、最后一层结点个数不满。
编号核对:8,9,10, 11,12,13,14,15位置都是空着的。
补充:满二叉树在同样深度的二叉树中结点个数最多。
满二叉树在同样深度的二叉树中叶子结点个数最多。
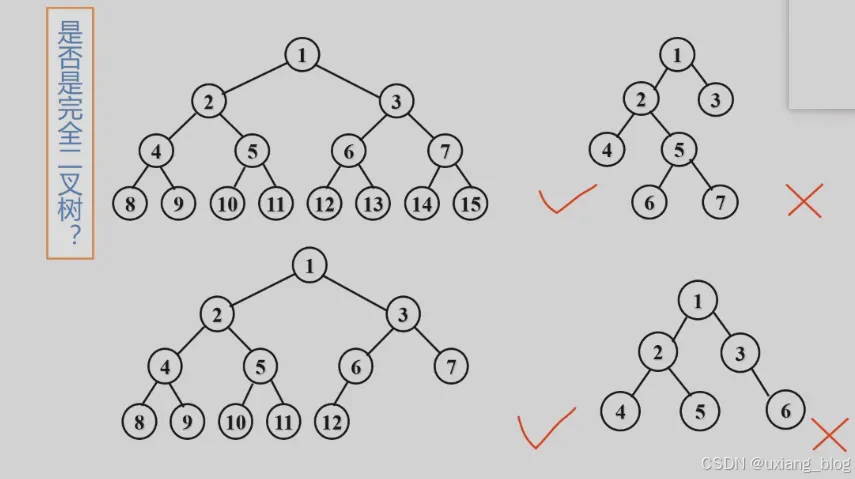
5.4.1.2、完全二叉树(Complete binary tree)
定义:深度为k的具有n个结点的二叉树,当且仅当其每一个结点都于深度为k的满二叉树中编号为1~n的结点一 一对应时,称之为完全二叉树。
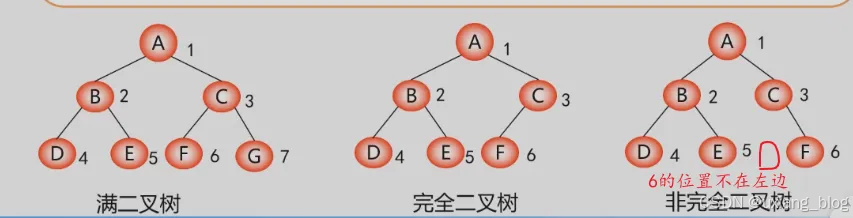
判断:
注意:在满二叉树中,从最后一个结点开始,连续去掉任意个结点,即时一棵完全二叉树。一定是连续的去掉,(包括数字位置和里面的)
特点:
● 1、叶子只可能分布在层次最大的两层上。
● 2、对于任一结点,如果其右子树的最大层次为i,则其左子树的最大层次必为i或i + 1。
性质4:具有n个结点的完全二叉树的深度为|Log2n| +1。
注意:|x|:称作x的底,表示不大于x的最大整数
这个性质是如果知道完全二叉树的结点个数(数据元素个数)就知道了它的深度了。
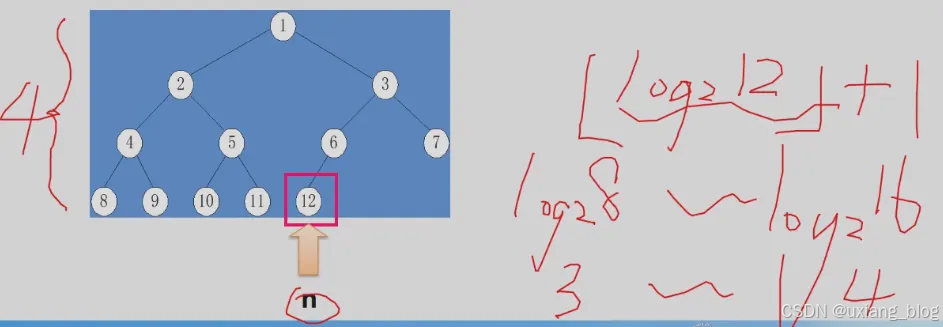
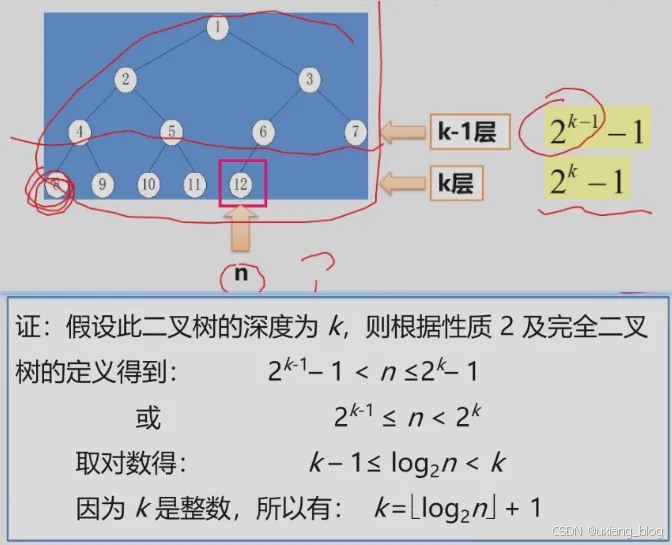
性质4表明了完全二叉树结点数n与完全二叉树深度k之间的关系。
性质5:如果对一棵有n个结点的完全二叉树(深度为|log2n| + 1 )的结点按层编号(从第1层第|log2n| + 1层,每层从左到右),则对任一结点i(1<= i<= n),有:

性质5表明了完全二叉树中双亲结点编号与孩子结点编号之间的关系。
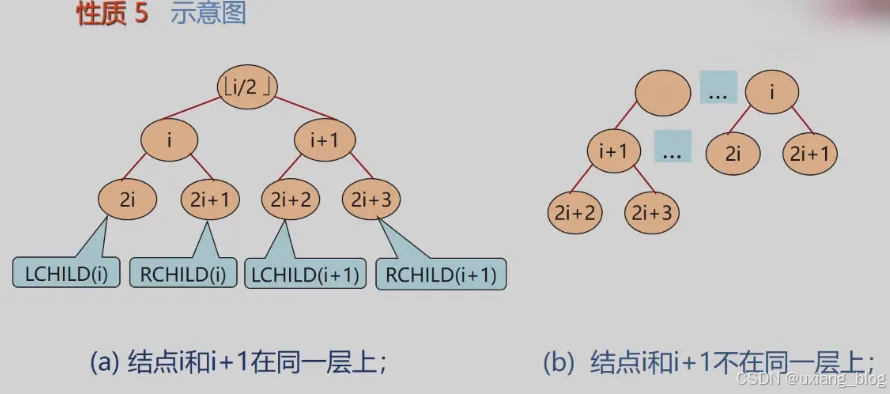
只需会计算即可。
5.4.2-a、二叉树顺序存储结构
实现:按满二叉树的结点层次编号,依次存放二叉树中的数据元素。
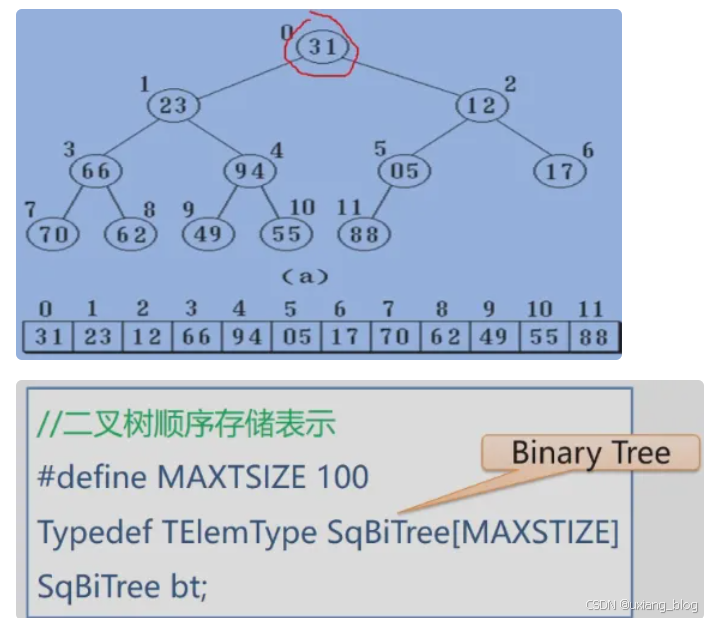
//二叉树顺序存储表示
#define MAXTSIZE 100 //定义数组的最大空间为100
Typedef TElemType SqBiTree[MAXSTIZE] //TElemType 中T(TREE)表示树,ElemType可以是int也可以示char类型
SqBiTree bt;//定义数组变量bt
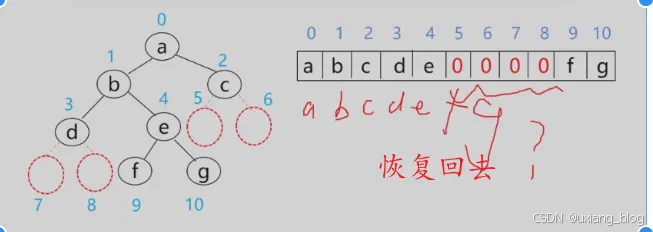
例如:
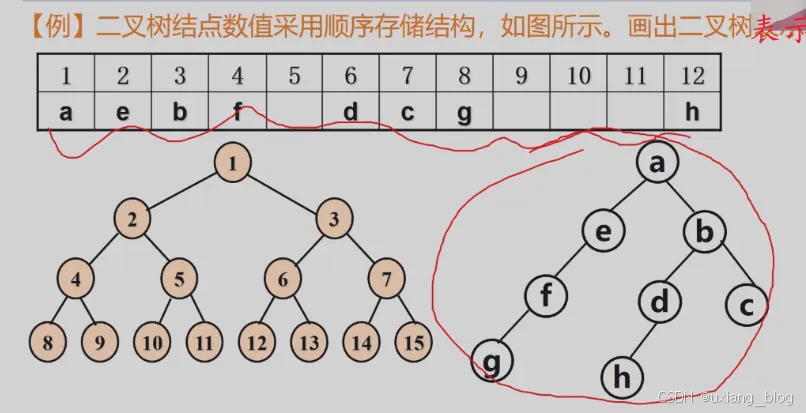
5.4.2.1、二叉树的顺序存储缺点:
最坏的情况:深度为k的且只有k个结点的单支树需要长度为2k-1 的数组。
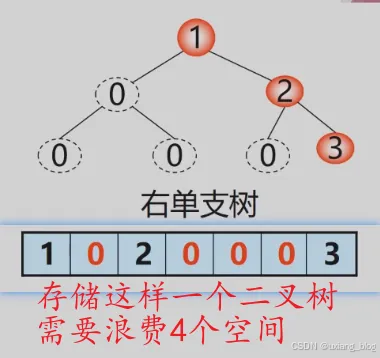
当树很高的时候就会浪费非常多的空间。
特点:结点间关系蕴含在其存储位置中,浪费空间,适于存满二叉树和完全二叉树
5.4.2-b、二叉树链式存储结构
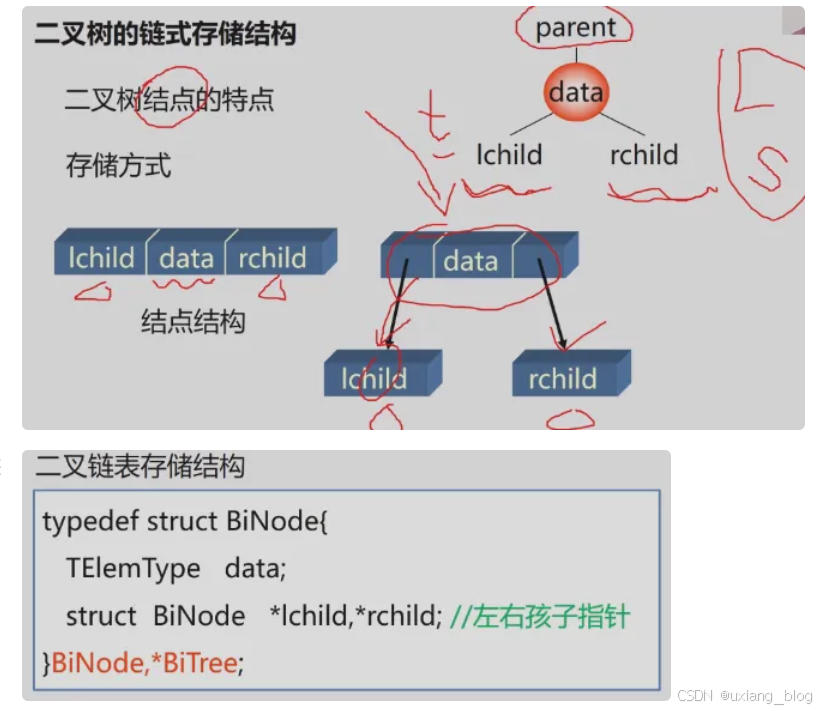
typedef struct BiNode{TElemType data;struct BiNode *lchild,*rchild;//左右孩子指针
}BiNode,*BiTree; //*BiTree指向结点的指针
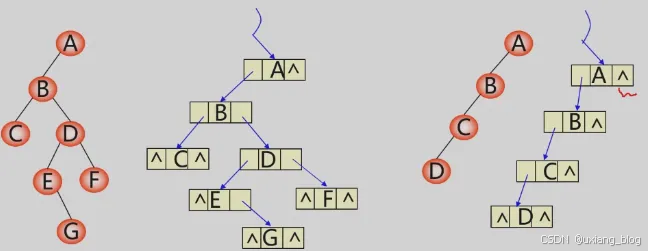
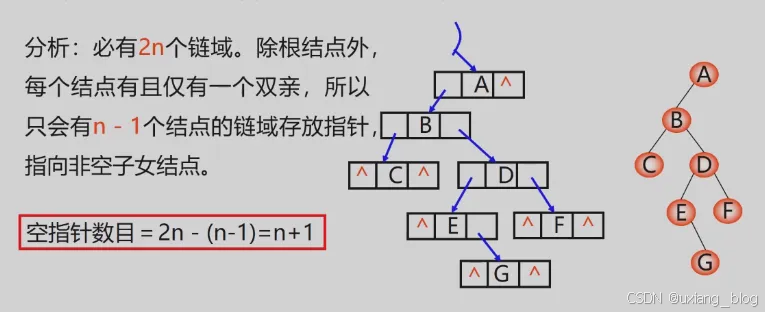
练习
在n个结点的二叉链表中,有________个空指针域。
5.4.2-c、三叉链表——二叉树链表的扩展
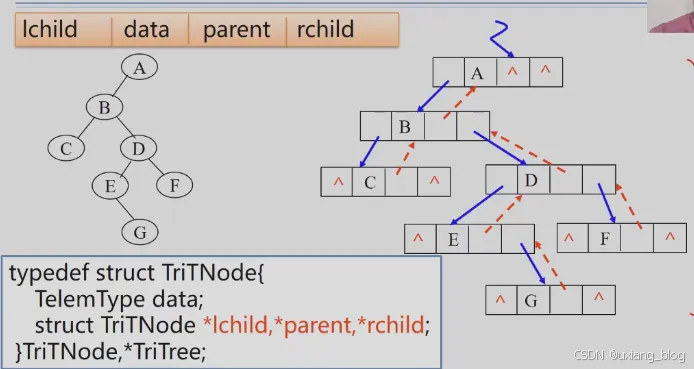
typedef struct TriTNode{TelemType data;struct TriTNode *lchild,*parent,*rchild;
}TriTNode,*TriTree;
5.5、遍历二叉树和线索二叉树
5.5.1、遍历二叉树
● 遍历定义——顺着某一条搜索路径巡防二叉树中的结点,使得每个结点均被访问一次,而且仅被访问一次(又称周游)。"访问”的含义很广,可以是对结点作各种处理,如:输出结点的信息、修改结点的数据值等,但要求这种访问不破坏原来的数据结构。
● 遍历目的——得到树中所有结点得一个线性排列。
● 遍历用途——它是树结构插入、删除、修改、查找和排序运算得前提,是二叉树一切运算得基础和核心。
1、遍历二叉树算法描述
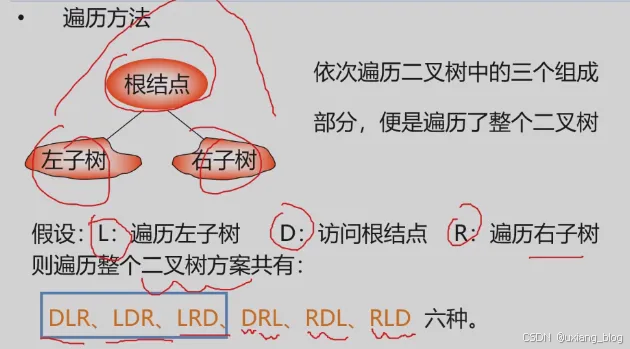
重点了解前三种,若规定先左后右,则只有前三种情况:
● DLR——先(根)序遍历
● LDR——中(根)序遍历
● LRD——后(根)序遍历
规则:先左后右,根在哪里就是那种序遍历。
| 先序遍历二叉树 | 中序遍历二叉树 | 后序遍历二叉树 |
| 若二叉树为空,则空操作;否则如下 | 若二叉树为空,则空操作;否则如下 | 若二叉树为空,则空操作;否则如下 |
| (1)访问根结点; | (1)中序遍历左子树; | (1)后序遍历左子树; |
| (2)先序遍历左子树; | (2)访问根结点; | (2)后序遍历右子树; |
| (3)先序遍历右子树。 | (3)中序遍历右子树。 | (3)访问根结点。 |
由二叉树的递归定义可知,遍历左子树和遍历右子树可如同遍历二叉树一样“递归”进行。
2、先、中、后序遍历二叉树的练习。
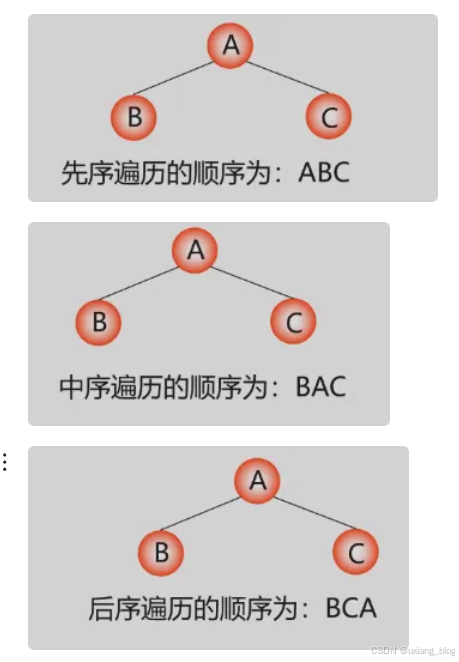
例题:
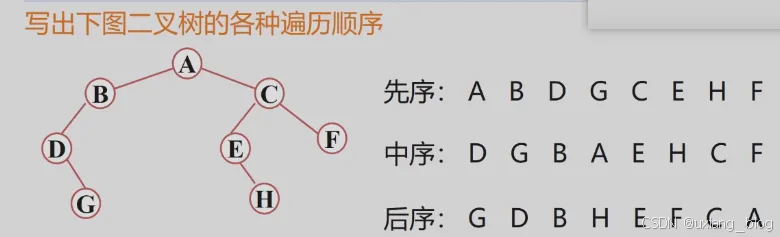
例:用二叉树表示算数表达式
写出下图所示二叉树的先序、中序和后序遍历顺序。
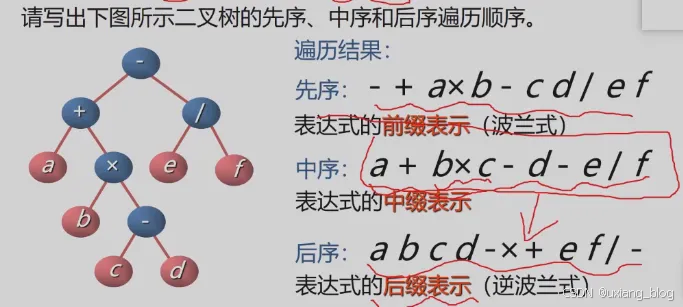
例——已知先序和中序序列求二叉树
例:已知二叉树的先序和中序序列,构造出相应的二叉树
● 先序: ABCDEFGHIJ
● 中序: CDBFEAIHGJ
分析:由先序序列确定根;由中序序列确定左右子树。
解:1、由先序知根为A,则由中序知左子树为CDBFE,右子树为IHGJ
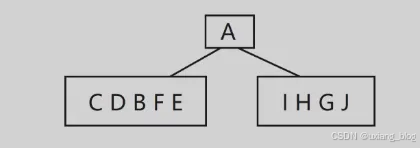
2、再分别在左、右子树的序列中找出根、左子树序列、右子数序列。
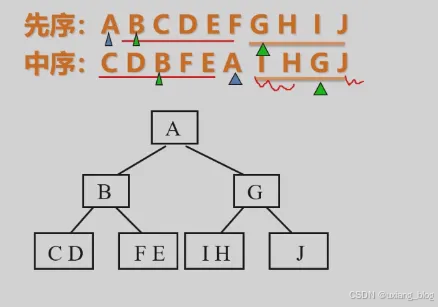
3、依次类推,直到得到二叉树
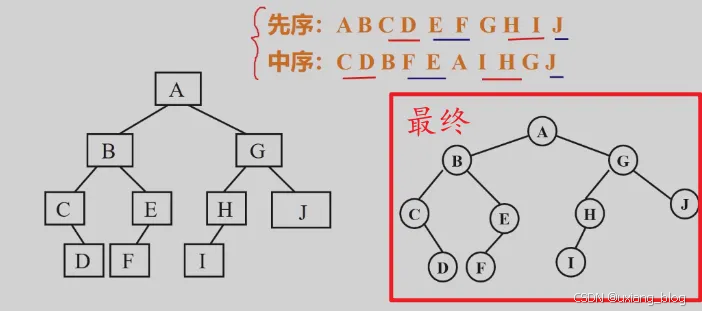
例:已知中序序列和后序序列求二叉树
实例分析:已知一棵树的中序:BDCEAFHG,后序:DECBHGFA,请画出这个树二叉树。

3、遍历的算法实现——先序,中序和后序遍历
二叉树先序遍历算法:先序遍历
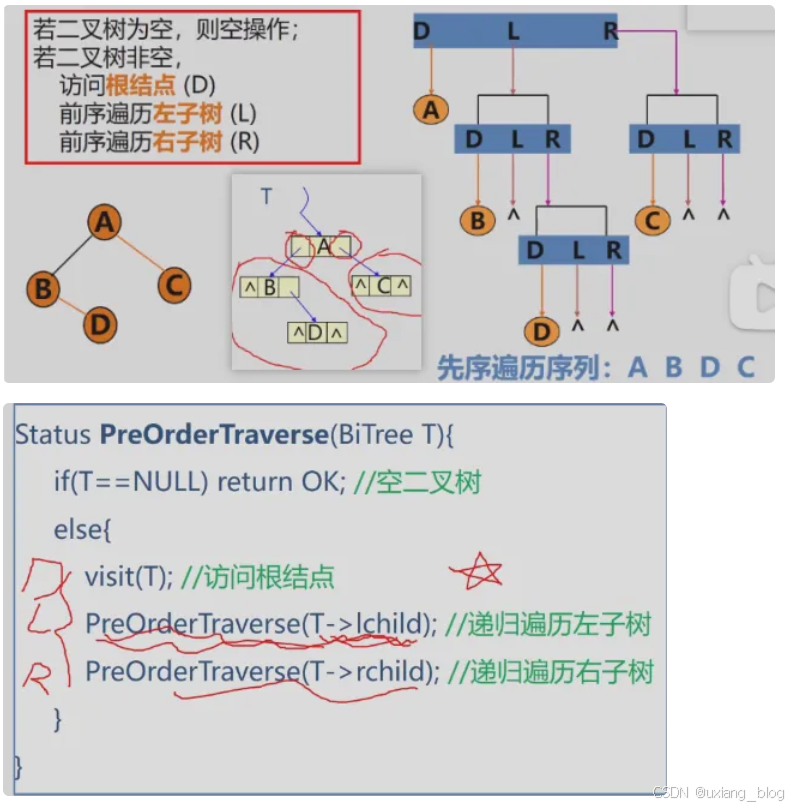
Status PreOrderTraverse(BiTree T){if(T == NULL)return OK; //空二叉树else{visit(T); //访问根结点PreOrderTraverse(T -> lchild); //递归遍历左子树PreOrderTraverse(T -> rchild); //递归遍历右子树}
}
递归过程详解
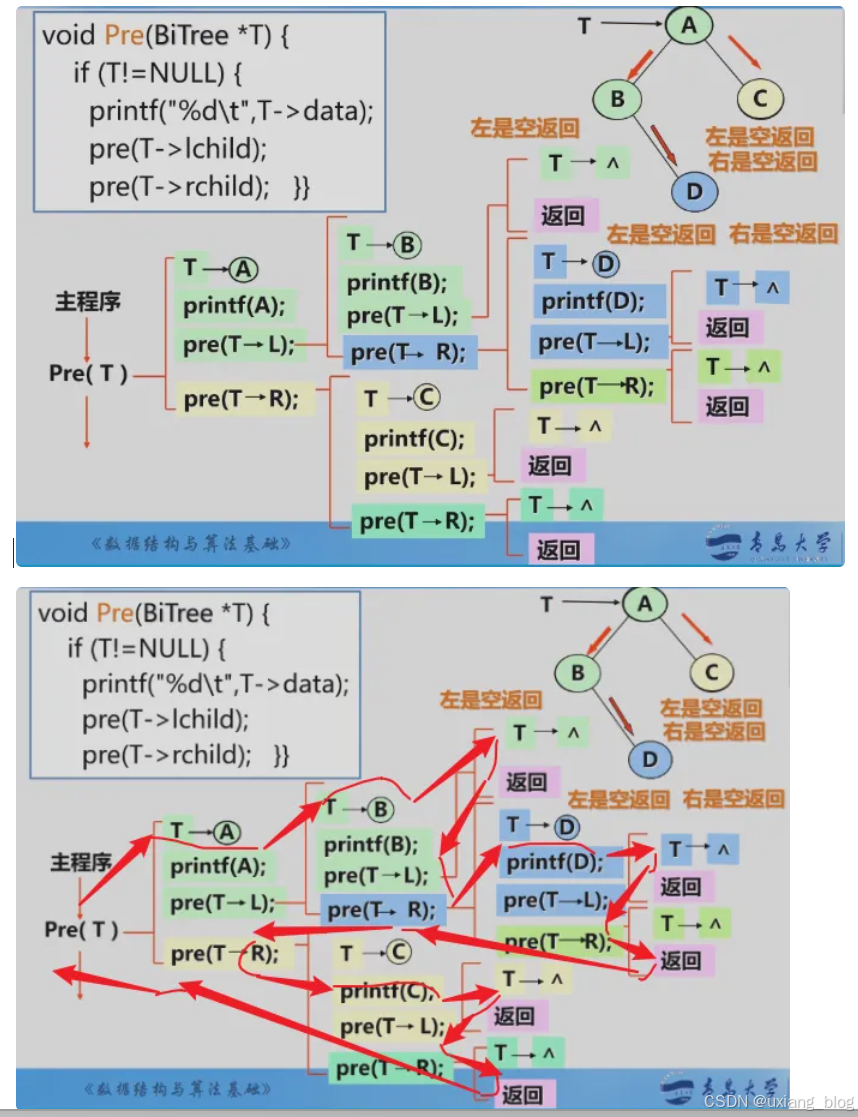
二叉树先序遍历算法:中序遍历
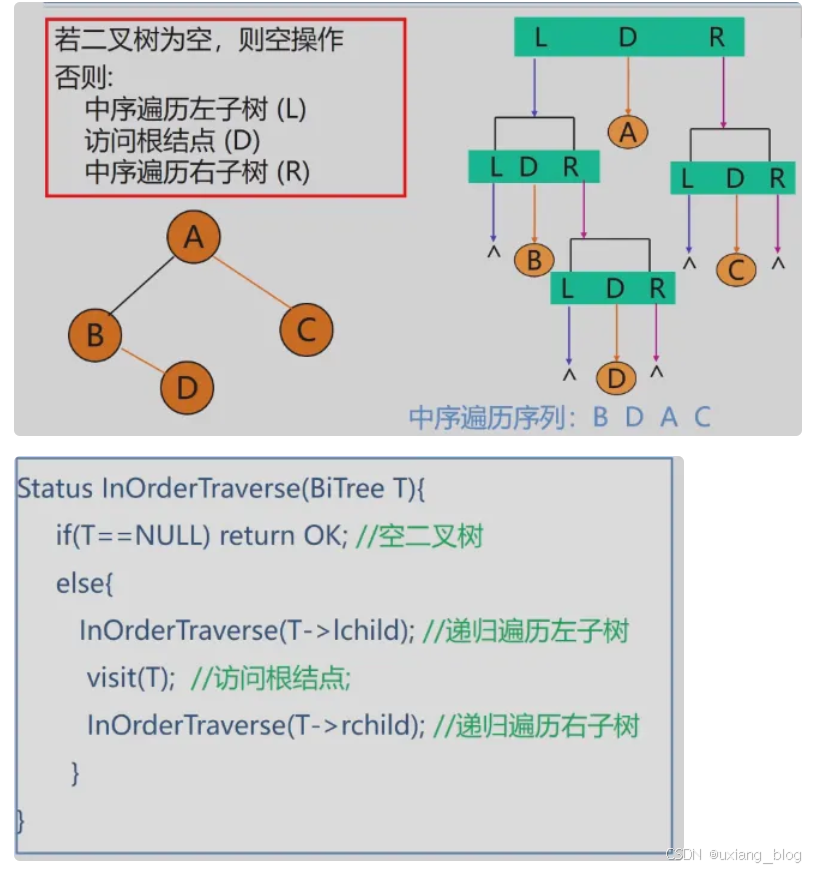
Status InOrderTraverse(BiTree T){if(T == NULL) return OK; //空二叉树else{InOrderTraverse(T -> lchild);//递归遍历左子树visit(T); //访问根结点;InOrderTraverse(T -> rchild); //递归遍历右子树}
}
二叉树先序遍历算法:后序遍历
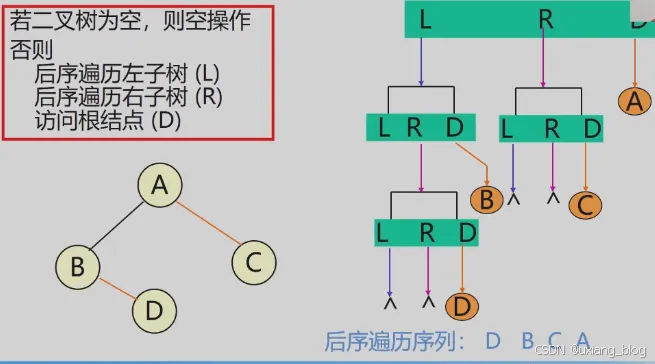
三个算法分别是:
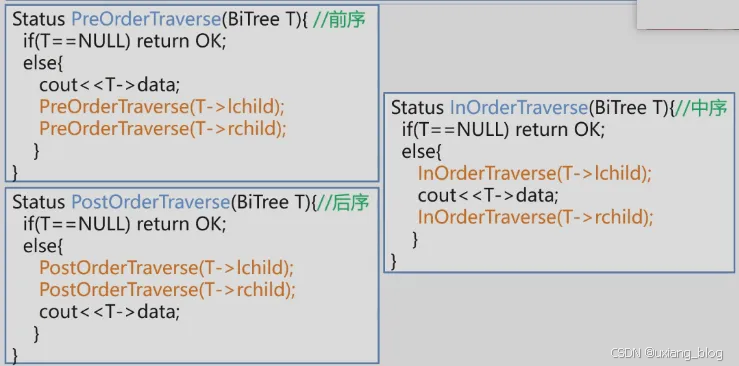
//前序遍历算法
Status PreOrderTraverse(BiTree T){if(T == NULL) return OK;else{cout<<T->data;PreOrderTraverse(T -> lchild);PreOrderTraverse(T -> rchild);}
}//中序遍历算法
Status InOrderTraverse(BiTree T){if(T == NULL) return OK;InOrderTraverse(T -> lchild);cout<<T -> data;InOrderTraverse(T -> rchild);
}//后序遍历算法
Status PostOrderTraverse(BiTree T){if(T == NULL) return OK;else{PostOrderTraverse(T -> lchild);PostOrederTraverse(T -> rchild);cout<<T -> data;}
}
4、遍历算法的分析
如果去掉输出语句,从递归的角度看,三种算法是完全相同的,或说这三种算法的访问路劲是相同的,只是访问点的实际不同。从虚线的出发点到终点的路劲上,每个结点经过3次。
| 第1次经过时访问 | 先序遍历 |
| 第2次经过时访问 | 中序遍历 |
| 第3次经过时访问 | 后续遍历 |
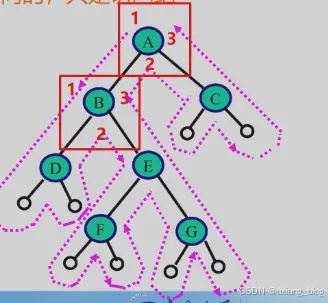
注解:时间复杂度都是一样的,都要每个结点经过一次,如果有n个结点的话,它的时间复杂度就是O(n);空间复杂度,遇上一个结点,如果我们不访问它,那就需要一个地方把它存上,然后等回来的时候访问,递归中记录这个地址的就是栈(BiTree T),最坏的情况是单只的,需要记录n个结点,所以空间复杂度为O(n)。
● 时间效率:O(n) //每个结点只访问一次
● 空间效率:O(n) //栈占用的最大辅助空间
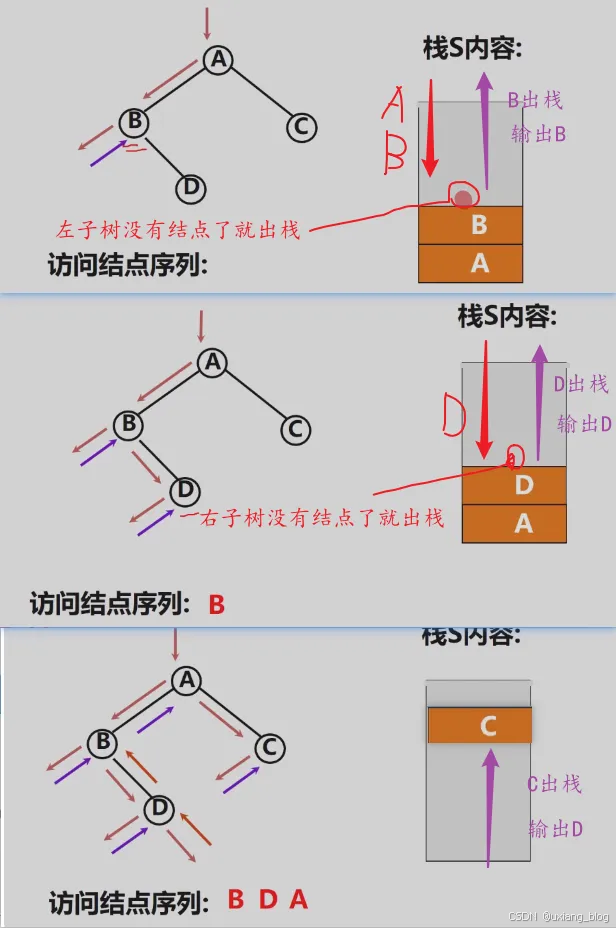
5、遍历二叉树的非递归算法——以中序为例
中序遍历非递归算法:二叉树中序遍历的非递归算法的关键:在中序遍历过某结点的整个左子树后,如何找到该结点的根以及右子树。
基本思想:
● 1、建立一个栈
● 2、根结点进栈,遍历左子树
● 3、根结点出栈,输出根结点,遍历右子树。
中序遍历的非递归操作演示:
遍历二叉树的非递归算法

Status InOrderTraverse(BiTree T){BiTreep;InotStack(S);p = T;while(p || !StackEmpty(S)){if(p){Push(S,p);p = p -> lchild;}else{Pop(S,q);p = q -> rchild;}}return OK;
}
6、二叉树的层次遍历及其算法实现
(1)二叉树的层次遍历
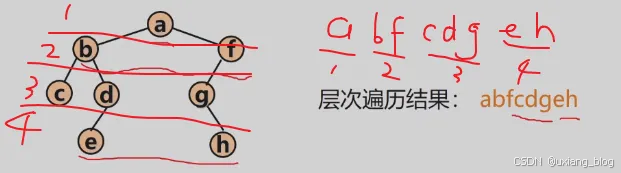
对于一个棵二叉树,从根结点开始,按从上到下、从左到右的顺序访问每一个结点。每一个结点仅仅访问一次。
算法设计思路:使用一个队列
● 1、将根结点进队;
● 2、队不空时循环:从队列中出列一个结点*p,访问它;
○ 若它有左孩子结点,将左孩子进队;
○ 若它有右孩子结点,将右孩子结点进队。
二叉树的层次遍历示意图
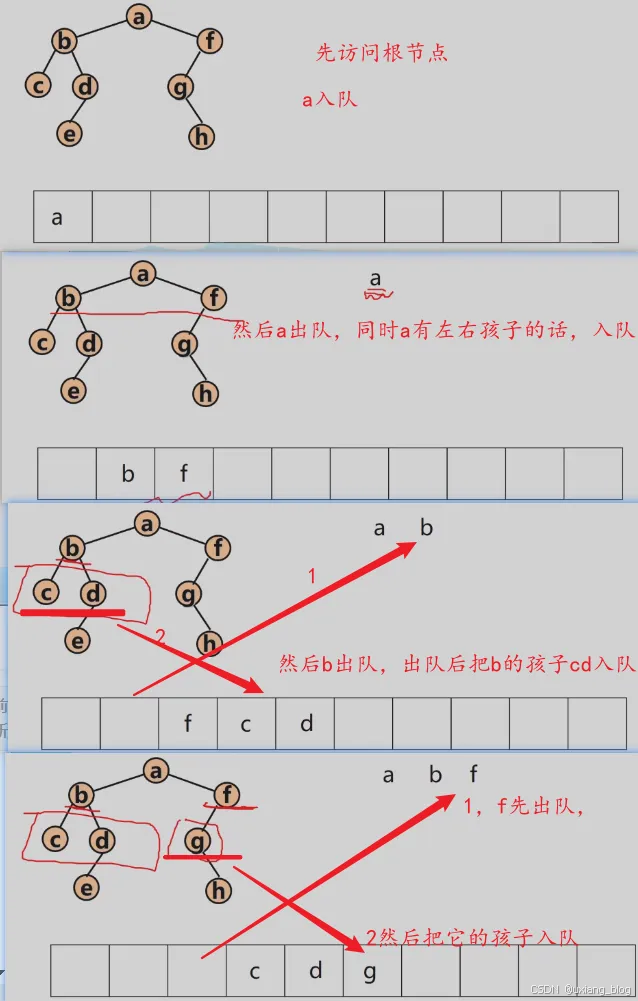
(2)二叉树的算法实现
使用队列类型定义如下:

typedef struct{BTNode data[MaxSize]; //存放队中元素int front, rear; //队头和队尾指针
}SqQueue; //顺序循环队列类型
二叉树层次遍历算法:

void LevelOrder(BTNode *b){BTNode *p;SqQueue *p;InitQueue(qu); //初始化队列enQueue(qu); //根结点指针进入队列while(!QueueEmpty(qu)){ //队不为空,则循环deQueue(qu,p); //出队结点pprintf("%c",p -> data); //访问结点p if(p -> lchild != NULL)enQueue(qu,p -> lchild); //有左孩子时将其进队if(p -> rchild != NULL)enQueue(qu,p -> rchild); //有右孩子时将其进队}
}
7、二叉树遍历算法的应用
二叉树的建立
按先序遍历序列建立二叉树的二叉链表
例:已知先序序列为:ABCDEGF
(1)从键盘输入二叉树的结点信息,建立二叉树的存储结构;
(2)在建立二叉树的过程中按照二叉树先序方式建立;
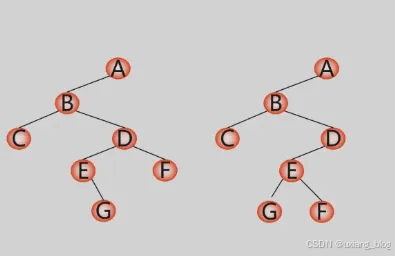
通过对这2个二叉树进行先序遍历会发现输出序列都为ABCDEGF,我们说对于一种方式(比如上述只有先序)很难确定是唯一的二叉树,那怎么才能确定就是左边一种而不是右边的一种呢?方法是给补充空(“#”)结点,这样我们构造出来的空结点就不一样啦。
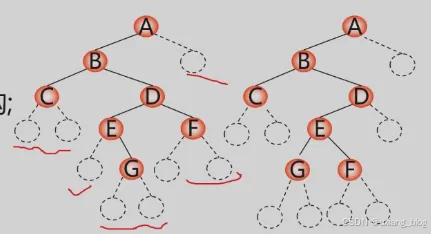
对于右图所示二叉树,按下列顺序读入字符:
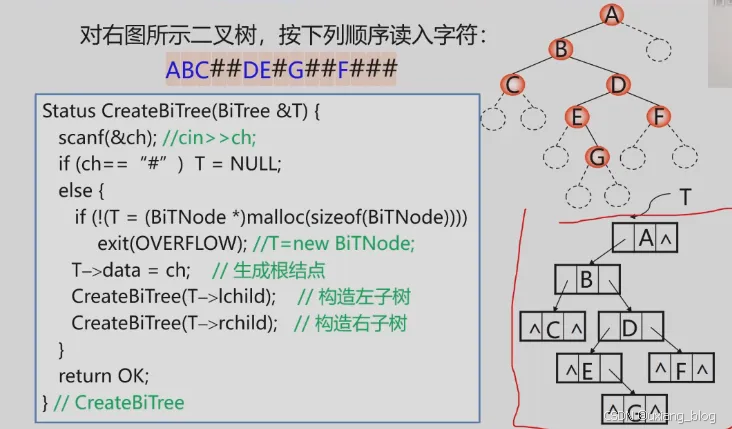
Status CreateBiTree(BiTree &T){scanf(&ch); //C++ 为 cin>>ch;if(ch == "#") T = NULL;else{if(!(T = (BiTNode *)malloc(sizeof(Node))))exit(OVERFLOW); //C++为 T = new BiTNode;T -> data = ch; //生成根结点CreateBiTree(T -> lchild); //构造左子树CreateBiTree(T -> rchild); //构造右子树}return OK;
}//CreateBiTree
复制二叉树
如果是空树,递归结束;
否则,申请新结点空间,复制根结点
● 递归复制左子树
● 递归复制右子树

int Copy(BiTree T, BiTree &NewT){if(T == NULL){ //如果是空树返回0NewT = NULL; return 0;}else{NewT = new BiTNode; NewT -> data = T -> data;Copy(T -> lChild, NewT -> lchild);Copy(T -> rChild, NewT -> rchild);}
}
计算二叉树的深度
如果是空树,则深度为0;
否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1。

int Depth(BiTree T){if(T == NULL) return 0;else{m = Depth(T -> lChild);n = Depth(T -> rChild);if( m > n) return(m + 1);else return(n + 1);}
}
计算二叉树结点总数
如果是空树,则结点个数为0;
否则, 结点个数为左子树的结点个数 + 右子树的结点个数再 + 1。

int NodeCount(BiTree T){if(T == NULL) return 0;else return NodeCount(T -> lchild)+ NodeCount(T -> rchild) + 1;
}
计算二叉树叶子结点数(补充)
如果是空树,则叶子结点个数为0;
否则,为左子树的叶子结点个数 + 右子树的叶子结点个数。

int LeadCount(BiTree T){if(T == NULL) return 0;//如果是空树返回0if(T -> lchild == NULL && T -> rchild == NULL) return 1; //如果是叶子结点返回1else return LeafCount(T -> lchild) + LeafCount(T -> rchild);
}
5.5.2、线索二叉树
问题:为什么要研究线索二叉树?
当用二叉链表作为二叉树的存储结构时,可以很方便地找到某个结点的左右孩子;但一般情况下,无法直接找到该结点再某种遍历序列中的前驱和后继结点。
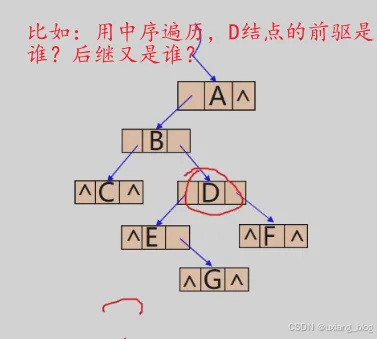
提出问题:如何寻找特定遍历序列中二叉树结点的前驱和后继???
解决的方法:
● 1、通过遍历寻找——费时间
● 2、再增设前驱、后继指针域——增加了存储负担。
● 3、利用二叉链表中的空指针域。
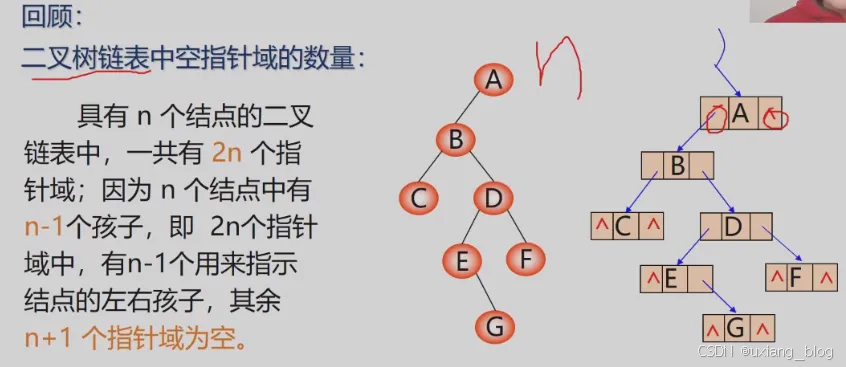
利用二叉链表中空指针域:
如果某个结点的左孩子为空,则将空的左孩子指针域改为指向其前驱;如果某结点的右孩子为空,则将空的右孩子指针域改为指向其后继——这种改变指向的指针称为“线索”加上这了线索的二叉树称为线索二叉树(Threaded Binary Tree),对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化。
线索二叉树
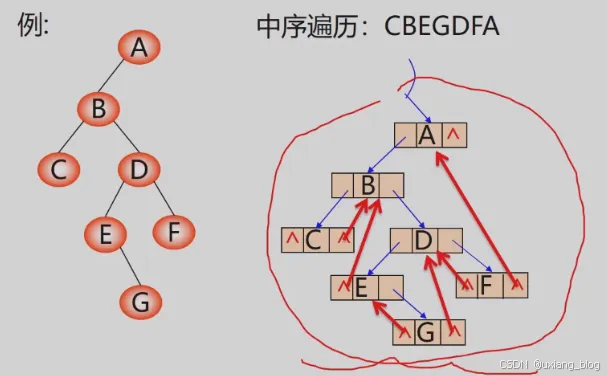
为区分lrchild和rchild指针到底指向孩子的指针,还是指向前驱或者后继的指针,对二叉链表中每个结点增设两个标志域ltag和rtag,并约定:
ltag = 0 lchild 指向该结点的左孩子
ltag = 1 lchild 指向该结点的前驱
rtag = 0 rchild 指向该结点的右孩子
rtag = 1 rchild 指向该结点的后继
这样, 结点的结构为:
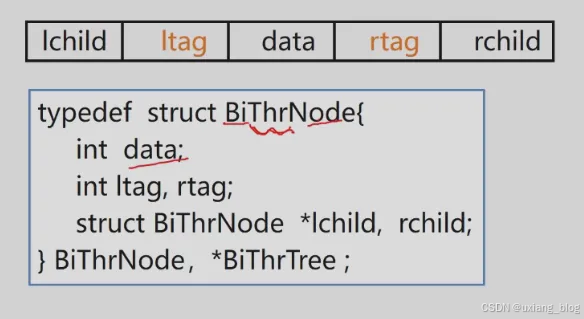
typedef struct BiThrNode{int data;int ltag,rtag;struct BiThrNode *lchild, rchild;
}BiThrNode, *BiThrTree;
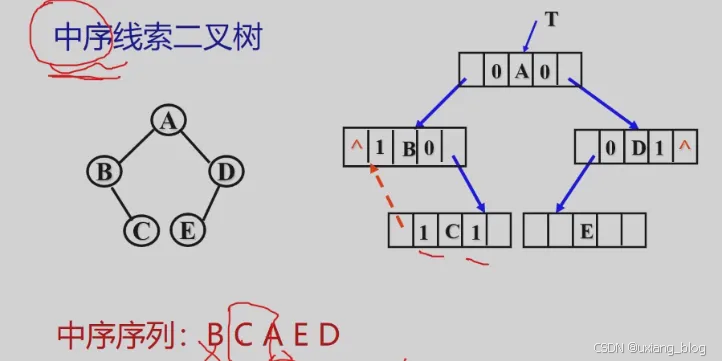
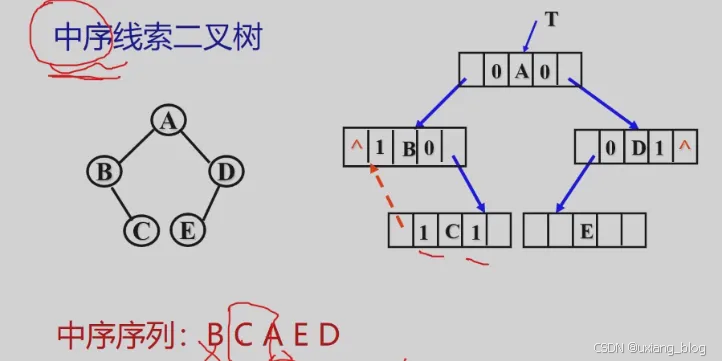
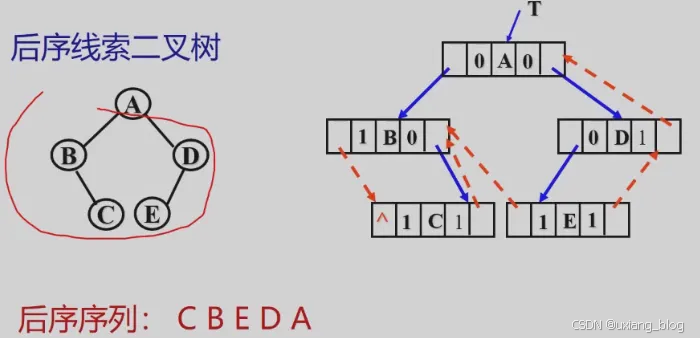
练习
画出以下二叉树对应的中序线索二叉树。
该二叉树中序遍历结果为:H,D,I,B,E,A,F,C,G
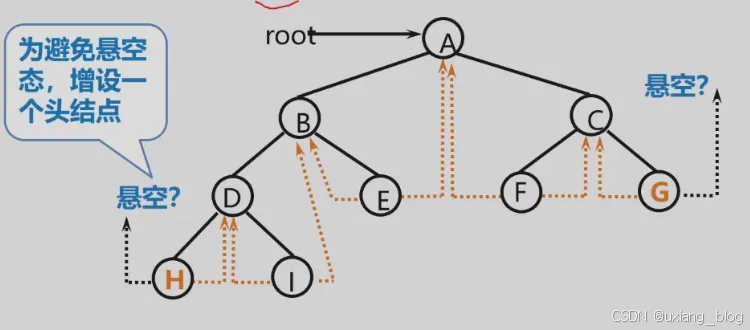
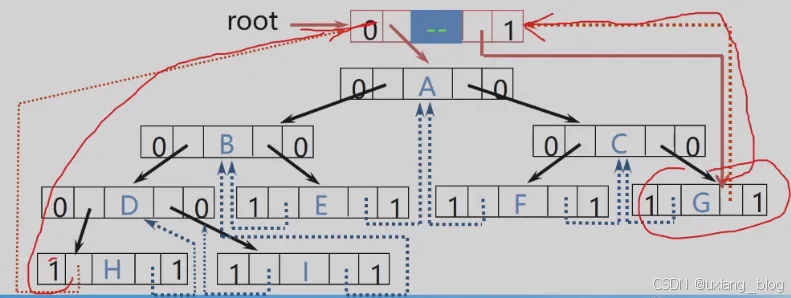
增加一个头结点:
ltag = 0, lchild 指向根结点,
rtag = 1,rchild 指向遍历序列中最后一个结点
遍历序列中第一个结点的lc域和最后一个结点的rc域都指向头结点
5.6、树和森林
5.6.1、常见的树的结构
1、双亲表示法
实现:定义结构数组存放树的结点,每个结点含两个域:
● 数据域:存放结点本身的信息。data
● 双亲域:指示本结点的双亲结点在数组中的位置。parent
特点:找双亲容易,找孩子难。
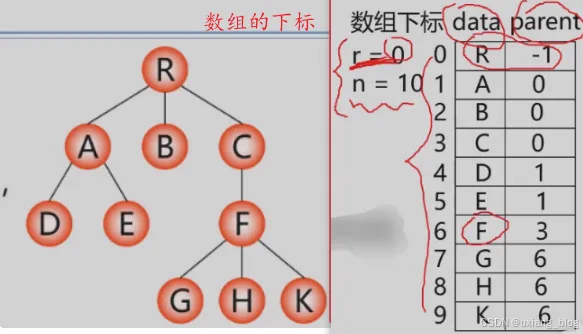
C语言的类型描述:

typedef struct PTNode{TElemType data;int parent; //双亲位置域
}PTNode;#define MAX_TREE_SIZE 100
typedef struct{PTNode nodes[MAX_TREE_SIZE];int r,n; //根结点的位置和结点个数
}PTree;
2、孩子链表
把每个结点的孩子结点列起来,看成是一个线性表,用单链表存储则n个结点有n个孩子链表(叶子的孩子链表为空表)。而n个头指针又组成一个线性表,用顺序表(含个元素的结构数组)存储。
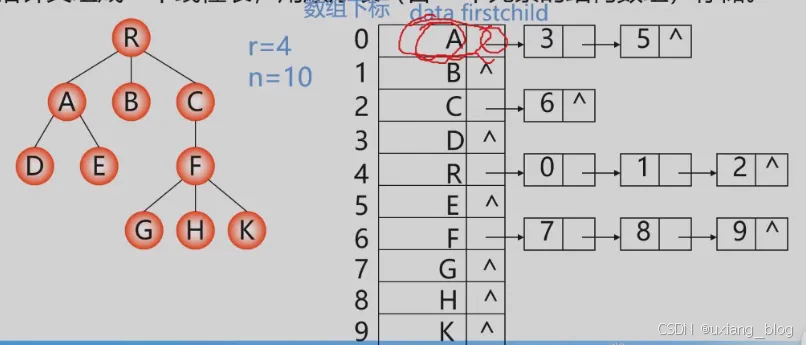
特点:找孩子容易,找双亲难。
C语言的类型描述:

//孩子结点结构
typedef struct CTNode{int child;struct CTNode *next;
}*ChildPtr;//双亲结点结构:
typedef struct{TElemType data;ChildPtr frrstchild;//孩子链表头指针
}CTBox;//树结构
typedef struct{CTBox nodes[MAx_TREE_SIZE];int n,r; //结点数和根结点的位置
}CTree;
带双亲的孩子链表
孩子链表找孩子容易,找双亲难,双亲链表找双亲容易,找孩子难。这里的带双亲的孩子链表结合了二者的优点,既找孩子容易,也找双亲容易。如其名就是在孩子链表中增加一个成员,这个成员是什么呢?就是双亲结点的下标。
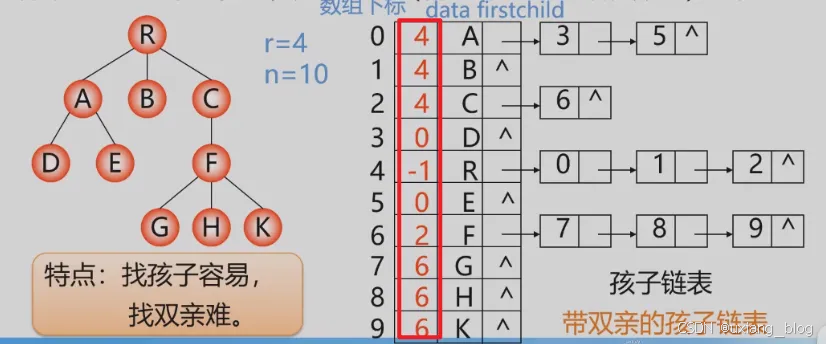
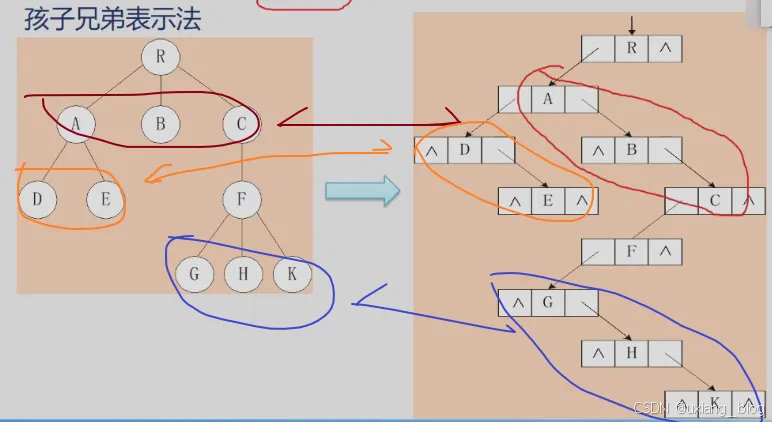
3、孩子兄弟表示法(二叉树表示法,二叉树链表表示法)
实现:用二叉链表作树的存储结构,链表中每个结点的两个指针域分别指向其第一个孩子结点和下一个兄弟结点。
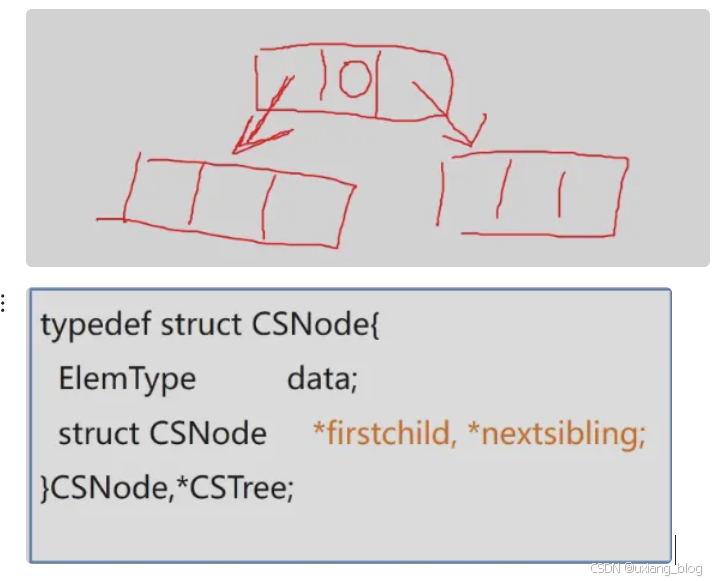
typedef struct CSNode{ElemType data;struct CSNode *firstchild,*nextsibling;
}CSNode,*CSTree;
二叉链表表示法
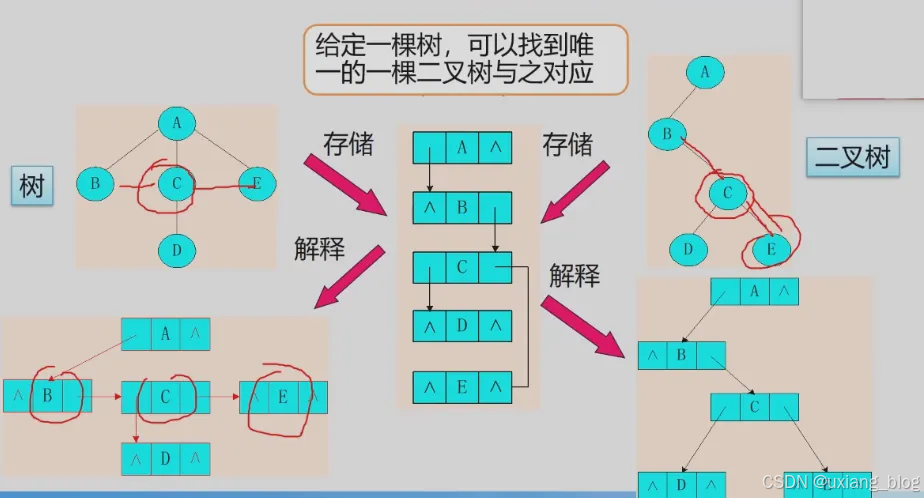
5.6.2、树、森林与二叉树的转换
1、树转换成二叉树
● 将树转换成为二叉树进行处理,利用二叉树的算法来实现对树的操作。
● 由于树和二叉树都可以用二叉链表作存储结构,则以二叉链表作媒介可以导出树与二叉树之间的一个对应关系。
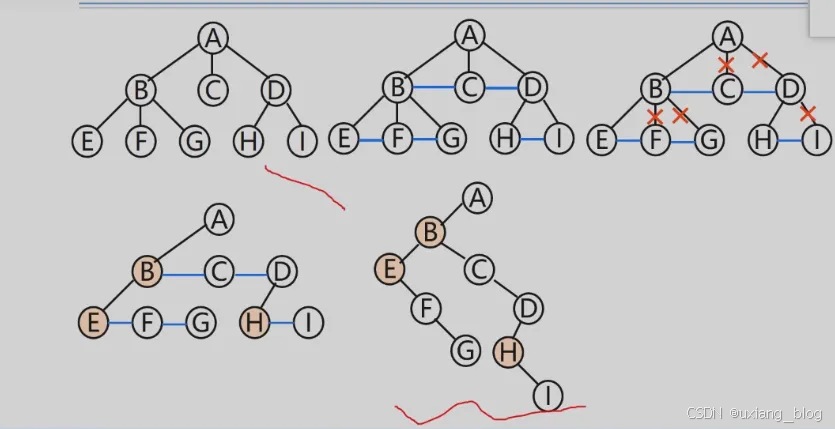
总结规律
● 1、加线:在兄弟之间加一连线
● 2、抹线:对每个结点,除了其左孩子外,去除其与其余孩子之间的关系
● 3、旋转:以树的根结点为轴心,将整个树顺时针转45°。
记为:兄弟相连留长子。(树变二叉树)
例如:将树转换成二叉树
2、二叉树转换成树——逆序操作
● 加线:若p结点是双亲结点的左孩子,则将p的右孩子,右孩子的右孩子…沿分支找到的所有右孩子,都与p的双亲用线连接起来。
● 抹线:抹掉原二叉树中双亲与右孩子之间的连线
● 调整:将结点按层次排列,形成树结构
例如:将二叉树转换成树
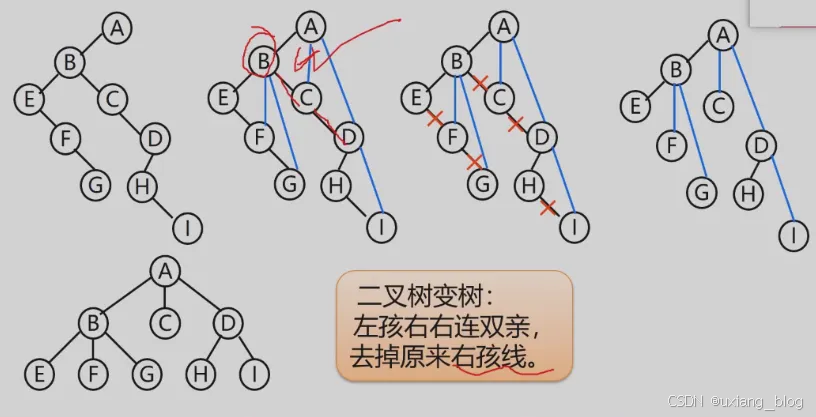
3、森林转化二叉树(二叉树与多棵树之间的关系)
● 1、将各棵树转换成二叉树
● 2、将每棵树的根结点用线相连
● 3、以第一棵树根结点为二叉树的根,再以根结点为轴心,顺时针旋转,构成二叉树型结构。
记作森林变二叉树:树变二叉树根相连。
例如:森林转化成二叉树
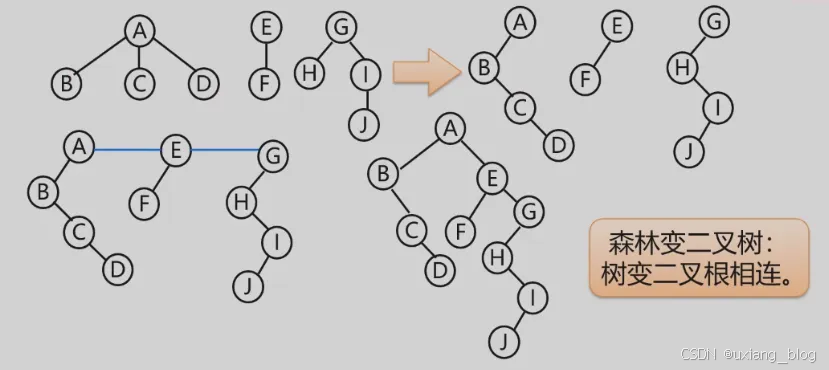
4、二叉树转化森林
● 1、抹线:将二叉树中根结点与其右孩子连线,及沿右分支搜索到的所有右孩子间连线全部抹掉,使之变成孤立的二叉树
● 2、还原:将孤立的二叉树还原成树。
记二叉树变森林:去掉全部右孩线,孤立二叉再还原。
例如:二叉树转换成森林
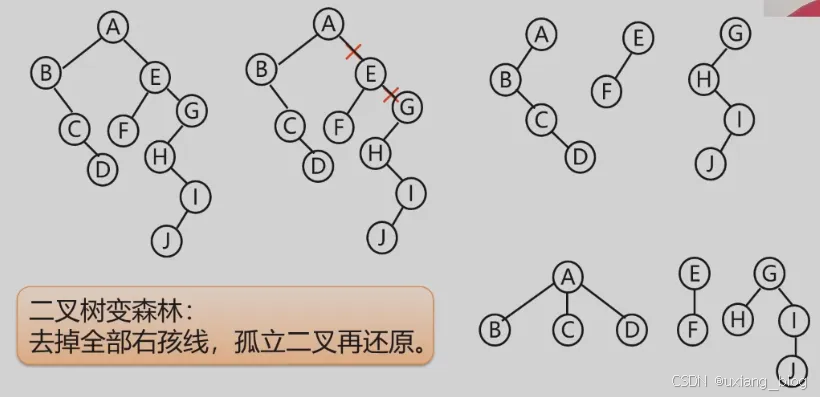
5.6.3、树与森林的遍历
1、树的遍历(三种方式)
● 先根(次序)遍历:若树不空,则先访问根结点,然后依次先根遍历各棵子树。
● 后根(次序)遍历:若树不空,则先依次后根遍历各棵子树,然后方法问根结点。
● 按层次遍历:若树不空,则自上而下,自左至右访问树中每个结点。

2、森林的遍历
将森林看作由三部分构成:
● 1、森林中第一棵树的根结点;
● 2、森林中第一棵树的子树森林;
● 3、森林中其他树构成的森林。
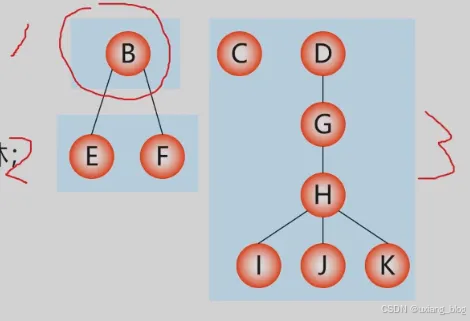
先序遍历:
若森林不空,则
● 1、访问森林中第一棵树的根结点;
● 2、先序遍历 森林中第一棵树的子树森林;
● 3、先序遍历森林中(除第一棵树之外)其余树构成的森林。
即:依次从左到右对森林中的每一棵树进行先根遍历。
中序遍历:
若森林不空,则
● 1、中序遍历森林中第一棵树的子树森林;
● 2、访问森林中第一棵树的根结点;
● 3、中序遍历森林中(除第一棵树之外)其余树构成的森林。
即:依次从左到右对森林中的每一棵树进行后根遍历。
例如:森林的遍历
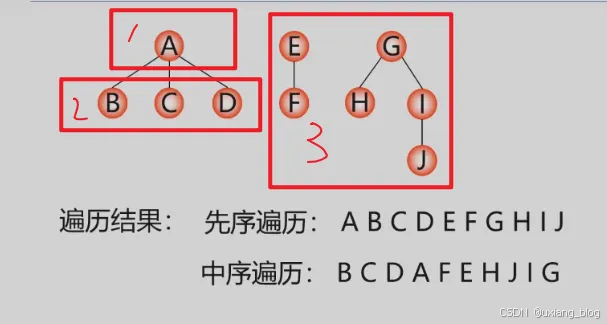
5.7 、哈夫曼树及其应用
哈夫曼:(霍夫曼、赫夫曼)David Albert Huffman (August 9,1925-October 7,1999)。计算机科学的先驱,以他的哈夫曼编码闻名,在他的一生中,对于有限状态自动机,开关电路,异步过程和信号设计有杰出的贡献。
他发明的Huffman编码能够使得我们通常的数据传输数量减少到最小。这个编码的发明和这个算法一样十分引人入胜。1950年,Huffman在MIT的信息理论与编码研究生班学习。Robert Fano教授让学生们自己决定是参加期末考试还是做一个大作业。而Huffman选择了后者,原因很简单,因为解决一个大作业可能比期末考试更容易通过。这个大作业促使了Huffman算法的诞生。
离开MIT后,Huffman来到University of Califrnia的计算系任教,并为此系的学术做出了许多杰出的工作。而他得算法也广泛应用于传真机,图像压缩和计算机安全领域。但是Huffman却从为算法申请过专利或其他相关能够为他带来经济利益的东西,他将他全部的精力放到教学上,以他自己的话来说,“我所要带来的就是我的学生。”
5.7.1 、哈夫曼树的基本概念
【例】编程:将学生的百分制成绩转换为五分制成绩
<60:E 60-90:D 70-79:C 80-89:B 90-100:A
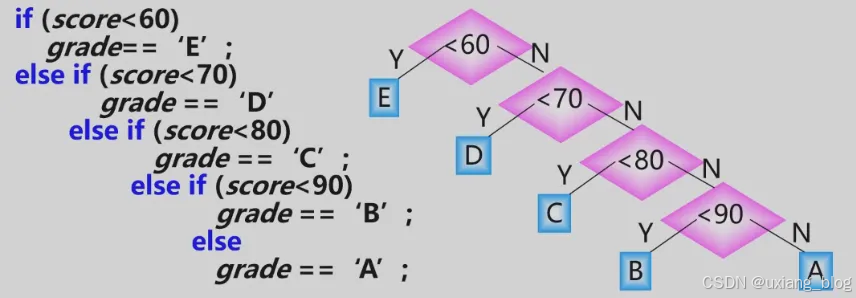
if(score<60) grade == 'E';
else if(score < 70)grade == 'D';
else if(score < 80)grade == 'C';
else if(score < 90)grade == 'B';
else grade == 'A';
判断树:用于描述分类过程的二叉树
例如:如果每的输入量很大,则应考虑程序的操作时间。
若学生成绩数据共10000个:则5%的数据需1次比较,15%的数据需2次比较,40%的数据需3次比较,40%的数据需4次比较,因此10000个数据比较的次数为:10000(15% + 215% + 340% + 410%)= 31500次
怎么才能让输入数据小一些呢?修改如下
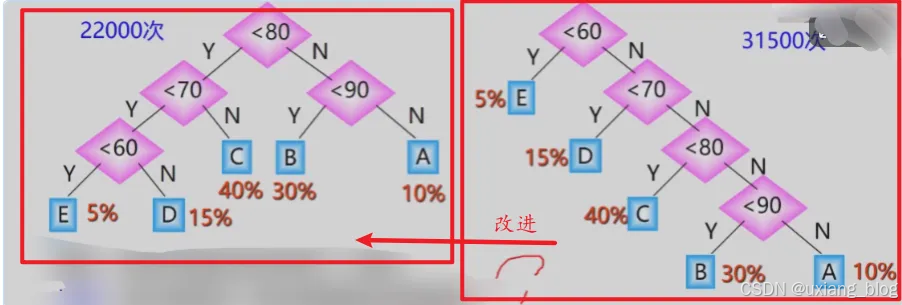
这种10000个数据比较的次数为:10000(320% + 280%)= 22000次
显然:两种判别树的效率是不一样的。问题:能不能找到一种效率最高的判别树呢?——————哈夫曼树(最优二叉树)
路径:从树中一个结点到另一个结点之间的分支构成这个两个结点间的路径。
结点的路径长度:两结点间路径上的分支数。

树的路径长度:从树根到每一个结点的路径长度之和。记作TL。
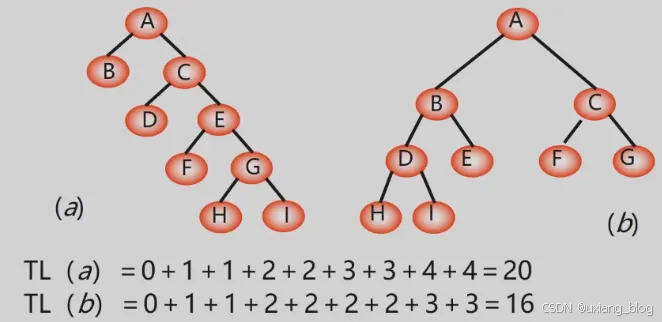
注意:结点数目相同的二叉树中,完全二叉树是路径长度最短的二叉树。
权(weight):将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。比如前面例子中60分以下的同学占5%,这些就是权,就是所占的比例。
结点的带权路径长度:从根结点到该结点之间的路径长度于该结点的权的乘积。
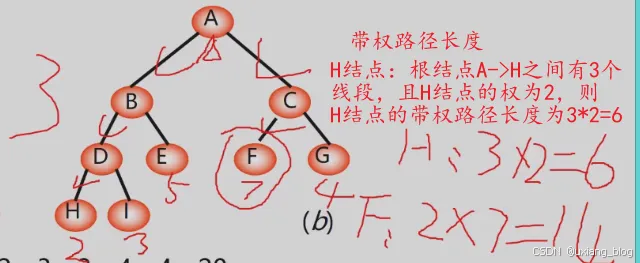
树的带权路径长度:树中所有叶子结点的带权路径长度之和。计算过程如例子所举
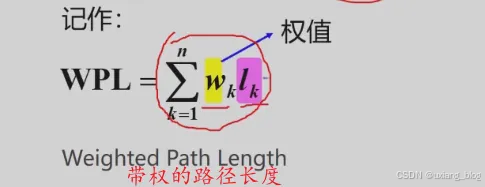
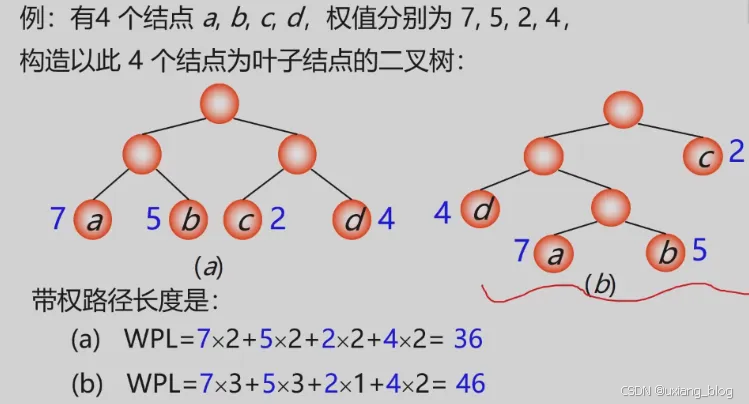
哈夫曼树:最优树 带权路径长度(WPL)最短的树
注意:“带权路径长度最短”是在“度相同“的树中比较而得的结果,因此有最优二叉树、最优三叉树之称等等。
哈夫曼树:最优二叉树 带权路径(WPL)最短的二叉树
因此构造这种树的算法是由哈夫曼教授于1952年提出的,所以被称为哈夫曼树,相应的算法称为哈夫曼算法。
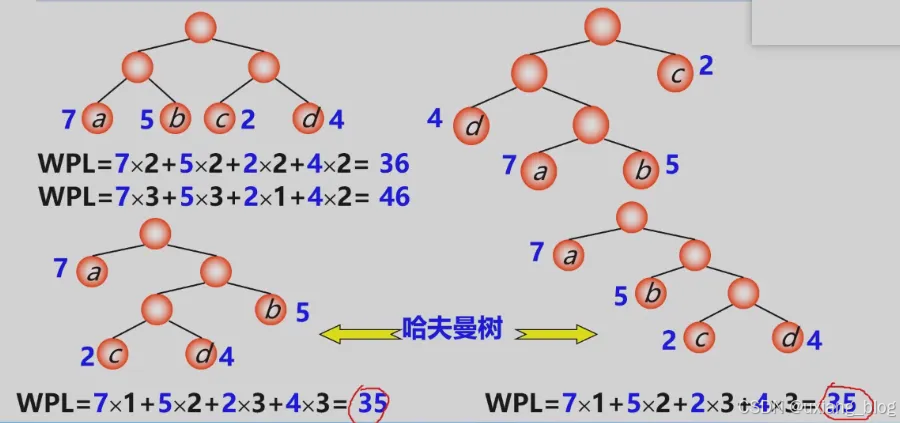
哈夫曼树的特点:
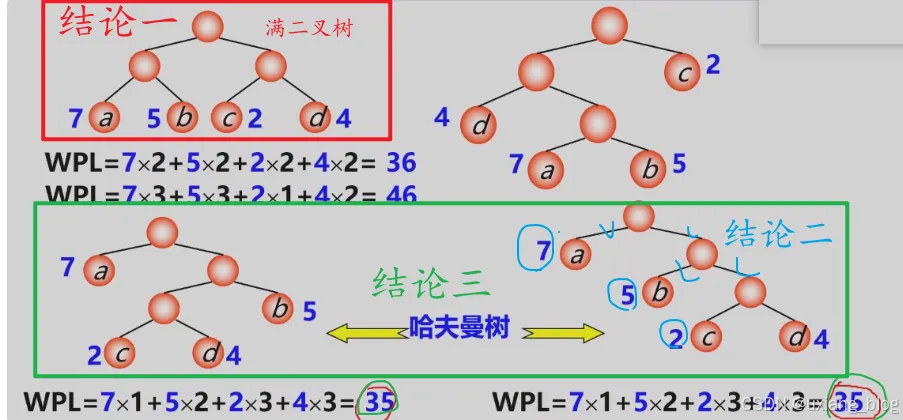
● 结论一:满二叉树不一定是哈夫曼树。
● 结论二:哈夫曼树中权越大的叶子离根越近。
● 结论三:具有相同带权结点的哈夫曼树不唯一。
5.7.2 、哈夫曼树的构造算法
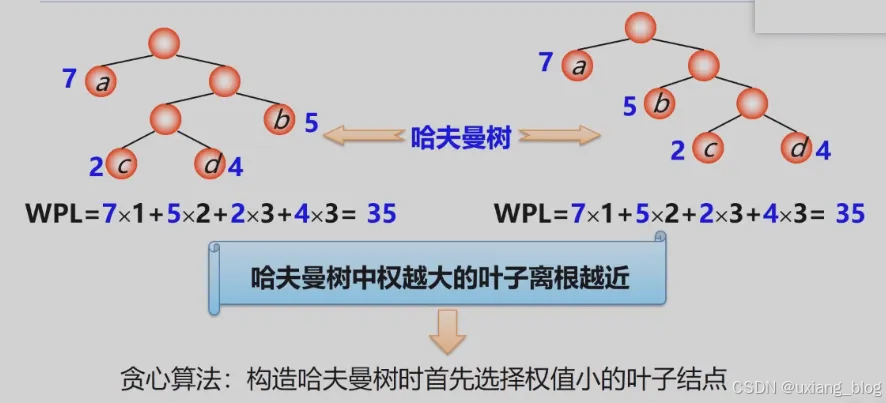
1、哈夫曼算法(构造哈夫曼树的方法):口诀+详细步骤描述
● (1)构造森林全是根:根据n个给定的权值{w1,w2,…,wn}构造n棵二叉树的森林F={T1,T2,…,Tn},其中Ti只有一个带权为wi的根结点。
● (2)选用两小造新树:在F中选取两棵根结点的权值最小的树作为左右子树,构造一棵新的二叉树,且设置新的二叉树的根结点的权值为其左右子树上根结点的权值之和
● (3)删除两小添新人:在F中删除这两棵树,同时将新得到的二叉树加入森林中
● (4)重复2、3剩单根:重复(2)和(3),直到森林中只有一棵树为止,这棵树即为哈夫曼树。
哈夫曼算法口诀:构造森林全是根,选用两小造新树,删除两小添新人,重复2、3剩单根。
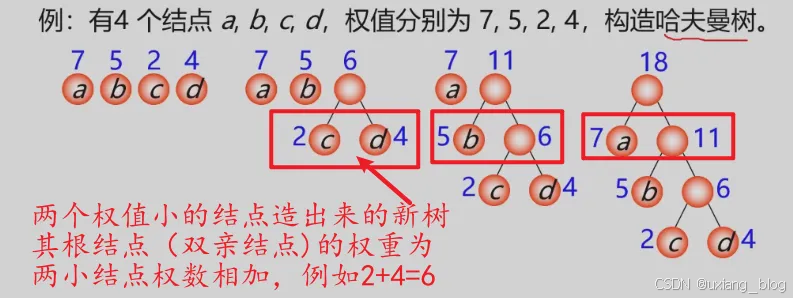
注意:
哈夫曼树的结点的度数为0或2,没有度数为1的结点。
包含n个叶子结点的哈夫曼树中共有2n-1个结点。
包含n棵树的森林要经过n - 1次才能形成哈夫曼树,共产生n - 1个新结点。
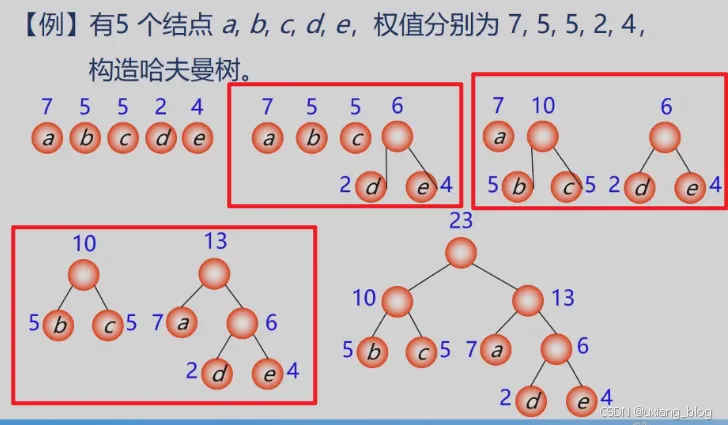
如何构造哈夫曼树
总结:
1、在哈夫曼算法中,初始时有n棵二叉树,要经过n - 1次合并最终形成哈夫曼树。
2、经过n - 1次合并并产生n - 1个新结点,且这n - 1个新结点都是具有两个孩子的分支结点。
可见:哈夫曼树中共有n + n -1 = 2n -1 个结点,且其所有的分支结点的度均不为1。
2、哈夫曼树构造算法的实现
采用顺序存储结构——一维结构数组 HuffmanTree H;
结点类型定义

例如:
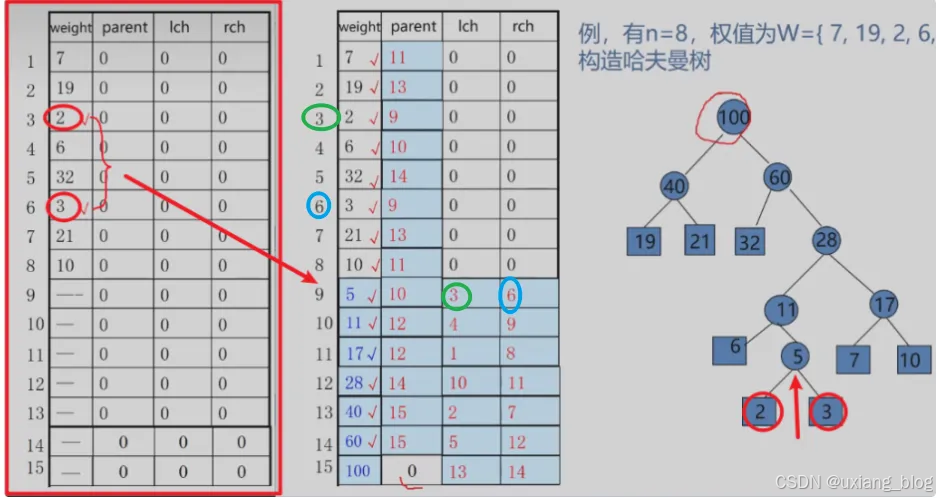
怎么实现哈夫曼算法呢?我们分3步来实现。
第一步,初始化HT [1…2n-1]:Ich = rch = parent = 0;
第二步,输入初始n个叶子结点:置HT[1…n]的weight值;

void CreatHuffmanTree(HuffmanTree HT, int n){//构造哈夫曼树——哈夫曼算法if(n <= 1) return;m = 2*n - 1;//数组共2n - 1个元素HT = new HTNode[m + 1]; //0号单元未用,HT[m]表示根结点for(i = 1; i <= m; ++i){//将2n - 1个元素的lch、rch、parent置为0HT[i].lch = 0;HT[i].rch = 0;HT[i].parent = 0;}for(i = 1; i <= n; ++i) cin >> HT[i].weight;//输入前n个元素的weight值//初始化结束,下面开始建立哈夫曼树
}
第三步,进行以下n -1次合并,依次产生n -1 个结点HT[i],i = n + 1…2n -1:
● (1)在HT[1…i-1]中选两个未被选过(从parent == 0 的结点中选)weight最小的两个结点HT[s1]和HT[s2],s1,s2为两个最小结点下标;
● (2)修改HT[s1]和HT[s2]的parent值:HT[s1].parent = i; HT[s2].parent = i;
● (3)修改新产生的HT[i]:
○ HT[i].weight = HT[s1].weight + HT[s2].weight;
○ HT[i].lch = s1; HT[i].rch = s2;
续

续上
for(i = n + 1;i <= m; i++){//合并产生n - 1个结点——构造Huffman树Select(HT,i - 1,s1,s2 ); //在HT[k](1<= k <= i-1)中选择两个其双亲域为0;//且权值最小的结点,并返回它们在HT中的序号s1和s2HT[s1].parent = i; HT[s2].parent = i; //表示从F中删除s1,s2HT[i].lch = s1; HT[i].rch = s2; //s1,s2分别作为i的左右孩子HT[i].weight = HT[s1].weight + HT[s2].weight; //i的权值为左右孩子权值之和
}
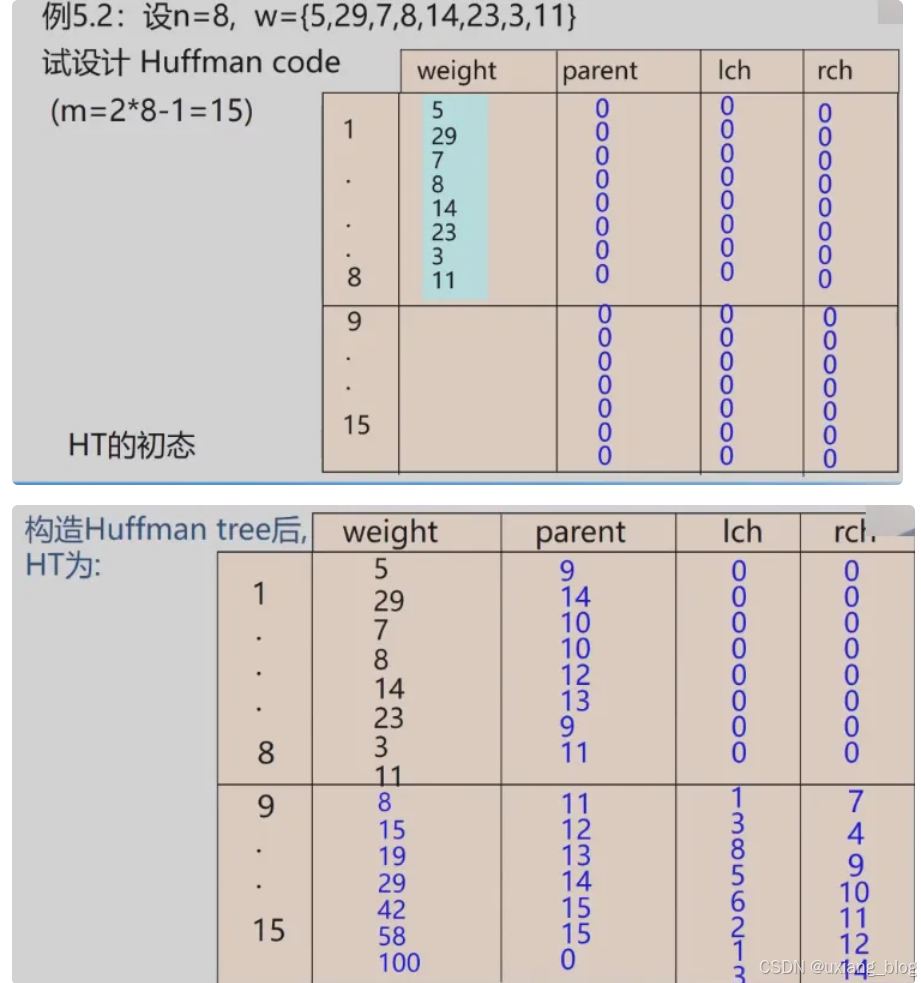
5.7.3 、哈夫曼编码
● 在远程通讯中,要将待传字符转换成由二进制的字符串:
● 设要传送的字符为: ABACCDA
| 若编码为 | 则ABACCDA为 |
| A-00 B-01 C-10 D-11 | 00 01 00 10 10 11 00(中间没有空格,仅是为方便表示) |
若是编码设计长度不等的二进制编码,即让待传字符串中出现次数较多的字符采用尽可能短的编码,则转换的二进制字符串便可能减少。
——————进一步优化
● 设要传送的字符为: ABACCDA
| 若编码为 | 则ABACCDA为 |
| A-0 B-00 C-1 D-01 | 0 00 0 11 01 0(中间没有空格,仅是为方便表示) |
此时0 00 0可以解读为0 0 0 0:AAAA or 00 00 :BB or 0 00 0: ABA等,使得不能还原成原来的样子。这样该如何解决呢?
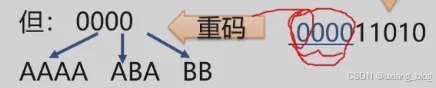
关键:要设计长度不等的编码,则必须使任一字符的编码都不是另一个字符的编码的前缀。——————这种编码称作前缀编码。
问题:什么样的前缀码能使得电文总长度最短? ——哈夫曼编码
方法:
● 1、统计字符集中大每个字符在电文中出现的平均概率(概率越大,要求编码越短)。
● 2、利用哈夫曼树的特点:权越大的叶子离根越近;将每个字符的概率值作为权值,构造哈夫曼树。则概率越大的结点,路径越短。
● 3、在哈夫曼树的每个分支上标上0或1:结点的左分支标0,右分支标1,把从根到每个叶子的路径上的标号连接起来,作为该叶子代表的字符的编码。
例子如下
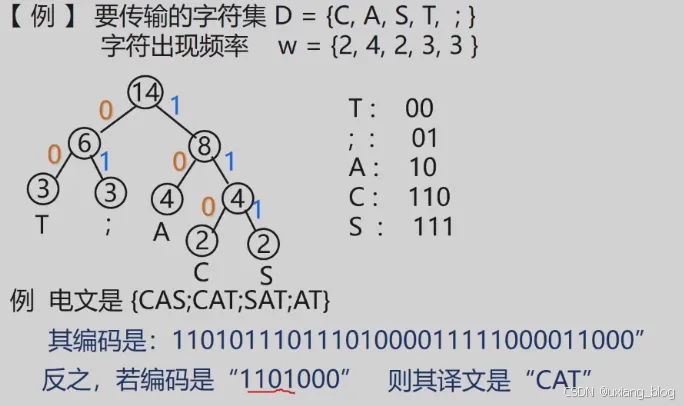
虽然哈夫曼编码是如此智慧,解决了电文最短的问题,但是怎么才能证明哈夫曼码确实不会产生歧义呢,或者说哈夫曼编码的原理是怎么样的?
两个问题:
1、为什么哈夫曼编码保证是前缀编码(个人暂且理解具有唯一性,不会产生歧义)?
因为没有一树叶是另一片树叶的祖先,所以每个叶结点的编码就不可能是其它叶结点编码的前缀。(每个叶子结点的路径唯一,且不同,所以谁也不可能包含谁)
2、为什么哈夫曼编码能够保证字符编码总长最短?
因为哈夫曼树的带权路径长度最短,故字符编码的总长度最短。
总结:哈夫曼编码的性质
● 性质1:哈夫曼编码是前缀码;
● 性质2:哈夫曼编码是最优前缀码。
练习

答案:
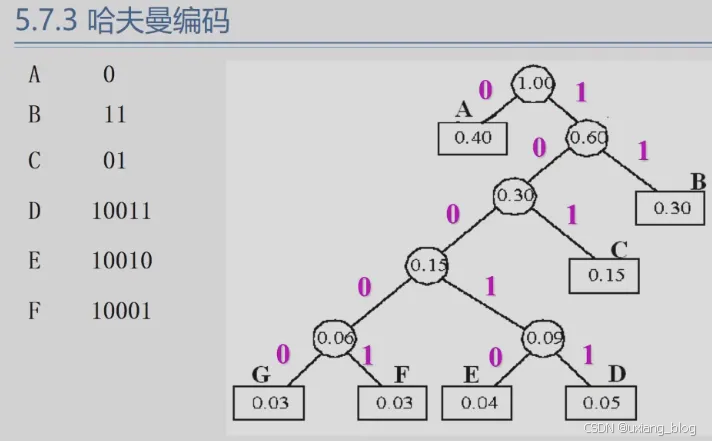
5.7.4 、哈夫曼编码的算法实现
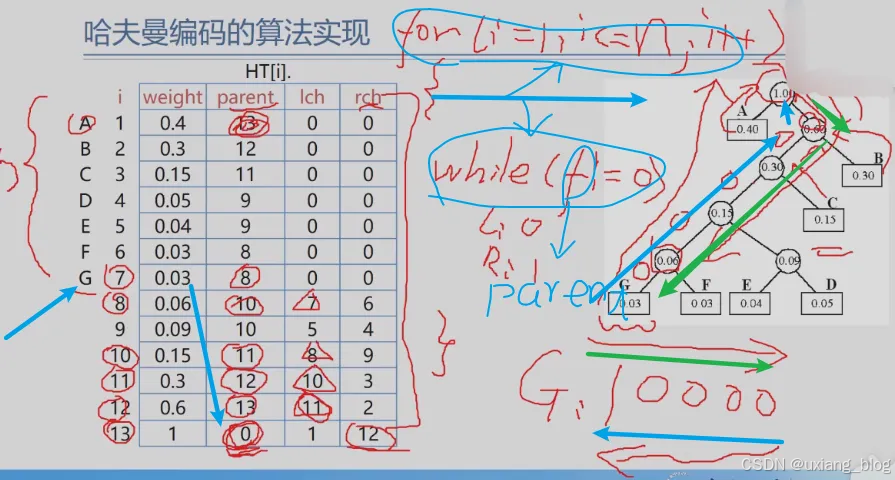
回溯的时候最开始从第n个元素开始,上图中由G开始,沿着路径往根结点走,最后确定根结点了之后,就开始从根结点开始寻找其他结点的位置,编制上其他结点哈夫曼编码。
注解:因为有n个结点,也就是决定了深度为n-1,最长回溯路径为n - 1,我们需要存储回溯中的0,1记录下来,这个长度怎么算了,有n-1个长度就够了,但在存储的数组中下标是从0——>n-1的,所以往往多出一个长度来,由于最长回溯路径只需要n-1个记录的就行,所以把数组中多出的这个用结束字符“\0”恰好合适。
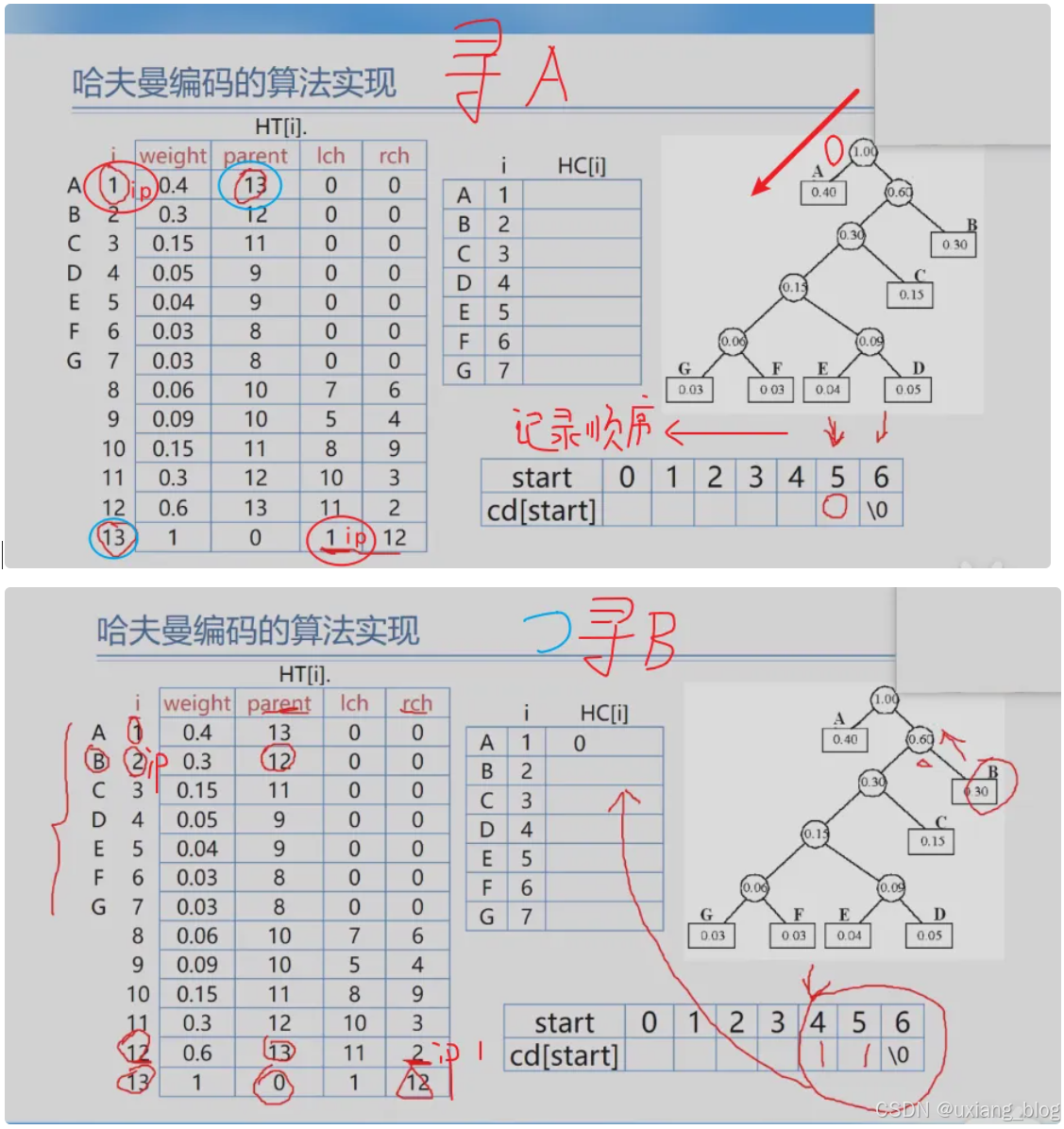
注解:B的ip地址是2,所以找到了它在12号结点的右侧,记为1,根据parent查出12号元素的双亲是13号元素,且在13号元素的右侧,记为1,最后找到13号元素的双亲是0,说明13号元素是根结点,所以遇到根结点结束。至此寻B的哈夫曼编码确定,为11,记录在数组B行。
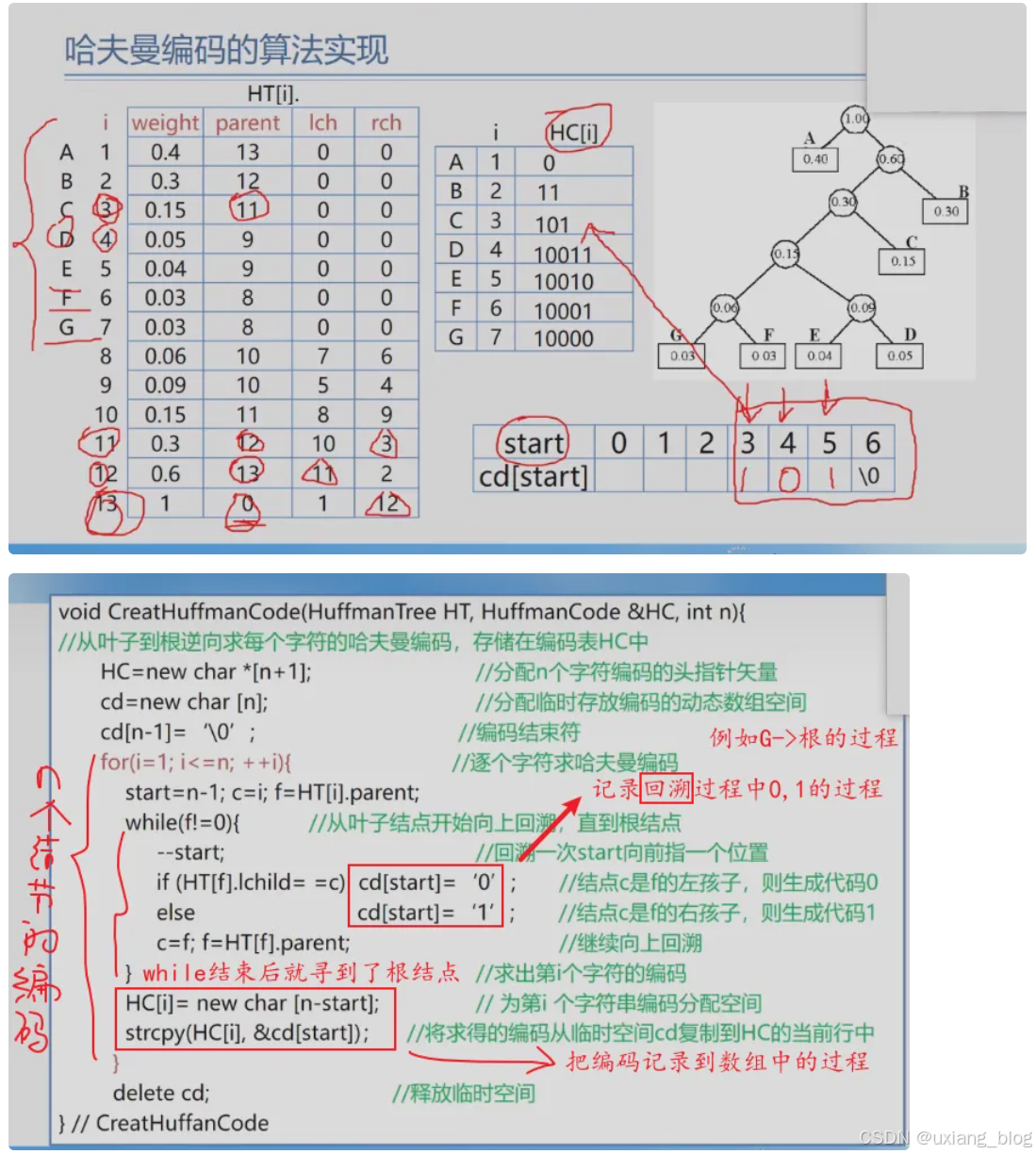
Void CreatHuffmanCode(HuffmanTree HT,HuffmanCode &HC, int n){
//从叶子到根逆向求每个字符的哈夫曼编码,存储在编码表HC中HC = new char *[n + 1];cd = new char[n];cd[n-1] = '\0';for(i = 1; i <= n; ++i){start = n - 1; c = i; f = HT[i].parent;while(f != 0){--start;if(HT[f].lchild == c) cd[start] = '0';else cd[start] = '1';c = f; f = HT[f].parent; }HC[i] = new char[n - start];strcpy(HC[i],&cd[strart]); }delete cd;
}//CreatHuffanCode
5.7.5 、哈夫曼编码的应用举例
1、文件的编码和解码

编码:
● 1、输入各字符及其权值:根据统计在单词中,英语书籍中的字母频率知道了权值。
● 2、构造哈夫曼树——HT[i]:结构数组,有n + n - 1=2n-1个结点,每个结点有权重w,双亲p,左孩子l和r右孩子。
● 3、进行哈夫曼编码——HC[i]:指针数组,
● 4、查HC[i],得到各字符的哈夫曼编码
英语中各字母出现频率
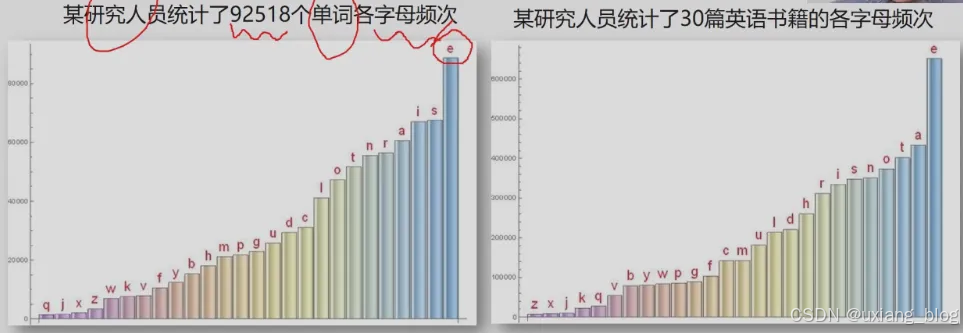
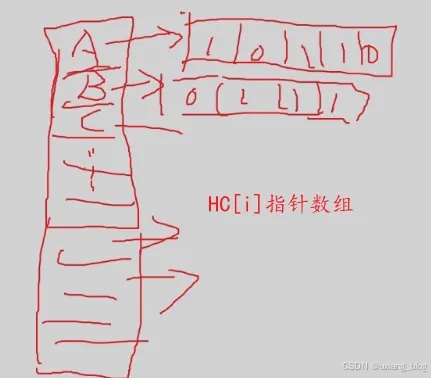
把明文转换成哈夫曼码的过程就叫做编码,利于计算机传输。同样的,也需要将哈夫曼码转换成明文,这叫做解码,方便人们识别穿过来的信息。
解码:
● 1、构造哈夫曼树
● 2、依次读入二进制码
● 3、读入0,则走向左孩子;读入1,则走向右孩子
● 4、一旦达到某叶子时,即可译出字符
● 5、然后再从根出发继续译码,指导结束
2、文件的编码和解码的案例
哈夫曼编码——解码
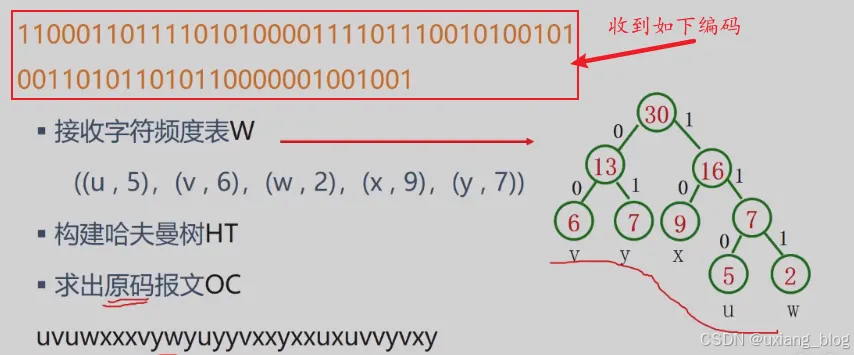
第六章 图
回顾:数据的逻辑结构
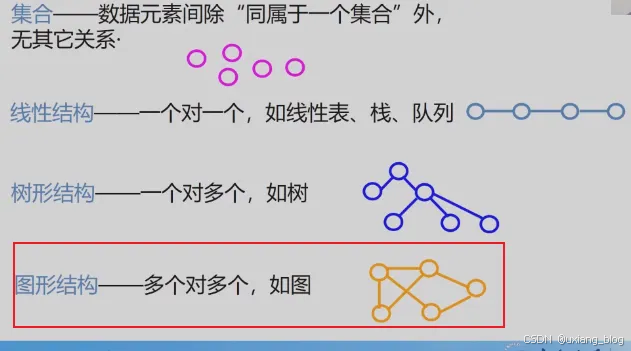
6.1、图的定义和基本术语
6.1.1、图的定义和术语
图:

//图:
G = (V,E)//V:顶点(数据元素)的有穷非空集合;//E:边的有穷集合。
无向图:每条边都是无方向的
有向图:每天条边都是有方向的
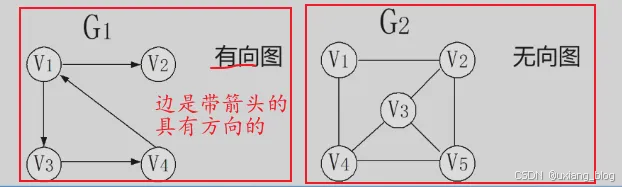
完全图:任意两个点都有一条边相连
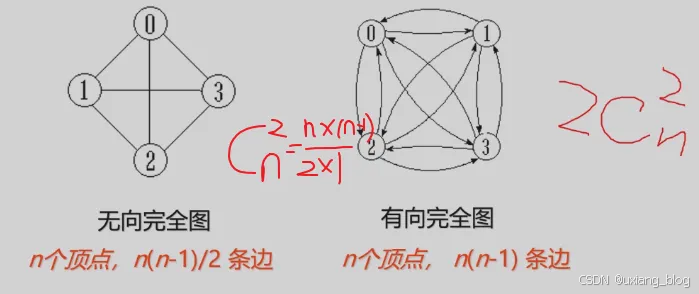
稀疏图:有很少边或弧的图(e<nlogn):e指代边数,n指代顶点个数
稠密图:有较多边或弧的图。
网:边/弧带权的图。:比如a地方到b地,两个地方之间有条路,这个路是10km,这个数值所指代的意义在不同的应用中有不同的体现,这里面指的是路程。
邻接:有边/弧相连的两个顶点之间的关系。
● 存在(vi,vj),则称vi和vj互为邻接点; ()代表没有方向
● 存在<vi,vj>,则称为vi邻接到vj,vj邻接于vi; <>代表有方向,括号中内容前面指向后面
关联(依附):边/弧与顶点之间的关系。
● 存在(vi,vj)/<vi,vj>,则称该边/弧关联于vi和vj
顶点的度与该顶点相关联的边的数目,记为TD(v)。在有向图中,顶点的度等于该顶点的入度与出度之和。顶点v的入度是以v为终点的有向边的条数,记作ID(v)。顶点v的出度是以v为始点的有向边的条数,记作OD(v)。
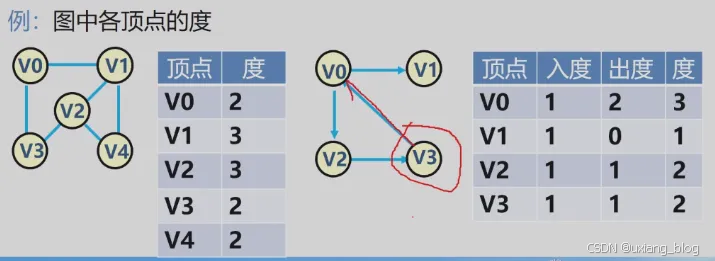
问:当有向图中仅1个顶点的入度为0,其余顶点的入度均为1,此时是何形状?
答:是树!而是一棵有向树!
路径:接续的边构成的顶点序列。
路径长度:路径上边或弧的数目/权值之和。
回路(环):第一个顶点二号最后一个顶点相同的路径。
简单路径:除路径起点和终点可以相同外,其余顶点均不相同的路径。
简单回路(简单环):除路径起点和终点相同外,其余顶点均不相同的路径。
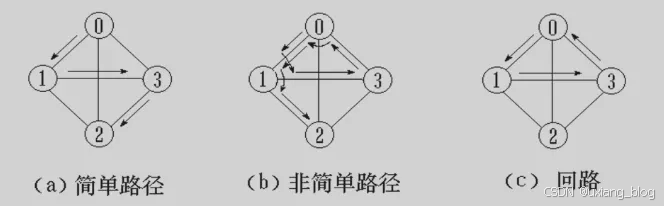
连通图(强连通图):在无(有)向图G=(V,{E})中,若对任何两个顶点v、u都存在从v到u的路径,则称G是连通图(强连通图)。
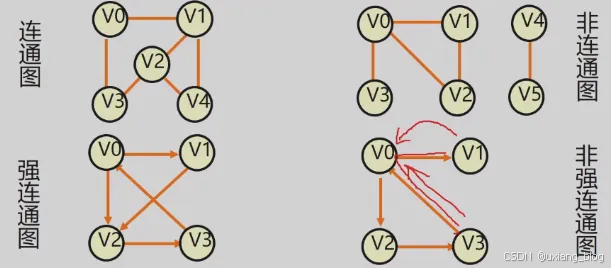
权与网:图中边或所具有的相关数称为权。表明一个顶点到另一个顶点的距离或耗费。待权的图称为网
子图:设有两个图G = (V,{E})、G1 = (V1,{E1}),若V1⊆ V,E1⊆ E,则称G1是G的子图。
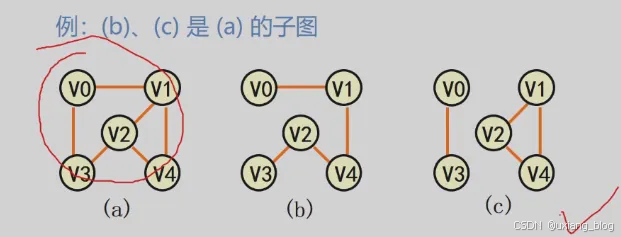
连通分量(强连通分量):
无向图G的极大连通子图称为G的连通分量。todo
极大连通子图的意思:该子图是G连通子图,将G的任何不在该孩子图中的顶点加入,子图不再连通。
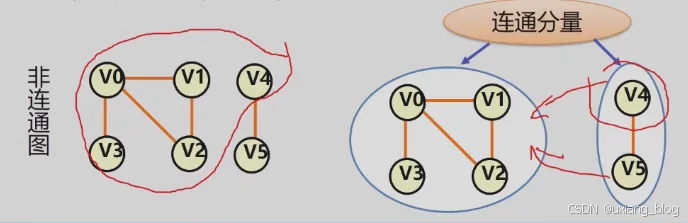
有向图G的极大强连通子图称为G的强连通分量。todo
极大强连通子图意思是:该子图是G的强连通子图,将D的任何不在该图中的顶点加入,子图不再是强连通的。
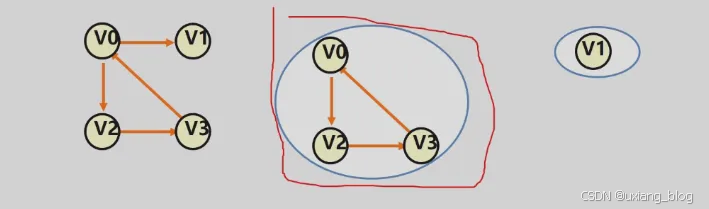
极小连通子图:该子图是G的连通子图,在该子图中删除任何一条边,子图不再连通。
生成树:包含无向图G所有顶点的极小连通子图。todo
生成森林:对非连通图,由各个连通分量的生成树的集合。todo
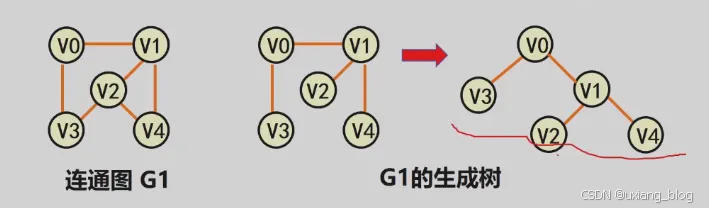
6.2、案例引入
6.2.1、六度空间理论
“六度空间”理论又称作六度分隔(Six Degrees of Separation)理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过六个人,你就能够认识任何一个陌生人。”该理论产生20世纪60年代,由美国心理学家米格伦提出。
6.2.2、六度空间理论验证:
但是米尔格兰姆的理论从来没有得到过严谨的证明,虽然屡屡应验,虽然很多社会学家一致都对其兴趣浓厚,但它只是一种假说。现在,许多科学家对此进行研究,它们都不约而同地使用了网络时代的新型通讯手段对“小世界现象"进行验证。
把六度空间理论种的人际关系网络抽象成一个无向图G。用图G中的一个顶点表示一个人,两个人认识与否代表这两个人的顶点之间是否有一条边来表示。从任一顶点出发用广度优先方法对图进行遍历,统计所有路径长度不超过7的顶点。(当所有路径长度不超过7的顶点占所有顶点的百分比超过了99%就说明得到了验证)
6.3、图的类型定义
//图的抽象数据类型定义如下:
ADT Graph{数据对象V:具有相同特性的数据元素的集合,称为顶点集。数据关系R:R = {VR}VR={<v,w>|<v,w>|v,w∈^p(v,w),<v,w>表示从v到w的弧,P(v,w)定义了弧<v,w>的信息}
}//基本操作
基本操作P:Create_Graph():图的创建操作。初始条件: 无。操作结果: 生成一个没有顶点的空图G。GetVex(G,v): 求图中的顶点v的值。初始条件: 图G存在,v是图中的一个顶点。操作结果: 生成一个没有顶点的空图G。。。。。。//对图的三个重要操作
//建立图
CreateGraph(&G,V,VR)初始条件: V是图的顶点集,VR是图中弧的集合。操作结果i: 按V和VR的定义构造图G。
//对图的两种遍历
FSTraverse(G) 初始条件: 图G存在。操作结果: 对图进行深度优先遍历。
BFTraverse(G)初始条件: 图G存在。操作结果: 对图进行广度优先遍历。
6.4、图的存储结构
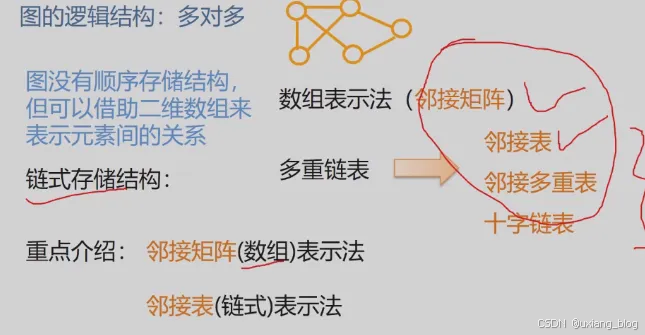
6.4.1、邻接矩阵
数组(邻接矩阵)表示法 todo
建立一个顶点表(记录各个顶点信息)和一个邻接矩阵(表示各个顶点之间的关系)。

无向图的邻接矩阵表示法

特点:
● 两个顶点之间有边就是1,没有边就是0;
● 对角线都为0,这代表顶点自身没有边;
● 分析1:无向图的邻接矩阵是对称的;
● 分析2:顶点i的度 = 第i行(列)中1的个数;
● 特别:完全图(每两个顶点之间都有边)的邻接矩阵中,对角元素为0,其余1。
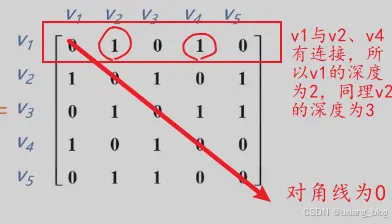
有向图的邻接矩阵表示法
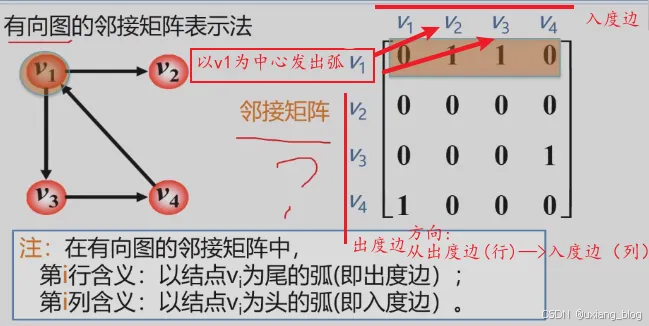
特点:
● 分析1:有向图中邻接矩阵可能是不对称的:因为指向具有方向,从V1指向V2和V2指向V1表示是不一样。
● 分析2:
○ 顶点的出度= 第i行元素之和。
○ 顶点的入度= 第i列元素之和
○ 顶点度= 第i行元素之和+第i行元素之和
网(即有权图)的邻接矩阵表示法
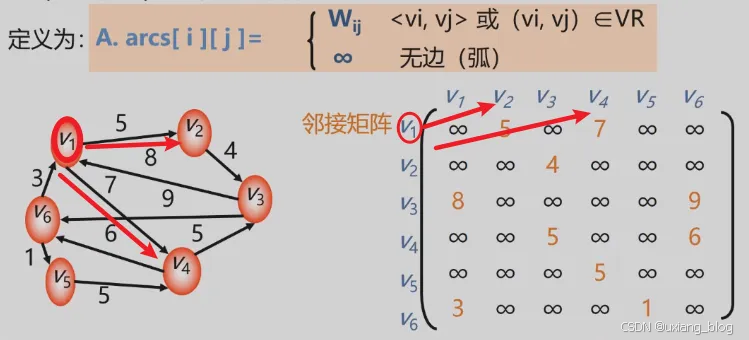
邻接矩阵的存储表示:用两个数组分别存储顶点表和邻接矩阵

#define MaxInt 32767 //表示极大值,即∞,计算机中不能表示无穷这个概念,通常只要是很大的数就表示无穷了
#define MVNum 100 //最大顶点数
typedef char VerTexType;//设顶点的数据类型为字符型
typedef int ArcType; //假设边的权值类型为整型
typedef struct{VerTexType vex[MVNum]; //顶点表ArcType arcs[MVNum][MVNum];//邻接矩阵int vexnum,arcnum; //图当前的顶点数和边数
}AMGraph; //Adiacency Matrix Graph
采用邻接矩阵表示创建无向网
无向网——>无向图
——>有向图
——>有向网
算法思想
● (1)输入总顶点数和总边数。
● (2)依次输入点的信息存入顶点表中。
● (3)初始化邻接矩阵,使每个权值初始化为极大值。
● (4)构造邻接矩阵。
采用邻接矩阵表示法创建无向网

//采用邻接矩阵表示创建无向网
Status CreateUDN(AMGraph &G){//采用邻接矩阵表示法,创建无向网Gcin>>G.vexnum>>G.arcnum; //输入总顶点数,总边数for(i = 0;i < G.vexnum; ++i)cin>>G.vexs[i]; //依次输入点的信息for(i = 0;i < G.vexnum; ++i) //初始化邻接矩阵for(j = 0;j < G.vexnum; ++j)G.arxs[i][j] = MaxInt; //边的权值均置为极大值for(k = 0;k < G.arcnum; ++k){//构造邻接矩阵cin>>v1>>v2>>w; //输入一条边所依附的顶点及边的权值i = LocateVex(G,v1);j = LocateVex(G,v2); //确定v1和v2在G中的位置G.arcs[i][j] = w; //边<v1,v2>的权值置为wG.arcs[j][i] = G.arcs[i][j]; //置<v1,v2>的对称边<v2,v1>的权值为w}//forreturn OK;
}// CreateUDNint LocateVex(AMGraph G,VertexType u){int i;for(i = 0; i < G.vexnum; ++i){if(u == G.vexs[i]){ return i;}}ruturn -1;
}

邻接矩阵——有什么好处?
● 直观、简单、好理解
● 方便检查任意一对顶点间是否存在边
● 方便找任一顶点的所有“邻接点”(有边直接相连的顶点)
● 方便计算任一顶点的“度”(从该点发出的边数为“出度”,指向该点的边数为“入度”)
○ 无向图:对应行(或列)非0元素的个数
○ 有向图:对应行非0元素的个数是“出度”;对应列非0元素的个数是“入度”
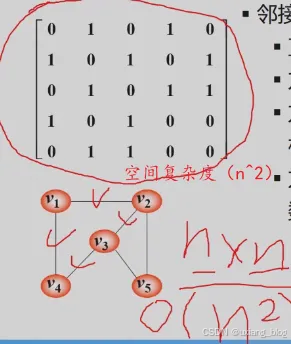
邻接矩阵——有什么不好?
● 不便于增加和删除顶点
● 浪费空间——存稀疏图(点很多而边很少)有大量无效元素
○ 对稠密图(特别是完全图)还是很合算的
● 浪费时间——统计稀疏图中一共有多少条边
6.4.2、链接表
邻接表的表示法(链式)
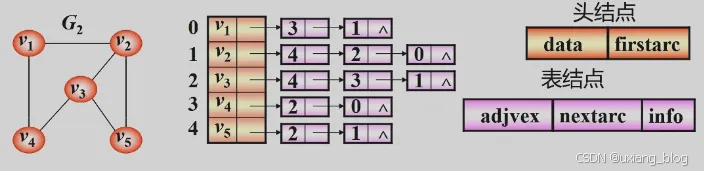
顶点:按编号顺序将顶点数据存储在一维数组中;
关联同一顶点的边(以顶点为尾的弧):用线性链表存储。
头结点:
● data:存放顶点的数据本身。
● firstarc:存储第一个结点地址的指针。
表结点:
● adjvex:邻接点域,存放与Vi邻接的顶点在表头数组中的位置。
● nextarc:链域,指示下一条边或弧。
● info:当前图中是一个网,就可增加info成员,用存放当前边的权值或者其他信息。
无向图
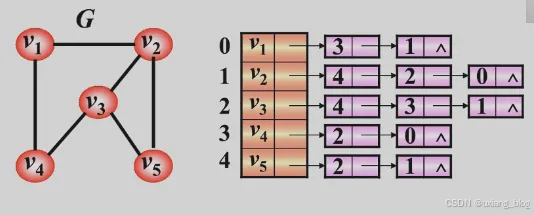
特点:
● 邻接表不唯一
● 若无向图中有n个顶点,e条边,则其邻接表需要n个头结点和2e个表结点,空间复杂度为O(n+2e)。适宜存储稀疏图。
● 无向图中顶点vi的度为第i个单链表中的结点数。
有向图
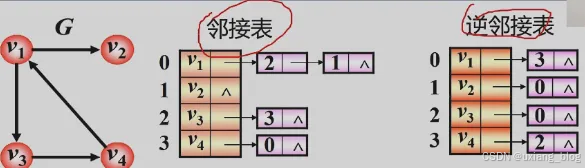
| 邻接表 | 逆邻接表 |
|---|---|
| 顶点vi的出度为第i个单链表中的结点个数。 | 顶点vi的入度为第i个单链表中的结点个数。 |
| 顶点vi的入度为整个单链表中邻结点域值是i-1的结点个数。 | 顶点vi的出度为整个单链表中邻接点阈值是i-1的结点个数。 |
| 特点总结:找出度易,找入度难。 | 特点总结:找入度易,找出度难。 |
练习:已知某网的邻接(出边)表,请画出该网络。
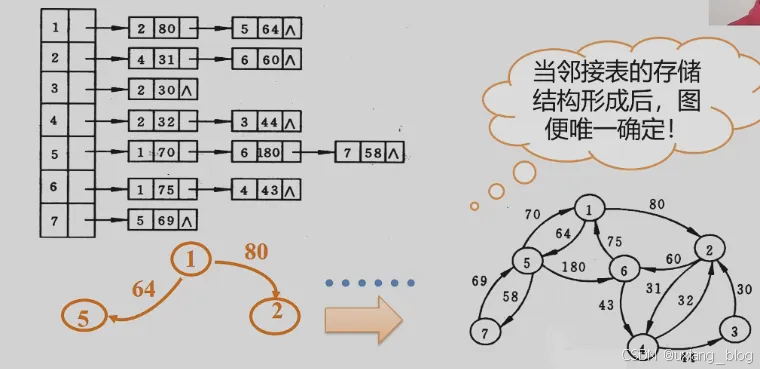
图的邻接表存储表示:
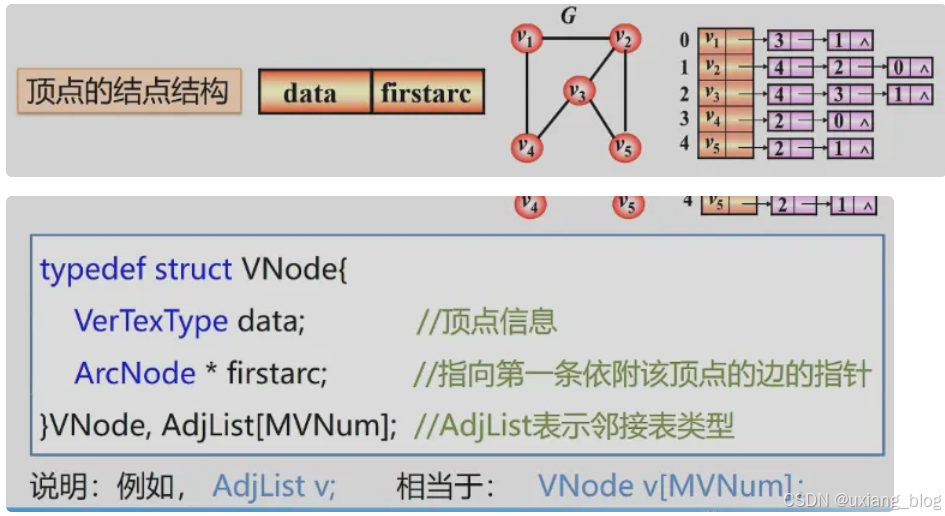
typedef struct VNode{VerTexType data; //顶点信息ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VNode,AdjList[MVNum]; //AdjList表示邻接表类型

#define MVNum 100 //最大顶点数
typedef struct ArcNode{ //边结点int adjvex; //该边指向的顶点的位置struct ArcNode *nextarc; //指向下一条边的指针OtherInfo info; //和边相关的信息
}ArcNode;

typedef struct{AdjList vertices; //vertices --vertex 的复数int vexnum,arcnum; //图得分当前顶点数和弧数
}ALGraph;
邻接表操作举例说明:
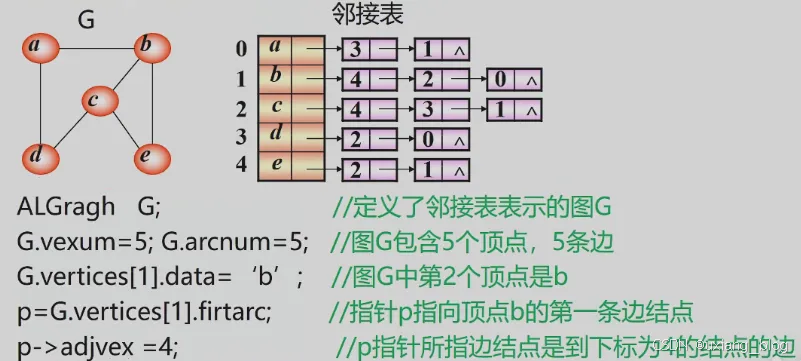
ALGragh G; //定义了邻接表表示的图G
G.vexum = 5; G.arcnum = 5; //图G包含5个顶点,5条边
G.vertices[1].data = 'b'; //图G中第2个顶点是b
p = G.vertices[1].firtarc; //指针p指向顶点b的第一条边结点
p -> adjvex = 4; //p指针所指边结点是到下标为4的结点的边
采用邻接表表示法创建无向网
算法思想
● (1)输入总顶点数和总边数。
● (2)建立顶点表:依次输入点的信息存入顶点表中使每个表头结点的指针域初始化为NULL
● (3)创建邻接表:依次输入每条边依附的两个顶点,确定两个顶点的序号i和j,建立边结点,将此边结点分别插入到vi和vj对应的两个边链表的头部

Status CreateUDG(ALGraph &G){ //采用邻接表表示法,创建无向图Gcin>>G.vexnum>>G.arcnum; //输入总顶点数,总边数for(i = 0;i < G.vexnum; ++i){ //输入个点,构造表头结点表cin>>G.vertices[i].data; //输入顶点值G.vertices[i].firstarc = NULL; } //forfor(k = 0;k < G.arcnum; ++k){ //输入各边,构造邻接表cin>>v1>>v2; //输入一条边依附的两个顶点i = LocateVex(G.v1);j = LocateVex(G,v2);p1 = new ArcNode; //生成一个新的边结点*p1p1 -> adjvex = j; //邻接点序号为jp1 -> nextarc = G.vertices[i].firstarc;G.vertices[i].firstarc = p1; //将新结点*p1插入顶点vi的边表头部p2 = new ArcNode; //生成另一个对称的新的边结点*p2p2 ->adjvex = i; //邻接点序号为ip2 -> nextarc = G.vertices[j].firstarc;G.vertices[j].firstarc = p2; //将新结点*p2插入顶点vj的边表头部}//forreturn OK;
}//CreateUDG
邻接表的特点:

● 方便找任一顶点的所有“邻接点”
● 节约稀疏图的空间
○ 需要N个头指针 + 2E个结点(每个结点至少2个域)
● 方便计算任一顶点的“度”?
○ 对无向图:是的
○ 对有向图:只能计算“出度”;需要构造“逆邻接表”(存指向自己的边),来方便计算“入度”
邻接矩阵与邻接表表示法的关系
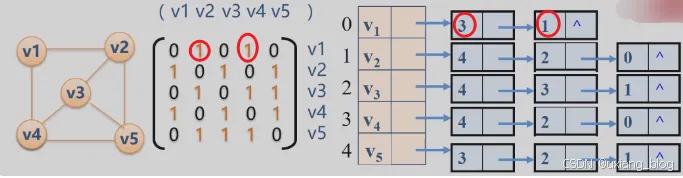
1、联系:邻接表中每个链表对应于邻接矩阵中的一行,邻表中结点个数等于一行中非零元素的个数。
2、区别:
● 对于任一确认的无向图,邻接矩阵式唯一的(行列号与顶点编号一致),但邻接表不唯一(链接次序与顶点编号无关)。
● 邻接矩阵的空间复杂度为O(n2),而邻接表的空间复杂度为O(n + e),有向的是O(n + e),无向的是O(n + 2e)。
3、用途:邻接矩阵多用于稠密图;而邻接表多用于稀疏图。
6.4.3、十字链表和邻接多重表

1、十字链表——用于有向图
十字链表(Orthogonal List)是有向图的另一种链式存储结构。我们也可以把它看成是有向图的邻接表和逆邻接表结合起来形成的一种链表。有向图中的每一条弧对应十字链表中的一个弧结点,同时有向图中的每个顶点在十字链表中对应有一个结点,叫做顶点结点。
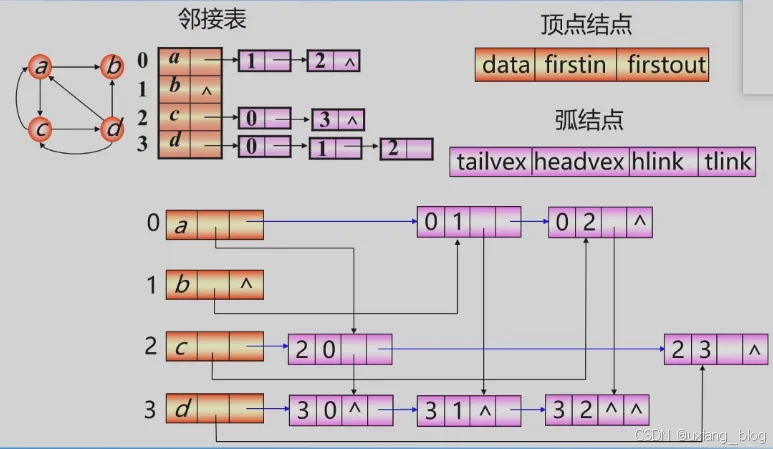
顶点结点
● data:存储头结点数据本身的数据域
● firstin :入度边,第一条入弧
● firstout:出度边,第一条出弧
弧结点
● tailvex:弧尾位置
● headvex:弧头位置
● hlink:弧头相同的下一条弧
● tlink:弧尾相同的下一个弧
2、邻接多重表——用于无向图的另一种链式存储结构
回顾:
邻接表优点:容易求得顶点和边的信息。
邻接表缺点:某些操作不方便(如:删除一条边需找表示此边的两个结点)。
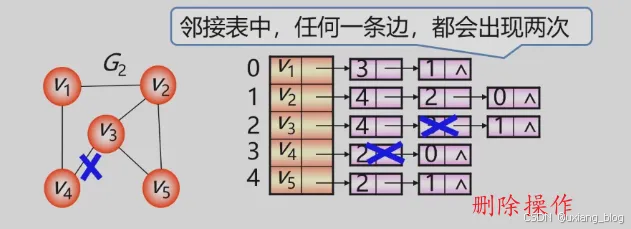
改进成邻接多重表
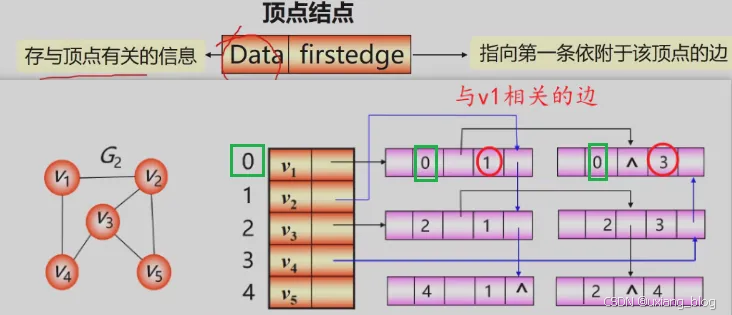
顶点结点
● Data:存与顶点有关的信息
● firstedge:指向第一条依附于该顶点的边
边结点
● mark :标志域标记此边是否被搜过过
● ivex:该边依附的两个顶点在表头数组中位置
● ilink:指向依附于ivex的的下一条边
● jvex:该边依附的两个点点在表头数组中位置
● jlink:指向于依附jvex的下一条边
● info:
6.5、图的遍历
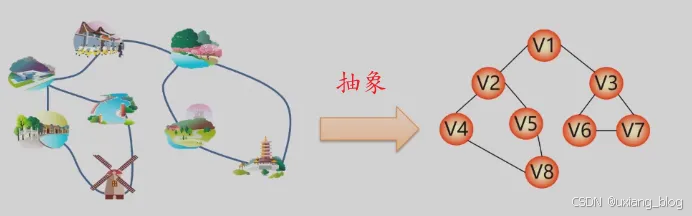
6.5.1、遍历定义:
遍历定义:从已给的连通图中某一顶点出发,沿着一些边访问图中所有的顶点,且每个顶点仅被访问一次,就叫做图的遍历,它是图的基本运算。
遍历实质:找每个顶点的邻接点的过程。
图的特点:图中可能存在回路,且图的任一顶点都可能与其他顶点相通,在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点。
怎么避免重复访问?
解决思路:设置辅助数组visited[n],用来标记每个被访问过的顶点。
● 初始状态visited[i]为0
● 顶点i被访问,改visited[i]为1,防止被多次访问
图常用的遍历:
● 深度优先搜索(Depth_First Search——DFS)
● 广度优先搜索(Breadth_First Search——BFS)
1、深度优先遍历(DFS)——一路走到黑,无路可走了往前退一步。
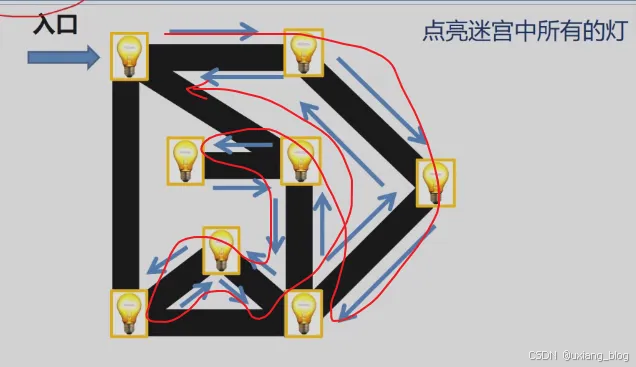
方法:
● 在访问图中某一起始顶点v后,由v出发,访问它的任一邻接顶点w1;
● 再从w1出发访问与w1邻接但还未被访问过的顶点w2;
● 然后再从w2出发,进行类似的访问,…
● 如此进行下去,直至到达所有的邻接顶点都被访问过的顶点u为止。
● 接着,退回一步,退到前一次刚访问过的顶点,看是否还有其他没有被访问的邻接顶点。
● 如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;
● 如果没有就退回一步进行搜索。重复上述过程,直达连通图中所有顶点都被访问过为止。

深度优先搜索遍历算法的实现:
邻接矩阵表示的无向图深度遍历实现:
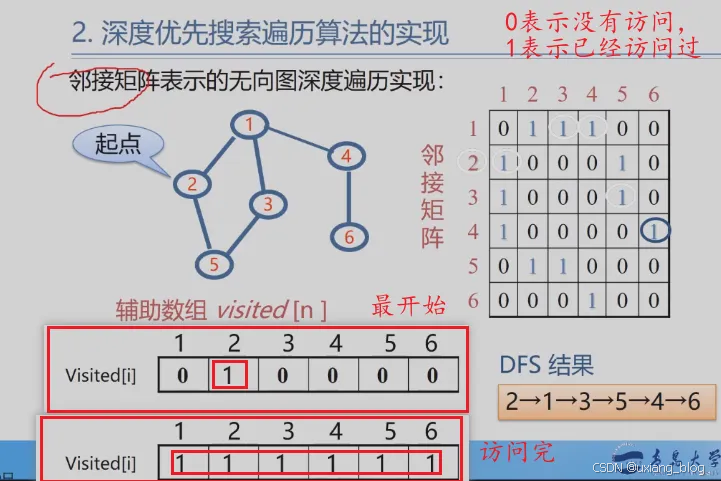
采用邻接矩阵表示图的深度优先搜索遍历

void DFS(AMGraph G,int v){ //图G为邻接矩阵类型cout << v; visited[v] = true; //访问第v个顶点for(w = 0;w < G.vexnum; w++) //依次检查邻接矩阵v所在的行//w是v的邻接点,如果w未访问,则递归调用DFSif(G.arcs[v][w] != 0) && (!visited[w]){DFS(G,w); }
}
DFS算法效率分析
● 用邻接矩阵来表示图,遍历图中每一个顶点都要从头扫描该顶点所在行,时间复杂度为O(n2)。
● 用邻接表来表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为O(n+e)
结论:
● 稠密图适于在邻接矩阵上进行深度遍历;
● 稀疏图适用于在理解表上进行深度遍历。
非连通图的遍历
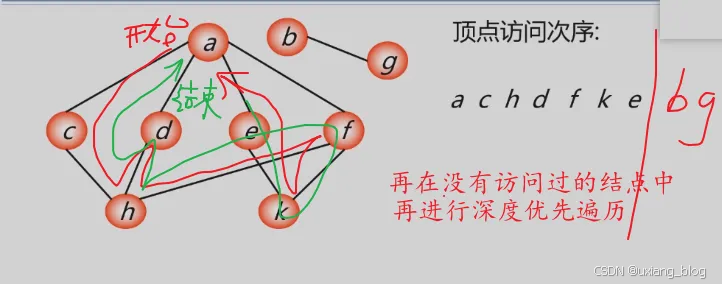
2、广度优先搜素(BFS - Breadth_First Search)
方法:从图中某一结点出发,首先依次访问该结点的所有邻接点vi1,vi2,…,vin再按照这些顶点被访问的先后次序依次访问与它们相邻接的所有未被访问的顶点。重复此过程,直到所有顶点均被访问为止。

非连通图的广度遍历
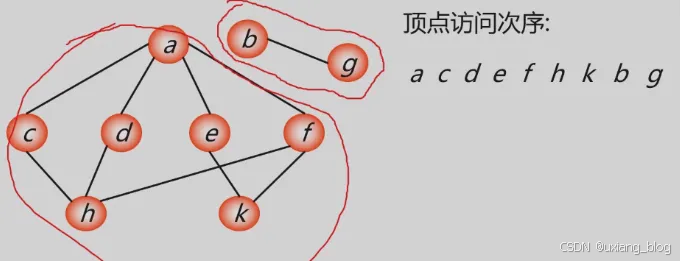
实现:
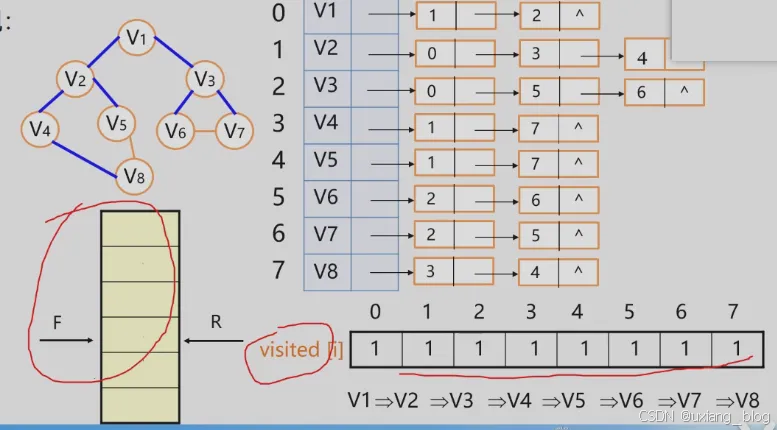
按广度优先非递归遍历连通图G

void BFS(Graph G,int v){ //按广度优先非递归遍历连通图Gcout << v; visited[v] = true; //访问第v个顶点InitQueue(Q); //辅助队列Q初始化,置空EnQueue(Q,v); //v进队while(!QueueEmpty(Q)){ //队列非空 DeQueue(Q,u); //对头元素出队并置为ufor(w = FirstAdjVex(G,u);w >= 0; w = NextAdjVex(G,u,w)){if(!visited[w]){ //w为u的尚未访问的邻接顶点cout<<w;visited[w] = true;EnQueue(Q,w);//w进队} //if}//for}//while
}BFS
BFS算法效率分析
● 如果使用邻接矩阵,则BFS对于每一个被访问到的顶点,都要循环检测矩阵中的整整一行(n个元素),总的时间代价未O(n2)。
● 用邻接表来表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为O(n + e)。
DFS与BFS算法效率比较
● 空间复杂度相同,都是O(n)(借用了栈或队列)
● 时间复杂度只与存储结构(邻接矩阵O(n2)或邻接表O(n+e))有关,而与搜索路径无关。
6.6、图的应用

6.6.1、最小生成树
概念回顾——生成树
生成树:所有顶点均由连接在一起,但不存在回路的图。

生成树的特点:
一个生成树可以有许多棵不同的生成树
所有生成树具有以下共同特点
● 生成树的顶点个数与图的顶点个数相同;
● 生成树是图的极小连通子图,去掉一条边则非连通;
● 一个有n个顶点的连通图的生成树有n-1条边;
● 在生成树中再加一条边必然形成回路;
● 生成树中任意两个顶点间的路径是唯一的;
含n个顶点n-1条边的图不一定是生成树。
无向图的生成树
提示:生成树不是要包含所有的顶点和边嘛,那就对它所有的顶点进行遍历,把访问过程中的边加上便是生成树了。(下图中顶点和蓝色边(访问过程的记录的边)就是得到生成图)。

说明:设图G=(V,E)是个连通图,当从图任一顶点出发遍历图G时,将边集E(G)分成两个集合T(G)和B(G)。其中T(G)是遍历图时所经过的边的集合,B(G)是遍历图时未经过的边的集合。显然,G1(V,T)是图G的极小连子图。即子图G1是连通图G的生成树。
最小生成树
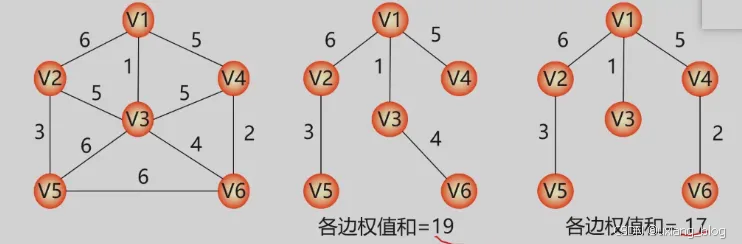
最小生成树:给定一个无向网络,在该网络的所有生成树中,使得各边权值之和最小的那棵生成树称为该网的最小生成树,也叫做最小代价生成树。辅助:让所有顶点相连,又使得连接其顶点的边最少,而且是其边权值最小的就是生成树。
最小生成树的典型用途
● 欲在n个城市间建立通信网,则n个城市应铺n-1条线路;
● 但因为每条线路都会有对应的经济成本,而n个城市最多有n(n-1)/2条线路,那么,如何选择n-1条线路,使得总费用最少呢?

构造最小生成树 Minimum Spanning Tree
构成最小生成树的算法很多,其中多数算法都利用了MST的性质。MST性质:设N = (V,E)是一个连通网,U是顶点集V的一个非空子集。若边(u,v)是一条具有最小权值的边,其中u∈U,v∈V-U,则必存在一棵包含边(u,v)的最小生成树。

MST性质解释:
在生成树的构造过程中,图中n个顶点分属两个集合:
● 已落在生成树上的顶点集:U
● 尚未落在生成树上的顶点集:V-U
接下来则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边。
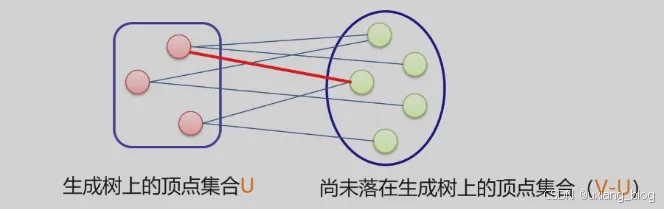
构成最小生成树方法一:普里姆(Prim)算法
算法思想:V中不断加周围权值最小的顶点构造生成树
● 设N=(V,E)是连通网,TE是N上最小生成树中的边的集合。
● 初始令 U={u0},(u0∈V),TE={}。
● 在所有u∈U,v∈V-U的边(u,v)∈E中,找一条代价最小的边(u0,v0)。
● 将(u0,v0)并入集合TE,同时v0并入U。
● 重复上述操作直到U=V为止,则T=(V,TE)为N的最小生成树。
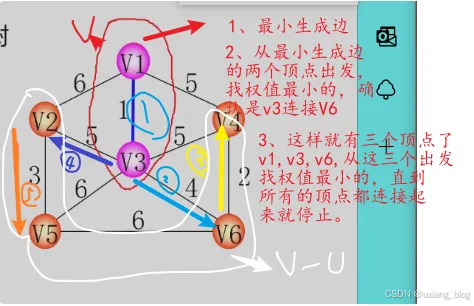
有个疑问,要是寻找过程中遇到这几个顶点都是连接的边的权值相同那么该怎么走呢?
构成最小生成树方法二:克鲁斯卡尔(Kruskal)算法。
算法思想:按照最小权值小大排序不成环构造生成树
● 设连通网 N = (V,E),令最小生成树初始状态为只有n个顶点而无边的连通图T=(V,{}),每个顶点自成一个连通分量。
● 在E中选取代价最小的边,若该边依附的顶点落在T中不同的连通分量上(即:不能形成环),则将此边加入到T中;否则,舍去此边,选取下一条代价最小的边。
● 依次类推,直至T中所有顶点都在同一连通分量上为止。
注意:以此算法构造出来的最小生成树可能不是唯一的。
两种算法比较:
| 算法名 | 普里姆算法 | 克鲁斯卡尔算法 |
|---|---|---|
| 算法思想 | 选择点 | 选择边 |
| 时间复杂度 | O(n2),n为顶点数 | O(eloge),e为边数 |
| 适应范围 | 稠密图 | 稀疏图 |
6.6.2、最短路径
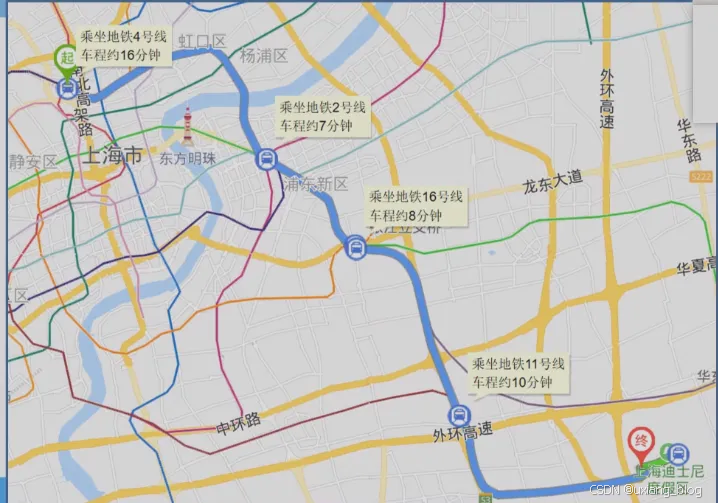
典型用途:交通网络的问题——从甲地到乙地之间是否有公路连通?在有许多条通路的情况下,哪一条路最短?
交通网络用有向图来表示:
顶点——表示地点
弧——表示两个地点有路连通
弧上的权值——表示两地之间的距离、交通或途中所花费的时间等。
如何能够使得一个地点到另一个地点的运输时间最短或运费最省?这个就是一个求两地点间的最短路径问题。
最短路经
问题抽象:在有向网中A点(源点)到达B点(终点)的多条路径中,寻找一条各边权值之和最小的路径,即最短路径。
注意:最短路径与最小生成树不同,路径上不一定包含n个顶点,也不一定包含n-1条边。
两种常见的最短路径问题
第一类问题:两点间最短路径
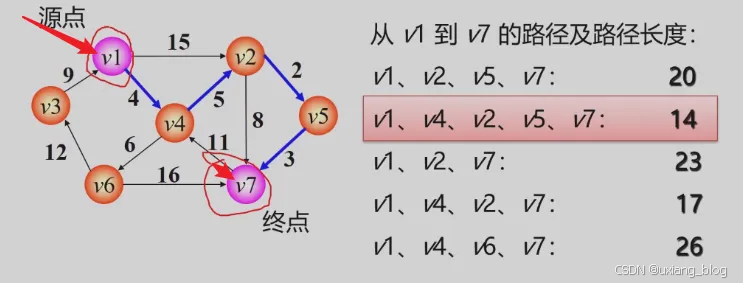
第二类问题:某源点到其他各点最短路径
在这里插入图片描述

两种常见的最短路径问题解决:
● 单源最短路径——用Dijkstra(迪杰斯特拉)算法
● 所有顶点间的最短路径——用Floyd(弗洛伊德)算法
Dijkstra(迪杰斯特拉)算法——单源最短路径
艾兹格.W.迪杰斯特拉(Edsger Wybe Dijkstra)
他是几位影响力最大的计算科学的奠基人之一,少数同时从工程和理论的角度塑造这个新学科的人。他的根本性贡献覆盖了很多领域,包括:编程器、操作系统、分布式系统、程序设计、编程语言、程序验证、软件工程、图论等等。他的很多论文为后人开拓了整个新的研究领域。我们现在熟悉的一些标准概念,比如互斥、死锁、信号量、等,都是Dijkstra发明和定义的。1994年时有人对约1000名计算机科学家进行了问卷调查,选出了38篇这个领域最有影响力的论文,其中有五篇是Dijkstra写的。——"有效的程序员不应该浪费很多时间用于程序调式,他们应该一开始1就不要把故障引入。”
Dijkstra(迪杰斯特拉)算法
● 1、初始化:先找到从源点v0到各终点vk的直到路径(v0,vk),即通过一条弧到达的路径。
● 2、选择:从这些路径中找出一条长度最短的路径(v0,u)。
● 3、更新:然后对其余各路径进行适当调整:若在途中存在弧(u,vk),且(v0,u) + (u,vk) < (v0,vk),则以路径(v0,u,vk)代替(v0,vk)。
在调整后的各条路径中,再找长度最短的路径,依次类推。
Dijkstra(迪杰斯特拉)算法总结:按路径长度依次产生最短路径
1、把V分成两组:
● (1)S:已求出最短路径的顶点的集合。
● (2)T=V - S: 尚未确定最短路径的顶点集合。
2、将T中顶点按最短路径依次递增的次序加入到S中,保证
● (1)从源点v0到S中各顶点的最短路径长度都不大于从v0到T中任何顶点的最短路径长度。
● (2)每个顶点对应一个距离值:
○ S中顶点:从v0到此顶点的最短路径长度。
○ T中顶点:从v0到此顶点的只包括S中顶点作中间顶点的最短路径长度。

Floyd(佛洛伊德)算法——所有顶点间的最短路径
方法一:每个以一个顶点为为源点,重复执行DijKstra算法n次,这个算法的时间复杂度为O(n3):n*O(n2)。
方法二:弗洛伊德算法
算法思想:
● 逐个顶点试探
● 从vi到vj的所有可能存在的路径中
● 选出一条长度最短的路径。
例子:采用Floyd算法,求图中各顶点之间最短路径
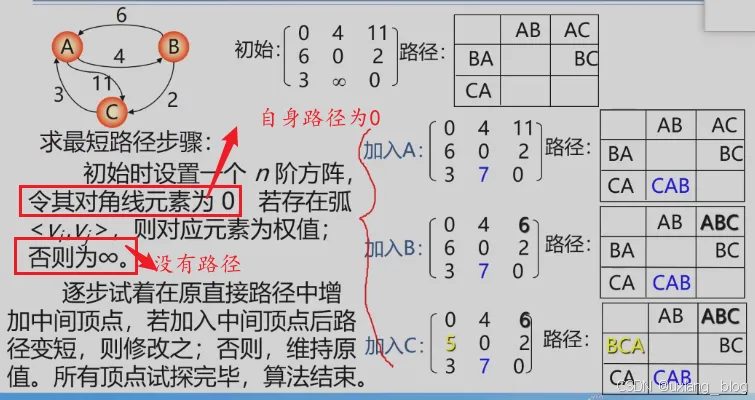
6.6.3、扩扑排序
有向无环图:无环的有向图,简称DAG图(Directed Acycline Graph)
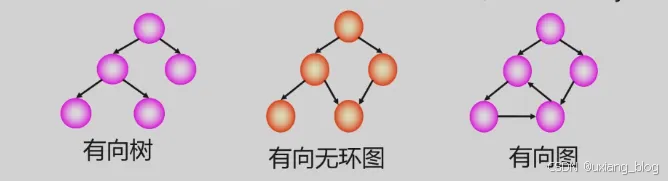
有向无环图常用来描述一个工程或系统的进行过程。(通常把计划、施工、生产、程序流程等当成一个工程)。
一个工程可以分为若干个子工程,只要完成了这些子工程(活动),就可以导致整个工程的完成。
有向无环图的应用:
AOV网:——括扑排序
用一个有向图表示一个工程的各子程及其相互制约的关系,其中以顶点表示活动,弧表示活动之间的优先制约关系,称这种有向图为顶点表示活动的网,简称AOV网(Activity On Vertex network)。
AOE网:——关键路径
用一个有向图表示一个工程的各子工程及其相互制约的关系,以弧表示活动,以顶点表示活动的开始或结束事件,称这种有向图为边表示活动的网,简称为AOE网(Activity On Edge)。
拓扑排序例:排课表
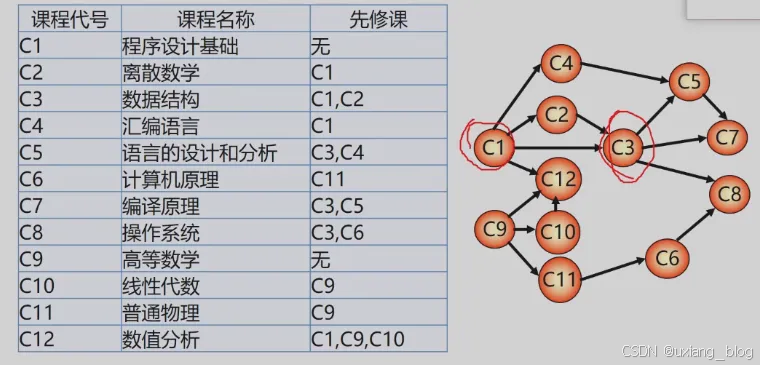
辅助:这种课程不能乱学,必须先要学啥,然后再学啥的先后顺序,把先后顺序用边表示的就是AOV网。
AOV网的特点:
● 若从i到j有一条有向路径,则i是j的前驱;j是i的后继。
● 若<i,j>是网中有向边,则i是j的直接前驱;j是i的直接后继。
● AOV网中不允许有回路,因为如果回路存在,则表明某项活动以自己为先决条件,显然这是荒谬的。
接着有个问题便来了,如何判别AOV网中是否存在回路?
拓扑排序
在AOV网没有回路的前提下,我们将全部活动(顶点)排序成一个线性序列,使得若AOV网中有弧<i,j>存在,则在这个序列中,i一定排在j的前面,具有这种性质的线性序列称为拓扑有序序列,相应的拓扑有序序列的算法称为拓扑排序。
拓扑排序的方法——如何进行拓扑排序?
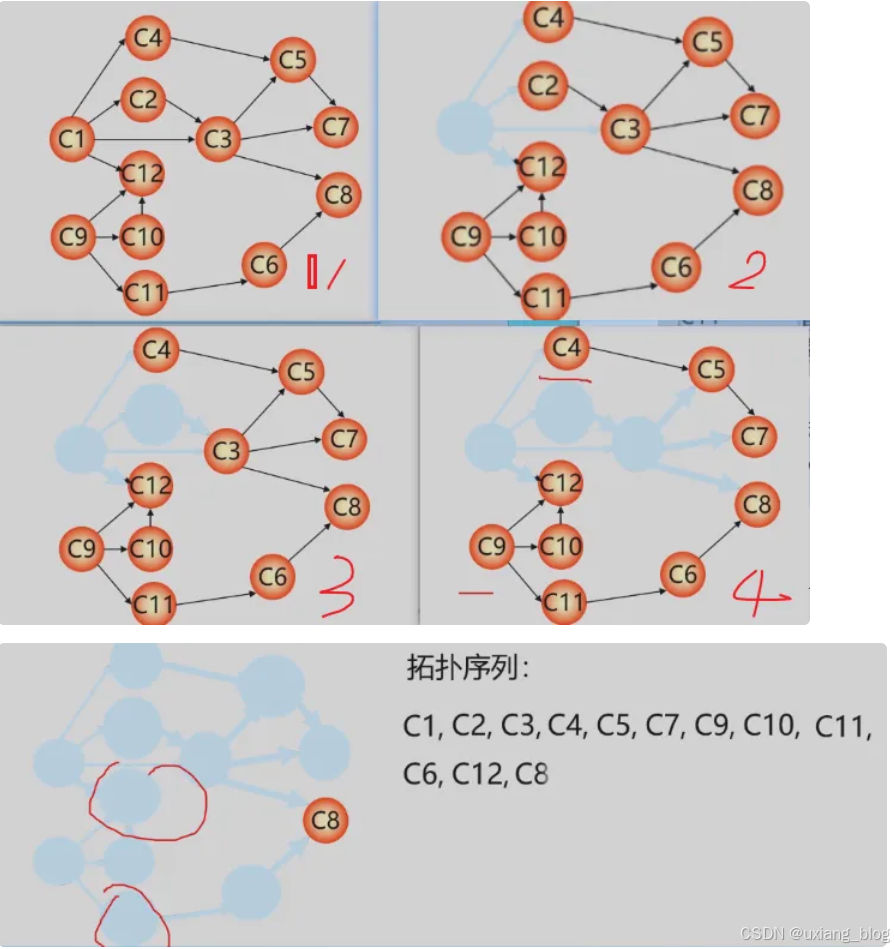
● 在有向图中选一个没有前驱的项目且输出之。
● 从图中删除该顶点和所有以它为尾的弧。
● 重复上述两步,直至全部顶点均已输出;或者当图中不存在无前驱的顶点为止。
注意:一个AOV网的拓扑序列不是唯一的,但是其中的一些先后顺序是不能颠倒的。
拓扑排序的一个重要应用:
检测AOV网中是否存在环方法:
对有向图构造的拓扑有序序列,若网中所有顶点都在它的扩扑有序序列中,则该AOV网必定不存在环。
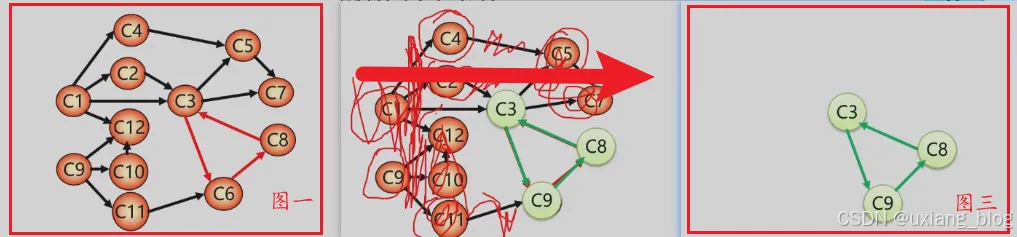
对拓扑排序是否真能检测AOV网中是否存在环方法判别证伪的说明:根据拓扑排序的方法,即遇到没有前驱的就删除其顶点以及其后继,直到最后会发现这个环,而这三个顶点选不出来意味着拓扑排列中缺少C3、C8和C9,说明有环,反证法得到拓扑排序确实能验证AOV网存在环这一结论。
6.6.4、关键路径
举例说明这个概念:有些事情的发生是有先后顺序的,必须先干啥后才能干啥,但是在遇到截止日期时,我们怎么排序使得这些活动所用的时间最少,且能对这些活动做出评估呢?
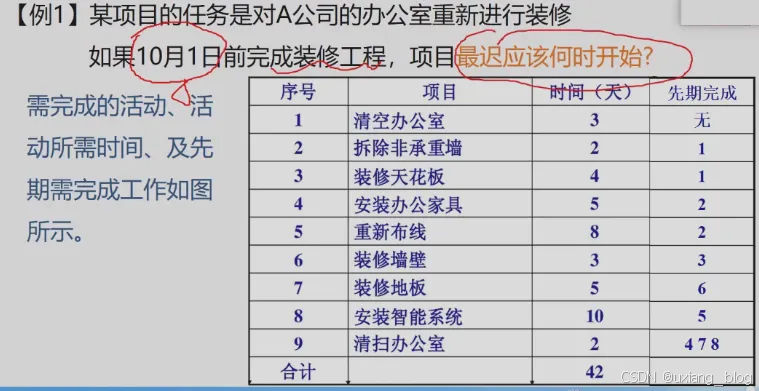
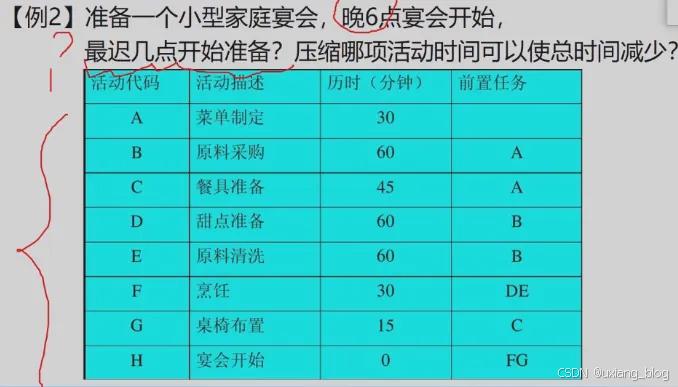
把工程计划表示为:边表示活动的网络,即AOV网,用顶点表示事件,弧表示活动,弧的权表示活动持续时间。
事件:表示在它之前的活动已经完成,在它之后的活动可以开始。
—————————————引入AOE中关键路径解决这些活动所用的时间最少的问题
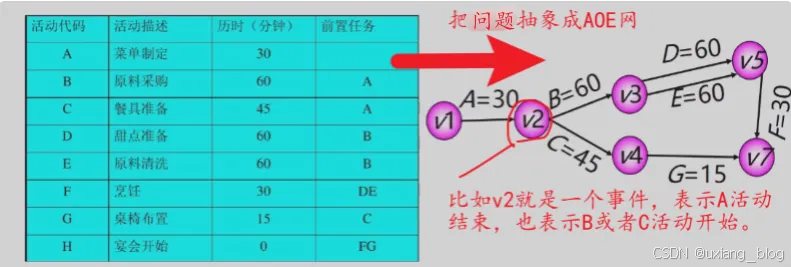
已知AOE网,怎么通过关键路径解决问题?如下例题说明。todo
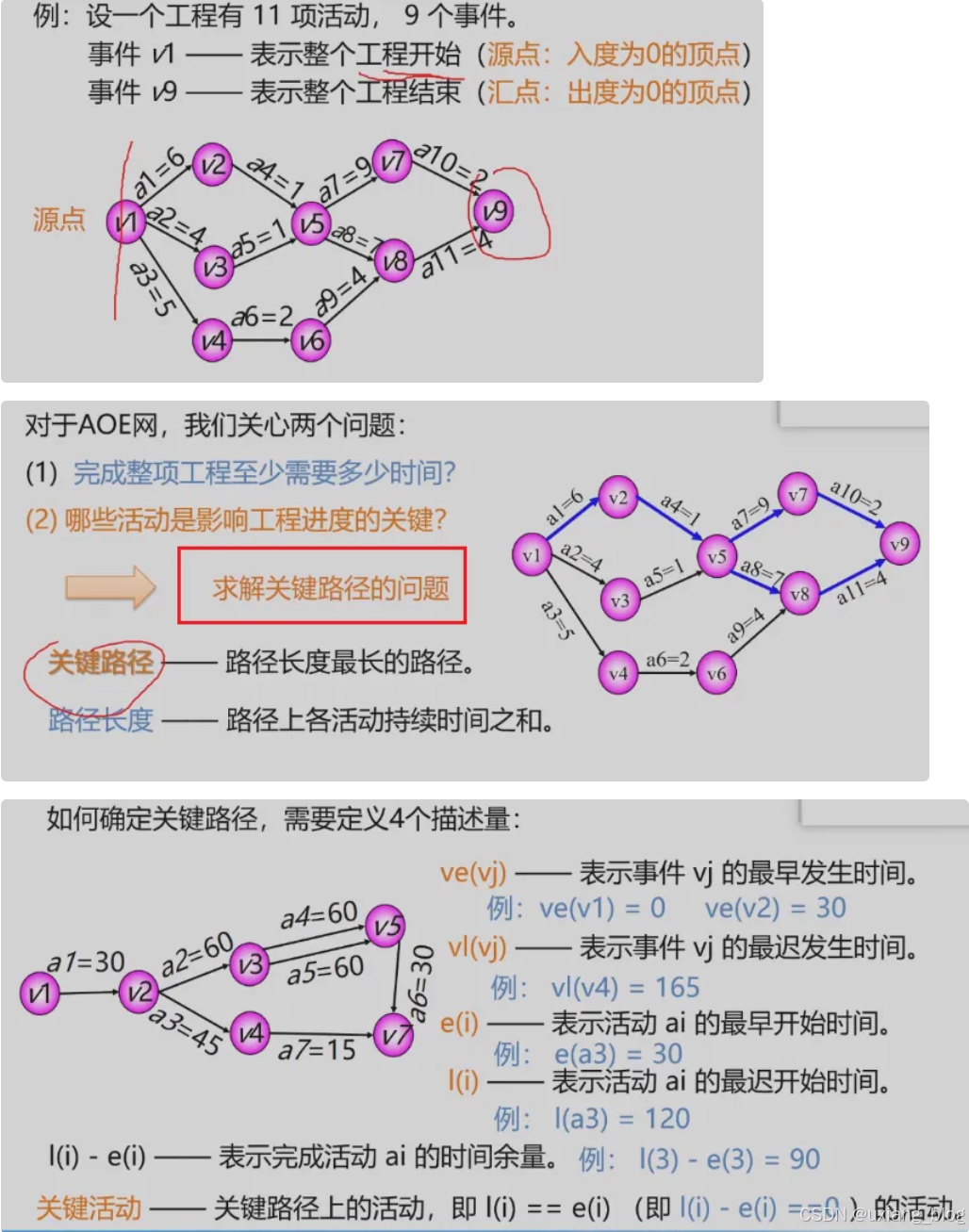
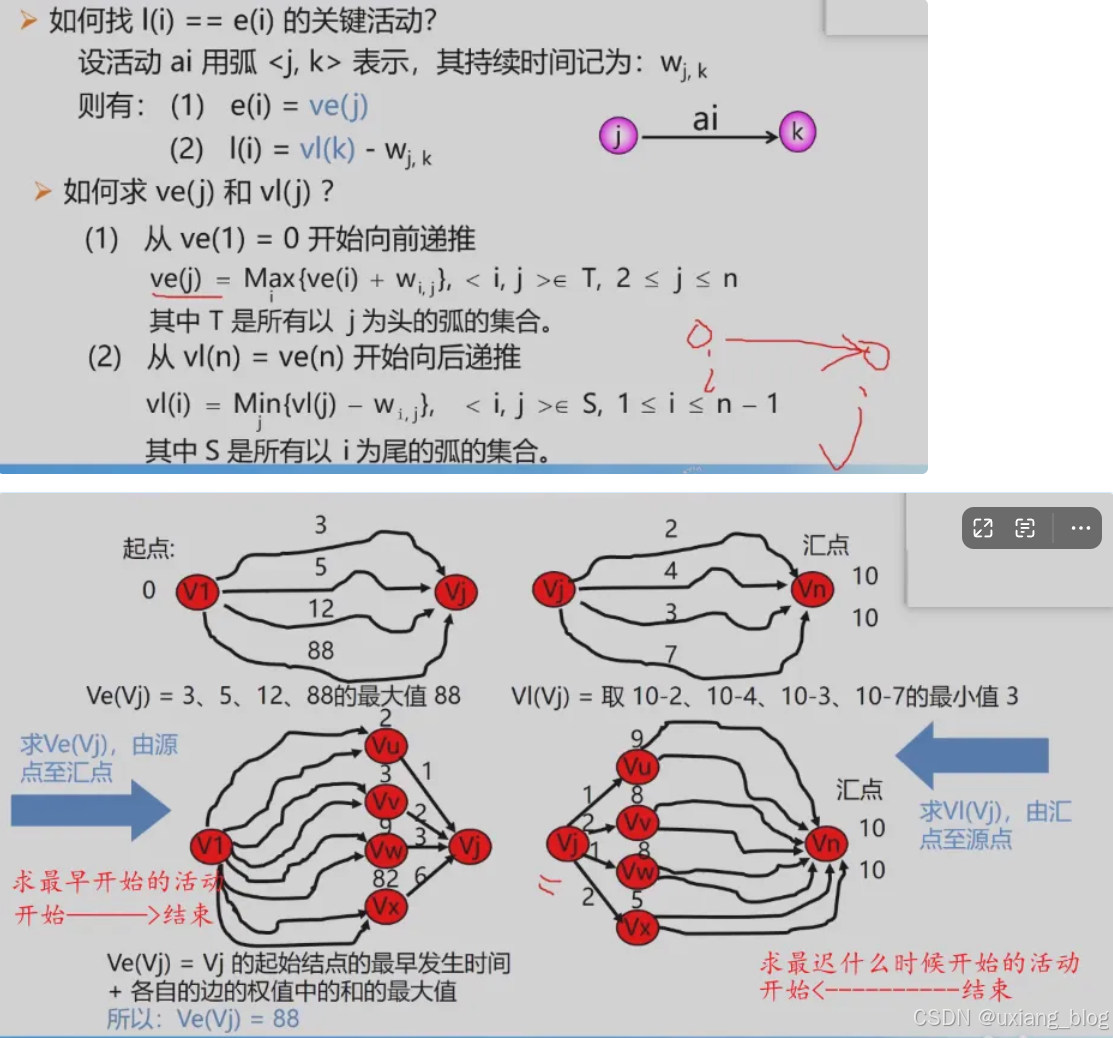
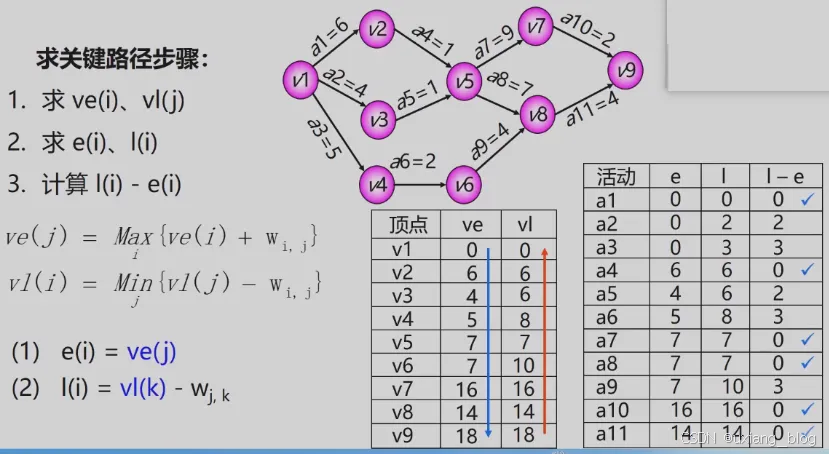
关键路径的讨论
1、若网中有几条关键路径,则需加快同时在几条关键路径上的关键活动。如:a11、a10、a8、a7。
2、如果一个活动处于所有的关键路径上,那么提高这个活动的速度,就能缩短整个工程的完成时间。如a1、a4。
3、处于所有的关键路径上的活动完成时间不能缩短太多,否则会使原来的关键路径变成不是关键路径。这时,必须重新寻找关键路径。如:a1由6天变成3天,就会改变关键路径。
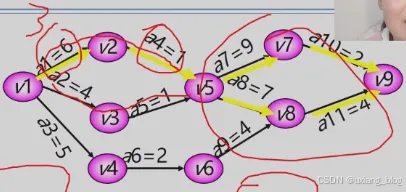
6.7、案例分析与实现
第七章 查找
知识回顾
7.1、查找的基本概念
问题:在哪里找?————查找表
查找表:是由统一类型的数据元素(或记录)构成的集合。由于“集合”中的数据元素之间存在着松散的关系,因此查找表是一种应用灵便的结构。
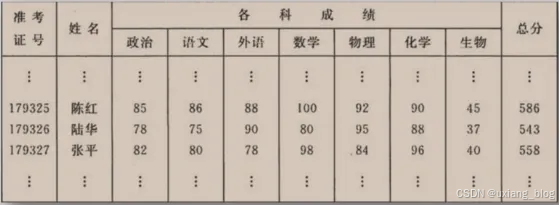
问题:什么查找?—————根据给定的某个值,在查找表中确定一个其关键子等于给定值的数据元素(或记录)
关键字:用来标识一个数据元素(或记录)的某个数据项的值,有主、次关键字之分。
● 主关键字:可唯一标识一个记录的关键字是主关键字;
● 次关键字:反之,用以识别若干记录的关键字是次关键字。
问题:查找成功否?————
查找—根据给定的某个值,在查找标中确定一个其关键字等于给定值的数据元素或(记录)
若查找表中存在这样的一个记录,则称“查找成功”:查找结构给出整个记录的信息,或指示该记录在查找表中的位置。
否则称“查找不成功”:查找结果给出“空记录”或“空指针”。
问题:查找目的是什么?
对查找表经常进行的操作:
● 1、查询某个“特定的”数据元素是否在查找表中;
● 2、检索某个“特定的”数据元素的各种属性;
● 3、在查找表中插入一个数据元素;
● 4、删除查找表中的某个数据元素。
问题:查找表怎么分类?
查找表可分为两类:
静态查找表:仅作“查询"(检索)操作的查找表。
动态查找表:作“插入”和“删除”操作的查找表。有时在查询之后,还需要将“查询”结果“不在查找表中”的数据元素插入到查找表中;或者,从查找表中删除其“查询”结果为“在查找表中”的数据元素,此类表为动态查找表。
问题:如何评价查找算法? ———查找算法的评价指标:
关键字的平均比较次数,也称平均查找长度ASL(Average Search Length)
ASL =∑i=0npici\sum_{i=0}^n p_ic_i∑i=0npici (关键字的比较次数的期望值)
n:记录的个数
pi:查找第i个记录的概率(通常认为pi = 1/n)
ci:找到第i个记录所需的比较次数
问题:查找过程中我们要研究什么?————研究查找表的各种组织方法及其查找过程的实施。
查找的方法取决于查找表的结构,即表中数据元素是依何种关系组织在一起的。
由于对查找表来说,在集合中查询或检索一个“特定的”数据元素时,若无规律可循,只能对集合中的元素——加以辨认直到找到为止。
而这样的“查询”或“检索”是任何计算机应用系统中使用频度都很高的操作,因此设法提高查找表的查找效率,是本章讨论问题的出发点。
为提高查找效率,一个办法就是在构造查找表时,在集合中的数据元素之间认为地加上某种确定的约束关系。
7.2、线性表的查找
7.2.1、顺寻查找(线性查找)
应用范围:
● 顺表表或线性链表表示的静态查找表
● 表内元素之间无序
顺序表的表示:
数据元素类型定义:

typedef struct{KeyType key; //关键字域...... //其他域
}ElemType;typedef struct{ElemType *R; //表基址int length; //表长
}SSTable; //Sequential Search Table
SSTable ST; //定义顺序表
在顺序表ST中从查找值为key的数据元素(从最后一个元素开始比较)

算法:

int Search_Seq(SSTable ST,KeyType key){//若成功返回其位置信息,否则返回0for(i = ST.length;i >= 1; --i){if(ST.R[i].key == key) return i;else return 0;}}
算法的其他形式:
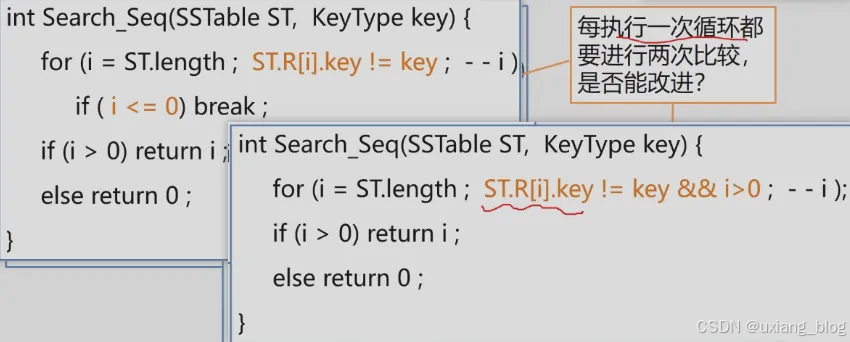
int Search_Seq(SSTable ST,KeyType key){for(i = ST.length;ST.R[i].key != key;--i){if(i <= 0) break;if(i > 0) return i;else return 0;}
}int Search_Seq(SSTable ST,KeyType key){for(i = ST.length; ST.R[i].key != key && i > 0; --i);//注意此处的分号if(i > 0) return i;else return 0;
}
问题:每次执行一次循环都要进行两次比较,是否能改进?————改进:设置监视哨的顺序查找
改进:把待查关键字key存入表头(“哨兵”,“监视哨”),从后往前逐个比较,可免去查找过程中每一步都要检测是否查找完毕,加快速度。

int Search_Seq(SSTable ST,KeyType key){ST.R[0].key = key;//把要查找的值存进下标为0的位置for(i = ST.length;ST.R[i].key != key; --i);return i;
}
当ST.length 较大时,此改进能使进行一次查找所需的平均时间几乎减少一半。
顺序查找的性能分析
时间效率分析

比较次数与key位置有关:
● 查找第i个元素,需要比较n-i+1次
● 查找失败,需比较n+1次。
时间复杂度:O(n):查找成功时的平均查找长度,设表中各记录查找概率相等。ASLs(n)=(1+2…+n)/n = (n+1)/2
空间复杂度:一个辅助空间——O(1);
讨论:todo
1、记录的查找概率不相等时如何提高查找效率?(查找表存储记录原则——按查找概率高低存储:)
● 1)查找概率越高,比较次数越少;
● 2)查找概率越低,比较次数较多。
2、记录的查找概率无法测定时如何提高查找效率?(方法——按查找概率动态调整记录顺序:)
● 1)在每个记录中设一个访问频度域;
● 2)始终保持记录按非递增有序的次序排列;
● 3)每次查找后均将刚查到的记录直接移至表头。
顺序查找的特点
优点:算法简单,逻辑次序无要求,且不同存储结构均适用。
缺点:ASL太长,时间效率太低。
7.2.2、折半查找(二分或对分查找)

折半查找:每次将待查记录所在区间缩小一半。
查找过程:
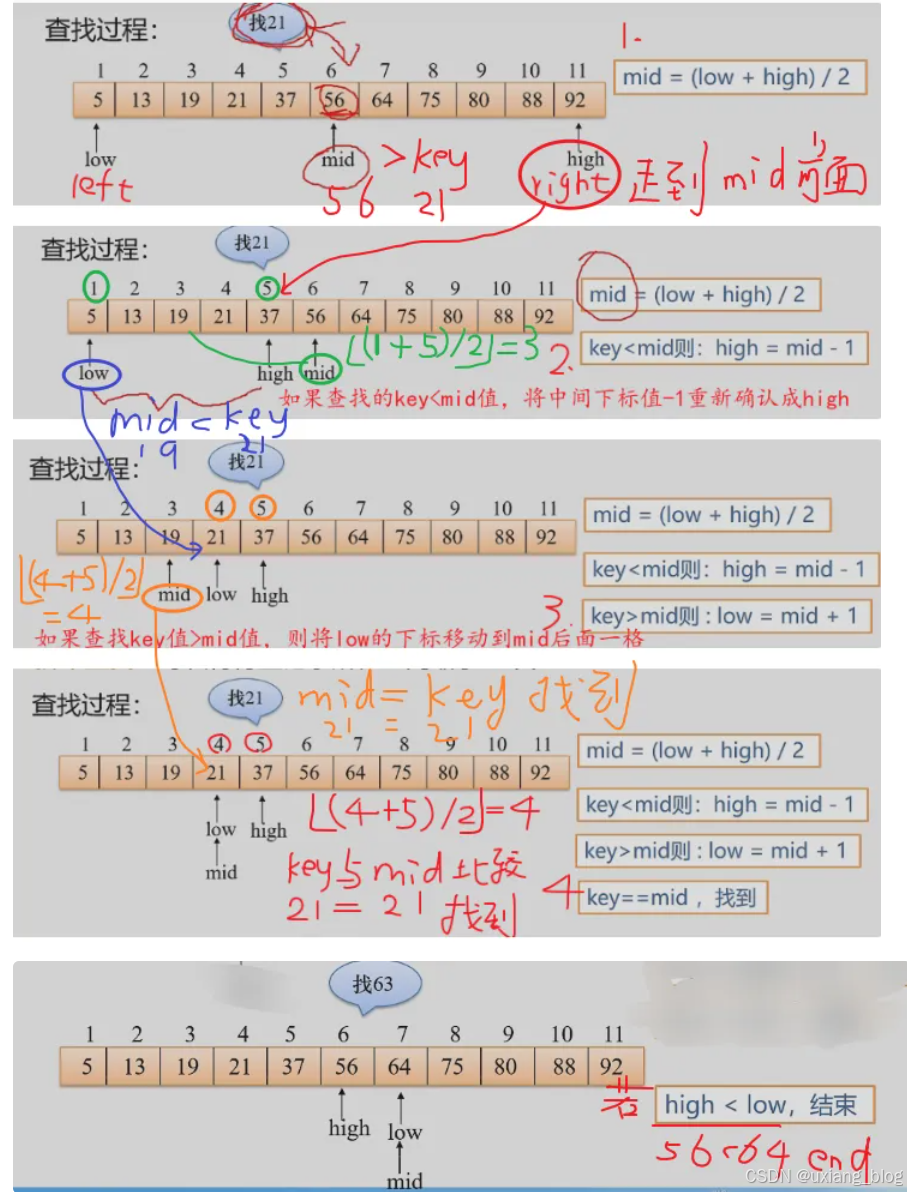
个人总结:
● 先确定最大的high和最小的low,然后根据最大的和最小的数组下标计算出两者中间的mid
● 中间的mid的确认后,mid所在的值立马与要查找到的key值比较大小,
○ 若是key<mid,low就移动mid后面一格;
○ 若是key>mid,high就移动mid前面一格;
● 最后依次比较下去,若是key=mid就是找到了,若是途中若high<low就结束,表示所找key不存在。
注意:mid移动是依靠的是high和low的下标遵守取整函数移动。low和high移动依靠的是mid与key值(存储在数组中的元素数据,而不是数组下标)的比较移动。
折半查找算法:(非递归算法)
● 设表长为n、low、high和mid分别指向待查元素所在区间的上界、下界和中点,key为给定的要查找的值:
● 初始时,令low=1,high=n,mid=|(low +high)/2)|
● 让k与mid指向的记录比较
○ 若key==R[mid].key,查找成功
○ 若key<R[mid].key,则high=mid-1
○ 若key>R[mid].key,则low = mid+1
● 重复上述操作,直到low>high时,查找失败

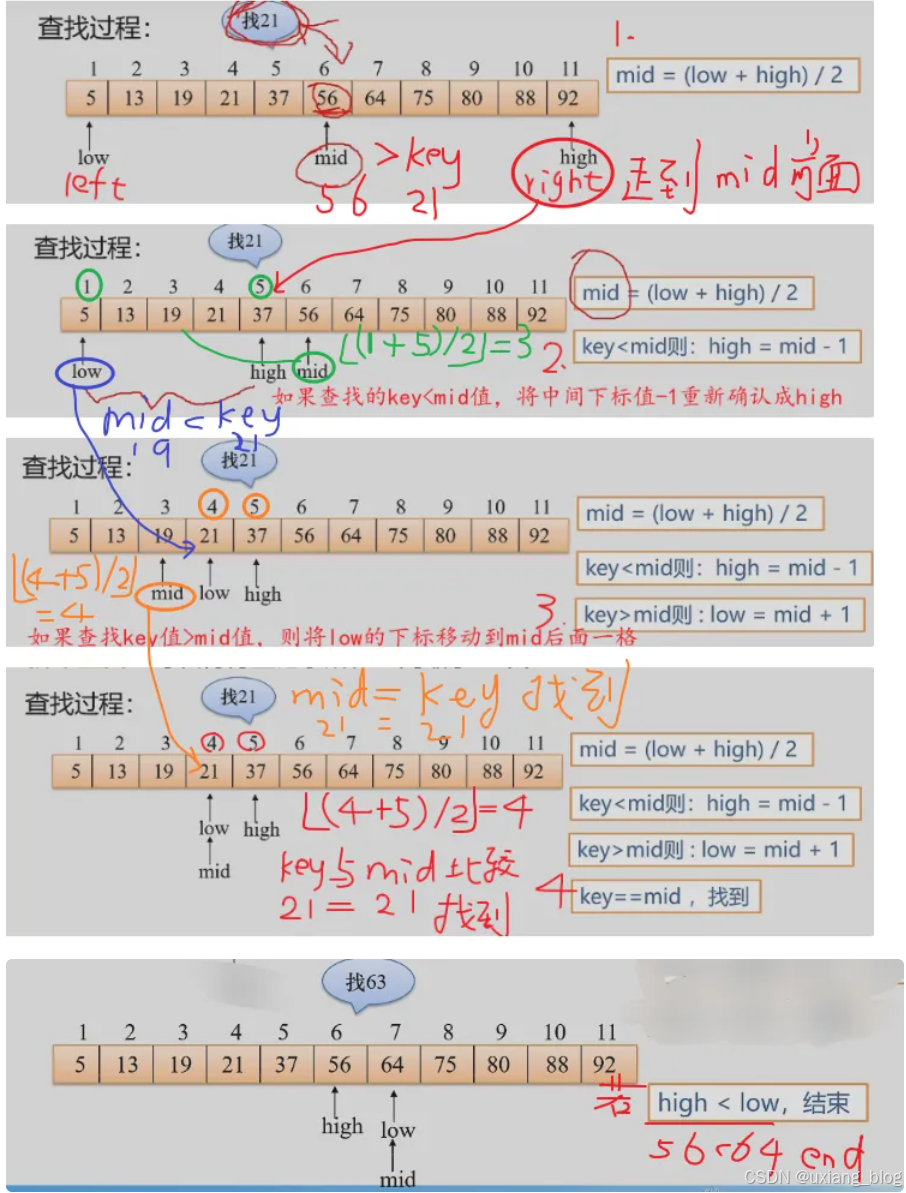
int Search_Bin(SSTable ST,KeyType key){//置区间初值low = 1;high = ST.length;while(low <= high){mid = (low + high)/2;if(ST.R[mid].key == key){ return mid;//找到待查元素}//缩小查找区间else if(key < ST.R[mid].key){high = mid -1 ; //继续在前半区间进行查找} else{ low = mid + 1; //继续在后半区间进行查找}return 0; //顺序表中不存在待查元素
}
折半查找——递归算法

int Search_Bin(SSTable ST,keyType key,int low, int high){if(low > high)return 0;mid = (low + high)/2;if(key == ST.elem[mid].key) return mid;else if(key < ST elem[mid].key)......//递归,在前半区间进行查找else ....
.. //递归,在后半区间进行查找
}
折半查找的性能分析——判定树
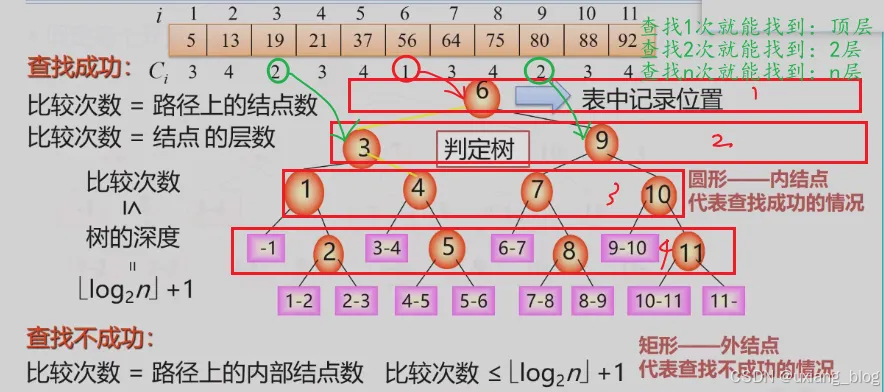
练习:
假定每个元素的查找概率相等,求查找成功时的平均查找长度。
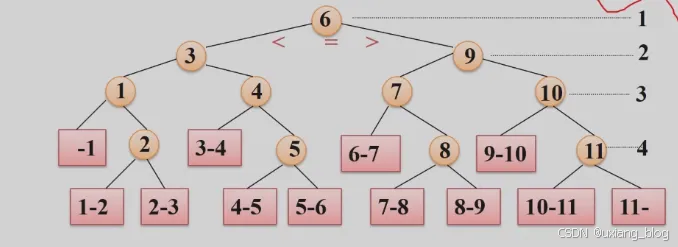
ASL = 1/11*(11 + 22 + 43 + 44) = 33/11 = 3 (红色字体为查找元素,乘以后面的查找次数)乘以总共查找元素的的倒数便是查找平均长度。
折半查找的性能分析——ASL
平均查找长度ASL(成功时):
设表长n=2h−1n = 2^h -1n=2h−1则h=log2(n+1)h = log_2(n+1)h=log2(n+1)(此时,判定树为深度 = h 的满二叉树),且表中记录的查找概率相等:Pi=1/nP_i =1/nPi=1/n。
则

折半查找优点:效率比较顺序查找高。空间性能是对数级别
折半查找缺点:只适用于有序表,且限于顺序存储结构(对线性链表无效)。
7.2.3、分块查找

分块查找(索引顺序查找)todo
条件:
● 1、将表分成几块,且表或者有序,或者分块有序;若i<j,块中所有记录的关键字均大于第i块中的最大关键字。
● 2、建立“索引表”(每个结点含有最大关键字域和指向本块第一个结点的指针,且按关键字有序)。
查找过程:先确定待查记录所在块(顺序或折半查找),索引表再在块内查找(顺序查找)。
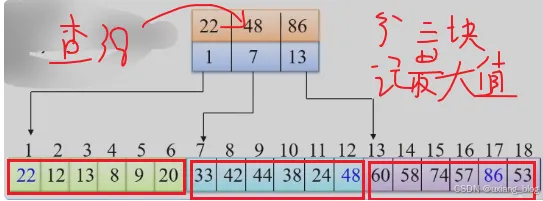
分块查找性能分析

分块查找优缺点
● 优点:插入和删除比较容易,无需进行大量移动。
● 缺点:要增加一个索引表的储存空间并对初始索引表进行排序运算。
● 适用情况:如果线性表既要快速查找又经常动态变化,则可采用分块查找。
查找方法比较
| 顺序查找 | 折半查找 | 分块查找 | |
|---|---|---|---|
| ASL | 最大 | 最小 | 中间 |
| 表结构 | 有序表、无序表 | 有序表 | 分块有序 |
| 存储结构 | 顺序表、线性链表 | 顺序表 | 顺序表、线性链表 |
7.3、树表的查找
当表插入、删除操作频繁时,为维护表的有序性,需要移动表中很多记录。——改用动态查找表:几种特殊的树。 表结构在查找过程中动态生成 对于给定值key,若表中存在,则成功返回;否则插入关键字等于key的记录。
几种特殊的树为
● 二叉排序树(重点)
● 平衡二叉树(重点)
● 红黑树
● B-树
● B+树
● 键树
7.3.1、二叉排序树
二叉排序树(Binary Sort Tree)又称为二叉搜索树、二叉查找树,
定义:
二叉排序树或是空树,或是满足如下性质的二叉树:
(1)若其左子树非空,则左子树上所有结点的值均小于根结点的值;
(2)若其右子树非空,则右子树上所有结点的值均大于等于根结点的值;
(3)其左右子树本身又各是一棵二叉树排序树
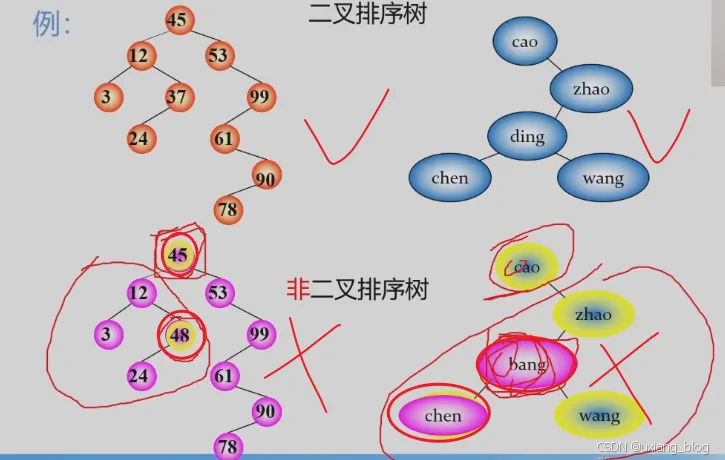
思考:todo
● 中序遍历二叉排序树
● 结果有什么规律?
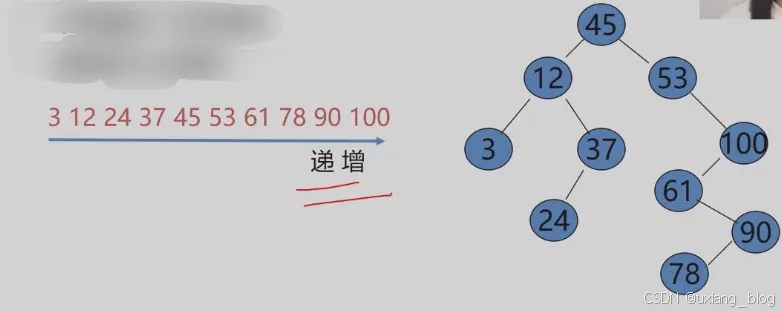
二叉排序树的性质:
中序遍历非空的二叉树排序树所得到的数据元素序列是一个按关键字排列的递增有序序列。
二叉树排序树的操作——查找
● 若查找的关键字等于根结点,成功
● 否则
○ 若小于根节点,查其左子树
○ 若大于根结点,查其右子树
● 在左子树上的操作类似
二叉树排序树的存储结构todo

typedef struct{KeyType key; // 关键字项InfoType otherinfo; //其他数据域
}ElemType;typedef struct BSTNode{ElemType data; //数据域struct BSTNode *lchild,*rchild;//左右孩子指针
}BSTNode,*BSTree;
BSTree T;//定义二叉排序树T
算法:二叉排序树的递归查找
算法思想:
(1)若二叉排序树为空,则查找失败,返回空指针。
(2)若二叉排序树非空,将给定值key与根结点的关键字T->data.key进行比较:
● 若key等于T -> data.key,则查找成功,返回根结点地址;
● 若key小于T -> data.key,则进一步查找左子树;
● 若key大于T ->data.key,则进一步查找右子树。
算法描述:

BSTree SearchBST(BSTree T,KeyType key){if((!T)||key == T -> data.key) return T;else if(key < T -> data.key) return SearchBST(T -> lchild,key);//在左子树中继续查找else return SearchBST(T -> rchild,key);//在右子树中继续查找
}//SearchBST
二叉排序树的查找分析
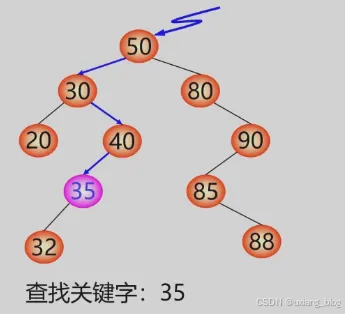
二叉树排序树上查找某关键字等于给定值的结点过程,其实就是走了一条从根到该结点的路径。
比较的关键字次数 = 此节点所在的层次数 最多的比较次数 = 树的深度 todo
二叉排序树的平均查找长度:

含有n个结点的二叉排序树的平均查找长度和树的形态有关
最好的情况:初始序列{45,24,53,12,37,93} ASL = log2(n+1)−1log_2(n+1)-1log2(n+1)−1;树的深度为:|log2nlog_2nlog2n|+1;与折半查找中的判定树相同。(形态比较均衡):O(log2nlog_2nlog2n)
最坏的情况:初始序列{12,24,37,45,53,93}插入的n个元素从一开始就有序——变成单枝树的形态!此时树的深度为n,ASL=(n+1)/2查找效率与顺序查找情况相同:O(n)
问题:如何提高形态不均衡的二叉排序树的查找效率?
解决办法:做"平衡化"处理,即尽量让二叉树的形状均衡!
二叉排序树的操作——插入
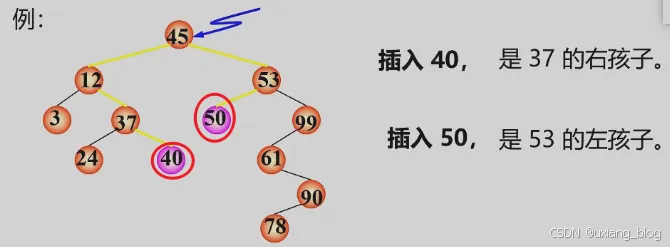
● 若二叉排序树为空,则插入结点作为根结点插入到空树中
● 否则,继续在其左、右子树上查找
○ 树中已有,不再插入
○ 树中没有
■ 查找直至某个叶子结点的左子树或右子树为空为止,则插入结点应为该叶子结点的左孩子或右孩子。
注意:插入的元素一定在叶子结点上。
二叉排序树的操作——生成
从空树出发,经过一系列的查找、插入操作之后,可生成一棵二叉排序树。
例:设查找的关键字序列为{45,24,53,45,12,24,90},可生成二叉排序树如下
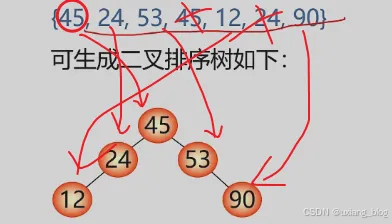
一个无序序列可通过构造二叉排序树而变成一个有序序列。构造树的过程就是对无序序列进行排序的过程。
插入的结点均为叶子结点,故无需移动其他结点。相当于在有序序列上插入记录而无需移动其他记录。
但是:关键字的输入顺序不同,建立的不同二叉排序树。
不同插入次序的序列生成不同形态的二叉排序树
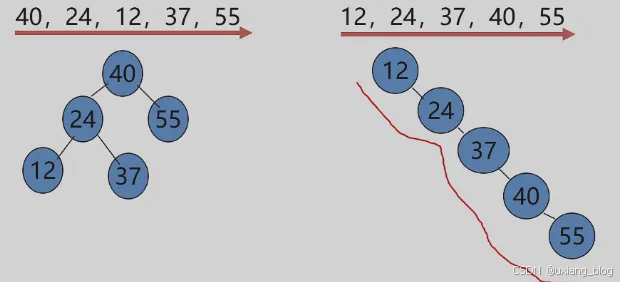
二叉排序树的操作——删除
从二叉排序树中删除一个结点,不能把以该结点为根的子树都删去,只能删掉该结点,并且还应保证删除后所得的二叉树仍然满足二叉排序树的性质不变。
由于中序遍历二叉排序树可以得到一个递增有序的序列。那么,在二叉排序树中删去一个结点相当于删去有序序列中的一个结点。
● 将因删除结点而断开的二叉链表重新链接起来
● 防止重新链接后树的高度增加。
(1)被删除的结点是叶子结点:直接删去该节点。例如:
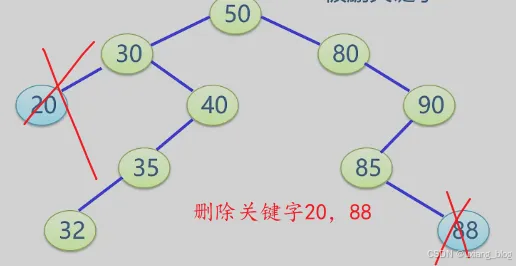
(2)被删除的结点只有左子树或者只有右子树,用其左子树或者右子树替换它(结点替换)。
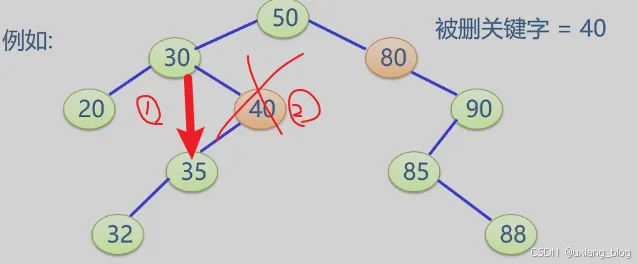
其双亲结点的相应指针域的值改为”指向被删除结点的左子树或右子树“。
(3)被删除的结点既有左子树,也有右子树。
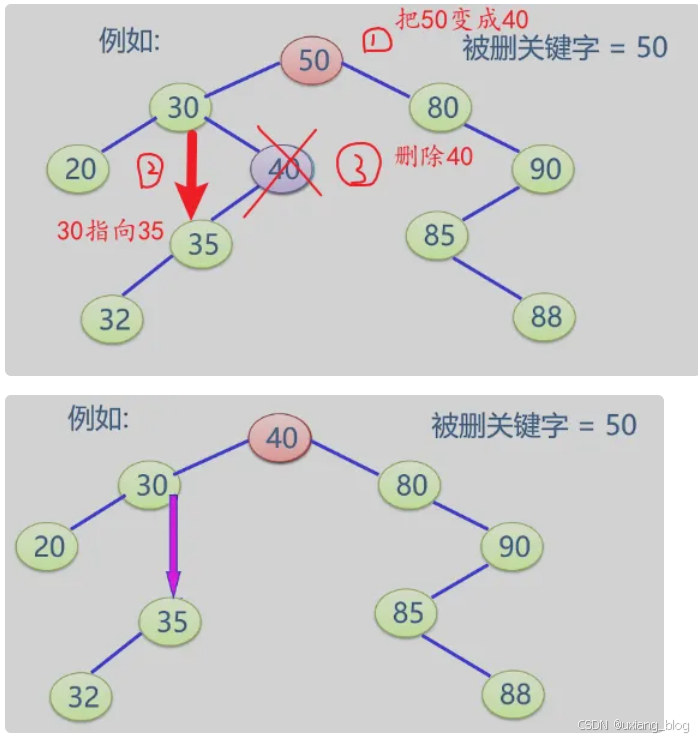
● 以其中序前趋值替换之(值替换),然后再删除该前趋结点。前趋是左子树中最大的结点。
● 也可以用其后继替换之,然后再删除后继结点。后继是右子树中最小的结点。
注意:是以前趋值替换,还是以后继值替换,取决于能那种方法能降低树的深度。
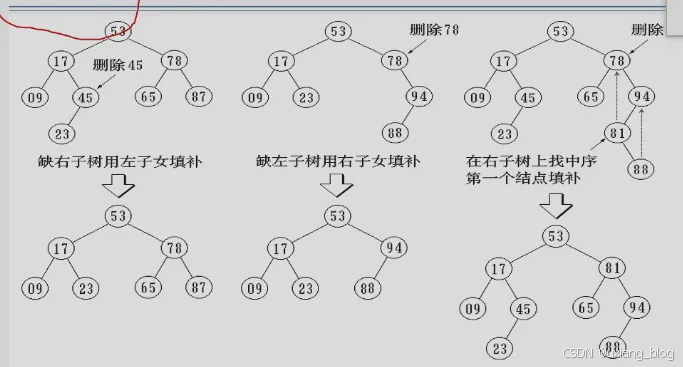
7.3.2、平衡二叉树
1、平衡二叉树的定义
平衡二叉树(balanced binary tree)
● 又称AVL树(Adelson-Velskii and Landis)。
● 一棵平衡二叉树或者是空树,或者是具有下列性质的二叉排序树:
○ a.左子树与右子树的高度之差的绝对值小于等于1;
○ b.左子树和右子树也是平衡二叉排序树。
为了方便起见,给每个结点附加一个数字,给出该结点左子树与右子树的高度差。这个数字称为结点的平衡因子(BF)。
平衡因子 = 结点左子树的高度 - 结点右子树的高度。
根据平衡二叉树的定义,平衡二叉树上所有的平衡因子只能是-1,0,或1。
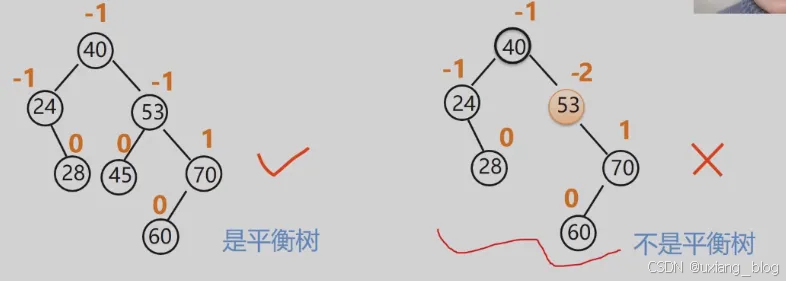
对于一棵有n个结点的AVL树,其高度保持在O(log2nlog_2nlog2n)数量级,ASL也保持在O(log2nlog_2nlog2n)量级。
2、失衡二叉排序树的分析与调整
当我们在一个平衡二叉排序树上插入一个结点时,有可能导致失衡,即出现平衡因子绝对值大于1的结点,如:2、-2。
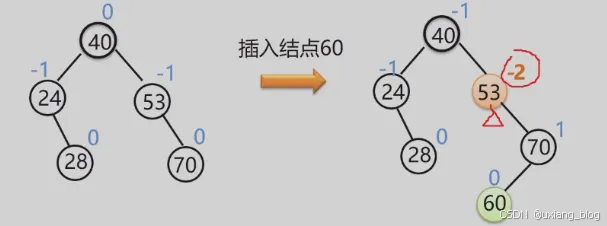
如果在一棵AVL树中插入一个新结点后造成失衡,则必须重新调整树的结构,使之恢复平衡。
平衡调整的四种类型:‘
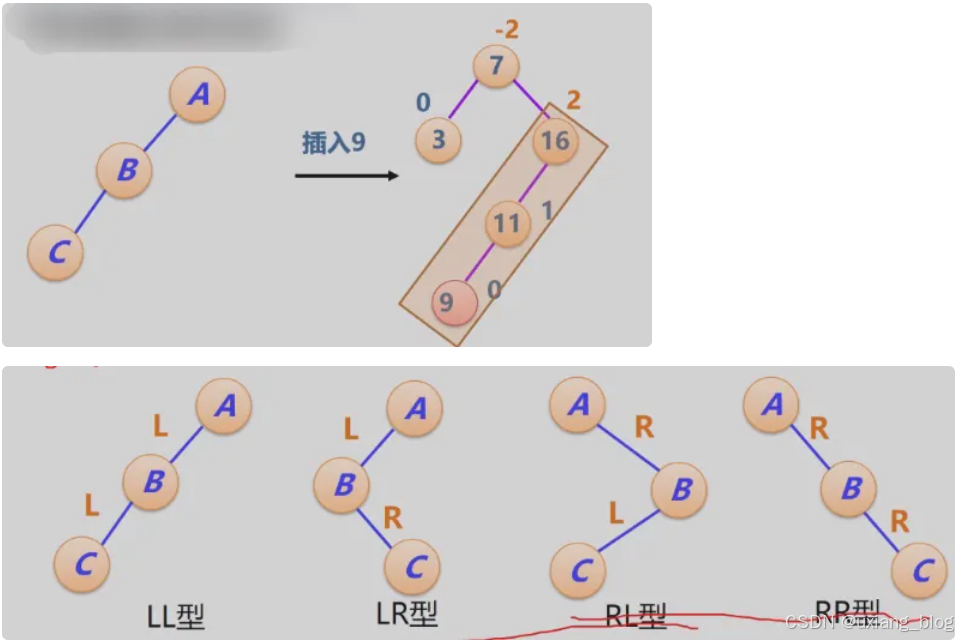
A:失衡结点,不止一个失衡结点时,为最小失衡子树的根结点
B:A结点的孩子,C结点的双亲。
C:插入新结点的子树。
调整原则:判断大小,把中间的作为根结点
● 降低高度
● 保持二叉排序树的性质
(1)LL型调整
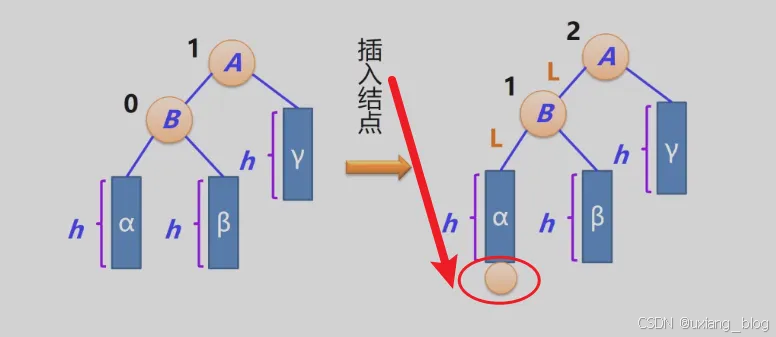
调整过程:α(阿尔法)、β(贝塔)、γ(伽马)
● B结点带左子树α
● A结点成为B的右孩子
● 原来B结点的右子树β作为A的左子树
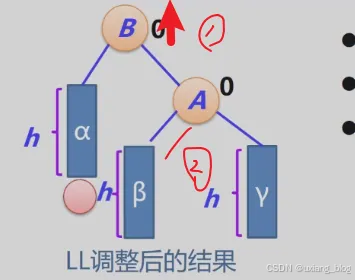
AVL树LL调整——例子:
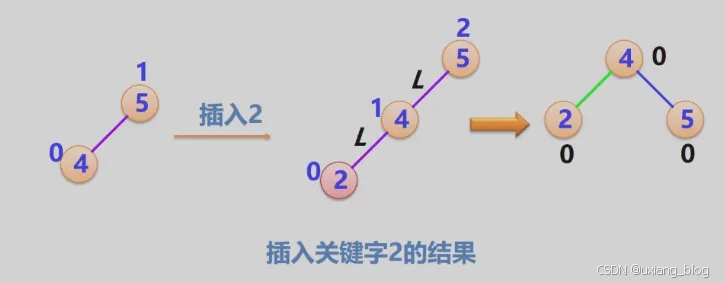
(2)RR型调整
RR型调整过程:
● B结点带右子树β一起升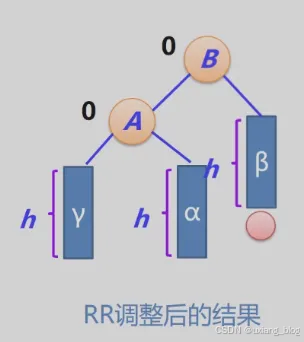
● A结点成为B的左孩子
● 原来B结点的左孩子α作为A的右子树
在这里插入图片描述
AVL树RR调整——例子:
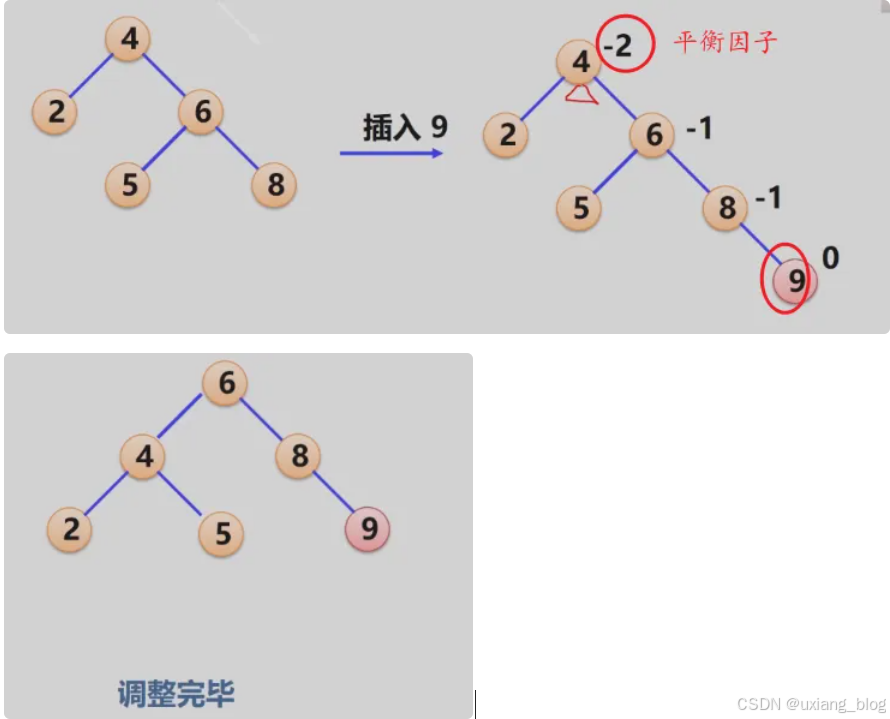
(3)LR型调整
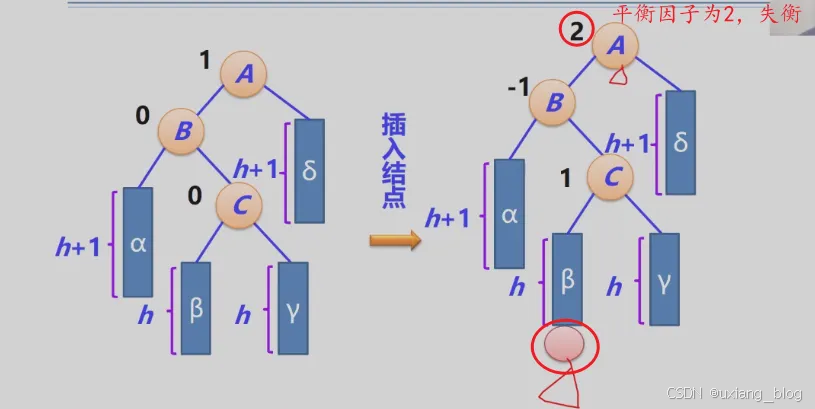
调整过程
● C结点穿过A、B结点上升
● B结点成为C的左孩子,A结点成为C的右孩子
● 原来C结点的左子树β作为B的右子树;原来C结点的右子树γ作为A的左子树。
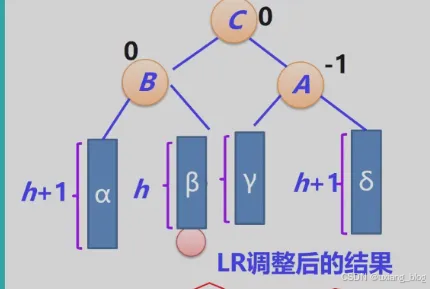
AVL树LR调整——例子:
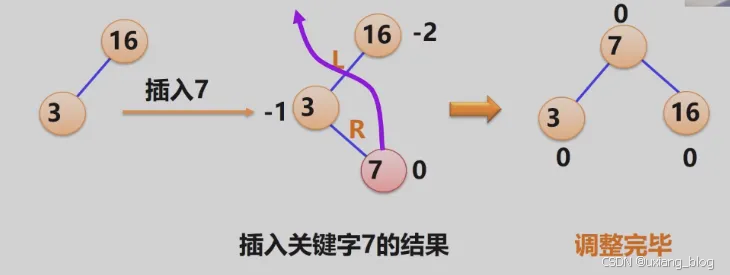
(4)RL型调整
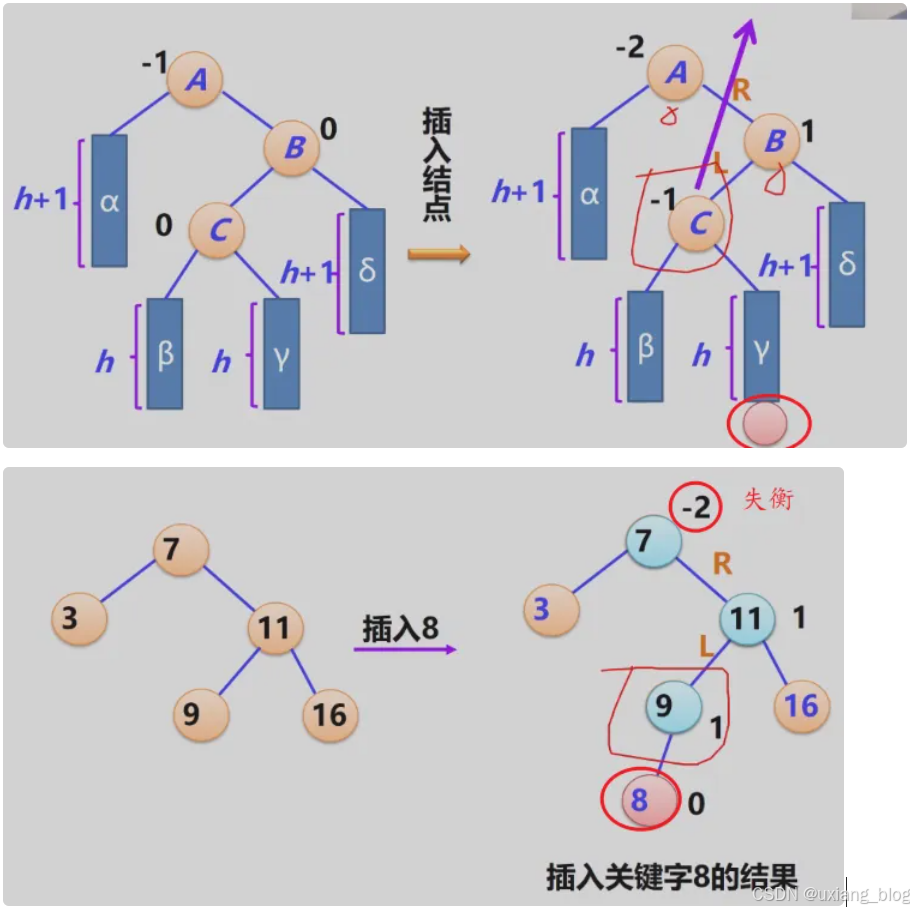
AVL树调整——例子:
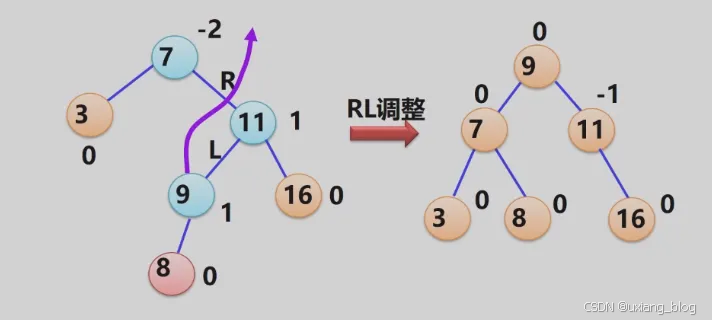
例题:输入关键字序列(16、3、7、11、9、26、18、14、15),给出构造AVL树的步骤。
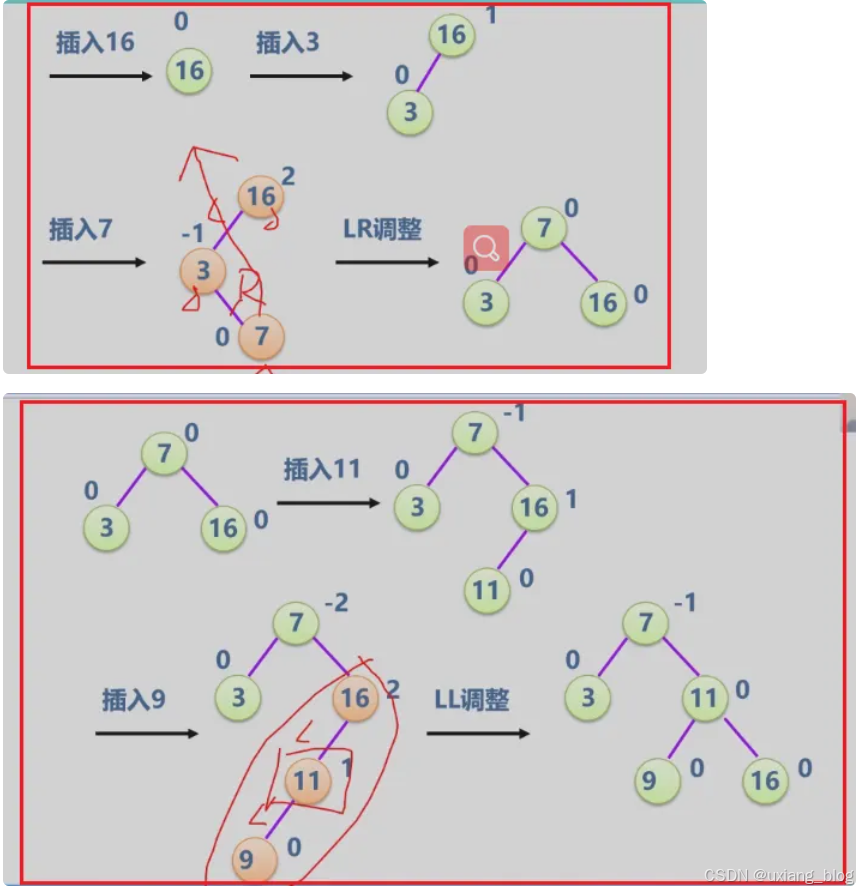
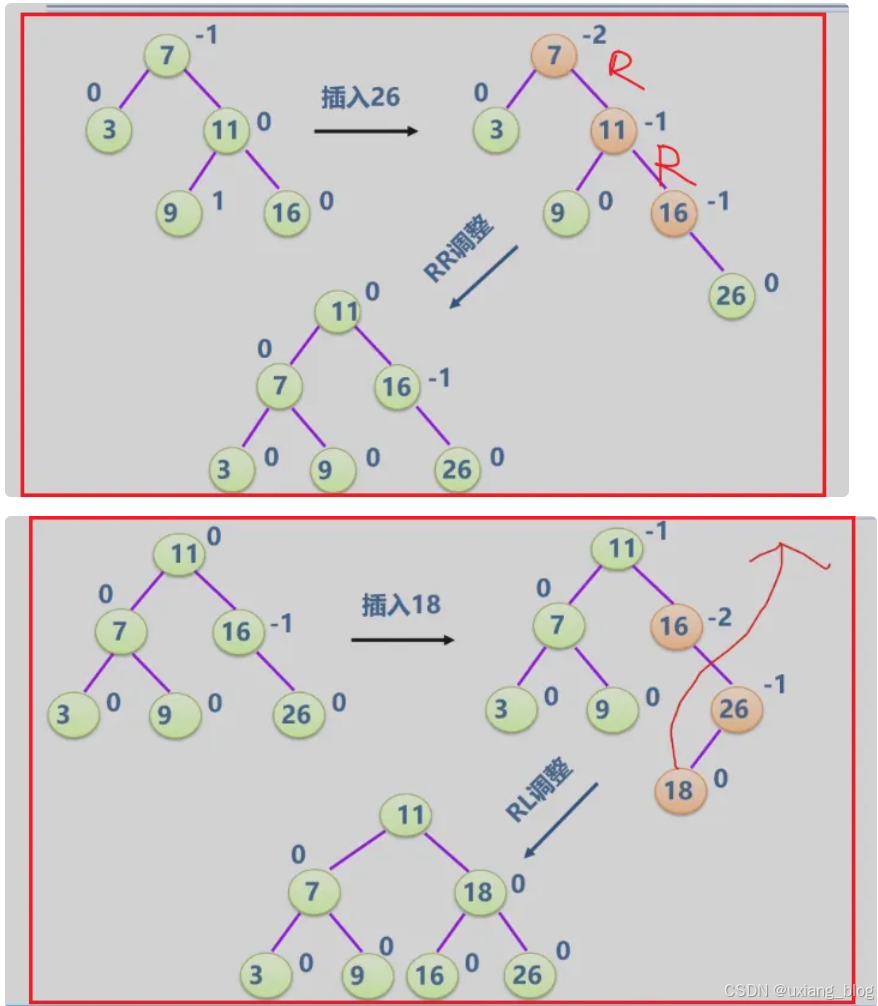
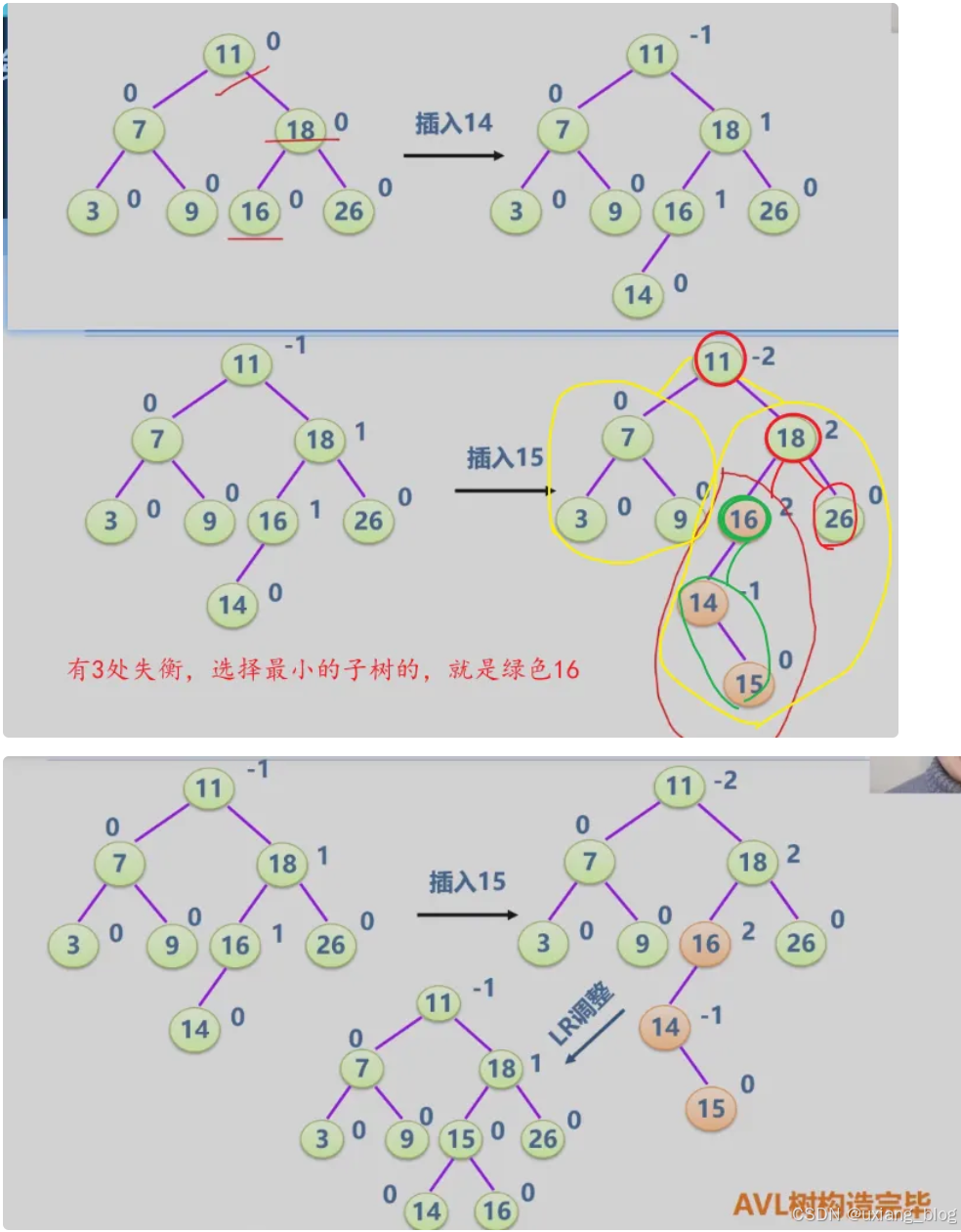
7.3.3、B-树
7.3.4、B+树
7.4、散列表的查找
7.4.1、散列表的基本概念
基本思想:记录的存储位置与关键字之间存在对应关系
对应关系——hash函数

Hash:哈希 翻译为:散列、杂凑——————散列表

例如要查找2001011180216的信息,可直接访问V[16]
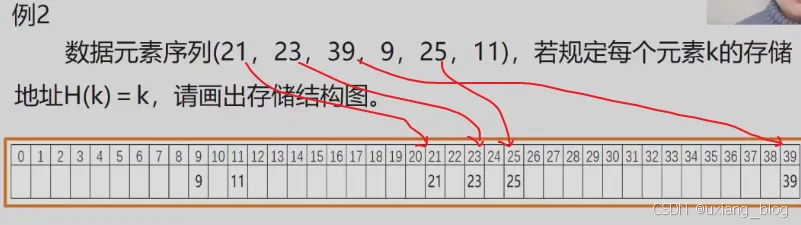
根据散列函数H(key)=k,查找key=9,则访问H(9) = 9号地址,若内容为9则成功;若查不到,则返回一个特殊值,如空指针或空记录。
优点:查找效率高。 缺点:空间效率低。
7.4.2、散列表的若干术语
散列方法(杂凑法)
选取某个函数,依次函数按关键字计算元素的存储位置,并按此存放;查找时,由同一个函数对给定值k计算地址,将k与地址单元中元素关键码进行比较,确定查找是否成功。
散列函数(杂凑函数):散列方法中使用的转换函数
散列表(杂凑表):按上述思想构造的表
散列函数:H(key)=k

冲突:不同的关键码映射到同一个散列地址key1 ≠key2,但是H(key1) = H(key2)
例:有6个元素的关键码分别为:(25、21、39、9、23、11)
● 选取关键码与元素位置间的函数为H(k) =k mod 7
● 地址编号从0-6.
通过散列函数对6个元素建立散列表:
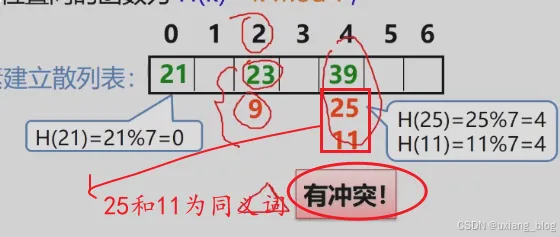
同义词:具有相同函数值的多个关键字
7.4.3、散列函数的构造方法
散列存储
选取某个函数,依该函数按关键字计算元素的存储位置 Loc(i) =H(keyi)
冲突 不同的关键码映射到同一个散列地址 key1≠key2,但是H(key1)=H(key2)
在散列查找方法中,冲突是不可能避免的,只能尽可能减少。——怎么减少?
使用散列表要解决好两个问题:
1、构造好的散列函数
● a.所选函数尽可能简单,以便提高转换速度;
● b.所选函数对关键码计算处的地址,应在散列地址集中致均匀分布,以减少空间浪费。
2、制定一个好的解决冲突的方案
查找时,如果从散列函数计算出的地址中查不到关键码,则应当依据冲突的规则,有规律地查询其他相关单元。
构造散列函数考虑的因素
● 1、执行速度(即计算散列函数所需时间);
● 2、关键字的长度;
● 3、散列表的大小;
● 4、关键字的分布情况;
● 5、查找频率。
根据元素集合的特性构造
● 要求1:n个数据原仅占用n个地址,虽然散列查找是以空间换时间,但仍希望散列的地址空间尽量小。
● 要求2:无论用什么方法存储,目的都是均匀地存放元素,以避免冲突。
散列函数的构造方法:
| 1、直接定址法 | 2、数字分析法 | 3、平方取中法 |
|---|---|---|
| 4、折叠法 | 5、除留余数法(最常用) | 6、随机数法 |
直接定址法
Hash(key) = a.key + b(a,b为常数)
优点:以关键码key的某个线性函数值为散列地址,不会产生冲突。
缺点:要占用连续地址空间,空间效率低。
例如:{100,300,500,700,800,900},散列函数Hash(key) = key/100(a = 1/100,b =0)

除留余数法
Hash(key) = key mod p(p是一个整数)
关键:如何选取合适的p?
技巧:设表长为m,取p<=m 且为质数
例:{15,23,27,38,53,61,70}
散列函数 Hash(key)= key mod 7

处理冲突的方法:
| 1、开放定址法(开地址法):重点 | 3、再散列法(双散列法) |
|---|---|
| 2、锁地址法(拉链法):重点 | 4、建立一个公共溢出区 |
1、开放地址法(开地址法)
基本思想:有冲突时就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总恩能够找到,并将数据元素存入。
例如:用留余数法 Hi=(Hash(key)+di)modmH_i = (Hash(key)+d_i)mod mHi=(Hash(key)+di)modm di为增量序列
常用方法:
| 线性探测法 | di为1,2,...,m−1线性序列d_i 为1,2,... ,m-1线性序列di为1,2,...,m−1线性序列 |
|---|---|
| 二次探测法 | di为12,−12,22,−22,...,q2二次序列d_i为1^2,-1^2,2^2,-2^2,...,q^2二次序列di为12,−12,22,−22,...,q2二次序列 |
| 伪随机探测法 | di为伪随机数列d_i为伪随机数列di为伪随机数列 |
线性探测法
Hi=(Hash(key)+di)modm(1≤i<m)H_i = (Hash(key)+d_i)mod m (1≤i<m)Hi=(Hash(key)+di)modm(1≤i<m)其中:m为散列表长度,did_idi为增量序列1,2,…,m-1,且did_idi=i(注意:一旦冲突,就找下一个地址,直到找到空地址存入)
例如:关键码集为{47,7,29,11,16,92,22,8,3},散列为m =11;散列函数为Hash(key)=key mod 11;拟用线性探测法…冲突。建散列表如下:
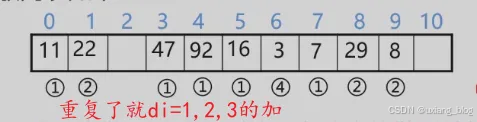
解释:
● ①47、7均是有散列函数得到的没有冲突的散列地址;
● ②Hash(29) = 7,散列地址有冲突,需寻找下一个空的散列地址:由H1=(Hash(29)+1)mod11=8H_1=(Hash(29)+1)mod 11=8H1=(Hash(29)+1)mod11=8,散列地址8为空,因此将29存入。
● ③11、16、92均是由散列函数得到拍的没有冲突的散列地址;
● ④另外,22、8、3同样在散列地址上有冲突,也是有H1H_1H1找到空的散列地址的。
所以,平均查找长度ASL = (1+2+1+1+1+4+1+1+2+2)/9=1.67
二次探测法
关键码集为{47,7,29,11,16,92,22,8,3},
设:散列函数为Hash(key) = key mod 11Hi=(Hash(key)+di)modmH_i=(Hash(key)+d_i)mod mHi=(Hash(key)+di)modm
其中:m为散列表长度,m要求是某个4k+3的质数;di为增量序列12,−12,22,−22,...,q21^2,-1^2,2^2,-2^2,...,q^212,−12,22,−22,...,q2
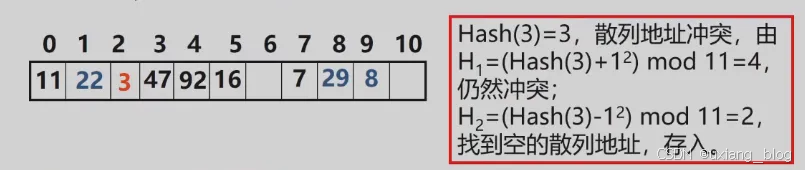
伪随机探测法
Hi=(Hash(key)+di)modm(1≤i<m)H_i=(Hash(key)+d_i)mod m(1 ≤i<m)Hi=(Hash(key)+di)modm(1≤i<m)
其中:m为散列表长度,di为伪随机数
2 、链地址法(拉链法)
基本思想:相同散列地址的记录链成一单链表
m个散列地址就设m个单链表,然后用一个数组将m个单链表的表头指针存储起来,形成一个动态的结构。
例如:一组关键字为{19.14,23,1,68,20,84,27,55,11,10,79},
散列函数为Hash(key)= key mod 13
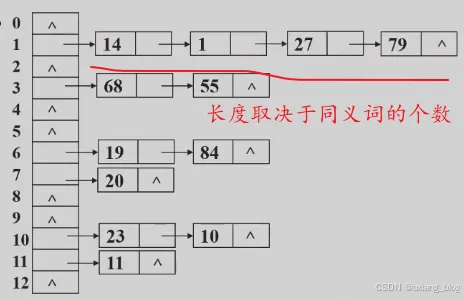
链地址法建立散列表步骤
● Step1:取数据元素的关键字key,计算其散列函数值(地址)。若该地址对应的链表为空,则将该元素插入次链表;否则执行Step2解决冲突。
● Step2:根据选择的冲突处理方法,计算关键字key的下一个存储地址。若该地址对应的链表不为空,则利用链表的前插法或后插法将该元素插入次链表。
链地址法的优点:
● 非同义词不会冲突,无“聚集”现象
● 链表上结点空间动态申请,更适合于表长不确定的情况
3 、再散列法(双散列函数法)
4、建立一个公共溢出区
7.4.4、散列表的查找
给定值查找值k,查找过程:
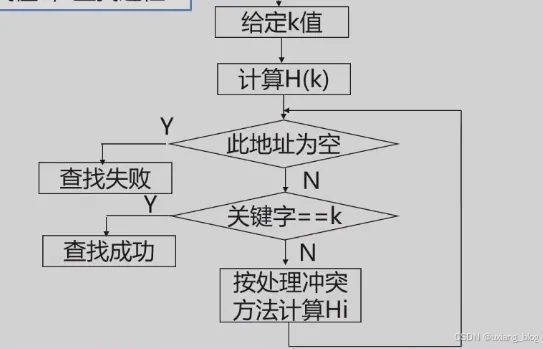
例题
已知一组关键字(19,14,23,1,68,20,84,27,55,11,10,79),散列函数为:H(key) = key Mod 13,散列表长m=16,设每记录的查找概率相等。
(1)用线性探测再链列处理冲突,即Hi=(H(key)+di) mod m

(2)用链地址法处理冲突
关键字(19,14,23,1,68,20,84,27,55,11,10,79)
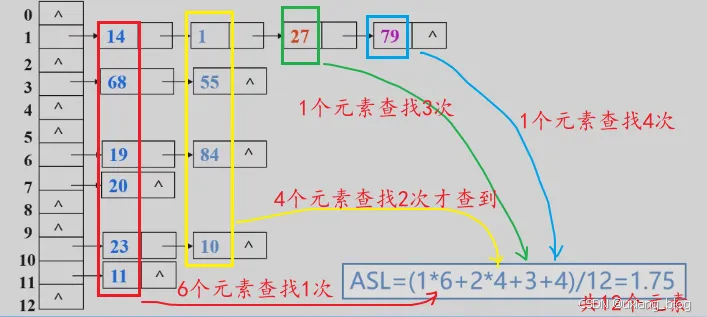
思考:对于关键字集(19,14,23,1,68,20,84,27,55,11,10,79), n = 12

散列表查找效率分析
使用平均查找长度ASL来衡量查找算法,ASL取决于
● 散列函数
● 处理 冲突的方法
● 散列表的装填因子α
装填因子α=(表中填入的记录数哈希表的长度)α = \begin{pmatrix} 表中填入的记录数\\ \hline 哈希表的长度\\ \end{pmatrix}α=(表中填入的记录数哈希表的长度),α越大,表中记录数越多,说明表装得越满,发生冲突得可能性就越大,查找时比较次数就越多。
ASL与装填因子α有关!既不是严格得O(1),也不是O(n)
● ASL≈1+(α2)ASL ≈ 1+ \begin{pmatrix} α\\ \hline 2\\ \end{pmatrix}ASL≈1+(α2)——————————拉链法
● ASL≈(12)[1+(11−α)]ASL ≈ \begin{pmatrix} 1\\ \hline 2\\ \end{pmatrix} [1+ \begin{pmatrix} 1\\ \hline 1-α\\ \end{pmatrix}]ASL≈(12)[1+(11−α)]——————线性探测法
● ASL≈−(1α)ln(1−α)ASL ≈ - \begin{pmatrix} 1\\ \hline α\\ \end{pmatrix}ln(1-α)ASL≈−(1α)ln(1−α)———————随机探测法
几点结论
● 散列表技术具有很好得平均性能,优于一些传统得技术
● 链地址法优于开地址法
● 除留余数法作散列函数优于其他类型函数
第八章 排序
知识回顾
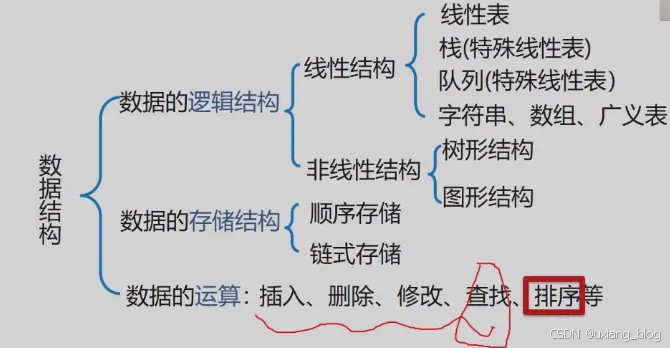
8.1、基本概念和排序方法概述
什么是排序?
排序:将一组杂乱无章得数据按一定规律顺次排列起来。即,将无序序列排成一个有序序列(由小到大或由大到小)的运算。
● 若参加排序的数据结点包含多个数据域,那么排序往往是针对域某个域而言。
8.1.1、概述
排序的应用非常广泛
● 软件中直接应用——见例如举例
● 程序中间接应用
○ 二分法查找
○ 最短路径、最小生成树
○ …
例如:

8.1.2、排序方法的分类

| 按照数据存储介质 | 内部排序 | 外部排序 |
|---|---|---|
| 按比较器个数 | 串行排序 | 并行排序 |
| 按主要操作 | 比较排序 | 基数排序 |
| 按辅助空间 | 原地排序 | 非原地排序 |
| 按稳定性 | 稳定排序 | 非稳定排序 |
| 按自然性 | 自然排序 | 非自然排序 |
按存储介质可分为:
● 内部排序:数据量不大、数据在内存,无需内外存交换数据
● 外部排序:数据量大,数据在外存(文件排序) 外部排序时,要将数据分批调入内存排序,中间结果还要即使放入外存,显然外部排序要复杂得多。
按比较器个数排序可分为:
● 比较排序:用比较的方法,插入排序、交换排序、选择排序、归并排序
● 基数排序:不比较元素的大小、仅仅根据元素本身的取值确定有序位置。
按辅助空间可分为:
● 原地排序:辅助空间用量为O(1)的排序方法。(所占的辅助空间与排序的数据量大小无关)
● 非原地排序:辅助空间用量超过O(1)的排序方法。
按稳定性可分为:
● 稳定排序:能够使任何数值相等的元素,排序以后相对次序不变。
● 非稳定性排序:不是稳定排序的方法。
排序的稳定性只对结构类型数据排序有意义
例如:n个学生信息(学号、姓名、语文、数学、英语、总分)
1、按数学成绩从高到低排序
2、按照总分从高到低排序
3、总分相同的情况下,数学成绩高的排在前面
按自然性可分为:
● 自然排序:输入数据越有序,排序的速度越快的排序方法。
● 非自然排序:不是自然排序的方法。
8.1.3、学习内容

按排序依据原则
● 插入排序:直接插入排序、折半插入排序、希尔排序
● 交换排序:冒泡排序、快速排序
● 选择排序:简单选择排序、堆排序
● 归并排序:2-路归并排序
● 基数排序
按排序所需工作量
● 简单的排序方法:T(n) =O(n2n^2n2) 基数排序:T(n) = O(d.n)
● 先进的排序方法:T(n) = O(nlogn)
存储结构——记录序列以顺序表存储

#define MAXSIZE 20 //设记录不超过20个
typedef int KeyType; //设关键字为整型量(int型)typedef struct { //定义每个记录(数据元素)的结构KeyType key; //关键字lnfoType othernfo;//其他数据项
}RedType; //Record TypeTypedef struct{ //定义顺序表的结构RedType r[MAXSIZE + 1]; //存储顺序表的向量//r[0]一般作哨兵或缓冲区int length; //顺序表的长度
}SqList;
8.2、插入排序
基本思想:
每步将一个待排序的对象,按其关键码大小,插入到前面已经排序好的一组对象的适当位置上,直到对象全部插入为止。
即边插入边排序,保证子序列中随时都是排好序的。
基本操作:有序插入
● 在有序序列中插入一个元素,保持序列有序,有序长度不断增加。
● 起初,a[0]是长度为1的子序列。然后,逐一将a[1]至a[n-1]插入有序子序列中。
● 在插入a[i]前,数组a的前半段(a[0]~a[i-1]) 是有序段,后半段(a[i]~a[n-1])是停留于输入次序的“无序段”。
● 插入a[i]使a[0]~a[i-1]有序,也就是要为a[i]找到有序位置j(0≤j≤i),将a[i]插入在a[j]的位置上。
插入位置图示
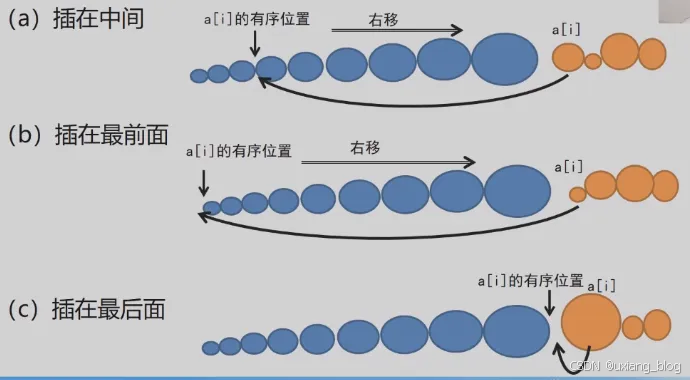
怎么找到插入位置j?
插入排序的种类
| 插入排序 | 插入排序的种类 |
|---|---|
| 顺序法定位插入位置 | 叫直接插入排序 |
| 二分法定位插入位置 | 叫二分插入排序 |
| 缩小增量多遍插入排序 | 叫希尔排序 |
8.2.1、直接插入排序:todo
直接插入排序———算法描述
直接插入排序——采用顺序查找法查找插入位置
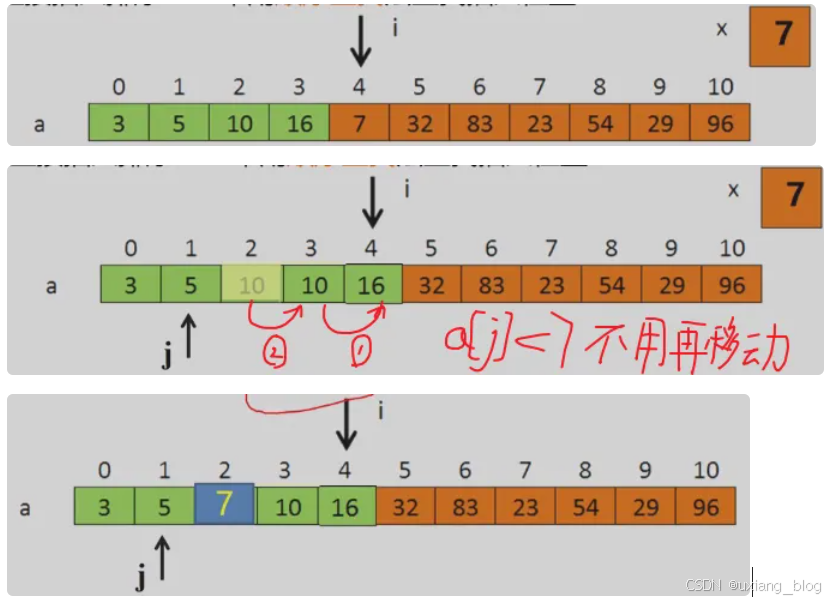
1、复制插入元素 x=a[i];
2、记录后移,查找插入位置 for(j=i-1;j>=0&&x<a[j];j–)a[j+1]=a[j];
3、插入到正确位置 a[j-1]=x;
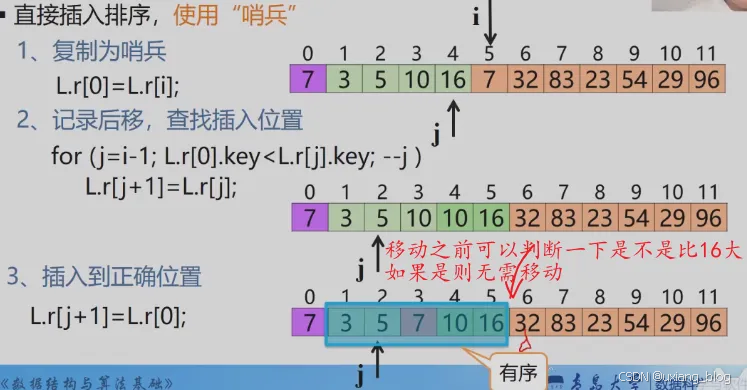
直接插入排序算法(i是插入元素,j是记录元素)

void lnsertSort(SqList &L){int i,j;for(i=2;i<=L.length;++i){if(L.r[i].key < L.r[i-1].key){//若“<”,需将L.r[i]插入有序子表L.r[0] = L.r[i]; //复制为哨兵for(j = i-1;L.r[0].key < L.r[j].key; --j){L.r[j+1] = L.r[j]; //记录后移}L.r[j+1] = L.r[0]; //插入到正确位置} }
}
直接插入排序——性能分析
实现排序的基本操作有两个:
(1)、"比较"序列中两个关键字的大小;
(2)、"移动"记录。
最好的情况(关键字在记录序列中顺序有序):
11 25 32 47 56 70 81 85 92 96
“比较”的次数:∑i=2n1=n−1\sum_{i=2}^n 1 = n -1∑i=2n1=n−1
“移动”的次数:O
最坏的情况(关键字在记录序列中逆序有序):
移动前:85 92 96 81(移动元素) 70 56 47 32 25 11
移动后: 81(移动元素) 85 92 96 70 56 47 32 25 11
"比较"的次数:∑i=2ni=(n+2)(n−1)2\sum_{i=2}^n i = \frac{(n+2)(n-1)}{2}∑i=2ni=2(n+2)(n−1)
"移动"的次数:∑i=2n(i+1)=(n+4)(n−1)2\sum_{i=2}^n (i + 1)= \frac{(n+4)(n-1)}{2}∑i=2n(i+1)=2(n+4)(n−1)
平均的情况:
比较次数:∑i=2ni+12=(n+2)(n−1)4\sum_{i=2}^n \frac{i + 1}{2}= \frac{(n+2)(n-1)}{4}∑i=2n2i+1=4(n+2)(n−1)
移动次数:∑i=2ni+12+1=(n+6)(n−1)4\sum_{i=2}^n \frac{i + 1}{2}+1= \frac{(n+6)(n-1)}{4}∑i=2n2i+1+1=4(n+6)(n−1)
时间复杂度结论
● 原始数据越接近有序,排序速度越快
● 最坏情况下(输入数据是逆有序的) Tw(n) = O(n2n^2n2)
● 平均情况下, 耗时差不多是最坏情况的一般 Te(n) = O(n2n^2n2)
● 要提高查找速度
○ 减少元素的 比较次数
○ 减少元素的移动次数
8.2.2、折半插入排序
查找插入位置时采用折半查找法
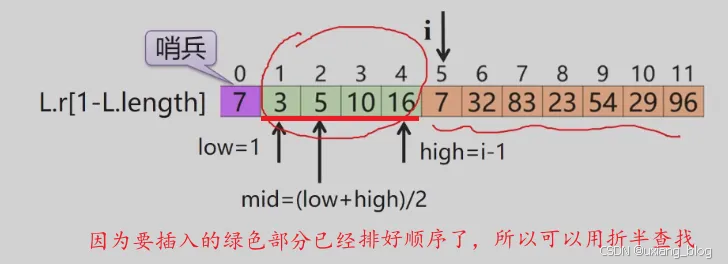
折半插入排序——算法描述

void BlnsertSort(SqList & L){for(i = 2; i <= L.length; ++i){//依次插入第2~第n个元素L.r[0] = L.r[i]; //当前插入元素到“哨兵”位置low = 1; high = i-1;//采用二分查找法插入位置while(low <= high){mid = (low + high)/2;if(L.r[0].key < L.r[mid].key) high = mid -1;else low = mid + 1;}//循环结束,high + 1则为插入位置for(j = i - 1;j >= high + 1; --j) L.r[j + 1] = L.r[j];L.r[high + 1] = L.r[0];//插入到正确的位置}
}//BlnserSort
折半插入排序——算法分析todo
● 折半查找比顺序查找快,所以折半插入排序就平均性能来说比较直接插入排序要快;
● 它所需要的关键码比较次数与待排序对象序列的初始排列无关,仅依赖于对象个数。在插入第i个对象时,需要经过|log2ilog_2ilog2i| +1次关键码比较,才能确定它应插入的位置;
○当n较大时,总关键码比较次数比直接插入排序的最坏情况要好得多,但比其最好情况要差;
○在对象的初始化排列已经按关键排好序或接近有序时,直接插入排序比折半插入排序执行的关键码比较次数要少;
● 折半插入排序的对象移动次数与直接插入排序相同,依赖于对象的初始化排列
○ 减少了比较次数,但没有减少移动次数
○ 平均性能优于直接插入排序
■ 时间复杂度为O(n2n^2n2)
■ 空间复杂度为O(1)
■ 是一种稳定的排序方法
8.2.3、希尔排序
希尔排序————算法描述
思考——希尔排序算法思想的出发点
● 可以增大移动的步幅吗? 比较一次,移动一步; 比较一次,移动一大步?
● 直接插入排序在什么情况下效率比较高?
○ 直接插入排序在基本有序时,效率较高
○ 在待排序的记录个数较少时,效率较高
基本思想:
先将整个待排序记录序列分割成若干子序列,分别进行直接插入排序,待震哥哥序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
例如:
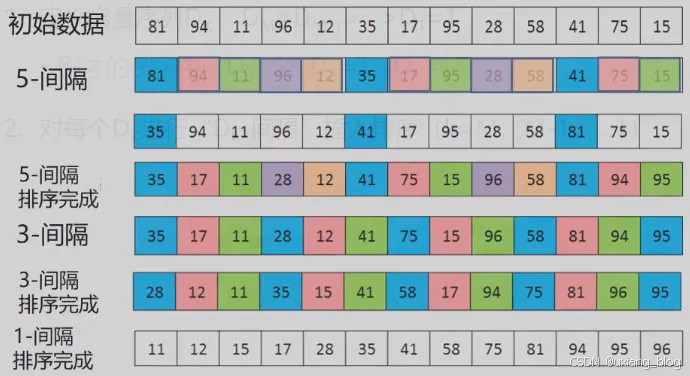
由图可以看出希尔排序思路:
1、定义增量序列DkD_kDk:DM>D(M−1)>...>D1=1D_M>D_(M-1)>...>D_1 = 1DM>D(M−1)>...>D1=1
● 刚才的例子中:D3=5,D2=3,D1=1D_3=5,D_2 = 3,D_1 =1D3=5,D2=3,D1=1
2、对每个Dk进行“Dk-间隔”插入排序(k = M, M-1, …1)
希尔排序特点
● 一次移动,移动位置较大,跳跃式地接近排序后的最终位置
● 最后一次只需要少量移动
● 增量序列必须式递减的,最后一个必须是1
● 增量序列应该是互质的
希尔排序算法(主程序)
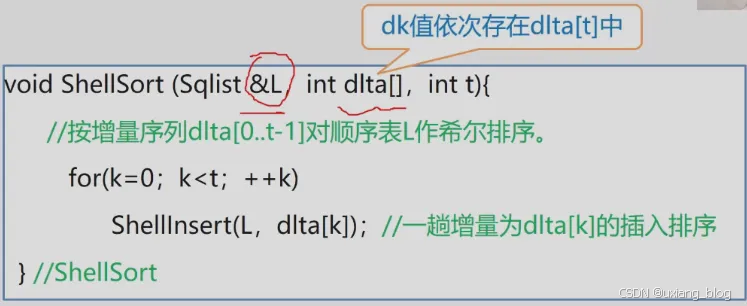
希尔排序算法(其中某一趟的排序操作)
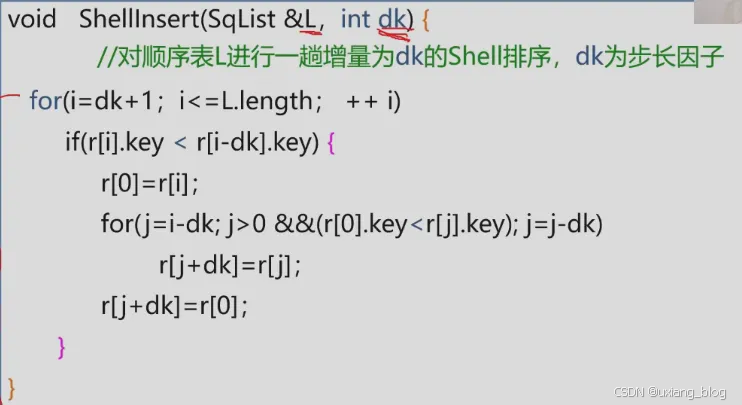
/*
希尔排序算法(主程序)
*/
void ShellSort(Sqlist &L int dlta[], int t){//按增量序列dlta[0...t-1]对顺序表L作希尔排序。for(k = 0; k < t; ++k)Shelllnsert(L,dlta[k]);//一趟增量为dlta[k]的插入排序
}//ShellSort
/*
希尔排序算法——其中某一趟的排序算法
*/
void Shelllnsert(SqList &L, int dk){//对顺序表L进行一趟增量为dk的Shell排序,dk为步长因子for(i = dk + 1; i <= L.length; ++i)if(r[i].key < r[i-dk].key){r[0] = r[i];for(j = i - dk; j > 0 &&(r[0].key < r[j].key);j = j - dk)r[j + dk] = r[j];r[j + dk] = r[0];}
}
希尔排序————算法分析
希尔排序算法效率与增量序列的取值有关
● Hibbard增量序列
○ Dk = 2k-1 ——
○ 最坏情况:Tworst = O(n3/2)
○ 猜想:Tavg = O(n5/4)
● Sedgewick增量序列
○ {1,5,19,41,109,…} ——94i-92i或4i-3*2i +1
○ 猜想:Tavg = O(n7/6) Tworst = O(n4/3)
希尔排序算法的稳定性
希尔排序法是一种不稳定的排序算法。
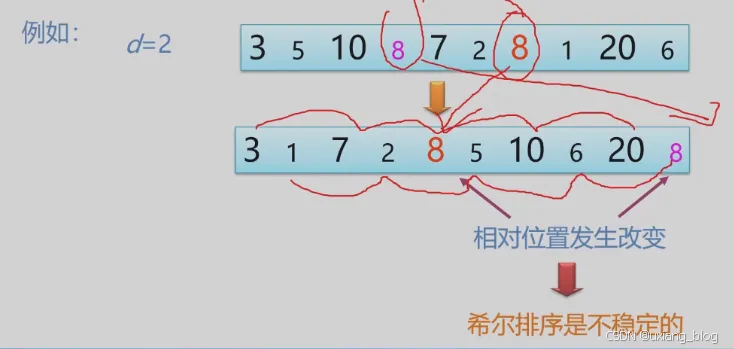
● 时间复杂度是n和d的函数:O(n1.25) ~ O(1.6n1.25)——经验公式
● 空间复杂度为O(1)
● 是一种不稳定的排序方法
○ 如何选最佳d序列,目前尚为解决
■ 最后一个增量值必须为1,无除了1之外的公因子
■ 不宜在链式存储结构上实现
8.3、交换排序
基本思想:
两两比较,如果发生逆序则交换,直到所有记录都排好序为止。
常见的交换排序方法:
● 冒泡排序O(n2n^2n2)
● 快速排序O(nlog2nnlog_2nnlog2n)
1、冒泡排序——基于简单交换思想
基本思想:每趟不断将记录两两比较,并按“前小后大”规则交换。
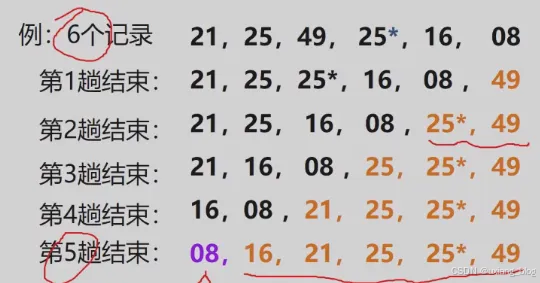
冒泡排序排序过程(升序)
初始:21, 25, 49, 25*, 16, 08 n =6
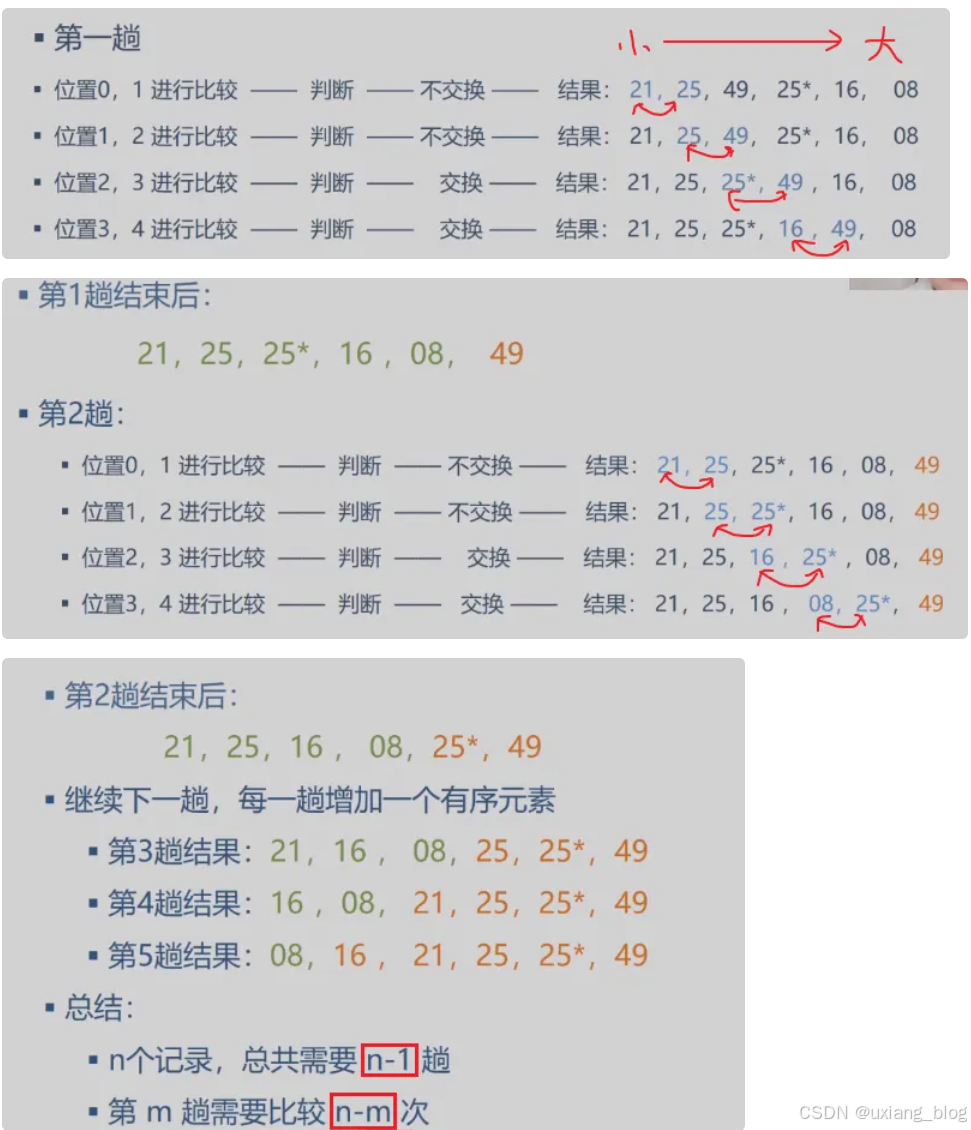
冒泡排序算法
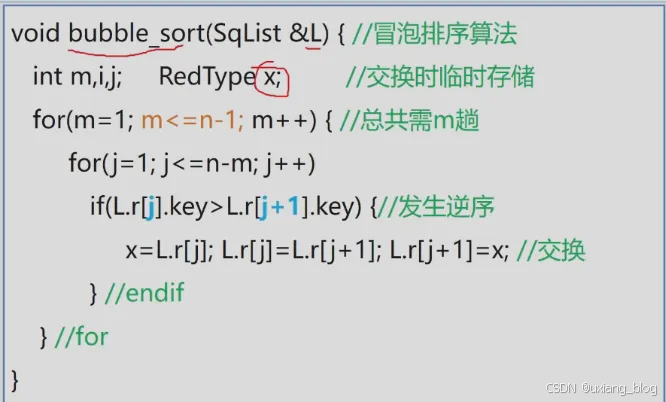
/*
冒泡排序算法
*/
void bubble_sort(SqList &L){int m,i,j; RedType x; //交换时临时存储for(m = 1; m < n -1; m++){//总共需m趟for(j = 1; j <= n - m; j++)if(L.r[j].key > L.r[j + 1].key){发生逆序x = L.r[j]; L.r[j] = L.r[j + 1]; L.r[j + 1] = x;//交换}//endif}//for
}
冒泡排序算法改进
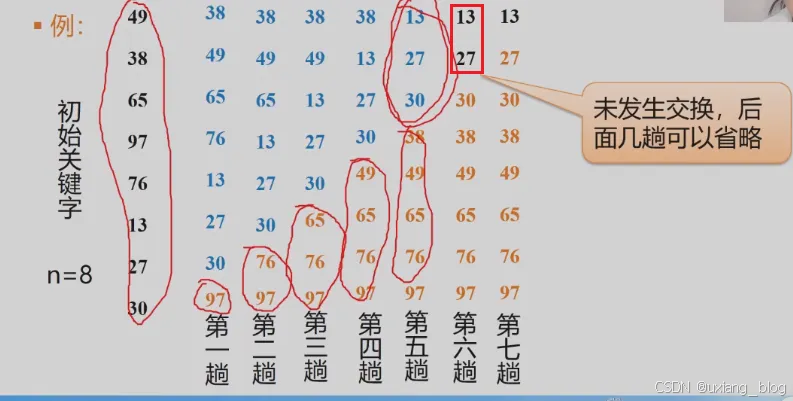
改进的冒泡排序算法

/*
改进的冒泡排序算法
*/
void bubble_sort(SqList &L){int m,i,j,flag = 1; RedType x;//flag 作为是否有交换的标记for(m = 1; m <= n-1 && flag == 1; m++){flog = 0;for(j = 1;j <= m; j++)if(L.r[j].key > L.r[j + 1].key){//发生逆序flag = 1;//若发生交换,flag置为1,若本趟没发生交换,flag保持为0x = L.r[j]; L.r[j] = L.r[j + 1]; r[j + 1] = x;//交换}//endif}//for
}
冒泡排序算法分析
时间复杂度
● 最好情况(正序)
○ 比较次数:n - 1
○ 移动次数: 0
● 最坏情况(正序)
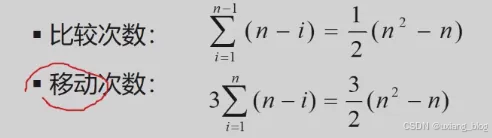
冒泡排序的算法评价
● 冒泡排序最好时间复杂度是O(n)
● 冒泡排序最坏时间复杂度为O(n2n^2n2)
● 冒泡排序平均时间复杂度为O(n2n^2n2)
● 冒泡排序算法中增加一个辅助空间temp,辅助空间为S(n) = O(1)
● 冒泡排序是稳定的
2、改进的交换排序——快速排序
基本思想:
● 任取一个元素(如:第一个)为中心(pivot: 枢轴、中心点)。
● 所有比它小的元素一律前放,比它大的元素一律后放,形成左右两个子表;
● 对各子表重新选择中心元素并依次规则调整——递归思想 ,
● 直到每个子表的元素只剩下一个
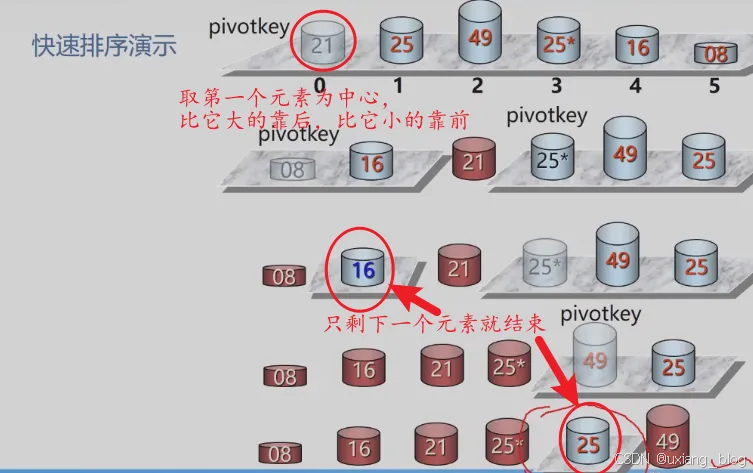
快速排序分析:
基本思想:通过一趟排序,将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分冀鲁豫进行排序,以达到整个序列有序
具体实现:选定一个中间数作为参考,所有元素与之比较,小的调到左边,大的调到右边。
(枢轴)中间数:可以是第一个数、最后一个数、最中间一个数、任选一个数等。——这里有个简单的规则,把第一个数作为中间数,然后其他的依次从1~8比较,放到左右两边,剩下的位置就留给中间数,此处49`可能在4号位置上,也可能在5号位置上,两种可能性都是正确的,但有个缺点是要用到额外空间。

——为了解决这个缺点,有另外一种方法,如下:
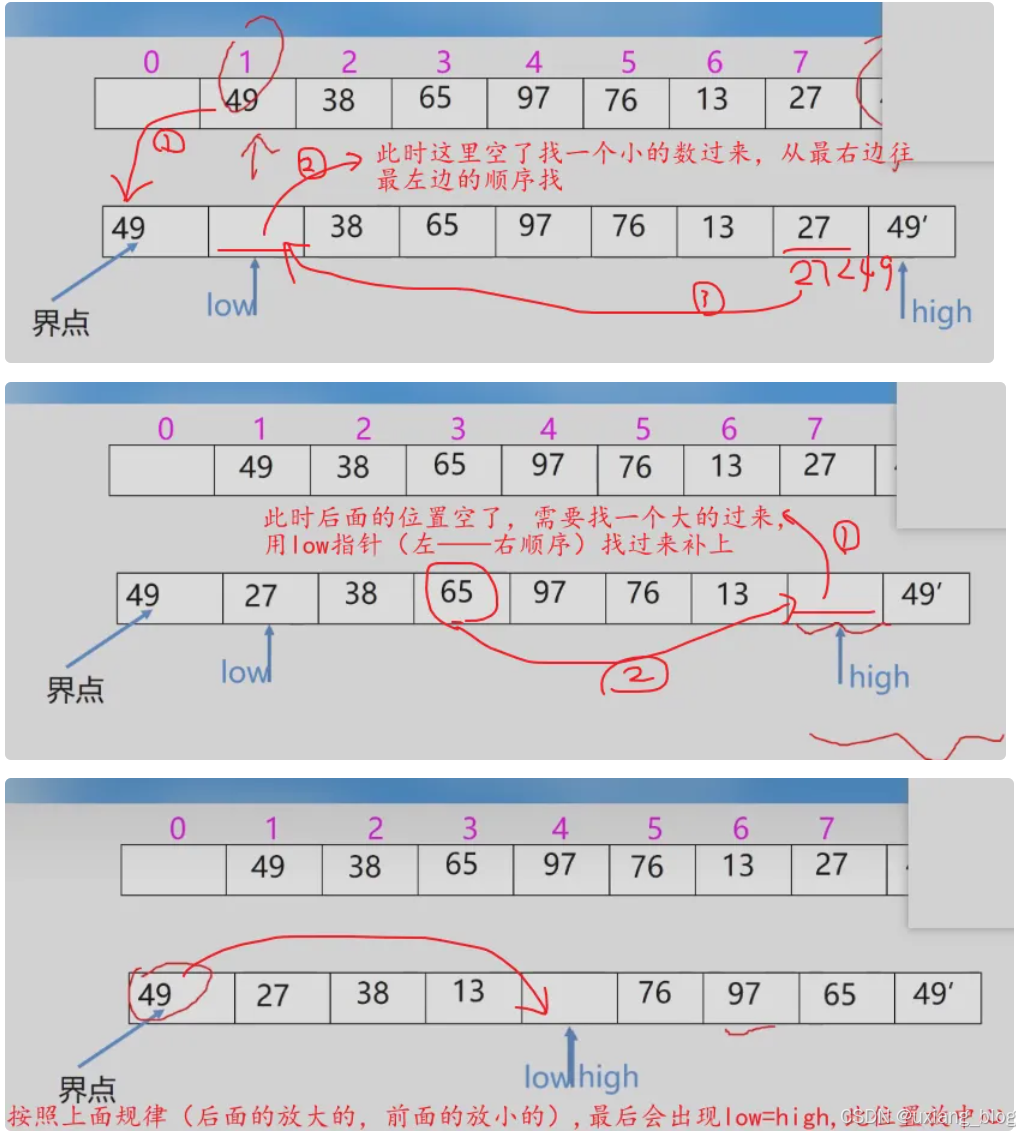
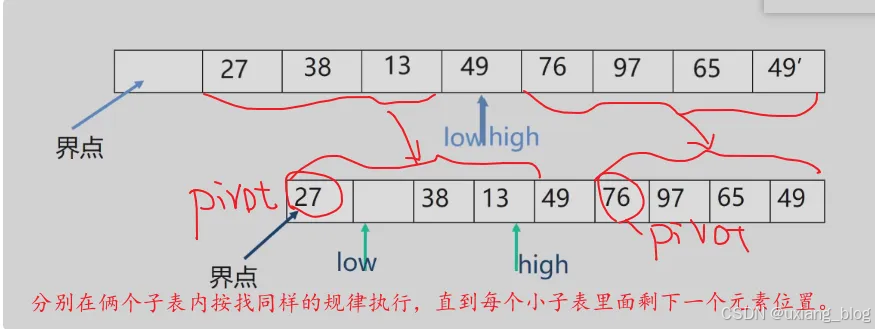
快速排序的特点:
● 每一趟的子表的形成是采用从两头向中间交替式逼近法;
● 由于每趟中对各子表的操作都相似,可采用递归算法。
快速排序算法:todo

void main(){QSort(L,1,L.length);
}
/*
对顺序表L快速排序
*/void QSort(SqList & L,int low, int high){//对顺序表L快速排序if(low < high){//长度大于1pivotloc = Partition(L,low,high);//将L.r[low..high]一分为二,pivotloc为枢轴元素排好序的位置QSort(L,low,pivotloc - 1);//对低子表递归排序QSort(L,pivotloc + 1,high);//对高子表递归排序}//endif
}//QSort/*
定位中心点位置
*/
int Partition(SqList & L, int low, int high){L.r[0] = L.r[low]; pivotkey = L.r[low].key;while(low < high){while(low < high && L.r[high].key >= pivotkey) --high;L.r[low] = L.r[high];while(low < high && L.r[low].key <= pivotkey) ++low;L.r[high] = L.r[low];}L.r[low] = L.r[0];return low;
}
快速排序算法分析:
时间复杂度
● 可以证明,平均计算时间是O(nlog2nnlog_2nnlog2n)。
○ Qsort()😮(nlog2nnlog_2nnlog2n)
○ Partition()😮(n)
● 实验结果表明:就平均计算时间而言,快速排序是我们所讨论的所有内排序方法中最好的一个。
空间复杂度
快速排序不是原地排序 由于程序中使用了递归,需要递归调用栈的支持,而栈的长度取决于递归调用的深度。(即使不用递归,也需要用用户栈)
● 在平均情况下:需要O(nlognnlognnlogn)的栈空间
● 最坏情况下:栈空间可达O(n)。
稳定性
快速排序是一种不稳定的排序方法。

思考:
试对(90、85、79、68、50、46)进行快速排序的划分
● 你是否发现什么特殊情况?
● 再对(46,50,68,74,85,90)进行快速排序划分呢?
由于每次枢轴记录的关键字都是大于其他所有记录的关键字,致使依次划分之后得到的子序列(1)的长度为0,这时已经退化成没有改进措施的冒泡排序。
● 快速排序不适用于对原本有序或基本有序的记录序列进行排序。
● 划分元素的选取是影响时间性能的关键
● 输入数据次序越乱,所划分元素值得随机性越好,排序速度越快。快速排序不是自然排序方法。
● 改变划分元素得选取方法,至多只能改变算法平均情况下得时间性能,无法改变最坏情况下的时间性能。即使最坏情况下,快速排序的时间复杂性总是O(n2n^2n2)
8.4、选择排序
1、简单选择排序
基本思想:在待排序的数据中选出最大(小)的元素放在其最终的位置。
基本操作:
● 1、首先通过n - 1 次关键字比较,从n个记录中找出关键字最小的记录,将它与第一个记录交换
● 2、再通过n - 2次比较,从剩余的 n - 1个记录中找出关键字次小的记录,将它与第二个记录交换
● 3、重复上述操作,共进行n - 1趟排序后,排序结束。
用图演示:
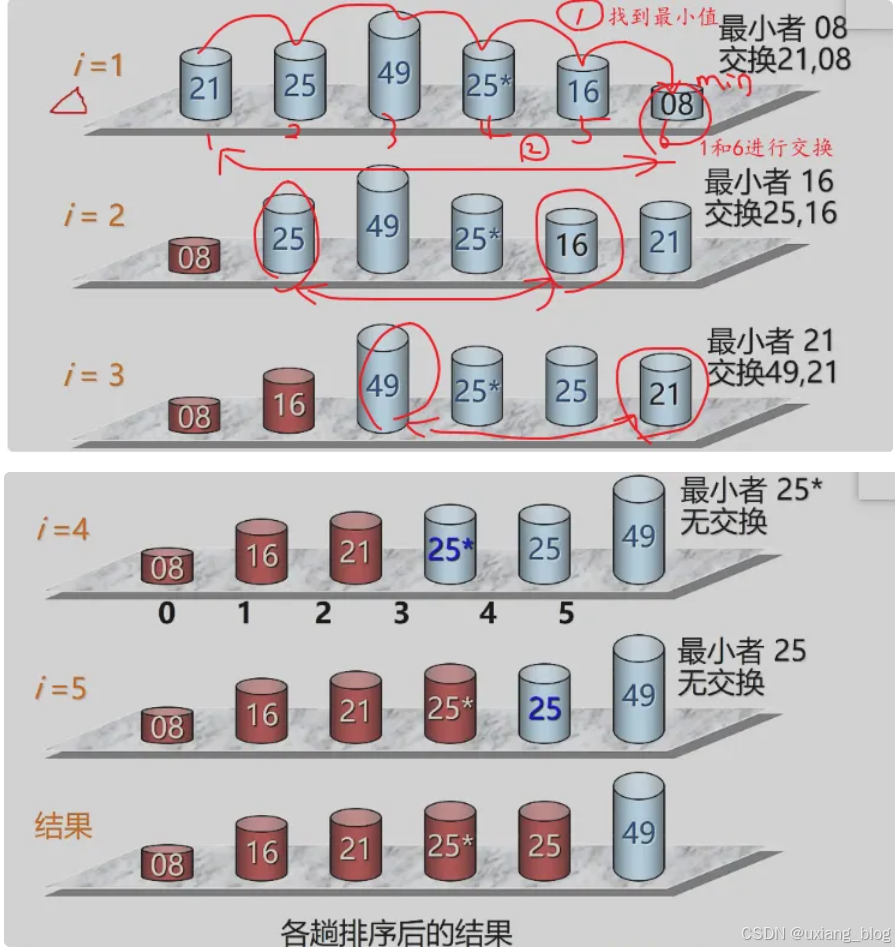
简单选择排序算法todo

void SelectSort(SqList &K){for(i = 1; i < L.length; ++i){k = i;for(j = i + 1; j < L.length; j++){if(L.r[j].key < L.r[k].key) k = j;//记录最小位置}if(k != i) L.r[i] <—— ——> L.r[k];//交换}
}
简单选择排序算法分析
时间复杂度
● 记录移动次数
○ 最好情况: 0
○ 最坏情况:3(n - 1)
● 比较次数:无论待排序列处于什么状态,选择排序所需进行的“比较”次数都相同∑i=1n−1(i−1)=n(n−1)2\sum_{i=1}^{n-1} (i-1) = \frac{n(n-1)}{2}∑i=1n−1(i−1)=2n(n−1)
算法稳定性
● 简单选择排序是不稳定排序
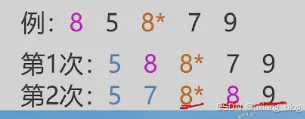
2、堆排序
堆定义

从堆的定义可以看出,堆实质是满足如下性质的完全二叉树:二叉树中任一非叶子结点均小于(大于)它的孩子结点。
例:判断是否是堆?
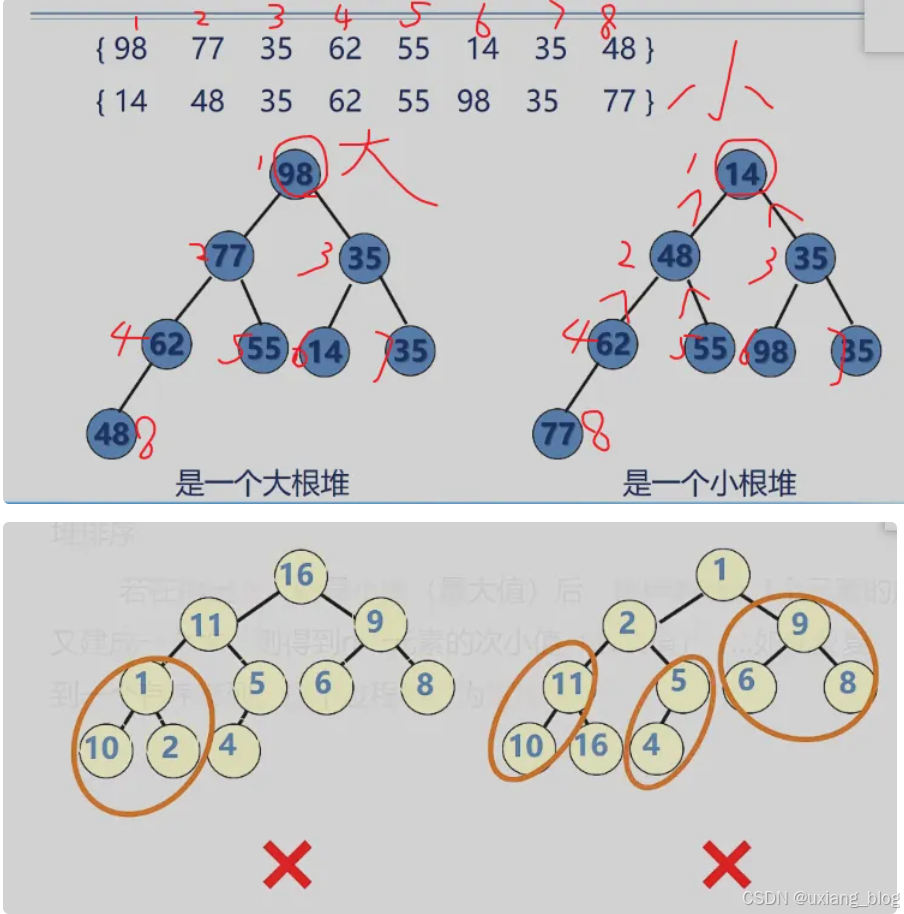
堆排序
若在输出堆顶的最小值(最大值)后,使得剩余n -1个元素的序列重又建成一个堆,则得到n个元素的次小值(次大值)…如此反复,便能得到一个有序序列,这个过程称之为堆排序。
实现推排序需要解决两个问题:
● 1、如何由一个无序序列建成一个堆?
● 2、如何在输出堆顶元素后,调整剩余元素为一个新的堆?
下面先讨论第二个问题:
堆的调整:
如何在输出堆顶元素后,调整剩余元素为一个新的堆?
小根堆:
● 1、输出堆顶元素之后,以堆中最后一个元素代替之;
● 2、然后将根结点值与左、右子树的根结点值进行比较,并与其中小者进行交换;
● 3、重复上述操作,直至叶子结点,将得到新的堆,将得到新的堆,称这个从堆顶至叶子的调整过程为“筛选”——那么大根堆的调整呢?
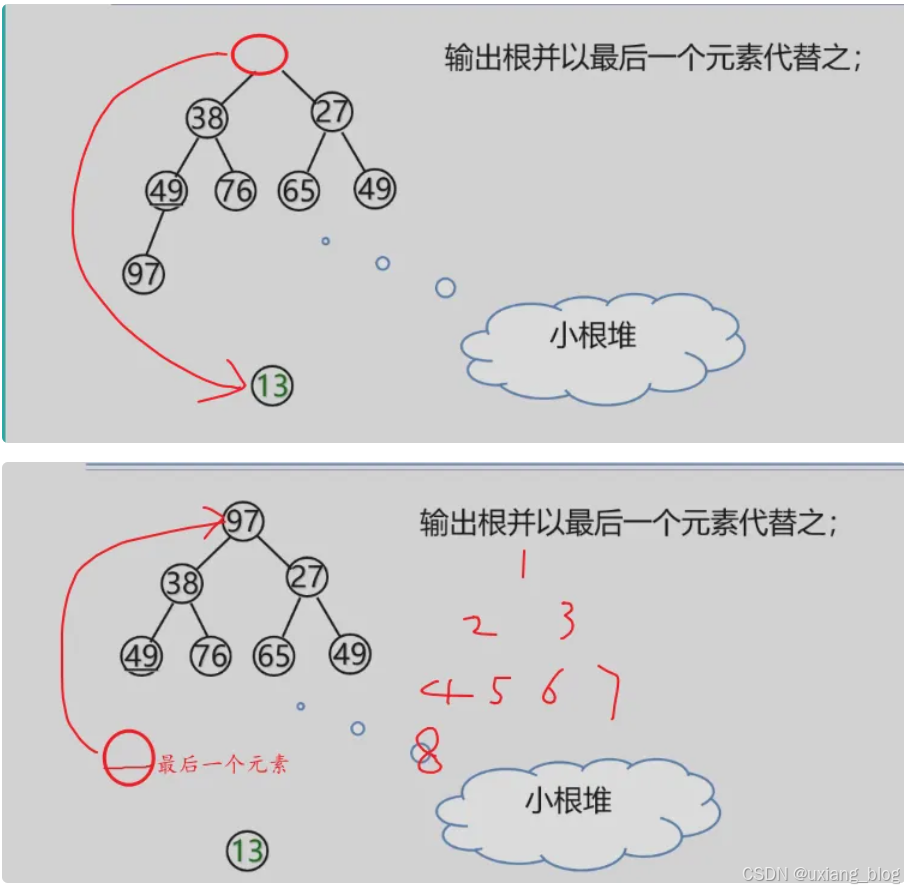
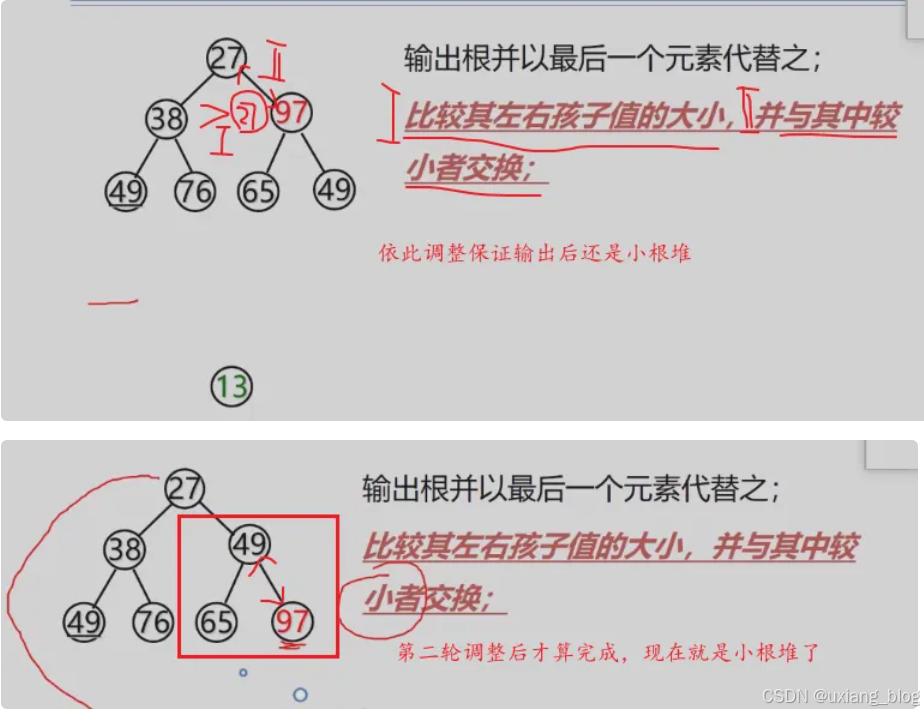
筛选过程的算法描述为:

void HeapAdjust(elem R[],int s,int m){
/*
已知R[s..m]中记录的关键字除R[s]之外均满足堆的定义,
本函数调整R[s..m]成为一个大根堆
*/rc = R[s];for(j = 2 * s;j <= m;j *= 2){//沿key较大的孩子结点向下筛选if(j < m && R[j] < R[j + 1])++j;//j为key较大的记录的下标if(rc >= R[j]) break;R[s] = R[j]; s = j; //rc应插入在位置s上}R[s] = rc;//插入
}//HeapAdjust
可以看出:对一个无序序列反复“筛选”就可以得到一个堆;即:从一个无序序列建堆的过程就是一个反复“筛选”的过程。那么:如何右一个无序序列建成一个堆?
显然:单结点的二叉树是堆;在完全二叉树中所有以叶子结点(序号i>n/2)为根的子树是堆。这样,我们只需依次将以序号为n/2, n/2 -1,…, 1的结点为根的子树均调整为堆即可。即:对应由n个元素组成的无序序列,“筛选”只需从第n/2个元素开始。
由于堆实质上是一个线性表,那么我们可以顺序存储一个堆。下面以一个实例介绍建一个小根堆的过程。
例如:有关键字为49,38,65,97,76,13,27,49的一组记录,将其按关键字调整为一个小根堆。
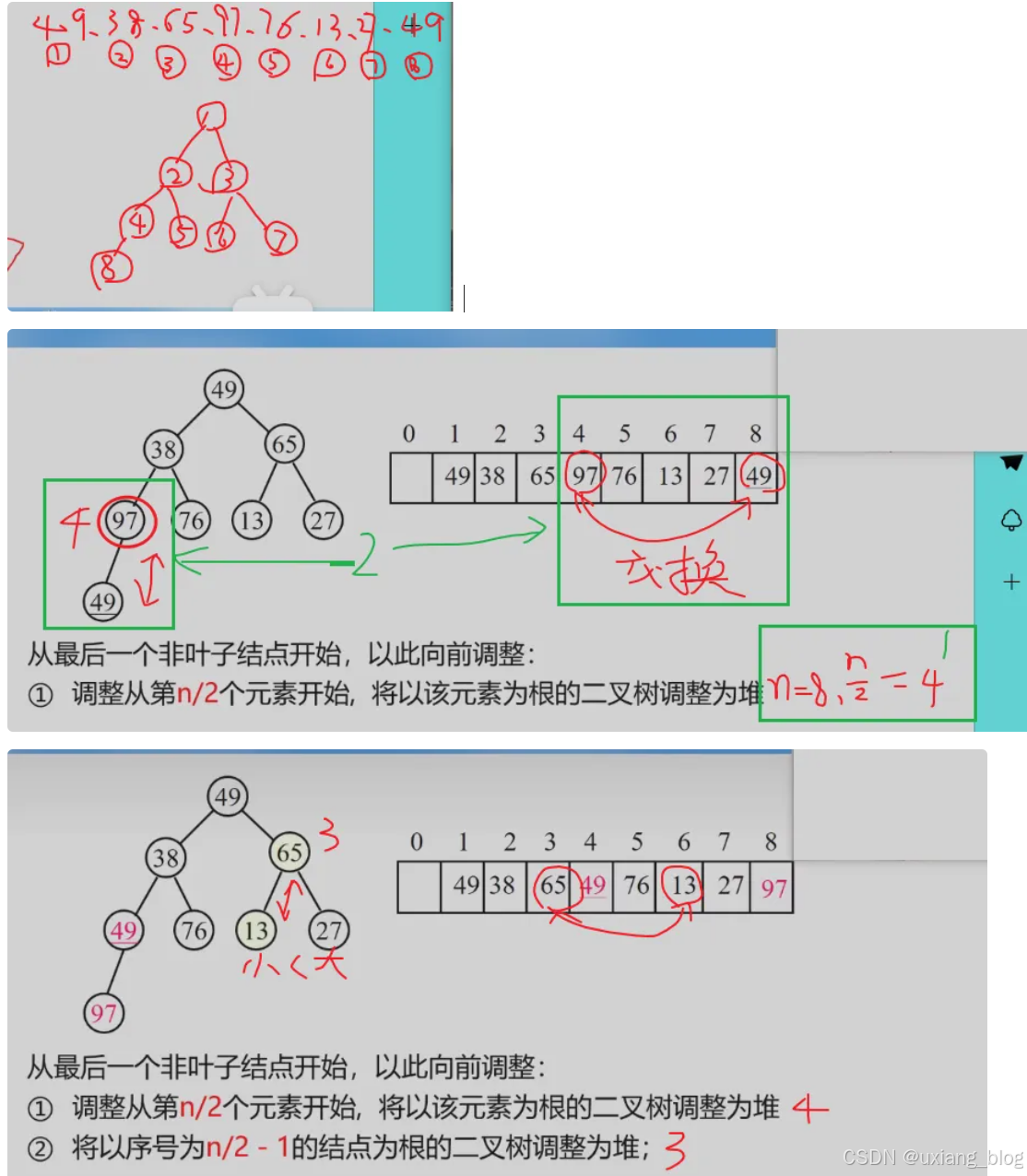
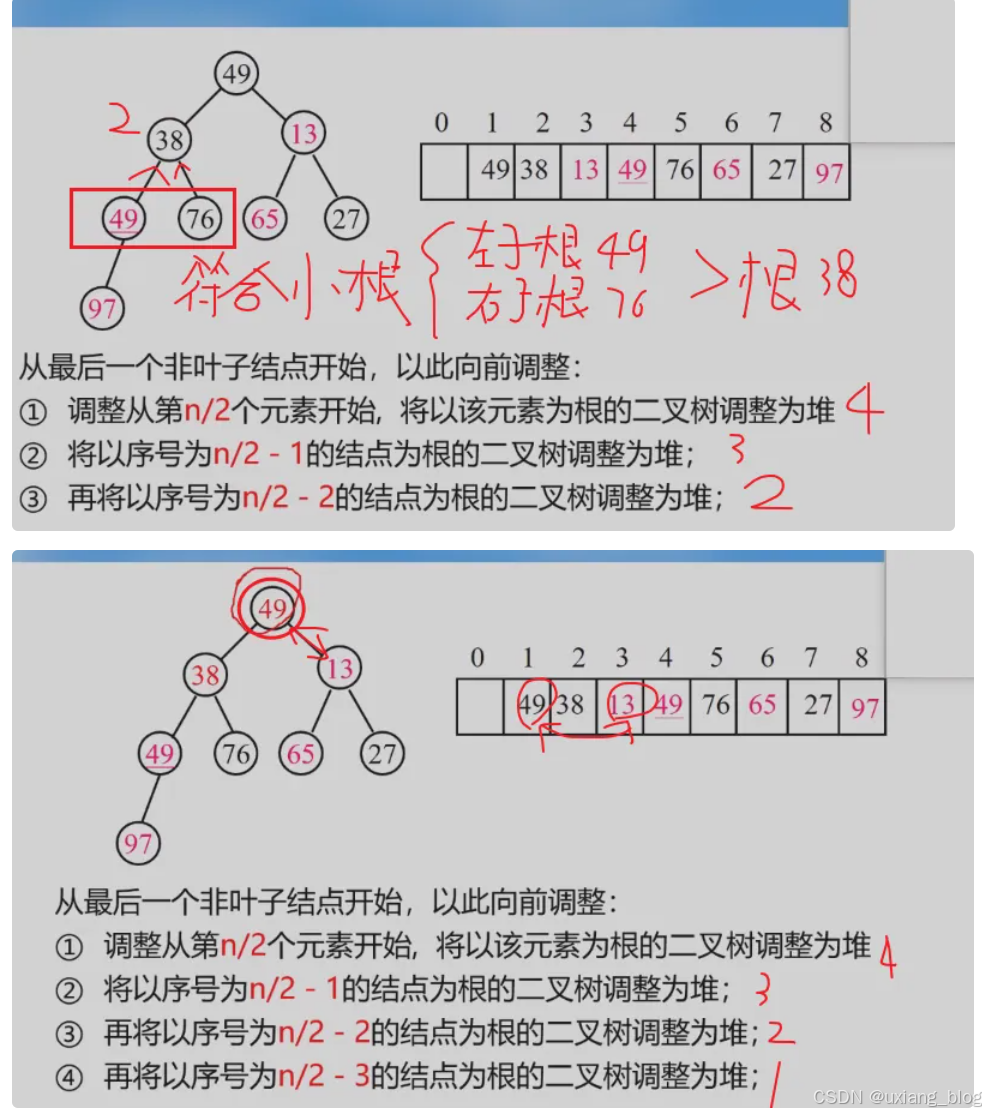
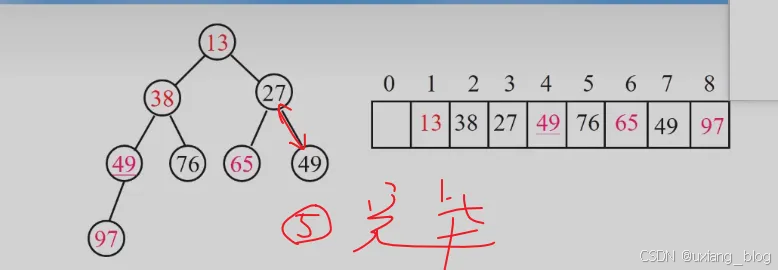
将初始无序的R[1]到R[n]建成一个小根堆,可用以下语句实现:
for(i = n/2;i >= 1; i–) HeapAdjust( R, i ,n);
由以上分析知:若对一个无序序列建堆,然后输出根;重复该过程就可以由一个无序序列输出有序序列。
实质上,堆排序就是利用完全二叉树中父节点与孩子结点之间的内在关系来排序的。
堆排序算法如下:

void HeapSort(elem R[]){//对R[1]到R[n]进行堆排序int i;for(i = n/2; i >= 1; i--)HeapAdjust(R,i,n);//建初始堆for(i = n; i > 1; i--){//进行n - 1趟排序Swap(R[1],R[i]);//根与最后一个元素交换HeapAdjust(R,1,i - 1);//对R[1]到R[i-1]重新建堆}
}//HeapSort
算法性能分析
● 初始堆化所需时间不超过O(n)
● 排序阶段(不含初始堆化)
○ 一次重新堆化所需时间不超过O(longn)
○ n - 1次循环所需要时间不超过O(nlogn)
Tw(n) = O(n) + O(nlogn) = O(nlogn)
● 堆排序的时间主要耗费在建初始堆和调整建新堆时进行的反复筛选上。堆排序在最坏情况下,其时间复杂度也为O(nlog2nnlog_2nnlog2n),这时堆排序的最大优点。无论待排序中的记录是正序还是逆序排列,都不会使堆排序处于“最好”或“最坏”的状态。
● 另外,堆排序仅需一个记录大小供交换用的辅助存储空间。
● 然而堆排序仅是一种不稳定的排序方法,它不适用于待排序记录个数n较少的情况,但对于n较大的文件还是很有效的。
8.5、归并排序
基本思想:将两个或两个以上的有序子序列“归并”为一个有序性序列。
在内部排序中,通常采用的是2-路归1并排序。
● 即:将两个位置相邻的有序子序列R[I…m]和R[m+1…n]归并为一个有序序列R[I…n]
归并排序示例
设初始关键字序列为:[48 34 60 80 75 12 26 48*]
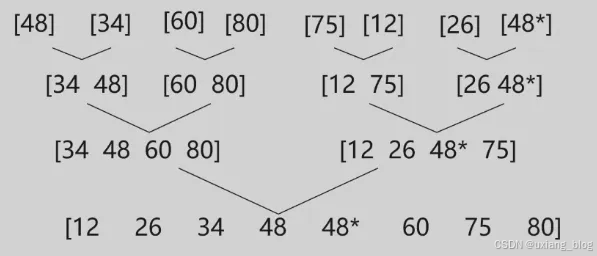
整个归并排序仅需[log2nlog_2nlog2n]趟,趟就是这个序列的深度。
关键问题:如何将两个有序序列合成一个有序序列?
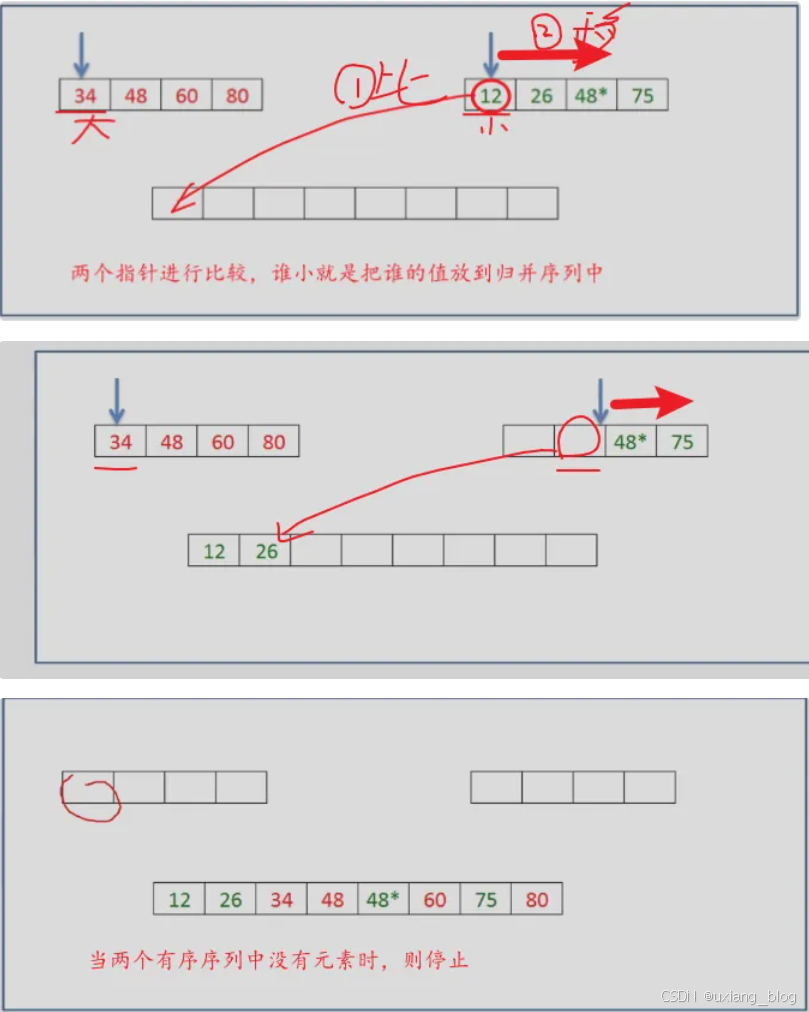
设R[low] - R[mid]和R[mid +1] - R[high]为相邻,归并成一个有序序列R1[low1]-R1[high]。

若SR[i].key <= SR[j].key, 则TR[k] = RS[i]; k++; j++;
否则,TR[k] = SR[j];k++;j++
归并排序算法分析
● 时间效率:O(nlog2nnlog_2nnlog2n)
● 空间效率:O(nnn) 因为需要一个与原始序列同样大小的辅助序列(R1)。这正时此算法的缺点。
● 稳定性:稳定
8.6、基数排序
基本思想:分配 + 收集
也叫桶排序或箱排序:设置若干个箱子,将关键字为k的记录放入第k个箱子,然后再按序号将非空的连接。
基数排序:数字是有范围的,均由0-9这十个数字组成,则只需设置十个箱子,相继按个、十、百…进行排序。


基数排序算法分析
时间效率:O(k*(n + m)) k:关键字个数,m:关键字取值范围为m个值
空间效率:O(n + m)
稳定性:稳定
例如:10000个人按照生日排序todo

8.7、外部排序(略)
8.8、综合比较
1、各种排序方法比较
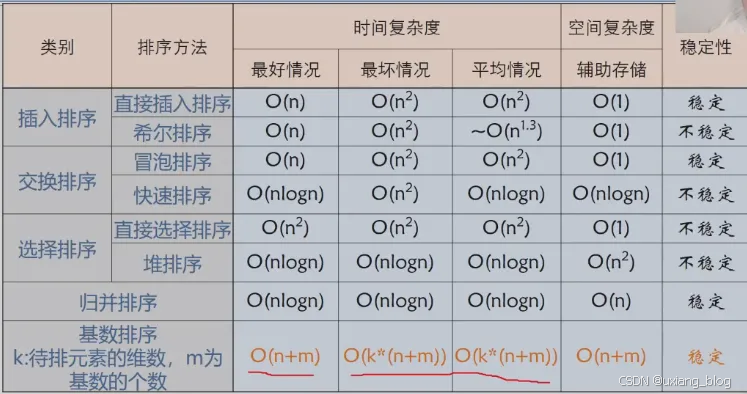
2、各种排序方法的综合比较
时间性能
1、按照平均的时间性能来分,有三类排序方法:
● 时间复杂度为O(nlognnlognnlogn)的方法有:
○ 快速排序、堆排序和归并排序,其中以快速排序为最好;
● 时间复杂度为O(n2n^2n2)的有:
○ 直接插入排序、冒泡排序和简单选择排序,其中以直接插入为最好,特别是对于哪些对关键近似有序的记录序列尤为如此;
● 时间符在度为O(n)的排序方法有:基数排序。
2、当待排记录序列按关键字顺序有序时,直接插入排序和冒泡排序能达到O(n)的时间复杂度;而对于快速排序而言,这是最不好的情况,此时的时间性能退化O(n2n^2n2),因此是应该尽量避免的情况。
3、简单选择排序、堆排序和归并排序的时间性能不随记录序列中的关键字的分布而改变。
空间性能
指的是排序过程所需的辅助空间大小
1、所有的简单排序方法(包括:直接插入、冒泡和选择)和堆排序的空间复杂度为O(1)
2、快速排序为O(longn),为栈所需的辅助空间
3、归并排序所需辅助空间最多,其空间复杂度为O(n)
4、链式基数排序需附设队列首尾指针,则空间复杂度为O(rd)
排序方法的稳定性能
● 稳定的排序方法指的式,对于两个关键字相等的记录,它们在序列中的相对位置,在排序之前和经过排序之后,没有改变。
● 当对多关键字的记录序列进行LSD方法排序时,必须采用稳定的排序方法。
● 对于不稳定的排序方法,只要能举出一个实例说明即可。
● 快速排序和堆排序是不稳定的排序方法。
关于“排序方法的时间复杂度的下限”
● 本章讨论的各种排序方法,除基数排序外,其它方法都是基于“比较关键字”进行排序的排序方法,可以证明,这类排序法可能达到的最快的时间复杂度为O(nlogn)。(基数排序不是基于“比较关键字”的排序方阿飞,所以它不受这个限制)。
● 可以用一棵判定树来描述这类基于“比较关键字”进行排序的排序方法。