【LeetCode热题100】No.128——最长连续序列
今天继续更新LeetCode热题100系列,第三题我们聚焦高频难题“最长连续序列”。这道题的核心考点是“时间复杂度优化”,常规的排序思路无法满足题目要求,需要借助哈希表实现高效查找。接下来,我们从题目分析、思路推导到Java代码实现,逐步拆解这道题的解题逻辑。
一、题目描述
首先明确题目要求(基于 LeetCode 官方原题):
- 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
- 进阶:你可以设计并实现时间复杂度为 O (n) 的解决方案吗?
示例
示例 1:输入:nums = [100,4,200,1,3,2]输出:4解释:最长数字连续序列是 [1,2,3,4],长度为 4。
示例 2:输入:nums = [0,3,7,2,5,8,4,6,0,1]输出:9解释:最长数字连续序列是 [0,1,2,3,4,5,6,7,8],长度为 9。
提示
- 0 <= nums.length <= 10⁵(数组长度可能为空,需特殊处理)
- -10⁹ <= nums [i] <= 10⁹(数值范围大,无法用数组下标映射)
二、解题思路分析
要解决这道题,首先要明确核心矛盾:题目要求时间复杂度 O (n),而常规的 “排序 + 遍历” 思路时间复杂度是 O (n log n),无法满足进阶要求。因此需要跳出排序思维,用 “哈希表快速查找” 的特性优化流程。
1. 排除无效思路:排序法(时间不达标)
先简单分析排序法的局限性,帮助理解优化方向:
- 思路:先对数组排序,再遍历数组统计连续序列长度(跳过重复元素)。
- 问题:排序的时间复杂度是 O (n log n),不符合 O (n) 的要求,仅适用于简单场景,无法通过进阶测试用例。
2. 最优思路:哈希表 +“起点判定”(O (n) 时间)
核心逻辑
要实现 O (n) 时间,关键是只对 “连续序列的起点” 进行遍历,避免重复处理非起点元素:
- 什么是 “连续序列的起点”?若某个数
x存在于数组中,但x-1不存在于数组中,那么x就是一个连续序列的起点(例如数组[100,4,200,1,3,2]中,100、200、1 是起点)。 - 如何高效判定起点?用哈希表存储数组中的所有元素,判定
x-1是否存在时,时间复杂度为 O (1)。 - 流程:
- 将数组元素存入哈希表(去重,避免重复处理相同数字)。
- 遍历哈希表中的每个元素
x,判断x是否为起点(即x-1不在哈希表中)。 - 若
x是起点,从x开始依次查找x+1、x+2... 是否在哈希表中,统计当前连续序列的长度。 - 记录所有连续序列的最大长度,即为答案。
为什么时间复杂度是 O (n)?
每个元素只会被 “作为起点的元素” 遍历一次(例如序列1,2,3,4中,只有 1 是起点,2、3、4 仅在 1 的遍历中被检查,不会单独作为起点遍历),因此整体遍历次数与元素个数成正比,时间复杂度 O (n)。
三、Java 代码实现
public class Solution {public int longestConsecutive(int[] nums) {// 1. 处理边界:数组为空时,返回0if (nums == null || nums.length == 0) {return 0;}// 2. 将数组元素存入哈希表(HashSet),实现O(1)查找和自动去重Set<Integer> numSet = new HashSet<>();for (int num : nums) {numSet.add(num);}int maxLength = 0; // 记录最长连续序列的长度// 3. 遍历哈希表中的每个元素,判定是否为起点并统计长度for (int num : numSet) {// 判定当前元素是否为连续序列的起点(x-1不在集合中)if (!numSet.contains(num - 1)) {int currentNum = num; // 当前序列的起点int currentLength = 1; // 当前序列的长度(至少包含起点本身)// 从起点开始,依次查找x+1、x+2...是否存在while (numSet.contains(currentNum + 1)) {currentNum++;currentLength++;}// 更新最长序列长度maxLength = Math.max(maxLength, currentLength);}}return maxLength;}
}
代码解析
- 边界处理:当数组为空时,直接返回 0,避免后续空指针异常。
- 哈希表存储:用
HashSet存储数组元素,既实现了 O (1) 的查找效率,又自动去重(例如数组中有重复元素[0,0,1],哈希表中仅保留0和1,避免重复计算)。 - 起点判定与长度统计:
- 对每个元素
num,先判断num-1是否存在:若不存在,说明num是起点。 - 以起点为基础,循环查找
currentNum+1是否存在,每找到一次,序列长度currentLength加 1。 - 用
Math.max更新全局最长序列长度maxLength。
- 对每个元素
- 返回结果:遍历结束后,
maxLength即为最长连续序列的长度。
四、测试案例验证
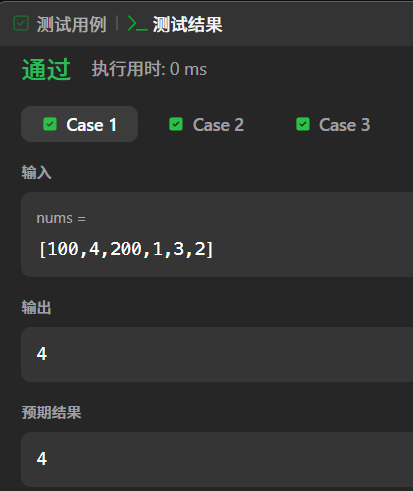
测试案例 1:基础示例
输入:nums = [100,4,200,1,3,2]处理过程:
- 哈希表存储:
{100,4,200,1,3,2}。 - 遍历哈希表元素:
- 100:100-1=99 不在集合中,是起点;查找 101 不存在,当前长度 1,maxLength=1。
- 4:4-1=3 在集合中,不是起点,跳过。
- 200:200-1=199 不在集合中,是起点;查找 201 不存在,当前长度 1,maxLength 仍为 1。
- 1:1-1=0 不在集合中,是起点;查找 2 存在(长度 2)→3 存在(长度 3)→4 存在(长度 4)→5 不存在,当前长度 4,maxLength=4。
- 3:3-1=2 在集合中,不是起点,跳过。
- 2:2-1=1 在集合中,不是起点,跳过。输出:
4,正确。
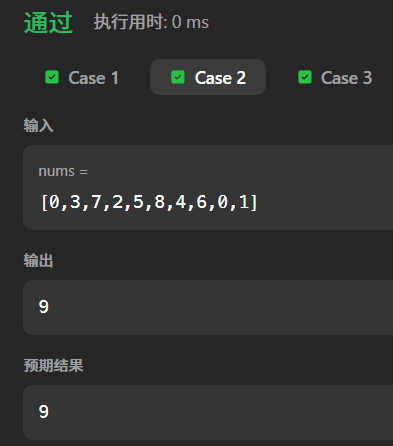
测试案例 2:含重复元素
输入:nums = [0,3,7,2,5,8,4,6,0,1]处理过程:
- 哈希表自动去重后:
{0,1,2,3,4,5,6,7,8}。 - 起点判定:0 是起点(0-1=-1 不存在),依次查找 1-8 均存在,当前长度 9,maxLength=9。输出:
9,正确。
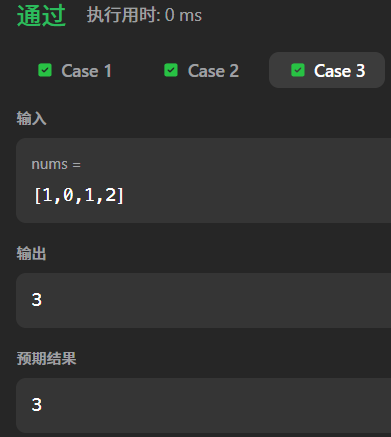
测试案例 3:含重复元素
输入:nums = [1,0,1,2]
- 哈希表自动去重后:
{0,1,2}。 - 起点判定:0是起点(0-1=-1 不存在,此时长度1),查找1(存在,长度2),查找2(存在,长度3),maxLength=3。输出:3,正确
五、复杂度分析
- 时间复杂度:O (n)。数组元素存入哈希表耗时 O (n);遍历哈希表时,每个元素仅被 “起点遍历” 一次,总耗时 O (n),整体时间复杂度 O (n)。
- 空间复杂度:O (n)。哈希表存储数组所有元素,空间与元素个数成正比,最坏情况下(无重复元素)为 O (n)。
六、总结
“最长连续序列” 的解题关键在于用哈希表实现高效查找,并通过 “起点判定” 避免重复遍历,核心要点如下:
- 拒绝排序思路:排序会导致 O (n log n) 时间复杂度,无法满足进阶要求。
- 哈希表的核心作用:既实现 O (1) 的查找效率,又自动去重,减少无效计算。
- 起点判定是关键:仅对 “x-1 不存在” 的元素开始统计序列长度,确保每个元素只被处理一次,最终实现 O (n) 时间复杂度。
如果在代码调试中遇到问题,或想进一步优化细节(如用HashMap存储额外信息),欢迎在评论区留言讨论!下一篇我们继续讲解 LeetCode 热题 100 的下一道题。
