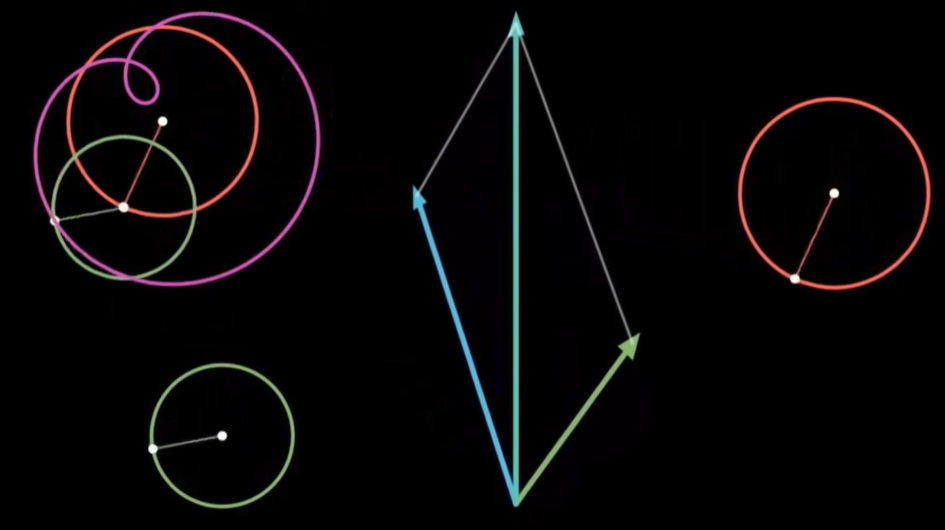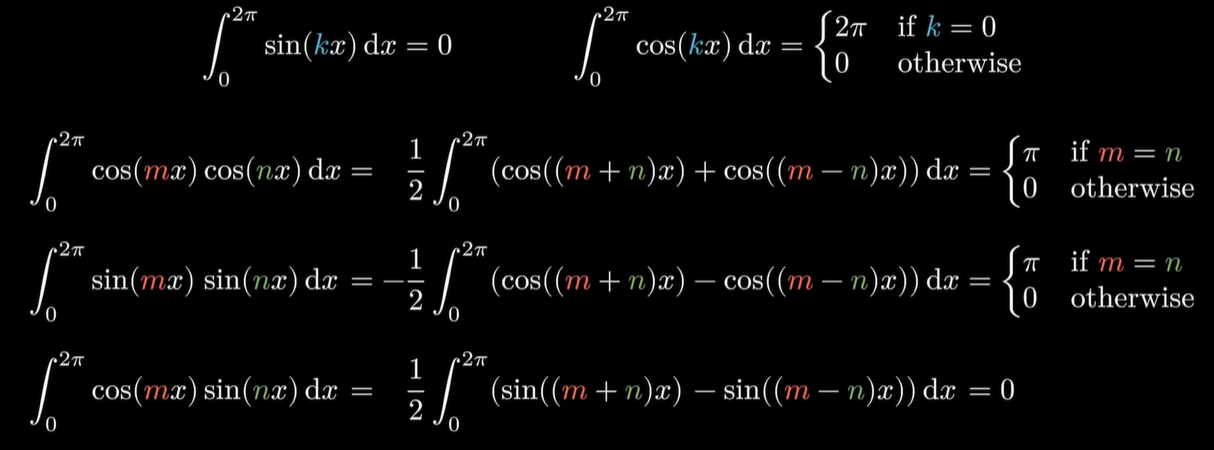【漫士】傅里叶变换，不过就是坐标分解而言

夏天了，很多人都会吃西瓜，可你知道该怎么挑一个好瓜吗，有一个经典的办法那就是听声音。

那这些瓜的声音到底有什么区别呢，初中物理有一个简单的回答叫音色，但这就引出另一个著名的难题，到底什么是音色呢？其实啊，答案要一直等到大学才会揭晓。那就是傅里叶变换。

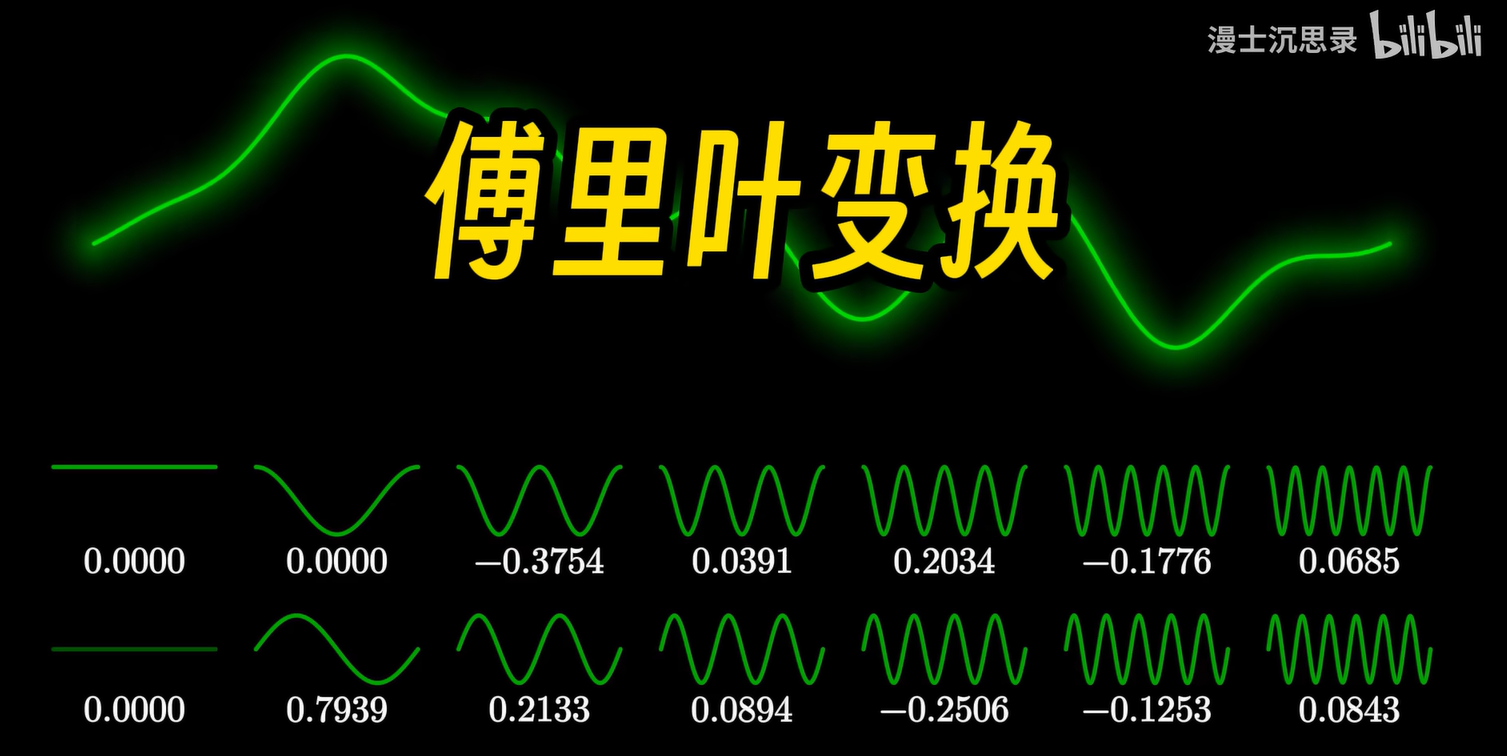
在信号处理、离散算法、偏微分方程中都有重要的应用，堪称现代信息社会的基石。

本期将会用动画，一点点拆解傅里叶变换，在这个过程中，你还能深刻地明白，贯穿数学和哲学里的一整套方法——还原论，的奥秘。

很多人可能都刷过这样的圆上加圆的视频，好几个复杂嵌套的圆，每个有各自的半径和旋转的速度，然后我们追踪这一连串向量最末端那个点的轨迹，神奇的事情发生了，这些看起来机械的转动组合起来，却突然像一个画笔有了生命一样，可以绘制出各种各样的图像

事实上，这些圆的半径和旋转速度是经过精密设计的，从而能够精准描摹出任何预先设定的形状。然而，在炫酷的动画过后，有许多疑惑依然没有解决：这些圆是怎么设计的呢？假如我想画一个自己的形状，我该怎么找到需要的那些神秘的半径和旋转速度呢？甚至有一个更深刻的问题，在整个的问题一开始，为什么会想到用圆上圆来画图？或者是用正弦波的叠加来拟合方波呢？这和视频开头所提到的音色又有什么关系？

几乎没有视频回答这些问题，而这些才是本期想要带你真正弄明白的——傅里叶变换底层的逻辑。

所以我会从一个看起来完全不相关的地方出发，最终带你自己发现并理解傅里叶变换。

① 平面直角坐标系

而旅程的起点是初中我们就很熟悉的平面直角坐标系

我们学过：

两个实数构成的二维坐标和平面上的点构成一一对应：

• 任何一个点往 X 轴和 Y 轴做垂线，在数轴上交点就是横纵坐标；

而反过来

• 横纵坐标的两根垂线，其交点也唯一确定了这个坐标所对应的点；

这些都是我们所熟知的知识，但正因为太熟知，所以我们常常忽略了他的伟大。

笛卡尔创立的坐标系，对未来数学产生最深远的影响，其实是这两根坐标轴，说得更本质一点，就是在这个纷繁复杂的平面几何的世界里，扔进去了两个互相垂直的单位向量——也就是我们俗称的——建系。

在平面几何和立体几何题里，建过系的人一定明白，引入坐标轴向量再计算，是一个多么伟大的发明。

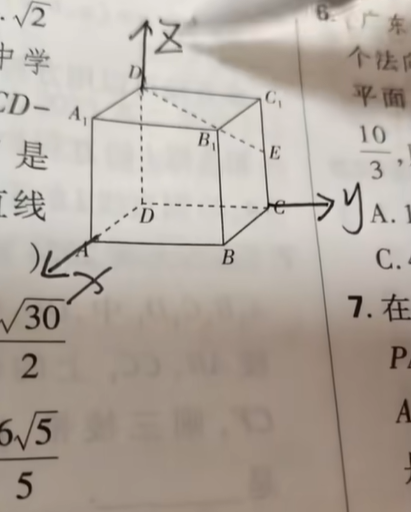
曾经要处理几何问题，人们必须像欧几里德那样，用玄妙的辅助线和辅助圆技巧，通过各种注意到
，用公理不断地推论得到证明。

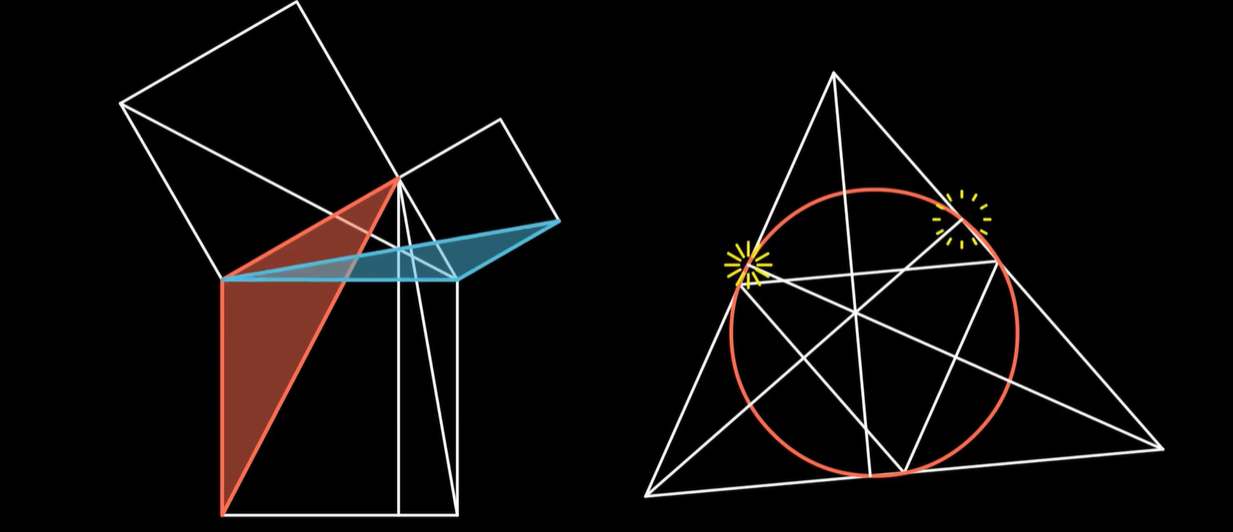
平面几何这种近乎艺术的特性使得它至今仍然活跃在数学奥林匹克的智力竞赛中。

但对于严肃的现代数学来说，相比于怀着膜拜的心情欣赏高斯浑然天成鬼才知道他怎么想到的解法
，我们更希望有一些不需要脑子，甚至机器来按部就班都能解决问题的办法，而建系计算就是这样的方法。

有了坐标系之后：

• 点的位置变成了两个数字；
• 曲线变成了方程；
• 而交点变成了解方程；

等等

算算术可比做辅助线机械暴力多了，也不需要什么天才的注意力，所以只需要按部就班的计算，就能解决几何问题。

总之：

• 坐标系的本质是用坐标轴分解位置。
• 而坐标轴的本质是基底向量。

一旦明确了基底向量，那我们就拥有了一套流畅的双向翻译体系。

• 那么就能用这些数字，线性组合基底，得到这个坐标所对应的抽象的几何空间的位置。
• 而反过来，只要能把一个抽象的向量，在基底下分解成线性组合，那么我们只需要这些组合的系数拼在一块就能得到坐标。

讲到这里，你可能会觉得，嗨呀，颠来倒去不就是“向量加和”和“坐标分解”吗，有什么了不起的。

关键在于，笛卡尔自己当年可能也没想到过：

【向量又何止是向量呢？】

除了二维平面上的点，我们还可以定义各种匪夷所思的向量。

• 只要它支持加法和数乘——线性叠加原理；
• 并且找出对应的基底；

你会发现，用坐标轴分解成坐标，这一套思路，依然能发挥奇效。

② 多项式函数

比如说多项式函数，就可以看成一种抽象意义的向量。

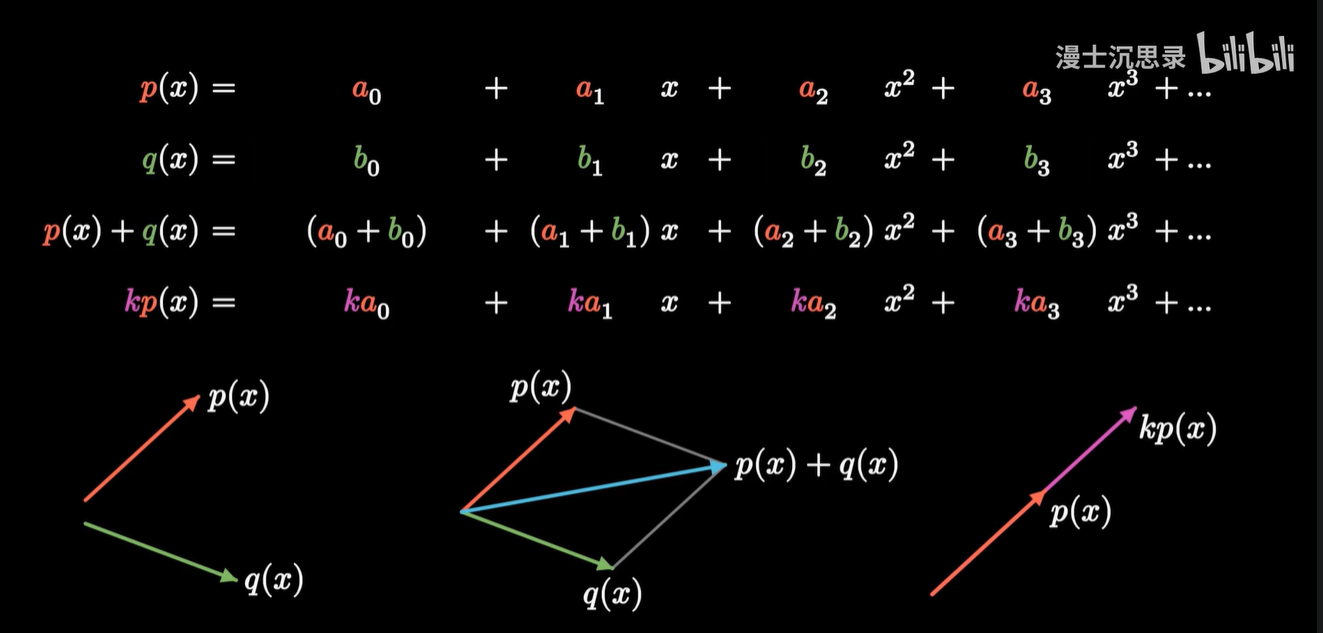
• 类比于向量的加法，两个多项式相加，就是各个系数相加，最终结果还是个多项式。
• 同样的，多项式乘以一个数字，就像向量的数乘，结果还是一个多项式。

那么我们能不能用一串数字来表示一个抽象的多项式呢？当然可以。

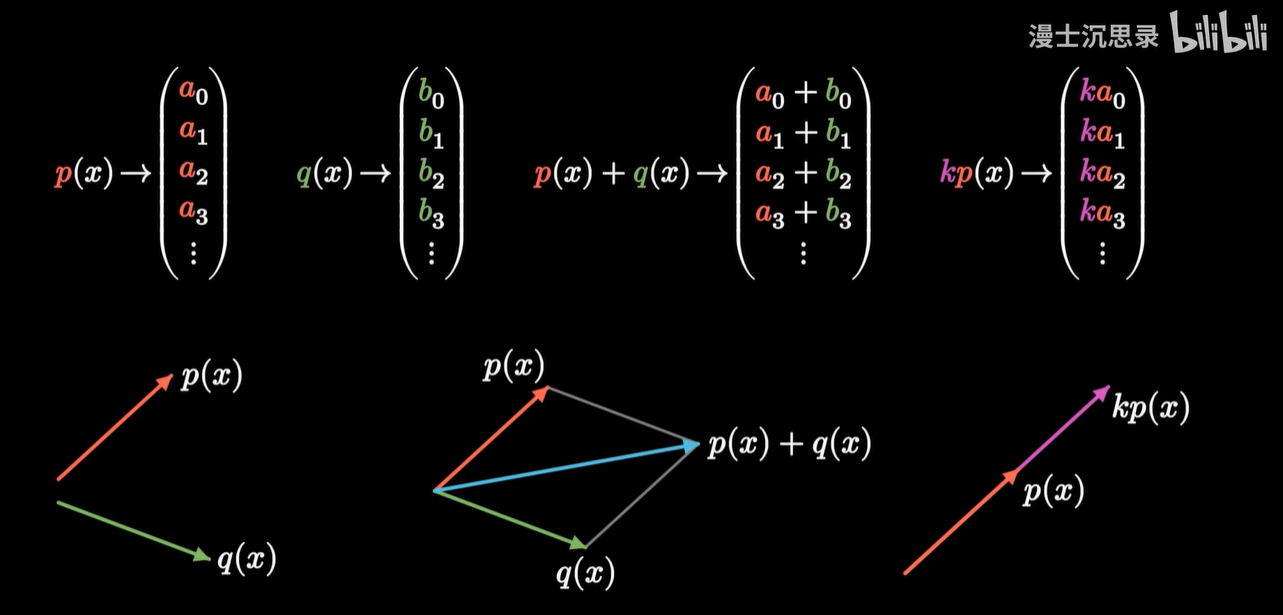
你会很自然地想到：

如果我们由低到高写出这个多项式的所有系数，就能用一串像坐标一样的数字，表示出多项式函数了。

---

---

事实上，这本质上是选择了一些特别的单项式：1、x、 x平方、 x3次方……等等，作为基底。

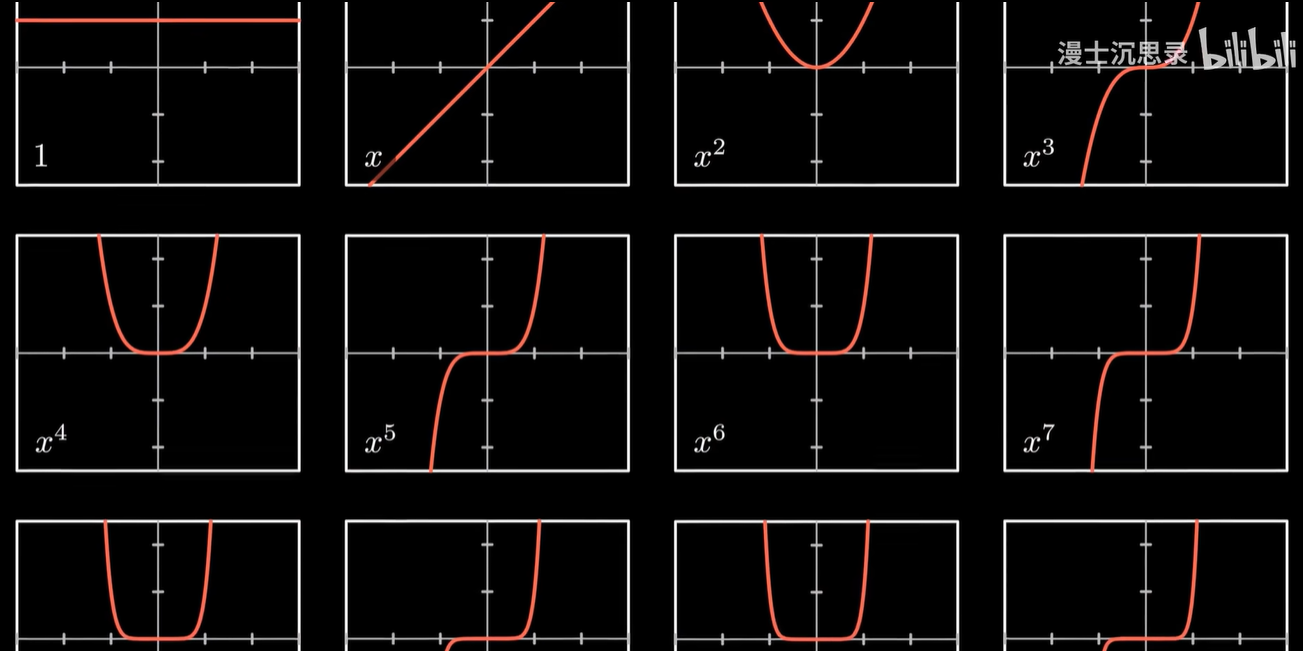
• 那么当我们从坐标翻译到向量时，本质上就是把每个单项式乘以坐标的各个系数，再加到一起，就还原了原本的多项式。
• 稍微有些不寻常的是，因为单项式的次数可以是任意正整数，所以我们需要无穷多个基底。

这种基底表示最强大的地方就在于：

即便你要分析的这个函数向量，是一个非常复杂的对象，比如说正弦函数、对数函数，但是在基底分解之后，就变成了一串坐标系数而已。

我承认分式函数很复杂，但是一串实数很简单啊。

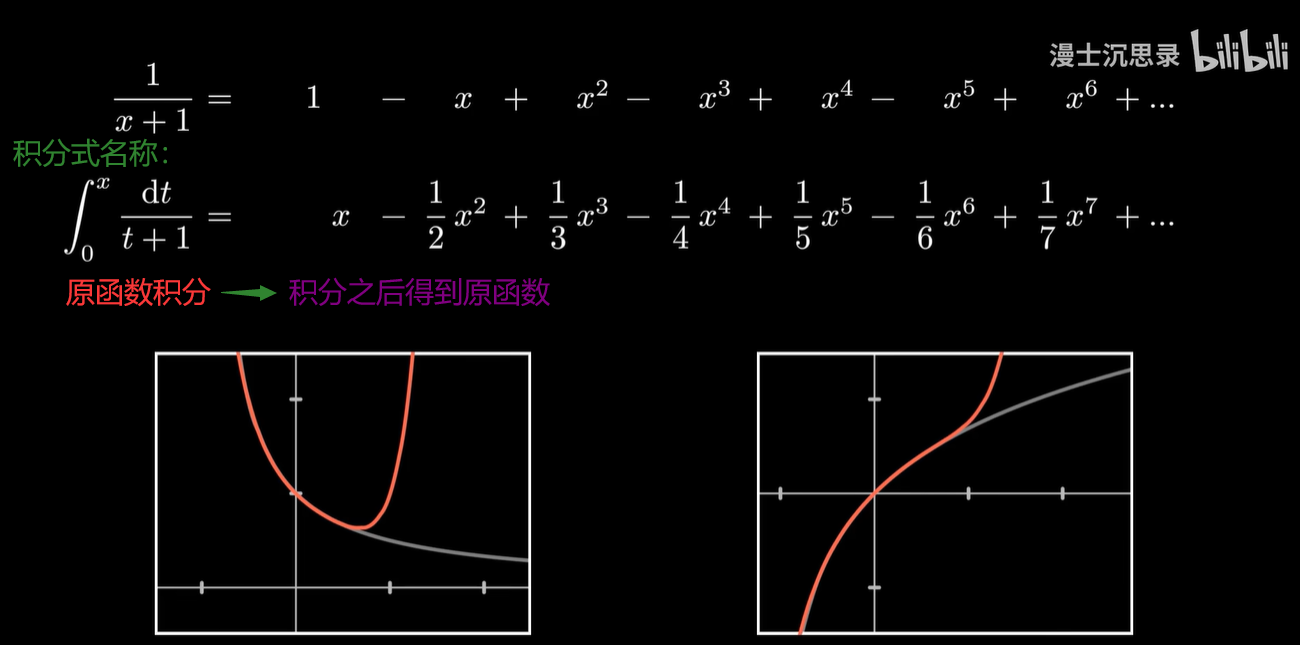
当我用单项式基底分解之后，这个分式函数你不会积分，但是这个坐标系里，一分解之后，每个单项式积分你总会吧，那么每个基底分别积分之后再加起来，你就自动获得了整个函数积分的原函数的这个坐标。

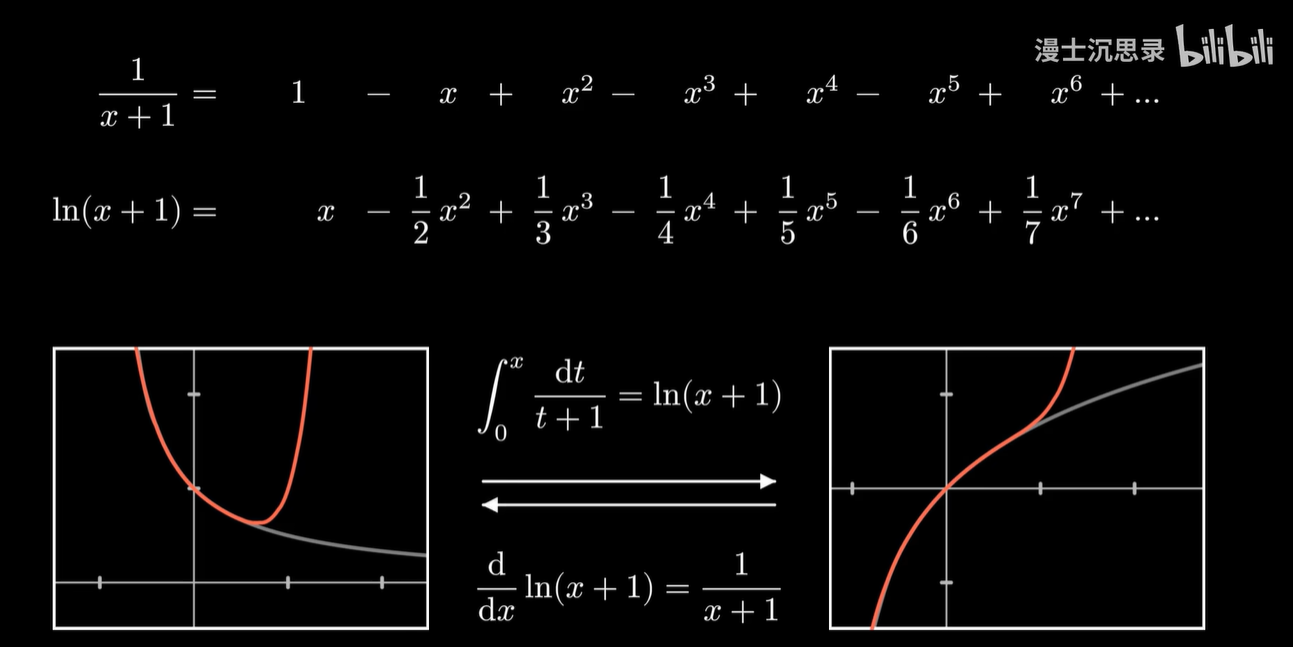
定睛细看，你会发现这不就是 ln(1+x) 吗，于是你就发现了一个不得了的秘密：

积分的原函数是 ln(1+x) ，而反过来，ln(1+x) 的导函数则是。

人类最早发现这两者的关系，真的就是我上面说的这条路线，从这种基底分解，来得到函数之间的积分求导的关系。

而这有一个现在耳熟能详的名字——那就是泰勒展开。

---

---

③ 剩余定理

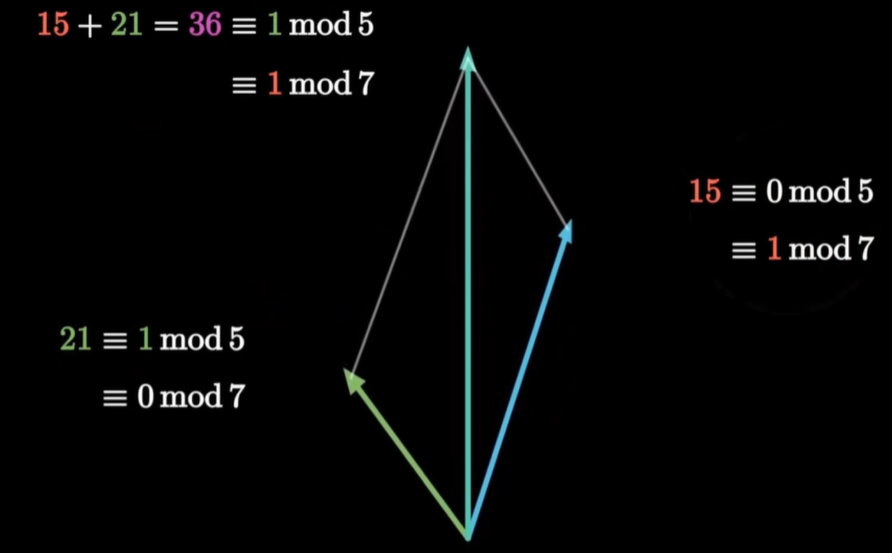
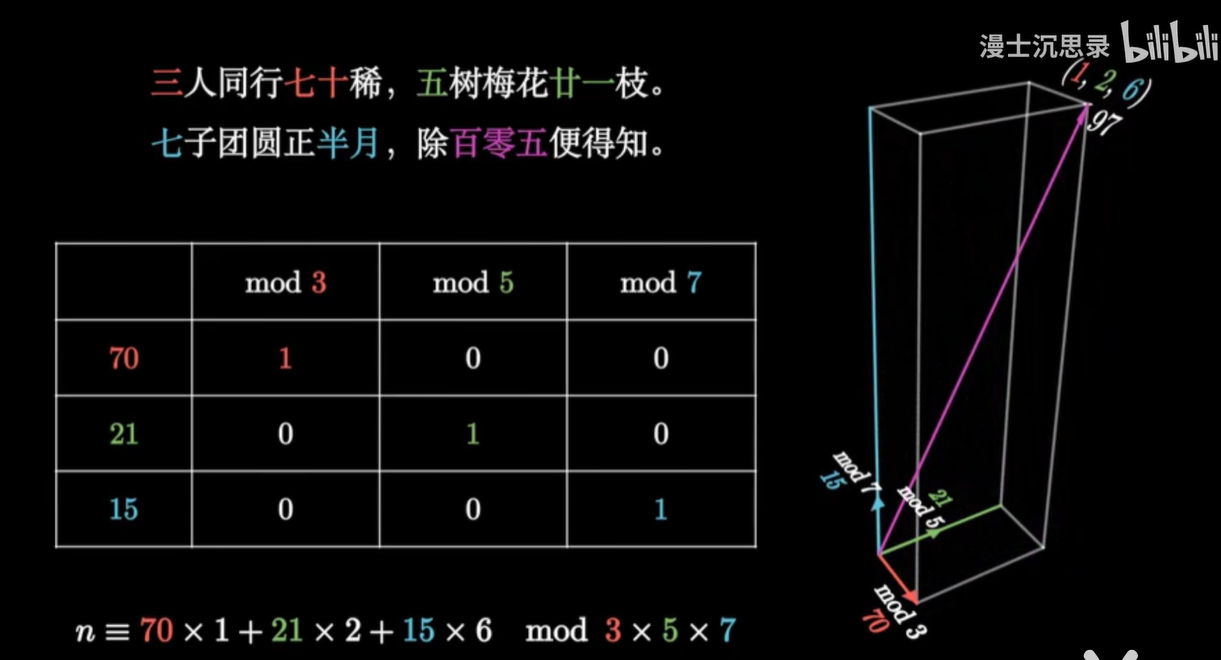
再举个例子，我们小学奥数都听过韩信点兵的故事，说韩信点兵啊，不需要一个一个数，只需要知道三个三个数剩一个人，五个五个数剩两个，七个七个数剩六个，韩信就立刻知道，整个队伍一共有97个人，这是怎么回事呢？

其实啊，你可以把：

• 整个队伍的人数（97）当成向量。
• 而把除以3、5、7的余数1、2、6当成三个坐标。

为什么可以这么看呢？

因为它满足向量和坐标之间最重要的对应关系——那就是线性相加。

把两个抽象的向量相加，那么得到和向量的坐标，一定是两者坐标一位位对应加起来。

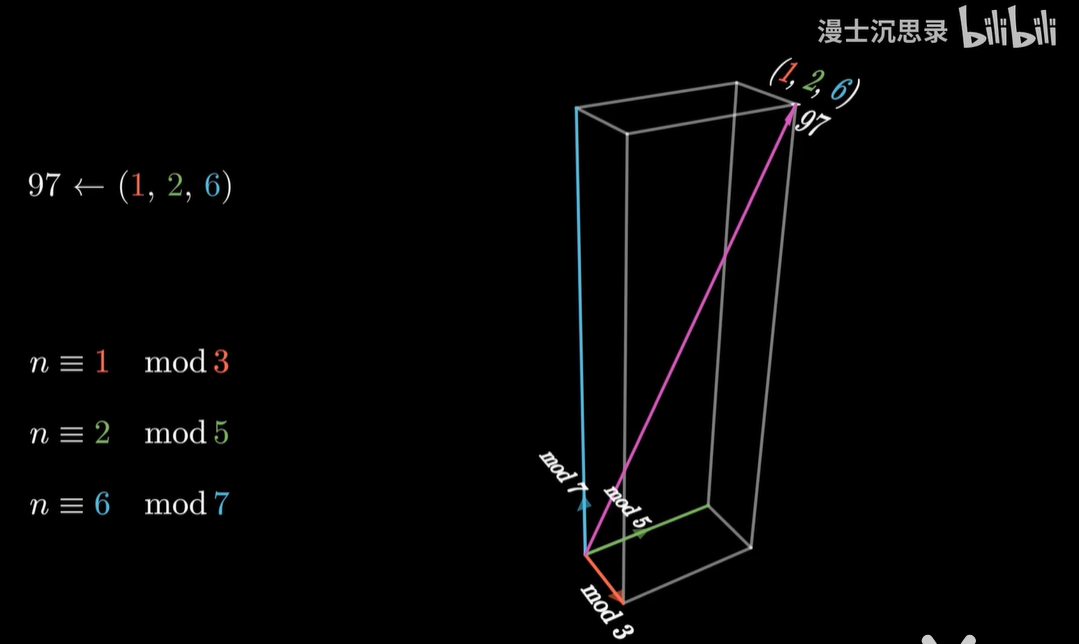
仔细想想，这对于余数来说不也是成立的吗，如果 X 除以 3 的余数是 1，Y 除以 3 的余数也是 1，那么 X 加 Y 除以 3 的余数一定是 1+1=2，除以5和七的余数同理。

所以韩信点兵的本质，就是把整数当成向量，把它分别除以三、五、七之后，得到三个坐标，来进行坐标轴的分解。

而要解这个问题，明朝数学家程大卫在他所著的算法统宗中，就用四句很通俗的口诀描述了

意思是：如果 X 除以3、5、7的余数分别是 A 、 B 、 C ，那么把 A 乘以70，加上 B 乘以21，再加上 C 乘以15，再对105除余数就是结果。

这里的70、21、15看起来像是很神秘的数字，但从我们刚才讲的坐标分解的思路来看，就是非常自然的。

70这个数字啊，除以3的余数是1，但是除以5和7都余数是零，所以：

70就是在这个余数坐标下，对应于三余数这个坐标轴的单位向量。

21和15类似的，都是除以某一个数的余数是1，而除以其他数的余数是零。

因此，如果把这个表达式整体除以3，你会发现后面两项，因为都乘以了一个3的倍数，对于除以3之后得到的余数没有影响，只留下70a这个第一项在发挥着模3取余数的影响。

而70÷3的余数是1，所以整个式子除以3的余数，的确就等于 a。

除以5同理， 前两项没有贡献，21÷5的余数是1，所以整体除以5的余数是 b。 

整个数字除以3、5、7的余数就分别是 A 、 B 、 C ，这恰是三个坐标（A，B，C）。

三个坐标（A，B，C）分别组合这三个基底，就能得到最终的向量——97。

这个巧妙的解法背后正体现了在这个余数坐标下，对恰当的基底线性组合，还原原来向量的过程。

---

最后模不模105，不重要，模完105只是得到最小正整数解，全解是（该数 + n*105）

---

④ 正弦基底

傅里叶变换想要分析的向量是所有的周期函数。

这里为了方便起见，我们固定周期是一个常数。

而他选择的基底向量，则是一系列不同周期的正余弦函数，为什么选正余弦函数作为基底呢？

唉，这个原因比较复杂微妙，因为自然世界的周期一般都来自于振动过程，而最简单的振动就是简谐振动。

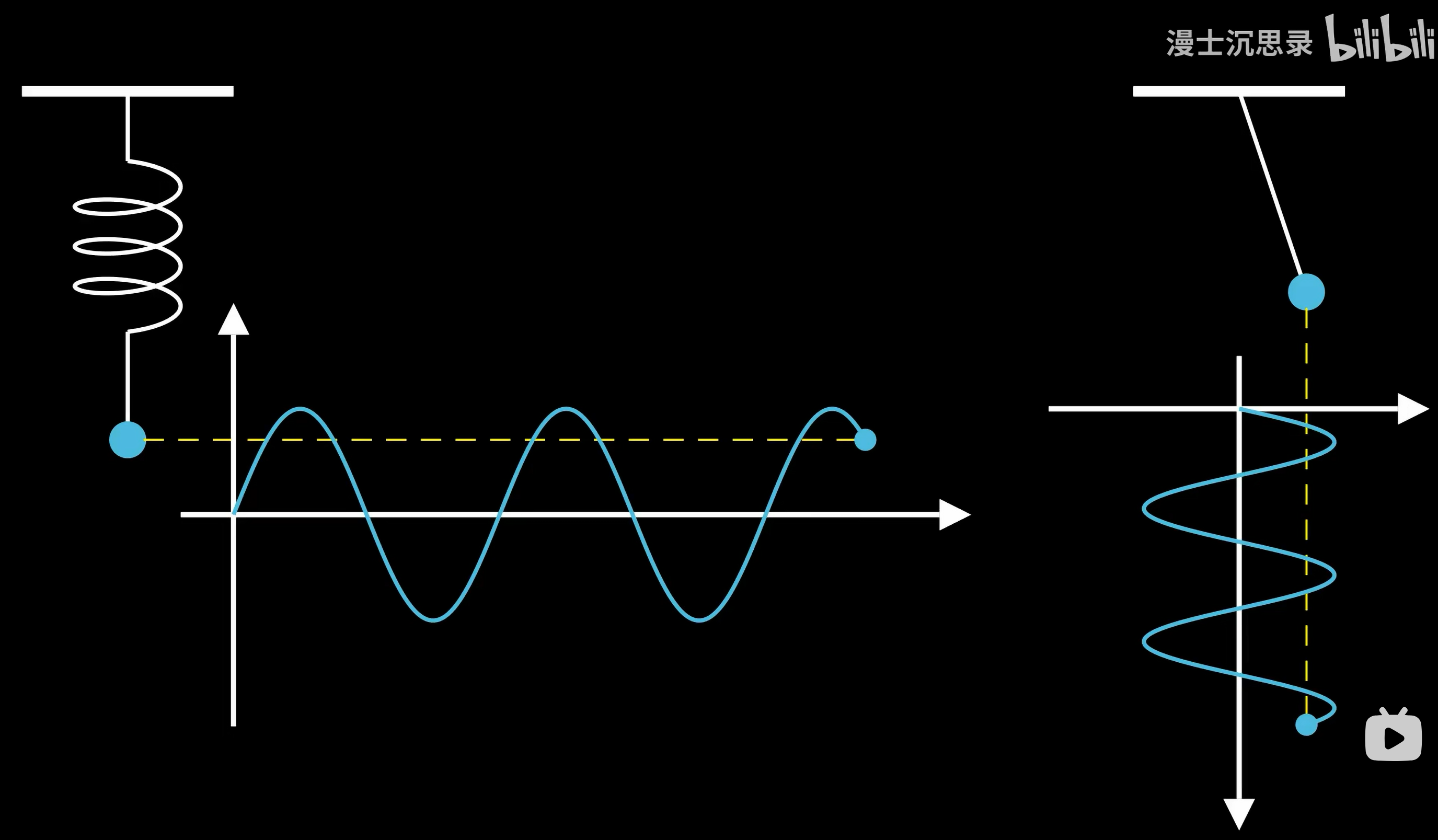
比如说弹簧挂着一个重物，上下震动或者单摆的左右摆动，而它们的位置随时间的关系都是正弦函数——>如果要再追究为什么振动里都是正弦，那是因为正弦函数有非常优美的数学性质：

• 它求一次导变成余弦
• 再求一次导又变回正弦，但多一个负号
  

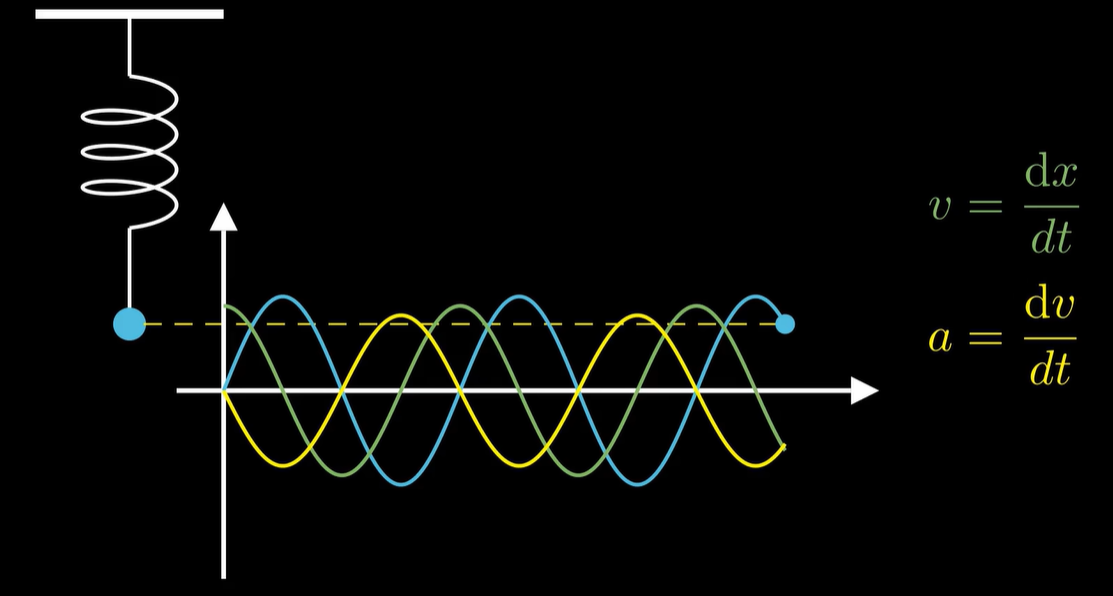
而这正是振动力过程底层的机理：离开平衡位置越远，回复力越大，加速度正比于偏移量。

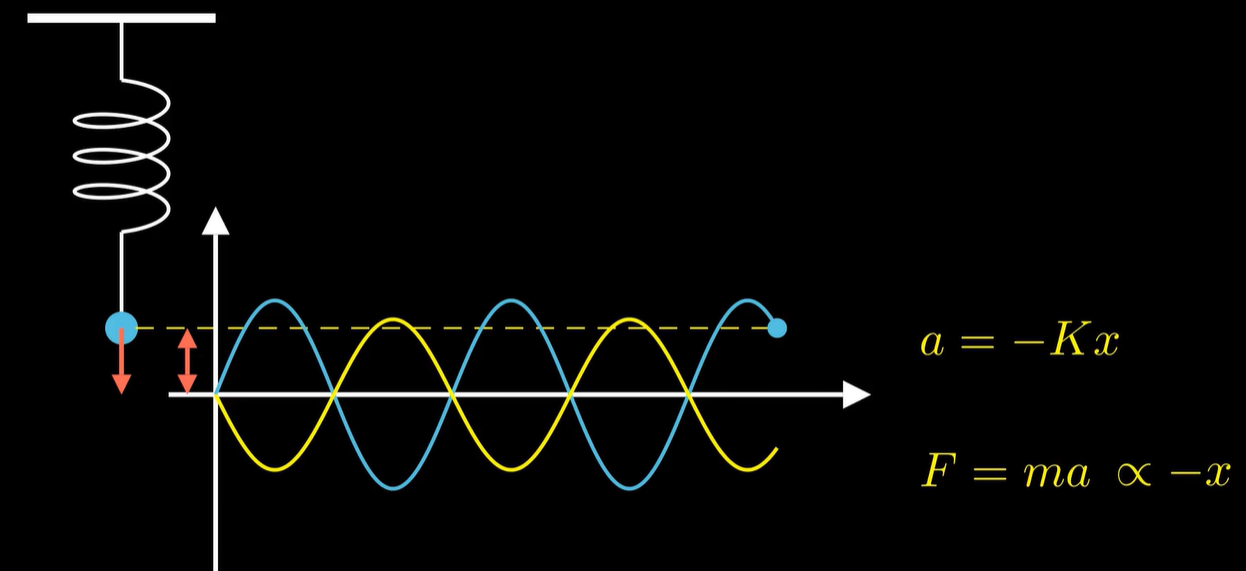
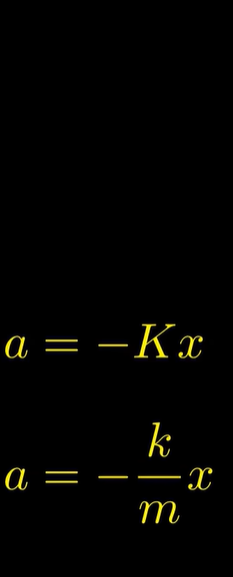
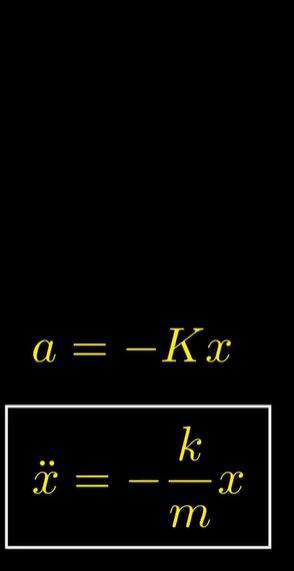
注：x上面两个点表示x的二阶导，这是牛顿发明微积分时的记法。

也就是二阶导与函数自身形式相同，差一个负的倍数。

这就注定了简谐振动的函数形式一定是正弦。巧合的是，热的传播、交流电等等，都有这种二阶导与函数值差一个负倍数的关系。

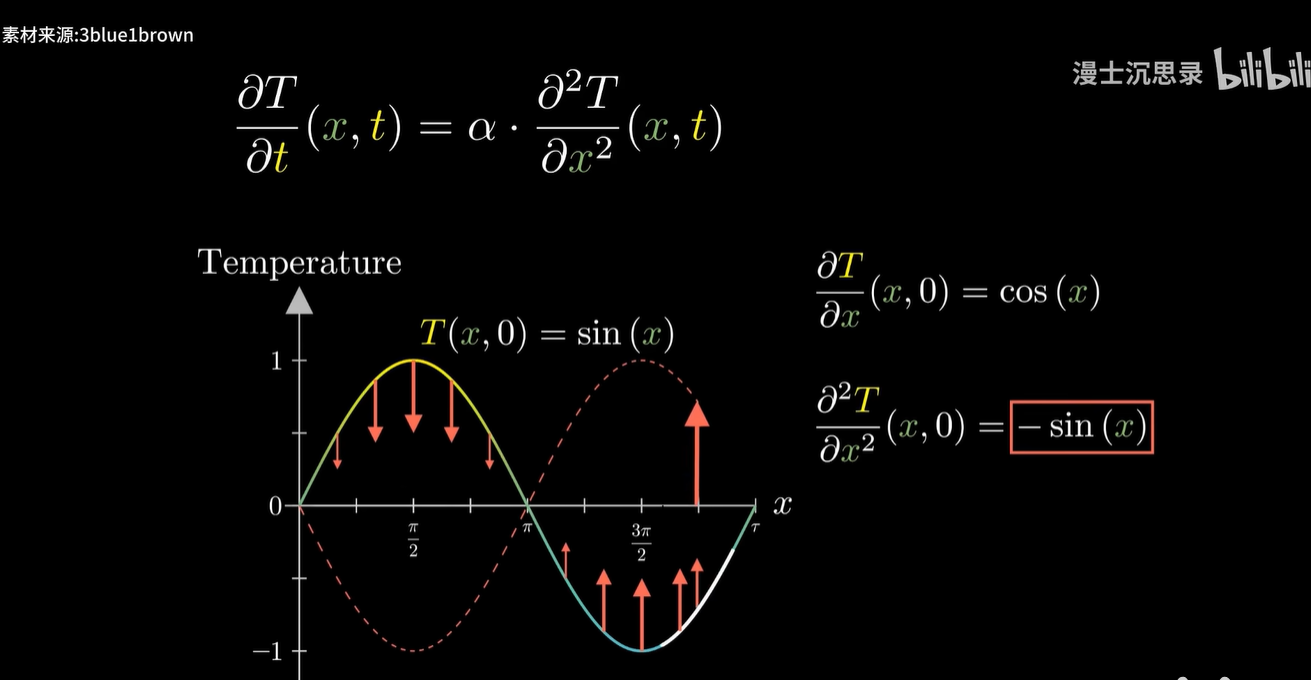
因此在这些场景里，正弦函数也经常出现。

正弦函数积分求导的计算都很方便，是性质最好的周期函数，甚至可以说是振动最基本的单元，所以就拿来做基底了。

可是，正当你选完基底，准备把各种杂七杂八的周期函数都一通分析的时候，突然就会意识到，哎呀，不太对呀，当年我们把多项式在单项式的基底下分解的时候，只需要盯着这个多项式每一项的系数，就自动得到坐标了，可现在给我这么一个乱七八糟的波，我哪里知道要用几倍的 cos x 加几倍的 cos 2x 加几倍的 cos 3x 得到它呢？？？

诶，好问题，这就是前面我们没有展开，但非常重要的内容。

⑤ 内积

x.1 向量内积

在抽象的向量和抽象的坐标系里，想要找到这些坐标所对应的系数，让基底线性组合得到我们想要的向量，我们同样需要一套抽象的办法，来系统性处理这些抽象的向量空间，而这个问题的答案就是——内积。

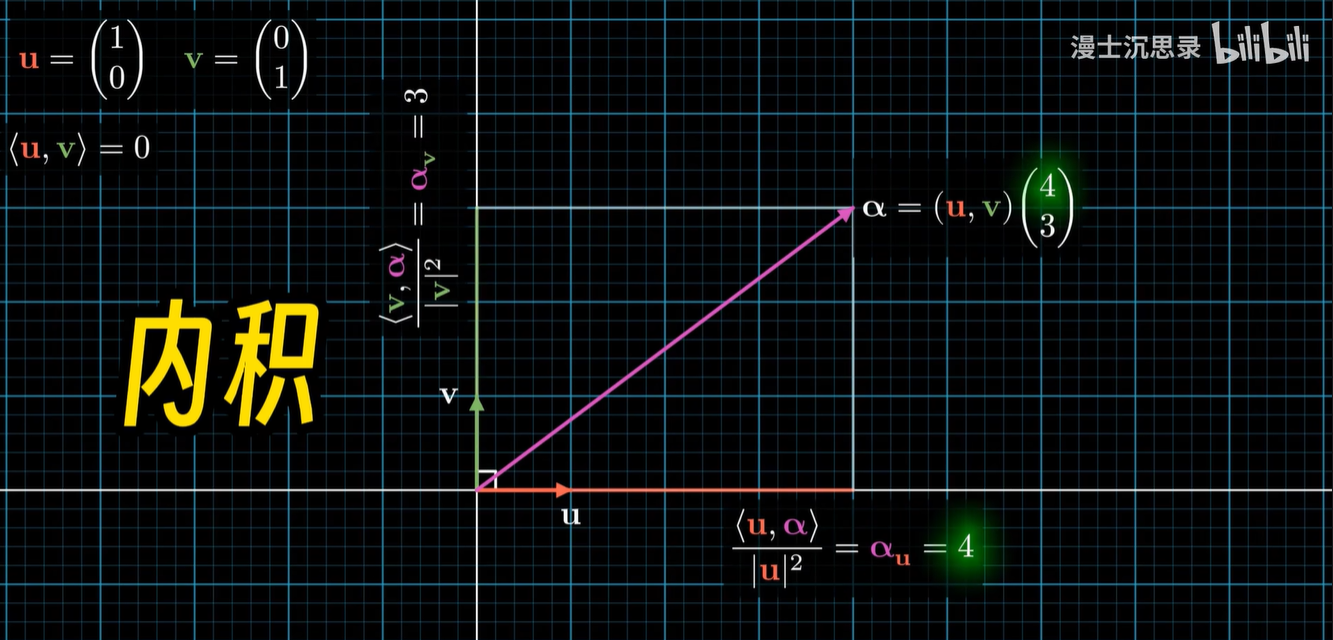
刚才我们说了，在坐标系里想要找到一个点的横坐标，是将它向 X 轴做垂线找交点，不过到了更抽象的空间里啊，其实我们很难定义垂线和焦点，这样几何背景过于浓厚的概念。

取而代之的是要用内积来寻找坐标。（线性组合系数）

高中数学里我们学过啊，向量点乘的几何意义是：

一个向量在另一个向量方向上的投影长度，乘以另外一个向量的模长。

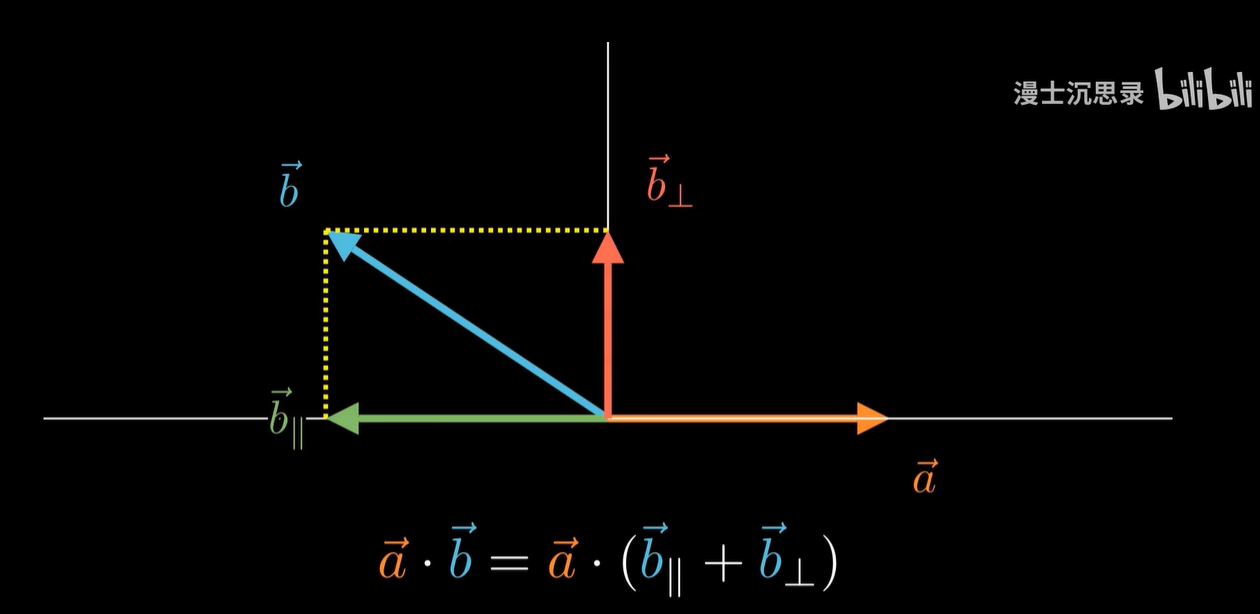
所以只要将一个向量和 X 轴的单位向量内积，我们就能自动得到在这个基底方向上的坐标。

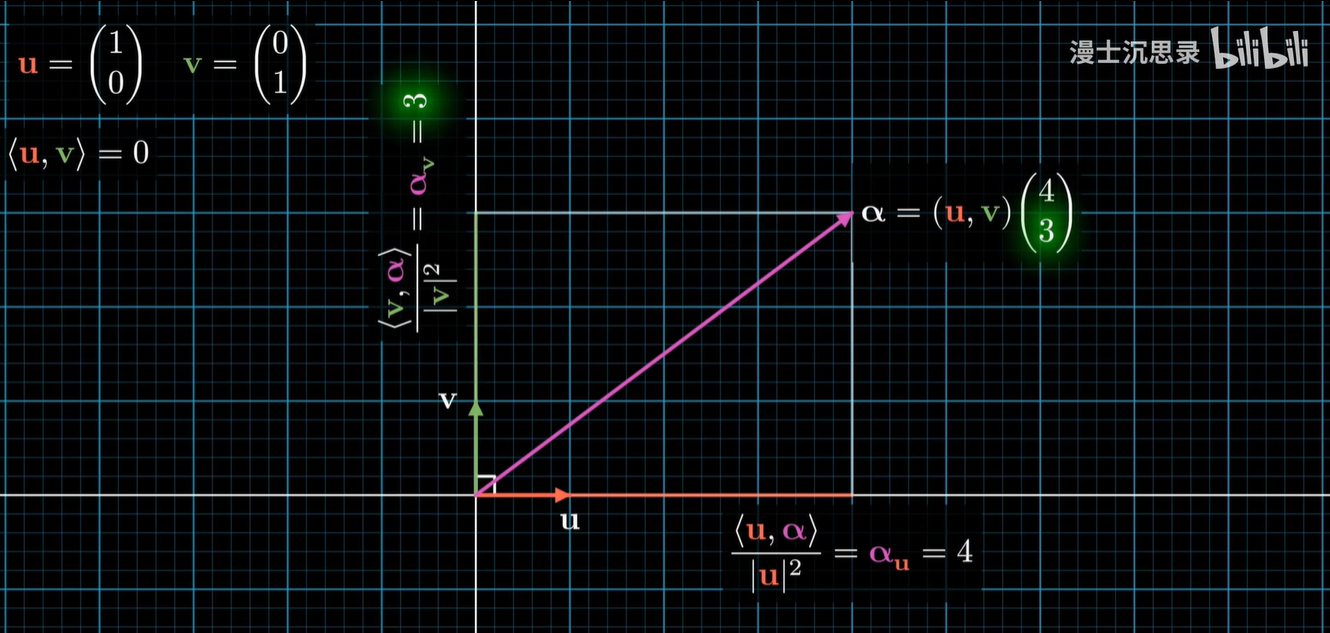
Y 轴也是同理，只需要把内积的基底改成（0,1）即可。

既然向量抽象了，那点乘也可以抽象一点，对于两个一般的向量，我们可以类比点乘来定义内积。

这个内积需要满足一些基本的性质，比如说

• 双线性性：一堆向量加在一起和另一个内积，等于每个分别内积之后再加到一起，就像乘法的分配律。
• 对称性：U 和 V 内积等于 V 和 U 内积，类似于乘法的交换律。
• 非负性：自己和自己的内积一定是非负的，只有当所有的坐标都是零时结果才等于零。
  

这样我们就可以通过把任何一个向量，直接和所有这些基底向量内积，自动得到线性组合这些基底所需要的系数。

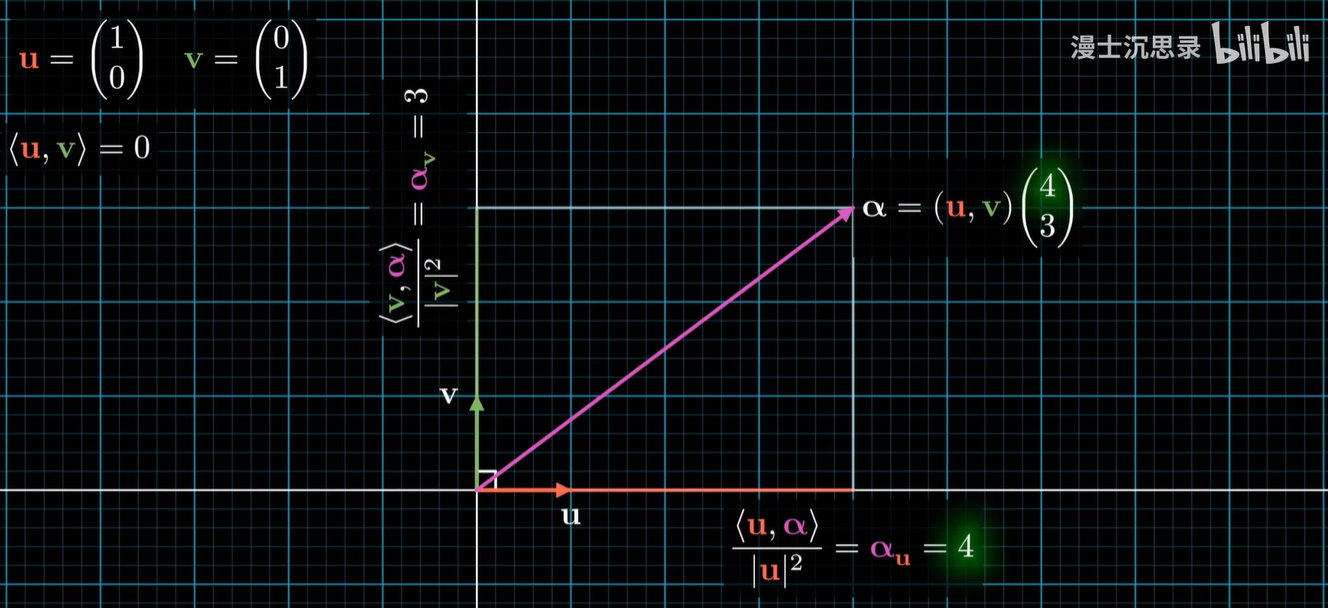
但是且慢，这里有一个隐蔽的问题，那就是我们的坐标轴一定得是正的。

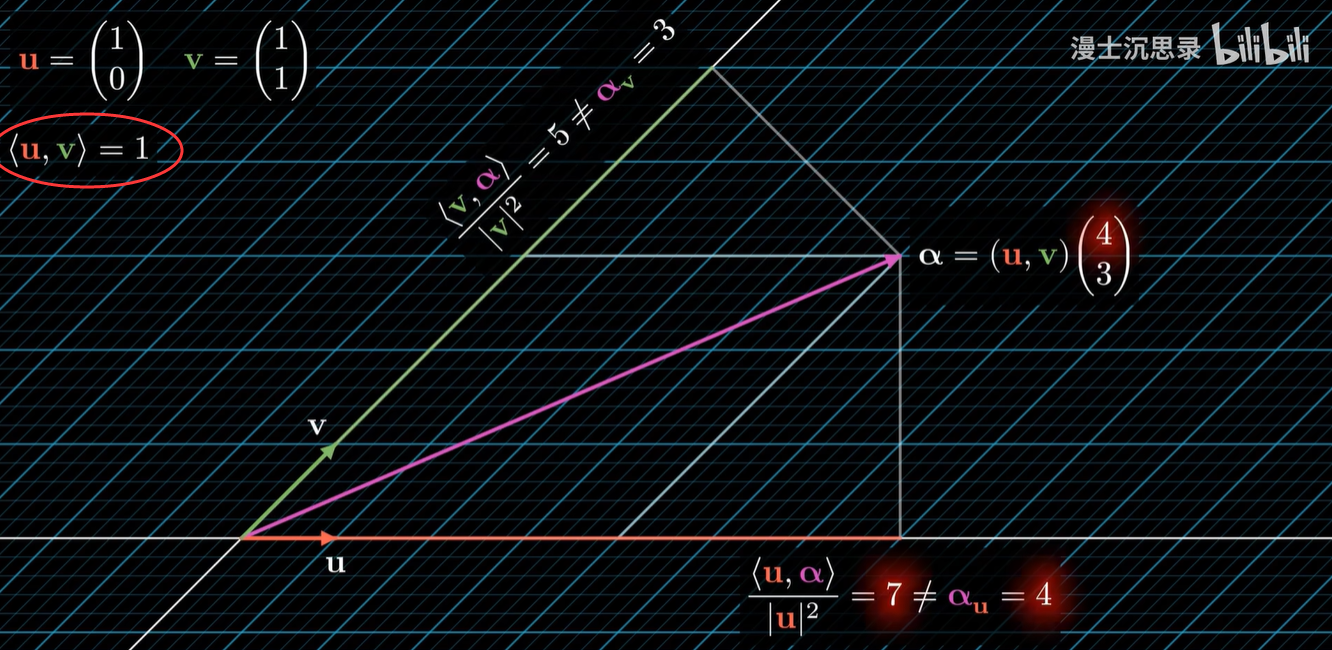
什么意思呢，假如我们选择的基底歪成了这个样子，那么这个坐标的向量和 X 轴基底内积的结果，并不能够还原出它 X 轴的坐标，究其原因啊，就是因为这个基底歪了，两个基底本身的内积不等于零。

能够利用基底内积直接还原出坐标系数，有一个前提，那就是任何两个基底的内积都得是零——正交基底。（施密特正交化）

而这就是很多人在学习线性代数时被反复强调，但可能不理解为啥要强调的正交基底了。

背后的原因正是因为：

只有单位正交的基底才能够通过内积的方式直接反向还原出它线性组合的坐标来。

好，让我们再回到傅里叶变换的正弦函数基底上来，我们该怎么定义两个函数的内积？？？

又该选择什么样的正交基底呢？？？

x.2 函数内积

仔细想想一个周期函数啊，本质上就是一段周期区间上，每个输入点的函数值。

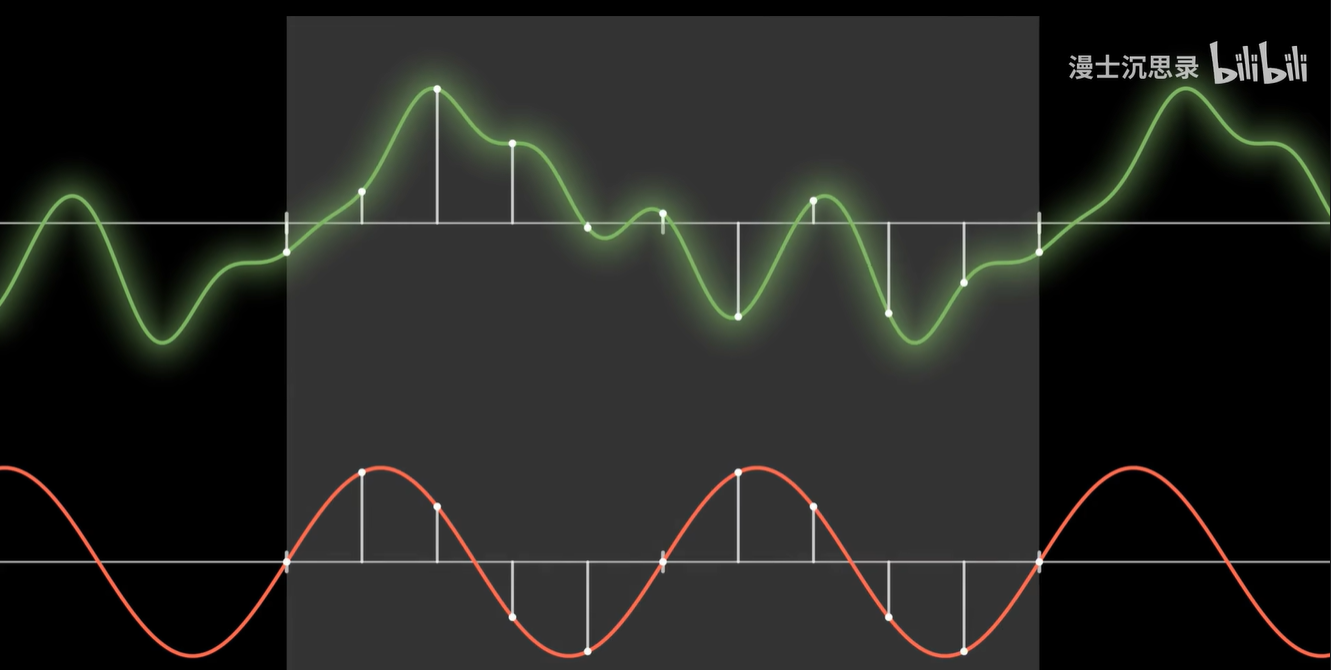
如果我们稍微离散化一下，把函数就当成很多个但有限个输入点函数值所构成的向量。

那么根据向量内积的坐标运算：两个向量的内积就是每个位置的坐标相乘再加在一起。

所以这相当于把两个函数各个不同自变量的函数值相乘（函数乘积），再加到一块儿（函数积分）

注意：函数积分 ≠ 函数卷积

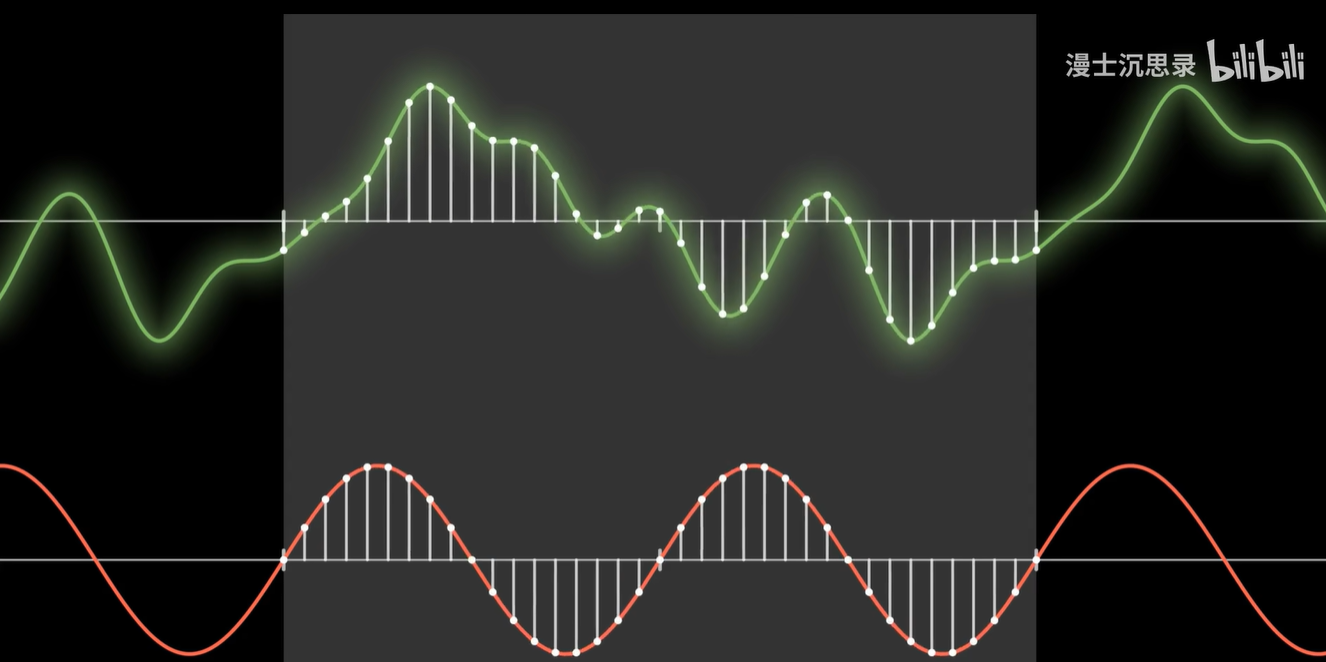
如果我们分的无限多，这本质上就相当于把两个函数相乘之后，在一段周期内把所有函数值加起来，唉，这有一个非常自然的表示，那就是——积分。

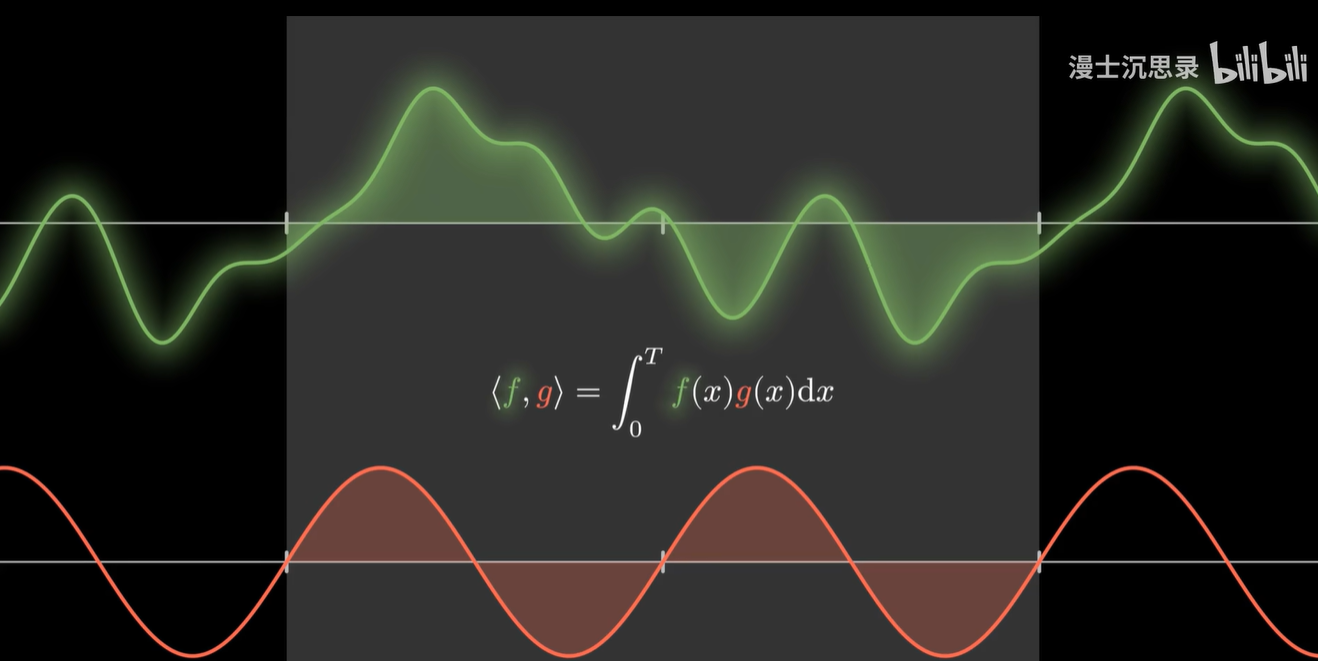
于是我们从这个角度，得到了一个可能最自然的两个函数的内积——那就是将两个周期函数相乘之后，在一段周期零到 T 的区间内积分的结果。

【结论】

于是我们终于验证了，这个看起来很恐怖的公式，其实就和向量的点乘一样，是：

• 把一个周期函数当成向量的内积运算。

---

还差最后一步，正交的性质怎么办，这里方便起见啊，我们不妨设关注的函数周期都是2π，那么正弦和余弦函数还有另外一个优势由此体现出来。

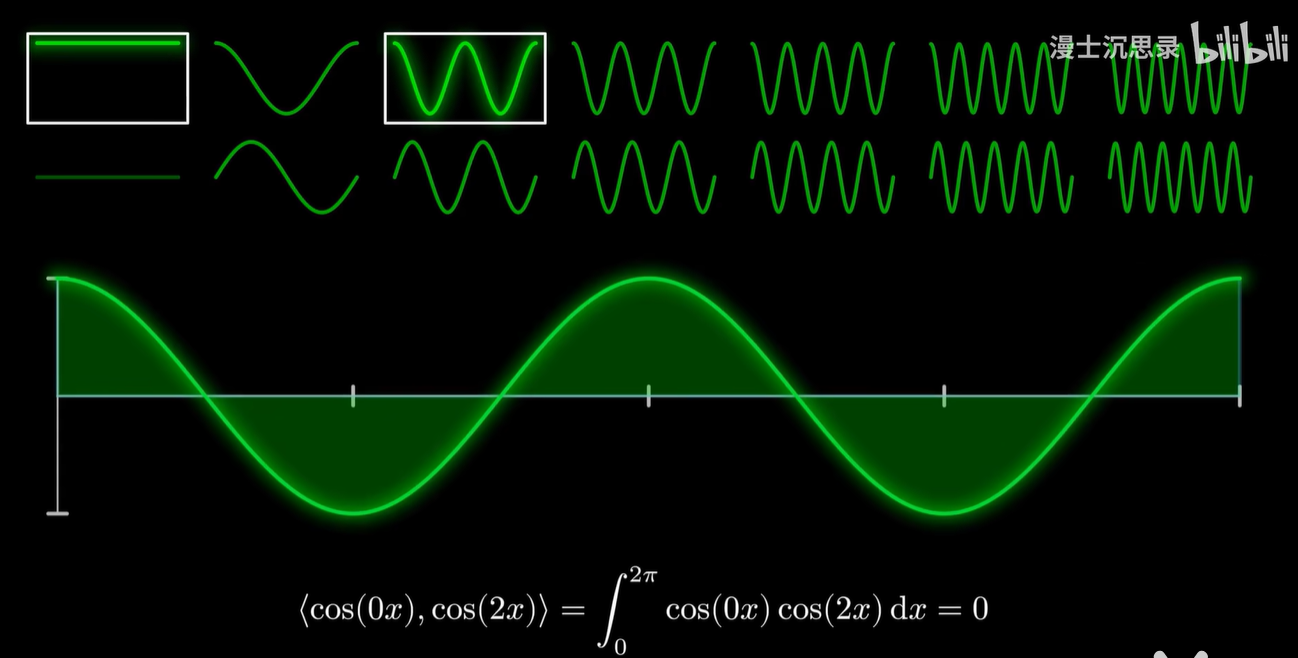
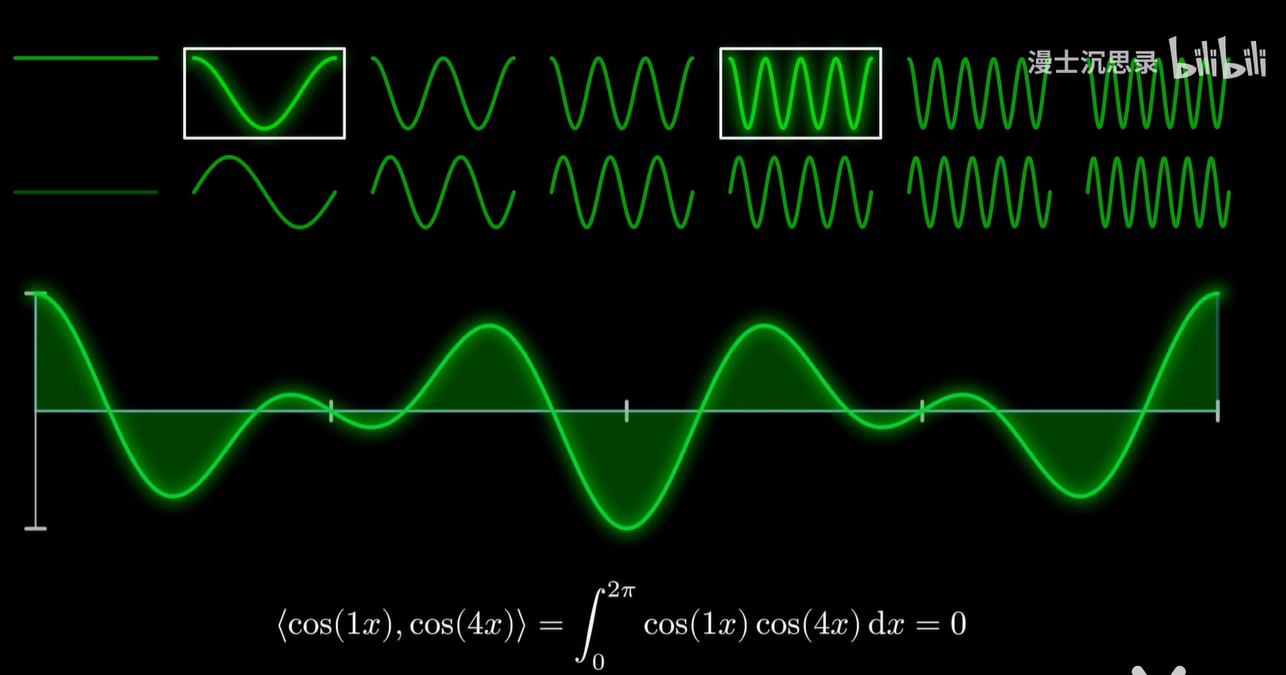
• 利用刚才定义的内积，这堆基底里啊，任意挑出两个正余弦函数，只要它们不是同一个，乘在一起，就可以积化和差，最后变成一个在0~2π区间内正负面积刚好相互抵消的函数。
  
• 换言之就是在刚才定义的乘积积分，两两正交。
• 所以这些正余弦函数的基底自动满足了正交性。
• 就像平面直角坐标系一样，只需要挑任何一个余弦函数的基底出来，内积一下，你就立刻知道这个基底应该乘以什么样的系数了。

---

到此，我们就破解了傅里叶变换的几乎所有密码：

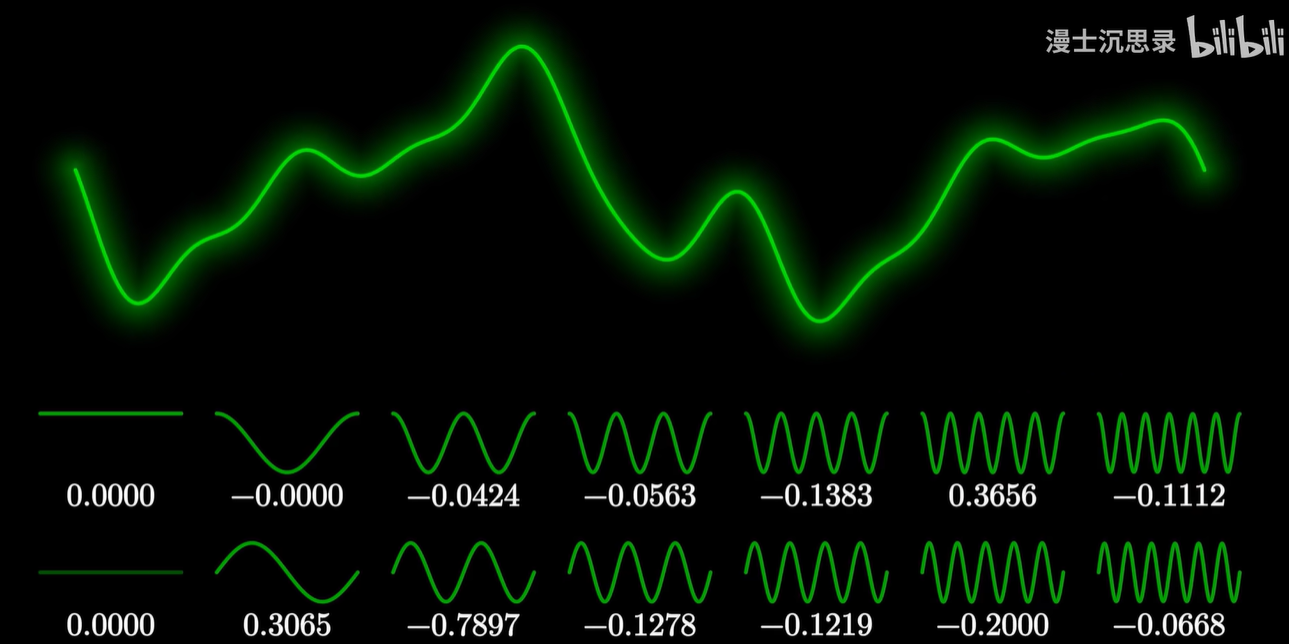
• 我们拥有了一个强大的周期函数的坐标系，它的基底是所有形如 sin nx 和 cos mx 的周期函数还有一个1，通过线性组合它们你可以表示出几乎所有周期为2π的函数。

比如说方波，用刚才内积的方法，你可以分别把方波和这些基底相乘，再积分，我们就可以得到一系列坐标的系数，再反向用这些坐标系数组合这些正余弦函数。

把越来越多的余弦函数叠加在一起，你就会惊奇地发现，这些波函数居然真的越来越接近方波。

这个过程看似玄妙，但实际上就跟用基底向量组合出空间的任何一个向量一样平常。

你肯定会说，好吧，傅里叶变换的确把函数变成了坐标，但这有什么用吗？？？

⑥ 频谱分析

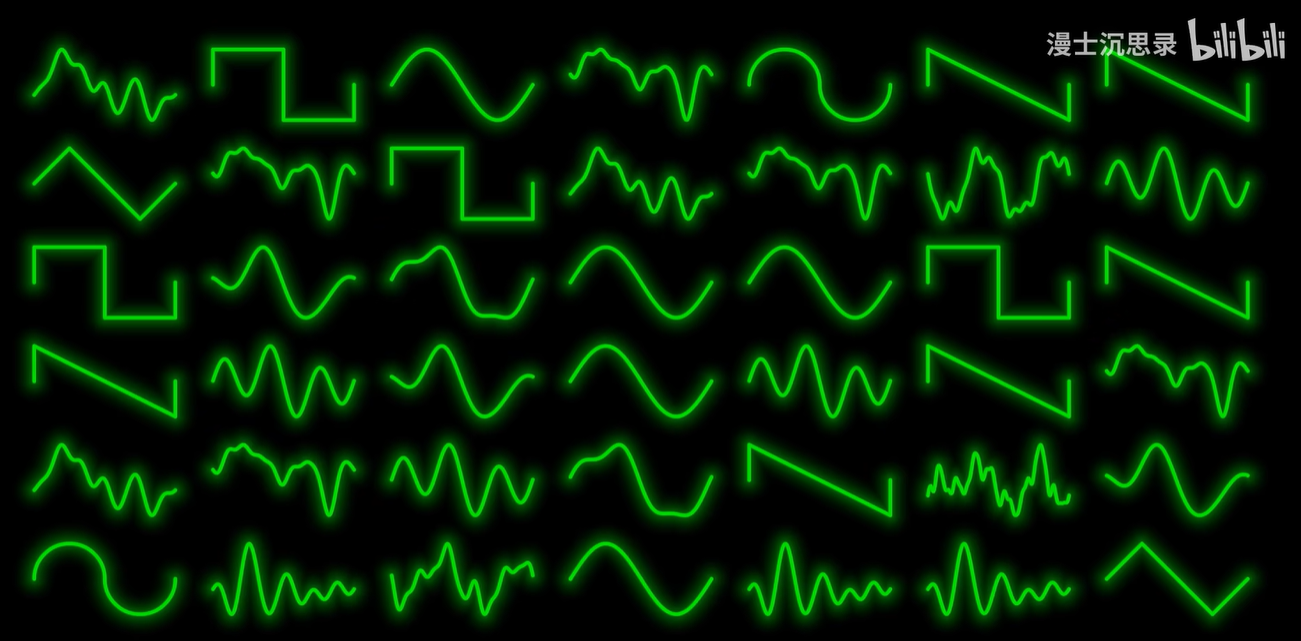
有的，如果用一句话来深刻概括傅里叶变换的意义，那就是他给出了另一个完全不同的看待函数的视角，那就是各个不同振动频率所对应的能量大小。

每一个正弦波前面的系数，就表示这个正弦周期的振动有多显著，将这些振动强度的系数一一列出，我们就可以还原出原来的函数形状。——频域分析法

所以这些系数就有一个专业的名词，叫做频谱。

频率周期大的基底对应的叫做低频区，而频率高周期小的那些基底则对应于高频区。

而这个频谱其实就是对这段波形所对应的声音音色最精确的定义。

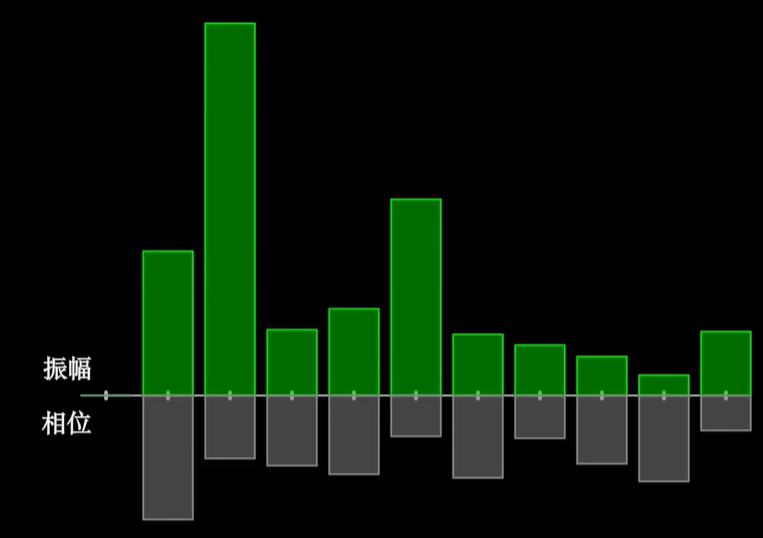
现在知道为啥初中不展开讲什么是音色了吧，真要跟你讲音色是对声音进行频谱分析之后的这个频谱形态，你遭得住吗。

---

⑦ 圆上圆

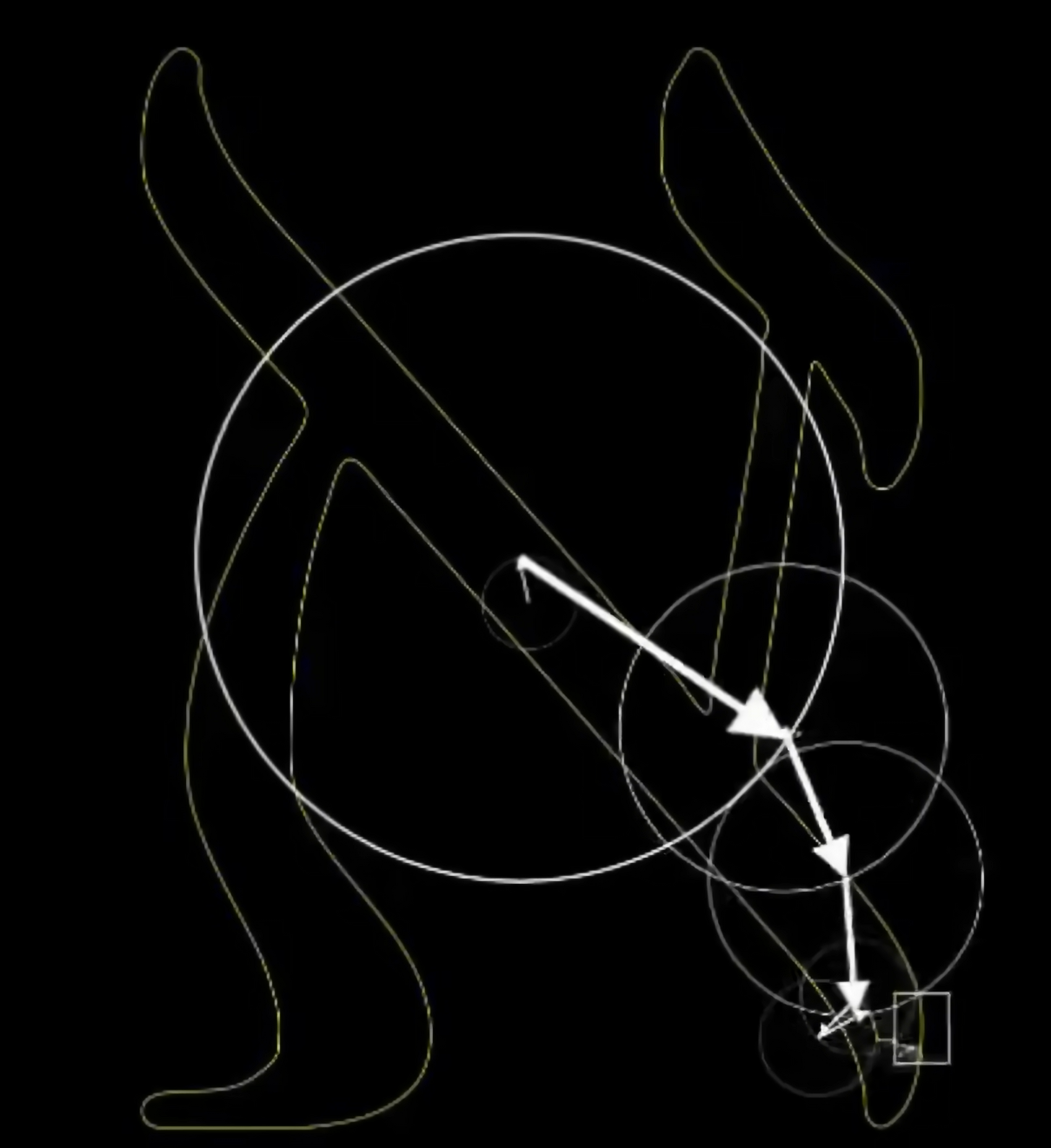
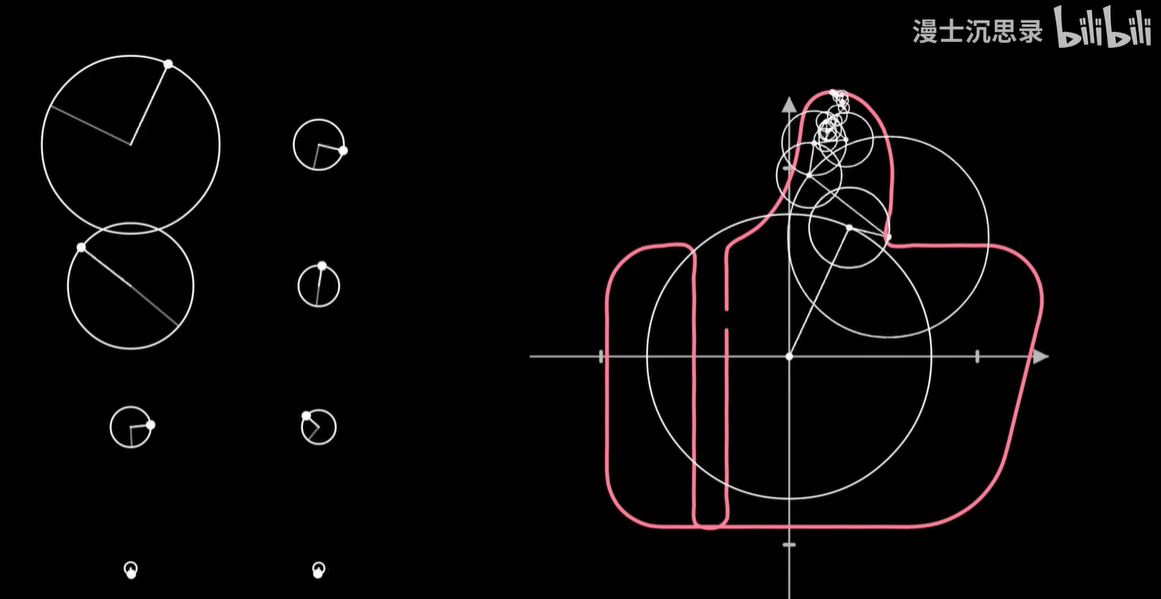
说完应用啊，我们再来回到整个开头的圆上圆。

其实在真正终极的傅里叶变换里，我们用的基底，是在这些圆周上以不同角速度旋转的向量，而不是正弦函数。

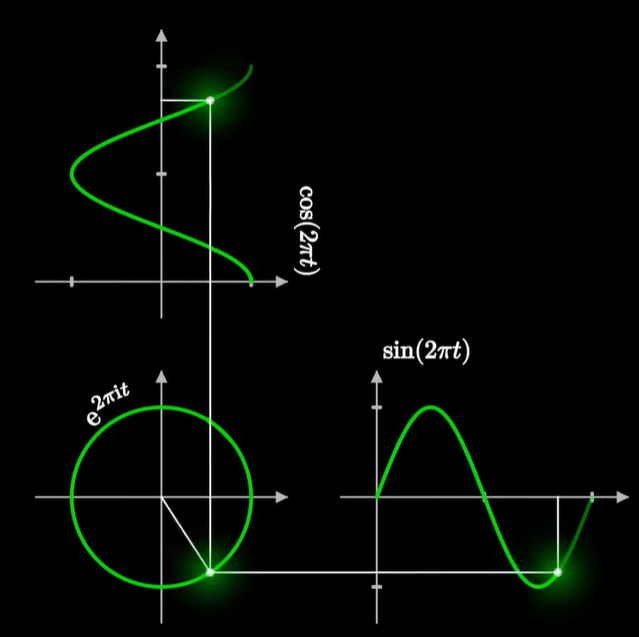
一个绕单位圆匀速旋转的运动，它在 X 轴和 Y 轴上两个投影，就各自是一个同样周期的正弦和余弦的运动。

这个结论有一个很直观的理解方式：那就是把二维的运动加上时间轴。

那么圆周运动就变成了螺旋线。

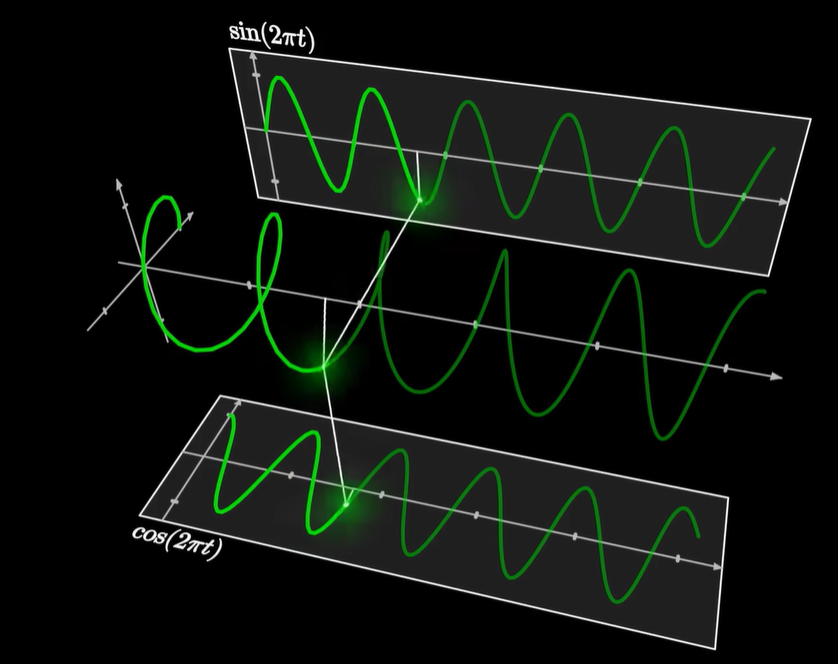
从不同的角度投影看过去，你就可以自动得到横坐标和纵坐标随时间变化的函数是正弦和余弦。

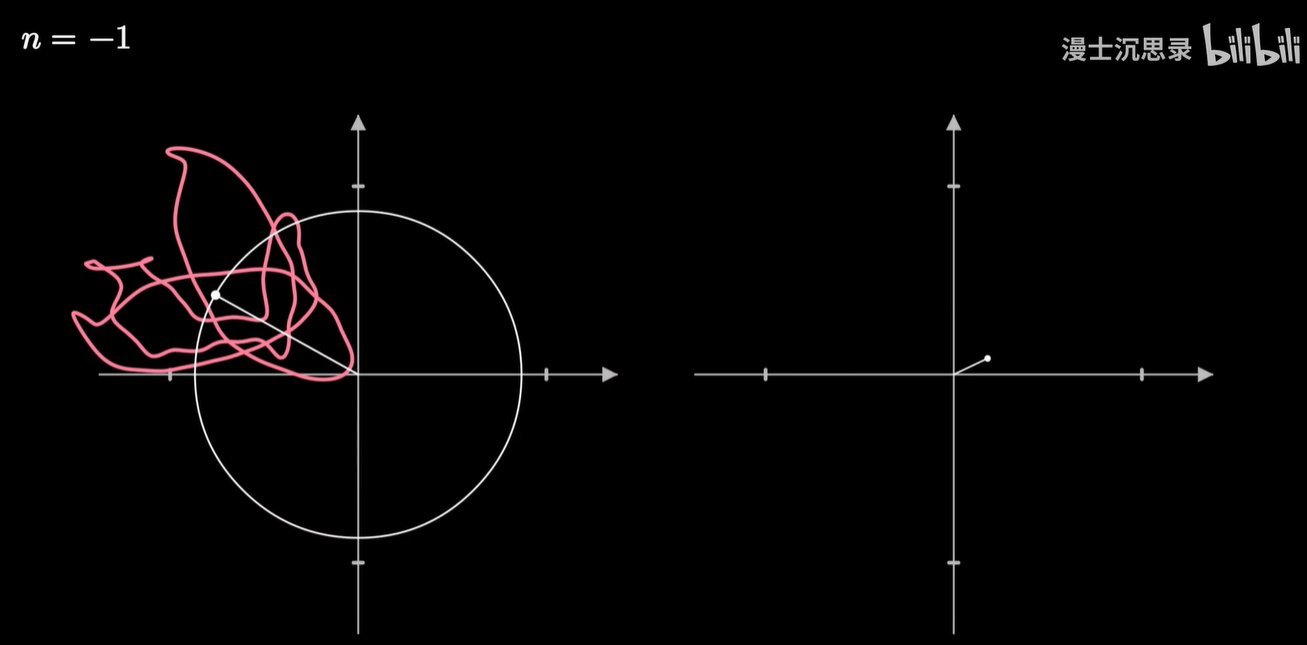
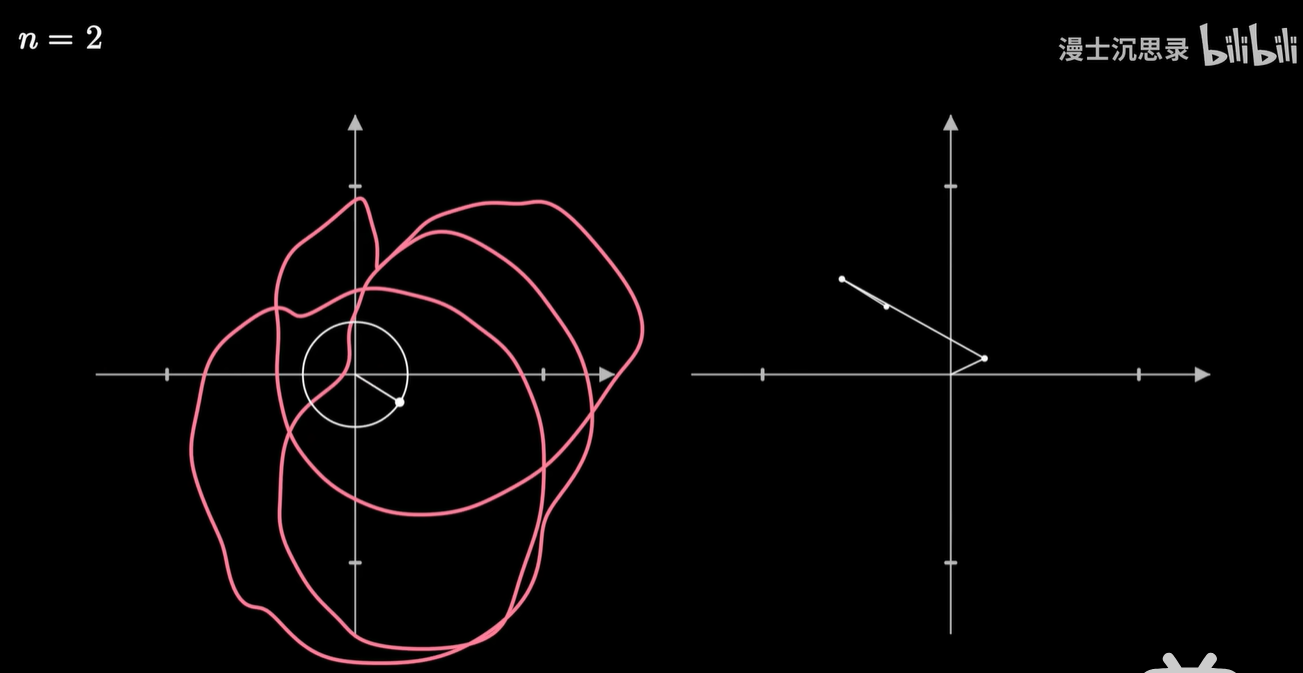
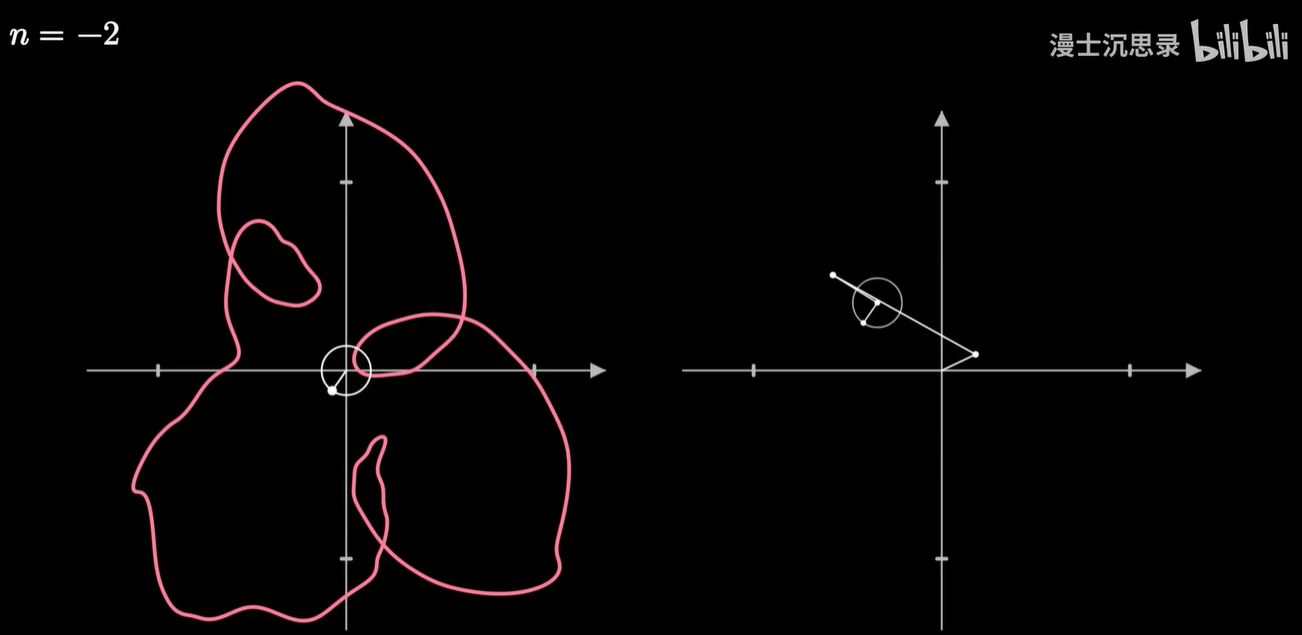
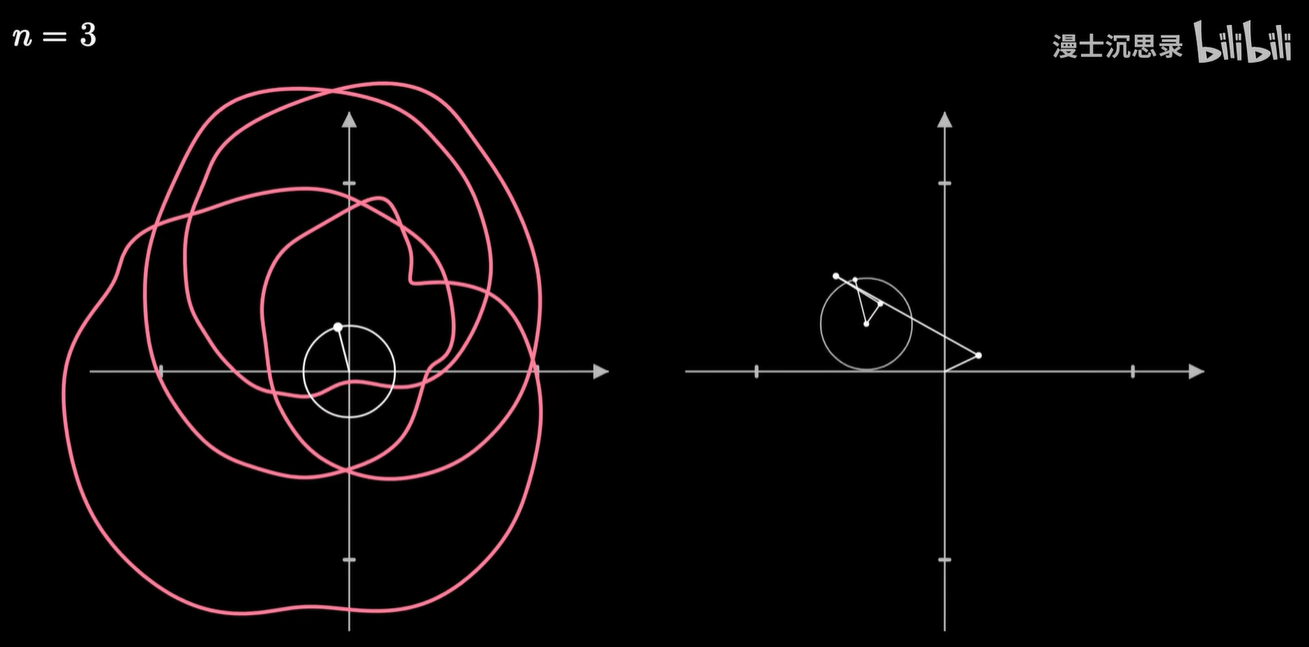
那现在我们就可以破解圆上圆画图的谜团了。

我们让一个点绕着任何形状的闭合曲线周期性地转圈，并同样加上时间维度，这也就变成了一种复杂的螺线，在两个不同的坐标轴看去这分别就是横坐标和纵坐标变化的周期函数。

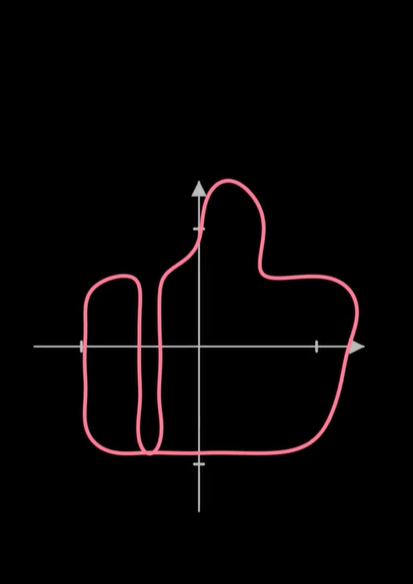
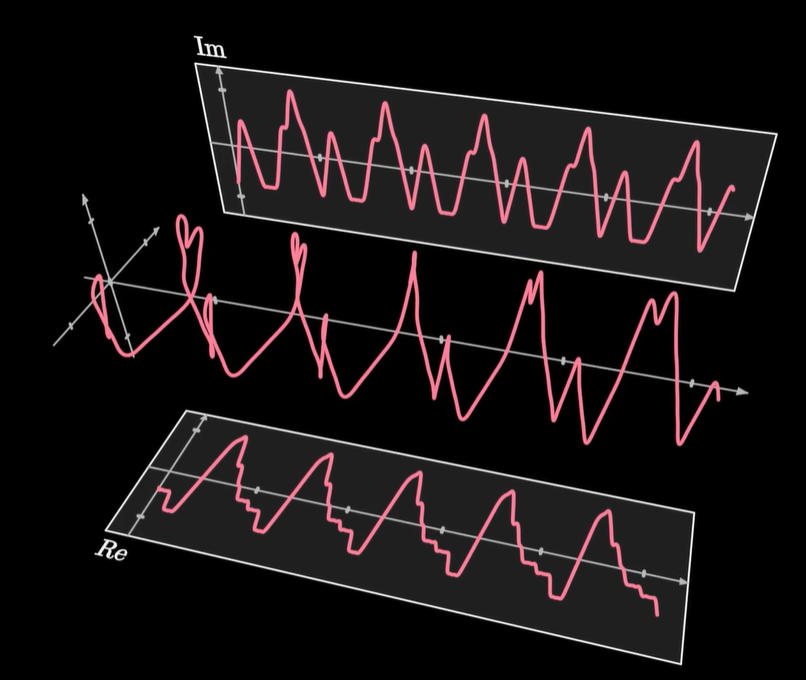
我们把画笔的运动当成一个向量，然后同样用一些基底向量运动的组合来搭建这个运动，而这些基底的运动就是以不同的速度和半径匀速画圈。

通常我们用复平面来表示这个二维的平面，那么基底的运动呢，就是 e 的 inπt 次方，随着整数n的不同，转动的速度也不同。而两个运动的相加就是把这些运动的向量首尾相连。

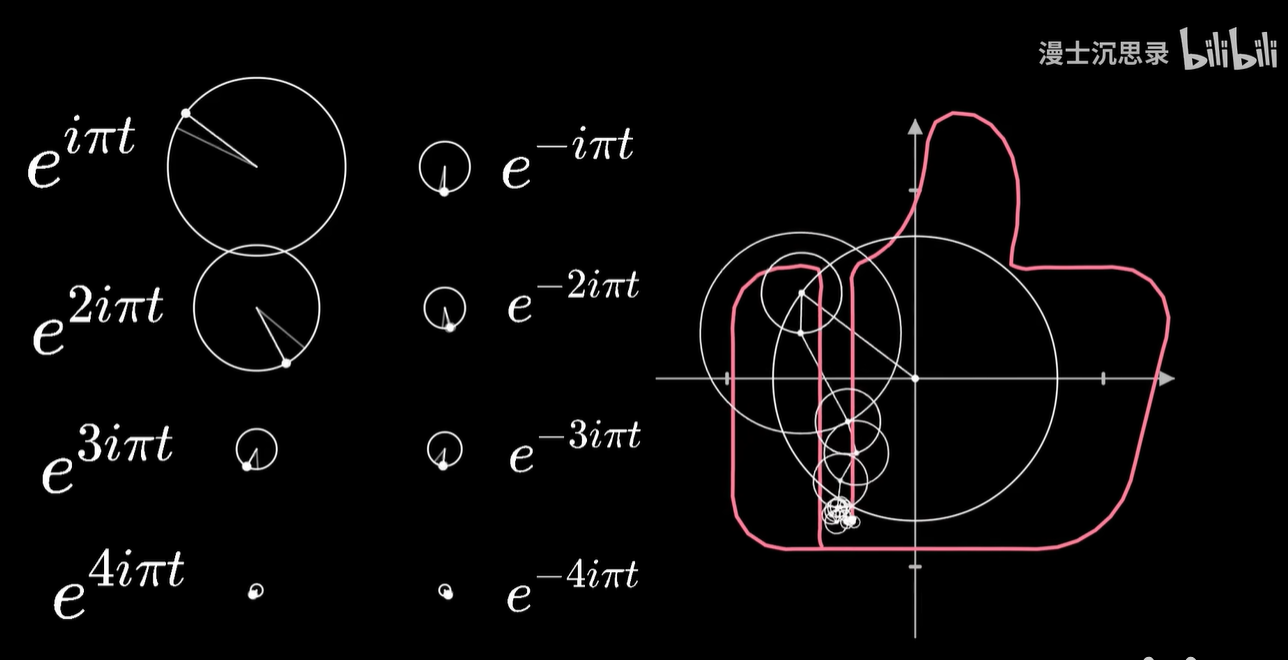
只需要给不同的基底乘以恰当的系数，缩放这些圆的半径大小，再加到一起，我们就可以表示出复杂的运动轨迹了，这就是对运动过程的傅立叶变换。

任何一个平面上连续的周期运动过程都可以用这种方式近似。

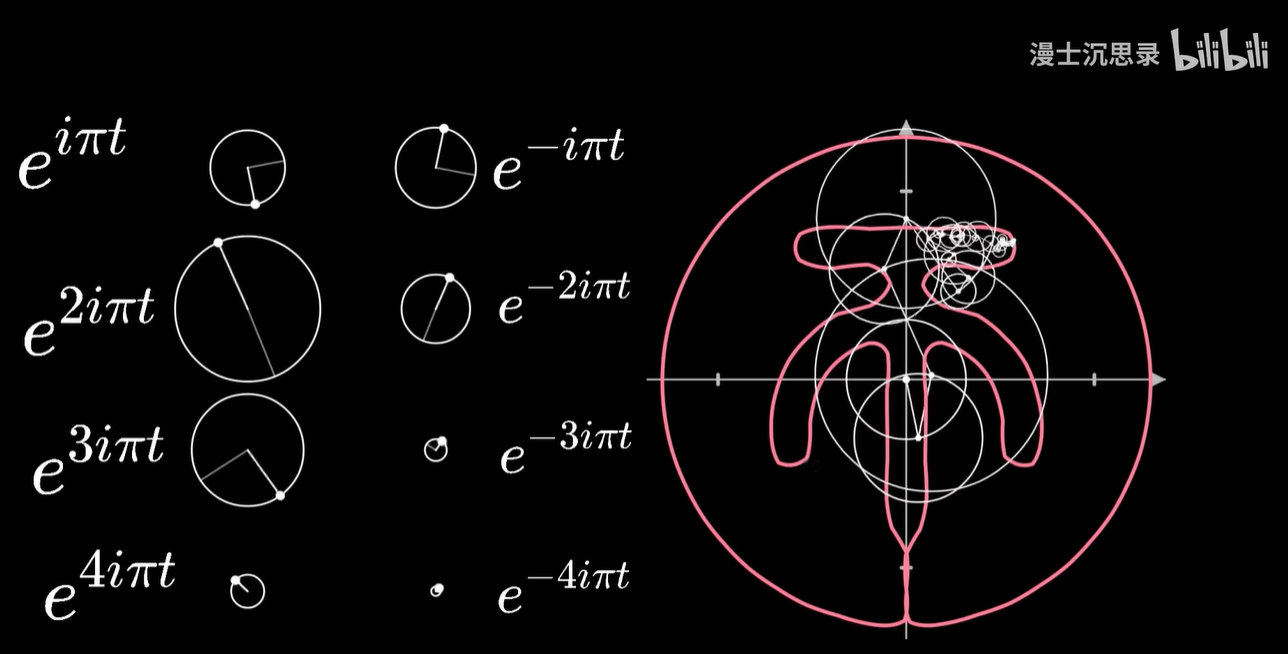
那你可能会问，我怎么知道每个圆周运动的半径要缩放多少倍呢？？？

那当然还是前面说过的内积了，这里的向量是在复平面上的运动，所以如果我们想要知道原来复杂的运动过程，这个向量和每秒钟转 n 圈的圆周运动两个向量的内积，那么我们可以根据复数相乘的几何意义，也做这个乘积的积分。

它的几何含义是：将原来的图像反向的缠绕 n 圈，那么此时整个曲线会有一个质心，这个质心所在的向量，就刚好对应于这个频率的圆周旋转所需要的半径和初始相位。

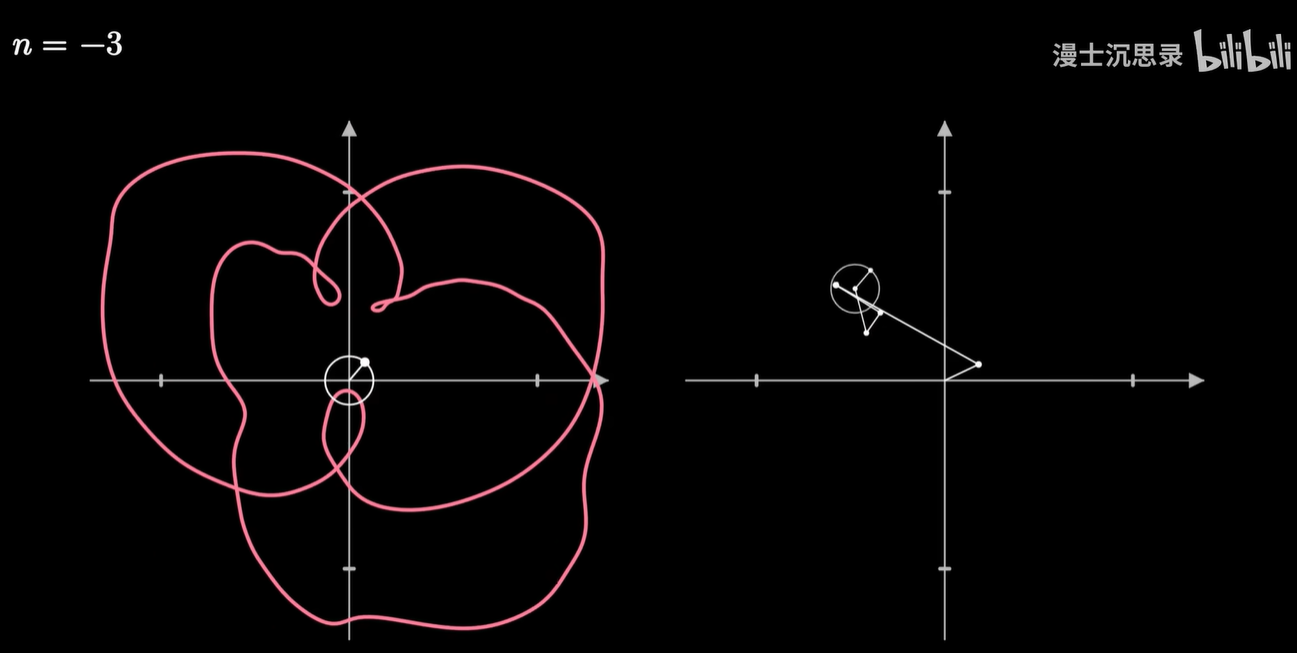
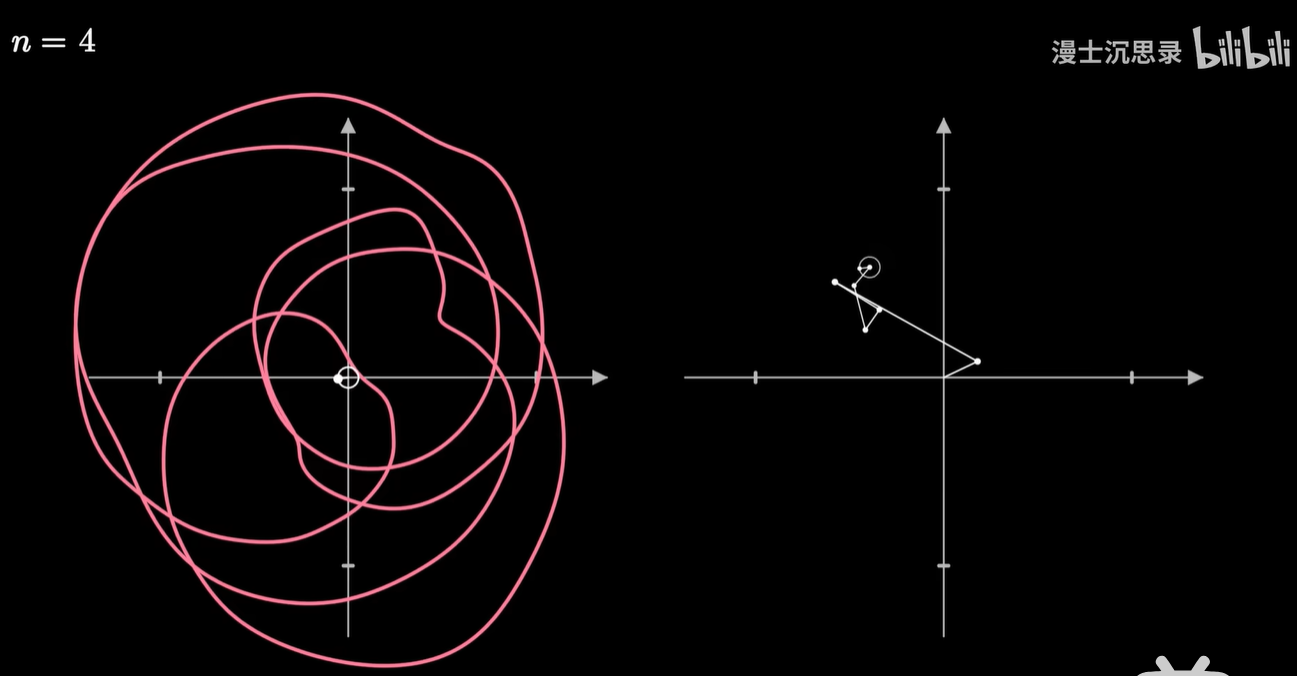
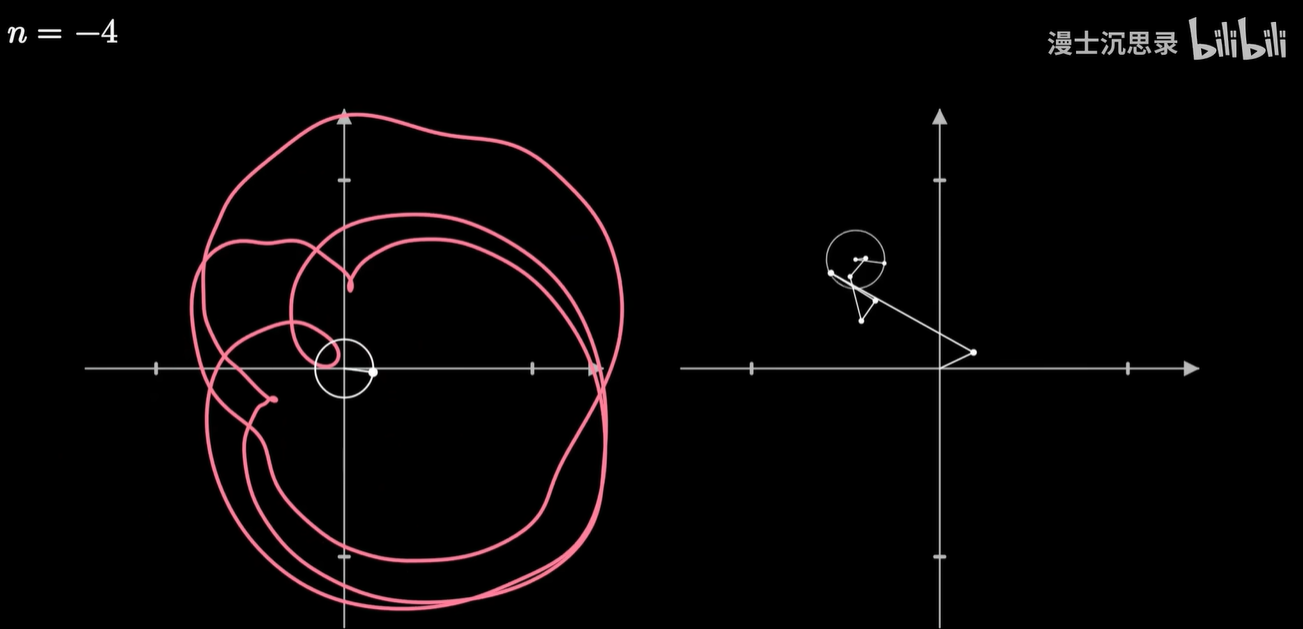
原有的这个旋转过程在某个频率下的旋转越强，这样反向缠绕之后质心就越偏离原点，获得的系数就越大。

我们可以将这样得到各种各样旋转的系数，把各种各样的圆组合起来，让它们一起转圈画一个。

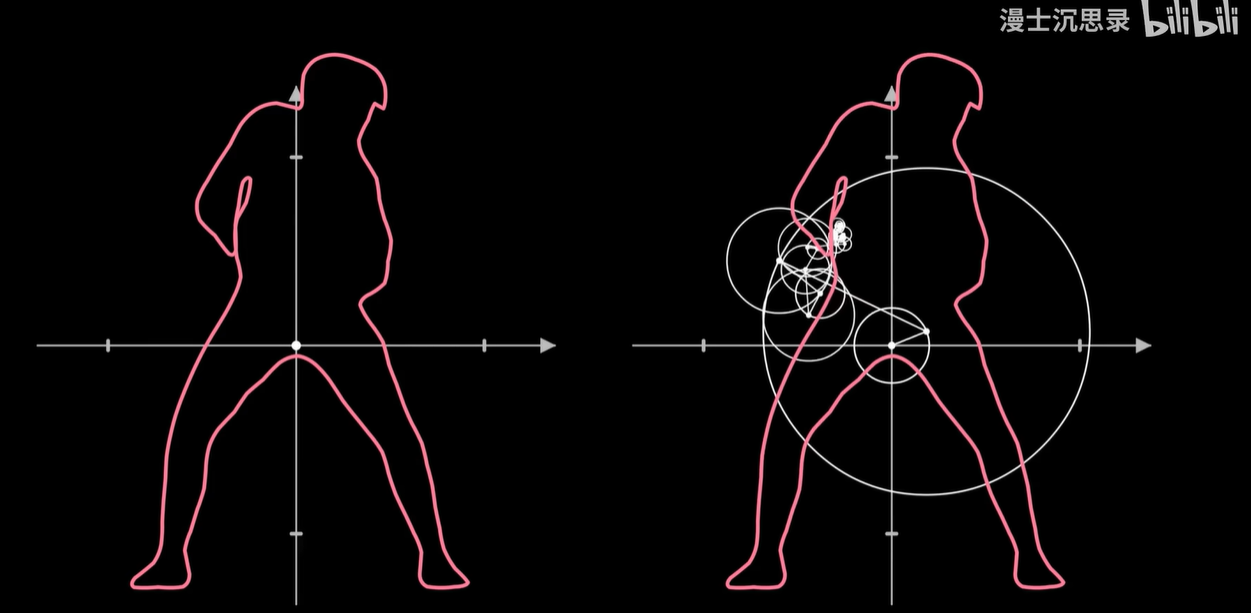
哎，我们确实还原了一开始的图像，使用的圆如果比较少。

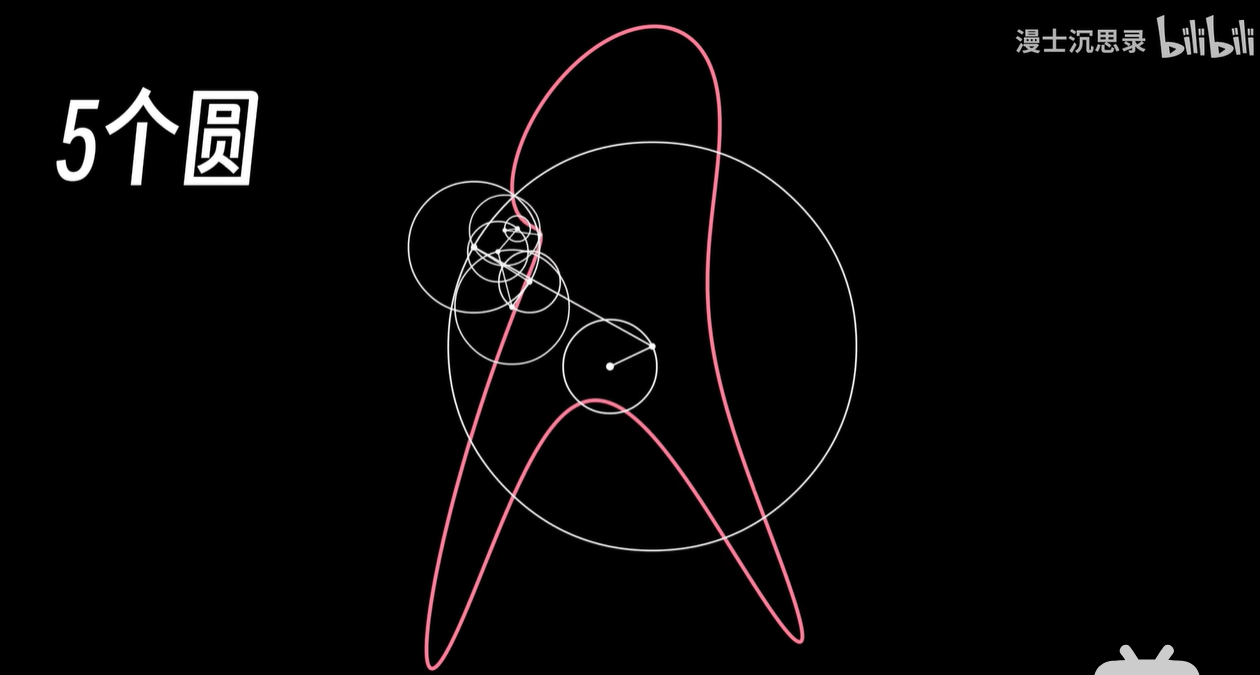
那么整体画的就会比较粗糙。

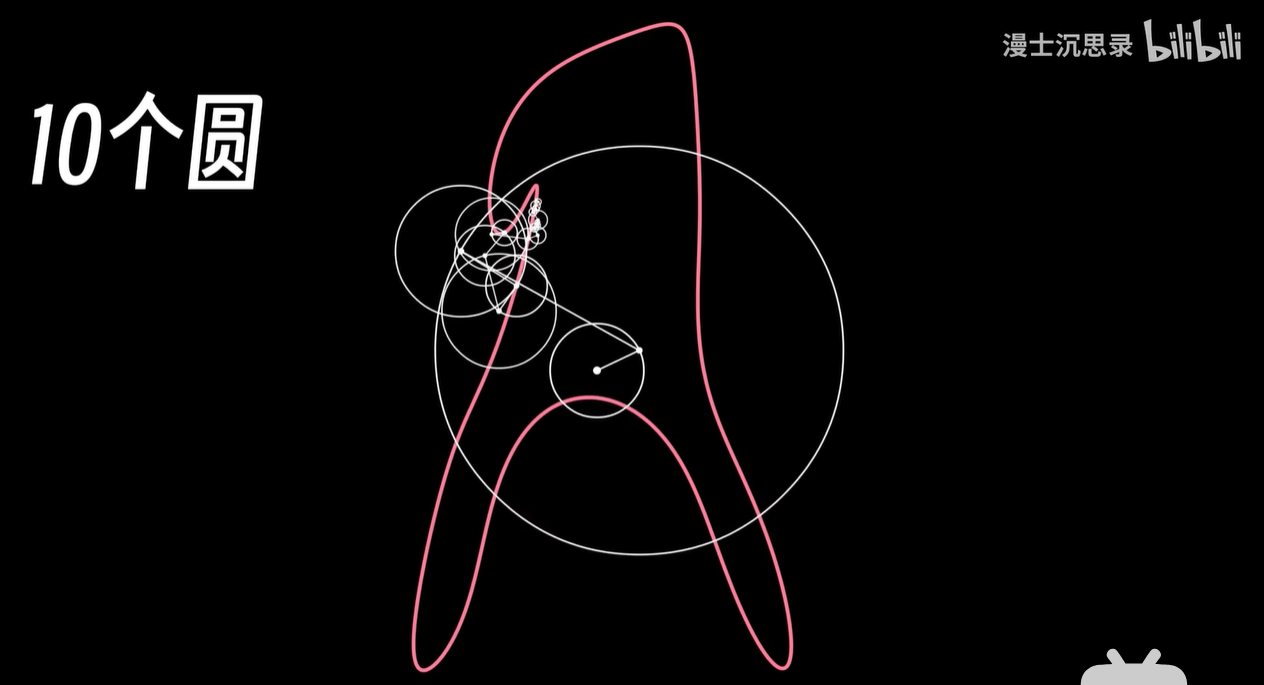
而用的圆越多，你画出来的这个图像就会越精致。

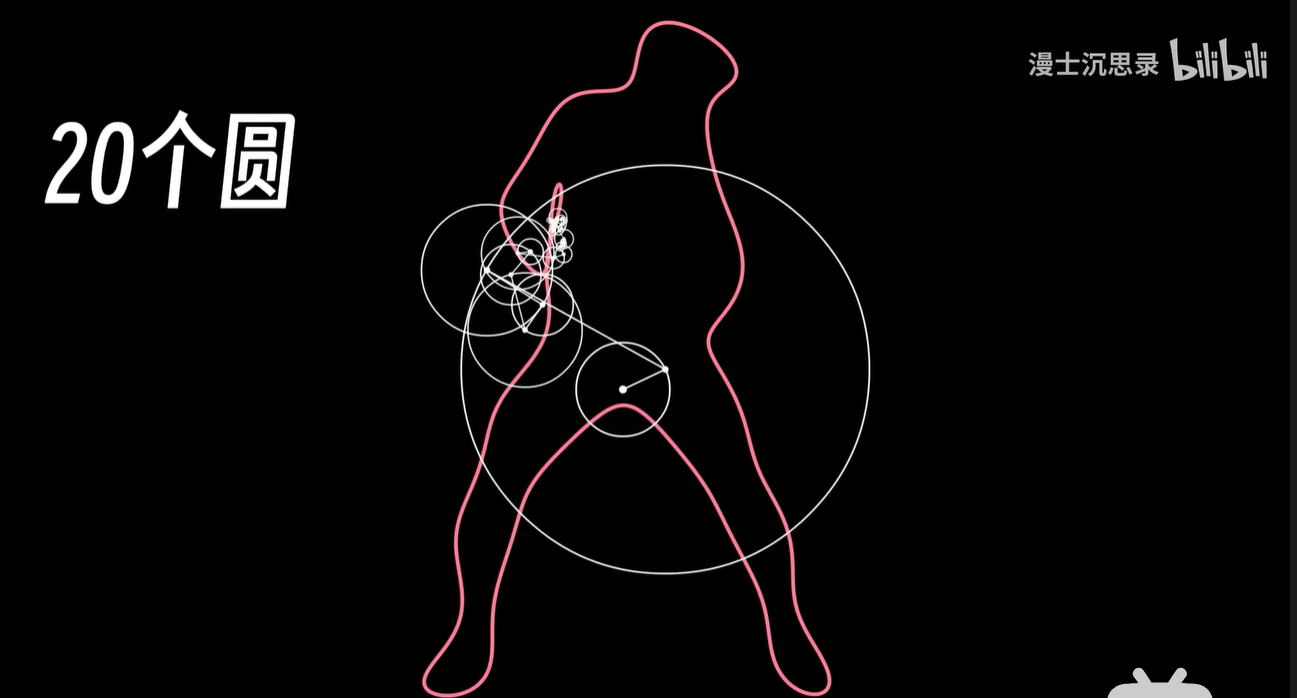
当使用20个圆上圆的时候，就可以基本上把各种各样的细节还原清晰。

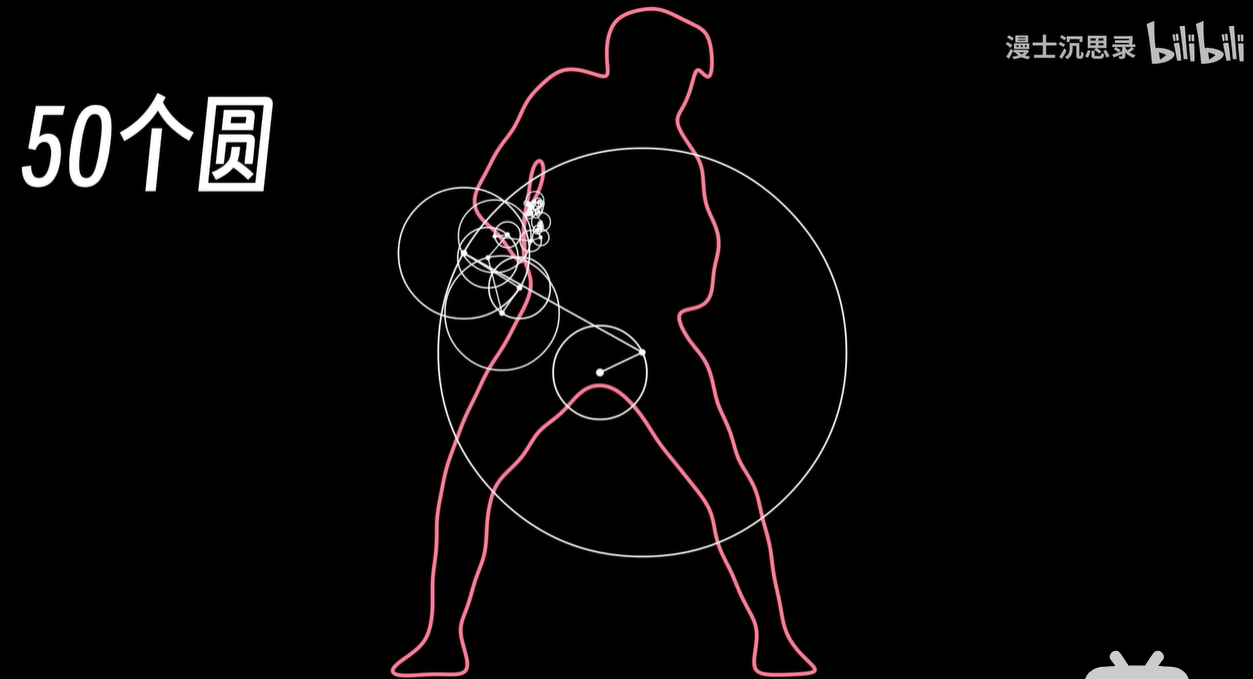
这和声音和图像等等都如出一辙，所以我们一般把这些都叫做高频细节。

我第一次学到这里的时候，突然意识到曾经我们学过人类历史上由托勒密提出的地心说，天文学家用本轮和均轮来解释复杂的行星逆行，诶，这本质上不就是用傅里叶变换的圆上圆来近似那些复杂魔幻的行星运动吗，也就是说，人类其实应用傅里叶变换的历史有千年之久。

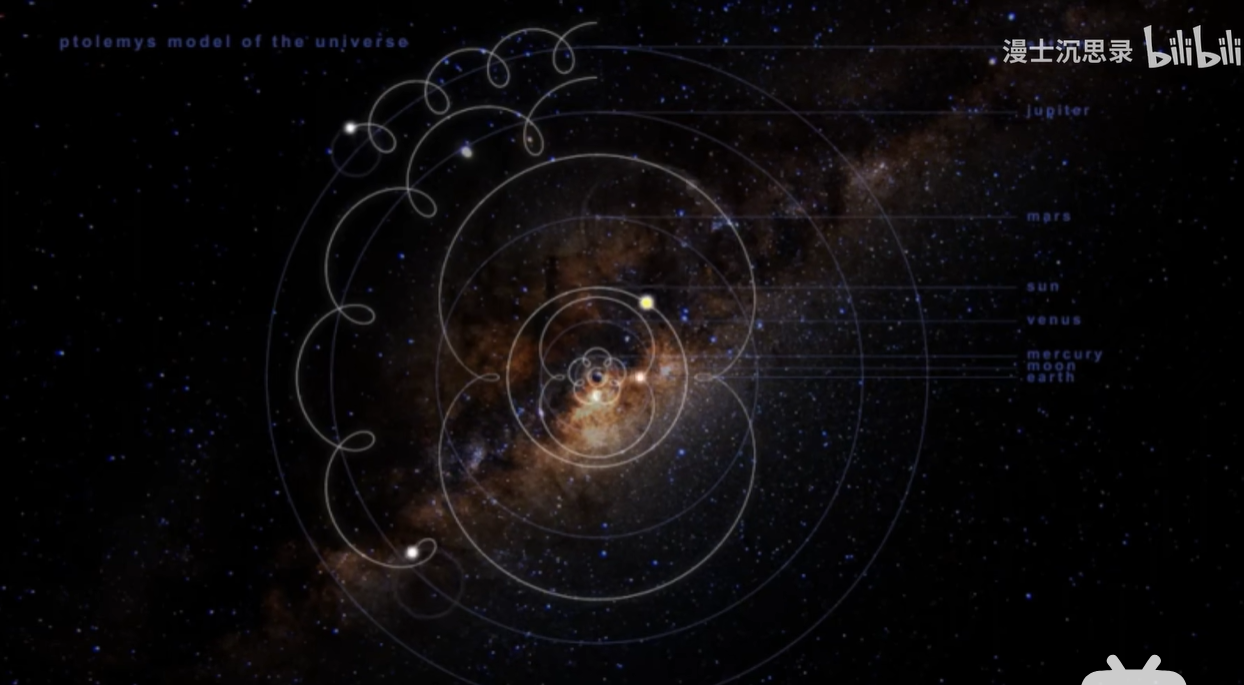
⑧ 还原论

其实无论是用圆上圆来表示任意的运动，还是用多项式函数来逼近任何一个函数，有一种类似的思维方式在反复的出现，它就是贯穿数学和哲学的一种思想方法——还原论。

简单来说，还原论认为理解一个复杂的事物最好的办法就是把它拆解成最基本的、更简单的部分，然后去研究这些部分、以及它们之间的相互作用，最终就能理解整个复杂的事物。

就像修钟表一样，一个钟表很复杂，直接研究它怎么坏的可能无从下手，但如果你懂还原论，就会把它拆开，研究里面的飞轮、齿轮、指针等等每一个零件，看看是哪个零件出了问题，或者哪两个零件之间的影响出现了故障，一旦找到了哪个小零件坏了，或者什么连接出了问题，你就理解为什么坏了，并且把它修好。

西方的科学和哲学一直秉持着这样的观念：把生物还原为细胞、把遗传还原为 DNA 和基因、把世间万物还原成分子和原子，并不断向下还原成更基本的单元。

正如傅里叶变换中，单个正弦波和圆周运动易于分析，所以我们就以此为根基，将任何一个周期函数还原为这些基底的组合。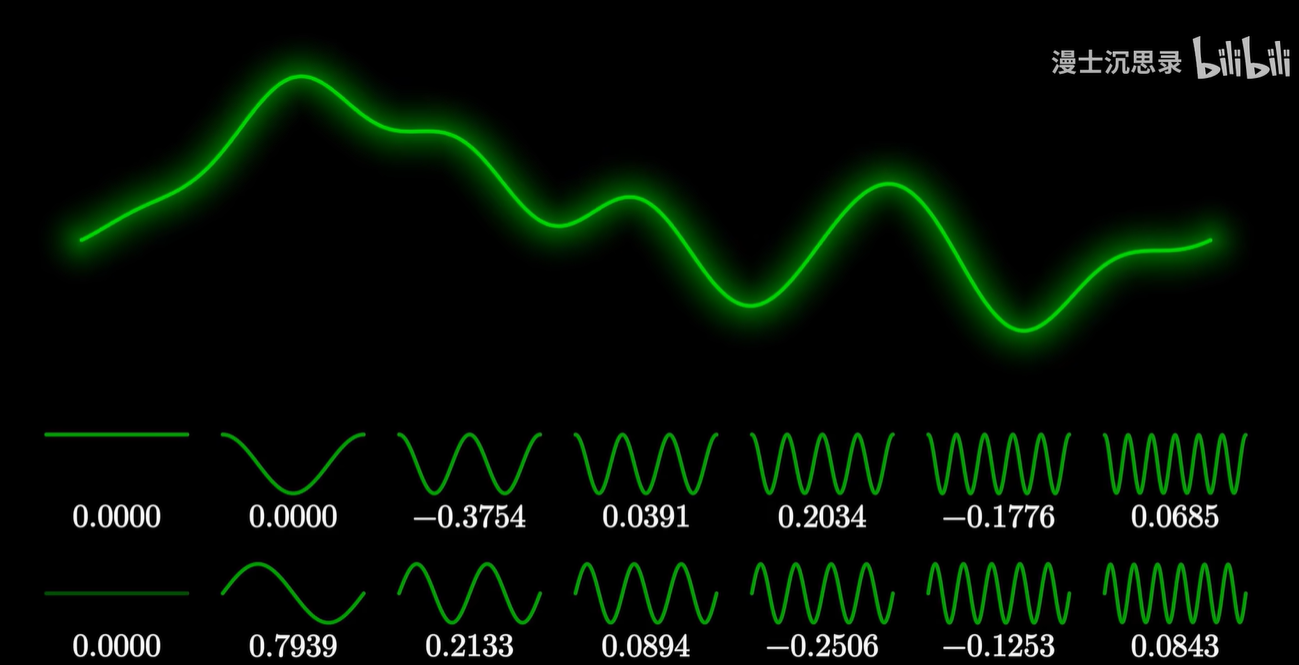

不过，虽然还原论鼎鼎有名威力巨大，但也有自己的局限之处，因为很多时候啊，透彻理解了每个部分和部分之间的联系，依然不能够理解整体，整体有时会大于部分之和，这形成了另一个研究领域，叫做复杂系统，这里不再过多展开。

⑨ 傅里叶变换的应用

x.1 信号处理

事实上，傅立叶变换除了能够帮助我们理解音色，绘制奇妙的轨迹之外，在信号处理分析领域还有着一系列十分神奇的应用。

举一个最常见的例子，你录制了一段语音，但背景却有恼人的电流声或者噪声。

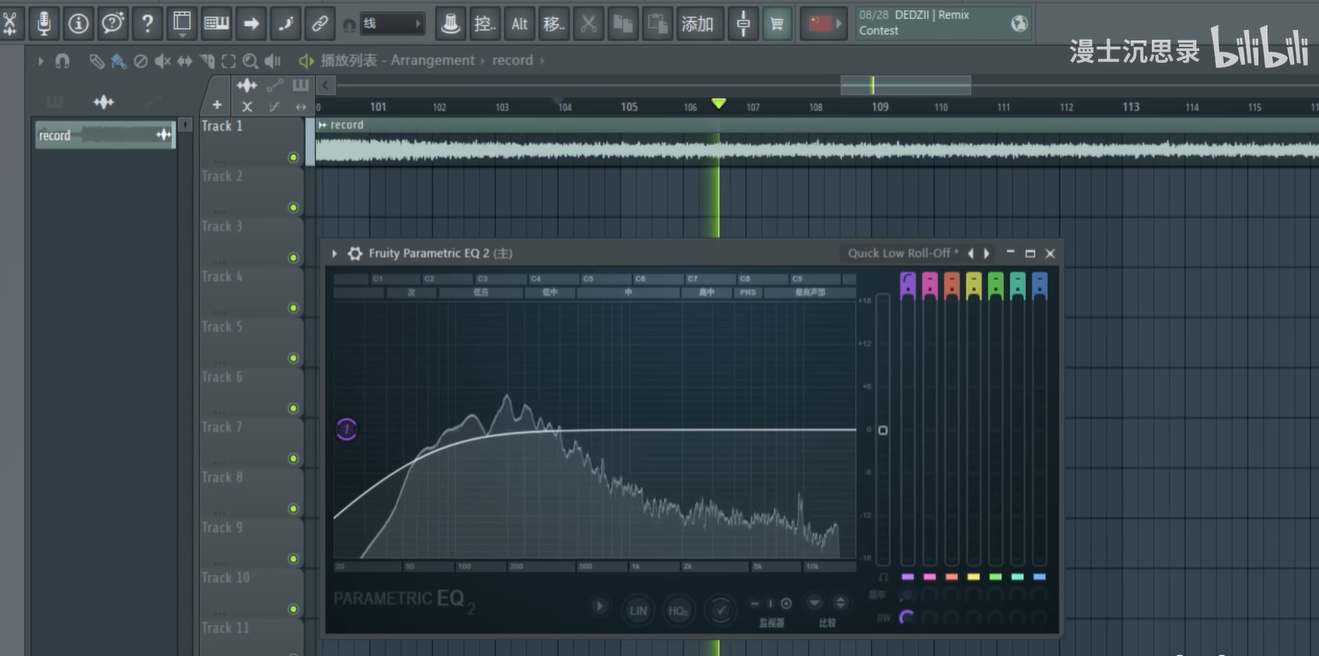
傅里叶变换提供了一种直观而强大的去噪方法，那就是信号在频域中，会显示为不同频率的成分，而恼人的噪声往往在频谱中对应着特定的频率区域。

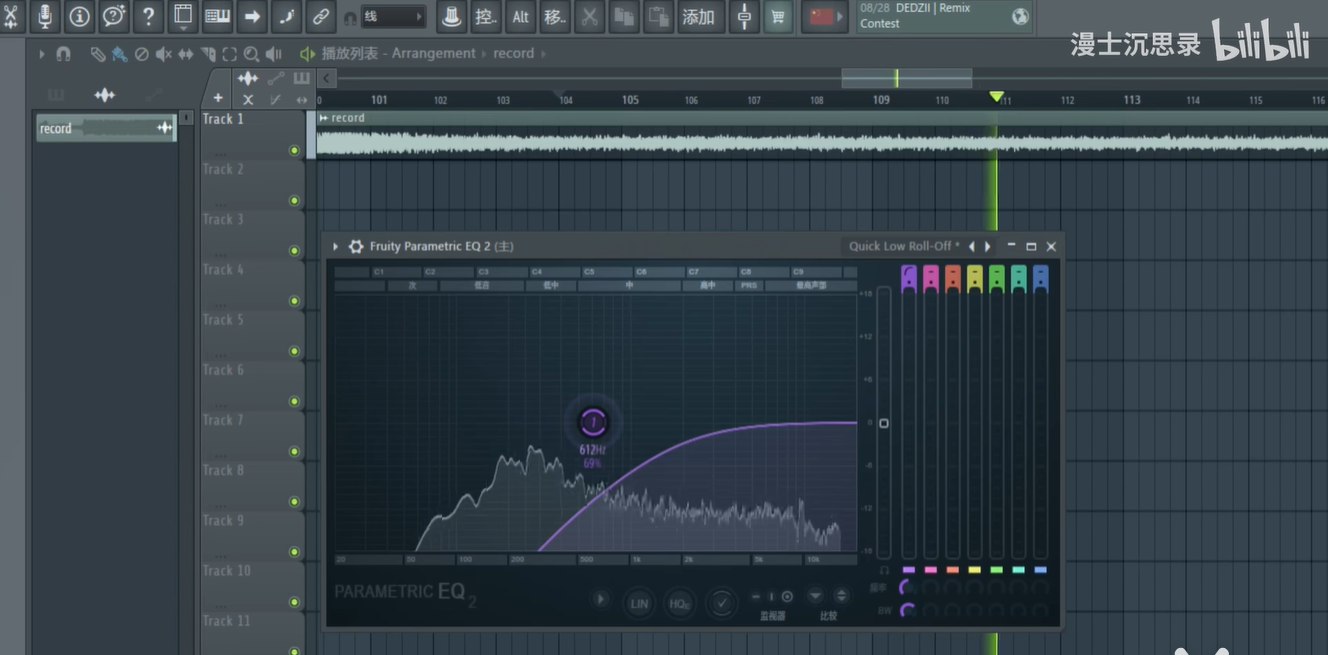
我们只需要在频域中直接降低甚至删除这些频率的能量，那么语音就可以奇迹般的变得清晰起来，这就是很多语音去噪的原理。（损失音色）

x.2 数字图像处理

又比如说拍摄照片时，有的时候会出现周期性的摩尔纹，或者网格状的条纹干扰，肉眼看起来非常烦人，但是如果直接处理像素，我们几乎无从下手。

通过傅里叶变换，将图像转到频域之后，你会看到周期性的噪声会清晰地显示为屏幕上几个特定的亮点。

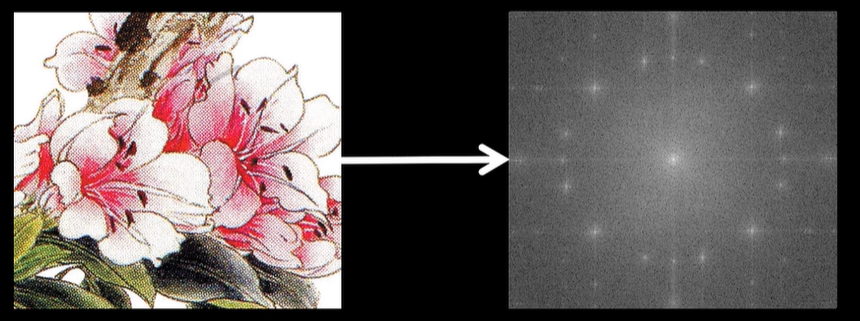
这是因为二维的图片信号也可以傅里叶变换，此时频域的每一个点对应的不再是正弦函数，而是二维的正弦波。

此时摩尔纹或者说网格纹的噪声会强烈激起某些特定频率和方向的基底的能量，我们只需要在频谱图中精准地抹掉这些频点，再将图像从频域逆变换回去，变回图片，令人头疼的这些条纹干扰便神奇地消失了，图像清晰了很多。

不仅如此，频域操作还可以用来锐化图像，当我们希望突出图像的边缘、纹理等细节时，只需要在频域对图像进行高通滤波，保留和增强图像的高频成分，便能将画面中的细节和轮廓清晰地凸显出来甚至修复一些看似模糊的图像。

你看这里的普朗克，他的头发和各种衣服都变得更清晰了。

此外，压缩技术恐怕是傅立叶变换与我们日常生活最紧密相连的应用之一了。

常见的 JPEG 图像压缩和 mp3的音频压缩，本质上都是在频域里巧妙地进行的。

在频域中啊，人类视觉和听觉，大多对低频的能量信号比较敏感，而对于高频的这些细节往往不太敏感，甚至可以直接去除。

于是，我们就可以在几乎不影响感官体验的前提下，只保留中间的这些低频能量，从而大幅减少文件的体积。

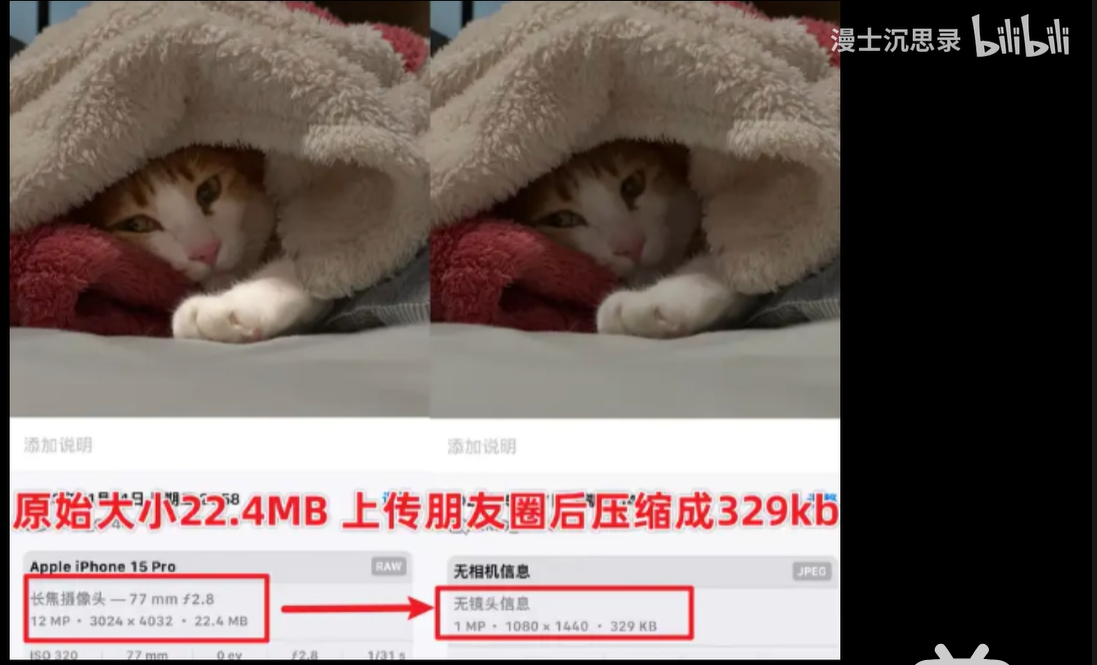
我们平时所享受到网络上各种高清图片、清晰的音乐可以快速地传递，其实背后都有傅里叶变换这种频率压缩技术的默默支持。

好了，以上就是这期的全部内容，这期视频来自B站up主“漫士沉思录”，精良的动画主要来自_F_X_P，他是一个热爱音乐又精通数学的 up 主，动画也做得很漂亮，推荐大家去关注他。

此外，还要特别感谢 starflyer23333、造梦师NGC7023以及南希的帮助，在此一并感谢。