低时延低复杂度QC-LDPC 编码技术（二）
接上篇：低时延低复杂度QC-LDPC 编码技术（一）-CSDN博客
3.校验矩阵设计
因为
矩阵不再是单位阵循环移位形式，无法使用移位逻辑进行矩阵计算，而是需要传统的矩阵计算电路完成，电路中包含大量的XOR2 和AND2，导致编码复杂度高。
针对上述分析，在
校验矩阵构造时，充分考虑矩阵计算环节，首先通过随机构造方式构造出D 矩阵，然后通过对
矩阵进行校验，实现对矩阵格式的限制，选取满足矩阵中子矩阵格式为全零矩阵或单位阵循环移位形式的D矩阵，即选择满足
为全零矩阵或单位阵循环移位形式的D矩阵，然后在D矩阵基础上，利用PEG（Progressive Edge Growth，PEG）构造方式构造出完整的校验矩阵。
经过格式限定后矩阵中的子矩阵与某一向量进行计算时，其本质上可以简化为一维向量数据按照单位循环阵的移位量进行循环移位。在此基础上，可以利用循环移位电路替代矩阵计算电路。
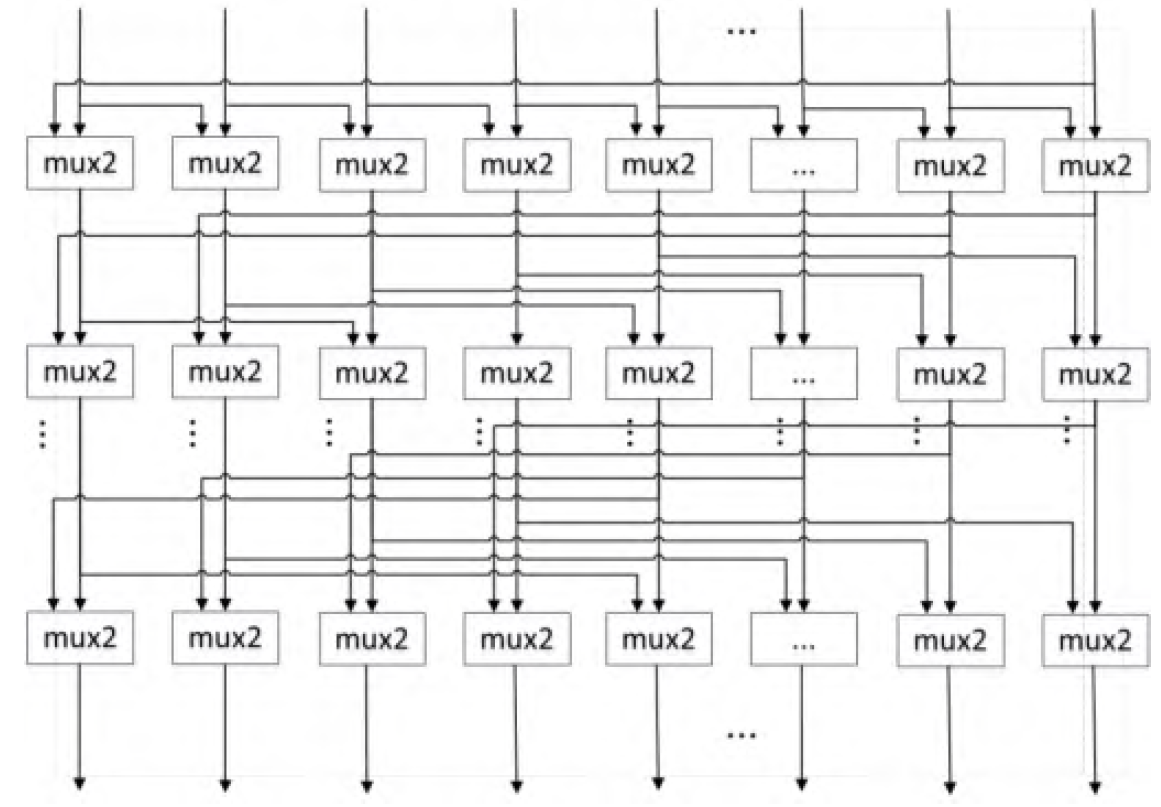
该循环移位电路由若干个选择器（mux2）组成， 其需要的mux2 数量为
，对于b=128的矩阵维度而言，需要的 mux2 数量仅为896 个，相比于传统矩阵计算需要的16384 个XOR2 和16383 个AND2 而言，单个矩阵计算的复杂度显著降低，通过代码综合结果显示，单个矩阵计算的逻辑复杂度降低接近80%。
基于上述校验矩阵构造规则，在进行D矩阵实际构造时，发现D矩阵列重（Column Weight，CW）为3时， D矩阵构造时间较短，当将D矩阵列重增加到5时，在对矩阵格式进行限定时发现构造时间明显增大，且存在构造失败的风险，因此从实际应用角度出发，在本文中D矩阵列重最终选用列重3。
在构造出D矩阵之后，以D矩阵为基础，在其基础上采用PEG 方式构造出完整的校验矩阵。需要指出在得到校验矩阵后，需要对其进行四环消除、六环优化、陷阱集优化操作。
4 按需级联算法架构
为解决D矩阵位置错误集中的问题，本文提出了LDPC+OD_BCH 级联架构，该级联架构将LDPC 作为内码，以BCH短码作为外码。其中，BCH外码为按需级联模式，仅针对易出错位置（错误集中位置）进行按需保护，即只对D矩阵所对应的parity 校验信息进行BCH编码保护，通过级联BCH 短码，解决D矩阵位置错误集中的问题。
BCH短码选取时需要与子矩阵维度对应，便于数据的对齐。
LDPC+OD_BCH 级联架构如下图所示
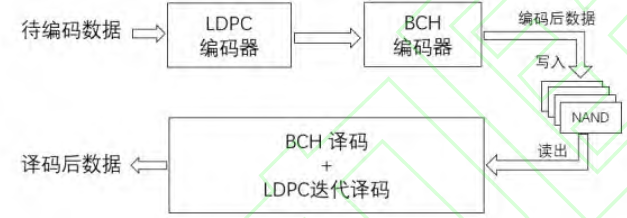
该级联架构在编码侧首先对待编码数据进行LDPC编码，得到LDPC校验信息（LDPC parity），然后将LDPC校验信息送入到BCH 编码器中，对LDPC校验信息进行BCH编码保护。
将BCH生成的校验信息（BCH parity）添加到LDPC码字后面，得到完整的经过LDPC与BCH按需级联编码后的码字。
以LDPC(18560,16512)+ OD_BCH(144,128,1,8)为例进行阐述，其中LDPC 校验矩阵中子矩阵维度为128bit，BCH 码长为144bit，保护的有效信息长度为128bit，纠错能力为1bit，对应的伽罗华域（ Galois Field ， GF ） 为
。
LDPC(18560,16512)对应的校验矩阵维度为16×145，该码字有16组LDPC校验信息。BCH 针对16 组LDPC 校验信息进行外码保护，生成BCH 校验信息，LDPC(18560,16512)+OD_BCH(144,128,1,8) 级联后的数据结构如下图所示。
因为LDPC 校验信息在整个LDPC 码字中占比较低，BCH按需级联方式带来的编码开销相比于传统的级联编码有显著降低。
以LDPC(18560,16512)+ BCH(144,128,1,8)级联码为例，传统级联编码引入的编码开销增加量为12.5%。
本文提出的LDPC(18560, 16512)+OD_BCH(144,128,1,8)按需级联方式，因为LDPC校验信息占比仅为11%，BCH所带来的开销增加量仅为1.38%，相比于传统级联方式，按需级联方式带来的编码开销增加量显著降低，与LDPC 本身的编码开销基本保持在一个水平。
LDPC+OD_BCH 按需级联架构不会对LDPC 码率产生显著影响，该特性在SSD 高码率应用场景下至关重要。