B树、B+树、B*树深度探索与解析：为什么数据库青睐于它们？

一、B树的概念介绍

提到“树”这种数据结构，咱们先想到的可能是二叉树、二叉搜索树。但如果数据量大到需要存在硬盘上（比如数据库里的海量数据），二叉树就有点“力不从心”了——它的高度可能很高，导致频繁的磁盘IO，效率大打折扣。

这时候，B树就该登场了。B树是一种多路平衡查找树，它的核心特点是“多路”——一个节点可以存储多个关键字，并有多个子树。这种结构能显著降低树的高度，减少磁盘访问次数，因此多用于数据库索引、文件系统等场景。

简单说，B树就像一个目录：一个目录下可以放多个文件（关键字），也可以包含多个子目录（子树），而且所有最底层的目录（叶节点）都在同一层，找东西时不用翻来翻去。

二、B树的性质

B树有严格的性质，以“阶数为M”的B树为例（M是一个大于2的整数，决定了节点能存多少关键字）：

1. 关键字数量：每个节点最多能存M-1个关键字（比如M=3时，最多2个关键字）；非根节点最少得有⌈M/2⌉ - 1个关键字（比如M=3时，最少1个；M=4时，最少1个）；根节点特殊，最少可以只有1个关键字。
2. 子树数量：有n个关键字的节点，一定有n+1个子树（比如2个关键字的节点，有3个子树）。
3. 有序性：节点内的关键字按升序排列，且某个子树里的所有关键字，一定介于它左右相邻的两个关键字之间（比如节点有关键字[5,8]，左子树的关键字都小于5，中间子树的都在5-8之间，右子树的都大于8）。
4. 平衡性：所有叶节点都在同一层，保证查找时不会出现“一条路特别长”的情况。

三、手搓B树插入功能

理解了性质，咱们来看看B树的插入功能是怎么实现的。以下代码基于C++，实现了一个模板类BTree<K, M>（K是关键字类型，M是阶数）。

1. 先定义B树的节点结构

B树的节点是存储关键字和子树的“容器”，咱们先定义它的结构：

template<class K, size_t M>
struct BTreeNode
{K _keys[M];// 最多存M个关键字（实际有效是n个，n<=M-1）BTreeNode<K, M>* _childs[M + 1];// 子树指针，数量比关键字多1BTreeNode<K, M>* _parent;// 父节点指针size_t n;// 当前有效关键字数量BTreeNode(): _parent(nullptr), n(0){// 初始化关键字和子树指针for (int i = 0; i < M; i++){_keys[i] = K();_childs[i] = nullptr;}_childs[M] = nullptr;}
};

这里有个细节：_keys数组大小是M，但实际最多只用M-1个（因为节点关键字不能超过M-1）；_childs数组大小是M+1，刚好比关键字数量多1，符合B树的性质。

2. 查找插入位置：FindNode函数

插入关键字前，得先找到该插在哪个节点里。FindNode函数的作用就是：如果关键字已存在，返回它所在的节点和索引；如果不存在，返回它应该插入的父节点和-1（表示未找到）。

pair<Node*, int> FindNode(const K& key)
{Node* cur = _root;Node* parent = nullptr;while (cur){int i = 0;for (; i < (int)cur->n; i++){if (key < cur->_keys[i]){// 关键字比当前小，去左子树找break;}else if (key > cur->_keys[i]){// 关键字比当前大，继续往后找continue;}else{// 找到关键字，返回节点和索引return { cur, i };}}// 没找到，记录父节点，继续往下找子树parent = cur;cur = cur->_childs[i];}// 找到最底层，返回父节点（就是要插入的节点）return { parent, -1 };
}

逻辑很直观：从根节点开始，按关键字大小遍历当前节点的关键字，小于就去左子树，大于就继续往后，直到找到位置或走到叶节点。

3. 插入关键字到节点：InsertKey函数

找到要插入的节点后，需要把关键字插入到节点的合适位置（保持有序），同时可能还要插入一个子树（分裂时会用到）。

void InsertKey(Node* cur, const K& key, Node* child)
{int youxu = cur->n - 1; // 从最后一个有效关键字开始K tmp = key;// 从后往前挪，给新关键字腾位置while (youxu >= 0){if (tmp < cur->_keys[youxu]){// 当前关键字比新的大，往后挪一位cur->_keys[youxu + 1] = cur->_keys[youxu];cur->_childs[youxu + 2] = cur->_childs[youxu + 1];// 子树也跟着挪youxu--;}else{// 找到位置了，跳出循环break;}}// 插入新关键字和子树cur->_keys[youxu + 1] = tmp;cur->_childs[youxu + 2] = child;cur->n++;// 有效关键字数量+1if (child){child->_parent = cur;// 更新子树的父节点}
}

这步类似数组的插入：从后往前移动元素，给新元素腾出位置，保证插入后节点内的关键字依然有序。

4. 关键一步：节点分裂（解决溢出）

B树插入最核心的操作是“分裂”。因为每个节点最多只能存M-1个关键字，如果插入后关键字数量达到M，就触发“溢出”，必须分裂成两个节点，否则就违反了B树的性质。

整个插入流程在Insert函数中实现：

bool Insert(const K& key)
{// 空树，直接创建根节点if (_root == nullptr){Node* newnode = new Node();newnode->_keys[0] = key;newnode->n = 1;_root = newnode;return true;}// 先检查关键字是否已存在pair<Node*, int> ret = FindNode(key);if (ret.second != -1){// 已存在，插入失败return false;}Node* cur = ret.first; // 要插入的节点K insertkey = key;Node* child = nullptr;while (true){// 插入关键字到当前节点InsertKey(cur, insertkey, child);// 如果节点关键字数量小于M，插入成功if (cur->n < M){return true;}// 否则，节点溢出，需要分裂int mid = M / 2; // 中间位置（分裂点）Node* brother = new Node(); // 分裂出的兄弟节点// 把mid右边的关键字和子树移到兄弟节点int i = mid + 1;int j = 0;for (; i < M; i++, j++){brother->_keys[j] = cur->_keys[i];brother->_childs[j] = cur->_childs[i];if (cur->_childs[i]){cur->_childs[i]->_parent = brother; // 更新子树的父节点}// 清空当前节点的对应位置cur->_keys[i] = K();cur->_childs[i] = nullptr;}// 移动最后一个子树brother->_childs[j] = cur->_childs[i];if (cur->_childs[i]){cur->_childs[i]->_parent = brother;}cur->_childs[i] = nullptr;// 更新两个节点的有效关键字数量brother->n = j;cur->n -= (j + 1); // 减去mid和右边的j个// 中间的关键字（mid位置）要上移到父节点K newkey = cur->_keys[mid];cur->_keys[mid] = K(); // 清空当前节点的mid位置// 如果当前节点是根节点，需要创建新的根节点if (cur->_parent == nullptr){_root = new Node();_root->_keys[0] = newkey;_root->_childs[0] = cur;_root->_childs[1] = brother;_root->n = 1;cur->_parent = _root;brother->_parent = _root;return true;}else{// 不是根节点，继续往上处理（父节点可能也要分裂）cur = cur->_parent;insertkey = newkey;child = brother;}}
}

分裂的逻辑可以总结为3步：

1. 找到中间位置mid = M/2，把mid右边的关键字和子树移到新的兄弟节点；
2. 把mid位置的关键字“上移”到父节点；
3. 如果父节点也溢出，重复分裂过程，直到没有溢出（如果根节点分裂，树的高度会+1）。

比如M=3（最多2个关键字）的B树，插入第3个关键字时就会分裂：中间的关键字上移，左右各留1个，形成两个子节点。

四、简要说明：B树删除

B树的删除操作比插入复杂，主要因为删除后可能导致节点关键字数量低于最小值，需要进行调整，这里不做具体实现，基本流程如下：

1. 定位节点：找到要删除的关键字所在的节点
2. 删除关键字：
   • 若为叶节点，直接删除
   • 若为非叶节点，用其前驱或后继关键字替换后删除
3. 平衡调整：
   • 若删除后节点关键字数仍满足最小值，操作结束
   • 若不满足，先尝试从兄弟节点"借"一个关键字（同时更新父节点对应关键字）
   • 若兄弟节点也无多余关键字，则与兄弟节点及父节点中间关键字合并

这个过程可能引发连锁反应，需要从叶节点一直向上调整到根节点，确保所有节点都满足B树的性质。

五、性能分析

B树的设计初衷是为了优化外存（如硬盘）中的数据访问，其性能优势主要体现在以下几个方面：

1. 时间复杂度分析

• 查找操作：最坏情况下需要访问树的高度h个节点，时间复杂度为O(h·logM)，其中h是树的高度，logM是每个节点内查找关键字的时间（可采用二分查找）。
• 插入操作：查找位置O(h·logM) + 插入关键字O(M)（节点内移动元素） + 可能的分裂操作O(M)（最多h次分裂），整体仍为O(h·M)。
• 删除操作：类似插入，时间复杂度为O(h·M)，因为可能需要多次合并或借调操作。

由于B树的高度h非常小（对于M=1000的B树，存储1亿个关键字的高度仅为3-4），所以实际性能非常优异。

2. 与二叉搜索树的对比

特性	二叉搜索树	B树（M阶）
树高度	O(logN)，但可能退化为O(N)	严格O(log_M N)，非常稳定
磁盘IO次数	O(h)，h可能很大	O(h)，h很小（通常3-5）
节点利用率	每个节点只存1个关键字	每个节点存O(M)个关键字
适合场景	内存中的小规模数据	外存中的大规模数据

对于存储在硬盘上的1亿条数据，二叉树可能需要30次IO操作，而M=1000的B树仅需要3-4次，性能差异显著。

3. 阶数M对性能的影响

阶数M是影响B树性能的关键参数：

• M越大，树高h越小：减少IO次数，但节点内的关键字查找时间增加
• M太小，树高h增大：增加IO次数，但节点内操作更快

实际应用中，M的选择通常与磁盘块大小匹配（如4KB磁盘块，M约为300-400），使每个B树节点刚好占用一个磁盘块，最大化单次IO的利用率。

4. 缓存友好性

B树的节点结构天然适合现代计算机的缓存机制：

• 一次加载一个节点到内存，可访问多个关键字
• 相邻节点通常在磁盘上物理位置接近，利于预读
• 节点内关键字连续存储，可高效利用CPU缓存

这种特性进一步提升了B树在实际应用中的性能表现。

5. 实际应用中的性能表现

在数据库系统中，B树（及变种B+树）作为索引结构时：

• 单条记录查询通常只需2-4次磁盘IO
• 范围查询可通过节点内连续扫描高效完成
• 插入删除操作不会导致索引结构剧烈变化，性能稳定

相比其他数据结构，B树在大数据量、高IO成本的场景下优势明显。

六、B树有什么价值？

B树通过"多路存储"和"平衡结构"的设计，完美解决了大量数据在外存中的高效访问问题。它的核心优势在于：

1. 低树高设计，显著减少磁盘IO次数
2. 严格的平衡性保证，提供稳定的查询性能
3. 节点结构与磁盘存储特性匹配，IO效率高
4. 支持高效的插入、删除和范围查询操作

理解B树的原理和实现，不仅能帮助我们更好地使用数据库等系统，也能培养我们从"内存思维"到"外存思维"的转变——在处理大规模数据时，减少IO操作往往比优化内存计算更重要。

七、B+树和B*树

B+树

B+树是B树的变形，是在B树基础上优化的多路平衡搜索树，B+树的规则跟B树基本类似，但是又
在B树的基础上做了以下几点改进优化：（注意这里不同版本可能实现不同，但原理都是类似的）

1. 分支节点的子树指针与关键字个数相同
2. 分支节点的子树指针p[i]指向关键字值大小在[k[i]，k[i+1])区间之间
3. 所有叶子节点增加一个链接指针链接在一起（这一点非常重要，这样我们去顺序查找的时候就不需要进行中序遍历了，可以直接根据链表来查找）
4. 所有关键字及其映射数据都在叶子节点出现

分支节点与叶子节点有重复的值，分支节点存的是叶子节点索引。父亲中存的是孩子节点中的最小值做索引。

B+树插入过程：

B+树的插入过程和B树类似，细节区别在于：第一次插入两层节点，一层做分支，一层做根，如果比第一个数大，就向叶子节点去插入，比第一个数小，就将索引更新为这个值，随后插入叶子节点，叶子节点满后分裂一半给兄弟节点，后往父亲插入一个关键字（兄弟节点中的最小值）和一个孩子…

B+树的特性：

1. 所有关键字都出现在叶子节点的链表中，且链表中的节点都是有序的。
2. 不可能在分支节点中命中。
3. 分支节点相当于是叶子节点的索引，叶子节点才是存储数据的数据层。

B*树

B*树是B+树的变形：在B+树的分支节点增加指向兄弟节点的指针。

B+树节点原来关键字个数最少是1/2M，B*树要求节点关键字最少是2/3M，最多是M

B+树的分裂：

当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。

B*树的分裂：

当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。

B 树 vs B+ 树 vs B* 树对比

对比维度	B 树	B+ 树	B* 树
节点关键字数量	非根非叶节点：关键字数在 ⌈M/2⌉ - 1 到 M-1 之间（M 为阶数）；根节点非叶时最少含 2 个关键字	非根非叶节点：关键字数在 ⌈M/2⌉ 到 M 之间（子树指针数 = 关键字数）	非根非叶节点：关键字数至少为 ⌈2M/3⌉（节点最低使用率 2/3，高于 B+ 树的 1/2）
数据存储位置	所有节点（非叶、叶节点）都存储关键字及对应数据	仅叶子节点存储全部关键字和数据；非叶节点是 “索引”（仅存关键字，无对应数据）	仅叶子节点存储全部关键字和数据；非叶节点是 “索引”（仅存关键字，无对应数据）
叶子节点特性	所有叶子节点在同一层，但无链表连接	所有叶子节点在同一层，且通过单向 / 双向链表连接（便于范围查询）	所有叶子节点在同一层，且通过单向 / 双向链表连接（便于范围查询）
查找结束位置	可在非叶节点命中（找到关键字后直接返回对应数据）	必须到叶子节点才命中（非叶节点仅做 “索引指引”，不存实际数据）	必须到叶子节点才命中（非叶节点仅做 “索引指引”，不存实际数据）
节点分裂策略	节点满时，分裂为两个新节点，各含约 M/2 个关键字，父节点新增子节点指针	节点满时，分裂出一个新节点，原节点复制约 1/2 数据到新节点，父节点新增子节点指针	优先尝试向兄弟节点转移数据（若兄弟节点未满）；若兄弟也满，才分裂为三个节点，各含约 1/3 数据，父节点新增子节点指针（分裂概率更低）
空间利用率	非根非叶节点最低使用率 1/2	非根非叶节点最低使用率 1/2	非根非叶节点最低使用率 2/3，空间利用率更高
典型应用场景	早期文件系统、少数数据库（现在较少直接使用）	数据库索引（如 MySQL InnoDB 的主键 / 辅助索引）、现代文件系统	对空间利用率要求极高的场景（是 B+ 树的优化变体，实际直接使用场景少于 B+ 树）

八、B树的应用

索引

B树最常见的应用就是用来做索引。索引通俗的说就是为了方便用户快速找到所寻之物，MySQL官方对索引的定义为：索引(index)是帮助MySQL高效获取数据的数据结构，简单来说：索引就是数据结构。

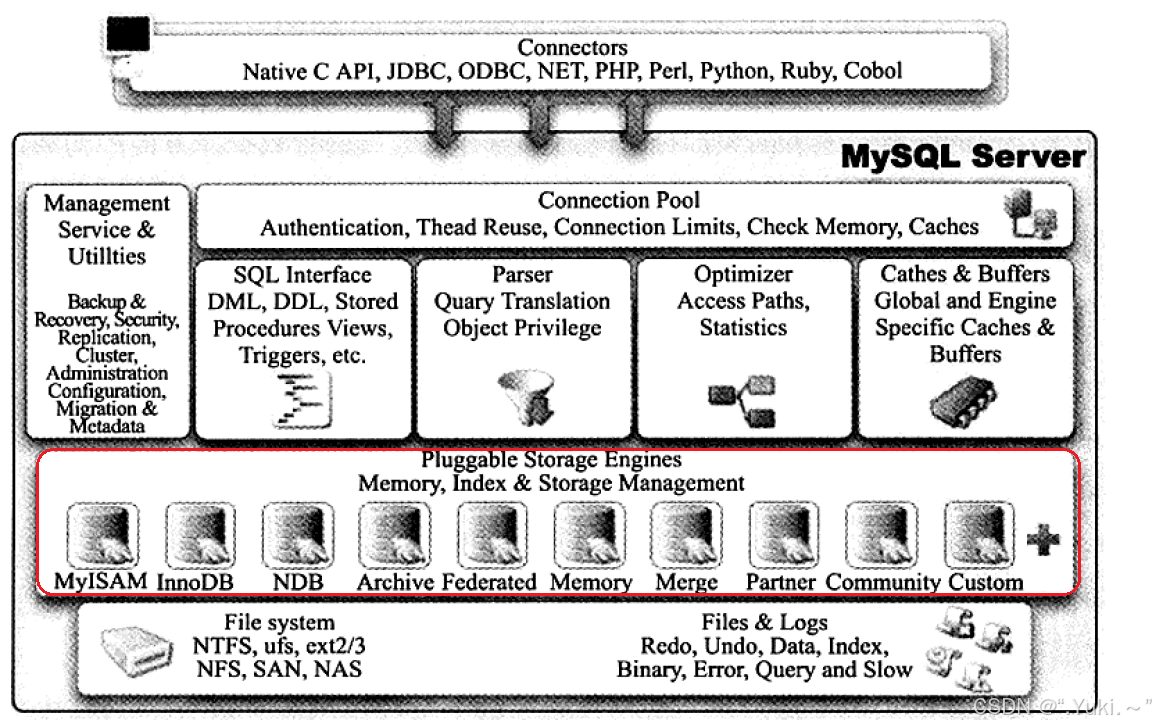
MySQL索引简介

MySQL中索引属于存储引擎级别的概念，不同存储引擎对索引的实现方式是不同的：

InnoDB

InnoDB 是 MySQL 的默认存储引擎，支持事务、行级锁和外键，其索引设计与数据存储深度耦合，以聚簇索引（主键索引）为核心，辅助索引依赖聚簇索引，两者均基于 B+ 树实现。

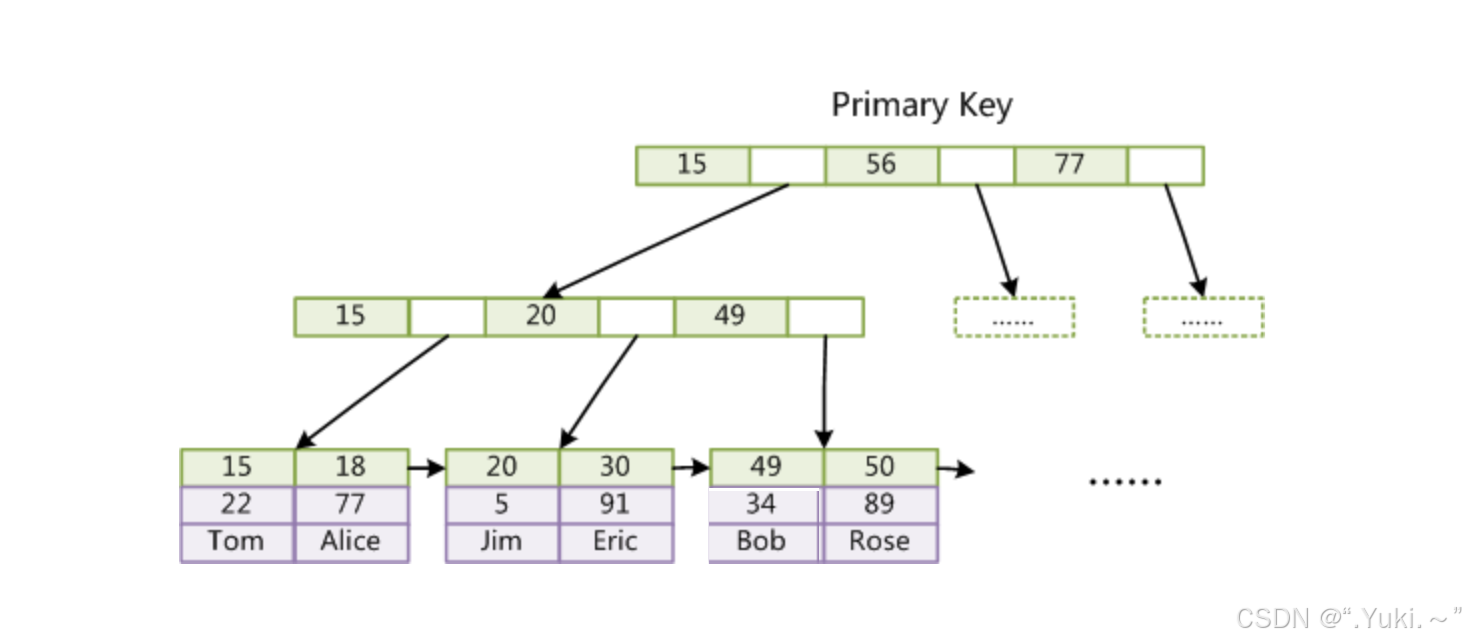
聚簇索引（主键索引）的 B+ 树结构

InnoDB 的聚簇索引直接将 数据与索引融合，B+ 树的叶子节点不再存储 “数据指针”，而是直接存储 整行数据（除主键外的其他字段内容）。

非叶子节点：存储 “主键值 + 子节点指针”，仅用于定位叶子节点的位置。
叶子节点：存储 “完整行数据”，且按主键顺序排序。
示例：若表 user 以 id 为主键，其聚簇索引的 B+ 树结构如下：

非叶子节点（上层）：[100, 指针A] → [200, 指针B] → [300, 指针C]↓          ↓          ↓
非叶子节点（下层）：[101, 指针A1] [102, 指针A2] ...  [201, 指针B1] ...↓          ↓                ↓
叶子节点（数据）：  (id=101, name=张三, age=20)  (id=102, name=李四, age=25)  ...  (id=201, name=王五, age=30)  ...

关键特点：
聚簇索引即 “数据本身”，查询主键时无需额外访问数据文件（直接从 B+ 树叶子节点获取数据），效率极高。

InnoDB 要求表必须有聚簇索引：
若显式定义 PRIMARY KEY，则该主键为聚簇索引；
若无主键，选择第一个 唯一非空索引 作为聚簇索引；
若既无主键也无唯一非空索引，InnoDB 会自动生成一个隐藏的 6 字节自增主键（DB_ROW_ID）作为聚簇索引。

辅助索引的 B+ 树结构

除主键外，其他字段（如 name、age）创建的索引均为辅助索引，其 B+ 树结构与聚簇索引不同：
非叶子节点：存储 “辅助索引键（如 name） + 子节点指针”，用于定位叶子节点。
叶子节点：不存储整行数据，仅存储 对应的主键值（如 id=101）。

查询流程：通过辅助索引查询时，需经历 “两次 B+ 树检索”（即 “回表”）：
先在辅助索引的 B+ 树中，根据辅助键找到对应的 主键值；
再到聚簇索引的 B+ 树中，根据主键值找到完整行数据。

示例：若为 user 表的 name 字段创建辅助索引，查询 WHERE name=‘张三’ 的流程：
辅助索引 B+ 树：根据 name=‘张三’ 找到叶子节点中的主键 id=101；
聚簇索引 B+ 树：根据 id=101 找到叶子节点中的完整数据 (101, 张三, 20)。

MyISAM

MyISAM 是 MySQL 早期的存储引擎，不支持事务和行级锁，仅支持表级锁，其索引设计的核心是 索引与数据完全分离，所有索引（包括主键索引）均为非聚簇索引，B+ 树的叶子节点仅存储 “数据的物理地址”（而非数据本身）。

MyISAM 中，主键索引和辅助索引的 B+ 树结构 完全一致，仅索引键不同：
非叶子节点：存储 “索引键（主键或辅助键） + 子节点指针”，用于定位叶子节点。
叶子节点：存储 “数据的物理地址”（即数据在 .MYD 文件中的偏移量，.MYD 是 MyISAM 的数据文件）。

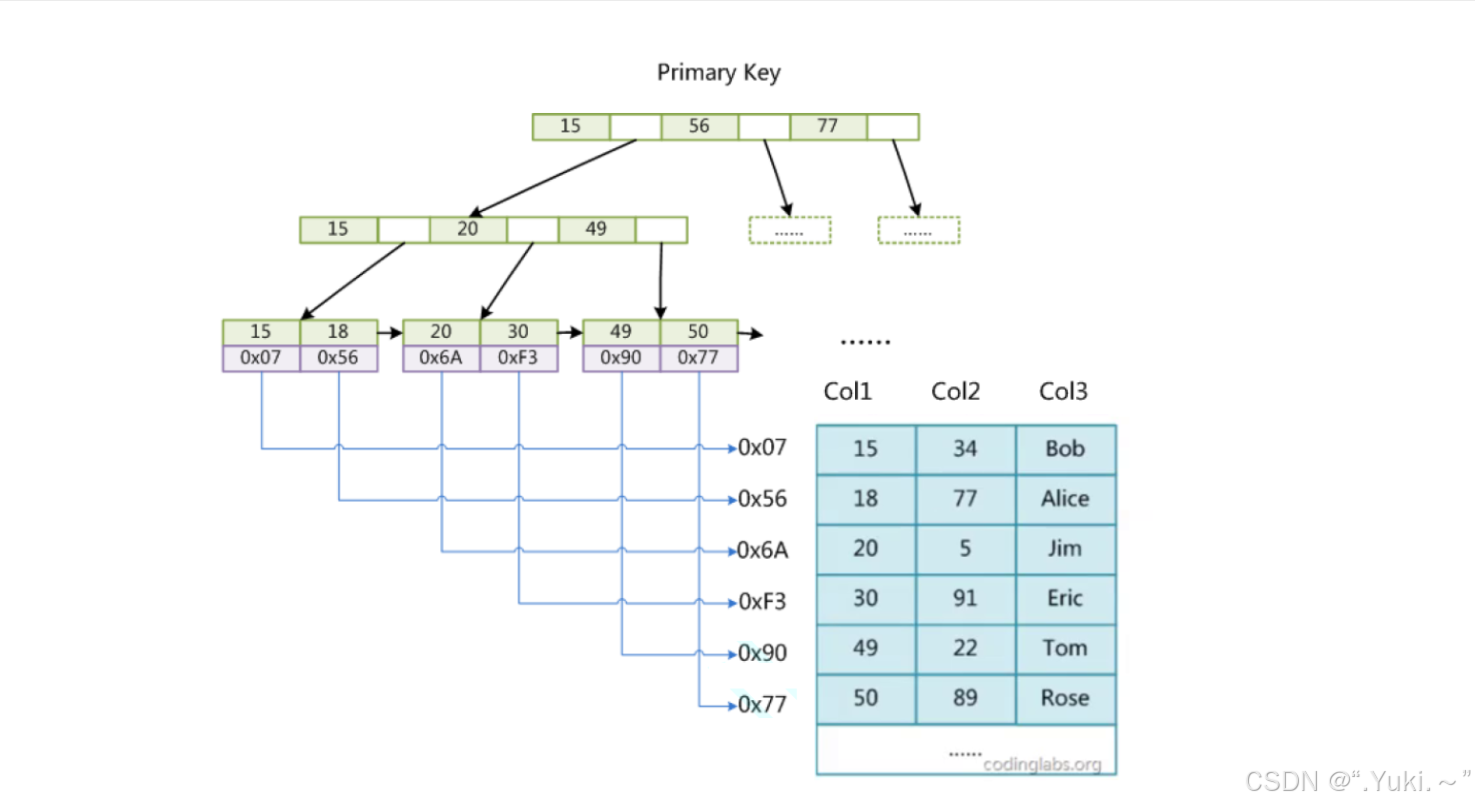
关键特点：
索引与数据分离：索引存储在 .MYI 文件（MyISAM 索引文件），数据存储在 .MYD 文件，查询时需先通过 B+ 树找到物理地址，再到 .MYD 文件中读取数据（一次索引检索 + 一次数据检索）。
主键无特殊地位：MyISAM 的主键可重复（甚至允许为 NULL），因为它仅作为普通索引键，叶子节点存储的是物理地址，而非数据本身，无需保证唯一性（但实际业务中仍建议主键唯一）。