【LeetCode】26、80、169、189、121、122、55、45、274题解

26. 删除有序数组中的重复项

给你一个 非严格递增排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：

• 更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。

• 返回 k 。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

提示：

• 1 <= nums.length <= 3 * 104

• -104 <= nums[i] <= 104

• nums 已按 非严格递增 排列

题解

class Solution:def removeDuplicates(self, nums):if not nums:return 0count = 0for i in range(len(nums)):if nums[count] != nums[i]:count += 1nums[count] = nums[i]return count + 1

因为数组是排序好的，重复元素会连续出现，这是关键！我们可以用两个指针：

• 慢指针 count：指向当前已经处理好的最后一个唯一元素

• 快指针 i：遍历整个数组寻找新的唯一元素

当快指针找到与慢指针不同的元素时，就把它放到慢指针的下一个位置，然后移动慢指针。

示例 nums = [0,0,1,1,1,2,2,3,3,4]

初始状态：

• count = 0（慢指针从第一个元素开始）

• 数组：[0,0,1,1,1,2,2,3,3,4]

1. i=0：nums[count] = nums[0] = 0，两元素相等，不做操作

2. i=1：nums[count]=0 与 nums[1]=0相等，不做操作

3. i=2：nums[count]=0与nums[2]=1不相等：count 变为 1

   把 nums[2]放到 nums[1]，数组变为 [0,1,1,1,1,2,2,3,3,4]

4. i=3：nums[count]=1 与 nums[3]=1相等，不做操作

5. i=4：nums[count]=1与nums[4]=1相等，不做操作

6. i=5：nums[count]=1与nums[5]=2不相等：count 变为 2

   把 nums[5]放到nums[2]，数组变为 [0,1,2,1,1,2,2,3,3,4]

7. i=6：nums[count]=2与nums[6]=2相等，不做操作

8. i=7：nums[count]=2与nums[7]=3不相等：count变为 3

   把 nums[7]放到nums[3]，数组变为 [0,1,2,3,1,2,2,3,3,4]

9. i=8：nums[count]=3与 nums[8]=3相等，不做操作

10. i=9：nums[count]=3与nums[9]=4不相等：count变为 4

    把 nums[9] 放到 nums[4]，数组变为 [0,1,2,3,4,2,2,3,3,4]

循环结束后，count=4，所以唯一元素个数是 count+1=5，数组前 5 个元素 [0,1,2,3,4]就是所有唯一元素

80. 删除有序数组中的重复项 II

给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使得出现次数超过两次的元素只出现两次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

说明：

为什么返回数值是整数，但输出的答案是数组呢？

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

示例 1：

输入：nums = [1,1,1,2,2,3]
输出：5, nums = [1,1,2,2,3]
解释：函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。 不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,1,2,3,3]
输出：7, nums = [0,0,1,1,2,3,3]
解释：函数应返回新长度 length = 7, 并且原数组的前七个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。

提示：

• 1 <= nums.length <= 3 * 104

• -104 <= nums[i] <= 104

• nums 已按升序排列

题解

class Solution:def removeDuplicates(self, nums: List[int]) -> int:n = len(nums)if n <= 2:return nslow, fast = 2, 2while fast < n:if nums[slow - 2] != nums[fast]:nums[slow] = nums[fast]slow += 1fast += 1return slow

示例演示：以nums = [1,1,1,2,2,3]为例

初始状态：slow=2, fast=2，数组[1,1,1,2,2,3]

1. fast=2：nums[slow-2]=nums[0]=1与nums[2]=1相等，不操作，fast=3

2. fast=3：nums[0]=1与nums[3]=2不等：

   nums[2] = 2，数组变为[1,1,2,2,2,3]

   slow=3，fast=4

3. fast=4：nums[1]=1与nums[4]=2不等：

   nums[3] = 2，数组变为[1,1,2,2,2,3]

   slow=4，fast=5

4. fast=5：nums[2]=2与nums[5]=3不等：

   nums[4] = 3，数组变为[1,1,2,2,3,3]

   slow=5，fast=6

循环结束，返回slow=5，前 5 个元素[1,1,2,2,3]就是符合条件的结果。

169. 多数元素

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：nums = [3,2,3]
输出：3

示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2

提示：

• n == nums.length

• 1 <= n <= 5 * 104

• -109 <= nums[i] <= 109

题解

class Solution:def majorityElement(self, nums: List[int]) -> int:votes = 0for num in nums:if votes == 0: x = numvotes += 1 if num == x else -1return x

摩尔投票算法：寻找数组中的多数元素，时间复杂度为 O (n)，空间复杂度为 O (1)

摩尔投票算法的核心思路是利用多数元素的特性：它出现的次数超过数组长度的一半（⌊n/2⌋）。这意味着如果我们将多数元素视为 "正票"，其他元素视为 "负票"，那么总体的 "得票" 一定是正数。

算法通过不断抵消不同元素的票数，最终剩下的元素必然是多数元素。

示例演示：以nums = [2,2,1,1,1,2,2]为例

1. 初始状态：votes=0，无候选元素

2. 第一个元素2：votes=0，所以x=2，votes=1

3. 第二个元素2：与x相同，votes=2

4. 第三个元素1：与x不同，votes=1

5. 第四个元素1：与x不同，votes=0

6. 第五个元素1：votes=0，所以x=1，votes=1

7. 第六个元素2：与x不同，votes=0

8. 第七个元素2：votes=0，所以x=2，votes=1

循环结束，返回x=2，正是数组中的多数元素。

189. 轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

提示：

• 1 <= nums.length <= 105

• -231 <= nums[i] <= 231 - 1

• 0 <= k <= 105

题解

class Solution:def rotate(self, nums: List[int], k: int) -> None:def reverse(i: int, j: int) -> None:while i < j:nums[i], nums[j] = nums[j], nums[i]i += 1j -= 1
​n = len(nums)k %= n  # 轮转 k 次等于轮转 k % n 次reverse(0, n - 1)reverse(0, k - 1)reverse(k, n - 1)

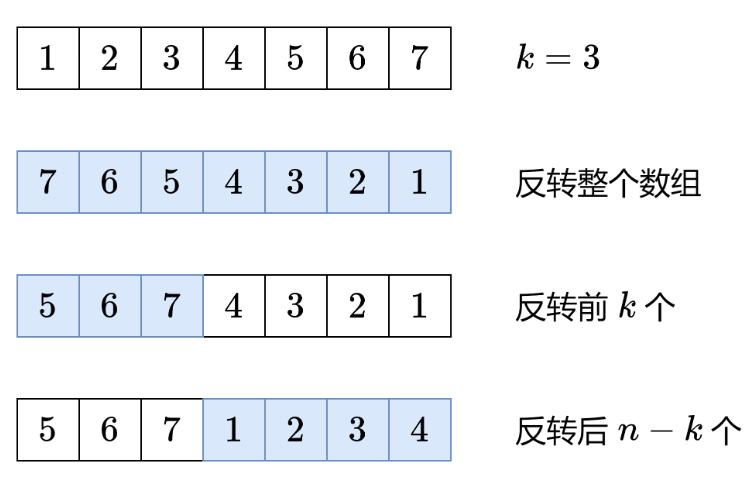
示例演示：以nums = [1,2,3,4,5,6,7], k = 3为例

1. 初始数组：[1,2,3,4,5,6,7]

2. 计算有效轮转次数：k = 3 % 7 = 3

3. 第一次反转（0 到 6）：

   • 整个数组反转 → [7,6,5,4,3,2,1]

4. 第二次反转（0 到 2，前 k 个元素）：

   • 反转前 3 个元素 → [5,6,7,4,3,2,1]

5. 第三次反转（3 到 6，剩余元素）：

   • 反转从索引 3 开始的元素 → [5,6,7,1,2,3,4]

最终结果正是我们需要的向右轮转 3 步的效果。

121. 买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

• 1 <= prices.length <= 105

• 0 <= prices[i] <= 104

题解

class Solution:def maxProfit(self, prices: List[int]) -> int:cost, profit = float('+inf'), 0for price in prices:cost = min(cost, price)profit = max(profit, price - cost)return profit

股票买卖的关键是 "低买高卖"，要找到历史最低点买入，然后在之后的最高点卖出。算法的核心思想是：

• 遍历过程中始终记录当前遇到的最低价格（买入点）

• 对于每个价格，计算如果现在卖出能获得的利润

• 保存最大的利润值

示例演示：以prices = [7,1,5,3,6,4]为例

1. 初始状态：cost = +∞，profit = 0

2. 第一个价格7：

   • cost = min(+∞, 7) = 7

   • profit = max(0, 7-7) = 0

3. 第二个价格1：

   • cost = min(7, 1) = 1（找到更低的买入点）

   • profit = max(0, 1-1) = 0

4. 第三个价格5：

   • cost保持 1 不变

   • profit = max(0, 5-1) = 4（利润更新为 4）

5. 第四个价格3：

   • cost保持 1 不变

   • profit = max(4, 3-1) = 4（利润保持 4）

6. 第五个价格6：

   • cost保持 1 不变

   • profit = max(4, 6-1) = 5（利润更新为 5）

7. 第六个价格4：

   • cost保持 1 不变

   • profit = max(5, 4-1) = 5（利润保持 5）

最终返回5，与示例结果一致。

122. 买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。然而，你可以在 同一天 多次买卖该股票，但要确保你持有的股票不超过一股。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0。

提示：

• 1 <= prices.length <= 3 * 104

• 0 <= prices[i] <= 104

题解

class Solution:def maxProfit(self, prices: List[int]) -> int:profit = 0for i in range(1, len(prices)):tmp = prices[i] - prices[i - 1]if tmp > 0: profit += tmpreturn profit

由于题目允许在同一天卖出后再买入（即当天可以完成一次完整的买卖），且不限制交易次数，那么最大利润的获取方式就是：抓住所有股价上涨的机会，在每个上涨区间都进行 "低买高卖"。

简单来说，就是把所有相邻两天的股价差为正的部分加起来，这些正差值的总和就是最大利润。

示例演示

以示例 1 prices = [7,1,5,3,6,4] 为例：

计算相邻两天的差价：

• 第 2 天 - 第 1 天：1-7 = -6（负数，不加）

• 第 3 天 - 第 2 天：5-1 = 4（正数，加 4，总利润 = 4）

• 第 4 天 - 第 3 天：3-5 = -2（负数，不加）

• 第 5 天 - 第 4 天：6-3 = 3（正数，加 3，总利润 = 7）

• 第 6 天 - 第 5 天：4-6 = -2（负数，不加）

最终总利润为 7，与示例结果一致。

再看示例 2 prices = [1,2,3,4,5]：

• 每天都比前一天涨 1，所有差价都是 1

• 总利润 = 1+1+1+1 = 4，与示例结果一致

55. 跳跃游戏

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

提示：

• 1 <= nums.length <= 104

• 0 <= nums[i] <= 105

题解

class Solution:def canJump(self, nums) :max_i = 0     for i, jump in enumerate(nums):   if max_i>=i and i+jump>max_i:max_i = i+jump return max_i>=i

贪心算法：跟踪当前能到达的最远位置

我们不需要提前规划具体的跳跃路径，只需要在遍历过程中不断更新 "当前能到达的最远位置"。如果在遍历结束前，这个最远位置已经能覆盖到最后一个下标，就说明可以到达；反之则不能。

enumerate(nums)会将数组转换成一个可迭代的对象，每次迭代会返回两个值：

• 第一个值 i：当前元素的索引（从 0 开始计数的位置编号）

• 第二个值 jump：当前索引位置的元素值（即 nums[i]）

示例演示

示例 1：nums = [2,3,1,1,4]

• 初始状态：max_i = 0

• i=0, jump=2：max_i >= 0且0+2>0，更新max_i=2

• i=1, jump=3：max_i >= 1且1+3>2，更新max_i=4

• i=2, jump=1：max_i >= 2但2+1=3 < 4，不更新

• i=3, jump=1：max_i >= 3但3+1=4 = 4，不更新

• i=4, jump=4：max_i >= 4但4+4=8 > 4，更新max_i=8

• 最终max_i=8 >= 4（最后一个下标），返回true

示例 2：nums = [3,2,1,0,4]

• 初始状态：max_i = 0

• i=0, jump=3：max_i >= 0且0+3>0，更新max_i=3

• i=1, jump=2：max_i >= 1且1+2=3 = 3，不更新

• i=2, jump=1：max_i >= 2且2+1=3 = 3，不更新

• i=3, jump=0：max_i >= 3但3+0=3 = 3，不更新

• i=4, jump=4：max_i=3 < 4（当前位置不可达），不处理

• 最终max_i=3 < 4（最后一个下标），返回false

45. 跳跃游戏 II

给定一个长度为 n 的 0 索引整数数组 nums。初始位置在下标 0。

每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说，如果你在索引 i 处，你可以跳转到任意 (i + j) 处：

• 0 <= j <= nums[i] 且

• i + j < n

返回到达 n - 1 的最小跳跃次数。测试用例保证可以到达 n - 1。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

提示:

• 1 <= nums.length <= 104

• 0 <= nums[i] <= 1000

• 题目保证可以到达 n - 1

题解

class Solution:def jump(self, nums: List[int]) -> int:ans = 0cur_right = 0  # 已建造的桥的右端点next_right = 0  # 下一座桥的右端点的最大值for i in range(len(nums) - 1):# 遍历的过程中，记录下一座桥的最远点next_right = max(next_right, i + nums[i])if i == cur_right:  # 无路可走，必须建桥cur_right = next_right  # 建桥后，最远可以到达 next_rightans += 1return ans

贪心算法

我们可以把跳跃过程想象成 "建造桥梁"：

• 每次跳跃相当于建造一座桥，桥的起点是当前位置，终点是能跳到的最远位置

• 我们需要用最少的桥连接起点 (0) 和终点 (n-1)

• 在每座桥的覆盖范围内，我们要找到下一座桥能到达的最远距离，这样才能用最少的桥

示例演示：以nums = [2,3,1,1,4]为例

1. 初始状态：ans=0，cur_right=0（第一座桥还没建），next_right=0

2. 遍历过程：

   • i=0：

     • next_right = max(0, 0+2) = 2（从 0 能跳到最远 2）

     • i == cur_right（0 == 0）：必须跳，cur_right=2，ans=1

   • i=1：

     • next_right = max(2, 1+3) = 4（从 1 能跳到更远的 4）

     • i < cur_right（1 < 2）：还在当前桥范围内，不跳

   • i=2：

     • next_right = max(4, 2+1) = 4（从 2 跳不如之前的远）

     • i == cur_right（2 == 2）：必须跳，cur_right=4，ans=2

   • 循环到i=3时，已经满足cur_right=4（到达最后位置），后续无需再跳

3. 最终返回ans=2，与示例结果一致

274. H 指数

给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。

根据维基百科上 h 指数的定义：h 代表“高引用次数” ，一名科研人员的 h 指数 是指他（她）至少发表了 h 篇论文，并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值，h 指数 是其中最大的那个。

示例 1：

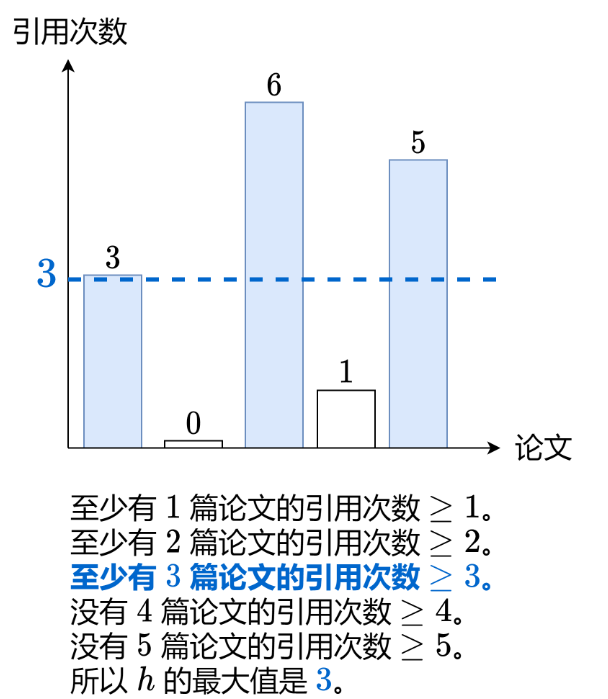
输入：citations = [3,0,6,1,5]
输出：3 
解释：给定数组表示研究者总共有 5 篇论文，每篇论文相应的被引用了 3, 0, 6, 1, 5 次。由于研究者有 3 篇论文每篇 至少 被引用了 3 次，其余两篇论文每篇被引用 不多于 3 次，所以她的 h 指数是 3。

示例 2：

输入：citations = [1,3,1]
输出：1

提示：

• n == citations.length

• 1 <= n <= 5000

• 0 <= citations[i] <= 1000

题解

class Solution:def hIndex(self, citations: List[int]) -> int:n = len(citations)cnt = [0] * (n + 1)for c in citations:cnt[min(c, n)] += 1 s = 0for i in range(n, -1, -1): s += cnt[i]if s >= i:  return i

h 指数的定义是 "至少有 h 篇论文被引用了至少 h 次"，且 h 是可能的最大值。题解的核心思路是：

1. 统计不同引用次数的论文数量

2. 从高到低检查可能的 h 值，找到满足条件的最大 h

示例演示：以citations = [3,0,6,1,5]为例

1. 初始化：n=5，cnt = [0,0,0,0,0,0]（大小为 6）

2. 统计引用次数：

   • 3 → min(3,5)=3 → cnt[3] = 1

   • 0 → min(0,5)=0 → cnt[0] = 1

   • 6 → min(6,5)=5 → cnt[5] = 1

   • 1 → min(1,5)=1 → cnt[1] = 1

   • 5 → min(5,5)=5 → cnt[5] = 2

   • 最终 cnt = [1,1,0,1,0,2]

3. 从高到低检查 h 值：

   • i=5：s += cnt [5] = 2 → s=2 < 5 → 不满足

   • i=4：s += cnt [4] = 0 → s=2 < 4 → 不满足

   • i=3：s += cnt [3] = 1 → s=3 ≥ 3 → 满足条件，返回 3

这与示例结果完全一致。