当前位置：首页 > news >正文

【第29话：路径规划】自动驾驶启发式搜索算法（A星搜索算法（ A* 搜索算法））详解及代码举例说明

news 2025/9/24 7:39:26

自动驾驶启发式搜索算法（A星算法）详解

启发式搜索算法在自动驾驶系统中扮演着核心角色，主要用于实时路径规划、障碍物避让和全局导航。它通过引入启发式函数（heuristic function）来智能地引导搜索过程，减少计算开销，提高效率。下面，我将逐步详解其原理、常见算法（以A*算法为例）、在自动驾驶中的应用实现，并提供代码示例。内容基于可靠的理论和实践，确保结构清晰。
在这里插入图片描述

1. 启发式搜索算法基础

什么是启发式搜索？
启发式搜索是一种智能搜索方法，它利用问题域的先验知识（即启发式信息）来估计从当前状态到目标状态的最优路径。相比盲目搜索（如广度优先搜索），它能显著降低搜索空间和时间复杂度。核心思想是：优先探索“最有希望”的节点。
- 关键组件：
  - 代价函数 $g (n)$ ：表示从起点到节点 $n$ 的实际代价（如距离或时间）。
  - 启发式函数 $h (n)$ ：估计从节点 $n$ 到目标的剩余代价（必须可接受，即 $\leq$ 实际代价）。
  - 总代价函数 $f (n)$ ：用于决策，定义为 $f (n) = g (n) + h (n)$ 。
- 例如，在路径规划中， $h (n)$ 可以是欧几里得距离或曼哈顿距离，帮助算法快速收敛。
为什么适合自动驾驶？
自动驾驶环境动态多变（如车辆、行人、交通灯），需要实时响应。启发式搜索能高效处理高维状态空间，确保路径安全、平滑且能量最优。常见场景包括：
- 全局路径规划：生成从A点到B点的最优路线。
- 局部避障：在感知到障碍物时，动态调整路径。

2. **核心算法：A*算法详解**

A* 算法是最常用的启发式搜索算法，因其最优性和效率被广泛应用于自动驾驶。它基于图搜索模型，将环境建模为网格或图结构（节点表示位置，边表示可行路径）。

算法原理：
- A* 使用优先队列（如最小堆）管理节点，优先扩展 $f (n)$ 最小的节点。
- 总代价公式为：
  $f (n) = g (n) + h (n)$
  其中：
  - $g (n)$ 是实际累积代价（例如，从起点到 $n$ 的移动距离）。
  - $h (n)$ 是启发式估计代价（例如， $n$ 到目标的直线距离）。
- 启发式函数 $h (n)$ 必须满足 可接受性（admissible）： $\leq$ 真实剩余代价，确保算法找到最优解。常用启发式包括：
  - 曼哈顿距离：适用于网格地图， $h(n) = |x_n - x_g| + |y_n - y_g|$ 。
  - 欧几里得距离：更精确， $\sqrt{(x_n - x_g)^2 + (y_n - y_g)^2}$ 。
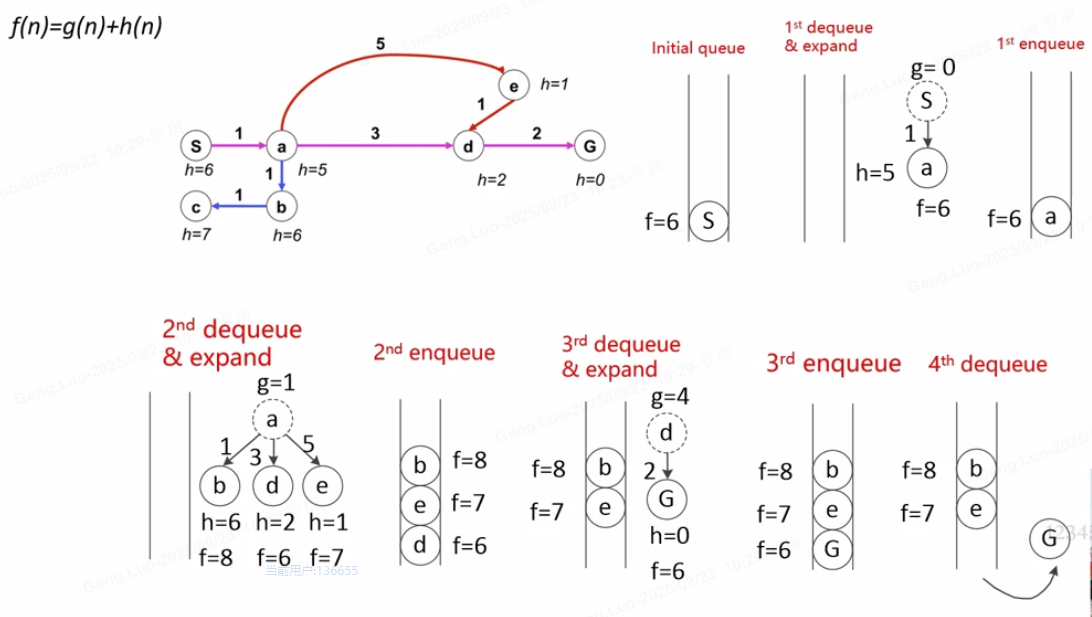
- 算法步骤：
  1. 初始化：起点加入开放列表（open list）， $g(start)=0g(\text{start}) = 0$ ， $f(start)=h(start)f(\text{start}) = h(\text{start})$ 。
  2. 循环：从开放列表取出 $f (n)$ 最小的节点 $n$ 。
  3. 如果 $n$ 是目标，则回溯路径；否则，扩展 $n$ 的邻居。
  4. 对每个邻居 $m$ ，计算新 $\text{cost}(n,m)$ 和 $f (m) = g (m) + h (m)$ 。
  5. 如果 $m$ 未在开放列表或新 $f (m)$ 更小，则更新并加入开放列表。
  6. 重复直到找到目标或开放列表为空。
在自动驾驶中的优化：
- 动态环境处理：A* 可扩展为 D* 或 LPA* 算法，支持实时更新地图（如新增障碍物）。
- 启发式设计： $h (n)$ 可结合交通规则（如速度限制）， $\frac{\text{距离}}{\text{最大速度}}$ ，以优化时间代价。
- 效率分析：时间复杂度为 $O(b^d)$ ，其中 $b$ 是分支因子， $d$ 是解深度。但在良好启发式下，可降至 $O (d)$ 。

3. 在自动驾驶中的具体应用

自动驾驶系统将环境感知数据（如激光雷达、摄像头）转换为搜索图，A* 算法用于生成可行路径。

实现步骤：
1. 环境建模：将道路地图离散化为网格图，每个网格单元表示一个状态（例如， $\times 1$ 米）。障碍物标记为不可通行。
2. 代价定义：
  - $g (n)$ ：基于移动距离（如单位网格代价为 1），或加入坡度、油耗等权重。
  - $h (n)$ ：使用欧几里得距离 $\sqrt{(x_n - x_g)^2 + (y_n - y_g)^2}$ ，确保可接受性。
  - 总代价 $f (n)$ 指导搜索，最小化路径长度或时间。
3. 实时规划：
  - 当传感器检测到障碍物时，算法重新计算 $h (n)$ 并更新路径。
  - 结合车辆动力学约束（如转弯半径），在扩展邻居时过滤无效节点。
4. 输出：生成路径点序列，控制模块执行转向和加速。
优势与挑战：
- 优势：高效、可证明最优（如果 $h (n)$ 可接受），易于实现。
- 挑战：启发式设计不当可能导致次优解；高动态环境需算法变种（如 D*）；计算资源需优化以适应实时性。

4. **代码示例：A*算法实现**

以下是一个简化的 Python 实现，用于网格地图路径规划。假设地图为 2D 网格，0 表示可行，1 表示障碍物。使用曼哈顿距离作为启发式函数。

import heapqdef heuristic(a, b):""" 曼哈顿距离启发式函数 """return abs(a[0] - b[0]) + abs(a[1] - b[1])def a_star(grid, start, goal):""" A* 算法实现:param grid: 2D 列表，0=可行, 1=障碍:param start: 起点坐标 (x, y):param goal: 目标坐标 (x, y):return: 路径列表，从起点到目标"""# 初始化：方向向量（上、下、左、右）neighbors = [(0, 1), (1, 0), (0, -1), (-1, 0)]open_list = []heapq.heappush(open_list, (0, start))came_from = {}g_score = {start: 0}f_score = {start: heuristic(start, goal)}while open_list:current = heapq.heappop(open_list)[1]if current == goal:# 回溯路径path = []while current in came_from:path.append(current)current = came_from[current]path.append(start)return path[::-1]  # 反转路径for dx, dy in neighbors:neighbor = (current[0] + dx, current[1] + dy)# 检查边界和障碍if (0 <= neighbor[0] < len(grid) and 0 <= neighbor[1] < len(grid[0]) and grid[neighbor[0]][neighbor[1]] == 0):tentative_g = g_score[current] + 1  # 假设每步代价为1if neighbor not in g_score or tentative_g < g_score[neighbor]:came_from[neighbor] = currentg_score[neighbor] = tentative_gf_score[neighbor] = tentative_g + heuristic(neighbor, goal)heapq.heappush(open_list, (f_score[neighbor], neighbor))return None  # 无路径# 示例用法
if __name__ == "__main__":grid = [[0, 0, 0, 0],[0, 1, 1, 0],  # 1表示障碍物[0, 0, 0, 0]]start = (0, 0)goal = (2, 3)path = a_star(grid, start, goal)print("路径:", path)  # 输出：[(0,0), (1,0), (2,0), (2,1), (2,2), (2,3)]

代码解释：
- heuristic 函数计算曼哈顿距离 $x_1 - x_2| + |y_1 - y_2|$ 。
- 算法使用优先队列（heapq）管理开放列表，确保高效。
- 输出路径为坐标序列，可直接用于车辆控制。
- 在实际自动驾驶中，需扩展为处理连续空间（如使用样条曲线平滑路径）。