第十七周 学习周报

摘要

本周初步学习了量子计算的基本概念和过去的发展历史等，为后期的学习打好基础，计算流体力学学习了流动与传热通用微分方程的通用形式，了解了守恒形式的能量方程，并学习了扩散和对流俩种不同的条件下的方程。

Abstract

This week I began studying the fundamental concepts and historical development of quantum computing, laying the groundwork for future learning. In computational fluid dynamics, I covered the general form of the governing differential equations for flow and heat transfer, examined the conservation form of the energy equation, and learned about the equations under both diffusion and convection conditions.

计算流体力学:

仔细观察上表中的方程形式，我们可以采用共同的形式将其概括表达，这种形式称为流动与传热的通用微分方程。通常使用表示通用变量。通用形式为：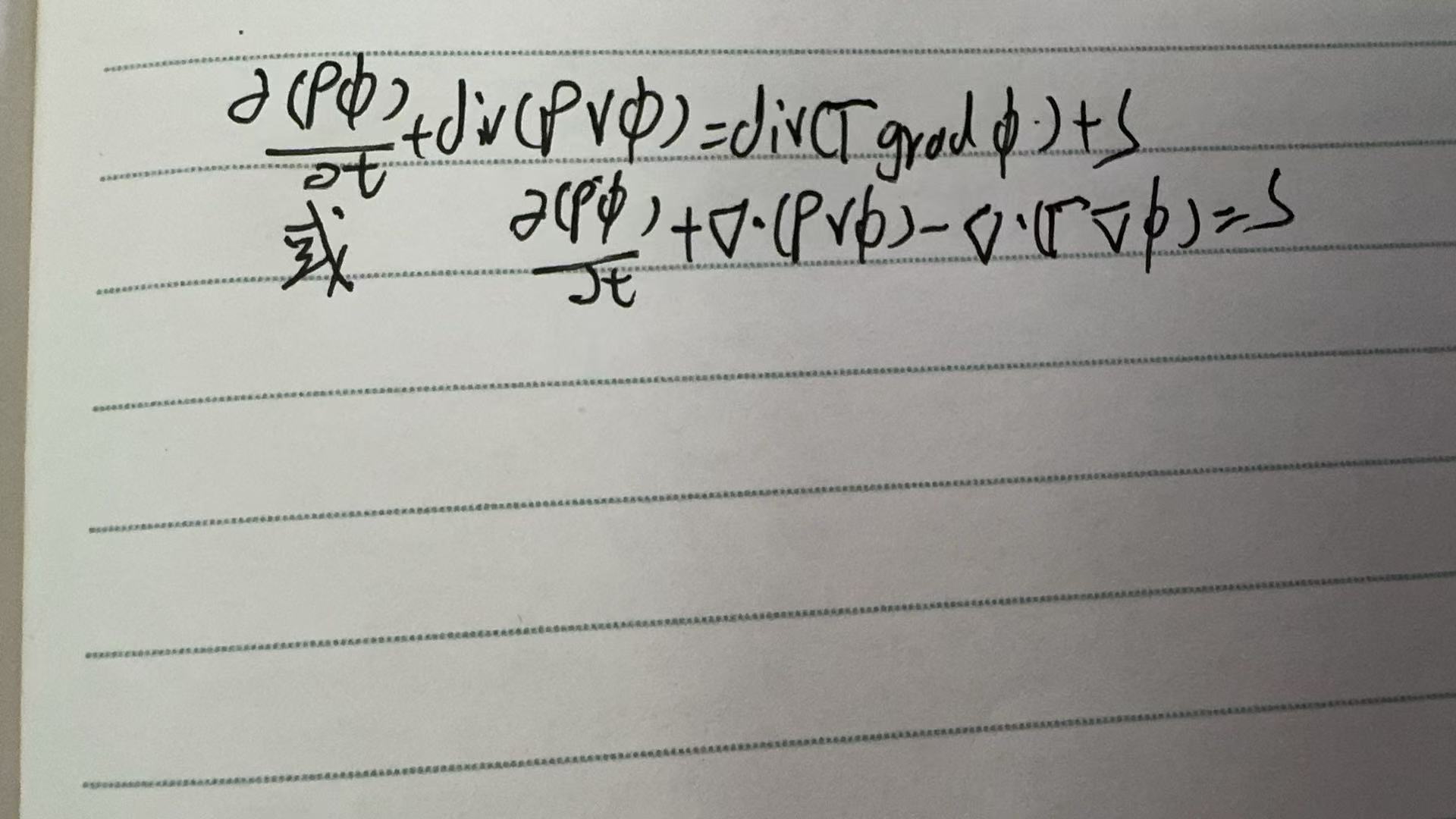

式中,第一项被称为非稳态项、瞬态项(transientterm)或时间项,第二项为对流项(convectiveterm)，第三项为扩散项(diffusiveterm)，末项S为源项(source term)。式中为通用变量,可以表示u、v、w、T等待求变量:为广义扩散系数，S之所以又被称为“广义”源项是因为处在和S位置上的项不必是原来物理意义上的量，而是数值计算模型方程中的一种定义。不同求解变量之间的区别除了边界条件与初始条件外，就在于和S的表达式的不同对于特定的方程，、和S具有特定的形式，表2-4给出了、和S这3个符号与特定方程的对应关系。如表所示，所有控制方程都可以经过适当的数学处理，将方程中的因变量、非稳态项、对流项和扩散项写成标准的形式，然后将方程其余各项集中在一起定义为广义源项，进而化为流动与传热的通用微分方程。接下来，我们只需要考虑通用微分方程的数值解，写出求解通用微分方程的程序。对于不同的，只需要重复调用该程序，并给定和S的适当表达式，以及对应的初始条件和边界条件，便可进行数值求解。总之，之所以写成通用形式，是为了方便编程求解(学过开源软件OpenFOAM的同学更能体会到这一点)。
当把 N-S方程写成通用形式时，压力梯度VP被写在了源项S中，适当的时候我们还要把压力梯度VP从源项S中拿出来。

量子计算：

量子计算是一种利用量子力学特性（​叠加​​和​​纠缠​​）来进行计算的新型计算模式。

对比了经典比特与量子比特的本质区别：经典比特采用二进制（0或1的确定状态），而量子比特表现为二维复向量空间的叠加态，其数学表达为a|0⟩ + b|1⟩（需满足概率守恒条件|a|² + |b|² = 1）。图中明确给出了基矢量定义：|0⟩ = (1, 0)ᵀ 和 |1⟩ = (0, 1)ᵀ（列向量形式）。量子比特的核心特性是通过概率幅（a, b）实现状态叠加，测量时会以|a|²概率坍缩到0、|b|²概率坍缩到1。这种向量空间表示是量子并行计算能力的数学基础。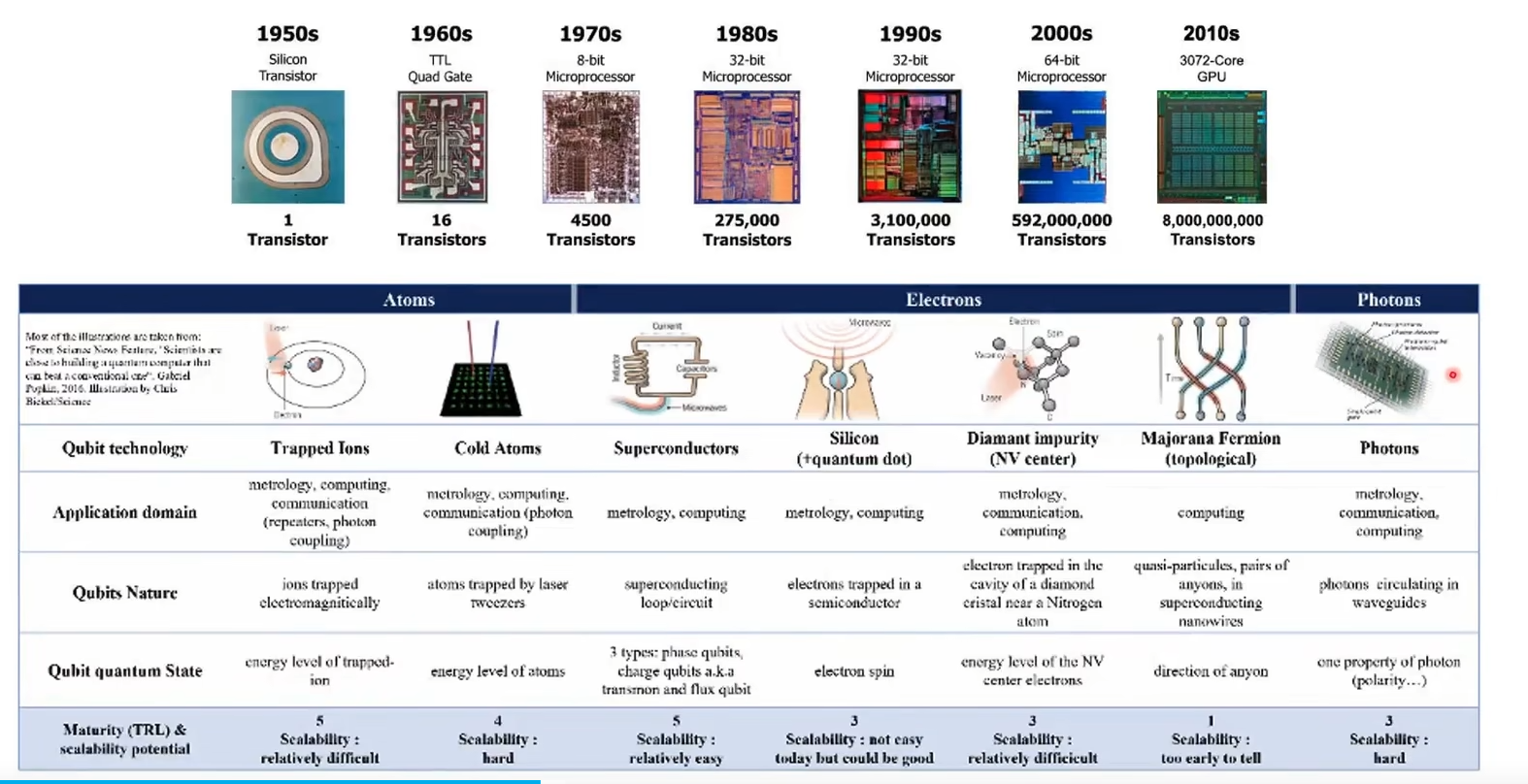经典半导体遵循摩尔定律持续微缩化，而量子计算通过多种物理载体实现量子比特，其可扩展性成为技术成熟度的关键指标。这种对比凸显了从经典计算到量子计算的技术范式转换。

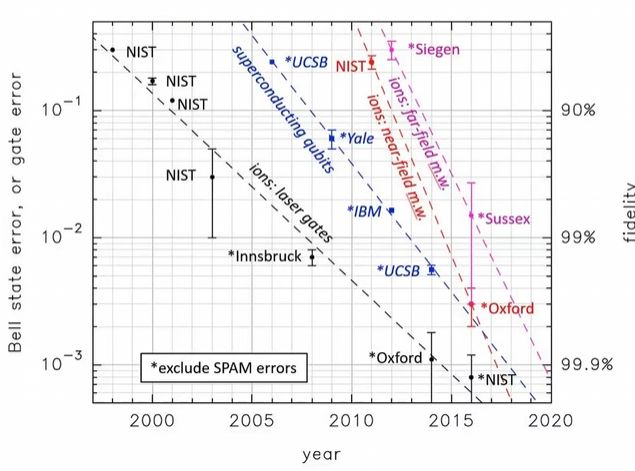
展示了2000至2020年间量子计算领域门操作错误率的演进趋势，采用对数坐标直观呈现技术发展历程。纵轴表示贝尔态错误率或门错误率（10⁻¹~10⁻³量级），右侧对应线性保真度刻度（90%~99.9%）。数据点标注NIST、UCSB、Yale等机构名称，反映超导量子比特（如IBM）与离子阱（如NIST）两大技术路线的竞争发展。整体错误率呈指数下降：从2000年的10⁻¹量级（保真度约90%）提升至2020年的10⁻³量级（保真度达99.9%），其中2016年后超导量子比特实现关键突破。部分数据点标注"*exclude SPAM errors"，表明已排除状态制备与测量误差的干扰。该图表揭示了量子门操作精度二十年来的持续优化，为大规模量子计算奠定了可靠性基础。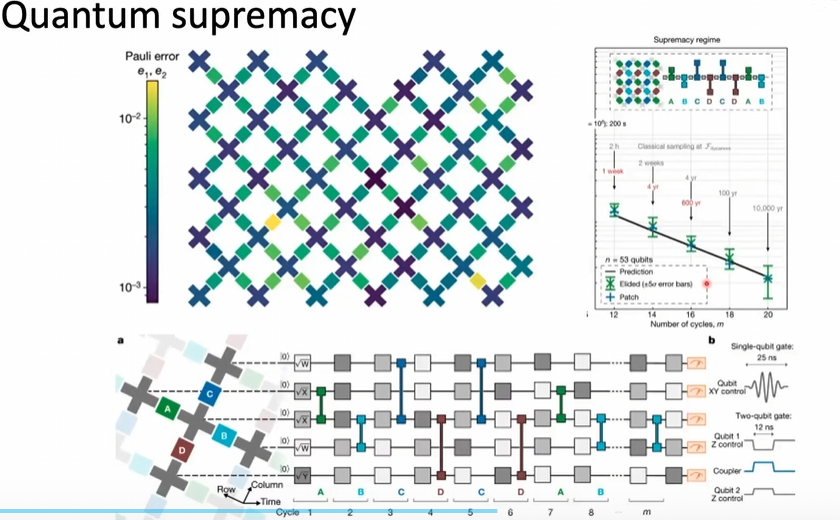该图从三个维度展示了量子霸权的实现机制：左上角量子比特阵列的Pauli错误率热力图显示门操作精度达10⁻²~10⁻³量级（蓝绿色低误差区域），满足量子计算可靠性要求；右上折线图通过对比经典采样与量子"Patch"方法，证明53量子比特处理器在200秒内完成特定任务时进入"霸权区域"（灰色背景标注），等效经典计算需万年量级时间；底部时序图详细展示了量子门与耦合器的精密控制信号（脉冲序列与XY/Z控制波形），其磁控参数精度达10⁻³量级（B₀、Bᵢₙ、Bₒᵤₜ均为10⁻³ mT）。整套系统通过高精度量子门控制、多比特耦合架构与电磁调控系统的协同，实现了量子计算对经典计算的指数级超越。