[优选算法专题三二分查找——NO.17二分查找]

题目链接：二分查找

题目描述：

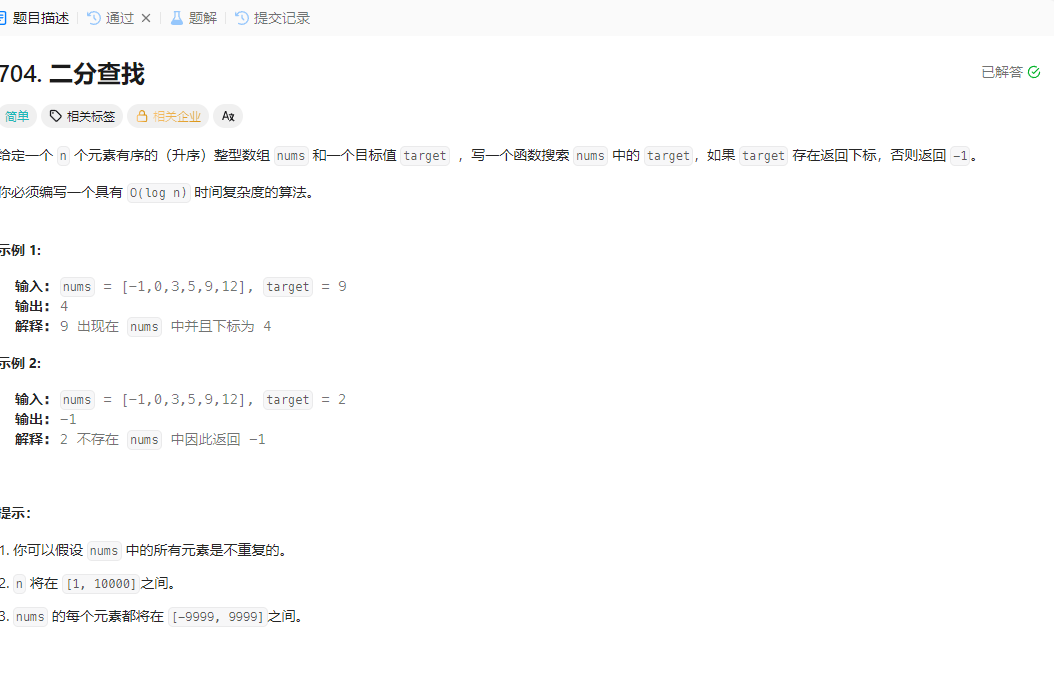
题目解答：

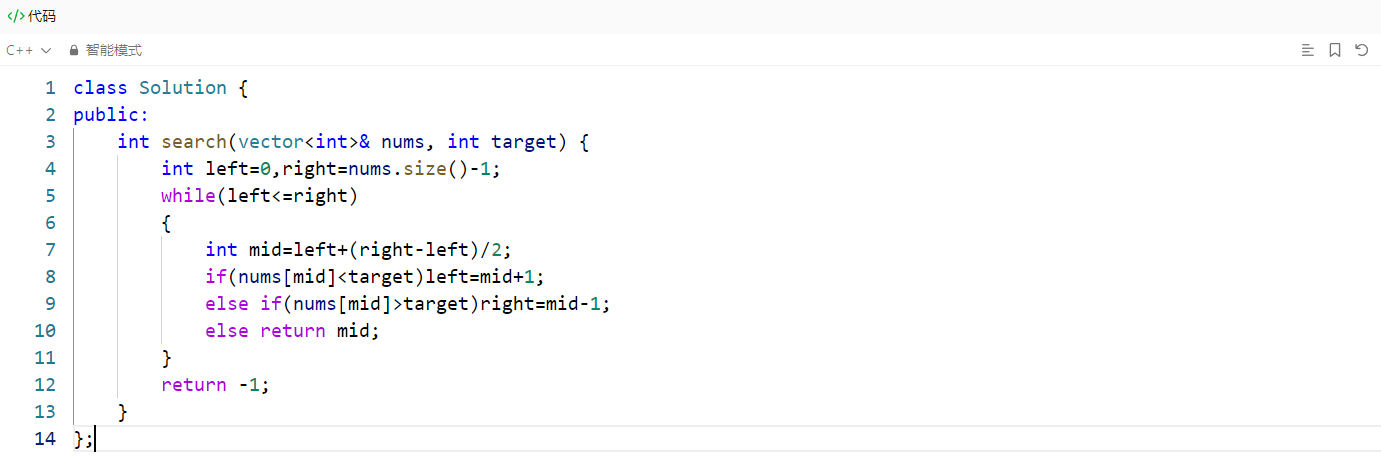
1. 使用闭区间 [left, right] 作为搜索范围
2. 循环条件 left <= right 确保当区间内还有元素时继续搜索
3. 中间值计算 mid = left + (right - left) / 2 有效避免了整数溢出问题
4. 根据中间元素与目标值的比较，动态调整搜索区间的边界
5. 找到目标值时直接返回索引，未找到则返回 -1

时间复杂度为 O (log n)，空间复杂度为 O (1)，是二分查找的经典应用。

---

总结朴素二分模板

朴素二分模板主要用来在有序数组中查找目标值，思路很简单：

通过不断将区间对半分，判断目标值在左半部分还是右半部分，直到找到或区间为空。

朴素二分模板（C++）

int binary_search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;  // 防溢出if (nums[mid] == target) {return mid;  // 找到目标} else if (nums[mid] < target) {left = mid + 1;  // 目标在右半部分} else {right = mid - 1;  // 目标在左半部分}}return -1;  // 未找到
}

关键点

• 循环条件：left <= right（闭区间 [left, right]）
• mid 计算：用 left + (right - left) / 2 避免溢出
• 区间调整：
  • nums[mid] < target → 目标在右侧 → left = mid + 1
  • nums[mid] > target → 目标在左侧 → right = mid - 1