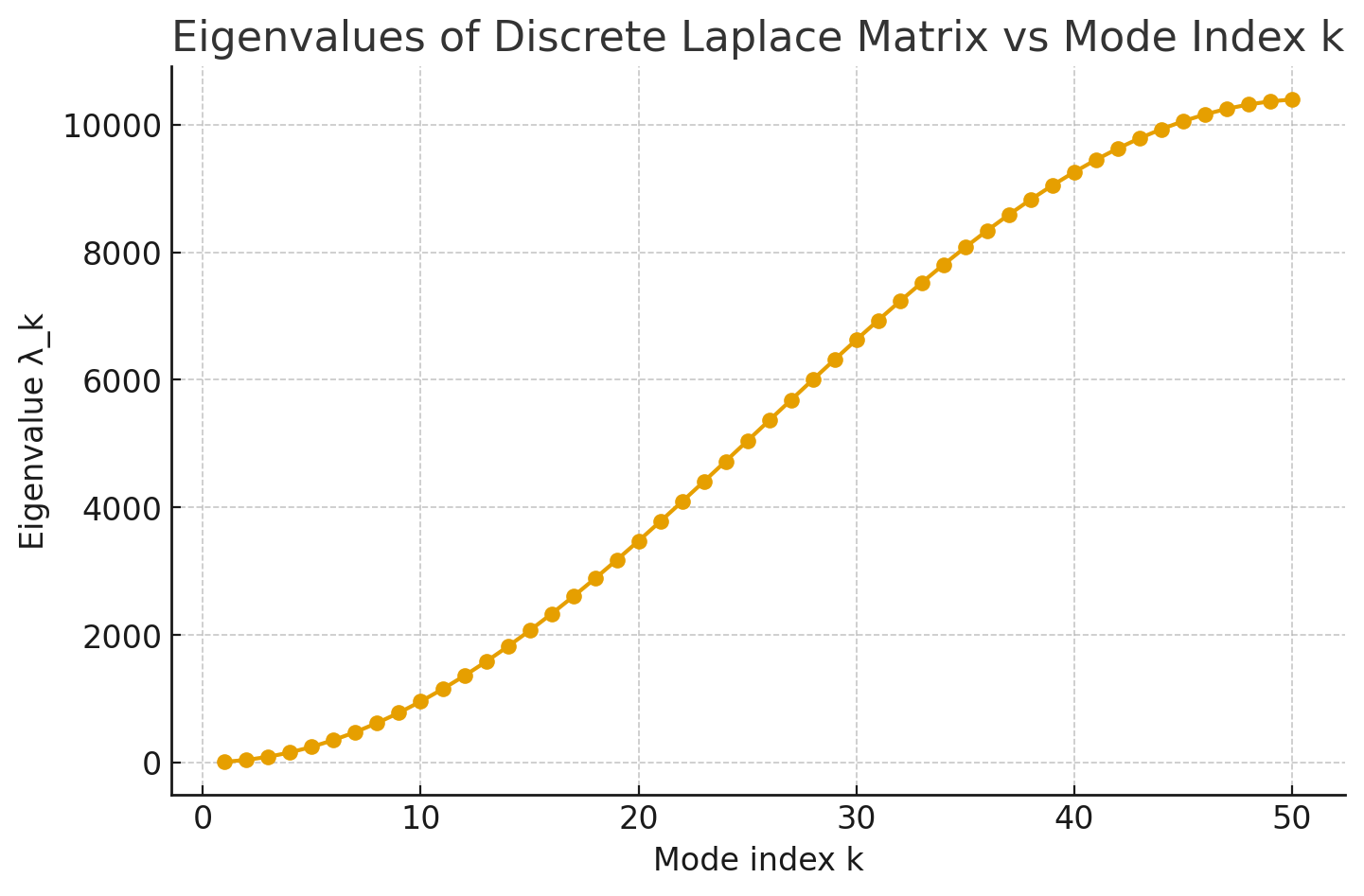
对1D poisson采用二阶中心差分格式离散,离散 Laplace 矩阵 A 的特征向量就是 Fourier 模式的离散化
以最常见的 1D Poisson 方程为例:
−u′′(x)=f(x),x∈(0,1),u(0)=u(1)=0 -u''(x) = f(x), \quad x \in (0,1), \quad u(0)=u(1)=0 −u′′(x)=f(x),x∈(0,1),u(0)=u(1)=0
用二阶中心差分离散化(网格步长 h=1/(n+1)h = 1/(n+1)h=1/(n+1)),得到线性系统:
Au=f, A u = f, Au=f,
其中 AAA 是 n×nn \times nn×n 的三对角矩阵:
A=1h2[2−1−12−1⋱⋱⋱−12−1−12]. A = \frac{1}{h^2} \begin{bmatrix} 2 & -1 & & & \\ -1 & 2 & -1 & & \\& \ddots & \ddots & \ddots & \\& & -1 & 2 & -1 \\& & & -1 & 2 \end{bmatrix}. A=h212−1−12⋱−1⋱−1⋱2−1−12.
这个矩阵的特征值与特征向量可以显式写出。
- 特征向量是正弦函数在离散点上的采样:
wk(j)=sin (kπjn+1),j=1,2,…,n,k=1,2,…,n. w_k(j) = \sin\!\Big(\frac{k \pi j}{n+1}\Big), \quad j = 1,2,\ldots,n, \quad k = 1,2,\ldots,n. wk(j)=sin(n+1kπj),j=1,2,…,n,k=1,2,…,n.
- 特征值为
λk=4h2sin2 (kπ2(n+1)). \lambda_k = \frac{4}{h^2} \sin^2\!\Big(\frac{k \pi}{2(n+1)}\Big). λk=h24sin2(2(n+1)kπ).
在多重网格方法的背景里, “Fourier modes” 是指离散函数空间上的 正弦/余弦基函数(类似于连续 Fourier 模式 eiπkxe^{i \pi k x}eiπkx 的离散版本)。
而上面得到的 wk(j)=sin (kπjn+1)w_k(j) = \sin\!\big(\tfrac{k\pi j}{n+1}\big)wk(j)=sin(n+1kπj) 正好就是这些 离散 Fourier 模式(正弦模态)。
也就是说,离散 Laplace 矩阵 AAA 的特征向量就是 Fourier 模式的离散化。
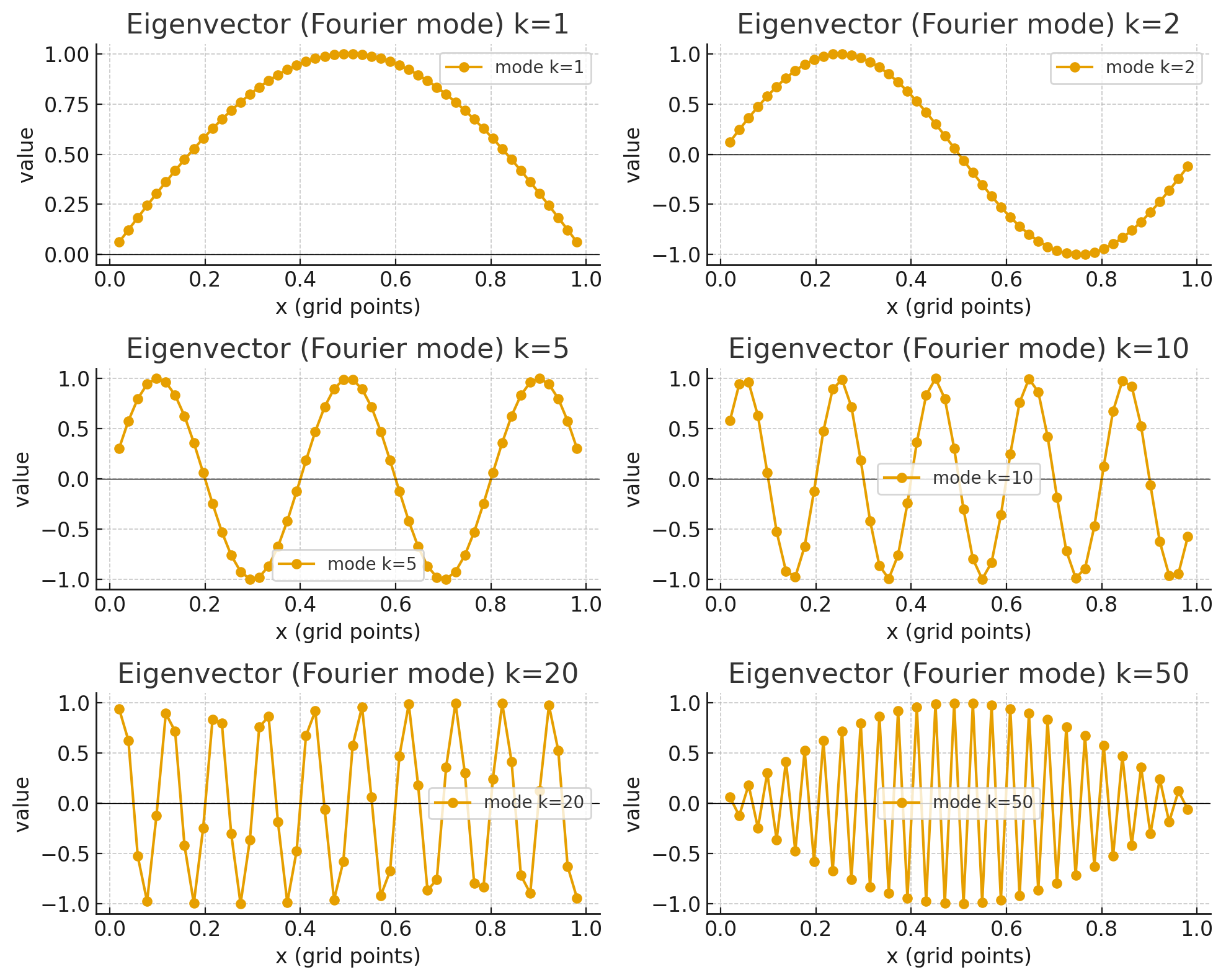
下图为几个傅里叶特征模态(比如 k=1,2,10,nk=1,2,10,nk=1,2,10,n)和特征向量的对应关系。
这里就是几个离散 Laplace 矩阵的特征向量(Fourier 模态)的形状:
- k=1k=1k=1:最低频,像一个半个正弦波。
- k=2,5k=2,5k=2,5:频率逐渐增高。
- k=10,20k=10,20k=10,20:波动更密集。
- k=nk=nk=n:最高频,几乎是一正负交替的锯齿状模式。
这就直观展示了 特征向量 = Fourier 模式 的含义。
下图为对应的 特征值随模态变化的曲线,高频模态对应的特征值更大。