当前位置： 首页 > news >正文

深度学习周报（9.15~9.21）

news 2025/9/22 8:34:46

目录

摘要

Abstract

1 transformer入门

1.1 Encoder

1.2 Decoder

2 量子计算基本定义

2.1 量子态

2.2 量子演化

2.3 复合系统

3 总结

摘要

本周首先初步了解了transformer的部分背景与基础，主要包括Seq2Seq模型、编码器与解码器的结构，AT与NAT的区别等；其次学习了量子计算的基本定义，包括狄拉克符号及其运算、布洛赫球、常见的单量子比特门与复合系统等。

Abstract

This week, I first gained a preliminary understanding of some background and fundamentals of the Transformer, primarily including the Seq2Seq model, the structure of encoders and decoders, and the differences between AT and NAT. Secondly, I studied the basic definitions of quantum computing, including Dirac notation and its operations, the Bloch sphere, common single-qubit gates, and composite systems.

1 transformer入门

Transformer 是一种在深度学习领域，特别是自然语言处理（NLP）中具有革命性意义的神经网络架构。它由 Google 的研究人员在 2017 年的论文《Attention is All You Need》中首次提出，它本质上也是一种Seq2Seq模型。

Seq2Seq模型主要用于处理变长输入与输出的序列映射问题，可以让机器自己决定输出序列的长度，广泛应用于机器翻译、文本摘要、对话生成等。该模型由两个核心组件构成：编码器（Encoder）和解码器（Decoder）。编码器负责将输入序列（如一个句子）逐步编码为一个固定维度的上下文向量（context vector），该向量被视为整个输入序列的语义摘要。解码器则以该上下文向量为初始状态，自回归地生成目标序列，每一步的输出作为下一步的输入，直至生成结束符。

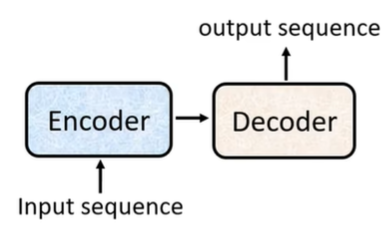
传统的、基于循环神经网络（RNN）或其变体实现的Seq2Seq模型有两个不足之处，一是编码器将整个序列压缩为单一向量，容易造成信息瓶颈；二是RNN的串行处理机制限制了训练效率，并难以捕捉长距离依赖关系。由此引入注意力机制和Transformer架构。

1.1 Encoder

Transformer的编码器包含多个相同的层，每层首先将输入的原始数据（离散的、符号化的单词或子词单元）转换为连续的、高维的数值向量，然后对其进行位置编码，让模型能学习到相对和绝对位置信息；其次，经过多头注意力机制；最后，经过前馈神经网络。另外，在每一层的输出处添加残差连接，并进行归一化处理。

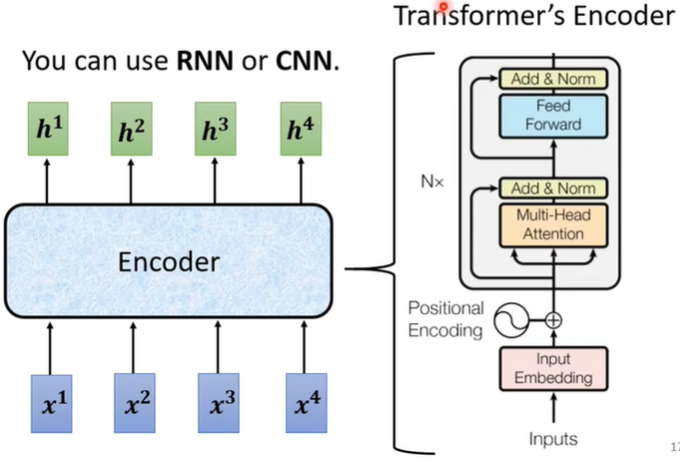
1.2 Decoder

Transformer的解码器与编码器结构类似，不同之处在于一方面它第一次经过的多头注意力机制是不考虑后面输入的（Masked），另一方面，它在中间多加了一层注意力机制以连接来自encoder的输出。这一层有两个输入来自Encoder，一个输入来自Decoder内部，最后输出时，残差连接的输入也来自Decoder内部。

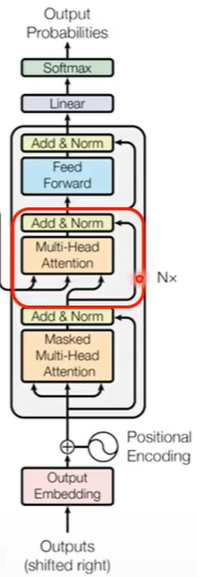
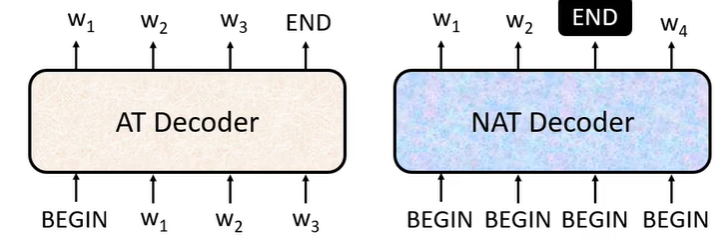
解码器主要有两种方式。一种是 AT (Auto-Regressive Translation，自回归翻译），这是最传统、最主流的序列生成方式。这种方式一次只生成一个词，在生成某个词时，模型的输入是之前已经生成的所有词以及编码器对输入的完整表示，生成过程一直重复，直到生成结束标记。它的生成质量较高，模型设计也相对成熟，但速度比较慢，而且如果中途错词的生成会影响后续所有词的生成。

另一种是 NAT (Non-Auto-Regressive Translation，非自回归翻译），它是为了解决 AT 的速度瓶颈而被提出的，其核心思想是并行生成整个输出序列，即尝试一次性（或在极少的步数内）生成输出序列中的所有词。这样每个输出词的预测无法依赖于其他已生成的输出词，而主要依赖于编码器对输入的表示。它需要先预测输出序列的长度 ，然后将所有位置的表示一次性送入解码器，由解码器并行地为所有位置输出预测的词。显而易见，它的优点是推理速度快，大大降低了延迟；缺点在于其生成质量较低。

2 量子计算基本定义

2.1 量子态

在量子力学和量子信息科学中，量子态（Quantum State）是描述一个量子系统物理状态的数学对象。它是量子理论的核心概念之一，用于预测系统在各种测量下的行为和结果的概率分布。

它通常由一个位于复数希尔伯特空间（Hilbert Space）中的单位向量表示。这个向量又通常用狄拉克符号（Dirac notation）写作 ket 形式：

|ψ⟩

对于单个量子比特（qubit），其希尔伯特空间是二维复向量空间。因此，任意单量子比特的纯态可表示为|0⟩、|1⟩两个基态的线性叠加：

|ψ⟩=α|0⟩+β|1⟩

其中：|0⟩、|1⟩分别可表示为 \begin{pmatrix} 1\\ 0 \end{pmatrix} 与 \begin{pmatrix} 0\\ 1 \end{pmatrix}。

希尔伯特空间（Hilbert Space）是一个完备的复内积空间。字面上就可以看出，它满足三个核心性质。首先，它是一个定义在复数域上的线性空间，其中的元素称为“向量”，这些向量可以相加、可以与复数相乘，且运算封闭；其次，这个空间中的任意两个向量可以定义一个复数内积；最后，这个空间中的任何柯西序列都收敛于该空间内的一个向量（完备性）。

狄拉克符号的核心由两部分构成，分别是ket符号（|ψ⟩）与bra符号（⟨ψ|）。 ket 相当于列向量，如前面所示； bra 是 ket 的共轭转置（Hermitian 共轭），相当于行向量，可用于与 ket 进行内积运算。

它的核心运算主要是内积运算（Inner Product）与外积运算（Outer Product）。两个量子态之间的内积写作  ⟨\phi|\psi⟩ ，表示态 |\psi⟩ 在 |\phi⟩ 方向上的投影幅度，结果是一个复数，当其为0时，称进行内积运算的两个态正交；他们之间外积的结果是一个算符（矩阵），常用于构造投影算符或量子门。

同时前文表述中，\alpha 与 \beta 均为复数，且满足 \left | \alpha \right |^{2} + \left | \beta \right |^{2} =1，由该公式可以联想到三角函数中的\left (cos \theta \right )^{2} + \left (sin \theta \right )^{2} = 1 ，因此，任意单量子比特的纯态又可表示为：

|ψ⟩= e^{i\eta }\cos\frac{\theta }{2} |0⟩+ e^{i\phi }\sin\frac{\theta }{2} |1⟩

其中 e^{i\eta } （ e^{i\phi} ）由欧拉公式给出，表示复平面上一个模长为 1 的复数，位于单位圆上，其与正实轴的夹角为 \eta （\phi）。

这个公式可以进一步演化为：|ψ⟩= e^{i\eta }（ \cos\frac{\theta }{2} |0⟩+ e^{i\left (\phi -\eta \right )}\sin\frac{\theta }{2} |1⟩）

那么可以进行下面的假设：

假设：\eta =0 ，那么 |ψ⟩=  \cos\frac{\theta }{2} |0⟩+ e^{i\left (\phi -\eta \right )}\sin\frac{\theta }{2} |1⟩ ， 可以用一个球体来直观理解，这个球体被称为布洛赫球（Bloch Sphere），如下图所示：

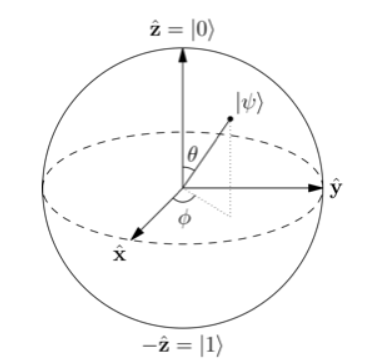
根据上图及公式：

当 \theta = 0 时，|ψ⟩=  |0⟩；

当 \theta = \pi 时，|ψ⟩=  |1⟩；

当 \theta =\frac{ \pi }{2} , \phi = 0 时，|ψ⟩=  \frac{\sqrt{2}}{2}（ |0⟩ + |1⟩）；

当 \theta =\frac{ \pi }{2} , \phi =\pi 时，|ψ⟩=  \frac{\sqrt{2}}{2}（ |0⟩ - |1⟩）；

当 \theta =\frac{ \pi }{2} , \phi =\frac{ \pi }{2} 时，|ψ⟩= \cos\frac{\theta }{2} （ |0⟩ + i|1⟩）；

当 \theta =\frac{ \pi }{2} , \phi =\frac{ 3\pi }{2} 时，|ψ⟩=  \cos\frac{\theta }{2} （ |0⟩ - i|1⟩）；

2.2 量子演化

量子动力学（Quantum Dynamics）是量子力学的一个核心分支，研究量子系统如何随时间演化。它回答的问题是：如果一个量子系统的初始状态已知，那么在后续任意时刻，它的状态将是什么？

量子动力学的一个核心原理是：封闭量子系统随时间演化的过程由酉算符（Unitary Operator）表示。这一理论来源于薛定谔方程（纯数学)：

i\frac{\mathrm{d} }{\mathrm{d} t} | \psi\left ( t \right ) ⟩ = H | \psi\left ( t \right ) ⟩ 

其中 H 可以看成是一个矩阵，而且通常是一个厄米矩阵（等于自己的共轭转置），它在薛定谔方程中被称为哈密顿量。

在量子计算中，量子动力学的思想被抽象为量子门操作和量子线路演化，每一个量子门都是一个特定的酉算符，对应一段量子动力学过程。常用的单量子比特门如下：

1. 泡利矩阵门（Pauli Gates），它包括三种，分别是X,Y,Z门。其中X 门（比特翻转门）相当于经典非门，在布洛赫球上表现为绕 x 轴旋转180度，它的矩阵表示为：

X = \begin{pmatrix} 0 &1 \\ 1& 0 \end{pmatrix}

Y 门可以同时实现比特和相位的翻转，在布洛赫球上表现为绕 y 轴旋转180度，它的矩阵表示为：

Y = \begin{pmatrix} 0 &-i \\ i& 0 \end{pmatrix}

Z 门（相位翻转门）可以改变 |1⟩ 的相位，在布洛赫球上表现为绕 z 轴旋转 180度，它的矩阵表示为：

Z= \begin{pmatrix} 1 &0 \\ 0& -1 \end{pmatrix}

2. 阿达玛门（Hadamard Gate, H），它能够创建等幅叠加态，是实现量子并行性的关键，在布洛赫球上表现为绕 y 轴旋转 90度后，再绕 x 轴旋转 180度，它的矩阵表示为：

H=\frac{1}{\sqrt{2}} \begin{pmatrix} 1 &1 \\ 1& -1 \end{pmatrix}

3. 相位门（Phase Gates）这类门不改变比特值，但引入相位变化。主要包括 S 门和 T 门。

S 门（ \frac{\pi}{2} 相位门）的矩阵表示为：

S=\begin{pmatrix} 1 &0 \\ 0& i \end{pmatrix}

T 门（ \frac{\pi}{4} 相位门）的矩阵表示为：

T= \begin{pmatrix} 1 &0 \\ 0& e^{i\frac{\pi}{4}} \end{pmatrix}

2.3 复合系统

量子力学中的一个基本公设是：一个复合系统的态空间是各个子系统态空间的张量积。

例如：假设有两个量子比特，第一个量子比特的态空间为 H_{A} = \mathbb{C}^{2}，第二个量子比特的态空间为 H_{B} = \mathbb{C}^{2}，则整个复合系统的态空间为：

H_{AB} =H_{A}\otimes H_{B} = \mathbb{C}^{2}\otimes\mathbb{C}^{2}=\mathbb{C}^{4}

标准基向量为：

∣0⟩⊗∣0⟩=∣00⟩；∣0⟩⊗∣1⟩=∣01⟩；∣1⟩⊗∣0⟩=∣10⟩；∣1⟩⊗∣1⟩=∣11⟩

其任意复合态都可写为这四个基向量的线性组合。

这儿可以回到量子态那一小节中狄拉克符号的运算部分，左 bra 右 ket 为内积运算，反之则为外积，若是多个 ket 则是张量积运算。

另外，在对一个复合系统进行操作时，对其子系统的独立操作由张量积来描述。

例如：假设有一个态： \frac{\sqrt{2}}{2}（ |00⟩ + |11⟩），需要对第二个量子比特进行比特翻转操作，其计算如下：

3 总结

本周主要学习了Transformer的部分入门知识与量子计算的一些基本定义，对于部分概念理解感觉比较浅显，后续深入学习考虑结合实例或论文理解，并多进行复盘。

http://www.dtcms.com/a/393990.html

相关文章：

  • MCP实战：使用 LangGraph 和 MCP 协议无缝集成外部工具
  • 【嵌入式总线通信协议库】
  • 06.【Linux系统编程】命令行参数(给main传参)、环境变量(概念+使用)、进程的虚拟地址空间(用户实际访问的空间)
  • esp32墨水屏天气预测学习
  • LabelImg 操作指南：提高标注速度
  • redhat7.2迁移ssh免密到麒麟v10
  • Linux基操
  • 如何解决 pip install 安装报错 ModuleNotFoundError: No module named ‘protobuf’ 问题
  • EXCEL中公式和文字混合和数字自动变成大写金额
  • Linux软件安装与项目部署
  • Config-配置中心2.0
  • Meta 开源 MobileLLM-R1 系列小参数高效模型，颠覆大模型竞赛
  • 【论文阅读】One-Minute Video Generation with Test-Time Training
  • 玄鸟12600M矿机ETC/ETHW挖矿性能解析与技术参数分析
  • Rust_2025：阶段1：day7.1 类型转换
  • Composer在PHP项目中的手动类自动加载策略
  • kubeasz二进制部署k8s生产环境集群
  • 浏览器缓存
  • 【PyTorch】梯度检查点 checkpoint 实现源码剖析
  • 学习嵌入式的第三十九天——ARM——汇编
  • 解决AI摘要不显示的三种方案 -AIsummary插件
  • 企业网盘，基于 .NET 技术开发，用于构建安全高效的文件云存储和云管理平台。
  • AFNetWorking
  • vscode连接ubuntu18报Gilbc2.28错
  • 华为超节点 384 集群： AI 算力的架构革新与实践
  • mescroll-uni 完全指南——Vue3 setup格式
  • 动态规划算法的欢乐密码(六)：子数组系列(下)
  • StringBuilder与StringBuffer区别详解
  • 深入浅出 Scikit-learn：从入门到实战的机器学习工具包指南
  • 乡村社区服务管理系统的设计与实现-（源码+LW+可部署）