论文阅读——隧道中毫米波MIMO信道特性的实验研究

隧道中毫米波MIMO信道特性的实验研究

X. Liu, X. Yin and G. Zheng, “Experimental Investigation of Millimeter-Wave MIMO Channel Characteristics in Tunnel,” in IEEE Access, vol. 7, pp. 108395-108399, 2019, doi: 10.1109/ACCESS.2019.2932576.

摘要

本文进行了28 GHz毫米波传播测量活动，旨在预测隧道环境中多输入多输出（MIMO）信道性能。研究了两种极化配置方案。为了克服毫米波传播的严重路径损耗，在隧道环境测量中使用了高增益定向喇叭天线。通过比较相同特定位置的测量结果和仿真结果，发现仿真模型与测量结果吻合良好。利用该仿真模型可以预测隧道其他位置的MIMO容量。研究推断，在恒定信噪比（SNR）条件下，水平极化配置的天线阵列元件比垂直极化配置具有更高的容量。

1. 引言

随着城市轨道交通系统对数据速率需求的不断增长，频谱短缺的现实问题日益严峻。为应对这一挑战，毫米波频段因其拥有大量原始带宽而备受关注。理解无线信道特性对于设计无线通信系统至关重要，因此研究地铁隧道中毫米波MIMO信道传播特性具有重要意义。

早期的MIMO信道性能研究主要集中在低频段（6 GHz以下）的地铁隧道环境。随后，基于模态分析的MIMO理论研究和实验活动在地铁隧道中展开。据我们所知，只有少数文献关注60 GHz频段的非地铁隧道（矿井隧道）研究。在矿井隧道的狭窄和宽阔环境下进行了单输入单输出（SISO）毫米波信道测量，结果表明狭窄环境中的SISO信道容量高于宽阔环境，其路径损耗指数低于自由空间。

由于矿井隧道的尺寸、材料或壁面粗糙度与地铁隧道存在显著差异，本文在中国南通中天科技公司（ZTT）的南通隧道中进行了28 GHz的MIMO信道测量，并利用这些测量结果预测地铁隧道中的毫米波MIMO信道性能。

2. 测量和仿真环境设置

2.1 测量环境

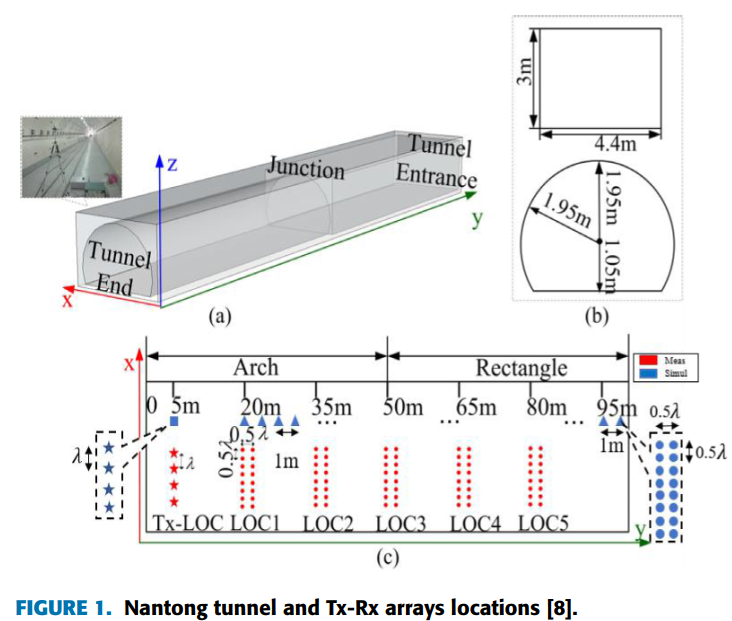
测量在中国南通ZTT的类地铁隧道中进行。隧道由50米矩形段和50米拱形段组成，总长100米。隧道宽4.4米，高3米。图1展示了南通隧道和发射-接收阵列位置的示意图，其中标记了发射机（Tx）和接收机（Rx）的具体位置，以及用于MIMO测量的虚拟阵列配置。

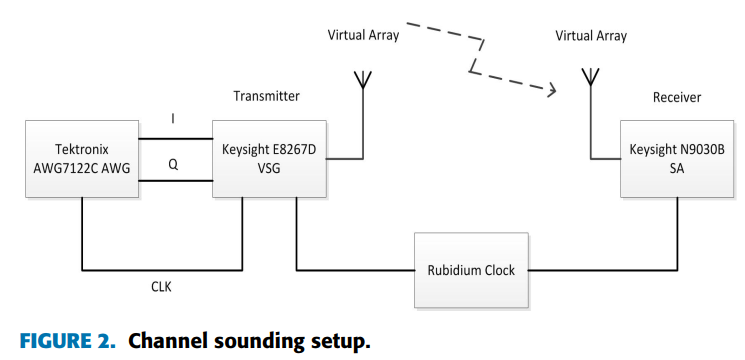
测量系统框图如图2所示，主要包括：

• 虚拟阵列用于实现MIMO测量
• 发射机使用Keysight E8267D矢量信号发生器
• 接收机使用Keysight N9030B信号分析仪
• 铷原子钟用于时间同步
• 控制计算机（CLK）进行数据采集和处理

关键测量参数如表1所示：

参数	数值
中心频率	28 GHz
发射功率	23 dBm
带宽	100 MHz
采样率	200 MHz
延迟分辨率	10 ns
最大延迟	5110 ns
发射信号	PN序列
PN序列长度	511码片
发射天线高度	1.6 m
接收天线高度	1.6 m

2.2 极化配置

研究了两种极化配置：

• VV配置：所有发射和接收天线阵列元件均为垂直极化
• HH配置：所有发射和接收天线阵列元件均为水平极化

通过将天线孔径的长边垂直于地面放置实现垂直极化信号的发射/接收，将其旋转90°平行于地面实现水平极化信号的发射/接收。使用的定向喇叭天线半功率波束宽度为16°，增益为19.25 dBi。

2.3 仿真设置

使用Wireless InSite射线追踪软件获取仿真结果。根据测量环境用AutoCAD建立3D模型。隧道壁的配置参数如表2所示：

材料	厚度(m)	粗糙度	电导率(S/m)	介电常数
混凝土	0.5	0.001	0.48	5.31

为了研究其他位置的MIMO容量，进一步仿真了发射-接收距离从15米到94米、间隔1米的情况。

3. 数据处理与分析

3.1 信道脉冲响应的获取

信道脉冲响应（CIR）通过收集数据与发射序列副本的互相关直接生成。为了从背景噪声中分离有效的多径分量（MPC），基于相对于原始功率延迟分布的平均热噪声底噪的5 dB信噪比阈值计算阈值。

相互信息容量是基于MIMO系统的基本属性。用于计算MIMO信道容量的窄带信道脉冲响应为：

$$h_{narr}(t,s,u)=\sum _{i=1}^{N_{\tau }}\tilde{h}(t,{\tau }_i,s,u)$$

其中$N_{\tau }$是多径数量，$s$表示第$s$个接收天线，$u$是第$u$个发射天线。

3.2 信道矩阵归一化

在分析MIMO信道容量之前，通常需要对MIMO信道矩阵进行归一化。每个信道实现的归一化信道矩阵表示为：

$${\mathbf{H}}_{nor}=\mathbf{H}\sqrt{\frac{N_{Tx}{N}_{Rx}}{||\mathbf{H}|{|}_F^2}}$$

其中$||\mathbf{H}|{|}_F$表示Frobenius范数，定义为：

$$||\mathbf{H}|{|}_F=\sqrt{\sum _{i=1}^{N_{Rx}}\sum _{j=1}^{N_{Tx}}|h_{ij}{|}^2}$$

3.3 MIMO信道容量计算

假设发射端没有信道状态信息，MIMO信道容量可计算为：

$$C={\log }_2\left(\det \left({\mathbf{I}}_{N_{Rx}}+\frac{\rho }{N_{Tx}}{\mathbf{H}}_{nor}{\mathbf{H}}_{nor}^{\ast }\right)\right)$$

其中$\rho$是平均SNR，$(•{)}^{\ast }$表示矩阵的共轭转置，$N_{Tx}$和$N_{Rx}$分别是发射和接收天线元件数量，${\mathbf{I}}_{N_{Rx}}$是$N_{Rx}\times N_{Rx}$的单位矩阵。

4. 反射系数的物理机制

造成HH配置性能优于VV配置的原因可以通过反射系数来解释。根据国际电信联盟（ITU）建议，28 GHz时混凝土的电导率为0.48 S/m，相对介电常数为5.31。对于非完全导电表面的反射，垂直极化（⊥）和水平极化（||）的平面波菲涅尔反射系数分别为：

垂直极化：
$$R_{\perp }(\theta )=\frac{\cos (\theta )-\sqrt{{\epsilon }^{\prime }-{\sin }^2(\theta )}}{\cos (\theta )+\sqrt{{\epsilon }^{\prime }-{\sin }^2(\theta )}}$$

水平极化：
$$R_{||}(\theta )=\frac{{\epsilon }^{\prime }\cos (\theta )-\sqrt{{\epsilon }^{\prime }-{\sin }^2(\theta )}}{{\epsilon }^{\prime }\cos (\theta )+\sqrt{{\epsilon }^{\prime }-{\sin }^2(\theta )}}$$

其中${\epsilon }^{\prime }=\epsilon /{\epsilon }_0-j\sigma /(\omega {\epsilon }_0)$，$\omega =2\pi f$，$\epsilon ={\epsilon }_r{\epsilon }_0$是材料的介电常数，$\sigma$是电导率，${\epsilon }_r$是相对介电常数，${\epsilon }_0=8.85\times 10^{-12}$ F/m是真空介电常数，$f$是载频，$\theta$是入射角。

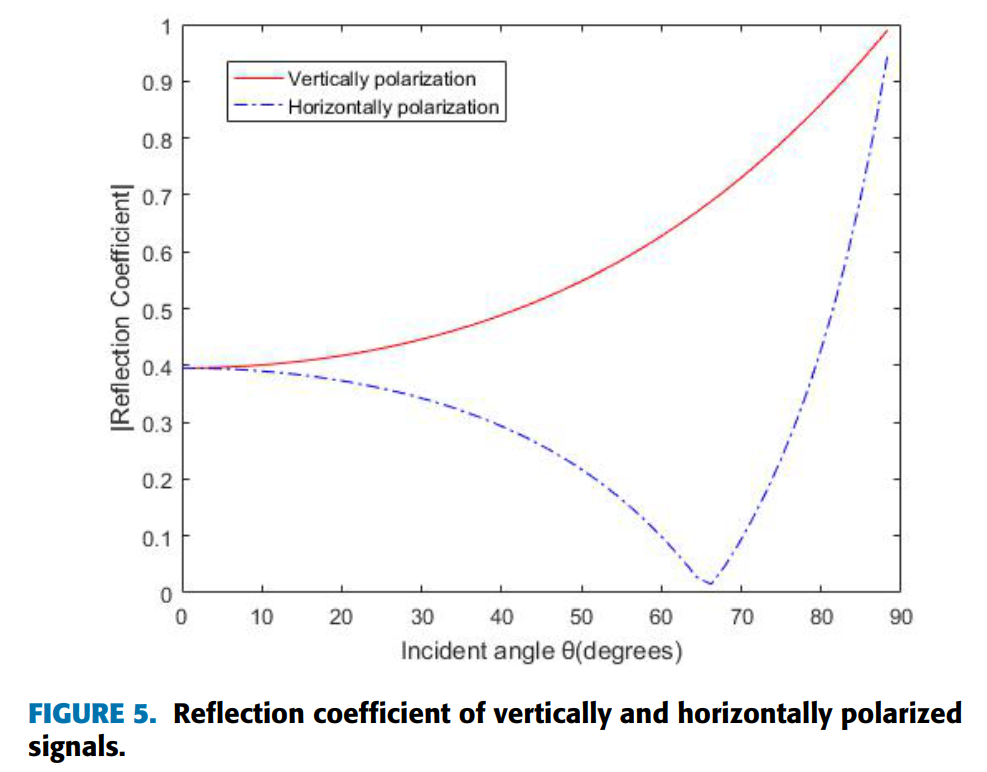
图5展示了垂直和水平极化的反射系数随入射角的变化。垂直极化系数随入射角增加而增加，但水平极化系数存在布儒斯特角，且始终低于垂直极化系数。对于水平极化信号，入射到隧道天花板和地板的射线是水平极化的，但在隧道壁上观察到垂直极化。对于垂直极化信号，观察到相反的响应。根据反射系数，HH配置在隧道壁上的反射射线功率大于VV配置。由于隧道宽度大于隧道高度，隧道壁上的反射射线具有比隧道天花板和地板更大的到达角。这导致HH配置比VV配置具有更高的角度扩展，从而HH配置具有比VV配置更大的信道容量。

5. 测量和仿真结果

5.1 恒定SNR下的MIMO信道容量比较

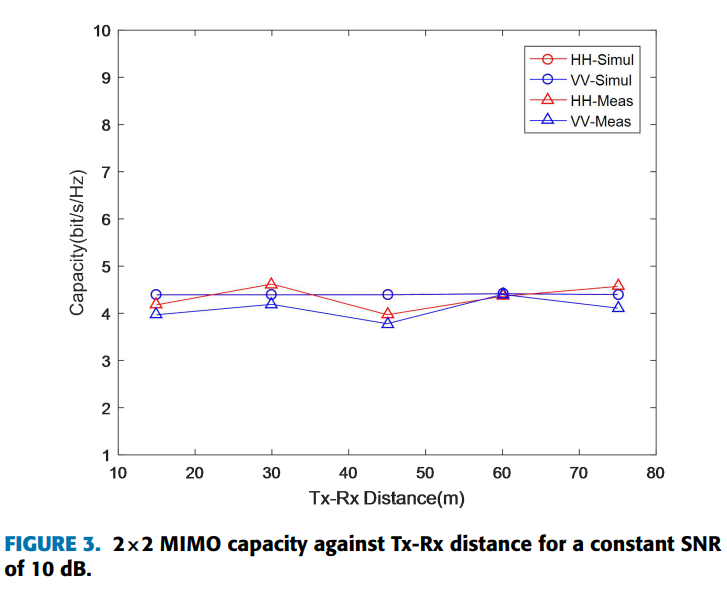
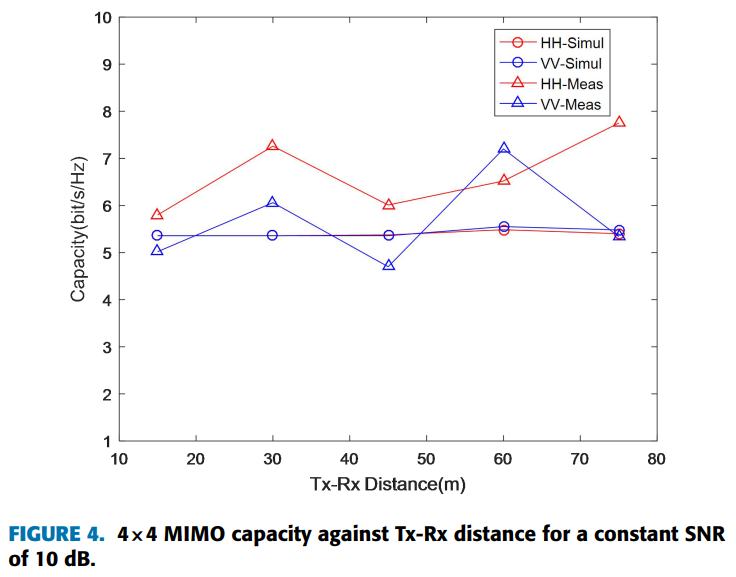
为了进行公平比较，考虑恒定SNR为10 dB的情况。图3和图4分别给出了2×2和4×4 MIMO信道容量。仿真结果低于测量结果，这是因为仿真是理想环境，而测量期间墙上存在一些小散射体，这些在仿真中未被考虑，因此仿真结果低于测量结果。尽管在30米位置存在差异，但仿真结果与测量结果具有相同的趋势。30米位置差异的原因是测量环境在该位置有金属材料导致强反射，使得测量中该位置附近的MIMO容量高于仿真。因此可以得出结论，仿真模型与测量结果吻合良好。

表3给出了HH和VV配置在所有发射-接收距离上的平均容量：

极化配置	平均容量 (bit/s/Hz)
	4×4	2×2
VV-测量	5.7	4.1
HH-测量	6.7	4.3
VV-仿真	5.42	4.39
HH-仿真	5.40	4.39

可以观察到HH配置的性能优于VV配置。

5.2 容量预测

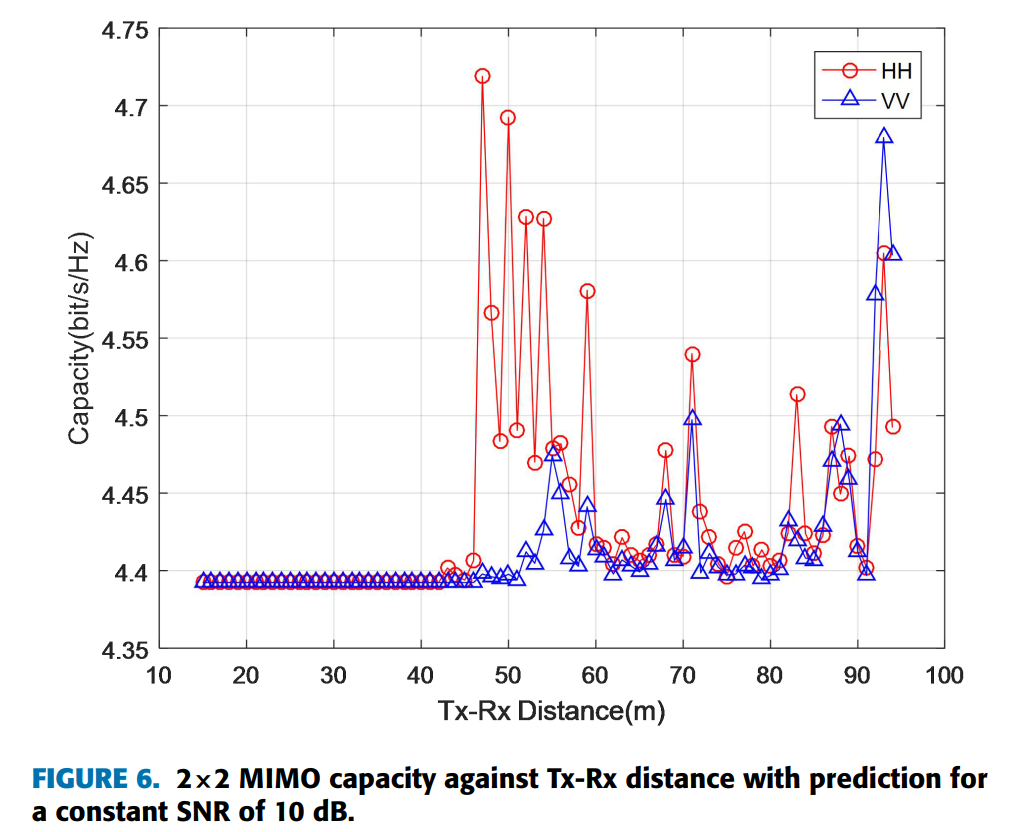
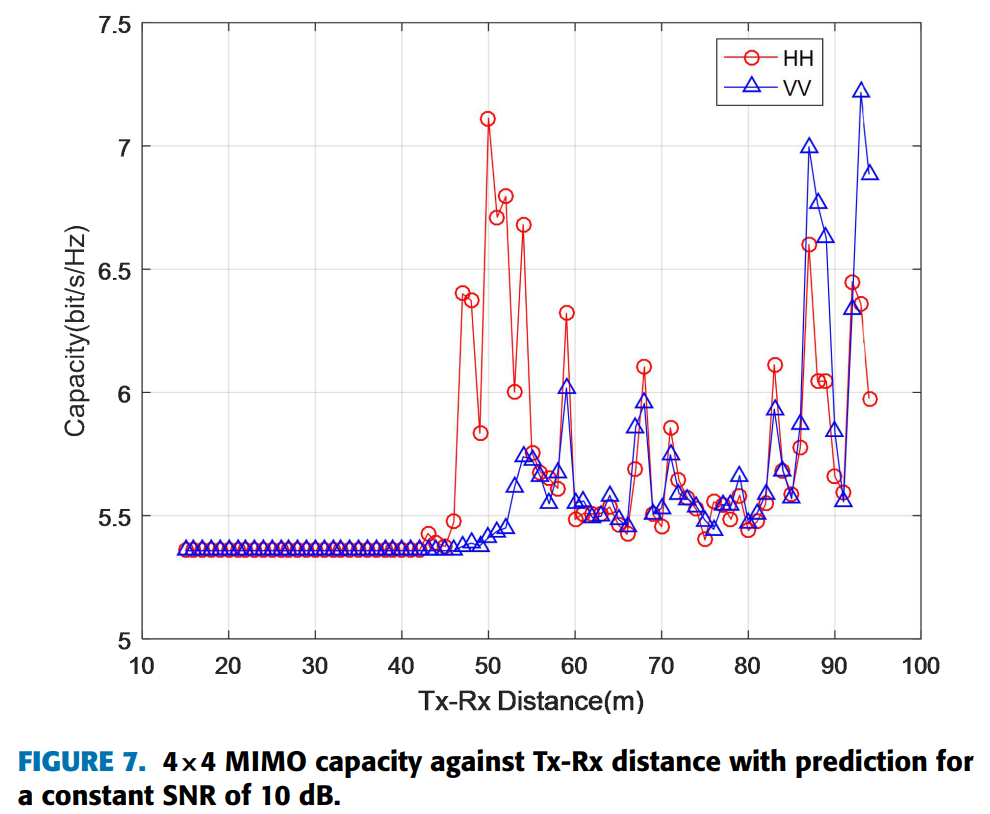
图6和图7分别展示了包含预测的2×2和4×4 MIMO容量随发射-接收距离的变化。当发射-接收距离在15米到45米范围内时，由于高莱斯K因子（定义为视距分量和非视距分量的功率比），HH和VV的MIMO信道容量几乎重叠。当发射-接收距离从45米增加到95米时，由于K因子的降低，HH和VV在恒定SNR 10 dB下的MIMO信道容量增加，且HH高于VV。

表4给出了包含预测的所有发射-接收距离的平均容量：

极化配置	平均容量 (bit/s/Hz)
	4×4	2×2	SISO
VV	5.59	4.41	3.46
HH	5.65	4.44	3.46

预测结果表明HH具有比VV更高的平均容量。由于MIMO系统相当复杂，将其性能与SISO系统进行比较非常重要。无论是实际测量还是仿真，2×2 MIMO和4×4 MIMO系统的平均容量都高于SISO系统。

6. 结论

本研究使用定向天线在中国南通的地铁隧道中进行了28 GHz的毫米波MIMO信道测量。为了克服毫米波频段的高衰减，在测量中使用了高增益定向锥形喇叭天线。研究考虑了两种极化配置（VV、HH）。

主要结论如下：

仿真结果的平均MIMO容量低于测量结果，这是因为测量环境中存在更多散射体导致强反射，而仿真无法完全模拟这些效应。

在地铁隧道中，无论是测量还是仿真，HH配置在恒定SNR下的容量都高于VV配置。这一现象的物理机制在于：水平极化在隧道侧壁的反射系数高于垂直极化，而隧道宽度大于高度使得侧壁反射占主导地位，导致HH配置具有更大的角度扩展和更高的信道容量。

因此，对于地铁隧道中的毫米波MIMO通信系统，HH是更好的极化配置选择。

---

附录A：MIMO信道容量的理论推导

A.1 信道模型的数学表示

考虑一个$N_{Tx}\times N_{Rx}$的MIMO系统，接收信号可以表示为：

$$\mathbf{y}=\mathbf{Hx}+\mathbf{n}$$

其中$\mathbf{y}\in {\mathbb{C}}^{N_{Rx}\times 1}$是接收信号向量，$\mathbf{x}\in {\mathbb{C}}^{N_{Tx}\times 1}$是发射信号向量，$\mathbf{H}\in {\mathbb{C}}^{N_{Rx}\times N_{Tx}}$是信道矩阵，$\mathbf{n}\in {\mathbb{C}}^{N_{Rx}\times 1}$是加性高斯白噪声向量。

假设噪声向量的协方差矩阵为：
$$\mathbb{E}[\mathbf{n}{\mathbf{n}}^{\ast }]={\sigma }_n^2{\mathbf{I}}_{N_{Rx}}$$

发射信号的协方差矩阵为：
$${\mathbf{R}}_x=\mathbb{E}[\mathbf{x}{\mathbf{x}}^{\ast }]$$

A.2 互信息量的推导

系统的互信息量定义为：
$$I(\mathbf{x};\mathbf{y})=h(\mathbf{y})-h(\mathbf{y}|\mathbf{x})$$

其中$h(\cdot )$表示差分熵。由于给定$\mathbf{x}$时，$\mathbf{y}$的条件分布为高斯分布：
$$\mathbf{y}|\mathbf{x}\sim \mathcal{C}\mathcal{N}(\mathbf{Hx},{\sigma }_n^2{\mathbf{I}}_{N_{Rx}})$$

因此条件熵为：
$$h(\mathbf{y}|\mathbf{x})={\log }_2\det (\pi e{\sigma }_n^2{\mathbf{I}}_{N_{Rx}})=N_{Rx}{\log }_2(\pi e{\sigma }_n^2)$$

对于边缘分布，$\mathbf{y}$也服从高斯分布：
$$\mathbf{y}\sim \mathcal{C}\mathcal{N}(0,\mathbf{H}{\mathbf{R}}_x{\mathbf{H}}^{\ast }+{\sigma }_n^2{\mathbf{I}}_{N_{Rx}})$$

其差分熵为：
$$h(\mathbf{y})={\log }_2\det (\pi e(\mathbf{H}{\mathbf{R}}_x{\mathbf{H}}^{\ast }+{\sigma }_n^2{\mathbf{I}}_{N_{Rx}}))$$

将上述结果代入互信息量公式：
$$I(\mathbf{x};\mathbf{y})={\log }_2\det (\pi e(\mathbf{H}{\mathbf{R}}_x{\mathbf{H}}^{\ast }+{\sigma }_n^2{\mathbf{I}}_{N_{Rx}}))-N_{Rx}{\log }_2(\pi e{\sigma }_n^2)$$

化简得：
$$I(\mathbf{x};\mathbf{y})={\log }_2\frac{\det (\mathbf{H}{\mathbf{R}}_x{\mathbf{H}}^{\ast }+{\sigma }_n^2{\mathbf{I}}_{N_{Rx}})}{\det ({\sigma }_n^2{\mathbf{I}}_{N_{Rx}})}$$

$$={\log }_2\det \left({\mathbf{I}}_{N_{Rx}}+\frac{1}{{\sigma }_n^2}\mathbf{H}{\mathbf{R}}_x{\mathbf{H}}^{\ast }\right)$$

A.3 最优功率分配

当发射端不知道信道状态信息时，最优的功率分配策略是等功率分配：
$${\mathbf{R}}_x=\frac{P}{N_{Tx}}{\mathbf{I}}_{N_{Tx}}$$

其中$P$是总发射功率。定义信噪比$\rho =P/{\sigma }_n^2$，则信道容量为：
$$C=\underset{{\mathbf{R}}_x}{\max }I(\mathbf{x};\mathbf{y})={\log }_2\det \left({\mathbf{I}}_{N_{Rx}}+\frac{\rho }{N_{Tx}}\mathbf{H}{\mathbf{H}}^{\ast }\right)$$

A.4 特征值分解与容量表达式

对$\mathbf{H}{\mathbf{H}}^{\ast }$进行特征值分解：
$$\mathbf{H}{\mathbf{H}}^{\ast }=\mathbf{U\Lambda }{\mathbf{U}}^{\ast }$$

其中$\mathbf{U}$是酉矩阵，$\mathbf{\Lambda }=\text{diag}({\lambda }_1,{\lambda }_2,...,{\lambda }_{N_{Rx}})$是特征值对角矩阵。

容量可以重写为：
$$C={\log }_2\det \left({\mathbf{I}}_{N_{Rx}}+\frac{\rho }{N_{Tx}}\mathbf{\Lambda }\right)=\sum _{i=1}^r{\log }_2\left(1+\frac{\rho }{N_{Tx}}{\lambda }_i\right)$$

其中$r=\text{rank}(\mathbf{H})$是信道矩阵的秩。

附录B：菲涅尔反射系数

B.1 边界条件与电磁场连续性

考虑平面电磁波从介质1（空气）入射到介质2（隧道壁材料）的界面。设入射角为${\theta }_i$，反射角为${\theta }_r$，折射角为${\theta }_t$。

根据斯涅尔定律：
$$n_1\sin {\theta }_i=n_2\sin {\theta }_t$$

其中$n_1$和$n_2$分别是两种介质的折射率。对于有损耗介质：
$$n_2=\sqrt{{\epsilon }_r-j\frac{\sigma }{\omega {\epsilon }_0}}$$

B.2 垂直极化（TE模式）

对于垂直极化，电场垂直于入射面。边界条件要求切向电场和磁场连续：

$$E_i+E_r=E_t$$
$$H_i\cos {\theta }_i-H_r\cos {\theta }_r=H_t\cos {\theta }_t$$

利用平面波中$H=\sqrt{\epsilon /\mu }E$的关系，以及${\theta }_i={\theta }_r$，可得：

$$E_i+E_r=E_t$$
$$\sqrt{\frac{{\epsilon }_1}{{\mu }_1}}(E_i-E_r)\cos {\theta }_i=\sqrt{\frac{{\epsilon }_2}{{\mu }_2}}{E}_t\cos {\theta }_t$$

定义反射系数$R_{\perp }=E_r/E_i$，透射系数$T_{\perp }=E_t/E_i$，求解上述方程组：

$$R_{\perp }=\frac{Z_2\cos {\theta }_i-Z_1\cos {\theta }_t}{Z_2\cos {\theta }_i+Z_1\cos {\theta }_t}$$

其中$Z_1=\sqrt{{\mu }_1/{\epsilon }_1}$和$Z_2=\sqrt{{\mu }_2/{\epsilon }_2}$是波阻抗。

利用$\cos {\theta }_t=\sqrt{1-{\sin }^2{\theta }_t}=\sqrt{1-(n_1/n_2{)}^2{\sin }^2{\theta }_i}$，并假设${\mu }_1={\mu }_2={\mu }_0$：

$$R_{\perp }=\frac{\cos {\theta }_i-\sqrt{{\epsilon }_r^{\prime }-{\sin }^2{\theta }_i}}{\cos {\theta }_i+\sqrt{{\epsilon }_r^{\prime }-{\sin }^2{\theta }_i}}$$

其中${\epsilon }_r^{\prime }={\epsilon }_r-j\sigma /(\omega {\epsilon }_0)$是复相对介电常数。

B.3 水平极化（TM模式）

对于水平极化，磁场垂直于入射面。类似地应用边界条件：

$$H_i+H_r=H_t$$
$$E_i\cos {\theta }_i-E_r\cos {\theta }_r=E_t\cos {\theta }_t$$

经过类似推导，得到水平极化的反射系数：

$$R_{||}=\frac{{\epsilon }_r^{\prime }\cos {\theta }_i-\sqrt{{\epsilon }_r^{\prime }-{\sin }^2{\theta }_i}}{{\epsilon }_r^{\prime }\cos {\theta }_i+\sqrt{{\epsilon }_r^{\prime }-{\sin }^2{\theta }_i}}$$

B.4 布儒斯特角

对于水平极化，当$R_{||}=0$时出现布儒斯特角${\theta }_B$：

$${\epsilon }_r^{\prime }\cos {\theta }_B=\sqrt{{\epsilon }_r^{\prime }-{\sin }^2{\theta }_B}$$

平方并整理：
$${\epsilon }_r^{\prime 2}{\cos }^2{\theta }_B={\epsilon }_r^{\prime }-{\sin }^2{\theta }_B$$
$${\epsilon }_r^{\prime 2}(1-{\sin }^2{\theta }_B)={\epsilon }_r^{\prime }-{\sin }^2{\theta }_B$$
$${\sin }^2{\theta }_B({\epsilon }_r^{\prime 2}-1)={\epsilon }_r^{\prime }({\epsilon }_r^{\prime }-1)$$

因此：
$$\tan {\theta }_B=\sqrt{{\epsilon }_r^{\prime }}$$

对于实数介电常数，布儒斯特角为：
$${\theta }_B=\arctan \sqrt{{\epsilon }_r}$$

附录C：隧道中的射线追踪模型

C.1 镜像法原理

在矩形隧道中，可以使用镜像法来计算多径传播。对于位于$(x_t,y_t,z_t)$的发射机和位于$(x_r,y_r,z_r)$的接收机，第$(m,n)$个镜像的位置为：

$$x_{mn}=\{\begin{array}{ll}{x}_t& m=0\\ 2ma-x_t& m\text{ 为偶数}\\ 2ma+x_t& m\text{ 为奇数}\end{array}$$

$$y_{mn}=\{\begin{array}{ll}{y}_t& n=0\\ 2nb-y_t& n\text{ 为偶数}\\ 2nb+y_t& n\text{ 为奇数}\end{array}$$

其中$a$和$b$分别是隧道的宽度和高度。

C.2 路径损耗计算

从第$(m,n)$个镜像到接收机的路径长度为：

$$d_{mn}=\sqrt{(x_r-x_{mn}{)}^2+(y_r-y_{mn}{)}^2+(z_r-z_t{)}^2}$$

相应的路径损耗（考虑反射损耗）为：

$$L_{mn}={\left(\frac{\lambda }{4\pi d_{mn}}\right)}^2\prod _{k=1}^{|m|}|R_x^{(k)}{|}^2\prod _{l=1}^{|n|}|R_y^{(l)}{|}^2$$

其中$R_x^{(k)}$和$R_y^{(l)}$是第$k$次和第$l$次反射的反射系数。

C.3 总接收功率

总接收功率为所有有效路径的相干叠加：

$$P_r=P_t{G}_t{G}_r{\left|\sum _{m=-M}^M\sum _{n=-N}^N\sqrt{L_{mn}}{e}^{-j{k}_0{d}_{mn}}\right|}^2$$

其中$P_t$是发射功率，$G_t$和$G_r$分别是发射和接收天线增益，$k_0=2\pi /\lambda$是波数，$M$和$N$是考虑的最大镜像阶数。

C.4 信道矩阵元素

对于MIMO系统，信道矩阵的第$(i,j)$个元素为：

$$h_{ij}=\sum _{m=-M}^M\sum _{n=-N}^N\sqrt{L_{mn}^{(ij)}}{e}^{-j{k}_0{d}_{mn}^{(ij)}}{F}_t^{(j)}({\theta }_{mn}^{(ij)},{\varphi }_{mn}^{(ij)})F_r^{(i)}({\theta }_{mn}^{(ij)},{\varphi }_{mn}^{(ij)})$$

其中$F_t^{(j)}$和$F_r^{(i)}$分别是第$j$个发射天线和第$i$个接收天线的方向图，$({\theta }_{mn}^{(ij)},{\varphi }_{mn}^{(ij)})$是相应的角度。