当前位置：首页 > news >正文

算法 --- BFS 解决最短路问题

news 2025/9/21 15:09:19

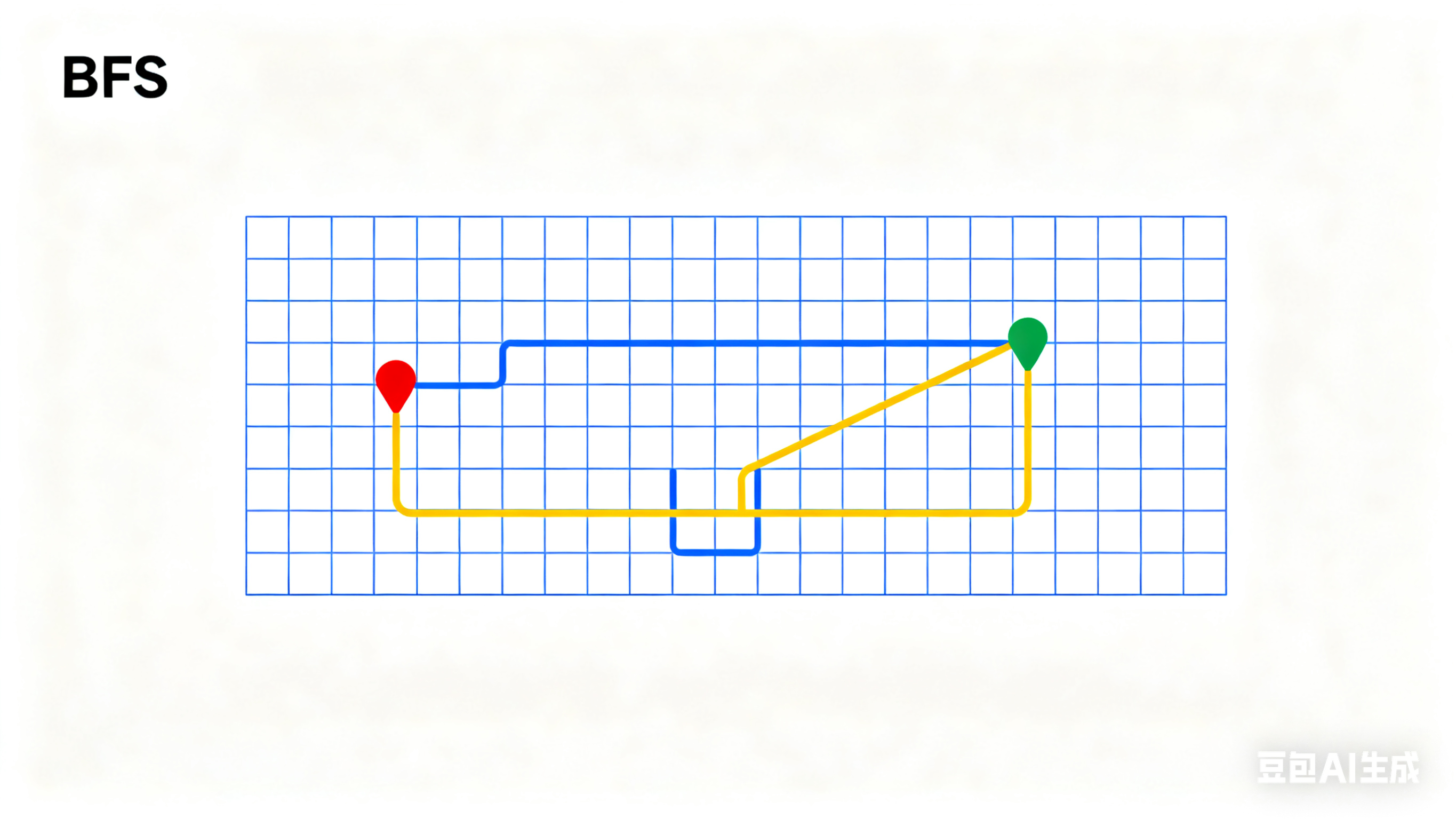
BFS 解决最短路问题

BFS最适合解决在无权图或所有边权重相等的图中，寻找从起点到终点的最短路径和最小步数的问题。

详细说明：

BFS解决最短路问题的题目通常具有以下特征，适用于这类场景：

图的类型：问题可以抽象为在一个无权图或者一个所有移动代价（权重）相同的图（如网格迷宫，每次移动一格代价为1）中进行搜索。

目标明确：要求找出从起点到终点的最短路径长度或最小操作步数。因为BFS的“一圈一圈”扩散的特性，第一次访问到某个节点的路径，一定是步数最短的路径，这是它相较于DFS的核心优势。

状态表示：问题的“状态”能够被清晰地定义为一个节点，并且状态之间的“转移”（即边）是明确且有限的。例如，在迷宫问题中，一个状态就是(x, y)坐标；在“单词接龙”问题中，一个状态就是一个具体的单词。

常见题型：

网格迷宫最短路径：经典的迷宫问题，从起点‘S’到终点‘T’，避开障碍物‘#’，求最少步数。
单词接龙：给定起始词和结束词，每次只能改变一个字母，且改变后的词必须在词典中，求从起始词到结束词的最短转换序列长度。
解开密码锁的最少次数：一个锁有多个数字转盘，每次只能将一个拨轮向上或向下转动一格，求从初始状态"0000"转到目标状态的最少次数。
在二叉树中找层数/深度：本质上也是BFS，每一层一步。
拓扑排序：也可以使用BFS（即Kahn算法）来实现。

反之，如果图中的边具有不同的权重（即加权图），那么BFS就不再适用，需要使用Dijkstra算法、Bellman-Ford算法等其他专门算法。

基本模型：

代码模板

// 初始化图和相关参数
graph = 读取图的邻接矩阵
n = 图的节点数
dist = 初始化为无穷大的数组，用于存储最短路径长度
dist[source] = 0 // 起点到自身的距离为0
visited = 初始化为false的数组，用于标记节点是否被访问// 使用队列实现BFS
queue = q初始化为空队列
q.push(???) // 将起点加入队列while queue 不为空:current = q.front(); // 从队列中取出一个节点int sz = q.size()//逻辑要求// 如果没有找到目标节点
return ??

这个伪代码模板描述了一个使用广度优先搜索（BFS）算法解决图中最短路径问题的通用流程。它包括了图的初始化、队列的使用、节点的访问标记以及最短路径的更新。这个模板可以应用于多种图结构，如无权图或有权图。

题目练习

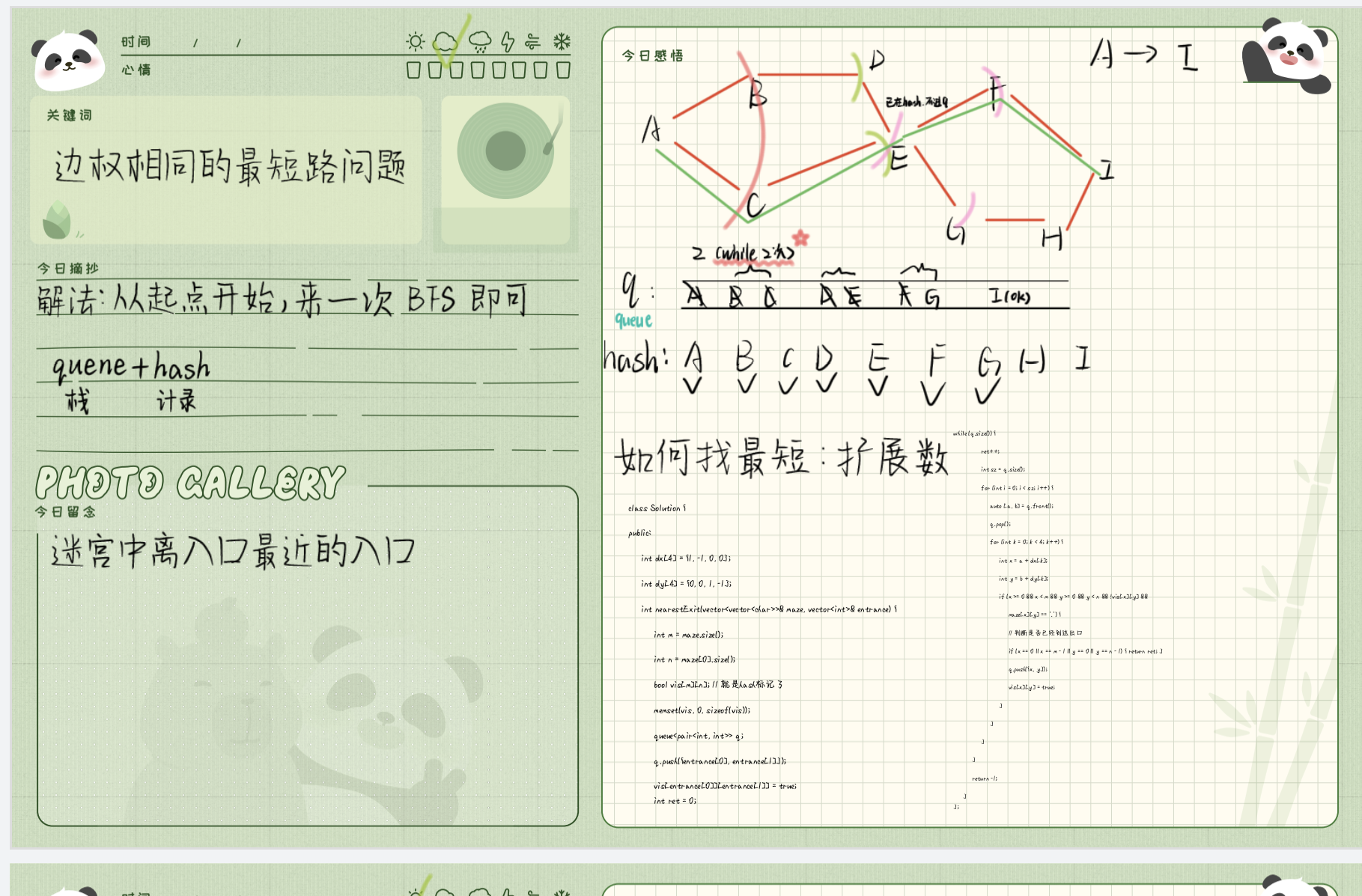
1926. 迷宫中离入口最近的出口 - 力扣（LeetCode）

解法（bfs 求最短路）：

算法思路：

利用层序遍历来解决迷宫问题，是最经典的做法。

我们可以从起点开始层序遍历，并且在遍历的过程中记录当前遍历的层数。这样就能在找到出口的时候，得到起点到出口的最短距离。

class Solution {
public:int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {int m = maze.size(), n = maze[0].size(), sr = entrance[0], sc = entrance[1];queue<pair<int, int>> q;bool vis[m][n];memset(vis, 0, sizeof vis);q.push({sr, sc});vis[sr][sc] = true;int ret = 0;while(q.size()){ret++;int sz = q.size();while(sz--){auto[x, y] = q.front();q.pop();for(int k = 0; k < 4; ++k){int a = x + dx[k], b = y + dy[k];if(a >= 0 && a < m && b >= 0 && b < n && maze[a][b] == '.' && !vis[a][b]){if(a == 0 || a == m - 1 || b == 0 || b == n - 1) return ret;vis[a][b] = true;q.push({a, b});}}}}return -1;}
};

433. 最小基因变化 - 力扣（LeetCode）

解法：

算法思路：

如果将「每次字符串的变换」抽象成图中的「两个顶点和一条边」的话，问题就变成了「边权为 1 的最短路问题」。

因此，从起始的字符串开始，来一次 bfs 即可。

class Solution {
public:int minMutation(string startGene, string endGene, vector<string>& bank) {unordered_set<string> vis;unordered_set<string> hash(bank.begin(), bank.end());string change = "ACGT";if(startGene == endGene) return 0;if(!hash.count(endGene)) return -1;queue<string> q;q.push(startGene);vis.insert(startGene);int ret = 0;while(q.size()){ret++;int sz = q.size();while(sz--){string t = q.front();q.pop();for(int i = 0; i < 8; ++i){string tmp = t;//细节for(int j = 0; j < 4; ++j){tmp[i] = change[j];if(hash.count(tmp) && !vis.count(tmp)){if(tmp == endGene) return ret;q.push(tmp);vis.insert(tmp);}}}}}return -1;}
};

127. 单词接龙 - 力扣（LeetCode）

解法同上一题一致！

class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> vis;unordered_set<string> hash(wordList.begin(), wordList.end());if(!hash.count(endWord)) return 0;if(beginWord == endWord) return 1;queue<string> q;q.push(beginWord);vis.insert(beginWord);int ret = 1;while(q.size()){ret++;int sz = q.size();while(sz--){string t = q.front();q.pop();for(int i = 0; i < t.size(); i++){string tmp = t;for(char ch = 'a'; ch <= 'z'; ++ch){tmp[i] = ch;if(hash.count(tmp) && !vis.count(tmp)){if(tmp == endWord) return ret;q.push(tmp);vis.insert(tmp);}}}}}return 0;}
};

675. 为高尔夫比赛砍树 - 力扣（LeetCode）

解法：

算法思路：

a. 先找出砍树的顺序；

b. 然后按照砍树的顺序，一个一个的用 bfs 求出最短路即可。

class Solution {
public:int m, n;int cutOffTree(vector<vector<int>>& forest) {m = forest.size(), n = forest[0].size();//顺序vector<pair<int, int>> trees;for(int i = 0; i < m; ++i)for(int j = 0; j < n; ++j)if(forest[i][j] > 1) trees.push_back({i, j});sort(trees.begin(), trees.end(), [&](const pair<int, int>& p1, const pair<int, int>& p2){return forest[p1.first][p1.second] < forest[p2.first][p2.second];});int bx = 0, by = 0, ret = 0;for(auto& [a, b] : trees){int step = bfs(forest, bx, by, a, b);if(step == -1) return -1;ret += step;bx = a, by = b;}return ret;}bool vis[51][51];int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int bfs(vector<vector<int>>& forest, int bx, int by, int ex, int ey){if(bx == ex && by == ey) return 0;queue<pair<int, int>> q;memset(vis, 0, sizeof vis);q.push({bx, by});vis[bx][by] = true;int step = 0;while(q.size()){step ++;int sz = q.size();while(sz--){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; ++k){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && forest[x][y] && !vis[x][y]){if(x == ex && y == ey) return step;q.push({x, y});vis[x][y] = true;}}}}return -1;}
};