当前位置：首页 > news >正文

浅谈矩阵在机器学习线性回归算法中的数学推导

news 2025/9/21 13:29:09

线性回归算法

是机器学习中最基础、最经典的监督学习算法之一，核心思想是建立输入特征（自变量）与输出目标（因变量）之间的线性映射关系，用于解决回归类问题（预测连续型数值，如房价、销量、温度等）。

即：
$Y$ = $α1\alpha_1$ $X_1$ + $α2\alpha_2$ $X_2$ + $α3\alpha_3$ $X_3$ + … + $αn\alpha_n$ $X_n$

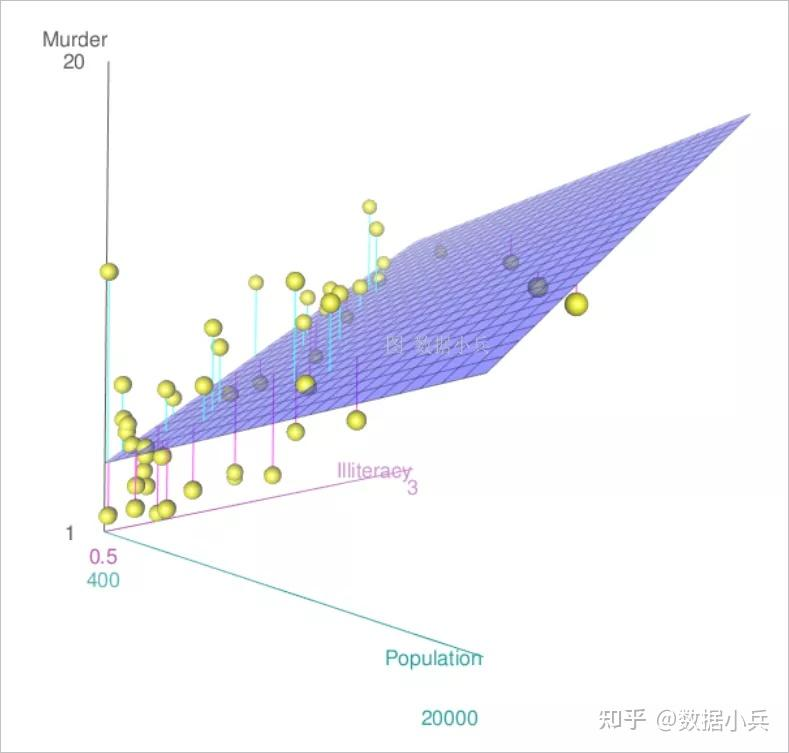
在这里插入图片描述
在机器学习中，我们往往可以获得大量数据集，

$($ $X_{11}$ , $X_{12}$ , $X_{13}$ , $Y_1$ $)$
$($ $X_{21}$ , $X_{22}$ , $X_{23}$ , $Y_2$ $)$
$($ $X_{31}$ , $X_{32}$ , $X_{33}$ , $Y_3$ $)$
$($ $X_{41}$ , $X_{42}$ , $X_{43}$ , $Y_4$ $)$
$($ $X_{51}$ , $X_{52}$ , $X_{53}$ , $Y_5$ $)$
…
$($ $X_{N1}$ , $X_{N2}$ , $X_{N3}$ , $Y_N$ $)$

若假定以上数据应满足线性回归，
则有：
$Y_1$ = $α11\alpha_{11}$ $X_{11}$ + $α12\alpha_{12}$ $X_{12}$ + $α13\alpha_{13}$ $X_{13}$ + … + $α1n\alpha_{1n}$ $X_{1n}$
$Y_2$ = $α21\alpha_{21}$ $X_{21}$ + $α22\alpha_{22}$ $X_{22}$ + $α23\alpha_{23}$ $X_{23}$ + … + $α2n\alpha_{2n}$ $X_{2n}$
$Y_3$ = $α31\alpha_{31}$ $X_{31}$ + $α32\alpha_{32}$ $X_{32}$ + $α33\alpha_{33}$ $X_{33}$ + … + $α3n\alpha_{3n}$ $X_{3n}$
…
$Y_N$ = $αN1\alpha_{N1}$ $X_{N1}$ + $αN2\alpha_{N2}$ $X_{N2}$ + $αN3\alpha_{N3}$ $X_{N3}$ + … + $αNn\alpha_{Nn}$ $X_{Nn}$

N 指数据集数量，
n 指自变量个数

上述方程组可以用矩阵来表示即为：

$\begin{bmatrix} X_{11} & X_{12} & X_{13} & X_{14} & ... & X_{1n} \\ X_{21} & X_{22} & X_{23} & X_{24} & ...& X_{2n} \\ X_{31} & X_{32} & X_{33} & X_{34} &...& X_{3n} \\ X_{41} & X_{42} & X_{43} & X_{44} &...& X_{4n} \\ ... & ... & ... & ... &... &...& \\ X_{N1} & X_{N2} & X_{N3} & X_{N4} &...& X_{Nn} \\ \end{bmatrix} \times \begin{bmatrix} \alpha_{1} \\ \alpha_{2} \\ \alpha_3 \\ \alpha_4 \\ ... \\ \alpha_n \\ \end{bmatrix} \ = \begin{bmatrix} Y_{1} \\ Y_{2} \\ Y_3 \\ Y_4 \\ ... \\ Y_n \\ \end{bmatrix}$

在尝试进行多元线性拟合的过程，就是一个简单的求点到直线/平面的最短距离的高中数学问题，即为求解当方程系数 $α\alpha$ 该为何值时，各个数据点距离直线\平面，或者说方程的距离之和最短。

即求：
$min||X\alpha - Y||^2 = min[V_1^2 + V_2^2 + V_3^2 + ... + Vn^2]$

所以对 J 求偏导
这里我们要注意，对于矩阵 $(Xα−Y)(X\alpha - Y)$ 其本质是一个列向量啊，
所以，求得上面的 J，只需要对列向量 $(Xα−Y)(X\alpha - Y)$ 进行一次内积，也就是：
$J=(Xα−Y)T(Xα−Y)=(αTXT−YT)(Xα−Y)=αTXTXα−αTXTY−YTXα+YTY\begin{align*}J &= (X\alpha - Y)^T(X\alpha - Y) \\&= (\alpha^TX^T - Y^T)(X\alpha - Y) \\&= \alpha^TX^TX\alpha - \alpha^TX^TY - Y^TX\alpha +Y^TY\end{align*}$

对 J 求偏导，当偏导=0时，即可得到极值 $min [J]$ 。
这里要用到三个矩阵求偏导的基础公式，见文章末尾。

$X^TX$ 必为对称阵，证明如下：对称阵即矩阵转秩等于矩阵本身 $X^TX)^T = X^TX$ ，
对于 $αTXTY\alpha^TX^TY$ 求偏导，很明显的， $[α1,α2,...αn]×[XTY][\alpha_1,\alpha_2, ... \alpha_n ] \times [X^TY]$ 其结果为标量，所以 $αT(XTY)=(XTY)Tα\alpha^T(X^TY) = (X^TY)^T\alpha$

$\frac{\partial J}{\partial \alpha} = 2X^TX\alpha - X^TY - X^TY + 0 = 0$
得： $X^TX\alpha = X^TY$

若 $X^TX$ 可逆，可得所求系数 $α=(XTX)−1XTY\alpha=(X^TX)^{-1}X^TY$

三个矩阵求偏导的基础公式，

$\alpha^T M \alpha$ $∂f∂α=2Mα\frac{\partial f}{\partial \alpha} = 2 M \alpha$
M 必须是对称矩阵 辅助记忆： $\alpha C \alpha$ $∂f∂α=2Cα\frac{\partial f}{\partial \alpha} = 2 C \alpha$ 证明： 若M是对称矩阵，此时我们才可以合并同类项，得到
$∂f∂α=2Mα\frac{\partial f}{\partial \alpha} = 2M\alpha$

$b^T \alpha$ $\frac{\partial f}{\partial \alpha} = b$ 证明：设： $\begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \end{bmatrix}$ $\alpha = \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \\ \alpha_4 \end{bmatrix}$ $b^T \alpha = b_1\alpha_1 + b_2\alpha_2 + b_3\alpha_3 + b_4\alpha_4$ $\frac{\partial f}{\partial \alpha} = \begin{bmatrix} b_1 \\ b_2 \\ b_3\\b_4 \end{bmatrix}$

对常量求偏导为0