【CF】Day146——杂题 (递归 | 规律与操作)

C. Mark and His Unfinished Essay

题目：

思路：

递归

看到如此巨大的 k 和 l r，显然不能暴力，因此考虑性质

可以想到一种递归的方式，因为后面的字符可以从前面转移过来，而这个转移的过程就很容易想到递归，但是就是有点不好写

我们定义 sum[i] 为执行到了第 i 次操作后的字符串长度，显然可以二分出第一个大于等于 k 的操作位置，然后根据这个进行转移，但是转移到哪呢？

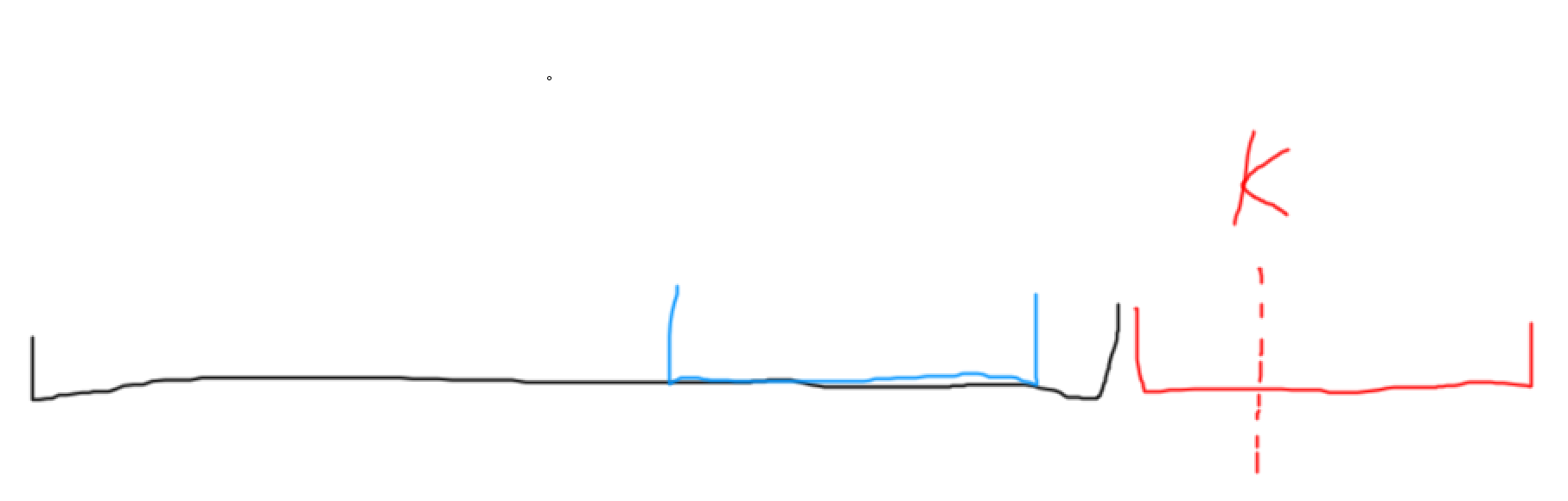
假设第一个大于等于 k 的区间是红色的操作区间，那么显然 k 的字符取决于上一次的操作区间，也就是如下图的蓝色部分

那么这个 k 的字符就对应着上一个操作的相对位置，即下图所示位置（绿色部分相同）

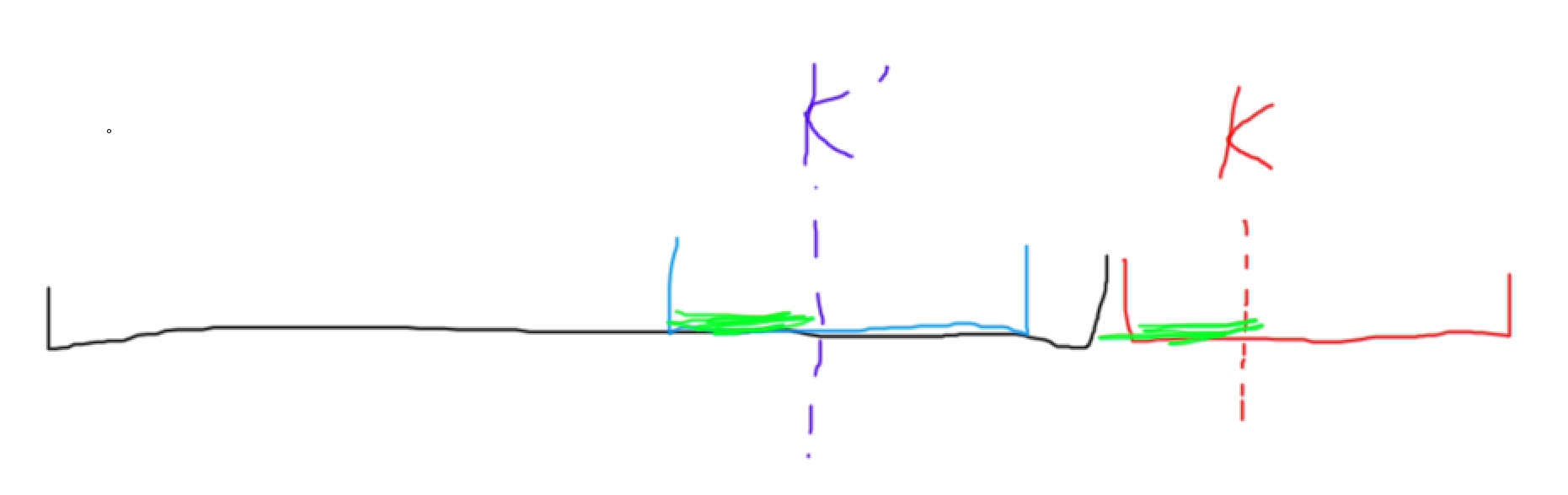
所以我们求出 k‘ 即可，然后不断递归到 1 ~ n 内即可

不难发现，k’ 的大小就是  (l[i] - 1) + (k - sum[i - 1])，这是显然的

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n,c,q;cin >> n >> c >> q;string s;cin >> s;s = ' ' + s;vector<int> sum(c+1,0);sum[0] = n;vector<int> l(c+1),r(c+1);for (int i = 1; i <= c; i++){cin >> l[i] >> r[i];sum[i] = sum[i-1] + r[i] - l[i] + 1;}auto query = [&](auto && self,int k)->int{if(k <= n)return k;auto index = lower_bound(sum.begin(),sum.end(),k) - sum.begin();int nk = k - sum[index - 1] + l[index] - 1;return self(self,nk);};while (q--){int k;cin >> k;cout << s[query(query,k)] << endl;}
}signed main()
{cin.tie(0)->sync_with_stdio(0);int t = 1;cin >> t;while (t--){solve();}return 0;
}

---

D. Magical Array

题目：

思路：

经典的找特征

参考：CodeTON Round 2 (Div. 1 + Div. 2, Rated, Prizes!) A~F - 知乎

还是熟悉的讨论，遇到操作类型的题目就是找规律，这一次的规律比较难找

如果注意力惊人，我们可以发现前缀和 pre[i] 满足以下特征

所以对于普通数组其 pre[i] 之和不变，但是特殊数组的 pre[i] 明显是减少的，且每次减少 1

因此求出 pre[i] 和最小的即可，操作数就是与普通数组的 pre[i] 的和之差

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n,m;cin >> n >> m;vector<int> sum(n);for (int i = 0; i < n; i++){int x = 0,s = 0;for (int j = 1; j <= m; j++){cin >> x;s += x;sum[i] += s;}}int mx = -1e18;for (int i = 0; i < n; i++){mx = max(mx,sum[i]);}int index = -1;for (int i = 0; i < n; i++){if(sum[i] != mx){index = i;break;}}cout << index + 1 << " " << mx - sum[index] << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(0);int t = 1;cin >> t;while (t--){solve();}return 0;
}