【记录】初赛复习 Day5 6(2021S第一轮错题,内附深井题目讲解)
我自己复习初赛的记录,是这个网站:
信息学奥赛-NOIP-少儿编程培训-有道小图灵 (youdao.com)
做初赛降低我的素质。
7.
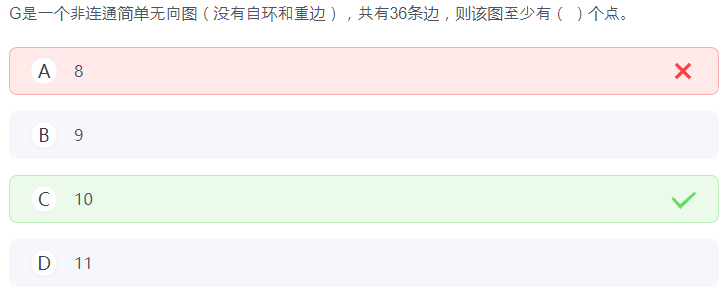

蠢,眼瞎了两次。
10.

虽然但是我小时候很疑惑,交换相邻元素为什么会和逆序对有关系?
因为每次交换,最多可以消除一个逆序对。
16.

做这道的时候脑子被门夹了,pi / 3 都没反应过来,acos(-1) 才是 pi。
(我刚升初三真不知道什么是球体积交。)

解释:
球冠(Spherical Cap):当一个平面切割球体时,截取的较小部分称为球冠。

这个公式硬背就可以了。
关于怎么求出这个 h:
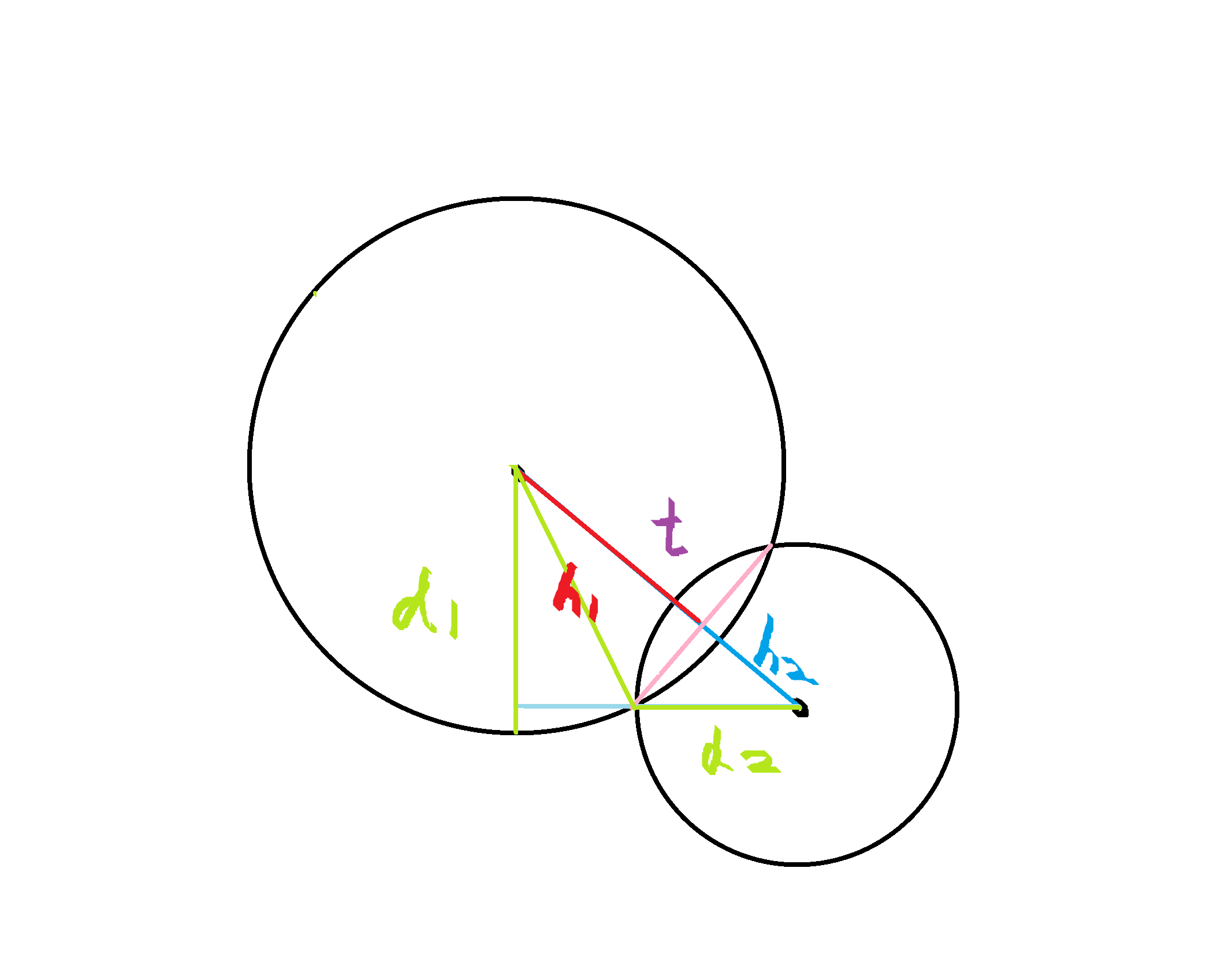
(我这里设半径 - 第一个球球冠的高为 h1,半径 - 第二个球球冠的高为 h2,t = h1 + h2)
根据勾股定理:
求出 h1:
半径再减掉 h1 就是球冠的高了。
注释代码:
#include<bits/stdc++.h>
using namespace std;// 数学常量:r = π/3
// 用于计算球体体积:(4 / 3) πR^3 = 4 * r * R^3
const double r = acos(0.5);int a1, b1, c1, d1;
int a2, b2, c2, d2;inline int sq(const int x) { return x * x; } // 平方函数
inline int cu(const int x) { return x * x * x; } // 立方函数int main() {// 保留 4位小数cout.flags(ios::fixed);cout.precision(4);cin >> a1 >> b1 >> c1 >> d1;cin >> a2 >> b2 >> c2 >> d2;// 存储两个球体的参数:// (a1, b1, c1) = 第一个球体的球心坐标,d1 = 半径// (a2, b2, c2) = 第二个球体的球心坐标,d2 = 半径int t = sq(a1 - a2) + sq(b1 - b2) + sq(c1 - c2);// 计算两球心之间距离的平方// 情况 1:一个球体完全包含在另一个球体内if (t <= sq(d2 - d1)) {cout << cu(min(d1, d2)) * r * 4;// 输出较小球体的体积:(4/3)πR3 = 4*r*R3}// 情况 2:两个球体完全分离(无交集)else if (t >= sq(d2 + d1)) {// 交集体积为 0cout << 0;}// 情况 3:两个球体部分相交else {// 计算球冠高度公式推导:// x = 第一个球体的球冠高度// y = 第二个球体的球冠高度double x = d1 - (sq(d1) - sq(d2) + t) / sqrt(t) / 2;double y = d2 - (sq(d2) - sq(d1) + t) / sqrt(t) / 2;// 计算相交部分体积(两个球冠体积之和):// 球冠体积公式 = πh^2(3R - h)/3 // 代入 r = π/3 后简化为:h^2(3R - h) * rcout << (x * x * (3 * d1 - x) + y * y * (3 * d2 - y)) * r;}cout << endl;return 0;
}17.
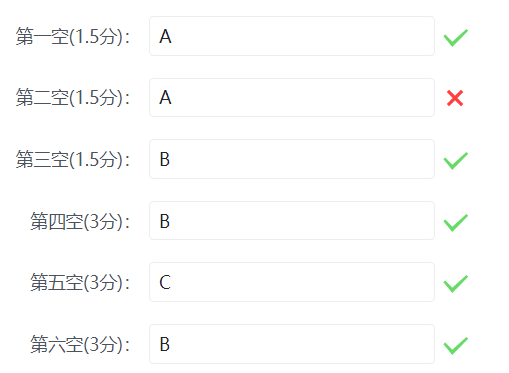
没啥好说的,分治求最大子段和。
第二题:除非开始的时候 n ≤ 0 会执行一次,否则一次也不会执行。
18.

全场最恶心转码解码题。
找张大点的草稿纸直接打表,当然真正考试直接蒙就行了。
时间太久了不值得。
第一题:将字符串解密后可能会出现 \n ,那就不只一行了。
我的意识流过程:
base
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51a b c d e f g h i j k l m n o p q r s t u v w x y z52 53 54 55 56 57 58 59 60 610 1 2 3 4 5 6 7 8 962 63+ /ASCLL
65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 123a b c d e f g h i j k l m n o p q r s t u v w x y z48 49 50 51 52 53 54 55 56 57 0 1 2 3 4 5 6 7 8 91 SGVsbG93b3JsZASGVs
18 6 21 441001011010101101100(下面按位或没有重合 1 直接加就好)
1001000 | 0 = 1001000 = (18 * 4) = 72 = H
1100000 | 101 = (6 * 16) + 5 = 101 = e
10101000000 | 101100 = 1010101101100 = 01101100 = l (强制转换成char会取后8位)bG93
27 6 61 55111001101111011101111110000 | 0 = 1110000 = (27 * 4) = 108 = l
1100000 | 1111 = (6 * 16) + 15 = 111 = o
111101000000 | 110111 = 111101110111 = 01110111 = 119 = w
(小写 w 选 F) 0 CSP2021csp
p ==
Q1NQMjAyMWNzcA==
Q1NQMjAyMGNzcA==
1cs
1 = 49 = 110001 = 1100 = 12 = M
c = 99 = 1100011 = 110
110001 & 11 = 010000 | 110 = 10110 = 22 = W
(W 选 D)
19.
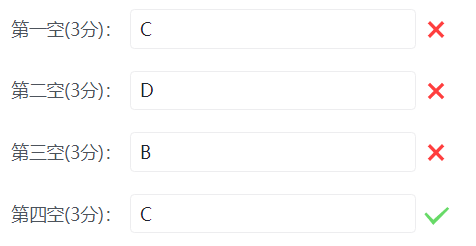
我一点招都没有了。

那个私人 r 合着没卵用啊?
20.
没学过,反正没在考模拟,先去学 RMQ 了。
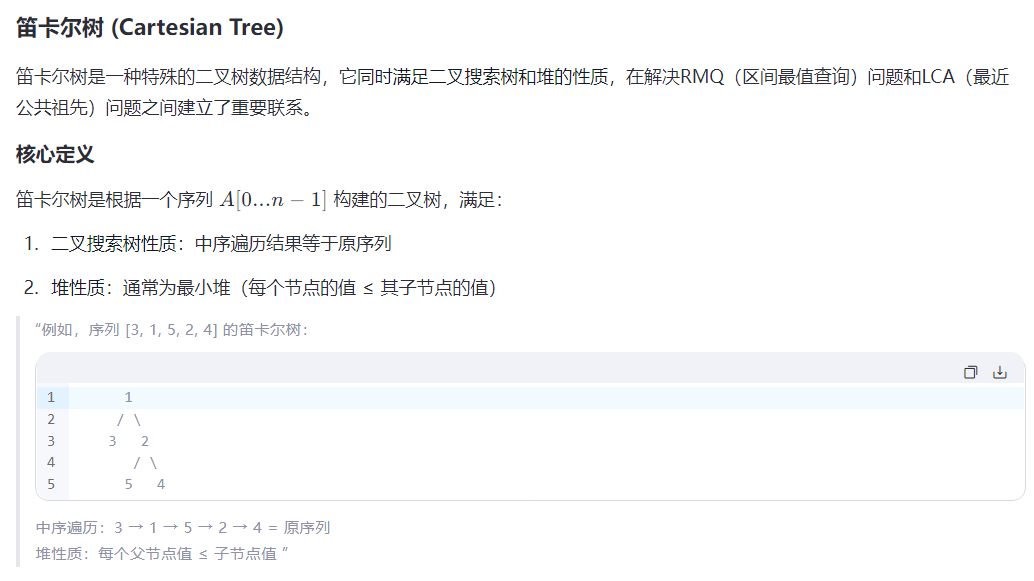
#include<bits/stdc++.h>
using namespace std;/* * 算法背景:* 这是一个理论最优的RMQ(区间最小值查询)实现,采用"笛卡尔树+欧拉环游+混合RMQ"方案* * 三步转化过程:* 1. RMQ -> LCA:通过构建笛卡尔树,将原数组RMQ问题转化为树上的LCA问题* 2. LCA -> RMQ:通过欧拉环游,将LCA问题转化为新序列上的RMQ问题* 3. RMQ优化:使用分块+ST表+位运算的混合策略解决新RMQ问题* * 复杂度:O(n)预处理时间,O(1)查询时间(理论最优)*/// 常量定义
const int MAXN = 100000, MAXT = MAXN << 1; // MAXT = 2*MAXN (欧拉环游序列最大长度,每个节点访问两次)
const int MAXL = 18, MAXB = 9, MAXC = MAXT / MAXB; // 分块参数struct node {int val; // 原始数组中的值int dep; // 在笛卡尔树中的深度(根节点深度为0)int dfn, end; // 欧拉环游中首次/末次出现的位置索引node *son[2]; // son[0]=左子树,son[1]=右子树
} T[MAXN];/** 全局变量说明:* n: 原始数组大小* t: 欧拉环游序列的实际长度(约2n-1)* b: 每个块的大小(理论最优值为log?n/2)* c: 块的总数量* Log2: 预处理的log?值数组,用于快速计算* Pos: 预处理的块内最小值位置表(关键优化)* Dif: 块内深度变化的位掩码表示* root: 笛卡尔树的根节点* A: 欧拉环游序列(核心数据结构)* Min: 块级稀疏表(ST表),Min[i][j]表示从第j块开始、长度为2^i的块区间中的最小值节点*/
int n, t, b, c, Log2[MAXC + 1];
int Pos[(1 << (MAXB - 1) + 5)], Dif[MAXC + 1];
node *root, *A[MAXT], *Min[MAXL][MAXC]; /** 笛卡尔树构建函数* * 笛卡尔树特性:* 1. 中序遍历结果等于原数组* 2. 是一个最小堆(但本代码实现的是最大堆,这是个潜在问题)* - 注意:对于RMQ问题,应该构建最小堆笛卡尔树* - 但代码中比较是`<`,构建的是最大堆,这可能导致结果错误* * 构建原理:* 使用单调栈算法,维护一个递减栈(因为是最大堆)* 对于新元素:* - 弹出栈中所有比它小的元素,这些元素成为新元素的左子树* - 新元素成为栈顶元素的右子树* * 为什么笛卡尔树能解决RMQ?* 原数组区间[l,r]的最小值对应笛卡尔树中节点l和r的LCA* (严格来说,对于最小堆笛卡尔树,LCA的值就是区间最小值)*/
void build() {static node *S[MAXN + 1]; // 用于构建的栈(静态分配提高效率)int top = 0;for (int i = 0; i < n; i ++) {node *p = &T[i];// 弹出栈中比当前值小的节点(这些节点将成为当前节点的左子树)while (top && S[top]->val < p->val) {p->son[0] = S[top--]; // 将栈顶节点作为当前节点的左子节点}// 当前节点成为栈顶节点的右子树if(top) {S[top]->son[1] = p;}S[++top] = p;}root = S[1]; // 栈底元素为最大值,作为根节点
}/** 欧拉环游遍历(生成DFS序列)* * 目的:将LCA问题转化为RMQ问题* * 欧拉环游特性:* - 每次进入节点和离开子树时都记录当前节点* - 节点u和v的LCA对应序列中u.dfn到v.dfn之间深度最小的节点* - 序列长度约为2n-1* * 例如,对于树:* 1* / \* 2 3* 欧拉环游序列为:[1, 2, 1, 3, 1]* * 关键性质:* 查询节点2和3的LCA,对应序列中位置1到3之间的最小深度节点(即位置2的节点1)*/
void DFS(node *p) {A[p->dfn = t++] = p; // 记录首次访问位置(dfn)for (int i = 0; i < 2; i ++) {if (p->son[i]) {p->son[i]->dep = p->dep + 1; // 子节点深度比父节点大1DFS(p->son[i]);A[t++] = p; // 返回父节点时再次记录(完成子树遍历)}} p->end = t - 1; // 记录末次访问位置(用于某些应用,本算法中未直接使用)
}/** 比较两个节点的深度(用于RMQ)* 返回深度较小的节点(即LCA候选)*/
node *min(node *x, node *y) {return x->dep < y->dep ? x : y;
}/** 初始化块级稀疏表(ST表)* * 混合RMQ策略的第一部分:处理块间查询* * 步骤:* 1. 计算最优块大小 b = ceil(log?t / 2)* - 为什么是log?n/2?这是理论最优值,平衡块内和块间处理开销* 2. 将序列分成c = t/b个块* 3. 预处理Log2数组,用于快速计算log?值* 4. 构建块级ST表:* - Min[0][i] = 第i块内的最小值节点* - Min[k][i] = 从第i块开始、长度为2^k的块区间中的最小值节点* * ST表查询原理:* 任何区间[l,r]可以表示为两个重叠区间的交集:* [l, l+2^k-1] 和 [r-2^k+1, r],其中k = log?(r-l+1)* 由于深度序列的特性,重叠不影响最小值结果*/
void ST_init() {b = (int) (ceil(log2(t) / 2)); // 计算理论最优块大小c = t / b; // 计算总块数Log2[1] = 0;// 预处理对数数组(用于快速计算log2)for (int i = 2; i <= c; i ++) {Log2[i] = Log2[i >> 1] + 1;}// 计算每块内的最小值(块级RMQ的基石)for (int i = 0; i < c; i ++) {Min[0][i] = A[i * b]; // 初始化为块首元素for (int j = 1; j < b; j ++) {// 更新块内最小值Min[0][i] = min(Min[0][i], A[i * b + j]);}}// 构建块级稀疏表(ST表)// Min[i][j] = min(Min[i-1][j], Min[i-1][j+2^(i-1)])for (int i = 1, l = 2; l <= c; i ++, l <<= 1) {for (int j = 0; j + l <= c; j ++) {Min[i][j] = min(Min[i - 1][j], Min[i - 1][j + (l >> 1)]);}}
}/** 块内预处理(位运算优化)- 混合RMQ策略的第二部分* * 核心思想:利用深度序列的特殊性质进行优化* * 深度序列特性:* - 相邻位置的深度差只能是+1或-1(因为是树的DFS序列)* - 块内深度变化只取决于相对变化模式,而非绝对深度* * 优化原理:* 1. 对于大小为b的块,有b-1个深度变化,每个变化是+1或-1* 2. 这些变化可以用一个b-1位的位掩码表示(1表示-1,0表示+1)* 3. 共有2^(b-1)种可能的模式,当b = log?n/2时,2^(b-1) = O(√n)* 4. 预处理所有可能模式的最小值位置,查询时直接查表* * 实现步骤:* 1. Dif[i]:记录第i块中深度下降的位置(位掩码)* 2. Pos[S]:预处理每种模式S的最小值位置(相对块起始位置的偏移)*/
void small_init() { // 为每个块生成差异位图for (int i = 0; i < c; i ++) { // 修正:应该是i < c,而非i <= cfor (int j = 1; j < b && i * b + j < t; j ++) {// 如果当前位置深度小于前一位置,表示深度下降if (A[i * b + j]->dep < A[i * b + j - 1]->dep) { Dif[i] |= 1 << (j - 1); // 设置对应位为1}}}// 预处理所有可能的块结构(共2^(b-1)种)for (int S = 0; S < (1 << (b - 1)); S ++) {int mx = 0, v = 0; // mx记录最小相对深度,v是当前相对深度for (int i = 1; i < b; i ++) {// 解码位掩码:1表示深度下降(-1),0表示深度上升(+1)v += (S >> (i - 1) & 1) ? -1 : 1;// 如果当前相对深度小于历史最小值,更新最小值位置if (v < mx) {mx = v;Pos[S] = i; // 记录最小值位置(相对块起始位置的偏移)}}}
}/** 块级ST表查询(查询多个完整块的最小值)* * 原理:使用ST表在O(1)时间内查询* 对于区间[l, r](块索引):* k = log?(r-l+1)* 返回 min(Min[k][l], Min[k][r-2^k+1])*/
node *ST_query(int l, int r) {int g = Log2[r - l + 1]; // 计算k值return min(Min[g][l], Min[g][r - (1 << g) + 1]);
}/** 块内查询(利用预处理的位掩码)* * 步骤:* 1. 确定所在块p = l/b* 2. 提取子区间[l, r]对应的位掩码S* - (Dif[p] >> (l - p*b)):将位掩码对齐到子区间起点* - & ((1 << (r-l)) - 1):只保留子区间长度的位* 3. 通过Pos[S]查表得到最小值位置(相对l的偏移)*/
node *small_query(int l, int r) {int p = l / b;// 提取子块对应的位掩码int S = (Dif[p] >> (l - p * b)) & ((1 << (r - l)) - 1);return A[l + Pos[S]];
}/** 混合RMQ查询(主查询函数)* * 处理三种情况:* 1. l和r在同一块内:直接使用small_query* 2. l和r在相邻块内:分别查询两端,取最小值* 3. l和r间隔多个块:* a. 查询左端不完整块(l到pl块末尾)* b. 查询右端不完整块(pr块开头到r)* c. 查询中间完整块(pl+1到pr-1),使用ST_query* d. 取三者最小值*/
node *query(int l, int r) {if (l > r) {return query(r, l); // 确保l <= r}int pl = l / b, pr = r / b; // 计算l和r所在的块索引if (pl == pr) {return small_query(l, r); // 单块查询}else {// 查询两端不完整块的最小值node *s = min(small_query(l, pl * b + b - 1), small_query(pr * b, r));// 查询中间完整块的最小值(如果存在)if (pl + 1 <= pr - 1) {s = min(s, ST_query(pl + 1, pr - 1));}return s;}
}int main() {ios::sync_with_stdio(false);cin.tie(0);int m;cin >> n >> m;for (int i = 0; i < n; i++) {cin >> T[i].val;}// 算法执行流程:// 1. 构建笛卡尔树(将RMQ转为LCA)build();// 2. 生成欧拉环游序列(将LCA转为新的RMQ问题)t = 0; // 重置欧拉序列计数器root->dep = 0; // 设置根节点深度为0DFS(root); // 生成欧拉环游序列// 3. 初始化RMQ数据结构ST_init(); // 初始化块级ST表small_init(); // 块内位运算预处理while (m --) {int l, r;cin >> l >> r;/** 查询解释:* 1. T[l].dfn和T[r].dfn是节点l和r在欧拉序列中的位置* 2. query(T[l].dfn, T[r].dfn)找到这两个位置间的最小深度节点* 3. 这个节点就是T[l]和T[r]在笛卡尔树中的LCA* 4. LCA节点的值就是原数组[l, r]区间内的最小值* * 注意:由于代码构建的是最大堆笛卡尔树,这里应该取最大值而非最小值* 正确做法应该是构建最小堆笛卡尔树(比较符应为>)*/cout << query(T[l].dfn, T[r].dfn)->val << "\n";}return 0;
}