当前位置：首页 > news >正文

模型进阶与神经网络

news 2025/9/21 9:36:37

模型进阶与神经网络

下面进一步分析数据特点，对函数重新定义（构建新的模型），同时对之前论述的损失、问题求解等步骤做进一步规范。

构造模型主要包含两个方向：

引入激活函数增加非线性：从线性模型扩展到非线性模型
扩充特征个数：增加输入特征的维度

方向一：引入激活函数增加非线性

线性模型的局限性

如果模型定义为一个或多个输入特征 $x$ 乘上对应权重，再加上一个偏置，这种模型称为线性模型（linear model），根据输入特征的个数，可以分为一元或多元线性模型。

线性模型往往导致预测结果和前一天的特征 $x$ 成一定比例，比如前一天观看量越大，预测的第二天结果也越大。但实际中可能存在周天至周四观看量很高，但是周五、周六观看量较低的周期性变化，所以线性模型无法模拟真实情况，这称为线性模型的偏差（model bias）。

观看量数据变化是一个复杂的连续曲线，类似下图。然而，任何连续曲线可以由分段线性曲线拟合，所以可以将预测观看量问题转化为如何拟合一个分段线性曲线（piecewise linear curve），并由此设计一个更优的模型。

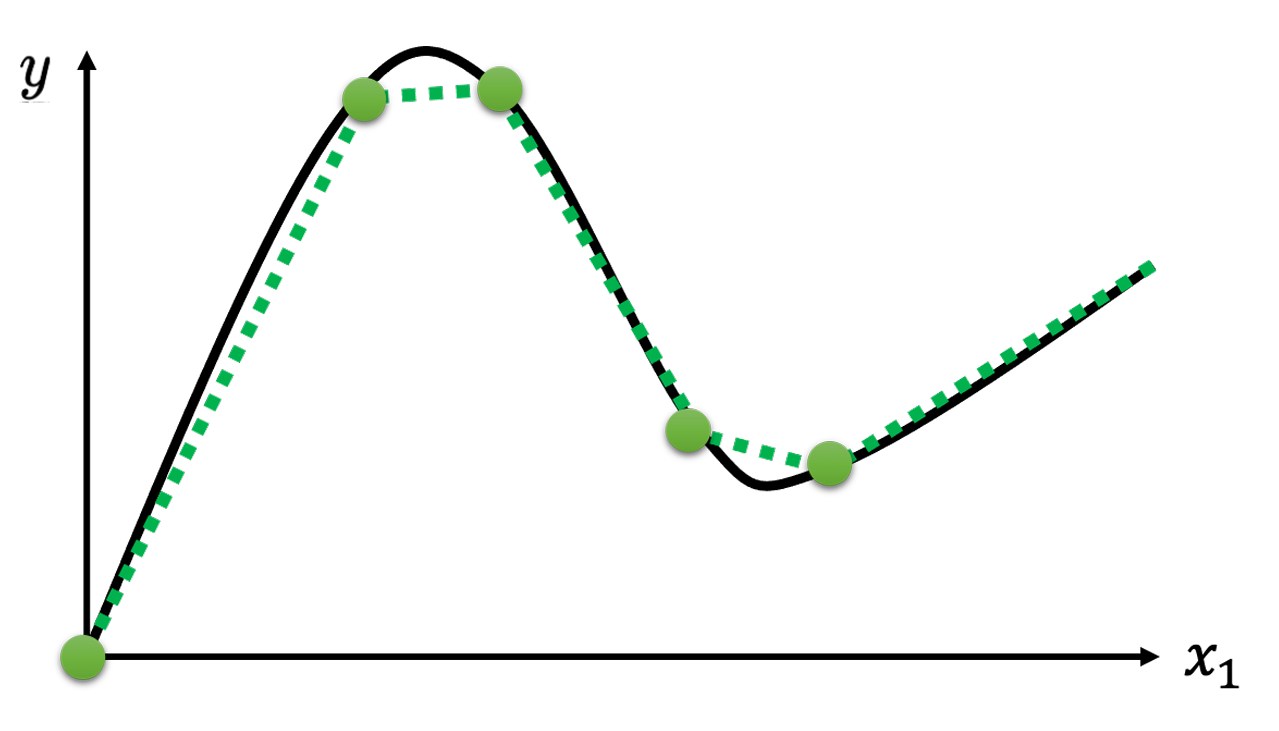
分段线性函数拟合

如下图所示，红色的为一个分段线性曲线，蓝色的为常数和一组hard sigmoid。根据每段区间上各曲线的斜率，可以看出蓝色基本可以拟合出红色的分段线性曲线。

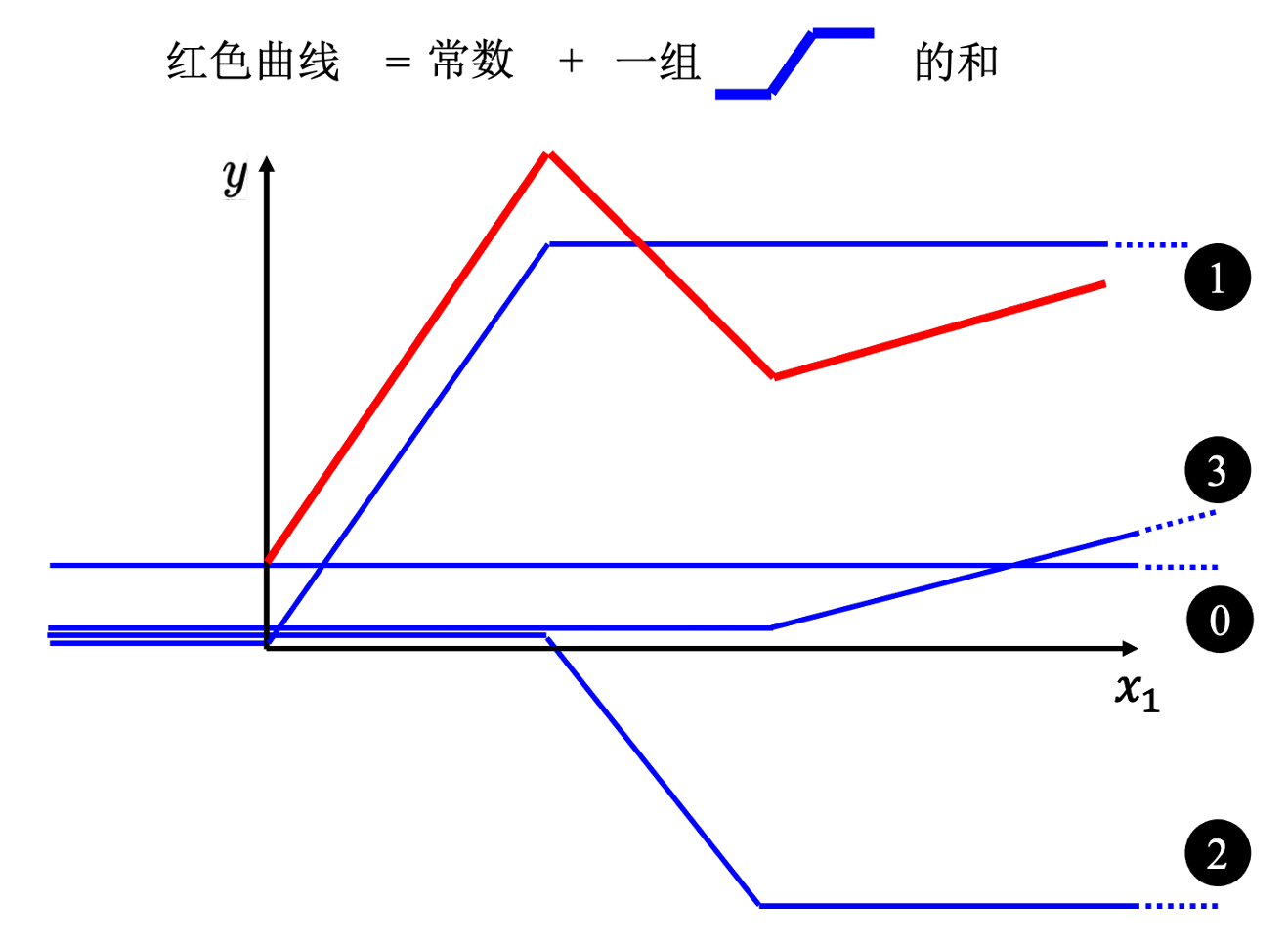
因此，可以得出结论：任意曲线 ≈ 分段线性曲线 = 常数 + 一组hard sigmoid。

sigmoid 与 hard sigmoid

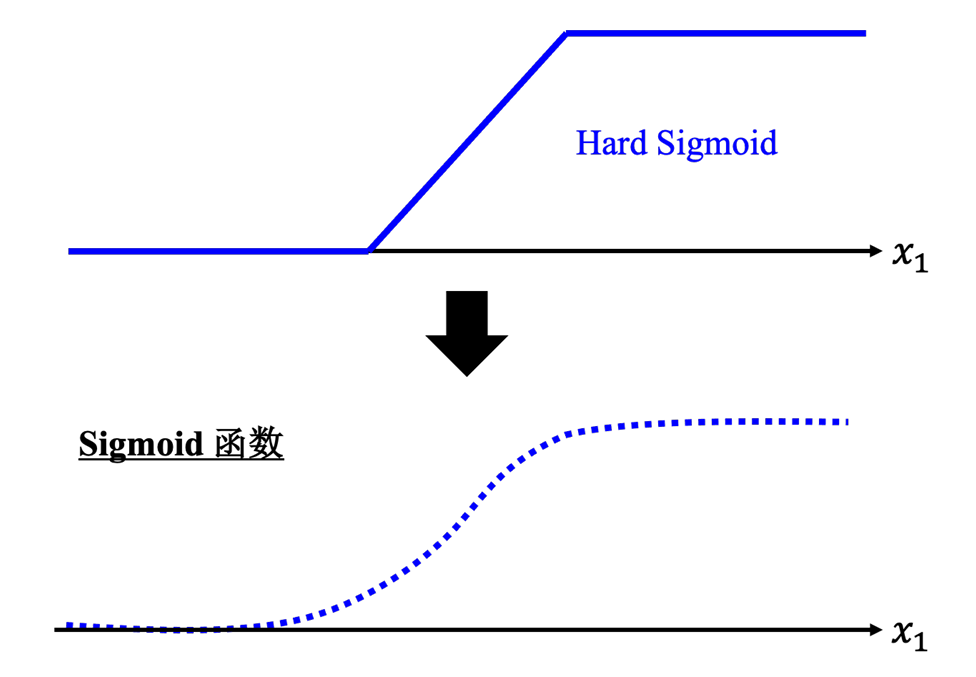
hard sigmoid 是一个分段函数，数学表达式形如： $y = ma x (0, min (1, (x + 1) /2))$ ，难以写出简洁的函数表达式，且不易计算梯度值。所以，通常采用 sigmoid 来代替 hard sigmoid，sigmoid 函数表达式为：

$\frac{1}{1+e^{wx+b}} = c \sigma(wx+b)$

上式中， $c$ 影响高度， $w$ 影响斜线的斜率， $b$ 影响 $x$ 轴平移位置。

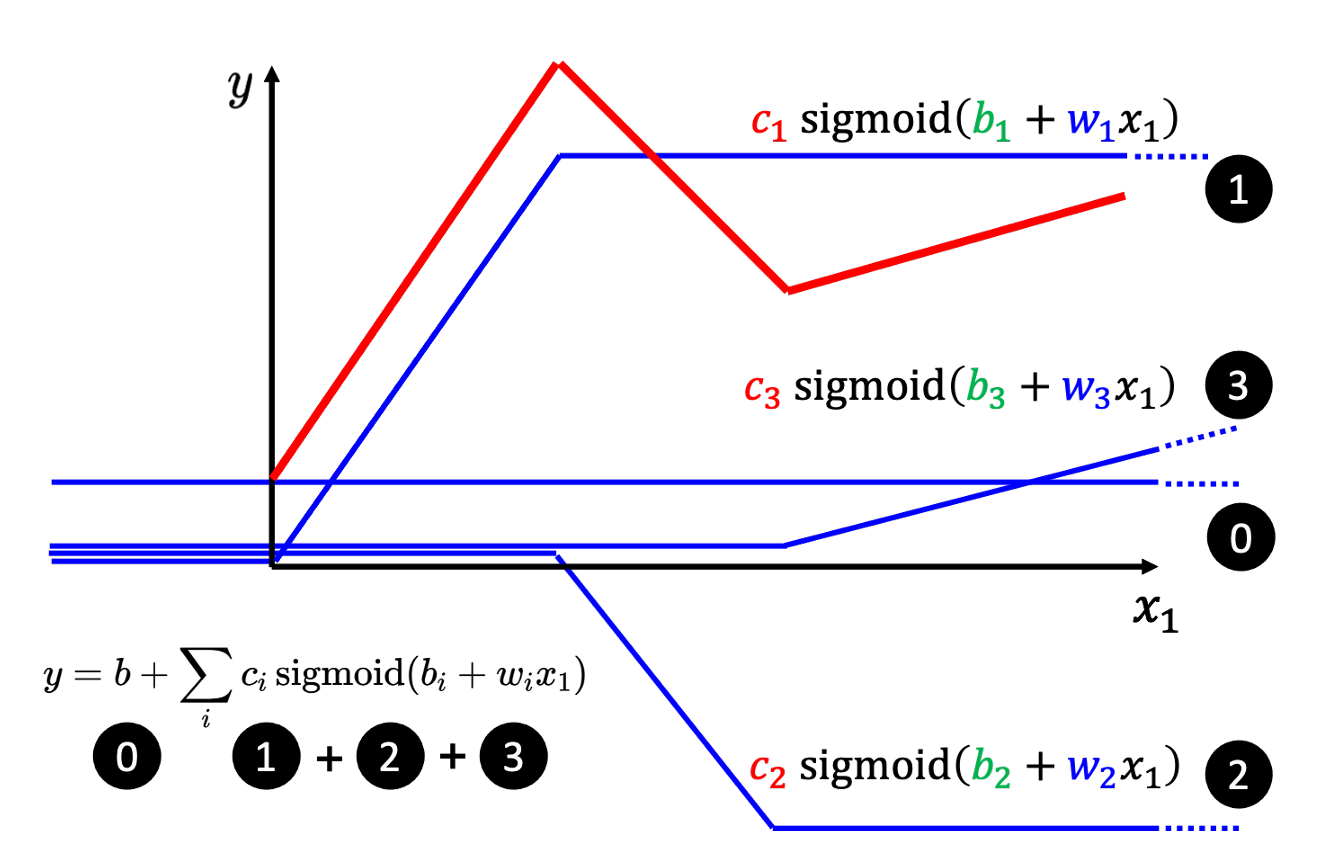
一般的，任一分段线性曲线可以写出数学表达式： $\sum_{i} c_i \sigma(b_i+w_i x)$

ReLU 与 hard sigmoid

表征 hard sigmoid 还可以使用 Rectified Linear Unit(ReLU)，ReLU 函数的一般表达式为： $y = ma x (0, x)$ 。

一般的，一个 hard sigmoid 函数需要使用两个 ReLU 来表示。下图直观展示，ReLU 和 hard sigmoid 的关系。其中，红色的 hard sigmoid，可以使用绿色的、由两个 ReLU 表示函数来表示。

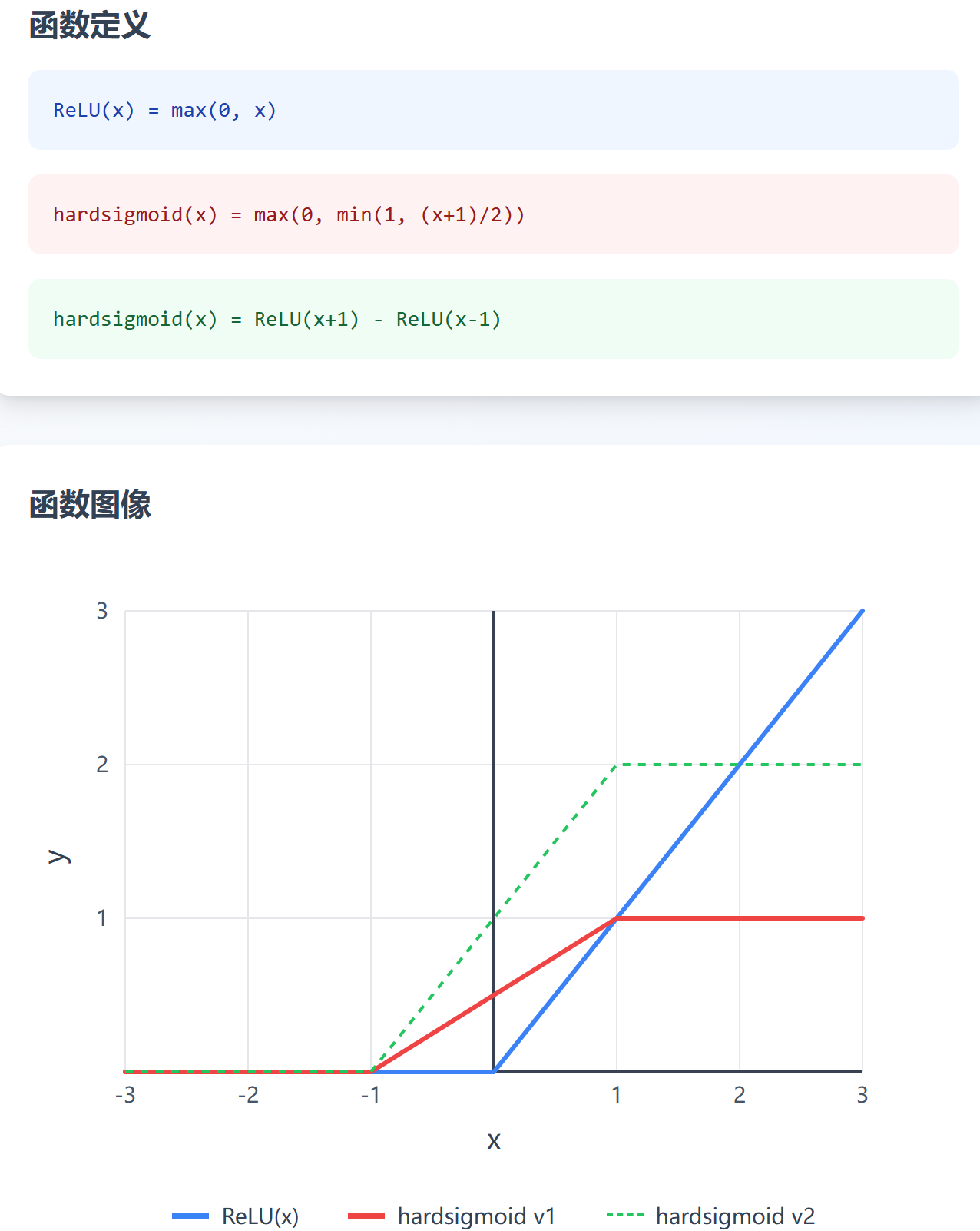
通常来说，使用 ReLU 来拟合分段线性函数，会使模型性能更优：

计算效率极高：ReLU 的操作极其简单：max(0, x)，这只是一个比较和一个选择操作
梯度消失问题：ReLU 在正区间梯度恒为1，避免了sigmoid函数的梯度消失问题
实现简单：相比hard sigmoid需要多个条件判断，ReLU的实现更加直接

方向二：扩充特征个数

上面是引入激活函数，将模型从线性模型扩展为非线性模型，从而增强了模型的灵活性（flexible）。

考虑可能多天前的视频观看量数据可能会影响未来一天的观看量，比如存在以周、月、季度的周期变化，所以下面考虑从输入特征个数出发改进模型。

对于 $s i g m o i d$ 函数来说，只能接收一个数值作为输入，如果增加多个特征作为输入，一个自然的想法是对多个特征做线性组合。第 $i$ 个sigmoid的输入为： $ri=bi+wi1x1+wi2x2+...wijxj+...=bi+∑jwijxjr_i=b_i+w_{i1}x_1+w_{i2}x_2+...w_{ij}x_j+...=b_i+\sum_j{w_{ij}x_j}$ ，其中， $x_j$ 是第 $j$ 个特征，表示前 $j$ 天的观看量。

最终模型表达式为：
$y=b+\sum_i{a_i}=b+\sum{\sigma(r_i)}=b+\sum_i{c_i*\sigma(b_i+\sum_j{w_{ij}x_j})}$

矩阵表示形式（以 $i = 3$ 为例）：

$[c_1, c_2, c_3] \cdot sigmoid( \left[\begin{array}{l} b_1 \\ b_2 \\ b_3 \end{array}\right]+\left[\begin{array}{lll} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \end{array}\right] \times\left[\begin{array}{l} x_1 \\ x_2 \\ x_3 \end{array}\right] ) \\ y=b+\vec{C}^{\top} \cdot \operatorname{sigmoid}(\vec{b}+ \mathbf{W} \vec{x})$

模型进阶总结

通过引入激活函数或增加特征个数，可以让模型具有更强的表征能力。

单个特征的形式：
$\rightarrow b+\sum_i{c_i*\sigma(b_i+w_i x)}$

多个特征的形式：
$y=b+∑jwijxj→b+∑ici∗σ(bi+∑jwijxj)y=b+\sum_j{w_{ij}x_j} \rightarrow b+\sum_i{c_i*\sigma(b_i+\sum_j{w_{ij}x_j})}$

优化求解的矩阵形式

定义损失

令 $θ={W,b,cT⃗,b⃗}=[θ1θ2θ3⋮]\boldsymbol{\theta}=\{W, b, \vec{c^T}, \vec{b}\}=\left[\begin{array}{c} \theta_1 \\ \theta_2 \\ \theta_3 \\ \vdots \end{array}\right]$ ，损失函数为 $L(θ)L(\boldsymbol{\theta})$ 。目标是找到一组使得损失值最小的一组 $θ\boldsymbol{\theta}$ ，称为 $θ∗\boldsymbol{\theta}^*$ 。

梯度下降

初始化： $θ0\boldsymbol{\theta}^0$

第一轮参数更新：
$\begin{gathered} \boldsymbol{g_0}=\nabla L\left(\boldsymbol{\theta}_0\right) = \left[\begin{array}{c} \left.\frac{\partial L}{\partial \theta_1}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_0} \\ \left.\frac{\partial L}{\partial \theta_2}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_0} \\ \vdots \end{array}\right] \end{gathered}$

$\boldsymbol{\theta_1} = \left[\begin{array}{c} \theta_1^1 \\ \theta_1^2 \\ \vdots \end{array}\right] = \boldsymbol{\theta_0} - \eta \boldsymbol{g_0}= \left[\begin{array}{c} \theta_0^1 \\ \theta_0^2 \\ \vdots \end{array}\right]-\left[\begin{array}{c} \left.\eta \frac{\partial L}{\partial \theta_1}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_0} \\ \left.\eta \frac{\partial L}{\partial \theta_2}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_0} \\ \vdots \end{array}\right]$

第二轮参数更新：
$\begin{gathered} \boldsymbol{g_1}=\nabla L\left(\boldsymbol{\theta}_1\right) = \left[\begin{array}{c} \left.\frac{\partial L}{\partial \theta_1}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_1} \\ \left.\frac{\partial L}{\partial \theta_2}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_1} \\ \vdots \end{array}\right] \end{gathered}$

$\boldsymbol{\theta_2} = \left[\begin{array}{c} \theta_2^1 \\ \theta_2^2 \\ \vdots \end{array}\right] = \boldsymbol{\theta_1} - \eta \boldsymbol{g_1}= \left[\begin{array}{c} \theta_1^1 \\ \theta_1^2 \\ \vdots \end{array}\right]-\left[\begin{array}{c} \left.\eta \frac{\partial L}{\partial \theta_1}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_1} \\ \left.\eta \frac{\partial L}{\partial \theta_2}\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_1} \\ \vdots \end{array}\right]$

在进行迭代时，会将数据划分成若干份，每份数据称为一个批量（batch），模型会计算在每个批量上的损失，然后更新（update）参数，再计算在下一个批量上的损失，在所有批量上更新完一轮称为一个回合（epoch）。

从模型到神经网络的理解

基于前面关于模型改进的讨论，可以引出对神经网络的理解。

神经元的概念

在前面的模型中，我们使用了 sigmoid 或 ReLU 等激活函数来处理输入的多个特征。这些激活函数对输入进行非线性变换的部分，在神经网络中被称为神经元（neuron）。

每个神经元的基本结构包括：

输入：接收来自前一层或多个特征的信息
线性变换：对输入进行加权求和： $r_i=b_i+w_{i1}x_1+w_{i2}x_2+...w_{ij}x_j+...$
激活函数：对线性变换结果进行非线性处理： $ai=σ(ri)a_i = \sigma(r_i)$ 或 $a_i = ReLU(r_i)$

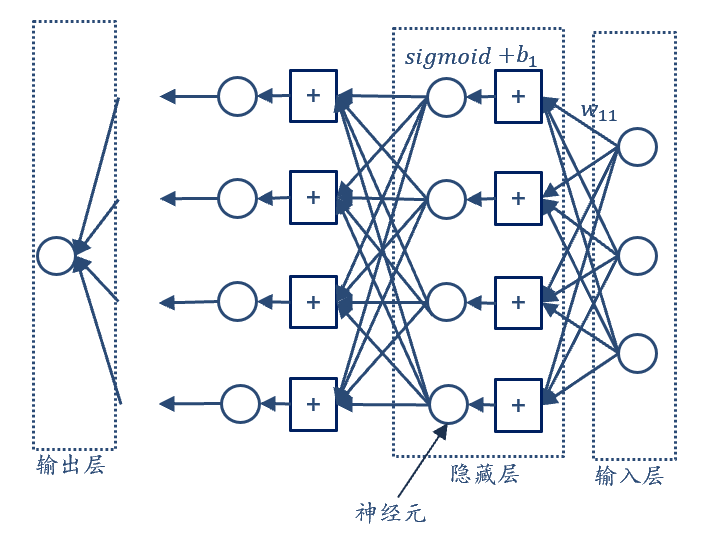
神经网络的结构

当我们将多个神经元按照一定的结构组织起来时，就形成了神经网络（neural network）：

输入层：接收原始特征数据
隐藏层：包含多个神经元，对输入进行非线性变换
输出层：产生最终的预测结果

每一层中的神经元都接收来自前一层所有神经元的输出，经过自己的处理后再传递给下一层。

深度学习的含义

当神经网络包含多个隐藏层时，就形成了深度学习（deep learning）。层数越多，网络的"深度"越大，模型的表达能力也越强。

模型训练与评估

假设训练集为： ${(x^1, y^1), (x^2, y^2), ...(x^N, y^N)\}$ ，测试集为： ${x^{N+1}, x^{N+2}, ...\}$

模型定义为： $y=fθ(x)y=f_{\boldsymbol{\theta}}(x)$ ，其中 $θ\boldsymbol{\theta}$ 表示模型中的所有参数

损失函数定义为： $L(θ)L(\boldsymbol{\theta})$

最优的参数组合为： $θ∗=arg⁡min⁡L(θ)\boldsymbol{\theta}^*=\arg\min L(\boldsymbol{\theta})$

最终训练好的模型为： $y=fθ∗(x)y=f_{\boldsymbol{\theta}^*}(x)$ ，将测试集作为输入，即可得到模型对测试集的预测结果

数据集划分

一般的，会将数据集划分为训练集、验证集、测试集。

其中，训练集作用是训练模型，调整模型的参数；验证集作用是评估不同模型的性能并选择模型；测试集作用是对模型做最终的性能评估。

数据集划分方式一般为：首先将整个数据集按照 8:2 的比例，划分为训练集和测试集，然后对 80% 的训练集按照 8:2 的比例进一步划分为训练集和验证集。也即，训练集：验证集：测试集为64%：16%：20%。

模型评估

竞赛中数据集划分

一般竞赛中会有两个测试集，一个是公开榜排名中的测试集（public testing data），另一个是在竞赛结束后用于测试模型的私有测试集（private testing data）。如果过度关注公开榜的测试集来修改模型，可能会影响在private testing data中的结果。竞赛结果的评价，会根据模型在公开榜和私榜结果综合评价，但是往往私榜的权重会更大。

所以在竞赛中，会划分数据集为训练、验证、测试，分别对应竞赛中的公开数据集、公开榜测试集、私榜测试集

k折交叉验证（k-fold cross validation）

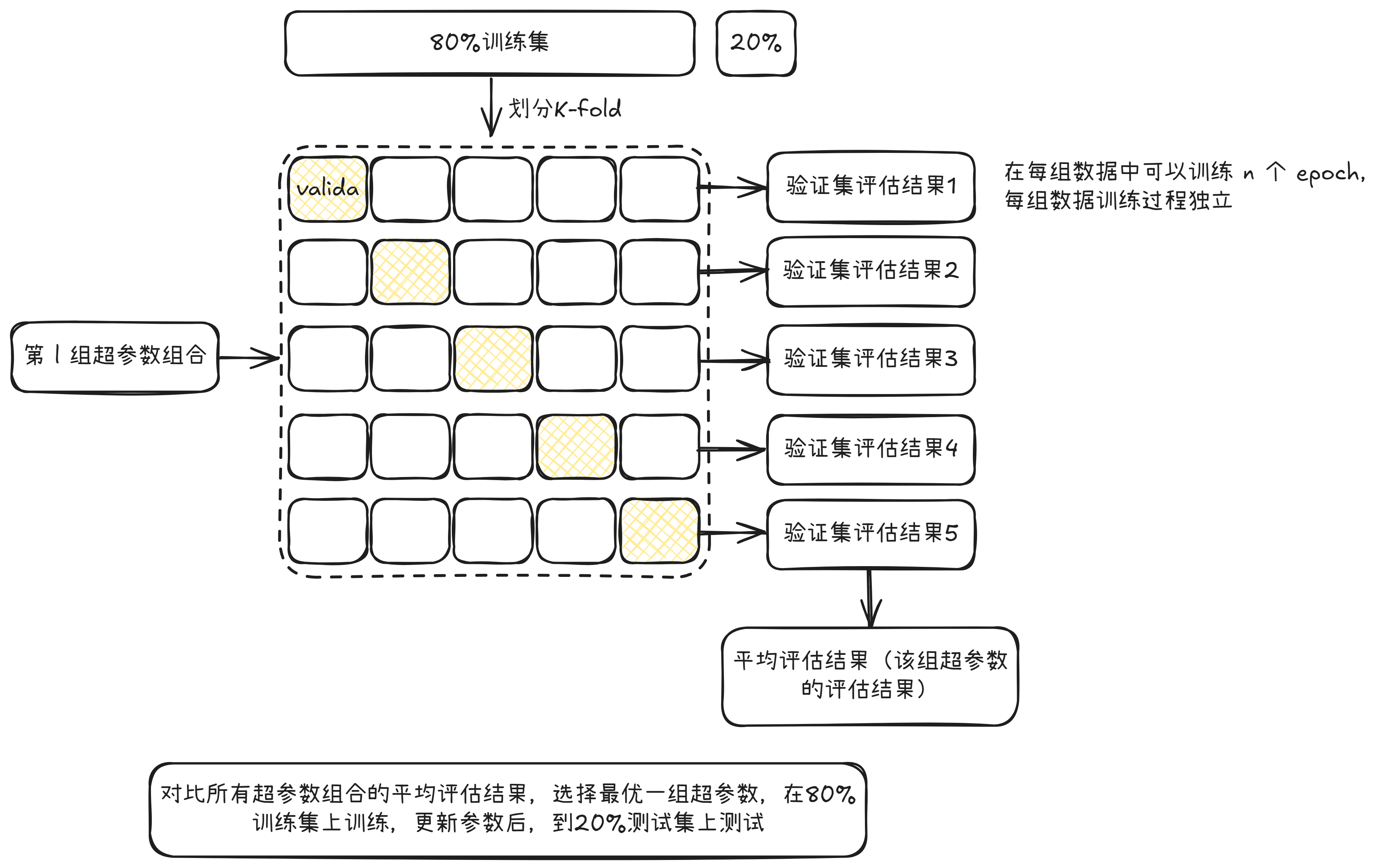
步骤：假设当前只有训练集和验证集，将训练集划分成 $k$ 份，取第 $1$ 份作为验证集，取后面 $k - 1$ 份作为训练集，模型在 $k - 1$ 份数据上训练特定的轮数（epoch），然后在验证集上评估，得到验证集上的损失值。然后取第 $2$ 份作为验证集，取剩下 $k - 1$ 作为训练集，得到在这一组数据下的损失值。计算 $k$ 份验证集的平均指标值作为该组参数下模型的指标。然后基于相同的步骤评估其他组参数下模型的指标，直到评估完所有的模型。选出最优模型后，基于全量的训练集做最终的训练，然后在测试集上获得评估指标。