pcl封装11 （快速定义）旋转矩阵

这个封装是为更好更快的进行组合。

分为绕xyz三个轴旋转的矩阵函数，和一个平移函数。

做一个案例进行快速的演示，代码用起来真的是一行搞定

目的：我们做一个矩阵满足点云绕z轴旋转45度，然后再平移（1,1,0）

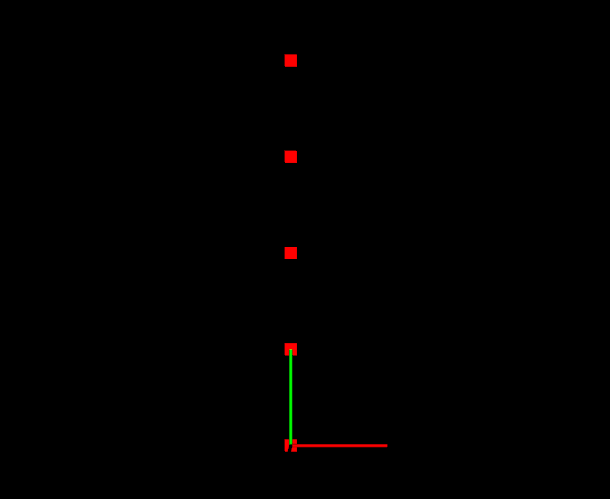
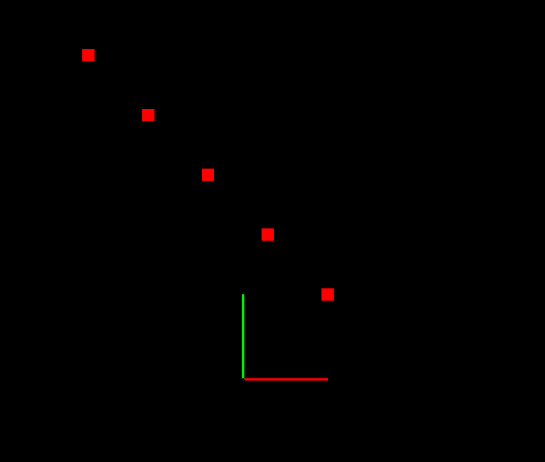
展示一下我的代码：超级方便

int main ()
{pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);cloud->push_back(pcl::PointXYZ(0, 0, 0));cloud->push_back(pcl::PointXYZ(0, 1, 0));cloud->push_back(pcl::PointXYZ(0, 2, 0));cloud->push_back(pcl::PointXYZ(0, 3, 0));cloud->push_back(pcl::PointXYZ(0, 4, 0));show_pointcloud<pcl::PointXYZ>(cloud, 12, 1);Eigen::Matrix4f trans_pose = Eigen::Matrix4f::Identity();trans_pose = matrix_trans({1, 1, 0}) * rotateZ(3.1415926 * 0.25) * trans_pose;pcl::transformPointCloud(*cloud, *cloud, trans_pose);show_pointcloud<pcl::PointXYZ>(cloud, 12, 1);return 0;
}

下面是矩阵的4个封装函数。它们主要用在了这一行，只用一行实现了旋转矩阵的定义

trans_pose = matrix_trans({1, 1, 0}) * rotateZ(3.1415926 * 0.25) * trans_pose;

//旋转矩阵
Eigen::Matrix4f rotateX(float angle_rad=3.14)
{Eigen::Matrix4f rot = Eigen::Matrix4f::Identity();float cos_a = cos(angle_rad);float sin_a = sin(angle_rad);rot(1, 1) = cos_a;rot(1, 2) = -sin_a;rot(2, 1) = sin_a;rot(2, 2) = cos_a;return rot;
};Eigen::Matrix4f rotateY( float angle_rad = 3.14)
{Eigen::Matrix4f rot = Eigen::Matrix4f::Identity();float cos_a = cos(angle_rad);float sin_a = sin(angle_rad);rot(0, 0) = cos_a;rot(0, 2) = sin_a;rot(2, 0) = -sin_a;rot(2, 2) = cos_a;return rot;
}Eigen::Matrix4f rotateZ( float angle_rad = 3.14)
{Eigen::Matrix4f rot = Eigen::Matrix4f::Identity();float cos_a = cos(angle_rad);float sin_a = sin(angle_rad);rot(0, 0) = cos_a;rot(0, 1) = -sin_a;rot(1, 0) = sin_a;rot(1, 1) = cos_a;return  rot;
}Eigen::Matrix4f matrix_trans(Eigen::Vector3f translation = { 1,1,1 })
{Eigen::Matrix4f rot = Eigen::Matrix4f::Identity();rot.block<3,1>(0,3) = translation;return  rot;
}