当前位置：首页 > news >正文

2.0、机器学习-数据聚类与分群分析

news 2025/9/21 7:54:04

聚类是机器学习中无监督学习的一种重要技术，旨在将数据集中的样本分成若干个组（簇），使得同一组内的样本相似度较高，而不同组的样本相似度较低，以下是常见的两种聚类算法。

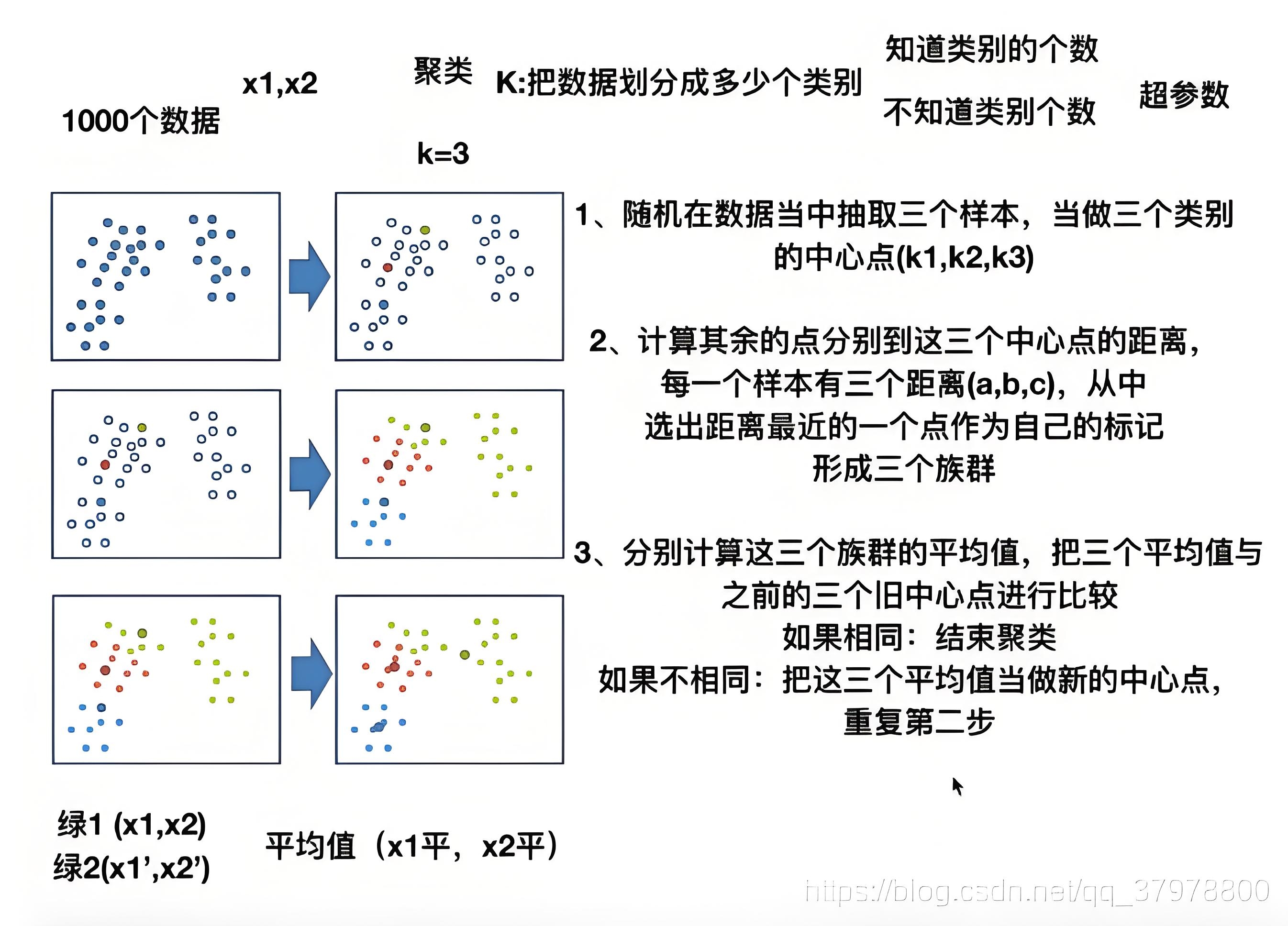
1、KMeans算法介绍

除了前面介绍的各种监督学习算法，在只有特征变量，没有目标变量的情况下，我们还可以通过聚类的方式来分析问题。比如对银行卡的申请人进行客户分群，对新闻进行分类等。

K-Means法（又称K-均值算法），是非监督学习下常用的一种聚类算法，核心思想是将数据点分配到k个簇中，使簇内数据点距离最⼩化。

K代表类别的数量
Means代表每个类的样本均值，

该算法通过不断迭代更新中心点，并重新分配数据点的方式，实现对数的聚类操作，如下是K-Means聚类构建过程：

1.1、实现案例

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt# ⽣成合成聚类数据
X, y = make_blobs(n_samples=10000,n_features=2,centers=4, # 4个聚类中⼼cluster_std=0.2, # 簇内标准差center_box=(-10.0, 10.0),random_state=0
)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)# 可视化原始数据分布
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.scatter(X_train[:, 0], X_train[:, 1], alpha=0.6)
plt.title('原始数据分布')
plt.xlabel('特征1')
plt.ylabel('特征2')
# K-Means聚类
kmeans = KMeans(n_clusters=4, random_state=0)
kmeans.fit(X_train) # ⽆监督学习，不需要标签
# 可视化聚类结果
plt.subplot(1, 2, 2)
plt.scatter(X_train[:, 0], X_train[:, 1], alpha=0.6)
plt.scatter(kmeans.cluster_centers_[:, 0],kmeans.cluster_centers_[:, 1],marker='*', s=200, c='red', label='聚类中⼼'
)
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']   
plt.rcParams['axes.unicode_minus'] = False  
plt.title('K-Means聚类结果')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend()
plt.tight_layout()
plt.show()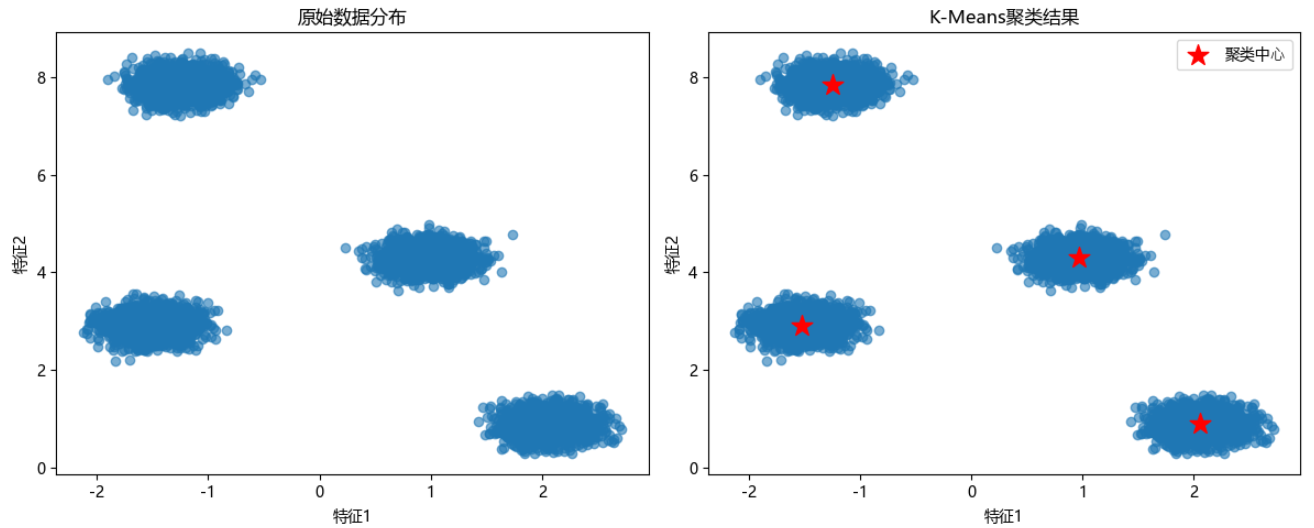

2、DBSCAN密度聚类算法

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种以密度为基础的空间聚类算法，可以用密度的概念剔除不属于任一类别的噪声点。

2.1、实现案例

import numpy as np
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt# 生成示例数据（半月形数据）
X, _ = make_moons(n_samples=300, noise=0.05, random_state=0)# 应用DBSCAN聚类
dbscan = DBSCAN(eps=0.3, min_samples=5) # eps是邻域半径，min_samples是形成核心对象的最小点数
labels = dbscan.fit_predict(X)# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.title('DBSCAN聚类结果')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.show()# 统计聚类结果
n_clusters = len(set(labels)) - (1 if -1 in labels else 0)
n_noise = list(labels).count(-1)print(f'估计的聚类数量: {n_clusters}')
print(f'估计的噪声点数量: {n_noise}')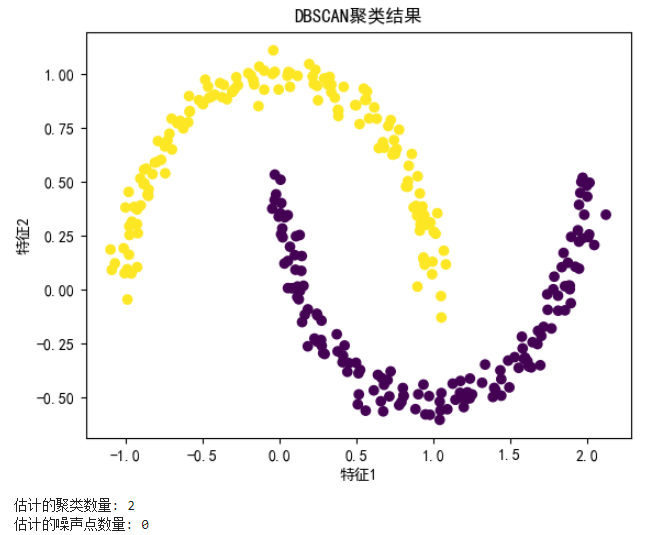

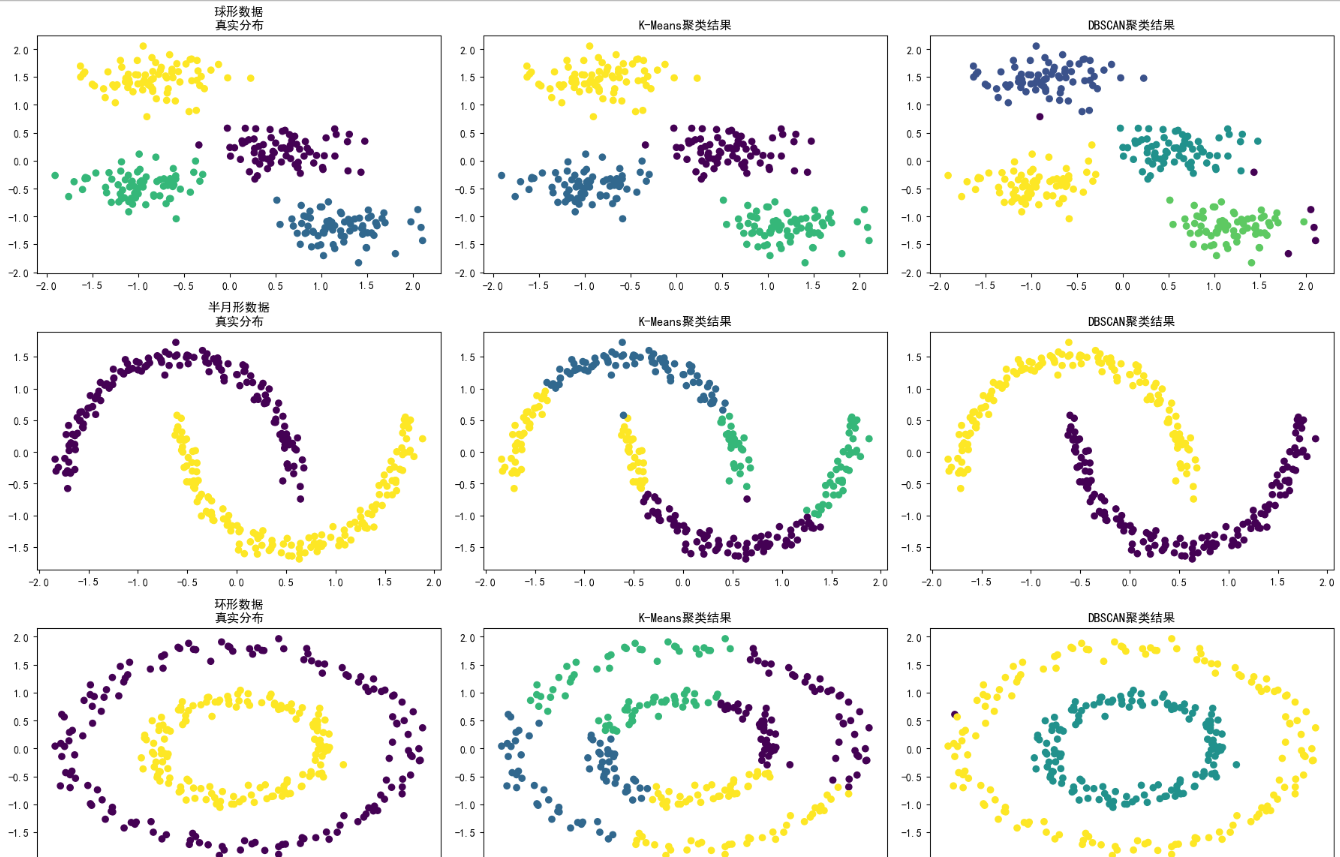
3、Kmeans和DBSCAN比较

特性维度	K-Means	DBSCAN
核心原理	基于质心。通过最小化簇内平方误差，将数据划分成K个球形簇。	基于密度。通过识别高密度区域并将其与低密度区域分离来发现任意形状的簇。
聚类形状	只能发现球形或凸形的簇。对非球形簇效果很差。	能发现任意形状的簇（如半月形、环形、条形）。
噪声处理	非常敏感。离群点会显著影响质心的位置，从而影响整个聚类结果。	非常鲁棒。能 explicitly（明确地）识别出噪声点/离群点，并将其标记为 `-1`。
所需参数	必须预先指定簇的数量 K。	需要指定邻域半径 (ε) 和最小点数 (MinPts)。不需要指定簇的数量。
簇的密度	假设所有簇的密度大致相同。	能够处理密度不同的簇。
数据分布假设	适用于凸数据集（各向同性）。	适用于非凸数据集。
算法输出	每个点都必须属于某一个簇。	将点分为三类：核心点、边界点、噪声点。
计算复杂度	相对较低，通常为 *O(n K * I * d)，其中 I 是迭代次数。计算效率高，适用于大规模数据集**。	最坏情况下可达 O(n²)，但在使用空间索引（如KD树、球树）后可优化至 O(n log n)。对大规模数据可能较慢。
结果稳定性	受初始质心影响，多次运行结果可能不一致。通常需要运行多次（`n_init`）取最优。	稳定。结果由数据和参数 (ε, MinPts) 决定，与运行顺序无关。