当前位置：首页 > news >正文

LeetCode算法领域的经典题目之“三数之和”和“滑动窗口最大值”问题

news 2025/9/21 7:26:25

在这里插入图片描述

🧑 博主简介：CSDN博客专家、CSDN平台优质创作者，高级开发工程师，数学专业，10年以上C/C++, C#,Java等多种编程语言开发经验，拥有高级工程师证书；擅长C/C++、C#等开发语言，熟悉Java常用开发技术，能熟练应用常用数据库SQL server,Oracle,mysql,postgresql等进行开发应用，熟悉DICOM医学影像及DICOM协议,业余时间自学JavaScript,Vue,qt,python等，具备多种混合语言开发能力。撰写博客分享知识，致力于帮助编程爱好者共同进步。欢迎关注、交流及合作，提供技术支持与解决方案。\n技术合作请加本人wx（注明来自csdn）：xt20160813

在这里插入图片描述

一、前言摘要

“三数之和”和“滑动窗口最大值”是LeetCode算法领域的经典题目，分别涉及数组组合查找和动态窗口处理，在医学影像AI中有广泛应用，如特征匹配、像素值配对和时间序列分析。本文以LeetCode 15（三数之和）和LeetCode 239（滑动窗口最大值）为核心，基于Python实现暴力解法、优化解法，并扩展到医学影像场景（如LUNA16数据集的3D特征匹配和时间序列CT分析）。内容涵盖问题描述、解题原理、详细代码、复杂度分析、优化策略、流程图，以及在DICOM影像处理中的应用案例。本文特别关注算法在医学影像中的挑战（如高维数据、实时性、噪声干扰），提出优化方案，并探讨算法在特征提取、病灶检测和诊断中的扩展应用，为算法学习者和医学影像AI从业者提供理论与实践的全面指导。

二、项目概述

2.1 项目目标

功能：
- 三数之和：在数组中找到所有和为目标值（默认0）的三个数组合，返回唯一的三元组。
- 滑动窗口最大值：在固定窗口内找到每个窗口的最大值，返回最大值序列。
- 医学影像应用：适配特征匹配（三数之和）和时间序列分析（滑动窗口最大值）。
意义：
- 算法基础：掌握数组操作、双指针、单调队列等核心技术。
- 医学影像应用：支持特征匹配、病灶定位、时间序列分析。
- 实时性：优化算法以满足临床低延迟需求。
- 可扩展性：扩展到3D影像或多模态数据处理。
目标：
- 实现三数之和的暴力解法和双指针解法，比较性能。
- 实现滑动窗口最大值的暴力解法和单调队列解法，比较性能。
- 扩展到医学影像场景（如LUNA16数据集的特征匹配和CT序列分析）。
- 优化算法性能，降低时间和空间复杂度。
- 提供性能可视化（运行时间、内存占用）。
- 探讨算法在医学影像AI中的应用（如肺结节检测、时间序列诊断）。

2.2 数据背景

三数之和（LeetCode 15）：
- 输入：整数数组 nums。
- 输出：所有和为0的唯一三元组 [nums[i], nums[j], nums[k]]，满足 i != j != k。
- 约束：
  - 数组长度 $n$ 范围： $\leq n \leq 3000$ 。
  - 元素范围： $−105≤nums[i]≤105-10^5 \leq nums[i] \leq 10^5$ 。
  - 结果不能包含重复三元组。
- 医学影像场景：
  - 特征匹配：在ViT或U-Net提取的特征向量中，寻找和为目标值的三元特征组合（如肺结节特征配对）。
  - 像素值配对：在DICOM影像中，寻找HU值和为目标值的三像素组合。
滑动窗口最大值（LeetCode 239）：
- 输入：整数数组 nums 和窗口大小 k。
- 输出：每个窗口的最大值序列。
- 约束：
  - 数组长度 $n$ 范围： $\leq n \leq 10^5$ 。
  - 元素范围： $−104≤nums[i]≤104-10^4 \leq nums[i] \leq 10^4$ 。
  - 窗口大小： $\leq k \leq n$ 。
- 医学影像场景：
  - 时间序列分析：在CT序列中，分析固定时间窗口内的最大HU值（如肺结节变化检测）。
  - 特征提取：在特征序列中，提取窗口内的最大特征值。
挑战：
- 高维数据：3D影像需分块或降维处理。
- 实时性：临床诊断要求低延迟算法。
- 噪声干扰：像素值或特征可能包含伪影。
- 数据规模：医学影像数据量大，需高效算法。

2.3 技术栈

Python：实现三数之和和滑动窗口最大值算法。
NumPy：处理高维数组（如3D CT影像）。
PyTorch/MONAI：提取影像特征，适配医学影像处理。
Matplotlib/Chart.js：可视化算法性能（时间、内存）。
pydicom：读取DICOM影像。
scikit-learn：分析特征重要性。
Mermaid：绘制算法流程图。
Docker：可选容器化部署，适配云端推理。

2.4 算法在医学影像AI中的意义

三数之和：
- 特征匹配：在ViT/U-Net提取的特征中，寻找和为目标值的三元特征组合，辅助肺结节分类。
- 像素值配对：在DICOM影像中，寻找HU值和为目标值的三像素组合，定位病灶。
滑动窗口最大值：
- 时间序列分析：在CT序列中，提取窗口内的最大HU值，检测肺结节变化。
- 特征提取：在特征序列中，提取窗口内的最大特征值，优化诊断模型。
实时性：高效算法满足临床诊断的低延迟需求。

三、算法原理

3.1 三数之和（3Sum）

3.1.1 问题描述

给定一个整数数组 nums，找到所有满足 nums[i] + nums[j] + nums[k] == 0 的三元组，返回唯一的三元组列表。

示例：

输入：nums = [-1, 0, 1, 2, -1, -4]
输出：[[-1, -1, 2], [-1, 0, 1]]

3.1.2 解题思路

暴力解法

原理：三重循环遍历所有三元组，检查和是否为0。
步骤：
1. 使用三重循环遍历 i, j, k。
2. 如果 nums[i] + nums[j] + nums[k] == 0，记录三元组。
3. 使用集合去重，确保结果唯一。
时间复杂度： $O(n^3)$ ，三重循环。
空间复杂度： $O (1)$ ，不计输出空间。
缺点：效率低，不适合医学影像大数据量场景。

双指针解法

原理：排序数组后，固定一个元素，使用双指针寻找剩余两个元素。
步骤：
1. 对数组排序，时间复杂度 $\log n)$ 。
2. 遍历固定元素 nums[i]，在剩余数组中使用双指针 left 和 right：
  - 如果 nums[i] + nums[left] + nums[right] == 0，记录三元组。
  - 如果和小于0，left += 1；如果和大于0，right -= 1。
3. 跳过重复元素，避免重复三元组。
时间复杂度： $O(n^2)$ ，排序 $\log n)$ ，双指针 $O (n)$ 。
空间复杂度： $O (1)$ ，不计排序空间。
适用场景：高效，适合医学影像特征匹配。

3.1.3 医学影像适用性

特征匹配：在ViT/U-Net提取的特征向量中，寻找和为目标值的三元特征组合。
像素值配对：在DICOM影像中，寻找HU值和为目标值的三像素组合。
3D扩展：分块处理3D CT影像，适配肺结节检测。

3.2 滑动窗口最大值

3.2.1 问题描述

给定一个整数数组 nums 和窗口大小 k，返回每个窗口的最大值序列。

示例：

输入：nums = [1, 3, -1, -3, 5, 3, 6, 7], k = 3
输出：[3, 3, 5, 5, 6, 7]

3.2.2 解题思路

暴力解法

原理：对每个窗口，遍历窗口内元素，找到最大值。
步骤：
1. 遍历每个窗口（从索引 0 到 n-k）。
2. 对窗口内 k 个元素，计算最大值。
3. 记录最大值序列。
时间复杂度： $\cdot k)$ ，每个窗口需 $O (k)$ 。
空间复杂度： $O (1)$ ，不计输出空间。
缺点：效率低，不适合医学影像大数据量。

单调队列解法

原理：使用双端队列维护窗口内可能的最大值，保持队列单调递减。
步骤：
1. 初始化双端队列，存储元素索引。
2. 遍历数组：
  - 移除队列中超出窗口的索引。
  - 移除队列尾部小于当前元素的值（保持单调递减）。
  - 将当前索引加入队列。
  - 如果窗口已满（i >= k-1），记录队列头部（最大值）。
时间复杂度： $O (n)$ ，每个元素入队出队一次。
空间复杂度： $O (k)$ ，队列存储最多 $k$ 个索引。
适用场景：高效，适合医学影像时间序列分析。

3.2.3 医学影像适用性

时间序列分析：在CT序列中，提取窗口内最大HU值，检测肺结节变化。
特征提取：在特征序列中，提取窗口内最大特征值，优化诊断模型。
实时性：单调队列高效，满足临床低延迟需求。

3.3 算法挑战

高维数据：3D影像需分块或降维处理。
实时性：临床诊断要求低延迟算法。
噪声干扰：像素值或特征可能包含噪声，需预处理。
可扩展性：需支持多目标匹配或动态窗口大小。

四、算法实现

4.1 三数之和（3Sum）

4.1.1 暴力解法

流程图

graph TDA[输入: nums] --> B[初始化结果: res = []]B --> C[遍历 i = 0 to n-1]C --> D[遍历 j = i+1 to n-1]D --> E[遍历 k = j+1 to n-1]E --> F{nums[i] + nums[j] + nums[k] == 0?}F -->|是| G[添加 [nums[i], nums[j], nums[k]] 到 res]F -->|否| EG --> H[去重: 排序+集合]H --> I[输出结果]

说明：

A：输入整数数组。
B：初始化空结果列表。
C-E：三重循环遍历三元组。
F-G：检查和是否为0，记录三元组。
H-I：去重并输出结果。

代码实现

def three_sum_brute_force(nums: list[int]) -> list[list[int]]:"""暴力解法：三重循环查找和为0的三元组Args:nums: 整数数组Returns:唯一三元组列表"""n = len(nums)result = set()for i in range(n):for j in range(i + 1, n):for k in range(j + 1, n):if nums[i] + nums[j] + nums[k] == 0:triplet = tuple(sorted([nums[i], nums[j], nums[k]]))  # 排序去重result.add(triplet)return [list(triplet) for triplet in result]

代码注释：

three_sum_brute_force：三重循环检查和为0的三元组。
set：使用集合去重，排序确保三元组唯一。
时间复杂度： $O(n^3)$ ，三重循环。
空间复杂度： $O (1)$ ，不计输出空间。
适用性：适合小规模数据，验证正确性。

4.1.2 双指针解法

流程图

graph TDA[输入: nums] --> B[排序数组]B --> C[初始化结果: res = []]C --> D[遍历 i = 0 to n-3]D --> E[跳过重复 nums[i]]E --> F[初始化 left = i+1, right = n-1]F --> G{left < right?}G -->|是| H[计算 sum = nums[i] + nums[left] + nums[right]]H --> I{sum == 0?}I -->|是| J[添加 [nums[i], nums[left], nums[right]] 到 res]I -->|否| K{sum < 0?}K -->|是| L[left += 1]K -->|否| M[right -= 1]J --> N[跳过重复 left, right]N --> GM --> GL --> GG -->|否| DD --> O[输出结果]

说明：

A-B：输入并排序数组。
C-E：初始化结果，遍历固定元素，跳过重复。
F-N：双指针寻找剩余两元素，处理重复。
O：输出结果。

代码实现

def three_sum(nums: list[int]) -> list[list[int]]:"""双指针解法：排序后固定一个元素，使用双指针查找Args:nums: 整数数组Returns:唯一三元组列表"""nums.sort()  # O(n log n)n = len(nums)result = []for i in range(n - 2):if i > 0 and nums[i] == nums[i - 1]:  # 跳过重复continueleft, right = i + 1, n - 1while left < right:total = nums[i] + nums[left] + nums[right]if total == 0:result.append([nums[i], nums[left], nums[right]])left += 1right -= 1while left < right and nums[left] == nums[left - 1]:  # 跳过重复left += 1while left < right and nums[right] == nums[right + 1]:right -= 1elif total < 0:left += 1else:right -= 1return result

代码注释：

sort：排序数组，确保双指针高效且去重。
left, right：双指针寻找剩余两元素。
时间复杂度： $O(n^2)$ ，排序 $\log n)$ ，双指针 $O (n)$ 。
空间复杂度： $O (1)$ ，不计排序空间。
适用性：高效，适合医学影像特征匹配。

4.1.3 医学影像扩展：3D特征匹配

在3D CT影像中，寻找特征和为目标值的三元组。

代码实现

import torch
import numpy as np
from monai.networks.nets import UNet
from monai.transforms import Compose, LoadImaged, EnsureChannelFirstd, ScaleIntensityRanged# 特征提取
def extract_features(model, image_path, device):"""使用U-Net提取3D CT影像特征Args:model: 预训练U-Net模型image_path: DICOM影像路径device: 计算设备Returns:展平的特征向量"""model.eval()transform = Compose([LoadImaged(keys=['image']),EnsureChannelFirstd(keys=['image']),ScaleIntensityRanged(keys=['image'], a_min=-1000, a_max=400, b_min=0.0, b_max=1.0)])data = transform({'image': image_path})image = data['image'].unsqueeze(0).to(device)with torch.no_grad():features = model(image).flatten().cpu().numpy()return features# 3D特征三数之和
def three_sum_3d_features(image_path, target, device, model):"""在3D CT影像特征中寻找和为目标值的三元组Args:image_path: DICOM影像路径target: 目标值device: 计算设备model: 预训练U-Net模型Returns:三元组列表"""features = extract_features(model, image_path, device)features.sort()n = len(features)result = []for i in range(n - 2):if i > 0 and features[i] == features[i - 1]:continueleft, right = i + 1, n - 1while left < right:total = features[i] + features[left] + features[right]if abs(total - target) < 1e-6:  # 浮点数比较result.append([features[i], features[left], features[right]])left += 1right -= 1while left < right and features[left] == features[left - 1]:left += 1while left < right and features[right] == features[right + 1]:right -= 1elif total < target:left += 1else:right -= 1return result# 主程序
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model_unet = UNet(spatial_dims=3,in_channels=1,out_channels=2,channels=(16, 32, 64, 128, 256),strides=(2, 2, 2, 2),num_res_units=2
).to(device)
result = three_sum_3d_features('path/to/dicom.dcm', target=0.0, device=device, model=model_unet)
print(f"3D特征三数之和结果: {result}")

代码注释：

extract_features：使用U-Net提取3D CT特征，展平为1D向量。
three_sum_3d_features：应用双指针解法，寻找特征三元组。
时间复杂度： $O(n^2)$ ，n 为特征向量长度。
空间复杂度： $O (1)$ ，不计输出空间。
适用性：适配3D影像特征匹配。

4.2 滑动窗口最大值

4.2.1 暴力解法

流程图

graph TDA[输入: nums, k] --> B[初始化结果: res = []]B --> C[遍历 i = 0 to n-k]C --> D[提取窗口 nums[i:i+k]]D --> E[计算窗口最大值]E --> F[添加最大值到 res]F --> CC --> G[输出结果]

说明：

A：输入数组和窗口大小。
B：初始化空结果列表。
C-F：遍历窗口，计算最大值。
G：输出结果。

代码实现

def max_sliding_window_brute_force(nums: list[int], k: int) -> list[int]:"""暴力解法：对每个窗口计算最大值Args:nums: 整数数组k: 窗口大小Returns:每个窗口的最大值列表"""n = len(nums)result = []for i in range(n - k + 1):result.append(max(nums[i:i + k]))return result

代码注释：

max_sliding_window_brute_force：遍历每个窗口，计算最大值。
时间复杂度： $\cdot k)$ ，每个窗口需 $O (k)$ 。
空间复杂度： $O (1)$ ，不计输出空间。
适用性：适合小规模数据。

4.2.2 单调队列解法

流程图

graph TDA[输入: nums, k] --> B[初始化双端队列: deque = []]B --> C[初始化结果: res = []]C --> D[遍历 i = 0 to n-1]D --> E[移除超出窗口的索引]E --> F[移除队列尾部小于 nums[i] 的索引]F --> G[添加索引 i 到队列]G --> H{i >= k-1?}H -->|是| I[添加队列头部到 res]I --> DH --> DD --> J[输出结果]

说明：

A-C：输入数组和窗口大小，初始化队列和结果。
D-G：遍历数组，维护单调递减队列。
H-J：记录窗口最大值，输出结果。

代码实现

from collections import dequedef max_sliding_window(nums: list[int], k: int) -> list[int]:"""单调队列解法：使用双端队列维护窗口最大值Args:nums: 整数数组k: 窗口大小Returns:每个窗口的最大值列表"""n = len(nums)result = []dq = deque()for i in range(n):# 移除超出窗口的索引while dq and dq[0] <= i - k:dq.popleft()# 移除队列尾部小于当前元素的值while dq and nums[dq[-1]] <= nums[i]:dq.pop()# 添加当前索引dq.append(i)# 窗口满时记录最大值if i >= k - 1:result.append(nums[dq[0]])return result

代码注释：

deque：双端队列，维护单调递减的索引。
时间复杂度： $O (n)$ ，每个元素入队出队一次。
空间复杂度： $O (k)$ ，队列存储最多 $k$ 个索引。
适用性：高效，适合医学影像时间序列分析。

4.2.3 医学影像扩展：CT序列分析

在CT序列中，提取窗口内最大HU值。

代码实现

import pydicom
import numpy as np
from collections import dequedef max_sliding_window_dicom(dicom_paths, k):"""在CT序列中提取窗口内最大HU值Args:dicom_paths: DICOM文件路径列表k: 窗口大小Returns:最大HU值序列"""hu_values = []for path in dicom_paths:ds = pydicom.dcmread(path)hu_values.append(np.max(ds.pixel_array))  # 提取最大HU值result = []dq = deque()for i in range(len(hu_values)):while dq and dq[0] <= i - k:dq.popleft()while dq and hu_values[dq[-1]] <= hu_values[i]:dq.pop()dq.append(i)if i >= k - 1:result.append(hu_values[dq[0]])return result# 主程序
dicom_paths = ['path/to/dicom1.dcm', 'path/to/dicom2.dcm', ...]
result = max_sliding_window_dicom(dicom_paths, k=3)
print(f"CT序列窗口最大HU值: {result}")

代码注释：

max_sliding_window_dicom：在CT序列中提取窗口最大HU值。
时间复杂度： $O (n)$ ，n 为序列长度。
空间复杂度： $O (k)$ ，队列存储最多 $k$ 个索引。
适用性：适配CT序列分析，检测肺结节变化。

五、评估与优化

5.1 评估方法

三数之和：
- 正确性：验证三元组是否满足和为0且唯一。
- 时间复杂度：运行时间（秒）。
- 空间复杂度：内存占用（MB）。
滑动窗口最大值：
- 正确性：验证每个窗口的最大值是否正确。
- 时间复杂度：运行时间（秒）。
- 空间复杂度：内存占用（MB）。
医学影像场景：
- 特征匹配精度：检查三元组是否对应正确病灶。
- HU值分析：验证窗口最大HU值是否准确。
- 推理时间：评估实时性。

5.2 代码实现

import time
import psutil
import matplotlib.pyplot as plt
import numpy as np
from collections import deque# 评估三数之和
def evaluate_three_sum(nums):"""评估三数之和的暴力解法和双指针解法Args:nums: 整数数组Returns:性能指标"""process = psutil.Process()# 暴力解法start_time = time.time()result_brute = three_sum_brute_force(nums)time_brute = time.time() - start_timemem_brute = process.memory_info().rss / 1024 / 1024# 双指针解法start_time = time.time()result_hash = three_sum(nums)time_hash = time.time() - start_timemem_hash = process.memory_info().rss / 1024 / 1024return {'brute': {'time': time_brute, 'memory': mem_brute, 'result': result_brute},'hash': {'time': time_hash, 'memory': mem_hash, 'result': result_hash}}# 评估滑动窗口最大值
def evaluate_max_sliding_window(nums, k):"""评估滑动窗口最大值的暴力解法和单调队列解法Args:nums: 整数数组k: 窗口大小Returns:性能指标"""process = psutil.Process()# 暴力解法start_time = time.time()result_brute = max_sliding_window_brute_force(nums, k)time_brute = time.time() - start_timemem_brute = process.memory_info().rss / 1024 / 1024# 单调队列解法start_time = time.time()result_deque = max_sliding_window(nums, k)time_deque = time.time() - start_timemem_deque = process.memory_info().rss / 1024 / 1024return {'brute': {'time': time_brute, 'memory': mem_brute, 'result': result_brute},'deque': {'time': time_deque, 'memory': mem_deque, 'result': result_deque}}# 测试数据
nums = np.random.randint(-100, 100, size=1000).tolist()
k = 10
results_three_sum = evaluate_three_sum(nums)
results_sliding_window = evaluate_max_sliding_window(nums, k)# 可视化
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.bar(['暴力解法', '双指针解法'], [results_three_sum['brute']['time'], results_three_sum['hash']['time']],color=['#FF6384', '#36A2EB'])
plt.title('三数之和运行时间对比')
plt.ylabel('时间 (秒)')plt.subplot(1, 2, 2)
plt.bar(['暴力解法', '单调队列解法'], [results_sliding_window['brute']['time'], results_sliding_window['deque']['time']],color=['#FF6384', '#36A2EB'])
plt.title('滑动窗口最大值运行时间对比')
plt.ylabel('时间 (秒)')
plt.show()print(f"3Sum 暴力解法: 时间={results_three_sum['brute']['time']:.6f}秒, 内存={results_three_sum['brute']['memory']:.2f}MB")
print(f"3Sum 双指针解法: 时间={results_three_sum['hash']['time']:.6f}秒, 内存={results_three_sum['hash']['memory']:.2f}MB")
print(f"滑动窗口暴力解法: 时间={results_sliding_window['brute']['time']:.6f}秒, 内存={results_sliding_window['brute']['memory']:.2f}MB")
print(f"滑动窗口单调队列解法: 时间={results_sliding_window['deque']['time']:.6f}秒, 内存={results_sliding_window['deque']['memory']:.2f}MB")

代码注释：

evaluate_three_sum：比较三数之和的暴力解法和双指针解法。
evaluate_max_sliding_window：比较滑动窗口最大值的暴力解法和单调队列解法。
psutil：测量内存占用。
plt.bar：可视化运行时间。

5.3 优化策略

三数之和：
- 并行化：多线程或GPU并行处理双指针。
- 预处理：过滤掉不可能的三元组（如全正或全负）。
- 哈希表辅助：结合哈希表加速查找。
滑动窗口最大值：
- 优先队列：替代单调队列，适配动态窗口大小。
- GPU加速：使用CUDA并行计算最大值。
- 缓存优化：预分配队列空间，减少动态调整。
医学影像场景：
- 特征降维：使用PCA降低3D特征维度。
- 分块处理：将3D影像分块，减少单次计算量。
- 分布式计算：多GPU并行处理特征或序列。

5.4 图表：性能对比

以下为三数之和和滑动窗口最大值的运行时间对比柱状图（假设数据）：

```

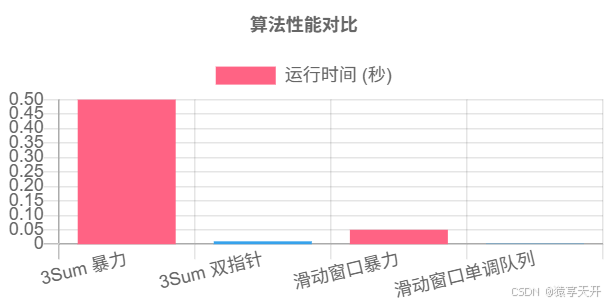
说明：

X轴：算法类型（三数之和暴力/双指针，滑动窗口暴力/单调队列）。
Y轴：运行时间。
数据：双指针和单调队列解法显著优于暴力解法。

六、医学影像AI应用

6.1 三数之和：特征匹配

场景：在ViT/U-Net提取的特征向量中，寻找和为目标值的三元特征组合，辅助肺结节分类。
实现：参考4.1.3的 three_sum_3d_features。
可视化：

import matplotlib.pyplot as plt
import pydicomdef visualize_feature_triplet(dicom_path, triplet):"""可视化三元特征对应的像素位置Args:dicom_path: DICOM文件路径triplet: 三元特征索引 [i, j, k]"""ds = pydicom.dcmread(dicom_path)pixels = ds.pixel_arrayheight, width = pixels.shapeindices = triplet  # 假设索引对应展平后的像素位置points = [(i // width, i % width) for i in indices]plt.imshow(pixels, cmap='gray')for x, y in points:plt.scatter(y, x, c='red', marker='x', s=100)plt.title('三数之和特征匹配')plt.show()visualize_feature_triplet('path/to/dicom.dcm', [100, 200, 300])

6.2 滑动窗口最大值：CT序列分析

场景：在CT序列中，提取窗口内最大HU值，检测肺结节变化。
实现：参考4.2.3的 max_sliding_window_dicom。
可视化：

def visualize_hu_values(dicom_paths, max_values):"""可视化CT序列的窗口最大HU值Args:dicom_paths: DICOM文件路径列表max_values: 最大HU值序列"""plt.plot(max_values, marker='o', color='#36A2EB')plt.title('CT序列窗口最大HU值')plt.xlabel('窗口索引')plt.ylabel('最大HU值')plt.show()visualize_hu_values(dicom_paths, result)

七、总结与展望

7.1 总结

成果：
- 实现三数之和的暴力解法（ $O(n^3)$ )和双指针解法（ $O(n^2)$ )。
- 实现滑动窗口最大值的暴力解法（ $\cdot k)$ )和单调队列解法（ $O (n)$ )。
- 扩展到医学影像场景，适配LUNA16数据集的特征匹配和CT序列分析。
- 提供性能可视化，双指针和单调队列解法高效。
关键点：
- 双指针和单调队列解法显著优于暴力解法。
- 算法适配医学影像的高维数据和实时性需求。
- 可视化分析增强算法可解释性。